SỞ GIÁO DỤC VÀ ĐÀO TẠO
MA TRẬN KIỂM TRA CUỐI HỌC KỲ I TỈNH ….
MÔN: Toán 11 (Bộ sách Cánh Diều)
Thời gian: 90 phút, không kể thời gian phát đề
Áp dụng từ năm học 2023 – 2024 (Tham khảo) I. CHỦ ĐỀ CHÍNH A. Đại số
Chương I: Hàm số lượng giác, phương trình lượng giác
1. Góc lượng giác. Giá trị lượng giác của góc lượng giác.
2. Các phép biến đổi lượng giác
3. Hàm số lượng giác và đồ thị.
4. Phương trình lượng giác cơ bản.
Chương II: Dãy số- cấp số cộng, cấp số nhân 1. Dãy số. 2. Cấp số cộng. 3. Cấp số nhân.
Chương III: Giới hạn. Hàm số liên tục. . Gi i h n của dãy số. 2. Gi i h n của hàm số. 3. Hàm số liên tục. B. Hình học
Chương IV: Đường thẳng và mặt phẳng trong không gian, quan hệ song song
1. Đường thẳng và mặt phẳng trong không gian.
2. Hai đường thẳng song song trong không gian.
3. Đường thẳng và mặt phẳng song song.
4. Hai mặt phẳng song song.
5. Hình lăng trụ và hình hộp.
6. Phép chiếu song song. Hình bi u di n của một hình trong không gian.
II. MA TRẬN (Thời gian: 90 phút)
Nhận biết và thông hiểu
Nội dung kiến thức vận dụng Chủ đề Nhận biết Thông hi u Cấp độ thấp Cấp độ cao Cộng Theo chương (Cấp độ ) (Cấp độ 2) (Cấp độ 3) (Cấp độ 4)
- Góc lượng giác. Giá trị lượng - Các phép biến đổi Chủ đề 1
giác của góc lượng giác lượng giác
- Hàm số lượng giác. - Phương trình lượng giác cơ bản. Số câu TN 3 2 1 6 Số điểm 0, 6 0, 4 0, 2 1, 2 Tỉ lệ 6% 4% 2% 12% Số câu TL 1 1 2 Số điểm 0, 5 0, 5 1, 0 Tỉ lệ 5% 5% 10% 1
- Dãy số- cấp số cộng, cấp số
Cấp số cộng, cấp số Chủ đề 2 nhân nhân Số câu TN 2 1 3 Số điểm 0, 4 0, 2 0, 6 Tỉ lệ 4% 2% 6% Số câu TL 1 1 2 Số điểm 0, 5 0, 5 1, 0 Tỉ lệ 5% 5% 10% - Gi i h n của dãy số. Chủ đề 3 - Gi i h n của hàm số - Hàm số liên tục. Số câu TN 3 1 1 5 Số điểm 0, 6 0, 2 0, 2 1, 0 Tỉ lệ 6% 2% 2% 10% Số câu TL 1 1 3 Số điểm 1, 0 0, 5 1, 5 Tỉ lệ 10% 5% 15%
- Đường thẳng và mặt phẳng
- Chứng minh ba đi m Chủ đề 4 trong không gian. thẳng hàng, ba đường
- Quan hệ song song trong không thẳng đồng quy, quan gian. hệ song song
- Hình lăng trụ và hình hộp. - Tìm giao đi m của
- Tìm giao đi m của đường thẳng đường thẳng và mặt
và mặt phẳng. Giao tuyến của hai phẳng. Giao tuyến của mặt phẳng. hai mặt phẳng. Số câu TN 5 1 6 Số điểm 1, 0 0, 2 1, 2 Tỉ lệ 10% 2% 12% Số câu TL 1 1 2 Số điểm 1, 5 0, 5 2, 0 Tỉ lệ 15% 5% 20% Bài toán tổng Sử dụng kiến hợp thức tổng hợp trong chương trình Số câu TN Số điểm Tỉ lệ Số câu TL 1 1 Số điểm 0, 5 0, 5 Tỉ lệ 5% 5% Tổng số câu 4TL + 13TN 4TL+ 5TN 1TL + 2TN 9TL+20TN 2 Số điểm 6, 1 3, 0 0, 9 10, 0 Tỉ lệ 61% 30% 9% 100% III. CẤU TRÚC ĐỀ Trắc nghiệm: 20 câu Tự luận:
Bài 1. (1, 0 điểm): Chủ đề . Bài 2. (1, 0 điểm): Chủ đề 2. Bài 3. (1, 5 điểm): Chủ đề 3.
Bài 4. (2, 0 điểm): Chủ đề 4. Bài 5. (0, 5 điểm): Tổng hợp
IV. HÌNH THỨC KIỂM TRA VÀ THỜI GIAN
- Hình thức tự luận và trắc nghiệm. - Thời gian làm bài: 90 phút Lưu ý:
+ Các trường tự soạn đề ôn tập theo ma trận đề trên.
+ Trong mỗi câu tự luận có thể gồm nhiều ý.
+ Học sinh làm phần trắc nghiệm lên phiếu trả lời trắc nghiệm, phần tự luận làm trên tờ giấy thi. 3
SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ MINH HỌA KIỂM TRA CUỐI HỌC KỲ I TỈNH …………
MÔN: Toán 11 (Bộ sách Cánh Diều)
Thời gian: 90 phút, không kể thời gian phát đề
Áp dụng từ năm học 2023 – 2024 (Tham khảo)
I. Phần trắc nghiệm (4 điểm).
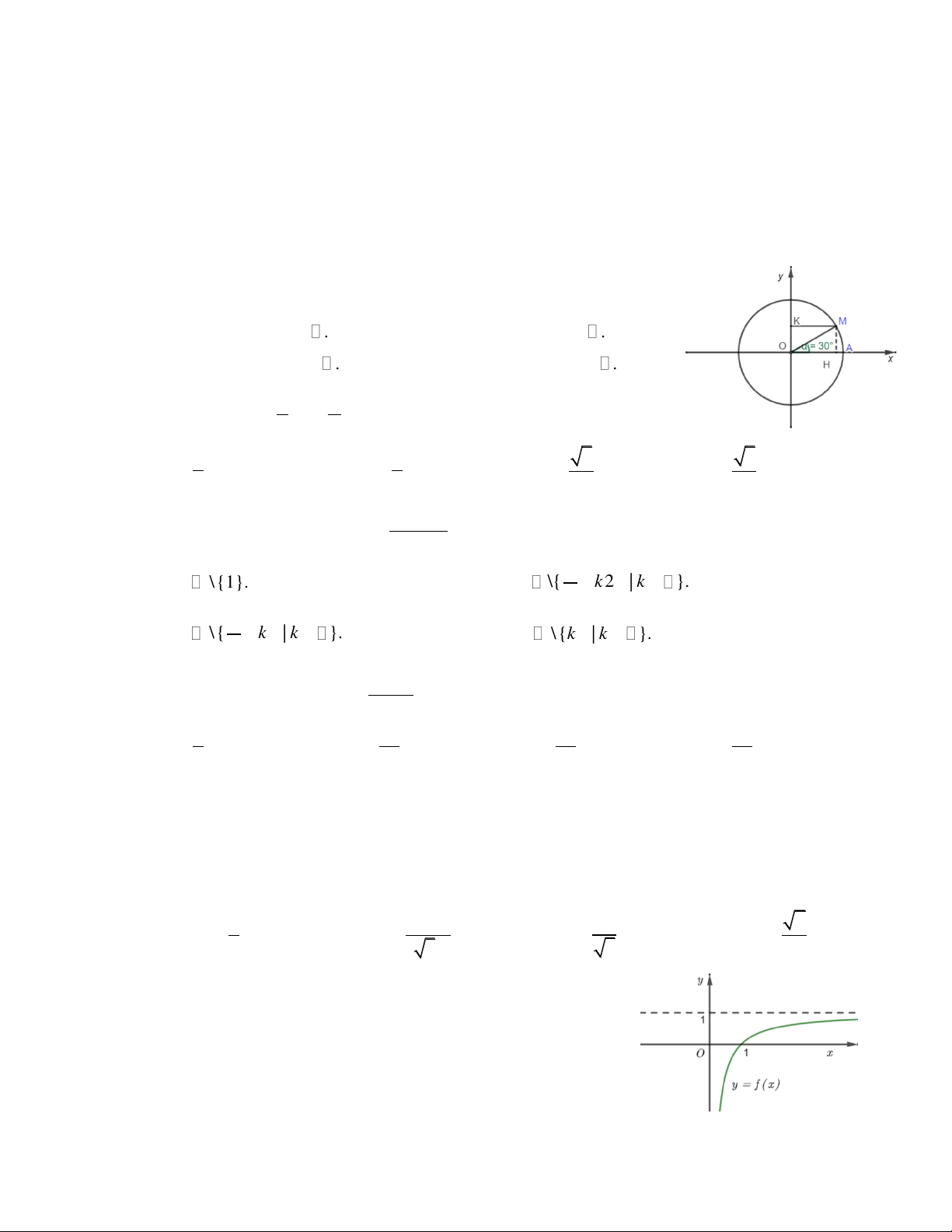
Câu 1. Cho đi m M trên đường tròn lượng giác như hình vẽ bên. Khi
đó số đo của góc lượng giác O , A OM  là A. 0 0 30  1
k 80 , k  . B. 0 0
30  k360 , k  . C. 0 0 3  0  1
k 80 , k  . D. 0 0 3
 0  k360 , k  . 2 
Câu 2. Cho cos   v i
   . Khi đó tan bằng 3 2 5 5 5 5 A. . B.  . C.  . D. . 4 4 2 2 x 
Câu 3. Tập xác định của hàm số sin 1
y  sin x  là 1  A. \ {1}. B. \{
 k2 | k  }. 2  C. \ {
 k | k  }. D.
\ {k | k  }. 2 n 
Câu 4. Cho dãy số u biết 3 2 u  .
u của dãy số u là n  n  n n  Số h ng 1 8 8 24 22 22 A. . B. . C. . D. . 9 9 9 8
Câu 5. Cho u là cấp số cộng có số h ng đầu u  2, công sai d  3.
 Số h ng thứ 11 của cấp số n  1 cộng đó là A. 32. B. 30. C. 31.  D. 28. 
Câu 6. Phát bi u nào sau đây sai? n n  n 2  4  2   2  A. lim  0.   B. lim  0. C. lim  0. D. lim     0.      3  ( 3)n  3  2  
Câu 7. Cho đồ thị hàm số y  f  x trong hình bên. Khi đó
lim f  x bằng x A. 0. B. 1. C. .  D. .  4
Câu 8. Trong các hàm số bên dư i, hàm số nào liên tục trên ? 1 A. y  . B. y  sin . x C. y  tan . x D. y  cot . x x
Câu 9. Cho hình chóp tứ giác S.ABC .
D Gọi O là giao đi m của AC và .
BD Trong các mặt phẳng
sau, đi m O nằm trên mặt phẳng nào?
A. SAB.
B. SAD.
C. SAC . D. SBC .
Câu 10. Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình bình hành. Gọi I , J lần lượt là trung
đi m của SB, SD. Trong các đường thẳng sau, đường thẳng nào song song v i IJ ? A. . AC B. . BD C. . AB D. . CD
Câu 11. Cho hai đường thẳng a, b cắt nhau và cùng song song v i mặt phẳng  P. Có bao nhiêu mặt
phẳng chứa a,b và song song v i mặt phẳng P? A. 0. B. 1. C. 2. D. Vô số.
Câu 12. Số c nh của hình lăng trụ ngũ giác là A. 5. B. 10. C. 15. D. 20.
Câu 13. Cho hình chóp tứ giác S.ABC .
D Gọi O là giao đi m của AC và .
BD Trong các đường thẳng
sau, đường thẳng nào là giao tuyến của hai mặt phẳng SAC và SBD? A. . SA B. . AD C. . SO D. . SC 1     Câu 14. Cho cos  v i 0    . Khi đó sin     bằng 3 2  6  1 2 6 2 2 3  4 2 2 6 1 A. . B. . C. . D. . 6 3 6 6
Câu 15. Số nghiệm của phương trình tan x  3 trên khoảng 0;3  là A. 0. B. 1. C. 2. D. 3.
Câu 16. Tổng 312 102 1002 10002 ...100...02 (10 số h ng) bằng 9 10 179 10 10 179 9 10 19 10 10 19 A. . B. . C. . D. . 9 9 9 9 2
x  x khi x 1
Câu 17. Giá trị của a đ hàm số f  x   liên tục trên là
x  a khi x 1 A. 1. B. 1.  C. 0. D. 2.
Câu 18. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Mặt phẳng   qua BD và song
song v i SA, mặt phẳng   cắt SC t i K. Khẳng định nào sau đây là khẳng định đúng? 1 A. SK  KC.
B. SK  2K . C
C. SK  3K . C
D. SK  K . C 2 5
Câu 19. Hằng ngày mực nư c của con kênh lên xuống theo thủy triều. Độ sâu h (mét) của mực nư c
trong kênh được tính t i thời đi m t (giờ) trong một ngày bởi công thức  t   h  3cos  12.  
Mực nư c của kênh cao nhất khi:  8 4 
A. t 15 (giờ).
B. t 16 (giờ).
C. t 13 (giờ).
D. t 14 (giờ). f  x 16 f  x 16
Câu 20. Cho f  x là một đa thức th a mãn lim
 24 . Tính I  lim . x 1  x 1 x 1  x  
1  2 f x  4  6 A. 2. B. 0. C. 24. D. . 
II. Phần tự luận (6 điểm). Bài 1 (1,0 điểm). 1. Cho biết 3 cos x 
. Tính giá trị của bi u thức 2 P  sin 2 . x 4   
2. Giải phương trình cos 2x  sin x   0.    3  Bài 2 (1,0 điểm).
. Cho cấp số cộng u có u  3,u 1.Tính u . n  1 2 11
2. Khi nghiên cứu về một lo i virus, người ta nhận thấy cứ sau mỗi phút, số lượng virus tăng lên gấp
ba lần trư c đó. Giả sử ban đầu từ 5 con virus, hãy tính số lượng virus có sau phút.
Bài 3 (1,5 điểm). Tính các gi i h n sau : 2 3n  2n  5
4x  5  2x  3 1. lim . lim . 2 4n  2. 7 x x  2 1 1
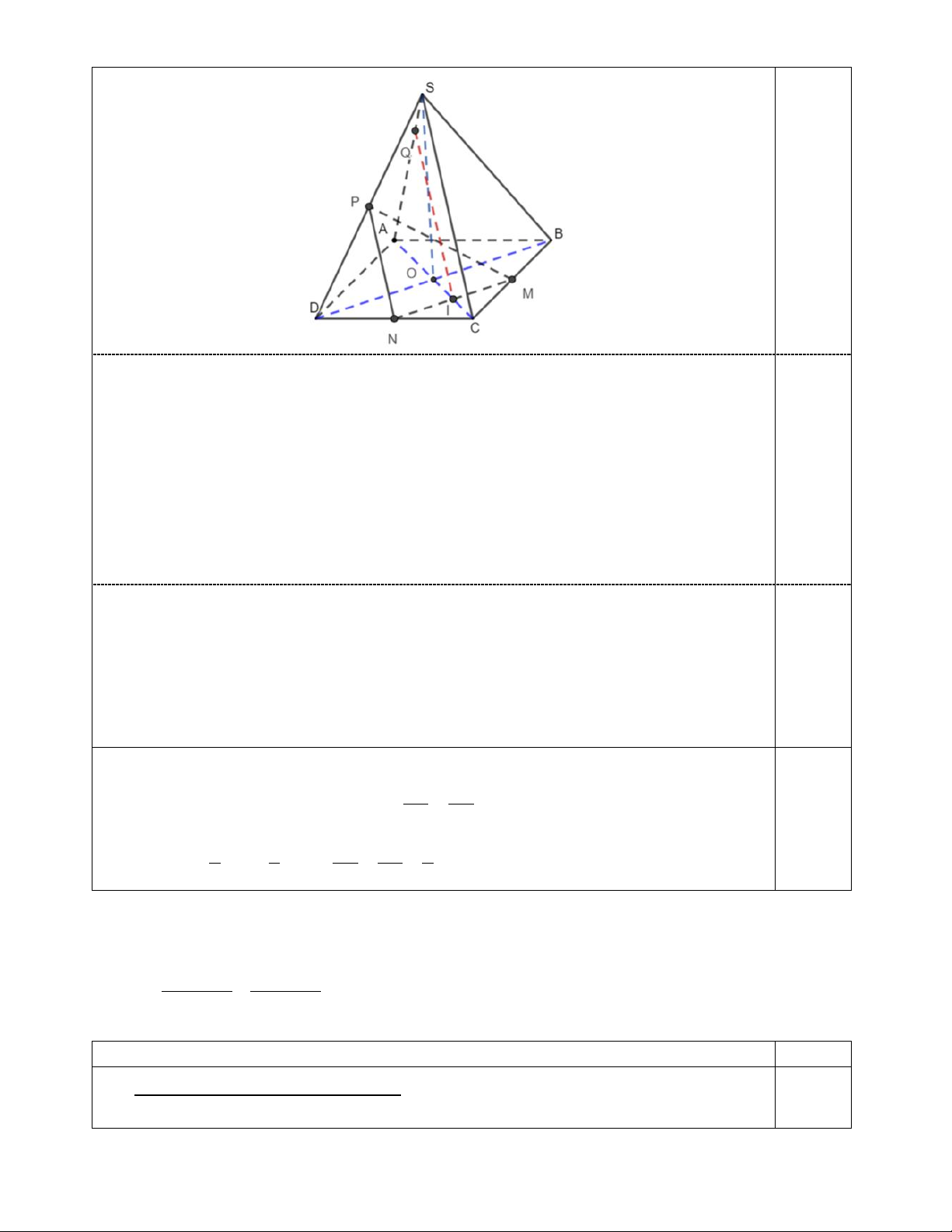
Bài 4 (2,0 điểm). Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi M , N, P lần lượt là trung đi m
của các c nh BC, CD, . SD
. Xác định giao tuyến của SAC ; SBD và chứng minh NP song song v i SBC. SQ
2. Gọi là Q giao đi m của SA v i MNP. Tính tỉ số . SA
Bài 5 (0,5 điểm). Cho hai số thực a,b th a mãn điều kiện sin a  b  2cosa b. Tính giá trị của bi u thức 1 1 P   . 2  sin 2a 2  sin 2b ---- HẾT ---- 6
SỞ GIÁO DỤC VÀ ĐÀO TẠO
HƯỚNG DẪN CHẤM KIỂM TRA CUỐI HỌC KỲ I TỈNH ………… MÔN: Toán 11
Thời gian: 90 phút, không kể thời gian phát đề
BẢNG ĐÁP ÁN TRẮC NGHIỆM 1.B 2.C 3.B 4.C 5.D 6.C 7.B 8.B 9.C 10.B 11.B 12.C 13.C 14.A 15.D 16.B 17.B 18.D 19.D 20.A
I. Phần trắc nghiệm (4 điểm). Câu 1:
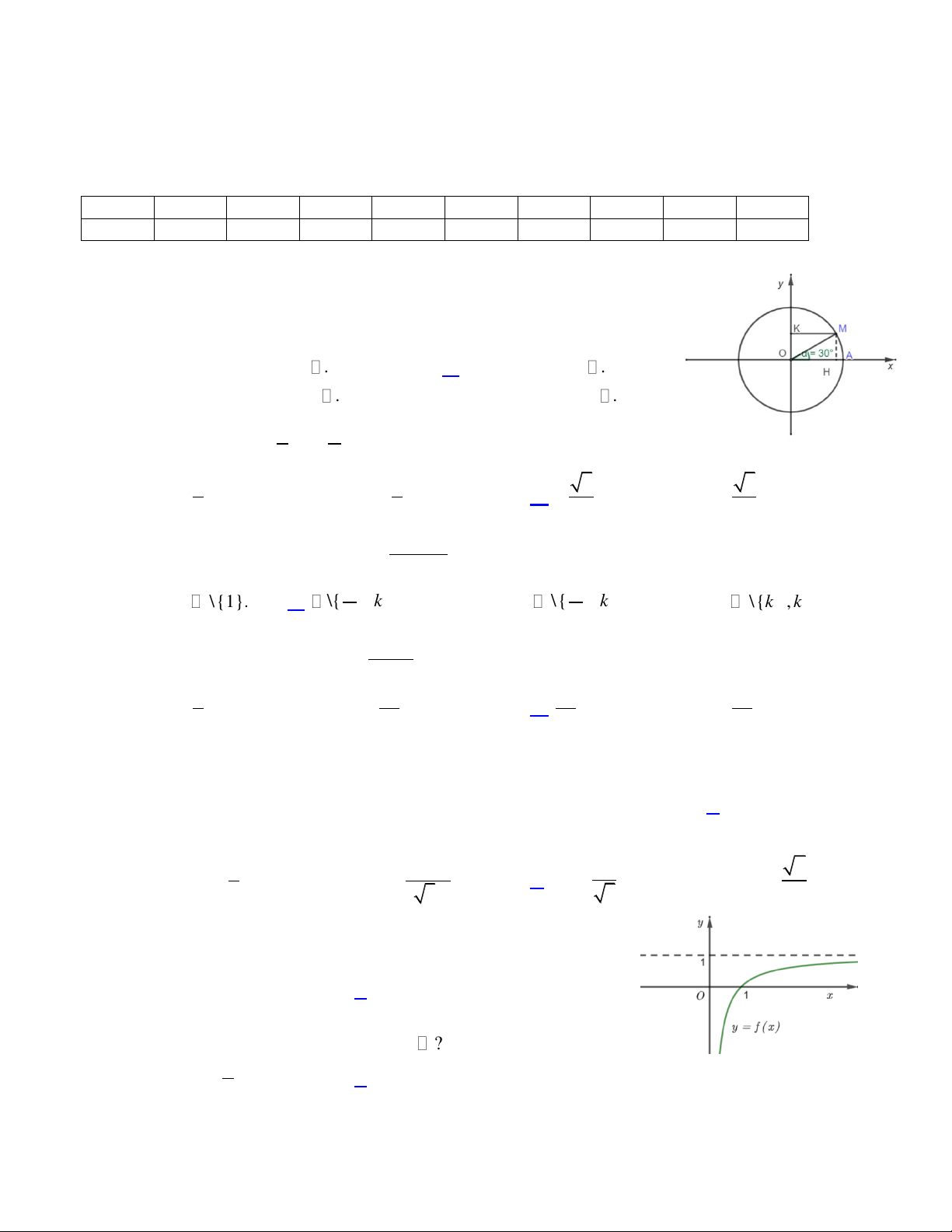
Cho đi m M trên đường tròn lượng giác (hình vẽ bên). Khi đó
số đo của góc lượng giác O , A OM  là A. 0 0 30  1
k 80 , k  . B. 0 0
30  k360 , k  . C. 0 0 3  0  1
k 80 , k  . D. 0 0 3
 0  k360 , k  . 2  Câu 2: Cho cos   v i
    Khi đó tan bằng 3 2 5 5 5 5 A. . B.  . C.  . D. . 4 4 2 2 x  Câu 3:
Tập xác định của hàm số sin 1
y  sin x  là 1   A. \ {1}. B. \{
 k2 , k  Z}. C. \ {
 k , k  Z}. D. \{k , k  Z}. 2 2 n  Câu 4:
Cho dãy số u biết 3 2 u  .
u của dãy số u là n  n  n n  Số h ng 1 8 8 24 22 22 A. . B. . C. . D. . 9 9 9 8 Câu 5:
Cho u là cấp số cộng có số h ng đầu u  2, công sai d  3.
 Số h ng thứ 11 của cấp số n  1 cộng đó là A. 32. B. 30. C. 31.  D. 28.  Câu 6:
Phát bi u nào sau đây sai? n n  n 2  4  2   2  A. lim  0.   B. lim  0. C. lim  0. D. lim     0.      3  ( 3)n  3  2   Câu 7:
Quan sát đồ thị hàm số trong hình bên và cho biết lim f  x x bằng A. 2. B. 1. C. .  D. .  Câu 8:
Hàm số nào sau đây liên tục trên ? 1 A. y  . B. y  sin . x C. y  tan . x D. y  cot . x x 7 Câu 9:
Cho hình chóp tứ giác S.ABC .
D Gọi O là giao đi m của AC và .
BD Trong các mặt phẳng
sau, đi m O nằm trên mặt phẳng nào?
A. SAB.
B. SAD.
C. SAC . D. SBC .
Câu 10: Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình bình hành. Gọi I , J lần lượt là trung
đi m của SB, SD. Trong các đường thẳng sau, đường thẳng nào song song v i IJ ? A. . AC B. . BD C. . AB D. . CD
Câu 11: Cho hai đường thẳng a, b cắt nhau và cùng song song v i mặt phẳng  P. Có bao nhiêu mặt
phẳng chứa a,b và song song v i mặt phẳng P? A. 0. B. 1. C. 2. D. Vô số.
Câu 12: Số c nh của hình lăng trụ ngũ giác là A. 5. B. 10. C. 15. D. 20.
Câu 13: Cho hình chóp tứ giác S.ABC .
D Gọi O là giao đi m của AC và .
BD Trong các đường thẳng
sau, đường thẳng nào là giao tuyến của hai mặt phẳng SAC và SBD? ? A. . SA B. . AD C. . SO D. . SC 1     Câu 14: Cho cos  v i 0    . Khi đó sin     bằng 3 2  6  1 2 6 2 2 3  4 2 2 6 1 A. . B. . C. . D. . 6 3 6 6
Câu 15: Số nghiệm của phương trình tan x  3 trên khoảng 0;3  là A. 0. B. 1. C. 2. D. 3.
Câu 16: Tổng 312 102 1002 10002 ...100...02 (10 số h ng) bằng 9 10 179 10 10 179 9 10 19 10 10 19 A. . B. . C. . D. . 9 9 9 9 2
x  x khi x 1
Câu 17: Giá trị của a đ hàm số f  x   liên tục trên là
x  a khi x 1 A. 1. B. 1.  C. 0. D. 2.
Câu 18: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Mặt phẳng   qua BD và song
song v i SA, mặt phẳng   cắt SC t i K. Khẳng định nào sau đây là khẳng định đúng? 1 A. SK  KC.
B. SK  2K . C
C. SK  3K . C
D. SK  K . C 2
Câu 19: Hằng ngày mực nư c của con kênh lên xuống theo thủy triều. Độ sâu h (mét) của mực nư c
trong kênh được tính t i thời đi m t (giờ) trong một ngày bởi công thức  t   h  3cos  12.  
Mực nư c của kênh cao nhất khi:  8 4 
A. t 15 (giờ).
B. t 16 (giờ).
C. t 13 (giờ).
D. t 14 (giờ). Hướng dẫn
Mực nư c của kênh cao nhất khi h l n nhất … 8  t   t   cos  1    k2  
 t  2 16k do 0  t  24 và k   8 4  8 4 k 1   t  14 f  x 16 f  x 16
Câu 20: Cho f  x là một đa thức th a mãn lim
 24 . Tính I  lim . x 1  x 1 x 1  x  
1  2 f x  4  6 A. 2. B. 0. C. 24. D. .  Hướng dẫn f  x 16 Vì 1 1 lim
 24 nên lim f x 16  0  lim f x 16  lim  . x 1  x 1 x 1  x 1  x 1 
2 f  x  4  6 12 f  x 16 f  x 16 Khi đó 1 I  lim  lim .lim  2 . x 1  x  
1  2 f x  4  6 x 1  x   x 1 1 
2 f  x  4  6
II. Phần tự luận (6 điểm). Bài 1 (1,0 điểm). . Cho biết 3 cos x 
. Tính giá trị của bi u thức 2 P  sin 2 . x 4   
2. Giải phương trình cos 2x  sin x   0.    3  Nội dung Điểm 9 7 0,25 1. Ta có : 2 2
sin x  1 cos x  1  . 16 16 0,25 Do đó 7 9 63 : 2 2 2
P  sin 2x  4 sin . x cos x  4. .  . 16 16 64      
2. Phương trình  cos 2x  sin x   cos 2x  cos  x      3   6      0,25 k 2 2x   x  k2 x     6 18 3     k  .     2x  x   k2 x    k2  0,25 6  6 Bài 2 (1,0 điểm).
. Cho cấp số cộng u có u  3,u 1.Tính u . n  1 2 11
2. Khi nghiên cứu về một lo i virus, người ta nhận thấy cứ sau mỗi phút, số lượng virus tăng lên gấp
ba lần trư c đó. Giả sử ban đầu từ 5 con virus, hãy tính số lượng virus có sau phút. Nội dung Điểm 9
. Gọi d là công sai của cấp số cộng u , d  u  u  2  0,25 n  2 1
u  u 10d  3  20  1  7. 11 1 0,25
2. Gọi u , là số virus sau phút thứ n. Vì có 5 virus ban đầu nên theo giả thiết, dãy số 0,25 n  u
là một cấp số nhân có u  5 và công bội q  3. Suy ra số virus có sau phút là n  1 0,25 10 10
u  u .q  5.3  295245 (ng-êi). 11 1
Bài 3 (1,5 điểm). Tính các gi i h n sau : 2 3n  2n  5
4x  5  2x  3 1. lim . lim . 2 4n  2. 7 x x  2 1 1 Nội dung Điểm 2 5   2 3 2 3n  2n  5 3 1. lim  lim n n  2 4n  7 7 4 4  0,5+0,5 2 n
4x  5  2x  3
4x  5  2x  32 2. lim  x x   lim 2 1
x  x  2 1 1
1  4x  5  2x  3 0,25 2 4
 x 8x  4   4 lim  lim  2  .
x  x  2 1
1  4x  5  2x  3 x 1 
4x  5  2x  3 0,25
Bài 4 (2,0 điểm). Cho chóp S.ABCD có đáy là hình bình hành. Gọi M , N, P lần lượt là trung đi m của
các c nh BC, CD, . SD
. Xác định giao tuyến của hai mặt phẳng SAC và SBD; chứng minh rằng NP / / SBC. SQ
2. Gọi là Q giao đi m của SA v i MNP. Tính tỉ số . SA Nội dung Điểm
. Hình vẽ đến ý (0,5 đi m) 0,5 10
Gọi O là giao đi m của AC và BD 0,25
Xét hai mp (SAC) và (SBD) có
+ S là đi m chung của hai mặt phẳng.
O  AC  SAC  +
  O là đi m chung của hai mặt phẳng. 0,25
O  BD  SBD
Vậy giao tuyến của hai mặt phẳng (SAC) và (SBD) là SO.
Chứng minh NP / / SBC.
NP  SBC   NP / /SC
 NP / / SBC.  SC   SBC 0,5
2. Gọi I  AC  MN. NP / /SC  CI SQ +    0,25   
  IQ / /SC   IQ PMN SAC CA SA 1 1 SQ CI 1 + Ta có: CI  CO  CA    0,25 2 4 SA CA 4
Bài 5 (0,5 điểm). Cho hai số thực a,b th a mãn điều kiện sin a  b  2cosa b. Tính giá trị của bi u thức 1 1 P   . 2  sin 2a 2  sin 2b Nội dung Điểm
4  sin 2a  sin 2b P 
4  2sin 2a  sin 2b  sin 2 . a sin 2b 11 Ta có   a  b  
a b a b 2   a b 2 4 sin 2 sin 2 4 2sin cos 4 4 cos
 4sin a b 0,25
Mặt khác : 4  2sin 2a  sin 2b  sin 2 . a sin 2b  
a b a b 1 4 4 sin cos
 cos2a  2b  cos2a  2b 2 1 2 
4  8 cos a  b   2
2 cos a  b 2
11 2sin a  b 2 2   a b 2  a b 2   a b 2 3 7 cos sin 3 3cos
 3sin a b Vậy 4 P  . 0,25 3
------------ Hết ------------ 12