Preview text:
UBND QUẬN HAI BÀ TRƯNG
ĐỀ KIỂM TRA CHẤT LƯỢNG HỌC KỲ I
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO Năm học 2021 -2022 MÔN: TOÁN 9 ĐỀ CHÍNH THỨC
Thời gian làm bài: 90 phút
Bài 1: (1,5 điểm)
1) Thực hiện phép tính: 2 4 2 5 5 1 1
2) Giải phương trình: 4x
36x 9x 2 2
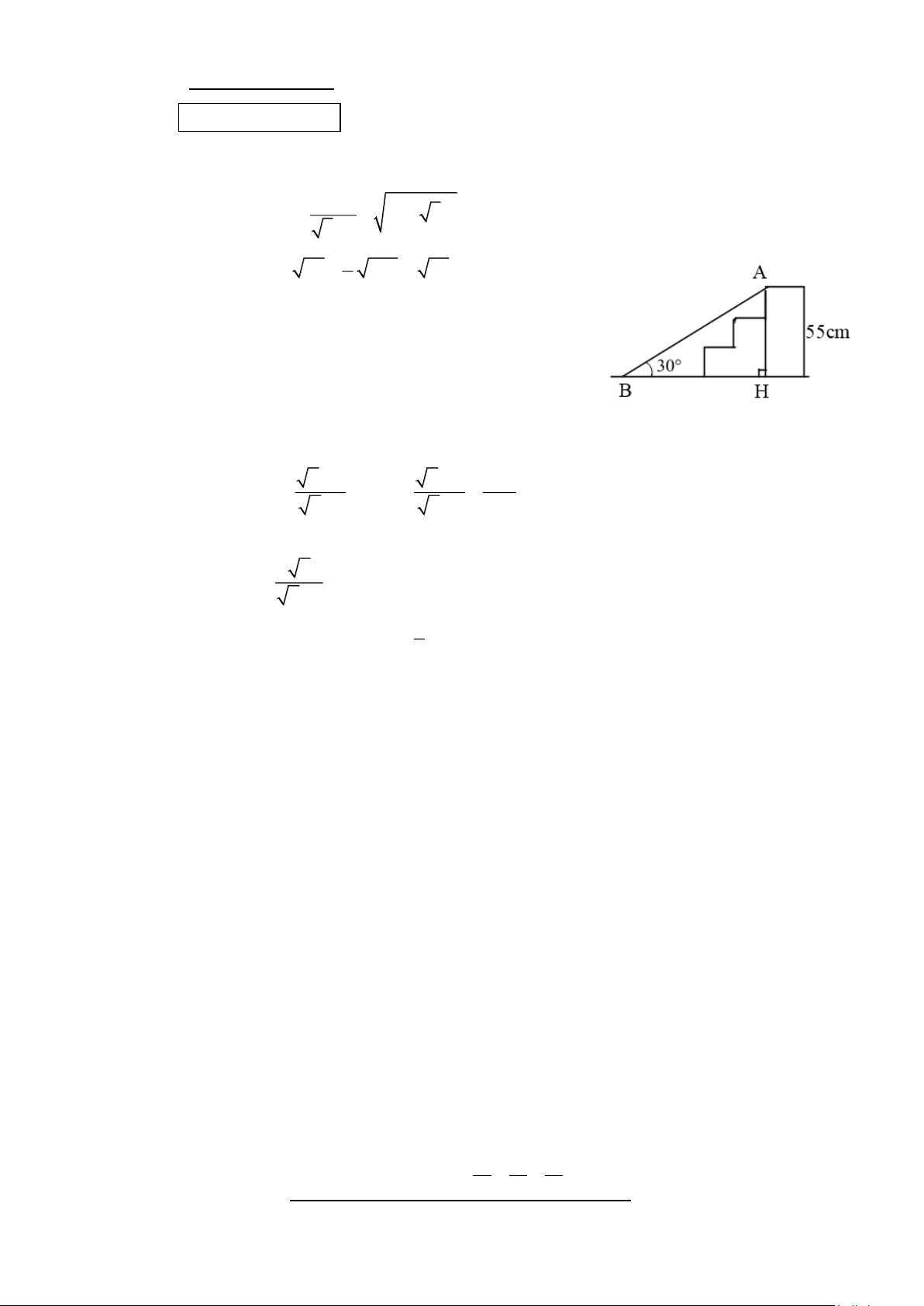
3) Bậc cửa nhà bác Nam cao 55 cm. Để đưa xe máy vào
nhà, bác cần đặt một chiếc cầu sắt để dắt xe sao cho góc giữa
mặt cầu và mặt đất khoảng 30 . Hỏi mặt cầu dài bao nhiêu
xăng-ti-mét? (Hình 1) Hình 1
Bài 2: (2,0 điểm) x 2 x 2 2
Cho hai biểu thức A và B
với x 0 và x 1. x 1 x 1 x 1
a) Tính giá trị của biểu thức A với x 4 . x b) Chứng minh B . x 1 1
c) Tìm các giá trị x nguyên để B : A . 2
Bài 3: (3,0 điểm).
2x y 5
1) Giải hệ phương trình . x y 1
2) Cho hàm số bậc nhất y m
1 x 2 ( m 1) có đồ thị là đường thẳng (d)
a) Vẽ đồ thị hàm số với m 2 .
b) Tìm m để đường thẳng (d) song song với đường thẳng y x 3.
c) Tìm m để đường thẳng (d) cắt Ox, Oy theo thứ tự tại điểm A, B sao cho OA 2OB .
Bài 4: (3,0 điểm).
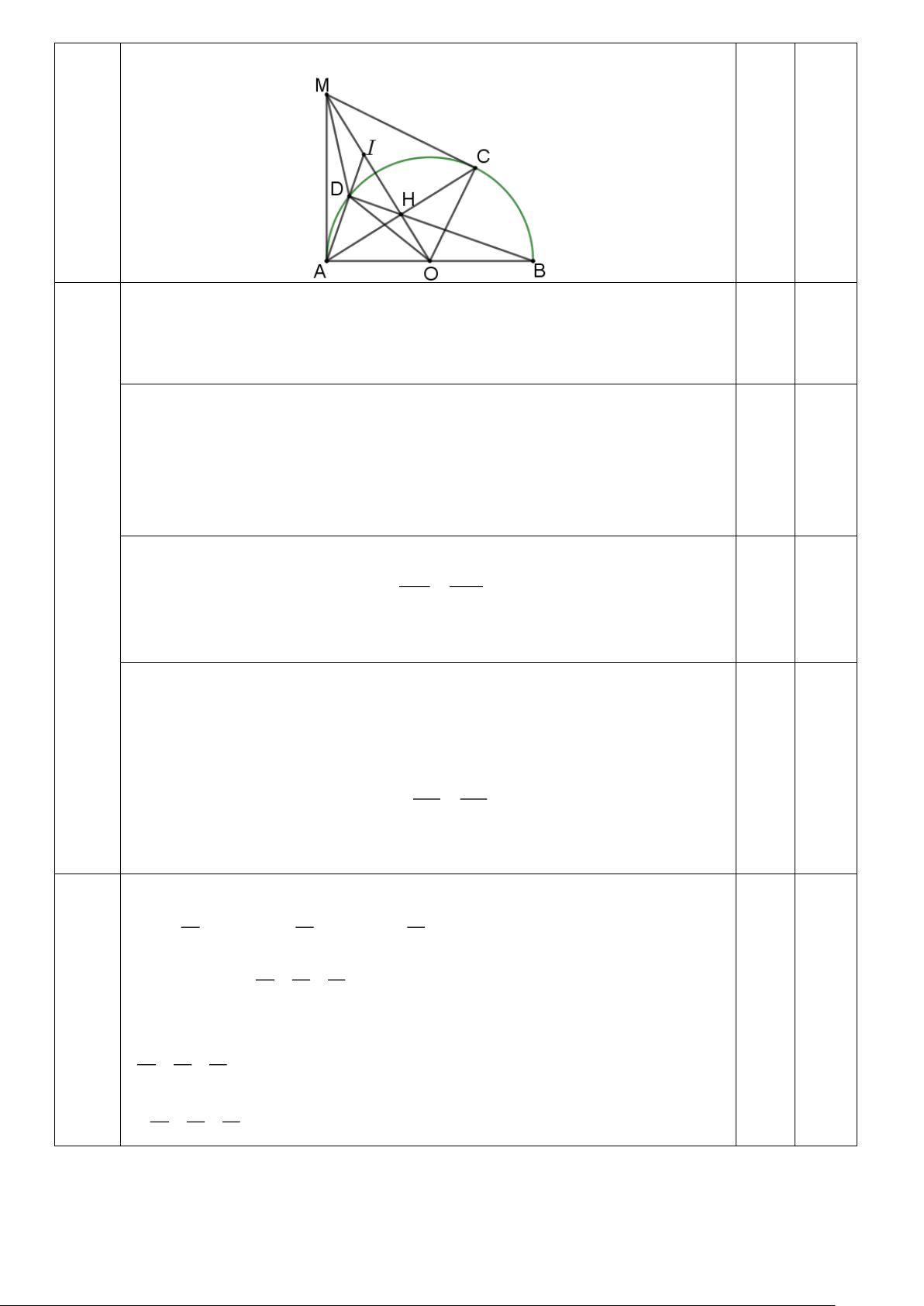
Cho nửa đường tròn tâm O, đường kính AB = 2R. Trên nửa đường tròn lấy điểm C bất kì (C
khác A và B). Tiếp tuyến tại C và tiếp tuyến tại A cắt nhau tại M.
a) Chứng minh bốn điểm, O, A, M, C cùng thuộc một đường tròn.
b) AC cắt OM tại H, chứng minh AC vuông góc với OM và 2
OH.OM R .
c) Tia BH cắt nửa đường tròn tại D.
Chứng minh tam giác ODM đồng dạng với tam giác OHD
d) Tia AD cắt MH tại I. Chứng minh I là trung điểm của MH.
Bài 5: (0,5 điểm). 3 3 3 a b c Cho các số dương , a ,
b c , chứng minh rằng:
ab bc ca b c a
Họ và tên thí sinh: ................................................................................. SBD: ............................
UBND QUẬN HAI BÀ TRƯNG
ĐỀ KIỂM TRA CHẤT LƯỢNG HỌC KỲ I
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
Năm học: 2021 - 2022
HƯỚNG DẪN CHẤM MÔN: TOÁN 9 ĐỀ CHÍNH THỨC
Thời gian làm bài: 90 phút Bài HƯỚNG DẪN CHẤM Điểm Bài 1 1,5
1) Thực hiện phép tính: 4 5 1 0,25 5 2 0,5 5 1 0,25
5 1 5 2 3
2) Giải phương trình ĐKXĐ: x 0 1 4x 36x 9x 2 2
2 x 3 x 3 x 2 0,5 0,25 x 1 x 1 (tmdk)
Vậy phương trình có nghiệm x = 1 0,25
3) Bài toán thực tế
Độ dài mặt cầu là AB. Xét tam giác ABH vuông tại H AH AH 55 sin B AB 0,25 0,5 AB sin B sin30
110 cm. Vậy mặt cầu dài 110cm 0,25 Bài 2 2,0
a) Tính giá trị biểu thức
Thay x 4 (TMĐK) vào biểu thức A 4 2 0,25 A 0,5 4 1
4 . Vậy với x 4 thì A 4 0,25 x
b) Chứng minh B x 1 x 2 2 B x 1 x 1
x 2 x 1 2 0,25 x 1 x 1
x 1 x 1 1,0
x x 2 2 x x 0,25 x 1 x 1
x 1 x 1 x x 1 0,25 x 1 x 1 x x 1 0,25
c) Tìm các giá trị x nguyên … x x 2 x B : A : x 1 x 1 x 2 0,5 1 x 1 x 2 B : A 0 2 x 2 2 0,25 2 x 2
Lập luận để: x 2 0 x 4
Kết hợp điều kiệu: x 0, x 1 và x là số nguyên: x 0;2;3 ; 0,25 Bài 3 3,0
1) Giải hệ phương trình
2x y 5 3 x 6 0,25 x y 1 x y 1 x 2 2 y 1 0,25 1,0 x 2 0,25 y 1
Vậy hệ phương trình có nghiệm ; x y 2; 1 0,25
2) Cho hàm số bậc nhất … 2,0
a) Vẽ đồ thị hàm số
Thay m 2 (TMĐK m 1), ta có hàm số: 0,25 y x 2 Lập bảng: x 0 - 2 0,25 0,75 y x 2 2 0
Đồ thị hàm số là đường thẳng đi qua hai điểm (0;2) và (-2;0).
Học sinh vẽ đúng đồ thị 0,25
(d) song song với đường thẳng y x 3 m 1 1 m 0 2 3 0,25 0,75
Đối chiếu điều kiện m 1 0,25 Kết luận 0,25 Do m 1 2 2 2
Tính được tọa độ A ;0 OA (đơn vị độ dài) m 1 m 1 m 1
tọa độ B0;2 OB 2 (đơn vị độ dài) 2 0,25 OA 2OB 4 0,5 m 1 3 m 1 2 m 1 (thỏa mãn điều kiện) 0,25 2 1 m 2
Vẽ hình đúng đến câu a được 0,25 Bài 4 3,0
a) Chứng minh bốn điểm A, O, C, M thuộc một đường tròn
Chứng minh OAM vuông tại A O, A, M thuộc đường tròn đk MO 0,25 0,75
Chứng minh OCM vuông tại C O, C, M thuộc đường tròn đk MO 0,25
4 điểm O, A, M, C cùng thuộc một đường tròn. 0,25
b) AC vuông góc với OM và OH.OM =R2
Áp dụng tính chất 2 tiếp tuyến cắt nhau: MA = MC
mà OA = OC OM là trung trực của AC OM AC 0,5 0,75
Xét tam giác OAM vuông tại A, đường cao AH, theo hệ thức lượng 2
OH.OM OA 0,25 Vì OA = R 2
OH.OM R
c) Tam giác ODM đồng dạng với tam giác OHD 2 2 OH OD
OH.OM R OH.OM OD 0,25 OD OM 0,75 Góc DOM chung 0,25 Vậy ODM
đồng dạng với OHD (c.g.c) 0,25
d) Chứng minh I là trung điểm MH * ODM
đồng dạng với OHD · ·
ODH OMD
mà: ODH OBD (tam giác ODB cân) OBD DAM
(cùng phụ DAB ) DAM OMD IAM IMD 0,5 IA IM I
AM đồng dạng với I MD 2 IM I . A ID IM ID 0,25 * I
HA vuông tại H, HD là đường cao: 2 IH I . D IA 0,25 Vậy 2 2
IM IH IM IH . Suy ra I là trung điểm MH Chứng minh… 3 a 3 b 3 c Ta có: 2 ab 2a ; 2 bc 2b ; 2 ac 2c b c a 3 3 3 a b c Cộng theo vế:
abbc ca 2 2 2
2 a b c b c a 0,25 Bài 5 0,5 Chứng minh 2 2 2
a b c abbc ca 3 3 3 a b c
abbc ca 2 2 2
2 a b c 2ab bc ca b c a 3 3 3 a b c
ab bc ca 0,25 b c a
Ghi chú: Mọi cách làm khác đúng giám khảo tự quyết định cho điểm theo thang điểm tương ứng




