Đề thi học kỳ 2 môn Toán lớp 11 Quảng Nam 2018-2019 (có đáp án)
Đề thi học kỳ 2 môn Toán lớp 11 Quảng Nam 2018-2019 có đáp án được soạn dưới dạng file PDF gồm 4 trang giúp các bạn ôn tập, tham khảo và chuẩn bị tốt cho kỳ thi sắp tới. Các bạn xem và tải về ở dưới.
Preview text:
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KIỂM TRA HỌC KỲ II NĂM HỌC 2018-2019 QUẢNG NAM
Môn: TOÁN – Lớp 11
Thời gian: 60 phút (không kể thời gian giao đề) ĐỀ CHÍNH THỨC MÃ ĐỀ 102
(Đề gồm có 02 trang)
A/ TRẮC NGHIỆM: (5,0 điểm)
Câu 1. Một chất điểm chuyển động theo phương trình 3 2
S = t - 4t + 7, trong đó t > 0, t được tính
bằng giây (s) và S được tính bằng mét (m) . Tính vận tốc của chất điểm tại thời điểm t = 3 ( giây) . A. 10 𝑚/𝑠. B. 3 𝑚/𝑠. C. 26 𝑚/𝑠. D. 19 𝑚/𝑠.
Câu 2. Cho tứ diện ABCD , gọi G là trọng tâm của tam giác ACD . Mệnh đề nào dưới đây đúng? A. GB ...⃗ + 𝐺𝐶 ...⃗ + 𝐺𝐷 ...⃗ = 𝑂.⃗. B. GA ...⃗ + 𝐺𝐶 ...⃗ + 𝐺𝐷 ...⃗ = 𝑂.⃗. C. GA ...⃗ + 𝐺𝐵 ...⃗ + 𝐺𝐶 ...⃗ = 𝑂.⃗. D. GA ...⃗ + 𝐺𝐵 ...⃗ + 𝐺𝐷 ...⃗ = 𝑂.⃗. 2 x + 3x - 4 Câu 3. Tính lim . x 1+ ® x -1 A. −5. B. 0. C. +∞. D. 5.
Câu 4. Tìm đạo hàm của hàm số y = 3sinx +1.
A. 𝑦! = −3 cos 𝑥. B. 𝑦! = cos 𝑥. C. 𝑦! = 3 cos 𝑥. D. 𝑦! = 3 cos 𝑥 + 1. Câu 5. Cho hàm số 2
y = cos x. Mệnh đề nào dưới đây đúng ?
A. 4𝑦. 𝑠𝑖𝑛"𝑥 − (𝑦!)" = 2𝑠𝑖𝑛"2𝑥.
B. 2 cos 𝑥 − 𝑦! = 0.
C. 𝑐𝑜𝑠"𝑥 + 𝑦! = 1.
D. 4𝑦. 𝑠𝑖𝑛"𝑥 − (𝑦!)" = 0.
Câu 6. Tìm vi phân của hàm số 2
y = 4x + 3x - 2.
A. 𝑑𝑦 = 8𝑥 + 3. B. 𝑑𝑥 = (8𝑥 + 3)𝑑𝑦. C. 𝑑𝑦 = (8𝑥 + 3)𝑑𝑥. D. 𝑑𝑦 = 8𝑥 + 3𝑑𝑥. 3 ì bx +1 - 1- ï ax khi x ¹ 0
Câu 7. Cho hàm số y = f (x) = í x . ïî2a -3b+1 khi x = 0
Tìm điều kiện của tham số a và b để hàm số trên liên tục tại điểm x = 0.
A. 𝑎 − 4𝑏 + 1 = 0.
B. 9𝑎 − 20𝑏 + 6 = 0.
C. 3𝑎 − 4𝑏 + 1 = 0.
D. 10𝑎 − 21𝑏 + 6 = 0. 1
Câu 8. Tìm đạo hàm cấp 2 của hàm số y = . x +1 -1 2 - 2 1 - A. 𝑦′′ = . B. 𝑦′′ = . C. 𝑦′′ = . D. 𝑦′′ = . 2 (x +1) 3 (x +1) 3 (x +1) 3 (x +1)
Câu 9. Cho hình chóp S.ABCD có SA ^ (ABCD) và đáy ABCD là hình vuông. Mệnh đề nào dưới đây đúng?
A. (𝑆𝐴𝐷) ^ (𝑆𝐵𝐶).
B. 𝐴𝐶 ^ (𝑆𝐴𝐵).
C. (𝑆𝐵𝐶) ^ (𝑆𝐴𝐵).
D. 𝐵𝐷 ^ (𝑆𝐴𝐷).
Câu 10. Tìm đạo hàm của hàm số 3
y = x + 5x . A. 𝑦! = 3𝑥" + 5.
B. 𝑦! = 3𝑥 + 5. C. 𝑦! = 𝑥# + 5. D. 𝑦! = 3𝑥" + 5𝑥. n + 5 Câu 11. Tính lim . 7n + 3 5 5 1 A. . B. . C. . D. 0. 7 3 7 x - 5 Câu 12. Tính lim . x®2 x +1 Trang 1 A. −1. B. 1. C. −5. D. +∞.
Câu 13. Cho hình lập phương ABCD.A' B'C ' D '. Gọi a là góc giữa hai đường thẳng AD ' và CB'. Tính a . A. 𝛼 = 60$. B. 𝛼 = 30$. C. 𝛼 = 45$. D. 𝛼 = 90$.
Câu 14. Cho hình chóp tứ giác đều S.ABCD có AB = a và 𝑆𝐵 = a. Tính khoảng cách từ A đến mặt phẳng (SBC). a 6 a 6
A. 𝑑O𝐴; (𝑆𝐵𝐶)Q = .
B. 𝑑O𝐴; (𝑆𝐵𝐶)Q = . 6 3 a
C. 𝑑O𝐴; (𝑆𝐵𝐶)Q = .
D. 𝑑O𝐴; (𝑆𝐵𝐶)Q = 𝑎. 2
Câu 15. Trong các mệnh đề sau, mệnh đề nào sai ?
A. Nếu 𝑎//𝑏 và (𝛼) ^ a thì (𝛼) // b .
B. Nếu 𝑎//(𝛼) và b ^ (𝛼) thì b ^ a.
C. Nếu (𝛼)//(𝛽) và a ^ (𝛼) thì a ^ (𝛽) .
D. Nếu a và b là hai đường thẳng phân biệt và a ^ (𝛼) , b ^(𝛼) thì 𝑎//𝑏 .
B/ TỰ LUẬN: (5,0 điểm)
Bài 1 (2,0 điểm). 5 - n x +14 - 4 a. Tìm lim . b. Tìm lim 3 + n x®2 x - 2 2 ì x - 7x +12 ï c. Cho hàm số khi x ¹ 4
y = f (x) = í . x - 4 ïî2m + 1 khi x = 4
Tìm điều kiện của tham số m để hàm số trên liên tục tại điểm x = 4.
Bài 2 (1,0 điểm). Cho hàm số 3 2
y = f (x) = x + 2x - 4, có đồ thị (C).
a. Tính đạo hàm của hàm số trên.
b. Viết phương trình tiếp tuyến của đồ thị (C) tại điểm có hoành độ x = 1. 0
Bài 3 (2,0 điểm). Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O, cạnh a; các cạnh bên
của hình chóp đều bằng 𝑎√3.
a. Chứng minh rằng 𝐴𝐶 ⊥ (𝑆𝐵𝐷).
b. Gọi (P) là mặt phẳng đi qua B và vuông góc với cạnh SD. Xác định thiết diện của hình chóp
S.ABCD cắt bởi mặt phẳng (P).
c. Tính góc giữa đường thẳng BC và mặt phẳng (P).
=================Hết=================
Họ và tên:……………….......…………………..SBD: …….......………….
Chú ý: Học sinh không được sử dụng tài liệu. Giám thị coi thi không giải thích gì thêm.
SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐÁP ÁN ĐỀ KIỂM TRA HỌC KỲ II QUẢNG NAM
MÔN TOÁN 11 – NĂM HỌC 2018-2019
Thời gian làm bài: 60 phút (Không kể thời gian phát đề) Trang 2
Gồm các mã đề 102; 105; 108; 111; 114; 117; 120; 123.
A. Phần trắc nghiệm: (5,0 điểm) Mã 102 8. C 1. B 9. C 2. B 10. A 3. D 11. C 4. C 12. A 5. D 13. D 6. C 14. B 7. B 15. A
B. Phần tự luận: (5,0 điểm) Bài Nội dung Điểm a) 5 -1 5 - n n lim = lim 0,25 3 + n 3 +1 n = 1 - 0,25 b) x + -
( x+14 -4)( x+14 +4 14 4 ) lim = lim 0,25 x®2 x®2 x - 2
(x - 2)( x +14 + 4) 1 1 = lim = 0,25 x®2 x +14 + 4 8 1 c) 2 - + - - x 7x 12 (x 3)(x 4) lim f (x) = lim = lim = lim(x -3) = 0,25 1 x®4 x®4 x®4 x - 4 x - 4 x 4 ® f (4) = 2m + 1 0,25
Hàm số liên tục tại x = 4 Û lim f (x) = f (4) x®4 0,25
Û 1 = 2m +1 Û m = 0 0,25
Kết luận với m = 0thì hàm số liên tục tại x = 4. 2 a. 2
f '(x) = 3x + 4x 0.25 b. Tính đúng: y = - 0 1 0,25
f '(x ) = f '(1) = 7 0,25 0
Phương trình tiếp tuyến cần tìm là y = 7x - 8 0,25
Bài 3 (2,0 điểm). Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O, cạnh a; các cạnh bên
của hình chóp đều bằng 𝑎√3.
a. Chứng minh rằng 𝐴𝐶 ⊥ (𝑆𝐵𝐷).
b. Gọi (P) là mặt phẳng đi qua B và vuông góc với cạnh SD. Xác định thiết diện của hình
chóp S.ABCD cắt bởi mặt phẳng (P).
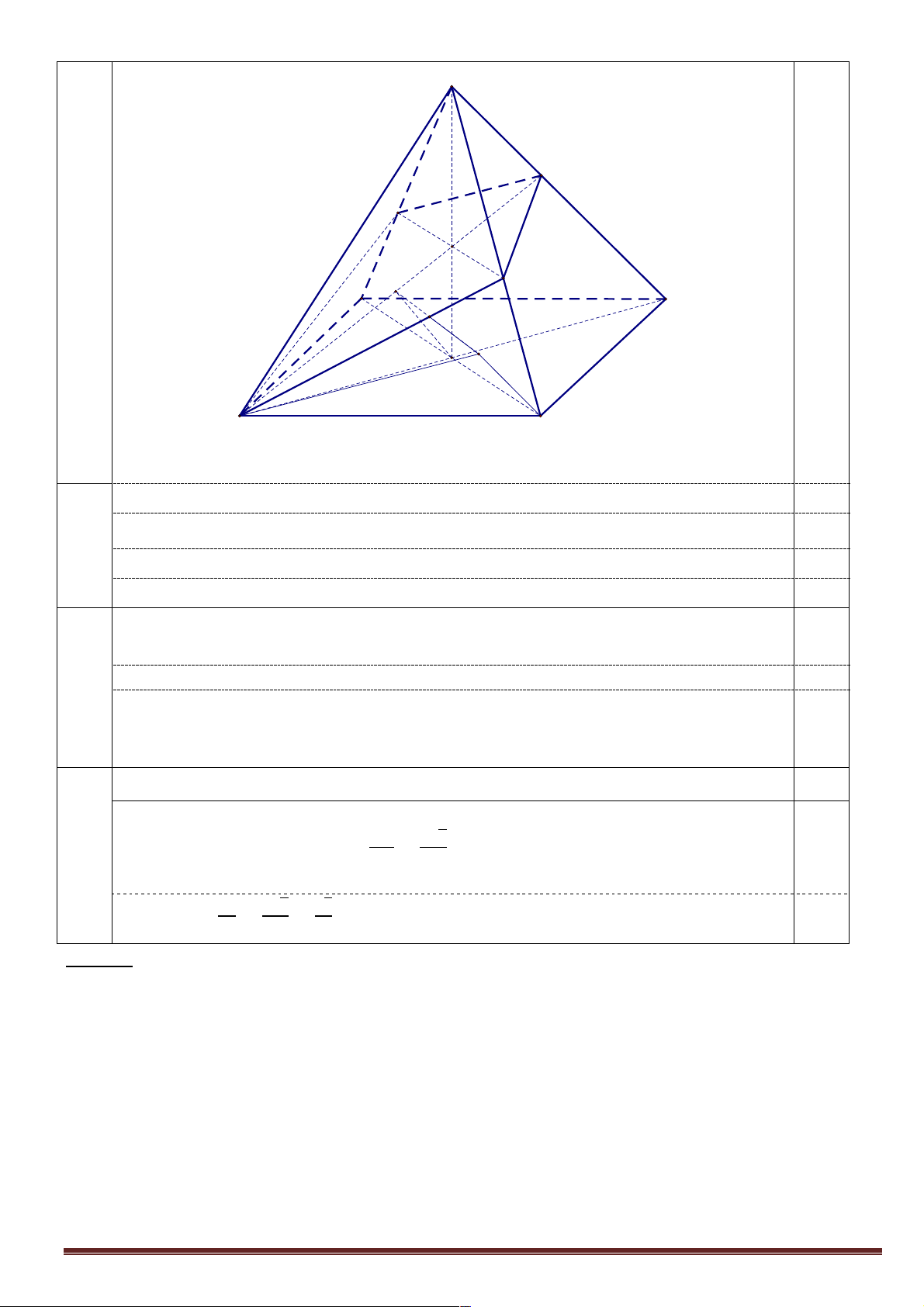
c. Tính góc giữa đường thẳng BC và mặt phẳng (P). Trang 3 S D' A' H C' 0,25 K A D F O B C
(Hình vẽ phục vụ câu a, đúng được 0,25 điểm).
Câu a) Chứng minh rằng 𝐴𝐶 ⊥ (𝑆𝐵𝐷). a
+ 𝐴𝐶 ⊥ 𝐵𝐷 (𝑔𝑡). 0,25
0,75 + 𝑆𝐴 = 𝑆𝐶 nên △ 𝑆𝐴𝐶 𝑐â𝑛 ⇒ 𝐴𝐶 ⊥ 𝑆𝑂. 0,25
𝐵𝐷 ⊂ (𝑆𝐵𝐷); 𝑆𝑂 ⊂ (𝑆𝐵𝐷). Vậy 𝐴𝐶 ⊥ (𝑆𝐵𝐷). 0,25
b. Gọi (P) là mặt phẳng đi qua B và vuông góc với cạnh SD. Xác định thiết diện b
của hình chóp S.ABCD cắt bởi mặt phẳng (P).
0,5 + Vì (𝑃) ⊥ 𝑆𝐷 nên hạ 𝐵𝐷! ⊥ 𝑆𝐷 (𝐷′ ∈ 𝑆𝐷); 𝐵𝐷′⋂ 𝑆𝑂 = {𝐻}. 0,25
+Vì 𝐴𝐶 ⊥ (𝑆𝐵𝐷) nên 𝐴𝐶 ⊥ 𝑆𝐷. Suy ra (𝑃)/⁄𝐴𝐶
⇒ (𝑃)⋂(𝑆𝐴𝐶) = 𝐴!𝐶!𝑣ớ𝑖 𝐴!𝐶!//𝐴𝐶; 𝐴! ∈ 𝑆𝐴, 𝐶′ ∈ 𝑆𝐶; 0,25
Vậy thiết diện cần tìm là tứ giác BC’D’A’(có hình vẽ đúng mới chấm).
c. Tính góc giữa đường thẳng BC và mặt phẳng (P). c
Hạ 𝑂𝐾 ⊥ 𝐵𝐷′ (K∈ 𝐵𝐷′). Suy ra 𝑂𝐾 ⊥ (𝑃). 0,5
Hạ 𝐶𝐹 ⊥ (𝑃) thì 𝐶𝐹 = 𝑂𝐾 = %%! = &√# (vì d (C;(P))= d (O; (P)). 0,25 " (
Vậy góc giữa đường thẳng BC và mặt phẳng (P) là góc 𝐶𝐵𝐹 g . 𝑠𝑖𝑛𝐶𝐵𝐹
g = )* = &√# = √# hay 𝐶𝐵𝐹 g = 16$46!43,16′′. 0,25 )+ (& (
Ghi chú: - Học sinh giải cách khác đúng thì được điểm tối đa tương ứng.
- Tổ Toán mỗi trường cần thảo luận kỹ HDC trước khi tiến hành chấm.
--------------------------------Hết-------------------------------- Trang 4