Đề thi học kỳ 2 Toán 11 năm 2018 – 2019 trường THPT Vinh Lộc – TT Huế

Nhằm kiểm tra đánh giá chất lượng học tập môn Toán của học sinh khối 11 trong giai đoạn học kỳ 2 năm học 2018 – 2019, vừa qua, trường THPT Vinh Lộc, tỉnh Thừa Thiên Huế tổ chức kỳ thi học kỳ 2 Toán 11 năm học 2018 – 2019.

Chủ đề:

Đề HK2 Toán 11 391 tài liệu

Môn:

Toán 11 3.3 K tài liệu

Thông tin:
18 trang 1 năm trước
Tác giả:
K
Kim Oanh
docx.com.vn

Bình luận

Vui lòng đăng nhập hoặc đăng ký để gửi bình luận.

Đề thi học kỳ 2 Toán 11 năm 2018 – 2019 trường THPT Vinh Lộc – TT Huế

Nhằm kiểm tra đánh giá chất lượng học tập môn Toán của học sinh khối 11 trong giai đoạn học kỳ 2 năm học 2018 – 2019, vừa qua, trường THPT Vinh Lộc, tỉnh Thừa Thiên Huế tổ chức kỳ thi học kỳ 2 Toán 11 năm học 2018 – 2019.

34 17 lượt tải Tải xuống

Chủ đề: Đề HK2 Toán 11 391 tài liệu

Môn: Toán 11 3.3 K tài liệu

Thông tin:

18 trang 1 năm trước

Tác giả:

Profile Kim Oanh
Trang 1/18 - Mã đề thi A
SỞ GD&ĐT THỪA THIÊN HUẾ
TR
Ư
ỜNG THPT VINH LỘC
KIỂM TRA HỌC KỲ II_NĂM HỌC 2018 - 2019
M
ôn: Toán - Lớ
p
11 - Chươn
g
trình chuẩn
ĐỀ CHÍNH THỨC Thời gian: 90 phút (Không kể thời gian phát đề)
(
Đề
g
ồm 04 tran
g)
Mã đề thi
A
Họ và tên:………………………………….Lớp:…………….............……..……
I. PHẦN TRẮC NGHIỆM KHÁCH QUAN (8,0 điểm)
Câu 1. Cho hình chóp
.SABCD
có đáy
ABCD
là hình vuông và

.SA ABCD
Mệnh đề nào dưới đây là sai?
A.

BC SAB
. B.

AC SBD
. C.

BD SAC
. D.

CD SAD
.
Câu 2. Xét chuyển động có phương trình
() sin( )st A t b

(,,Ab
là các hằng số). Tìm gia tốc tức thời tại
thời điểm
t
của chuyển động.
A.
2
a( ) sin( ).tA tb


B.
a( ) cos( ).tA tb

C.
2
a( ) cos( ).tA tb


D.
2
a( ) sin( ).tA tb


Câu 3. Cho

2 3 khi 2
1 khi 2
xx
fx
ax x


. Để

2
lim
x
fx
tồn tại, giá trị của
a
phải bằng bao nhiêu?
A. 1. B. 3. C. 4. D. 2.
Câu 4. Một nhóm bạn trao đổi về kết quả khi tính
*
111 1
...
248 2
lim ,( )
n
n
n
a

đã đưa ra các nhận xét như sau:
(1) Giới hạn lớn hơn
0
nếu
1.a
(2) Giới hạn bằng
1
nếu
1.a
(3) Giới hạn bằng

nếu
01.a
Hỏi có tất cả bao nhiêu nhận xét đúng?
A. Không có nhận xét nào đúng. B. Chỉ có một nhận xét đúng.
C. Có hai nhận xét đúng. D. Cả ba nhận xét đều đúng.
Câu 5. Hàm số bậc hai nào sau đây thỏa mãn điều kiện:

(1) 5, 1 3 ?ff

A.

2
93.fx x x
B.

2
9.fx x x
C.
2
38.
xxx
D.
2
391.fx x x
Câu 6. Cho hình hộp
111 1
.ABCD A B C D
. Tìm giá trị của k để đẳng thức vectơ:
11 1 1
AB B C DD k AC
   
là đúng.
A.
0k
. B.
2k
. C.
4k
. D.
1k
.
Câu 7. Trong không gian cho điểm
O
và bốn điểm
,,,ABCD
không thẳng hàng. Điều kiện cần và đủ để
,,,ABCD
tạo thành hình bình hành là gì?
A.
0OA OB OC OD
 
. B.
OA OC OB OD
   
.
C. .
11
22
OA OB OC OD

. D.
11
22
OA OC OB OD

.
Câu 8. Thông qua việc tìm giới hạn của các hàm số khi
0,xx
hãy xác định xem đường cong dưới đây là đồ
thị của hàm số nào?
A.

32
2
1
.
xx
gx
x

B.

2
4
1
.
x
hx
x

C.

4
2
1
.
x
kx
x
D.

2
2
1
.
x
fx
x
Trang 2/18
Câu 9. Có bao nhiêu giá trị
0; 2x
sao cho tiếp tuyến với đồ thị hàm số
2cosyx x
tại các tiếp điểm có hoành
độ đó song song với đường thẳng
y2?
x
A.
4.
B.
3.
C.
1.
D.
2.
Câu 10. Cho tứ diện
A
BCD
có
A
BCDa
,
3
2
IJ
a
(
,IJ
lần lượt là trung điểm của
B
C
và
A
D
). Số đo góc
giữa hai đường thẳng
A
B
và
CD
bằng bao nhiêu độ?
A.
4 5 .
B.
6 0 .
C.
90 .
D.
30 .
Câu 11. Tính
2
2
4
lim .
2
x
x
x
A.
2.
B.
2.
C.
4.
D.
4.
Câu 12. Tìm đạo hàm của hàm số
2
1yx
.
A.
2
2
1
1
xx
x
.
B.
2
2
1
x
x
. C.
2
1
x
x
. D.
2
21
x
x
.
Câu 13.
Tính
3
2
3
lim .
nn
n
A.
1.
B.
.
C. 0. D.
.
Câu 14.
Cho hàm số

1
fx
x
. Tính

2.y
A.
1
.
2
B.
1
.
2
C.
1
.
2
D.
1
.
2
Câu 15.
Cho hình lăng trụ tam giác
.
A
BC A B C

. Đặt
,,,
A
A a AB b AC c BC d

   
. Trong các đẳng thức vectơ
đã cho dưới đây, đẳng thức nào đúng?
A.
0abcd

. B.
0bcd

. C.
abc d

. D.
abc

.
Câu 16.
Cho tứ diện
A
BCD
, các điểm
M
,
N
lần lượt là trung điểm của
A
B
,
CD
. Không thể kết luận
G
là trọng
tâm của tứ diện
A
BCD
trong trường hợp nào dưới đây?
A.
GM GN
.
B.
0GA GB GC GD
   
.
C.
4PG PA PB PC PD
 
với
P
là điểm bất kỳ.
D.
0GM GN

.
Câu 17.
Cho hình hộp
.
A
BCDABCD

. Gọi
,IK
lần lượt là tâm của hình bình hành
A
BB A

và
B
CC B

. Khẳng
định nào sau đây là
sai?
A.
22
B
DIK BC
  
. B. Bốn điểm
I
,
K
,
C
,
A
đồng phẳng.
C.
11
22
IK AC A C


  
. D. Ba vectơ
,,
B
DIKBC

  
không đồng phẳng.
Câu 18.
Cho hàm số

2
2
khi 2
.
2
5 khi 2
xx
x
fx
x
xx


Khẳng định nào sau đây là sai?
A.
Hàm số liên tục trên
.
B. Hàm số có tập xác định là
.
C.
Hàm số gián đoạn tại
0
0.x
D. Hàm số liên tục tại
0
2.x
Câu 19.
Cho tứ diện
A
BCD
. Gọi
,IJ
lần lượt là trung điểm của
A
B
và
CD
,
G
là trung điểm của
I
J
.
Đẳng thức nào dưới đây là đúng?
A.
GA GB GC GD JI
   
. B.
2GA GB GC GD JI

.
C.
0GA GB GC GD
   
. D.
2GA GB GC GD IJ
    
.
Câu 20.
Cho hàm số
3
31 .
y
xx C
Viết phương trình tiếp tuyến của đồ thị

C
tại điểm có hoành độ bằng 0.
A.
3 12.yx
B.
311.yx
C.
31.yx
D.
32.yx
Trang 3/18 - Mã đề thi A
Câu 21. Tính
4
4
3
3
212
lim .
3
nn n
nnn


A.
.
B. . C.
3
3
.
31
D.
1.
Câu 22.
Gọi
C
là đồ thị của hàm số
2
2
x
y
x
.
M
là một điểm trên
C
không trùng với gốc tọa độ và có hoành
độ là số nguyên sao cho khoảng cách từ
M
đến trục hoành gấp đôi khoảng cách từ
M
đến trục tung. Phương
trình nào sau đây là một phương trình tiếp tuyến của
C
tại
?
M
A.
8.y 
B.
64.y 
C.
12.y 
D.
9.y 
Câu 23.
Cho hình hộp chữ nhật
.
A
BCD A B C D

có
6cmAB
,
2cmBC BB

. Điểm
E
là trung điểm cạnh
B
C
. Một tứ diện đều
M
NPQ
có hai đỉnh
M
và
N
nằm trên đường thẳng
E
C
, hai đỉnh
P
và
Q
nằm trên đường thẳng
đi qua điểm
B
và cắt đường thẳng
A
D
tại điểm
F
. Khoảng cách
D
F
bằng bao nhiêu?
A.
3cm.
B.
6cm.
C.
1cm.
D.
2cm.
Câu 24.
Cho
cos 1x 
. Tính
246 2
1 cos cos cos ... cos ...
n
Sxxx x
A.
2
1
cos
x
. B.
2
1
sin
x
. C.
2
sin
x
. D.
2
cos
x
.
Câu 25.
Nếu

y
f
x
và
y
g
x
đều liên tục tại
0
x
thì hàm số nào sau đây chưa chắc liên tục tại
0
?
x
A.
y().
f
x
g
x
B.

y().
f
x
g
x
C.
y.().
f
x
g
x
D.
y.
()
f
x
g
x
Câu 26.
Cho
2
2
2
1 khi 1
() .
1
3 2 1 khi 1
xx
mx x
fx
x
mx m x



Tính tổng tất cả các giá trị
m
thỏa mãn điều kiện hàm số có giới
hạn khi
1.x
A.
5.
B.
0.
C.
217.
D.
17.
Câu 27.
Biết rằng
lim ,lim ,
nn
ua v b
với
0.b
Khẳng định nào sau đây là đúng?
A.
lim .
n
n
u
a
vb



B.
lim .
nn
uv ab
C.
lim .
nn
uv ab
D.

lim . .
nn
uv ab
Câu 28.
Tìm
m
để hàm số

2 9 khi 0
3 khi 0
xx
fx
mx

liên tục tại
0
0.x
A.
3.m
B.
2.m 
C.
0.m
D.
1.m
Câu 29.
Cho đường thẳng
aP
và đường thẳng
bQ
. Mệnh đề nào sau đây là đúng?
A.
// //
P
QaQ
và
// .bP
B.
a
và
b
chéo nhau.
C.

// // .
P
Qab
D.
// // .ab P Q
Câu 30. Cho hình chóp
.SABCD
có tất cả các cạnh bên và cạnh đáy đều bằng nhau.
A
BCD
là hình vuông. Khẳng định
nào sau đây là đúng?
A.
BD SAC
. B.

SB ABCD
. C.

BD SAD
. D.
BD SCD
.
Câu 31.
Tính
1
lim .
1n
A.
3. B. 0. C. 1. D. 2.
Câu 32.
Tính
1
23
lim .
1
x
x
x
A.
.
B.
.
C.
2.
D.
2.
Câu 33.
Tìm đạo hàm của hàm số

ysin, .xx
Trang 4/18
A.
ycos.
x
B.
ycos.
x

C.
ytan.
x
D.
2
1
y.
cos
x
Câu 34.
Cho 3, 5ab

góc giữa
a
và
b
bằng
120 .
Chọn khẳng định sai trong các khẳng định sau.
A.
2 139ab
. B.
19ab
. C.
29ab
. D.
7ab
.
Câu 35.
Cho hình hộp
.
A
BCDABCD

. Nếu mp
()
chứa
A
B
cắt hình hộp theo thiết diện là một tứ giác thì
tứ giác đó là hình gì?
A.
Hình chữ nhật. B. Hình bình hành. C. Hình thoi. D. Hình vuông.
Câu 36.
Tính đạo hàm của hàm số
2
y,('0).
''
ax bx c
aa
ax b


A.
2
'2' ''
.
''
aa x ab x bb a c
y
ax b

B.
2
2
'2' ''
.
(' ')
aa x ab x bb a c
y
ax b

C.
2
2
'2' ''
.
(' ')
aa x ab x bb a c
y
ax b

D.
2
2
'2' ''
.
(' ')
aa x ab x bb a c
y
ax b

Câu 37.
Cho hình lăng trụ
.
A
BC A B C

. Gọi
H
là trung điểm của
A
B

. Đường thẳng
B
C
song song với mặt phẳng
nào dưới đây?
A.
.
A
AH
B.
.
H
AB
C.
.
H
AC
D.
.
A
HC
Câu 38.
Cho hình lăng trụ đều
.
A
BC A B C

có tất cả các cạnh bằng .a Gọi
M
là trung điểm của
,AB
là góc tạo
bởi đường thẳng
M
C
và mặt phẳng
A
BC
. Khi đó
tan
bằng bao nhiêu?
A.
3
7
. B.
23
3
. C.
27
7
. D.
3
2
.
Câu 39.
Biết rằng
lim , lim .
xx
fx gx
 
 
Khẳng định nào sau đây là đúng?
A.
lim 0.
x
fx gx



B.

lim 1.
x
fx
gx





C.
 
11
lim lim 0.
xx
fx gx
 

D.
lim . ,
x
Lf x




với
0.L
Câu 40. Cho hình chóp
.S ABC
có
, SA ABC ABC
vuông tại
.
B
Gọi
A
M
là đường cao của tam giác
SAB
(
M
thuộc cạnh
SB
). Khi đó,
A
M
không vuông góc với đường thẳng nào dưới đây?
A.
.
B
C
B.
.
A
C
C.
.SB
D.
.SC
II. PHẦN TỰ LUẬN (2,0 điểm)
Bài 1 (1,0 điểm).
a) Tính giới hạn:
52
5
236
lim .
nn
I
nn

b)
Cho hàm số

23
1
x
yfx
x

có đồ thị

.C
Viết phương trình tiếp tuyến của đồ thị
C
song song với
đường thẳng
: 5 2019.dy x
Bài 2 (1.0 điểm). Cho hàm số:
2
1.yxx
Chứng minh rằng:
2
41 4.
x
yyxy


------------- HẾT -------------
(Học sinh không được sử dụng tài liệu. Cán bộ coi thi không giải thích gì thêm.)
Trang 5/18 - Mã đề thi A
SỞ GD&ĐT THỪA THIÊN HUẾ
TRƯỜNG THPT VINH LỘC
KIỂM TRA HỌC KỲ II_NĂM HỌC 2018 - 2019
Môn: Toán - Lớp 11 - Chương trình chuẩn
ĐỀ CHÍNH THỨC Thời gian: 90 phút (Không kể thời gian phát đề)
(Đề gồm 04 trang)
Mã đề thi
B
Họ và tên:………………………………….Lớp:…………….............……..……
I. PHẦN TRẮC NGHIỆM KHÁCH QUAN (8,0 điểm)
Câu 1.
Cho hình chóp
.SABCD
có tất cả các cạnh bên và cạnh đáy đều bằng nhau.
A
BCD
là hình vuông. Khẳng định
nào sau đây là đúng?
A.

SB ABCD
. B.
BD SAD
. C.
BD SCD
. D.
BD SAC
.
Câu 2.
Cho tứ diện
A
BCD
, các điểm
M
,
N
lần lượt là trung điểm của
A
B
,
CD
. Không thể kết luận
G
là trọng tâm
của tứ diện
A
BCD
trong trường hợp nào dưới đây?
A.
4PG PA PB PC PD
   
với
P
là điểm bất kỳ.
B.
0GM GN

.
C.
GM GN
.
D.
0GA GB GC GD
   
.
Câu 3.
Biết rằng
lim , lim .
xx
fx gx
 
 
Khẳng định nào sau đây là đúng?
A.
lim . ,
x
Lf x




với
0.L
B.
lim 0.
x
fx gx




C.

lim 1.
x
fx
gx





D.
 
11
lim lim 0.
xx
fx gx
 

Câu 4.
Một nhóm bạn trao đổi về kết quả khi tính
*
111 1
...
248 2
lim ,( )
n
n
n
a

đã đưa ra các nhận xét như sau:
(1) Giới hạn lớn hơn
0
nếu
1.a
(2) Giới hạn bằng
1
nếu
1.a
(3) Giới hạn bằng

nếu
01.a
Hỏi có tất cả bao nhiêu nhận xét đúng?
A.
Chỉ có một nhận xét đúng. B. Có hai nhận xét đúng.
C.
Không có nhận xét nào đúng. D. Cả ba nhận xét đều đúng.
Câu 5.
Tìm
m
để hàm số

2 9 khi 0
3 khi 0
xx
fx
mx

liên tục tại
0
0.x
A.
1.m
B.
3.m
C.
2.m 
D.
0.m
Câu 6.
Tính
2
2
4
lim .
2
x
x
x
A.
2.
B.
4.
C.
2.
D.
4.
Câu 7.
Cho hình hộp
.
A
BCD A B C D

. Gọi
,IK
lần lượt là tâm của hình bình hành
A
BB A

và
B
CC B

. Khẳng định
nào sau đây là
sai?
A.
Ba vectơ
,,
B
DIKBC

  
không đồng phẳng. B.
22
B
DIK BC
  
.
C.
Bốn điểm
I
,
K
,
C
,
A
đồng phẳng. D.
11
22
IK AC A C


  
.
Câu 8.
Cho
cos 1x 
. Tính
246 2
1 cos cos cos ... cos ...
n
Sxxx x
A.
2
1
sin
x
. B.
2
cos
x
. C.
2
1
cos
x
. D.
2
sin
x
.
Câu 9.
Trong không gian cho điểm
O
và bốn điểm
,,,ABCD
không thẳng hàng. Điều kiện cần và đủ để
,,,ABCD
tạo thành hình bình hành là gì?
A.
11
22
OA OC OB OD

. B.
0OA OB OC OD
   
.
Trang 6/18
C.
OA OC OB OD
   
. D. .
11
22
OA OB OC OD

.
Câu 10.
Cho hình chóp
.S ABC
có
, SA ABC ABC
vuông tại
.
B
Gọi
A
M
là đường cao của tam giác
SAB
(
M
thuộc cạnh
SB
). Khi đó,
A
M
không vuông góc với đường thẳng nào dưới đây?
A.
.
B
C
B.
.
A
C
C.
.SB
D.
.SC
Câu 11.
Cho
3, 5ab

góc giữa
a
và
b
bằng
120 .
Chọn khẳng định sai trong các khẳng định sau.
A.
2 139ab
. B.
19ab
. C.
29ab
. D.
7ab
.
Câu 12.
Tính đạo hàm của hàm số
2
y,('0).
''
ax bx c
aa
ax b


A.
2
'2' ''
.
''
aa x ab x bb a c
y
ax b

B.
2
2
'2' ''
.
(' ')
aa x ab x bb a c
y
ax b

C.
2
2
'2' ''
.
(' ')
aa x ab x bb a c
y
ax b

D.
2
2
'2' ''
.
(' ')
aa x ab x bb a c
y
ax b

Câu 13.
Tính
4
4
3
3
212
lim .
3
nn n
nnn


A.
.
B. . C.
3
3
.
31
D.
1.
Câu 14.
Tính
1
23
lim .
1
x
x
x
A.
2.
B.
.
C.
.
D.
2.
Câu 15.
Cho hình lăng trụ đều
.
A
BCABC

có tất cả các cạnh bằng
.a
Gọi
M
là trung điểm của
,AB
là góc tạo
bởi đường thẳng
M
C
và mặt phẳng
A
BC
. Khi đó
tan
bằng bao nhiêu?
A.
23
3
. B.
3
2
. C.
3
7
. D.
27
7
.
Câu 16.
Cho hình chóp
.SABCD
có đáy
A
BCD
là hình vuông và
.SA ABCD
Mệnh đề nào dưới đây là sai?
A.
BC SAB
. B.
A
CSBD
. C.
BD SAC
. D.
CD SAD
.
Câu 17.
Hàm số bậc hai nào sau đây thỏa mãn điều kiện:
(1) 5, 1 3 ?ff

A.
2
93.fx x x
B.

2
9.
f
xxx
C.

2
38.
xxx
D.

2
391.fx x x
Câu 18.
Tìm đạo hàm của hàm số
2
1yx
.
A.
2
2
1
x
x
. B.
2
1
x
x
. C.
2
21
x
x
. D.
2
2
1
1
xx
x
.
Câu 19.
Cho hàm số
3
31 .
y
xx C
Viết phương trình tiếp tuyến của đồ thị

C
tại điểm có hoành độ bằng 0.
A.
31.yx
B.
32.yx
C.
312.yx
D.
3 11.yx
Câu 20.
Xét chuyển động có phương trình
() sin( )
s
tA tb

(,,Ab
là các hằng số). Tìm gia tốc tức thời tại
thời điểm
t
của chuyển động.
A.
2
a( ) sin( ).tA tb


B.
2
a( ) sin( ).tA tb


C.
a( ) cos( ).tA tb

D.
2
a( ) cos( ).tA tb


Câu 21.
Gọi
C
là đồ thị của hàm số
2
2
x
y
x
.
M
là một điểm trên

C
không trùng với gốc tọa độ và có hoành
độ là số nguyên sao cho khoảng cách từ
M
đến trục hoành gấp đôi khoảng cách từ
M
đến trục tung. Phương
trình nào sau đây là một phương trình tiếp tuyến của

C
tại
?
M
A.
12.y 
B.
8.y 
C.
9.y 
D.
64.y 
Trang 7/18 - Mã đề thi A
Câu 22.
Cho tứ diện
A
BCD
. Gọi
,IJ
lần lượt là trung điểm của
A
B
và
CD
,
G
là trung điểm của
I
J
.
Đẳng thức nào dưới đây là đúng?
A.
2GA GB GC GD JI
   
. B.
2GA GB GC GD IJ
    
.
C.
GA GB GC GD JI
   
. D.
0GA GB GC GD
   
.
Câu 23.
Cho đường thẳng
aP
và đường thẳng
bQ
. Mệnh đề nào sau đây là đúng?
A.

// // .
P
Qab
B.
// // .ab P Q
C.
// //
P
QaQ
và
// .bP
D.
a
và
b
chéo nhau.
Câu 24.
Cho hàm số

1
fx
x
. Tính

2.y
A.
1
.
2
B.
1
.
2
C.
1
.
2
D.
1
.
2
Câu 25.
Tìm đạo hàm của hàm số

ysin, .xx
A.
ytan.
x
B.
2
1
y.
cos
x
C.
ycos.
x
D.
ycos.
x

Câu 26.
Biết rằng

lim ,lim ,
nn
ua v b
với
0.b
Khẳng định nào sau đây là đúng?
A.
lim .
nn
uv ab
B.
lim . .
nn
uv ab
C.
lim .
n
n
u
a
vb



D.
lim .
nn
uv ab
Câu 27.
Cho tứ diện
A
BCD
có
A
BCDa
,
3
2
IJ
a
(
,IJ
lần lượt là trung điểm của
B
C
và
A
D
). Số đo góc
giữa hai đường thẳng
A
B
và
CD
bằng bao nhiêu độ?
A.
6 0 .
B.
90 .
C.
30 .
D.
4 5 .
Câu 28.
Cho hình hộp chữ nhật
.
A
BCD A B C D

có
6cmAB
,
2cmBC BB

. Điểm
E
là trung điểm cạnh
B
C
. Một tứ diện đều
M
NPQ
có hai đỉnh
M
và
N
nằm trên đường thẳng
E
C
, hai đỉnh
P
và
Q
nằm trên đường thẳng
đi qua điểm
B
và cắt đường thẳng
A
D
tại điểm
F
. Khoảng cách
DF
bằng bao nhiêu?
A.
3cm.
B.
2cm.
C.
6cm.
D.
1cm.
Câu 29.
Cho hình hộp
.
A
BCD A B C D

. Nếu mp
()
chứa
A
B
cắt hình hộp theo thiết diện là một tứ giác thì tứ
giác đó là hình gì?
A.
Hình vuông. B. Hình chữ nhật. C. Hình bình hành. D. Hình thoi.
Câu 30.
Cho hình hộp
111 1
.
A
BCD A B C D
. Tìm giá trị của k để đẳng thức vectơ:
11 1 1
A
BBC DD kAC
   
là đúng.
A.
2k
. B.
4k
. C.
1k
. D.
0k
.
Câu 31.
Tính
1
lim .
1n
A.
3. B. 1. C. 2. D. 0.
Câu 32.
Nếu
y
f
x
và
y
g
x
đều liên tục tại
0
x
thì hàm số nào sau đây chưa chắc liên tục tại
0
?
x
A.
y.
()
f
x
g
x
B.

y().
f
x
g
x
C.
y.().
f
x
g
x
D.
y().
f
x
g
x
Câu 33.
Cho hình lăng trụ tam giác
.
A
BC A B C

. Đặt
,,,
A
A a AB b AC c BC d

   
. Trong các đẳng thức vectơ
đã cho dưới đây, đẳng thức nào đúng?
A.
0abcd

. B.
abc d

. C.
abc

. D.
0bcd

.
Câu 34.
Cho hàm số

2
2
khi 2
.
2
5 khi 2
xx
x
fx
x
xx


Khẳng định nào sau đây là sai?
A.
Hàm số gián đoạn tại
0
0.x
B. Hàm số liên tục trên
.
Trang 8/18
C. Hàm số có tập xác định là
.
D. Hàm số liên tục tại
0
2.x
Câu 35. Cho

2 3 khi 2
1 khi 2
xx
fx
ax x


. Để

2
lim
x
fx
tồn tại, giá trị của
a
phải bằng bao nhiêu?
A. 4. B. 1. C. 2. D. 3.
Câu 36. Cho
2
2
2
1 khi 1
() .
1
3 2 1 khi 1
xx
mx x
fx
x
mx m x



Tính tổng tất cả các giá trị
m
thỏa mãn điều kiện hàm số có giới
hạn khi
1.x
A.
5.
B.
0.
C.
217.
D.
17.
Câu 37. Cho hình lăng trụ
.ABC A B C

. Gọi
H
là trung điểm của
AB

. Đường thẳng
BC
song song với mặt phẳng
nào dưới đây?
A.

.HAB
B.

.HA C
C.

.AHC
D.

.AA H
Câu 38. Thông qua việc tìm giới hạn của các hàm số khi
0,xx
hãy xác định xem đường cong dưới đây là đồ
thị của hàm số nào?
A.

2
4
1
.
x
hx
x

B.

4
2
1
.
x
kx
x
C.

2
2
1
.
x
fx
x
D.

32
2
1
.
xx
gx
x

Câu 39. Tính
3
2
3
lim .
nn
n
A.
1.
B.
.
C. 0. D.
.
Câu 40. Có bao nhiêu giá trị

0; 2x
sao cho tiếp tuyến với đồ thị hàm số
2cosyx x
tại các tiếp điểm có hoành
độ đó song song với đường thẳng
y2?x
A.
2.
B.
3.
C.
1.
D.
4.
II. PHẦN TỰ LUẬN (2,0 điểm)
Bài 1 (1,0 điểm).
a) Tính giới hạn:
52
5
236
lim .
nn
I
nn

b) Cho hàm số

23
1
x
yfx
x

có đồ thị

.C
Viết phương trình tiếp tuyến của đồ thị

C
song song với
đường thẳng
: 5 2019.dy x
Bài 2 (1.0 điểm). Cho hàm số:
2
1.yxx
Chứng minh rằng:

2
41 4.xyyxy


------------- HẾT -------------
(Học sinh không được sử dụng tài liệu. Cán bộ coi thi không giải thích gì thêm.)
Trang 9/18 - Mã đề thi A
SỞ GD&ĐT THỪA THIÊN HUẾ
TR
Ư
ỜNG THPT VINH LỘC
KIỂM TRA HỌC KỲ II_NĂM HỌC 2018 - 2019
M
ôn: Toán - Lớ
p
11 - Chươn
g
t
r
ình chu
ẩ
n
ĐỀ CHÍNH THỨC Thời gian: 90 phút (Không kể thời gian phát đề)
(
Đ
ề
gồ
m 04 tran
g)
Mã đề thi
C
Họ và tên:………………………………….Lớ
p
:…………….............……..……
I. PHẦN TRẮC NGHIỆM KHÁCH QUAN (8,0 điểm)
Câu 1.
Tính
1
lim .
1n
A.
3. B. 0. C. 1. D. 2.
Câu 2.
Cho hình lăng trụ tam giác
.
A
BC A B C

. Đặt
,,,
A
AaABbACcBCd

   
. Trong các đẳng thức vectơ đã
cho dưới đây, đẳng thức nào đúng?
A.
0abcd

. B.
0bcd

. C.
abc d

. D.
abc

.
Câu 3.
Tìm đạo hàm của hàm số

ysin, .xx
A.
2
1
y.
cos
x
B.
ycos.
x

C.
ytan.
x
D.
ycos.
x
Câu 4.
Cho hình hộp
111 1
.
A
BCD A B C D
. Tìm giá trị của k để đẳng thức vectơ:
11 1 1
A
BBC DD kAC
   
là đúng.
A.
0k
. B.
2k
. C.
4k
. D.
1k
.
Câu 5.
Gọi

C
là đồ thị của hàm số
2
2
x
y
x
.
M
là một điểm trên
C
không trùng với gốc tọa độ và có hoành
độ là số nguyên sao cho khoảng cách từ
M
đến trục hoành gấp đôi khoảng cách từ
M
đến trục tung. Phương
trình nào sau đây là một phương trình tiếp tuyến của

C
tại
?
M
A.
8.y 
B.
64.y 
C.
12.y 
D.
9.y 
Câu 6.
Tính đạo hàm của hàm số
2
y,('0).
''
ax bx c
aa
ax b


A.
2
2
'2' ''
.
(' ')
aa x ab x bb a c
y
ax b

B.
2
2
'2' ''
.
(' ')
aa x ab x bb a c
y
ax b

C.
2
'2' ''
.
''
aa x ab x bb a c
y
ax b

D.
2
2
'2' ''
.
(' ')
aa x ab x bb a c
y
ax b

Câu 7.
Cho hình lăng trụ
.
A
BCABC

. Gọi
H
là trung điểm của
A
B

. Đường thẳng
B
C
song song với mặt phẳng
nào dưới đây?
A.
.
A
AH
B.
.
H
AB
C.
.
H
AC
D.
.
A
HC
Câu 8.
Cho
3, 5ab

góc giữa
a
và
b
bằng
120 .
Chọn khẳng định sai trong các khẳng định sau.
A.
29ab
. B.
7ab
. C.
2139ab
. D.
19ab
.
Câu 9.
Cho hình hộp chữ nhật
.
A
BCD A B C D

có
6cmAB
,
2cmBC BB

. Điểm
E
là trung điểm cạnh
B
C
.
Một tứ diện đều
M
NPQ
có hai đỉnh
M
và
N
nằm trên đường thẳng
E
C
, hai đỉnh
P
và
Q
nằm trên đường thẳng đi
qua điểm
B
và cắt đường thẳng
A
D
tại điểm
F
. Khoảng cách
DF
bằng bao nhiêu?
A.
3cm.
B.
6cm.
C.
1cm.
D.
2cm.
Câu 10.
Cho hình lăng trụ đều
.
A
BCABC

có tất cả các cạnh bằng
.a
Gọi
M
là trung điểm của
,AB
là góc tạo
bởi đường thẳng
M
C
và mặt phẳng
A
BC
. Khi đó
tan
bằng bao nhiêu?
A.
27
7
. B.
3
2
. C.
3
7
. D.
23
3
.
Câu 11.
Cho đường thẳng
aP
và đường thẳng
bQ
. Mệnh đề nào sau đây là đúng?
A.
// //
P
QaQ
và
// .bP
B.
a
và
b
chéo nhau.
C.

// // .
P
Qab
D.
// // .ab P Q
Trang 10/18
Câu 12. Xét chuyển động có phương trình
() sin( )
s
tA tb

(,,Ab
là các hằng số). Tìm gia tốc tức thời tại
thời điểm
t
của chuyển động.
A.
2
a( ) sin( ).tA tb

 B.
a( ) cos( ).tA tb

C.
2
a( ) cos( ).tA tb

 D.
2
a( ) sin( ).tA tb


Câu 13.
Một nhóm bạn trao đổi về kết quả khi tính
*
111 1
...
248 2
lim ,( )
n
n
n
a

đã đưa ra các nhận xét như sau:
(1) Giới hạn lớn hơn
0
nếu
1.a
(2) Giới hạn bằng
1
nếu
1.a
(3) Giới hạn bằng

nếu
01.a
Hỏi có tất cả bao nhiêu nhận xét đúng?
A.
Có hai nhận xét đúng. B. Không có nhận xét nào đúng.
C.
Chỉ có một nhận xét đúng. D. Cả ba nhận xét đều đúng.
Câu 14.
Cho
2
2
2
1 khi 1
() .
1
3 2 1 khi 1
xx
mx x
fx
x
mx m x



Tính tổng tất cả các giá trị m thỏa mãn điều kiện hàm số có giới
hạn khi
1.x
A.
217. B. 17. C.
5.
D.
0.
Câu 15.
Cho

23khi 2
1 khi 2
xx
fx
ax x


. Để
2
lim
x
f
x
tồn tại, giá trị của a phải bằng bao nhiêu?
A.
2. B. 3. C. 4. D. 1.
Câu 16.
Cho hàm số

1
fx
x
. Tính

2.y
A.
1
.
2
B.
1
.
2
C.
1
.
2
D.
1
.
2
Câu 17.
Cho hình chóp
.S ABC
có
, SA ABC ABC
vuông tại
.
B
Gọi
A
M
là đường cao của tam giác
SAB
(
M
thuộc cạnh
SB
). Khi đó,
A
M
không vuông góc với đường thẳng nào dưới đây?
A.
.
A
C
B.
.SC
C.
.
B
C
D.
.SB
Câu 18.
Cho tứ diện
A
BCD
. Gọi
,IJ
lần lượt là trung điểm của
A
B
và
CD
,
G
là trung điểm của
I
J
.
Đẳng thức nào dưới đây là đúng?
A.
GA GB GC GD JI
   
. B.
2GA GB GC GD JI

.
C.
0GA GB GC GD
   
. D.
2GA GB GC GD IJ
  
.
Câu 19.
Cho hình chóp
.SABCD
có tất cả các cạnh bên và cạnh đáy đều bằng nhau.
A
BCD
là hình vuông. Khẳng định
nào sau đây là đúng?
A.
BD SAD
. B.
BD SCD
. C.
BD SAC
. D.

SB ABCD
.
Câu 20.
Có bao nhiêu giá trị
0; 2x
sao cho tiếp tuyến với đồ thị hàm số
2cosyx x
tại các tiếp điểm có hoành
độ đó song song với đường thẳng
y2?
x
A.
2.
B.
3.
C.
1.
D.
4.
Câu 21.
Cho tứ diện
A
BCD
, các điểm
M
,
N
lần lượt là trung điểm của
A
B
,
CD
. Không thể kết luận
G
là trọng
tâm của tứ diện
A
BCD
trong trường hợp nào dưới đây?
A.
4PG PA PB PC PD
   
với
P
là điểm bất kỳ.
B.
0GM GN

.
C.
GM GN
.
D.
0GA GB GC GD
   
.
Câu 22.
Cho
cos 1x 
. Tính
246 2
1 cos cos cos ... cos ...
n
Sxxx x
A.
2
1
cos
x
. B.
2
1
sin
x
. C.
2
sin
x
. D.
2
cos
x
.
Trang 11/18 - Mã đề thi A
Câu 23. Nếu

y
f
x
và
y
g
x
đều liên tục tại
0
x
thì hàm số nào sau đây chưa chắc liên tục tại
0
?
x
A.
y.().
f
x
g
x
B.
y.
()
f
x
g
x
C.
y().
f
x
g
x
D.

y().
f
x
g
x
Câu 24.
Biết rằng
lim , lim .
xx
fx gx
 
 
Khẳng định nào sau đây là đúng?
A.
lim 0.
x
fx gx




B.

lim 1.
x
fx
gx





C.
 
11
lim lim 0.
xx
fx gx
 

D.
lim . ,
x
Lf x



với
0.L
Câu 25.
Cho hình chóp
.SABCD
có đáy
A
BCD
là hình vuông và
.SA ABCD
Mệnh đề nào dưới đây là sai?
A.
BD SAC
. B.
CD SAD
. C.
BC SAB
. D.
A
CSBD
.
Câu 26.
Trong không gian cho điểm
O
và bốn điểm
,,,ABCD
không thẳng hàng. Điều kiện cần và đủ để
,,,ABCD
tạo thành hình bình hành là gì?
A.
0OA OB OC OD
   
. B.
OA OC OB OD
   
.
C. .
11
22
OA OB OC OD
  
. D.
11
22
OA OC OB OD

.
Câu 27.
Biết rằng

lim ,lim ,
nn
ua v b
với
0.b
Khẳng định nào sau đây là đúng?
A.
lim . .
nn
uv ab
B. lim .
n
n
u
a
vb



C.
lim .
nn
uv ab
D.
lim .
nn
uv ab
Câu 28.
Tìm
m
để hàm số

2 9 khi 0
3 khi 0
xx
fx
mx

liên tục tại
0
0.x
A.
3.m
B.
2.m 
C.
0.m
D.
1.m
Câu 29.
Hàm số bậc hai nào sau đây thỏa mãn điều kiện:
(1) 5, 1 3 ?ff

A.
2
391.fx x x
B.
2
93.fx x x
C.

2
9.
f
xxx
D.

2
38.
xxx
Câu 30.
Cho hình hộp
.
A
BCDABCD

. Gọi
,IK
lần lượt là tâm của hình bình hành
A
BB A

và
B
CC B

. Khẳng
định nào sau đây là
sai?
A.
11
22
IK AC A C


  
. B. Ba vectơ
,,
B
DIKBC

  
không đồng phẳng.
C.
22
B
DIK BC
  
. D. Bốn điểm
I
,
K
,
C
,
A
đồng phẳng.
Câu 31.
Tính
3
2
3
lim .
nn
n
A.
1.
B.
.
C.
.
D. 0.
Câu 32.
Cho hàm số

3
31 .
y
xx C
Viết phương trình tiếp tuyến của đồ thị

C
tại điểm có hoành độ bằng 0.
A.
32.yx
B.
312.yx
C.
311.yx
D.
31.yx
Câu 33.
Tính
2
2
4
lim .
2
x
x
x
A.
2.
B.
2.
C.
4.
D.
4.
Trang 12/18
Câu 34. Thông qua việc tìm giới hạn của các hàm số khi
0,xx
hãy xác định xem đường cong dưới đây là đồ
thị của hàm số nào?
A.

4
2
1
.
x
kx
x
B.

2
2
1
.
x
fx
x
C.

32
2
1
.
xx
gx
x

D.

2
4
1
.
x
hx
x

Câu 35. Tìm đạo hàm của hàm số
2
1yx
.
A.
2
2
1
x
x
. B.
2
1
x
x
. C.
2
21
x
x
. D.

2
2
1
1
xx
x
.
Câu 36. Tính
4
4
33
212
lim .
3
nn n
nnn


A.
3
3
.
31
B.
1.
C.
.
D.
.
Câu 37. Cho tứ diện
ABCD
có
AB CD a
,
3
2
IJ
a
(
,IJ
lần lượt là trung điểm của
BC
và
AD
). Số đo góc
giữa hai đường thẳng
AB
và
CD
bằng bao nhiêu độ?
A.
30 .
B.
4 5 .
C.
6 0 .
D.
90 .
Câu 38. Cho hình hộp
.ABCD A B C D

. Nếu mp
()
chứa
AB
cắt hình hộp theo thiết diện là một tứ giác thì tứ
giác đó là hình gì?
A. Hình chữ nhật. B. Hình bình hành. C. Hình thoi. D. Hình vuông.
Câu 39. Tính
1
23
lim .
1
x
x
x
A.
2.
B.
.
C.
.
D.
2.
Câu 40. Cho hàm số

2
2
khi 2
.
2
5 khi 2
xx
x
fx
x
xx


Khẳng định nào sau đây là sai?
A. Hàm số liên tục trên
.
B. Hàm số có tập xác định là
.
C. Hàm số gián đoạn tại
0
0.x
D. Hàm số liên tục tại
0
2.x
II. PHẦN TỰ LUẬN (2,0 điểm)
Bài 1 (1,0 điểm).
a) Tính giới hạn:
52
5
236
lim .
nn
I
nn

b) Cho hàm số

23
1
x
yfx
x

có đồ thị

.C
Viết phương trình tiếp tuyến của đồ thị

C
song song với
đường thẳng
: 5 2019.dy x
Bài 2 (1.0 điểm). Cho hàm số:
2
1.yxx
Chứng minh rằng:

2
41 4.xyyxy


------------- HẾT -------------
(Học sinh không được sử dụng tài liệu. Cán bộ coi thi không giải thích gì thêm.)
Trang 13/18 - Mã đề thi A
SỞ GD&ĐT THỪA THIÊN HUẾ
TR
Ư
ỜNG THPT VINH LỘC
KIỂM TRA HỌC KỲ II_NĂM HỌC 2018 - 2019
M
ôn: Toán - Lớ
p
11 - Chươn
g
t
r
ình chu
ẩ
n
ĐỀ CHÍNH THỨC Thời gian: 90 phút (Không kể thời gian phát đề)
(
Đ
ề
gồ
m 04 tran
g)
Mã đề thi
D
Họ và tên:………………………………….Lớ
p
:…………….............……..……
I. PHẦN TRẮC NGHIỆM KHÁCH QUAN (8,0 điểm)
Câu 1.
Tìm đạo hàm của hàm số

ysin, .xx
A.
ycos.
x
B.
ycos.
x

C.
ytan.
x
D.
2
1
y.
cos
x
Câu 2.
Cho hình hộp
111 1
.
A
BCD A B C D
. Tìm giá trị của k để đẳng thức vectơ:
11 1 1
A
BBC DD kAC
   
là đúng.
A.
1k
. B.
0k
. C.
2k
. D.
4k
.
Câu 3.
Cho tứ diện
A
BCD
, các điểm
M
,
N
lần lượt là trung điểm của
A
B
,
CD
. Không thể kết luận
G
là trọng tâm
của tứ diện
A
BCD
trong trường hợp nào dưới đây?
A.
0GM GN

.
B.
GM GN
.
C.
0GA GB GC GD
   
.
D.
4PG PA PB PC PD
   
với
P
là điểm bất kỳ.
Câu 4.
Trong không gian cho điểm
O
và bốn điểm
,,,ABCD
không thẳng hàng. Điều kiện cần và đủ để
,,,ABCD
tạo thành hình bình hành là gì?
A.
11
22
OA OC OB OD

. B.
0OA OB OC OD
   
.
C.
OA OC OB OD
   
. D. .
11
22
OA OB OC OD

.
Câu 5.
Cho hình chóp
.S ABC
có
, SA ABC ABC
vuông tại
.
B
Gọi
A
M
là đường cao của tam giác
SAB
(
M
thuộc cạnh
SB
). Khi đó,
A
M
không vuông góc với đường thẳng nào dưới đây?
A.
.SC
B.
.
B
C
C.
.
A
C
D.
.SB
Câu 6.
Cho hình chóp
.SABCD
có đáy
A
BCD
là hình vuông và
.SA ABCD
Mệnh đề nào dưới đây là sai?
A.

CD SAD
. B.

BC SAB
. C.

A
CSBD
. D.

BD SAC
.
Câu 7.
Cho
3, 5ab

góc giữa
a
và
b
bằng
120 .
Chọn khẳng định sai trong các khẳng định sau.
A.
2 139ab
. B.
19ab
. C.
29ab
. D.
7ab
.
Câu 8.
Cho hình hộp
.
A
BCD A B C D

. Nếu mp
()
chứa
A
B
cắt hình hộp theo thiết diện là một tứ giác thì tứ
giác đó là hình gì?
A.
Hình thoi. B. Hình vuông. C. Hình chữ nhật. D. Hình bình hành.
Câu 9.
Cho hàm số
3
31 .
y
xx C
Viết phương trình tiếp tuyến của đồ thị

C
tại điểm có hoành độ bằng 0.
A.
3 11.yx
B.
31.yx
C.
32.yx
D.
3 12.yx
Câu 10.
Cho
2
2
2
1 khi 1
() .
1
3 2 1 khi 1
xx
mx x
fx
x
mx m x



Tính tổng tất cả các giá trị
m
thỏa mãn điều kiện hàm số có giới
hạn khi
1.x
A.
17.
B.
5.
C.
0.
D.
217.
Câu 11.
Tìm
m
để hàm số

2 9 khi 0
3 khi 0
xx
fx
mx

liên tục tại
0
0.x
A.
2.m 
B.
0.m
C.
1.m
D.
3.m
Câu 12.
Cho đường thẳng
aP
và đường thẳng
bQ
. Mệnh đề nào sau đây là đúng?
A.
// //
P
QaQ
và
// .bP
B.
a
và
b
chéo nhau.
Trang 14/18
C.

// // .
P
Qab
D.
// // .ab P Q
Câu 13.
Cho

23khi 2
1 khi 2
xx
fx
ax x


. Để
2
lim
x
f
x
tồn tại, giá trị của a phải bằng bao nhiêu?
A.
1. B. 2. C. 3. D. 4.
Câu 14.
Hàm số bậc hai nào sau đây thỏa mãn điều kiện:
(1) 5, 1 3 ?ff

A.
2
391.fx x x
B.
2
93.fx x x
C.
2
9.
f
xxx
D.

2
38.
xxx
Câu 15.
Nếu

y
f
x
và
y
g
x
đều liên tục tại
0
x
thì hàm số nào sau đây chưa chắc liên tục tại
0
?
x
A.

y().
f
x
g
x
B.
y.().
f
x
g
x
C.
y.
()
f
x
g
x
D.
y().
f
x
g
x
Câu 16.
Cho hình lăng trụ đều
.
A
BCABC

có tất cả các cạnh bằng .a Gọi
M
là trung điểm của
,AB
là góc tạo
bởi đường thẳng
M
C
và mặt phẳng
A
BC
. Khi đó
tan
bằng bao nhiêu?
A.
23
3
. B.
3
2
. C.
3
7
. D.
27
7
.
Câu 17.
Biết rằng
lim , lim .
xx
fx gx
 
 
Khẳng định nào sau đây là đúng?
A.
lim 0.
x
fx gx



B.

lim 1.
x
fx
gx





C.
 
11
lim lim 0.
xx
fx gx
 

D.
lim . ,
x
Lf x




với
0.L
Câu 18.
Tính đạo hàm của hàm số
2
y,('0).
''
ax bx c
aa
ax b


A.
2
2
'2' ''
.
(' ')
aa x ab x bb a c
y
ax b

B.
2
2
'2' ''
.
(' ')
aa x ab x bb a c
y
ax b

C.
2
'2' ''
.
''
aa x ab x bb a c
y
ax b

D.
2
2
'2' ''
.
(' ')
aa x ab x bb a c
y
ax b

Câu 19.
Tính
4
4
3
3
212
lim .
3
nn n
nnn


A.
1.
B.
.
C.
.
D.
3
3
.
31
Câu 20.
Tính
1
lim .
1n
A.
3. B. 1. C. 2. D. 0.
Câu 21.
Một nhóm bạn trao đổi về kết quả khi tính
*
111 1
...
248 2
lim ,( )
n
n
n
a

đã đưa ra các nhận xét như sau:
(1) Giới hạn lớn hơn
0
nếu
1.a
(2) Giới hạn bằng
1
nếu
1.a
(3) Giới hạn bằng

nếu
01.a
Hỏi có tất cả bao nhiêu nhận xét đúng?
A.
Chỉ có một nhận xét đúng. B. Có hai nhận xét đúng.
C.
Không có nhận xét nào đúng. D. Cả ba nhận xét đều đúng.
Câu 22.
Cho hàm số

1
fx
x
. Tính

2.y
Trang 15/18 - Mã đề thi A
A.
1
.
2
B.
1
.
2
C.
1
.
2
D.
1
.
2
Câu 23. Cho hình lăng trụ tam giác
.ABCABC

. Đặt
,,,AA a AB b AC c BC d

 
. Trong các đẳng thức vectơ
đã cho dưới đây, đẳng thức nào đúng?
A.
0bcd

. B.
abc d

. C.
abc

. D.
0abcd

.
Câu 24. Xét chuyển động có phương trình
() sin( )st A t b

(,,Ab
là các hằng số). Tìm gia tốc tức thời tại
thời điểm
t
của chuyển động.
A.
2
a( ) sin( ).tA tb


B.
a( ) cos( ).tA tb

C.
2
a( ) cos( ).tA tb


D.
2
a( ) sin( ).tA tb


Câu 25. Cho hình hộp
.ABCDABCD

. Gọi
,IK
lần lượt là tâm của hình bình hành
ABB A

và
BCC B

. Khẳng
định nào sau đây là sai?
A.
22BD IK BC
  
. B. Bốn điểm
I
,
K
,
C
,
A
đồng phẳng.
C.
11
22
IK AC A C


  
. D. Ba vectơ
,,BD IK B C

  
không đồng phẳng.
Câu 26. Tìm đạo hàm của hàm số
2
1yx
.
A.
2
2
1
x
x
. B.
2
1
x
x
. C.
2
21
x
x
. D.

2
2
1
1
xx
x
.
Câu 27. Cho tứ diện
ABCD
. Gọi
,IJ
lần lượt là trung điểm của
AB
và
CD
,
G
là trung điểm của
IJ
.
Đẳng thức nào dưới đây là đúng?
A.
0GA GB GC GD
 
. B.
2GA GB GC GD IJ
 
.
C.
GA GB GC GD JI
    
. D.
2GA GB GC GD JI
   
.
Câu 28. Gọi

C
là đồ thị của hàm số
2
2
x
y
x
.
M
là một điểm trên

C
không trùng với gốc tọa độ và có hoành
độ là số nguyên sao cho khoảng cách từ
M
đến trục hoành gấp đôi khoảng cách từ
M
đến trục tung. Phương
trình nào sau đây là một phương trình tiếp tuyến của

C
tại
?M
A.
12.y 
B.
8.y 
C.
9.y 
D.
64.y 
Câu 29. Thông qua việc tìm giới hạn của các hàm số khi
0,xx
hãy xác định xem đường cong dưới đây là đồ
thị của hàm số nào?
A.

2
2
1
.
x
fx
x
B.

32
2
1
.
xx
gx
x

C.

2
4
1
.
x
hx
x

D.

4
2
1
.
x
kx
x
Câu 30. Cho hàm số

2
2
khi 2
.
2
5 khi 2
xx
x
fx
x
xx


Khẳng định nào sau đây là sai?
A. Hàm số liên tục tại
0
2.x
B. Hàm số liên tục trên
.
C. Hàm số có tập xác định là
.
D. Hàm số gián đoạn tại
0
0.x
Câu 31. Có bao nhiêu giá trị

0; 2x
sao cho tiếp tuyến với đồ thị hàm số
2cosyx x
tại các tiếp điểm có hoành
độ đó song song với đường thẳng
y2?x
A.
2.
B.
3.
C.
1.
D.
4.
Trang 16/18
Câu 32. Tính
3
2
3
lim .
nn
n
A.
0. B.
1.
C.
.
D.
.
Câu 33.
Tính
2
2
4
lim .
2
x
x
x
A.
2.
B.
2.
C.
4.
D.
4.
Câu 34.
Cho hình lăng trụ
.
A
BCABC

. Gọi
H
là trung điểm của
A
B

. Đường thẳng
B
C
song song với mặt phẳng
nào dưới đây?
A.
.
A
AH
B.
.
H
AB
C.
.
H
AC
D.
.
A
HC
Câu 35.
Tính
1
23
lim .
1
x
x
x
A.
.
B.
.
C.
2.
D.
2.
Câu 36.
Cho hình hộp chữ nhật
.
A
BCD A B C D

có
6cmAB
,
2cmBC BB

. Điểm
E
là trung điểm cạnh
B
C
. Một tứ diện đều
M
NPQ
có hai đỉnh
M
và
N
nằm trên đường thẳng
E
C
, hai đỉnh
P
và
Q
nằm trên đường thẳng
đi qua điểm
B
và cắt đường thẳng
A
D
tại điểm
F
. Khoảng cách
DF
bằng bao nhiêu?
A.
3cm.
B.
6cm.
C.
1cm.
D.
2cm.
Câu 37.
Cho tứ diện
A
BCD
có
A
BCDa
,
3
2
IJ
a
(
,IJ
lần lượt là trung điểm của
B
C
và
A
D
). Số đo góc
giữa hai đường thẳng
A
B
và
CD
bằng bao nhiêu độ?
A.
30 .
B.
4 5 .
C.
6 0 .
D.
90 .
Câu 38.
Cho
cos 1x 
. Tính
246 2
1 cos cos cos ... cos ...
n
Sxxx x
A.
2
1
sin
x
. B.
2
cos
x
. C.
2
1
cos
x
. D.
2
sin
x
.
Câu 39.
Cho hình chóp
.SABCD
có tất cả các cạnh bên và cạnh đáy đều bằng nhau.
A
BCD
là hình vuông. Khẳng định
nào sau đây là đúng?
A.
BD SCD
. B.
BD SAC
. C.

SB ABCD
. D.
BD SAD
.
Câu 40.
Biết rằng

lim ,lim ,
nn
ua v b
với
0.b
Khẳng định nào sau đây là đúng?
A.
lim .
n
n
u
a
vb



B.
lim .
nn
uv ab
C.
lim .
nn
uv ab
D.
lim . .
nn
uv ab
II. PHẦN TỰ LUẬN (2,0 điểm)
Bài 1 (1,0 điểm).
a) Tính giới hạn:
52
5
236
lim .
nn
I
nn

b)
Cho hàm số

23
1
x
yfx
x

có đồ thị

.C
Viết phương trình tiếp tuyến của đồ thị
C
song song với
đường thẳng
: 5 2019.dy x
Bài 2 (1.0 điểm). Cho hàm số:
2
1.yxx
Chứng minh rằng:
2
41 4.
x
yyxy


------------- HẾT -------------
(Học sinh không được sử dụng tài liệu. Cán bộ coi thi không giải thích gì thêm.)
Trang 17/18 - Mã đề thi A
ĐÁP ÁN ĐỀ THI HỌC KÌ II – KHỐI 11 – NĂM HỌC 2018 - 2019
------------------------
I. PHẦN TRẮC NGHIỆM:Mã đề [ A ]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
B A D C D D B A D B C C D D B A D C C C
21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40
C A D B D A C A A A B A A C B B D B C B
Mã đề [ B ]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
D C D B B D A A C B C B C B A B D B A B
21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40
B D C D C A A B C C D A D A C A C D D A
Mã đề [ C ]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
B B D D A D D A D D A A A C A C A C C A
21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40
C B B C D B D A A B B D C C B A C B B C
Mã đề [ D ]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
A A B C C C C D B B D A B A C A C D D D
21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40
B B A D D B A B B D A C C D A D C A B C
II. PHẦN TỰ LUẬN:
Bài Ý Lời
g
iải và hướn
g
dẫn chấm Điểm
1
a)
Tính giới hạn:
52
5
236
lim .
nn
I
nn

0,5 điểm
5
52
35
35
5
5
4
4
36
36
2
2
236
lim lim lim 2.
1
1
1
1
n
nn
nn
nn
I
nn
n
n
n










0,5
b)
Cho hàm số

23
1
x
yfx
x

có đồ thị

.C
Viết phương trình tiếp tuyến của đồ thị

C
song song với đường thẳng
: 5 2019.dy x
0,5 điểm
Gọi
00
;
M
x
y
là tiếp điểm của tiếp tuyến với đồ thị
.C
Hệ số góc của tiếp tuyến tại
:
M



00
2
0
5
,1.
1
kfx x
x

0,25
Ta có:

2
00
0
00
03
511
27
xy
kx
xy



Vậy có hai tiếp tuyến với phương trình lần lượt là:
12
:53; :517.yx yx
0,25
2
Cho hàm số:
2
1.yxx
Chứng minh rằng:
2
41 4.
x
yyxy


1,0 điểm
Ta có:
2
2
222
2
1
111
.1 .
22
1121
21
xx
xxxy
y
yy
xxx
x
x








0,5

22
2
.2 1 . 2 1
41
yx y x
y
x


0,25
Trang 18/18

22
22
24
41.2.1. 4.
121
xxy
x
yyx y y yxy
x
x



(đpcm)
0,25
| 1/18

Tài liệu khác của Toán 11

Preview text:


SỞ GD&ĐT THỪA THIÊN HUẾ
KIỂM TRA HỌC KỲ II_NĂM HỌC 2018 - 2019
TRƯỜNG THPT VINH LỘC
Môn: Toán - Lớp 11 - Chương trình chuẩn ĐỀ CHÍNH THỨC
Thời gian: 90 phút (Không kể thời gian phát đề) (Đề gồm 04 trang) Mã đề thi
Họ và tên:………………………………….Lớp:…………….............……..…… A
I. PHẦN TRẮC NGHIỆM KHÁCH QUAN (8,0 điểm)
Câu 1. Cho hình chóp S.ABCD có đáy ABCD là hình vuông và SA   ABCD. Mệnh đề nào dưới đây là sai?
A. BC  SAB .
B. AC  SBD .
C. BD  SAC .
D. CD  SAD .
Câu 2. Xét chuyển động có phương trình s(t)  Asin(t b) ( ,
A ,b là các hằng số). Tìm gia tốc tức thời tại
thời điểm t của chuyển động. A. 2
a(t)  A sin(t b).
B. a(t)  Acos(t b). C. 2
a(t)  A cos(t b). D. 2
a(t)  A sin(t b).  x   x
Câu 3. Cho f x 2 3 khi 2  
. Để lim f x tồn tại, giá trị của a phải bằng bao nhiêu? ax 1 khi x  2 x 2  A. 1. B. 3. C. 4. D. 2. 1 1 1 1   ... n
Câu 4. Một nhóm bạn trao đổi về kết quả khi tính 2 4 8 2 * lim
, (n   ) đã đưa ra các nhận xét như sau: n a
(1) Giới hạn lớn hơn 0 nếu a 1.
(2) Giới hạn bằng 1 nếu a 1.
(3) Giới hạn bằng  nếu 0  a 1.
Hỏi có tất cả bao nhiêu nhận xét đúng?
A. Không có nhận xét nào đúng.
B. Chỉ có một nhận xét đúng.
C. Có hai nhận xét đúng.
D. Cả ba nhận xét đều đúng.
Câu 5. Hàm số bậc hai nào sau đây thỏa mãn điều kiện: f (1)  5, f   1  3?
A. f x 2
 x  9x  3.
B. f x 2  x  9 . x
C. f x 2  3  x  8 . x
D. f x 2  3
x  9x 1.
   
Câu 6. Cho hình hộp ABC .
D A B C D . Tìm giá trị của k để đẳng thức vectơ: AB B C DD k AC là đúng. 1 1 1 1 1 1 1 1
A. k  0 .
B. k  2 .
C. k  4 .
D. k  1.
Câu 7. Trong không gian cho điểm O và bốn điểm ,
A B,C, D không thẳng hàng. Điều kiện cần và đủ để ,
A B,C, D
tạo thành hình bình hành là gì?
        
A. OA OB OC OD  0 .
B. OA OC OB OD .
 1   1 
 1   1 
C. .OA OB OC OD .
D. OA OC OB OD . 2 2 2 2
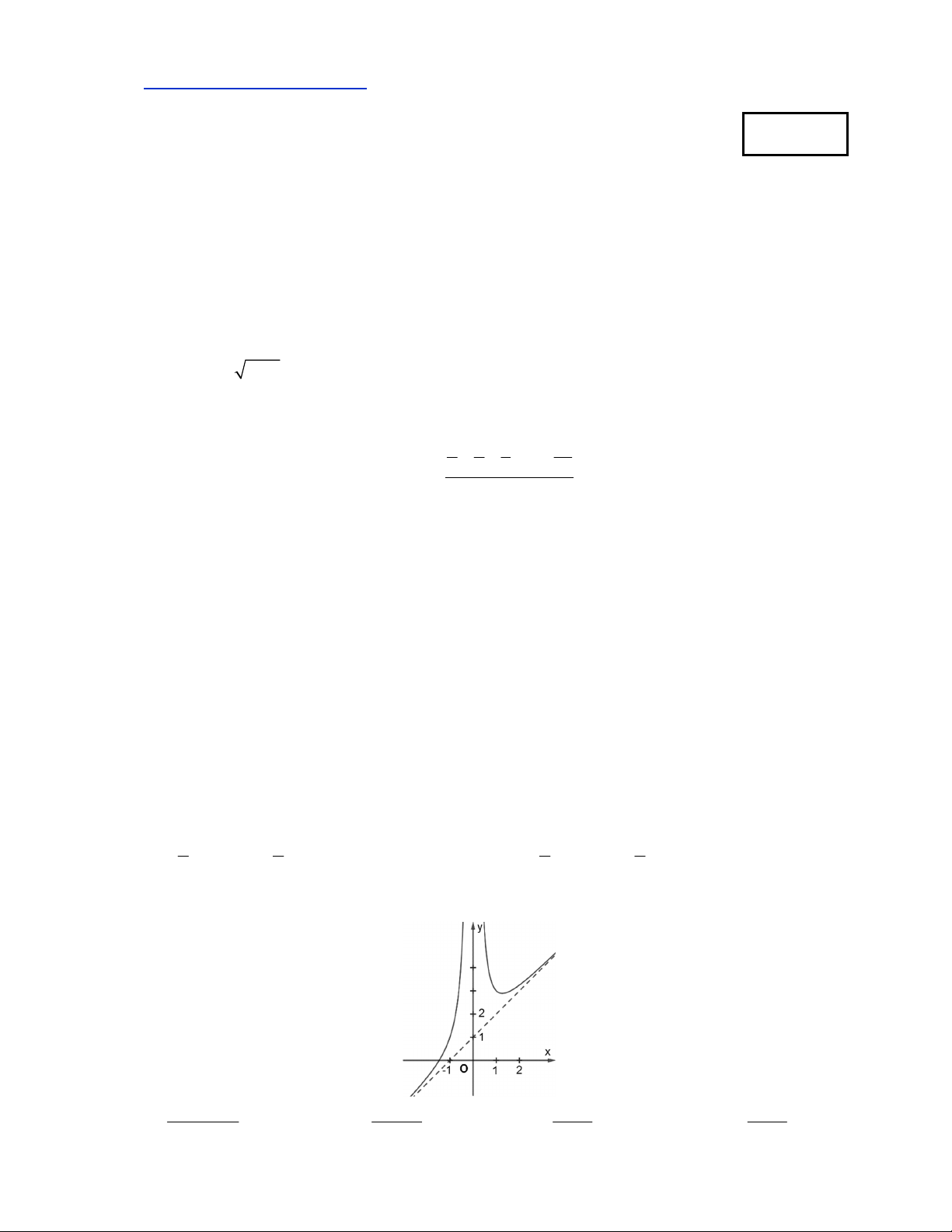
Câu 8. Thông qua việc tìm giới hạn của các hàm số khi x  0, x   hãy xác định xem đường cong dưới đây là đồ thị của hàm số nào? 3 2 x x 1 2 x 1 4 x 1 2 1 x
A. g x  .
B. h x  .
C. k x  .
D. f x  . 2 x 4 x 2 x 2 x Trang 1/18 - Mã đề thi A
Câu 9. Có bao nhiêu giá trị x 0;2  sao cho tiếp tuyến với đồ thị hàm số y x  2cos x tại các tiếp điểm có hoành
độ đó song song với đường thẳng y  2x ? A. 4. B. 3. C. 1. D. 2. a 3
Câu 10. Cho tứ diện ABCD có AB CD a , IJ
( I , J lần lượt là trung điểm của BC và AD ). Số đo góc 2
giữa hai đường thẳng AB và CD bằng bao nhiêu độ? A. 45 .  B. 60 .  C. 90 .  D. 30 .  2 x  4 Câu 11. Tính lim . x2 x  2 A. 2. B. 2.  C. 4. D. 4. 
Câu 12. Tìm đạo hàm của hàm số 2
y x 1. x  2 x   1 2x x x A.  . B. . C. . D. . 2 x 1 2 x 1 2 x 1 2 2 x 1 3 3n n Câu 13. Tính lim . 2 n A. 1. B. .  C. 0. D. .
Câu 14. Cho hàm số   1
f x  . Tính y 2. x 1 1 1 1 A. . B.  . C. . D.  . 2 2 2 2 
      
Câu 15. Cho hình lăng trụ tam giác ABC.A BC
 . Đặt AA  a, AB b, AC c, BC d . Trong các đẳng thức vectơ
đã cho dưới đây, đẳng thức nào đúng?                
A. a b c d  0 .
B. b c d  0 .
C. a b c d .
D. a b c .
Câu 16. Cho tứ diện ABCD , các điểm M , N lần lượt là trung điểm của AB , CD . Không thể kết luận G là trọng
tâm của tứ diện ABCD trong trường hợp nào dưới đây?
A. GM GN .
    
B. GA GB GC GD  0 .
    
C. 4PG PA PB PC PD với P là điểm bất kỳ.
  
D. GM GN  0 .
Câu 17. Cho hình hộp ABC . D A BCD
  . Gọi I, K lần lượt là tâm của hình bình hành ABB A   và BCC B  . Khẳng
định nào sau đây là sai?   
A. BD  2IK  2BC .
B. Bốn điểm I , K , C , A đồng phẳng.  1  1 
  
C. IK AC AC.
D. Ba vectơ BD, IK, B C
  không đồng phẳng. 2 2 2
x x  2  khi x  2
Câu 18. Cho hàm số f x   x  2
. Khẳng định nào sau đây là sai?
5 x khi x  2
A. Hàm số liên tục trên . 
B. Hàm số có tập xác định là . 
C. Hàm số gián đoạn tại x  0.
D. Hàm số liên tục tại x  2. 0 0
Câu 19. Cho tứ diện ABCD . Gọi I , J lần lượt là trung điểm của AB và CD , G là trung điểm của IJ .
Đẳng thức nào dưới đây là đúng?
    
    
A. GA GB GC GD JI .
B. GA GB GC GD  2JI .
    
    
C. GA GB GC GD  0 .
D. GA GB GC GD  2IJ . Câu 20. Cho hàm số 3
y x  3x 1 C. Viết phương trình tiếp tuyến của đồ thịC tại điểm có hoành độ bằng 0.
A. y  3x 12.
B. y  3x 11.
C. y  3x 1.
D. y  3x  2. Trang 2/18 4 4
n  2n 1  2n Câu 21. Tính lim . 3 3
3n n n 3 A. .  B. .  C. . D. 1. 3 3 1 2 x
Câu 22. Gọi C là đồ thị của hàm số y
. M là một điểm trên C không trùng với gốc tọa độ và có hoành 2  x
độ là số nguyên sao cho khoảng cách từ M đến trục hoành gấp đôi khoảng cách từ M đến trục tung. Phương
trình nào sau đây là một phương trình tiếp tuyến của C tại M ?
A. y  8.
B. y  64.
C. y  12.
D. y  9.
Câu 23. Cho hình hộp chữ nhật ABC . D A BCD
  có AB  6cm , BC BB  2cm . Điểm E là trung điểm cạnh BC
. Một tứ diện đều MNPQ có hai đỉnh M và N nằm trên đường thẳng EC , hai đỉnh P và Q nằm trên đường thẳng
đi qua điểm B và cắt đường thẳng AD tại điểm F . Khoảng cách DF bằng bao nhiêu? A. 3cm. B. 6 cm. C. 1cm. D. 2 cm.
Câu 24. Cho cos x  1  . Tính 2 4 6 2  1 cos  cos  cos  ... cos n S x x x x  ... 1 1 A. . B. . C. 2 sin x . D. 2 cos x . 2 cos x 2 sin x
Câu 25. Nếu y  f x và y  g x đều liên tục tại x thì hàm số nào sau đây chưa chắc liên tục tại x ? 0 0 f x
A. y  f x  g(x).
B. y  f x  g(x).
C. y  f x.g(x). D. y  . g(x) 2
x x  2 2 
m x 1 khi x  1
Câu 26. Cho f (x)   1 x
. Tính tổng tất cả các giá trị m thỏa mãn điều kiện hàm số có giới 3
 mx 2m1 khi x 1 hạn khi x 1. A. 5. B. 0. C. 2 17. D. 17.
Câu 27. Biết rằng limu a,limv   ,
b với b  0. Khẳng định nào sau đây là đúng? n nu a A. lim n    .
B. limu v a b n n  . v bn
C. limu v   a  . b D. lim u
 .v  ab n n  . n nx x
Câu 28. Tìm m để hàm số f x 2 9 khi 0  
liên tục tại x  0. 3
m khi x  0 0
A. m  3. B. m  2. 
C. m  0.
D. m 1.
Câu 29. Cho đường thẳng a  P và đường thẳng b  Q . Mệnh đề nào sau đây là đúng?
A. P // Q  a // Q và b// P.
B. a và b chéo nhau.
C. P // Q  a // . b
D. a // b  P // Q.
Câu 30. Cho hình chóp S.ABCD có tất cả các cạnh bên và cạnh đáy đều bằng nhau. ABCD là hình vuông. Khẳng định nào sau đây là đúng?
A. BD  SAC .
B. SB   ABCD .
C. BD  SAD .
D. BD  SCD . 1 Câu 31. Tính lim . n 1 A. 3. B. 0. C. 1. D. 2. 2x  3 Câu 32. Tính lim . x 1  x 1 A. .  B. .  C. 2.  D. 2.
Câu 33. Tìm đạo hàm của hàm số y  sin ,
x x. Trang 3/18 - Mã đề thi A 1 A. y  cos . x B. y   cos . x C. y  tan . x D. y  . 2 cos x    
Câu 34. Cho a  3, b  5 góc giữa a và b bằng 120 .
 Chọn khẳng định sai trong các khẳng định sau.        
A. a  2b  139 .
B. a b  19 .
C. a  2b  9 .
D. a b  7 .
Câu 35. Cho hình hộp ABC . D A BCD
  . Nếu mp ( ) chứa AB cắt hình hộp theo thiết diện là một tứ giác thì
tứ giác đó là hình gì?
A. Hình chữ nhật.
B. Hình bình hành. C. Hình thoi.
D. Hình vuông. 2
ax bx c
Câu 36. Tính đạo hàm của hàm số y 
, (aa '  0).
a ' x b ' 2
aa ' x  2ab ' x bb ' a 'c 2
aa ' x  2ab ' x bb ' a 'c A. y  . B. y  .
a ' x b ' 2
(a ' x b ') 2
aa ' x  2ab ' x bb ' a 'c 2
aa ' x  2ab ' x bb ' a 'c C. y  . D. y  . 2
(a ' x b ') 2
(a ' x b ')
Câu 37. Cho hình lăng trụ A . BC A BC
 . Gọi H là trung điểm của AB . Đường thẳng B C
 song song với mặt phẳng nào dưới đây? A. AA H  .
B. HAB. C. HA C  .
D. AHC.
Câu 38. Cho hình lăng trụ đều A . BC A BC
  có tất cả các cạnh bằng .
a Gọi M là trung điểm của AB,  là góc tạo
bởi đường thẳng MC và mặt phẳng  ABC . Khi đó tan  bằng bao nhiêu? 3 2 3 2 7 3 A. . B. . C. . D. . 7 3 7 2
Câu 39. Biết rằng lim f x   ,
 lim g x   .
 Khẳng định nào sau đây là đúng? x x  f x A. lim  f
  x  g x  0.  B. lim    1  . x x g   x  1 1 C. lim   D. lim  . L f  x   ,   với L  0.    lim    0. x x f x g x x
Câu 40. Cho hình chóp S.ABC có SA   ABC, ABC  vuông tại .
B Gọi AM là đường cao của tam giác SAB (
M thuộc cạnh SB ). Khi đó, AM không vuông góc với đường thẳng nào dưới đây? A. B . C B. AC. C. . SB D. SC.
II. PHẦN TỰ LUẬN (2,0 điểm)
Bài 1 (1,0 điểm). 5 2  
a) Tính giới hạn: 2n 3n 6 I  lim . 5 n n x
b) Cho hàm số y f x 2 3 
có đồ thị C. Viết phương trình tiếp tuyến của đồ thị C song song với x 1
đường thẳng d : y  5x  2019.
Bài 2 (1.0 điểm). Cho hàm số: 2
y x x 1. Chứng minh rằng:  2
4 1 x y  y  4 .xy
------------- HẾT -------------
(Học sinh không được sử dụng tài liệu. Cán bộ coi thi không giải thích gì thêm.) Trang 4/18
SỞ GD&ĐT THỪA THIÊN HUẾ
KIỂM TRA HỌC KỲ II_NĂM HỌC 2018 - 2019
TRƯỜNG THPT VINH LỘC
Môn: Toán - Lớp 11 - Chương trình chuẩn ĐỀ CHÍNH THỨC
Thời gian: 90 phút (Không kể thời gian phát đề) (Đề gồm 04 trang) Mã đề thi
Họ và tên:………………………………….Lớp:…………….............……..…… B
I. PHẦN TRẮC NGHIỆM KHÁCH QUAN (8,0 điểm)
Câu 1. Cho hình chóp S.ABCD có tất cả các cạnh bên và cạnh đáy đều bằng nhau. ABCD là hình vuông. Khẳng định nào sau đây là đúng?
A. SB   ABCD .
B. BD  SAD .
C. BD  SCD .
D. BD  SAC .
Câu 2. Cho tứ diện ABCD , các điểm M , N lần lượt là trung điểm của AB , CD . Không thể kết luận G là trọng tâm
của tứ diện ABCD trong trường hợp nào dưới đây?
    
A. 4PG PA PB PC PD với P là điểm bất kỳ.
  
B. GM GN  0 .
C. GM GN .
    
D. GA GB GC GD  0 .
Câu 3. Biết rằng lim f x   ,
 lim g x   .
 Khẳng định nào sau đây là đúng? x x A. lim  . L f  x   ,   với L  0. B. lim  f
  x  g x  0.  x x  f x 1 1 C. lim     D. lim  lim  0.  g   x 1. xx   x f x
 g x 1 1 1 1   ... n
Câu 4. Một nhóm bạn trao đổi về kết quả khi tính 2 4 8 2 * lim
,(n   ) đã đưa ra các nhận xét như sau: n a
(1) Giới hạn lớn hơn 0 nếu a 1.
(2) Giới hạn bằng 1 nếu a 1.
(3) Giới hạn bằng  nếu 0  a 1.
Hỏi có tất cả bao nhiêu nhận xét đúng?
A. Chỉ có một nhận xét đúng.
B. Có hai nhận xét đúng.
C. Không có nhận xét nào đúng.
D. Cả ba nhận xét đều đúng. x x
Câu 5. Tìm m để hàm số f x 2 9 khi 0  
liên tục tại x  0. 3
m khi x  0 0
A. m 1.
B. m  3. C. m  2. 
D. m  0. 2 x  4 Câu 6. Tính lim . x2 x  2 A. 2.  B. 4.  C. 2. D. 4.
Câu 7. Cho hình hộp ABC . D A BCD
  . Gọi I, K lần lượt là tâm của hình bình hành ABB A   và BCC B  . Khẳng định
nào sau đây là sai?
     
A. Ba vectơ BD, IK, B C
  không đồng phẳng.
B. BD  2IK  2BC .  1  1 
C. Bốn điểm I , K , C , A đồng phẳng.
D. IK AC AC. 2 2
Câu 8. Cho cos x  1  . Tính 2 4 6 2  1 cos  cos  cos  ... cos n S x x x x  ... 1 1 A. . B. 2 cos x . C. . D. 2 sin x . 2 sin x 2 cos x
Câu 9. Trong không gian cho điểm O và bốn điểm ,
A B,C, D không thẳng hàng. Điều kiện cần và đủ để ,
A B,C, D
tạo thành hình bình hành là gì?
 1   1 
    
A. OA OC OB OD .
B. OA OB OC OD  0 . 2 2 Trang 5/18 - Mã đề thi A    
 1   1 
C. OA OC OB OD .
D. .OA OB OC OD . 2 2
Câu 10. Cho hình chóp S.ABC có SA   ABC, ABC  vuông tại .
B Gọi AM là đường cao của tam giác SAB (
M thuộc cạnh SB ). Khi đó, AM không vuông góc với đường thẳng nào dưới đây? A. B . C B. AC. C. . SB D. SC.    
Câu 11. Cho a  3, b  5 góc giữa a và b bằng 120 .
 Chọn khẳng định sai trong các khẳng định sau.        
A. a  2b  139 .
B. a b  19 .
C. a  2b  9 .
D. a b  7 . 2
ax bx c
Câu 12. Tính đạo hàm của hàm số y  ,(aa '  0).
a ' x b ' 2
aa ' x  2ab ' x bb ' a 'c 2
aa ' x  2ab ' x bb ' a 'c A. y  . B. y  .
a ' x b ' 2
(a ' x b ') 2
aa ' x  2ab ' x bb ' a 'c 2
aa ' x  2ab ' x bb ' a 'c C. y  . D. y  . 2
(a ' x b ') 2
(a ' x b ') 4 4
n  2n 1  2n Câu 13. Tính lim . 3 3
3n n n 3 A. .  B. .  C. . D. 1. 3 3 1 2x  3 Câu 14. Tính lim . x 1  x 1 A. 2. B. .  C. . D. 2. 
Câu 15. Cho hình lăng trụ đều AB . C A BC
  có tất cả các cạnh bằng .
a Gọi M là trung điểm của AB,  là góc tạo
bởi đường thẳng MC và mặt phẳng  ABC . Khi đó tan  bằng bao nhiêu? 2 3 3 3 2 7 A. . B. . C. . D. . 3 2 7 7
Câu 16. Cho hình chóp S.ABCD có đáy ABCD là hình vuông và SA   ABCD. Mệnh đề nào dưới đây là sai?
A. BC  SAB .
B. AC  SBD .
C. BD  SAC .
D. CD  SAD .
Câu 17. Hàm số bậc hai nào sau đây thỏa mãn điều kiện: f (1)  5, f   1  3?
A. f x 2
 x  9x 3.
B. f x 2  x  9 . x
C. f x 2  3  x 8 . x
D. f x 2  3
x  9x 1.
Câu 18. Tìm đạo hàm của hàm số 2
y x 1. 2x x x x  2 x   1 A. . B. . C. . D.  . 2 x 1 2 x 1 2 2 x 1 2 x 1 Câu 19. Cho hàm số 3
y x  3x 1 C. Viết phương trình tiếp tuyến của đồ thịC tại điểm có hoành độ bằng 0.
A. y  3x 1.
B. y  3x  2.
C. y  3x 12.
D. y  3x 11.
Câu 20. Xét chuyển động có phương trình s(t)  Asin(t b) ( ,
A ,b là các hằng số). Tìm gia tốc tức thời tại
thời điểm t của chuyển động. A. 2
a(t)  A sin(t b). B. 2
a(t)  A sin(t b).
C. a(t)  Acos(t b). D. 2
a(t)  A cos(t b). 2 x
Câu 21. Gọi C là đồ thị của hàm số y
. M là một điểm trên C  không trùng với gốc tọa độ và có hoành 2  x
độ là số nguyên sao cho khoảng cách từ M đến trục hoành gấp đôi khoảng cách từ M đến trục tung. Phương
trình nào sau đây là một phương trình tiếp tuyến của C  tại M ?
A. y  12.
B. y  8.
C. y  9.
D. y  64. Trang 6/18
Câu 22. Cho tứ diện ABCD . Gọi I , J lần lượt là trung điểm của AB và CD , G là trung điểm của IJ .
Đẳng thức nào dưới đây là đúng?
    
    
A. GA GB GC GD  2JI .
B. GA GB GC GD  2IJ .
    
    
C. GA GB GC GD JI .
D. GA GB GC GD  0 .
Câu 23. Cho đường thẳng a  P và đường thẳng b  Q . Mệnh đề nào sau đây là đúng?
A. P // Q  a // . b
B. a // b  P // Q.
C. P // Q  a // Q và b// P.
D. a và b chéo nhau.
Câu 24. Cho hàm số   1
f x  . Tính y 2. x 1 1 1 1 A. . B.  . C. . D.  . 2 2 2 2
Câu 25. Tìm đạo hàm của hàm số y  sin ,
x x. 1 A. y  tan . x B. y  . C. y  cos . x D. y   cos . x 2 cos x
Câu 26. Biết rằng limu a,limv   ,
b với b  0. Khẳng định nào sau đây là đúng? n n
A. limu v   a  . b B. lim u
 .v  ab n n  . n nu a C. lim n    .
D. limu v a b n n  . v bn a 3
Câu 27. Cho tứ diện ABCD có AB CD a , IJ
( I , J lần lượt là trung điểm của BC và AD ). Số đo góc 2
giữa hai đường thẳng AB và CD bằng bao nhiêu độ? A. 60 .  B. 90 .  C. 30 .  D. 45 . 
Câu 28. Cho hình hộp chữ nhật ABC . D A BCD
  có AB  6cm , BC BB  2cm . Điểm E là trung điểm cạnh BC
. Một tứ diện đều MNPQ có hai đỉnh M và N nằm trên đường thẳng EC , hai đỉnh P và Q nằm trên đường thẳng
đi qua điểm B và cắt đường thẳng AD tại điểm F . Khoảng cách DF bằng bao nhiêu? A. 3cm. B. 2 cm. C. 6 cm. D. 1cm.
Câu 29. Cho hình hộp A . BCD A BCD
  . Nếu mp ( ) chứa AB cắt hình hộp theo thiết diện là một tứ giác thì tứ giác đó là hình gì? A. Hình vuông.
B. Hình chữ nhật.
C. Hình bình hành. D. Hình thoi.
   
Câu 30. Cho hình hộp A .
BCD A B C D . Tìm giá trị của k để đẳng thức vectơ: AB B C DD k AC là đúng. 1 1 1 1 1 1 1 1
A. k  2 .
B. k  4 .
C. k  1.
D. k  0 . 1 Câu 31. Tính lim . n 1 A. 3. B. 1. C. 2. D. 0.
Câu 32. Nếu y  f x và y  g x đều liên tục tại x thì hàm số nào sau đây chưa chắc liên tục tại x ? 0 0 f x A. y  .
B. y  f x  g(x).
C. y  f x.g(x).
D. y  f x  g(x). g(x) 
      
Câu 33. Cho hình lăng trụ tam giác ABC.A BC
 . Đặt AA  a, AB b, AC c, BC d . Trong các đẳng thức vectơ
đã cho dưới đây, đẳng thức nào đúng?                
A. a b c d  0 .
B. a b c d .
C. a b c .
D. b c d  0 . 2
x x  2  khi x  2
Câu 34. Cho hàm số f x   x  2
. Khẳng định nào sau đây là sai? 5
  x khi x  2
A. Hàm số gián đoạn tại x  0.
B. Hàm số liên tục trên .  0 Trang 7/18 - Mã đề thi A
C. Hàm số có tập xác định là . 
D. Hàm số liên tục tại x  2. 0  x   x
Câu 35. Cho f x 2 3 khi 2  
. Để lim f x tồn tại, giá trị của a phải bằng bao nhiêu? ax 1 khi x  2 x 2  A. 4. B. 1. C. 2. D. 3. 2
x x  2 2 
m x 1 khi x  1
Câu 36. Cho f (x)   1 x
. Tính tổng tất cả các giá trị m thỏa mãn điều kiện hàm số có giới 3
 mx2m1 khi x 1 hạn khi x 1. A. 5. B. 0. C. 2 17. D. 17.
Câu 37. Cho hình lăng trụ ABC.A BC
 . Gọi H là trung điểm của AB . Đường thẳng B C
 song song với mặt phẳng nào dưới đây?
A. HAB. B. HA C  .
C. AHC.
D. AAH .
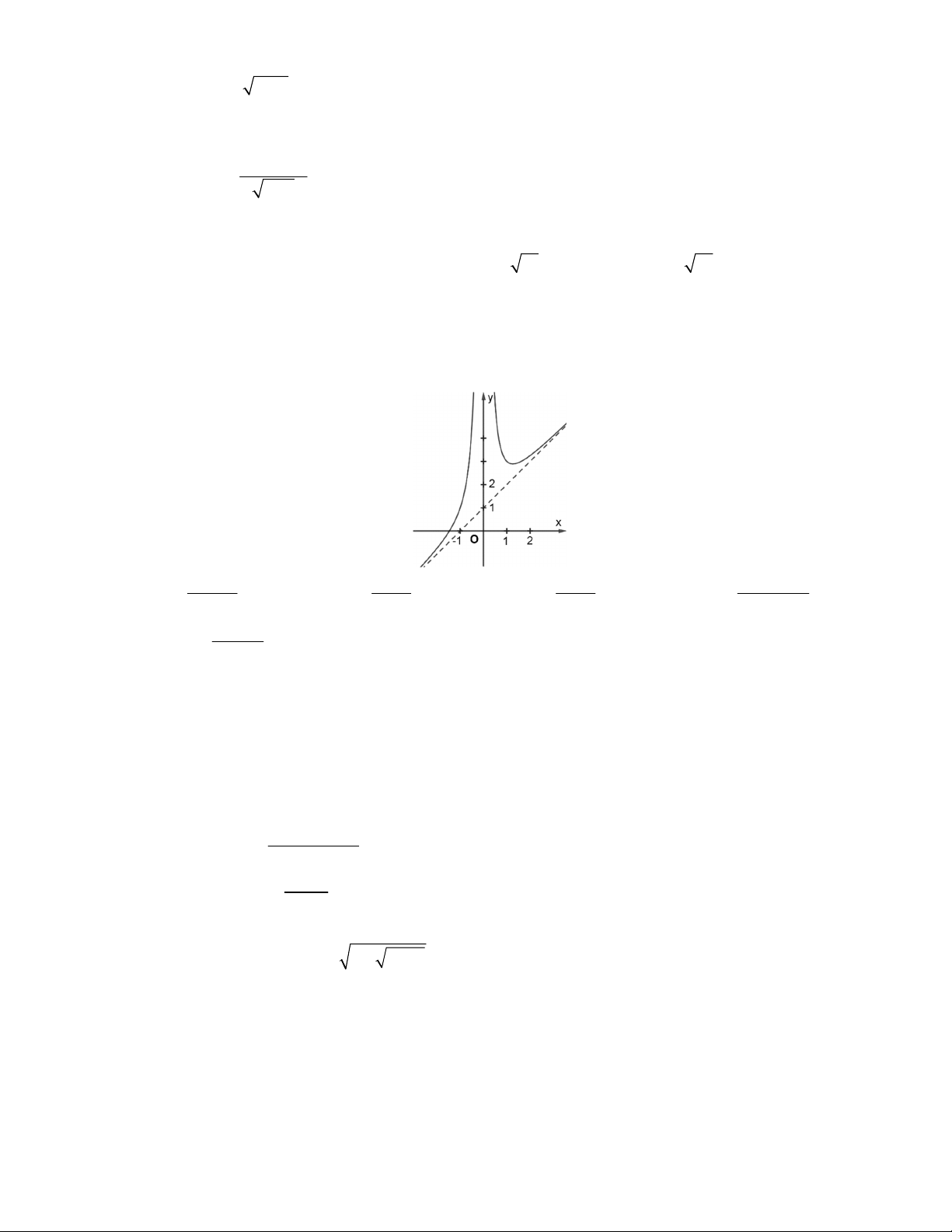
Câu 38. Thông qua việc tìm giới hạn của các hàm số khi x  0, x   hãy xác định xem đường cong dưới đây là đồ thị của hàm số nào? 2 x 1 4 x 1 2 1 x 3 2 x x 1
A. h x  .
B. k x  .
C. f x  .
D. g x  . 4 x 2 x 2 x 2 x 3 3n n Câu 39. Tính lim . 2 n A. 1. B. .  C. 0. D. . 
Câu 40. Có bao nhiêu giá trị x 0;2  sao cho tiếp tuyến với đồ thị hàm số y x  2cos x tại các tiếp điểm có hoành
độ đó song song với đường thẳng y  2x ? A. 2. B. 3. C. 1. D. 4.
II. PHẦN TỰ LUẬN (2,0 điểm)
Bài 1 (1,0 điểm). 5 2  
a) Tính giới hạn: 2n 3n 6 I  lim . 5 n n x
b) Cho hàm số y f x 2 3 
có đồ thị C. Viết phương trình tiếp tuyến của đồ thị C  song song với x 1
đường thẳng d : y  5x  2019.
Bài 2 (1.0 điểm). Cho hàm số: 2
y x x 1. Chứng minh rằng:  2
4 1 x y  y  4 .xy
------------- HẾT -------------
(Học sinh không được sử dụng tài liệu. Cán bộ coi thi không giải thích gì thêm.) Trang 8/18
SỞ GD&ĐT THỪA THIÊN HUẾ
KIỂM TRA HỌC KỲ II_NĂM HỌC 2018 - 2019
TRƯỜNG THPT VINH LỘC
Môn: Toán - Lớp 11 - Chương trình chuẩn ĐỀ CHÍNH THỨC
Thời gian: 90 phút (Không kể thời gian phát đề) (Đề gồm 04 trang) Mã đề thi
Họ và tên:………………………………….Lớp:…………….............……..…… C
I. PHẦN TRẮC NGHIỆM KHÁCH QUAN (8,0 điểm) 1 Câu 1. Tính lim . n 1 A. 3. B. 0. C. 1. D. 2. 
      
Câu 2. Cho hình lăng trụ tam giác ABC.A BC
 . Đặt AA  a, AB b, AC c, BC d . Trong các đẳng thức vectơ đã
cho dưới đây, đẳng thức nào đúng?                
A. a b c d  0 .
B. b c d  0 .
C. a b c d .
D. a b c .
Câu 3. Tìm đạo hàm của hàm số y  sin ,
x x. 1 A. y  . B. y   cos . x C. y  tan . x D. y  cos . x 2 cos x
   
Câu 4. Cho hình hộp A .
BCD A B C D . Tìm giá trị của k để đẳng thức vectơ: AB B C DD k AC là đúng. 1 1 1 1 1 1 1 1
A. k  0 .
B. k  2 .
C. k  4 .
D. k  1. 2 x
Câu 5. Gọi C là đồ thị của hàm số y
. M là một điểm trên C không trùng với gốc tọa độ và có hoành 2  x
độ là số nguyên sao cho khoảng cách từ M đến trục hoành gấp đôi khoảng cách từ M đến trục tung. Phương
trình nào sau đây là một phương trình tiếp tuyến của C  tại M ?
A. y  8.
B. y  64.
C. y  12.
D. y  9. 2
ax bx c
Câu 6. Tính đạo hàm của hàm số y  ,(aa '  0).
a ' x b ' 2
aa ' x  2ab ' x bb ' a 'c 2
aa ' x  2ab ' x bb ' a 'c A. y  . B. y  . 2
(a ' x b ') 2
(a ' x b ') 2
aa ' x  2ab ' x bb ' a 'c 2
aa ' x  2ab ' x bb ' a 'c C. y  . D. y  .
a ' x b ' 2
(a ' x b ')
Câu 7. Cho hình lăng trụ ABC.A BC
 . Gọi H là trung điểm của AB . Đường thẳng B C
 song song với mặt phẳng nào dưới đây? A. AA H  .
B. HAB. C. HA C  .
D. AHC.    
Câu 8. Cho a  3, b  5 góc giữa a và b bằng 120 .
 Chọn khẳng định sai trong các khẳng định sau.        
A. a  2b  9 .
B. a b  7 .
C. a  2b  139 .
D. a b  19 .
Câu 9. Cho hình hộp chữ nhật ABC . D A BCD
  có AB  6cm , BC BB  2cm . Điểm E là trung điểm cạnh BC .
Một tứ diện đều MNPQ có hai đỉnh M và N nằm trên đường thẳng EC , hai đỉnh P và Q nằm trên đường thẳng đi
qua điểm B và cắt đường thẳng AD tại điểm F . Khoảng cách DF bằng bao nhiêu? A. 3cm. B. 6 cm. C. 1cm. D. 2 cm.
Câu 10. Cho hình lăng trụ đều ABC.A BC
  có tất cả các cạnh bằng .
a Gọi M là trung điểm của AB,  là góc tạo
bởi đường thẳng MC và mặt phẳng  ABC . Khi đó tan  bằng bao nhiêu? 2 7 3 3 2 3 A. . B. . C. . D. . 7 2 7 3
Câu 11. Cho đường thẳng a  P và đường thẳng b  Q . Mệnh đề nào sau đây là đúng?
A. P // Q  a // Q và b// P.
B. a và b chéo nhau.
C. P // Q  a // . b
D. a // b  P // Q. Trang 9/18 - Mã đề thi A
Câu 12. Xét chuyển động có phương trình s(t)  Asin(t b) ( ,
A ,b là các hằng số). Tìm gia tốc tức thời tại
thời điểm t của chuyển động. A. 2
a(t)  A sin(t b).
B. a(t)  Acos(t b). C. 2
a(t)  A cos(t b). D. 2
a(t)  A sin(t b). 1 1 1 1   ... n
Câu 13. Một nhóm bạn trao đổi về kết quả khi tính 2 4 8 2 * lim
,(n   ) đã đưa ra các nhận xét như sau: n a
(1) Giới hạn lớn hơn 0 nếu a 1.
(2) Giới hạn bằng 1 nếu a 1.
(3) Giới hạn bằng  nếu 0  a 1.
Hỏi có tất cả bao nhiêu nhận xét đúng?
A. Có hai nhận xét đúng.
B. Không có nhận xét nào đúng.
C. Chỉ có một nhận xét đúng.
D. Cả ba nhận xét đều đúng. 2
x x  2 2 
m x 1 khi x 1
Câu 14. Cho f (x)   1 x
. Tính tổng tất cả các giá trị m thỏa mãn điều kiện hàm số có giới 3
 mx2m1 khi x 1 hạn khi x 1. A. 2 17. B. 17. C. 5. D. 0.  x   x
Câu 15. Cho f x 2 3 khi 2  
. Để lim f x tồn tại, giá trị của a phải bằng bao nhiêu? ax 1 khi x  2 x 2  A. 2. B. 3. C. 4. D. 1.
Câu 16. Cho hàm số   1
f x  . Tính y 2. x 1 1 1 1 A.  . B. . C.  . D. . 2 2 2 2
Câu 17. Cho hình chóp S.ABC có SA   ABC, ABC  vuông tại .
B Gọi AM là đường cao của tam giác SAB (
M thuộc cạnh SB ). Khi đó, AM không vuông góc với đường thẳng nào dưới đây? A. AC. B. SC. C. B . C D. . SB
Câu 18. Cho tứ diện ABCD . Gọi I , J lần lượt là trung điểm của AB và CD , G là trung điểm của IJ .
Đẳng thức nào dưới đây là đúng?
    
    
A. GA GB GC GD JI .
B. GA GB GC GD  2JI .
    
    
C. GA GB GC GD  0 .
D. GA GB GC GD  2IJ .
Câu 19. Cho hình chóp S.ABCD có tất cả các cạnh bên và cạnh đáy đều bằng nhau. ABCD là hình vuông. Khẳng định nào sau đây là đúng?
A. BD  SAD.
B. BD  SCD .
C. BD  SAC .
D. SB   ABCD .
Câu 20. Có bao nhiêu giá trị x 0;2  sao cho tiếp tuyến với đồ thị hàm số y x  2cos x tại các tiếp điểm có hoành
độ đó song song với đường thẳng y  2x ? A. 2. B. 3. C. 1. D. 4.
Câu 21. Cho tứ diện ABCD , các điểm M , N lần lượt là trung điểm của AB , CD . Không thể kết luận G là trọng
tâm của tứ diện ABCD trong trường hợp nào dưới đây?
    
A. 4PG PA PB PC PD với P là điểm bất kỳ.   
B. GM GN  0 .
C. GM GN .
    
D. GA GB GC GD  0 .
Câu 22. Cho cos x  1  . Tính 2 4 6 2  1 cos  cos  cos  ... cos n S x x x x  ... 1 1 A. . B. . C. 2 sin x . D. 2 cos x . 2 cos x 2 sin x Trang 10/18
Câu 23. Nếu y  f x và y  g x đều liên tục tại x thì hàm số nào sau đây chưa chắc liên tục tại x ? 0 0 f x
A. y  f x.g(x). B. y  .
C. y  f x  g(x).
D. y  f x  g(x). g(x)
Câu 24. Biết rằng lim f x   ,
 lim g x   .
 Khẳng định nào sau đây là đúng? x x  f x A. lim  f
  x  g x  0.  B. lim    1  . x x g   x  1 1 C. lim   D. lim  . L f  x  ,  với L  0.    lim    0. x x f x g x x
Câu 25. Cho hình chóp S.ABCD có đáy ABCD là hình vuông và SA   ABCD. Mệnh đề nào dưới đây là sai?
A. BD  SAC .
B. CD  SAD .
C. BC  SAB .
D. AC  SBD .
Câu 26. Trong không gian cho điểm O và bốn điểm ,
A B,C, D không thẳng hàng. Điều kiện cần và đủ để ,
A B,C, D
tạo thành hình bình hành là gì?
    
   
A. OA OB OC OD  0 .
B. OA OC OB OD .
 1   1 
 1   1 
C. .OA OB OC OD .
D. OA OC OB OD . 2 2 2 2
Câu 27. Biết rằng limu a,limv   ,
b với b  0. Khẳng định nào sau đây là đúng? n nu a A. lim u
 .v   a . b B. lim n    . n n v bn
C. limu v   a  . b
D. limu v a b n n  . n nx x
Câu 28. Tìm m để hàm số f x 2 9 khi 0  
liên tục tại x  0. 3
m khi x  0 0
A. m  3. B. m  2. 
C. m  0.
D. m 1.
Câu 29. Hàm số bậc hai nào sau đây thỏa mãn điều kiện: f (1)  5, f   1  3?
A. f x 2  3
x  9x 1.
B. f x 2
 x  9x 3.
C. f x 2  x  9 . x
D. f x 2  3  x 8 . x
Câu 30. Cho hình hộp ABC . D A BCD
  . Gọi I, K lần lượt là tâm của hình bình hành ABB A   và BCC B  . Khẳng
định nào sau đây là sai?  1  1 
  
A. IK AC AC.
B. Ba vectơ BD, IK, B C
  không đồng phẳng. 2 2   
C. BD  2IK  2BC .
D. Bốn điểm I , K , C , A đồng phẳng. 3 3n n Câu 31. Tính lim . 2 n A. 1. B. . C. .  D. 0. Câu 32. Cho hàm số 3
y x  3x 1 C. Viết phương trình tiếp tuyến của đồ thịC tại điểm có hoành độ bằng 0.
A. y  3x  2.
B. y  3x 12.
C. y  3x 11.
D. y  3x 1. 2 x  4 Câu 33. Tính lim . x2 x  2 A. 2. B. 2.  C. 4. D. 4.  Trang 11/18 - Mã đề thi A
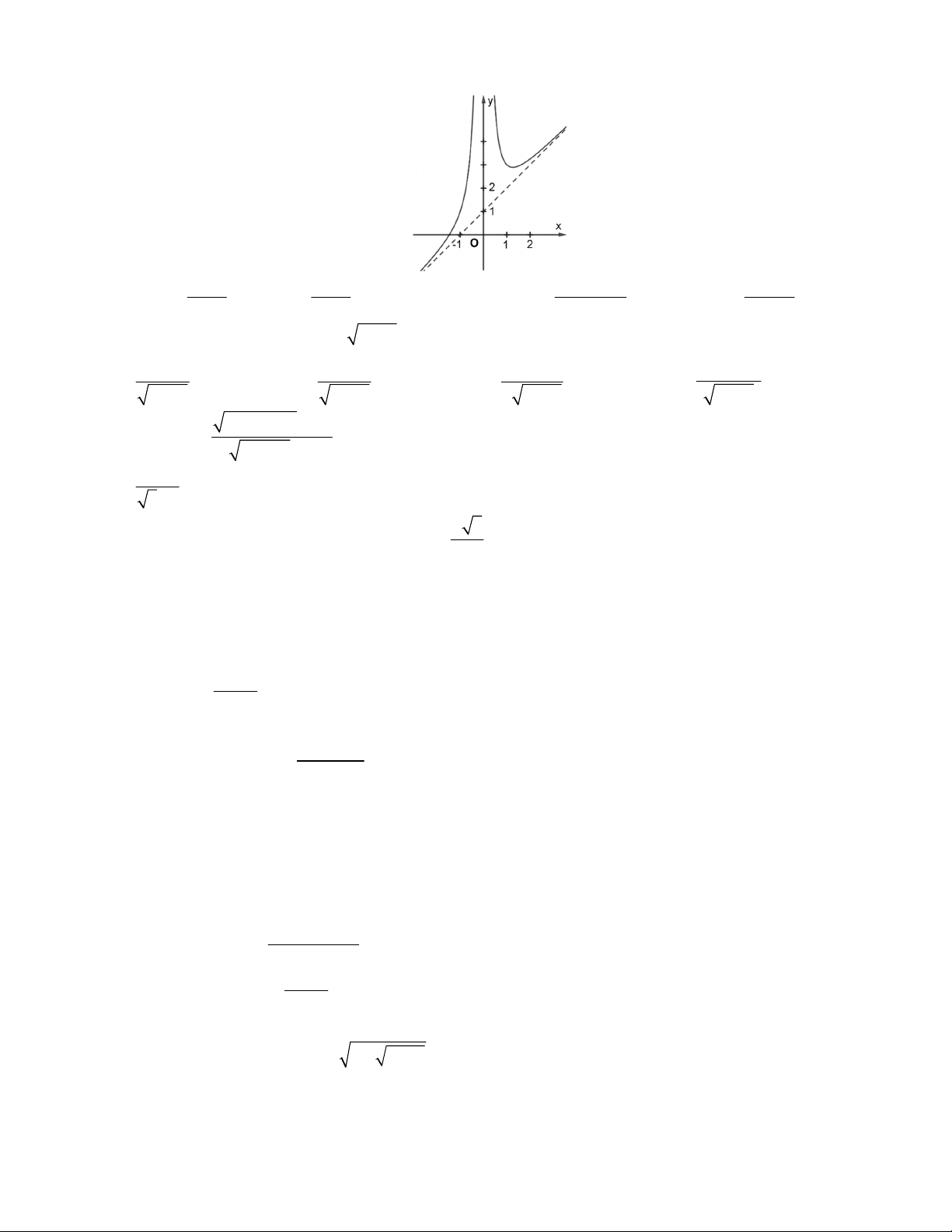
Câu 34. Thông qua việc tìm giới hạn của các hàm số khi x  0, x   hãy xác định xem đường cong dưới đây là đồ thị của hàm số nào? 4 x 1 2 1 x 3 2 x x 1 2 x 1
A. k x 
. B. f x  .
C. g x  .
D. h x  . 2 x 2 x 2 x 4 x
Câu 35. Tìm đạo hàm của hàm số 2
y x 1. 2x x x x  2 x   1 A. . B. . C. . D.  . 2 x 1 2 x 1 2 2 x 1 2 x 1 4 4
n  2n 1  2n Câu 36. Tính lim . 3 3
3n n n 3 A. . B. 1. C. . D. .  3 3 1 a 3
Câu 37. Cho tứ diện ABCD có AB CD a , IJ
( I , J lần lượt là trung điểm của BC và AD ). Số đo góc 2
giữa hai đường thẳng AB và CD bằng bao nhiêu độ? A. 30 .  B. 45 .  C. 60 .  D. 90 . 
Câu 38. Cho hình hộp ABC . D A BCD
  . Nếu mp ( ) chứa AB cắt hình hộp theo thiết diện là một tứ giác thì tứ giác đó là hình gì?
A. Hình chữ nhật.
B. Hình bình hành. C. Hình thoi.
D. Hình vuông. 2x  3 Câu 39. Tính lim . x 1  x 1 A. 2. B. .  C. . D. 2.  2
x x  2  khi x  2
Câu 40. Cho hàm số f x   x  2
. Khẳng định nào sau đây là sai? 5
  x khi x  2
A. Hàm số liên tục trên . 
B. Hàm số có tập xác định là . 
C. Hàm số gián đoạn tại x  0.
D. Hàm số liên tục tại x  2. 0 0
II. PHẦN TỰ LUẬN (2,0 điểm)
Bài 1 (1,0 điểm). 5 2 2n  3n  6
a) Tính giới hạn: I  lim . 5 n n x
b) Cho hàm số y f x 2 3 
có đồ thị C. Viết phương trình tiếp tuyến của đồ thị C  song song với x 1
đường thẳng d : y  5x  2019.
Bài 2 (1.0 điểm). Cho hàm số: 2
y x x 1. Chứng minh rằng:  2
4 1 x y  y  4 .xy
------------- HẾT -------------
(Học sinh không được sử dụng tài liệu. Cán bộ coi thi không giải thích gì thêm.) Trang 12/18
SỞ GD&ĐT THỪA THIÊN HUẾ
KIỂM TRA HỌC KỲ II_NĂM HỌC 2018 - 2019
TRƯỜNG THPT VINH LỘC
Môn: Toán - Lớp 11 - Chương trình chuẩn ĐỀ CHÍNH THỨC
Thời gian: 90 phút (Không kể thời gian phát đề) (Đề gồm 04 trang) Mã đề thi
Họ và tên:………………………………….Lớp:…………….............……..…… D
I. PHẦN TRẮC NGHIỆM KHÁCH QUAN (8,0 điểm)
Câu 1. Tìm đạo hàm của hàm số y  sin ,
x x. 1 A. y  cos . x B. y   cos . x C. y  tan . x D. y  . 2 cos x
   
Câu 2. Cho hình hộp A .
BCD A B C D . Tìm giá trị của k để đẳng thức vectơ: AB B C DD k AC là đúng. 1 1 1 1 1 1 1 1
A. k  1.
B. k  0 .
C. k  2 .
D. k  4 .
Câu 3. Cho tứ diện ABCD , các điểm M , N lần lượt là trung điểm của AB , CD . Không thể kết luận G là trọng tâm
của tứ diện ABCD trong trường hợp nào dưới đây?   
A. GM GN  0 .
B. GM GN .
    
C. GA GB GC GD  0 .
    
D. 4PG PA PB PC PD với P là điểm bất kỳ.
Câu 4. Trong không gian cho điểm O và bốn điểm ,
A B,C, D không thẳng hàng. Điều kiện cần và đủ để ,
A B,C, D
tạo thành hình bình hành là gì?
 1   1 
    
A. OA OC OB OD .
B. OA OB OC OD  0 . 2 2    
 1   1 
C. OA OC OB OD .
D. .OA OB OC OD . 2 2
Câu 5. Cho hình chóp S.ABC có SA   ABC, ABC  vuông tại .
B Gọi AM là đường cao của tam giác SAB ( M
thuộc cạnh SB ). Khi đó, AM không vuông góc với đường thẳng nào dưới đây? A. SC. B. B . C C. AC. D. . SB
Câu 6. Cho hình chóp S.ABCD có đáy ABCD là hình vuông và SA   ABCD. Mệnh đề nào dưới đây là sai?
A. CD  SAD.
B. BC  SAB .
C. AC  SBD .
D. BD  SAC .    
Câu 7. Cho a  3, b  5 góc giữa a và b bằng 120 .
 Chọn khẳng định sai trong các khẳng định sau.        
A. a  2b  139 .
B. a b  19 .
C. a  2b  9 .
D. a b  7 .
Câu 8. Cho hình hộp ABC . D A BCD
  . Nếu mp ( ) chứa AB cắt hình hộp theo thiết diện là một tứ giác thì tứ giác đó là hình gì? A. Hình thoi.
B. Hình vuông.
C. Hình chữ nhật.
D. Hình bình hành. Câu 9. Cho hàm số 3
y x  3x 1 C. Viết phương trình tiếp tuyến của đồ thịC tại điểm có hoành độ bằng 0.
A. y  3x 11.
B. y  3x 1.
C. y  3x  2.
D. y  3x 12. 2
x x  2 2 
m x 1 khi x 1
Câu 10. Cho f (x)   1 x
. Tính tổng tất cả các giá trị m thỏa mãn điều kiện hàm số có giới 3
 mx2m1 khi x 1 hạn khi x 1. A. 17. B. 5. C. 0. D. 2 17. x x
Câu 11. Tìm m để hàm số f x 2 9 khi 0  
liên tục tại x  0. 3
m khi x  0 0 A. m  2. 
B. m  0.
C. m 1.
D. m  3.
Câu 12. Cho đường thẳng a  P và đường thẳng b  Q . Mệnh đề nào sau đây là đúng?
A. P // Q  a // Q và b// P.
B. a và b chéo nhau. Trang 13/18 - Mã đề thi A
C. P // Q  a // . b
D. a // b  P // Q.  x   x
Câu 13. Cho f x 2 3 khi 2  
. Để lim f x tồn tại, giá trị của a phải bằng bao nhiêu? ax 1 khi x  2 x 2  A. 1. B. 2. C. 3. D. 4.
Câu 14. Hàm số bậc hai nào sau đây thỏa mãn điều kiện: f (1)  5, f   1  3?
A. f x 2  3
x  9x 1.
B. f x 2
 x  9x 3.
C. f x 2  x  9 . x
D. f x 2  3  x 8 . x
Câu 15. Nếu y  f x và y  g x đều liên tục tại x thì hàm số nào sau đây chưa chắc liên tục tại x ? 0 0 f x
A. y  f x  g(x).
B. y  f x.g(x). C. y  .
D. y  f x  g(x). g(x)
Câu 16. Cho hình lăng trụ đều AB . C A BC
  có tất cả các cạnh bằng .
a Gọi M là trung điểm của AB,  là góc tạo
bởi đường thẳng MC và mặt phẳng  ABC . Khi đó tan  bằng bao nhiêu? 2 3 3 3 2 7 A. . B. . C. . D. . 3 2 7 7
Câu 17. Biết rằng lim f x   ,
 lim g x   .
 Khẳng định nào sau đây là đúng? x x  f x A. lim  f
  x  g x  0.  B. lim    1  . x x g   x  1 1 C. lim   D. lim  . L f  x  ,  với L  0.    lim    0. x x f x g x x 2
ax bx c
Câu 18. Tính đạo hàm của hàm số y  ,(aa '  0).
a ' x b ' 2
aa ' x  2ab ' x bb ' a 'c 2
aa ' x  2ab ' x bb ' a 'c A. y  . B. y  . 2
(a ' x b ') 2
(a ' x b ') 2
aa ' x  2ab ' x bb ' a 'c 2
aa ' x  2ab ' x bb ' a 'c C. y  . D. y  .
a ' x b ' 2
(a ' x b ') 4 4
n  2n 1  2n Câu 19. Tính lim . 3 3
3n n n 3 A. 1. B. . C. .  D. . 3 3 1 1 Câu 20. Tính lim . n 1 A. 3. B. 1. C. 2. D. 0. 1 1 1 1   ... n
Câu 21. Một nhóm bạn trao đổi về kết quả khi tính 2 4 8 2 * lim
,(n   ) đã đưa ra các nhận xét như sau: n a
(1) Giới hạn lớn hơn 0 nếu a 1.
(2) Giới hạn bằng 1 nếu a 1.
(3) Giới hạn bằng  nếu 0  a 1.
Hỏi có tất cả bao nhiêu nhận xét đúng?
A. Chỉ có một nhận xét đúng.
B. Có hai nhận xét đúng.
C. Không có nhận xét nào đúng.
D. Cả ba nhận xét đều đúng.
Câu 22. Cho hàm số   1
f x  . Tính y 2. x Trang 14/18 1 1 1 1 A. . B.  . C. . D.  . 2 2 2 2 
      
Câu 23. Cho hình lăng trụ tam giác ABC.A BC
 . Đặt AA  a, AB b, AC c, BC d . Trong các đẳng thức vectơ
đã cho dưới đây, đẳng thức nào đúng?                
A. b c d  0 .
B. a b c d .
C. a b c .
D. a b c d  0 .
Câu 24. Xét chuyển động có phương trình s(t)  Asin(t b) ( ,
A ,b là các hằng số). Tìm gia tốc tức thời tại
thời điểm t của chuyển động. A. 2
a(t)  A sin(t b).
B. a(t)  Acos(t b). C. 2
a(t)  A cos(t b). D. 2
a(t)  A sin(t b).
Câu 25. Cho hình hộp ABC . D A BCD
  . Gọi I, K lần lượt là tâm của hình bình hành ABB A   và BCC B  . Khẳng
định nào sau đây là sai?   
A. BD  2IK  2BC .
B. Bốn điểm I , K , C , A đồng phẳng.  1  1 
  
C. IK AC AC.
D. Ba vectơ BD, IK, B C
  không đồng phẳng. 2 2
Câu 26. Tìm đạo hàm của hàm số 2
y x 1. 2x x x x  2 x   1 A. . B. . C. . D.  . 2 x 1 2 x 1 2 2 x 1 2 x 1
Câu 27. Cho tứ diện ABCD . Gọi I , J lần lượt là trung điểm của AB và CD , G là trung điểm của IJ .
Đẳng thức nào dưới đây là đúng?
    
    
A. GA GB GC GD  0 .
B. GA GB GC GD  2IJ .
    
    
C. GA GB GC GD JI .
D. GA GB GC GD  2JI . 2 x
Câu 28. Gọi C là đồ thị của hàm số y
. M là một điểm trên C  không trùng với gốc tọa độ và có hoành 2  x
độ là số nguyên sao cho khoảng cách từ M đến trục hoành gấp đôi khoảng cách từ M đến trục tung. Phương
trình nào sau đây là một phương trình tiếp tuyến của C  tại M ?
A. y  12.
B. y  8.
C. y  9.
D. y  64.
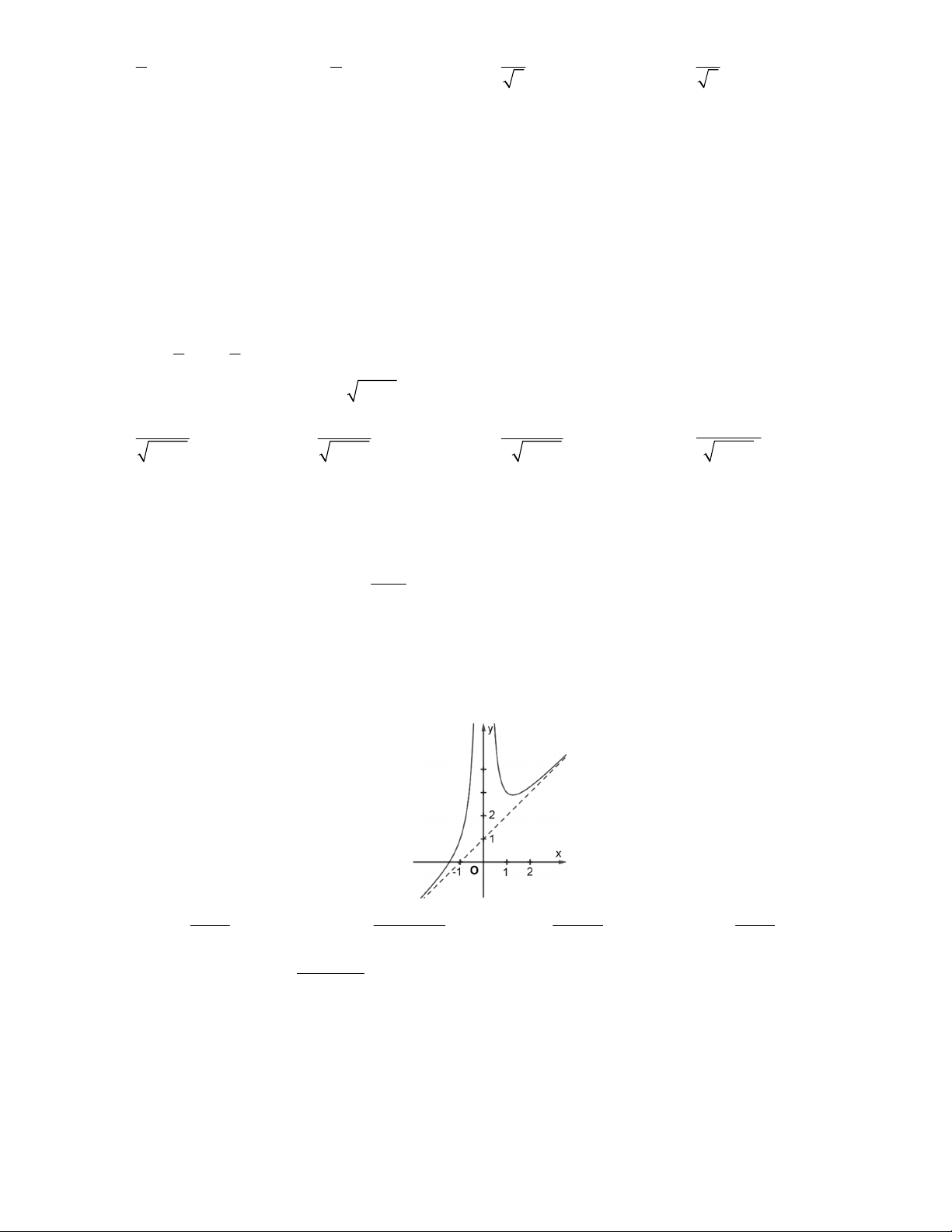
Câu 29. Thông qua việc tìm giới hạn của các hàm số khi x  0, x   hãy xác định xem đường cong dưới đây là đồ thị của hàm số nào? 2 1 x 3 2 x x 1 2 x 1 4 x 1
A. f x  .
B. g x  .
C. h x  .
D. k x  . 2 x 2 x 4 x 2 x 2
x x  2  khi x  2
Câu 30. Cho hàm số f x   x  2
. Khẳng định nào sau đây là sai? 5
  x khi x  2
A. Hàm số liên tục tại x  2.
B. Hàm số liên tục trên .  0
C. Hàm số có tập xác định là . 
D. Hàm số gián đoạn tại x  0. 0
Câu 31. Có bao nhiêu giá trị x 0;2  sao cho tiếp tuyến với đồ thị hàm số y x  2cos x tại các tiếp điểm có hoành
độ đó song song với đường thẳng y  2x ? A. 2. B. 3. C. 1. D. 4. Trang 15/18 - Mã đề thi A 3 3n n Câu 32. Tính lim . 2 n A. 0. B. 1. C. .  D. .  2 x  4 Câu 33. Tính lim . x2 x  2 A. 2. B. 2.  C. 4. D. 4. 
Câu 34. Cho hình lăng trụ ABC.A BC
 . Gọi H là trung điểm của AB . Đường thẳng B C
 song song với mặt phẳng nào dưới đây? A. AA H  .
B. HAB. C. HA C  .
D. AHC. 2x  3 Câu 35. Tính lim . x 1  x 1 A. .  B. . C. 2.  D. 2.
Câu 36. Cho hình hộp chữ nhật ABC . D A BCD
  có AB  6cm , BC BB  2cm . Điểm E là trung điểm cạnh BC
. Một tứ diện đều MNPQ có hai đỉnh M và N nằm trên đường thẳng EC , hai đỉnh P và Q nằm trên đường thẳng
đi qua điểm B và cắt đường thẳng AD tại điểm F . Khoảng cách DF bằng bao nhiêu? A. 3cm. B. 6 cm. C. 1cm. D. 2 cm. a 3
Câu 37. Cho tứ diện ABCD có AB CD a , IJ
( I , J lần lượt là trung điểm của BC và AD ). Số đo góc 2
giữa hai đường thẳng AB và CD bằng bao nhiêu độ? A. 30 .  B. 45 .  C. 60 .  D. 90 . 
Câu 38. Cho cos x  1  . Tính 2 4 6 2  1 cos  cos  cos  ... cos n S x x x x  ... 1 1 A. . B. 2 cos x . C. . D. 2 sin x . 2 sin x 2 cos x
Câu 39. Cho hình chóp S.ABCD có tất cả các cạnh bên và cạnh đáy đều bằng nhau. ABCD là hình vuông. Khẳng định nào sau đây là đúng?
A. BD  SCD .
B. BD  SAC .
C. SB   ABCD .
D. BD  SAD .
Câu 40. Biết rằng limu a,limv   ,
b với b  0. Khẳng định nào sau đây là đúng? n nu a A. lim n    .
B. limu v a b n n  . v bn
C. limu v   a  . b D. lim u
 .v  ab n n  . n n
II. PHẦN TỰ LUẬN (2,0 điểm)
Bài 1 (1,0 điểm). 5 2  
a) Tính giới hạn: 2n 3n 6 I  lim . 5 n n x
b) Cho hàm số y f x 2 3 
có đồ thị C. Viết phương trình tiếp tuyến của đồ thị C  song song với x 1
đường thẳng d : y  5x  2019.
Bài 2 (1.0 điểm). Cho hàm số: 2
y x x 1. Chứng minh rằng:  2
4 1 x y  y  4 .xy
------------- HẾT -------------
(Học sinh không được sử dụng tài liệu. Cán bộ coi thi không giải thích gì thêm.) Trang 16/18
ĐÁP ÁN ĐỀ THI HỌC KÌ II – KHỐI 11 – NĂM HỌC 2018 - 2019
------------------------
I. PHẦN TRẮC NGHIỆM:Mã đề [ A ] 1 2 3 4 5 6 7 8 9
10 11 12 13 14 15 16 17 18 19 20 B A D C D D B A D B C C D D B A D C C C
21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 C A D B D A C A A A B A A C B B D B C B Mã đề [ B ] 1 2 3 4 5 6 7 8 9
10 11 12 13 14 15 16 17 18 19 20 D C D B B D A A C B C B C B A B D B A B
21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 B D C D C A A B C C D A D A C A C D D A Mã đề [ C ] 1 2 3 4 5 6 7 8 9
10 11 12 13 14 15 16 17 18 19 20 B B D D A D D A D D A A A C A C A C C A
21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 C B B C D B D A A B B D C C B A C B B C Mã đề [ D ] 1 2 3 4 5 6 7 8 9
10 11 12 13 14 15 16 17 18 19 20 A A B C C C C D B B D A B A C A C D D D
21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 B B A D D B A B B D A C C D A D C A B C II. PHẦN TỰ LUẬN: Bài Ý
Lời giải và hướng dẫn chấm Điểm 5 2  
Tính giới hạn: 2n 3n 6 I  lim . 0,5 điểm 5 n n a) 5  3 6  3 6 n 2   5 2     3 5 2 3 5 2n  3n  6  n n lim lim     lim n n I  2. 0,5 5 n n  1  1 5 n 1 1  4  4  n n x
Cho hàm số y f x 2 3 
có đồ thị C. Viết phương trình tiếp tuyến của đồ thị x 1 0,5 điểm 1
C song song với đường thẳng d : y  5x  2019.
Gọi M x ; y là tiếp điểm của tiếp tuyến với đồ thị C. 0 0  5 0,25 b)
Hệ số góc của tiếp tuyến tại M : k f  x  , x  1 . 0  2  0  x 1 0 
x  0  y  3 
Ta có: k  5   x  2 0 0 1  1  0 x  2   y  7  0 0 0,25
Vậy có hai tiếp tuyến với phương trình lần lượt là:
 : y  5x  3;  : y  5x 17. 1 2 Cho hàm số: 2
y x x 1. Chứng minh rằng:  2
4 1 x y  y  4 .xy1,0 điểm   2 x x 1 2 1  x  1 x x 1 y Ta có: y   .1   .  0,5 2 2 2 2 2 2y    x 1 2yx 1 2 x 1 2 x x 1  2 y .2  x 1  . y  2 2 x 1 y  0,25 4 2 x   1 Trang 17/18 - Mã đề thi A   2 x   2 2x 4xy 4
1 .y  2y . x 1  . yy   y  4 . x y (đpcm) 0,25 2 2 x 1 2 x 1 Trang 18/18