SỞ GD-ĐT QUẢNG TRỊ ĐỀ KIỂM TRA HỌC KỲ II NĂM HỌC 2020-2021
TRƯỜNG THPT THỊ XÃ QUẢNG TRỊ Môn: Toán Lớp: 11
Thời gian làm bài: 90 phút, không kể thời gian giao đề Đề KT chính thức (Đề có 01 trang) Mã đề:111
Câu 1:(1,0điểm). Cho cấp số cộng biết u  3;u  5. Tính số hạng đầu và công sai của cấp số 2 3 cộng đó.
Câu 2:(1,0điểm). Cho cấp số nhân biết u  u  3 và u  u  6 . Tính u và S của cấp số 1 2 2 3 5 6 nhân đó.
Câu 3:(2,0điểm). Tính các giới hạn sau: 4n  5 3  x  7 a) lim lim n  . b) 1 x2 x  . 2
Câu 4:(1,0 điểm). Chứng ming rằng phương trình 7 2
11x  3x  2020x  2021  0 có ít nhất một
nghiệm thuộc khoảng  1  ;  1 .
Câu 5: (1,0 điểm). 2
 x  5x  6  ; khi x  3
Cho hàm số: f (x)   x  3
m  2; khi x  3
Tìm m để hàm số đã cho liên tục tại x  3 .
Câu 6:(3,0 điểm).
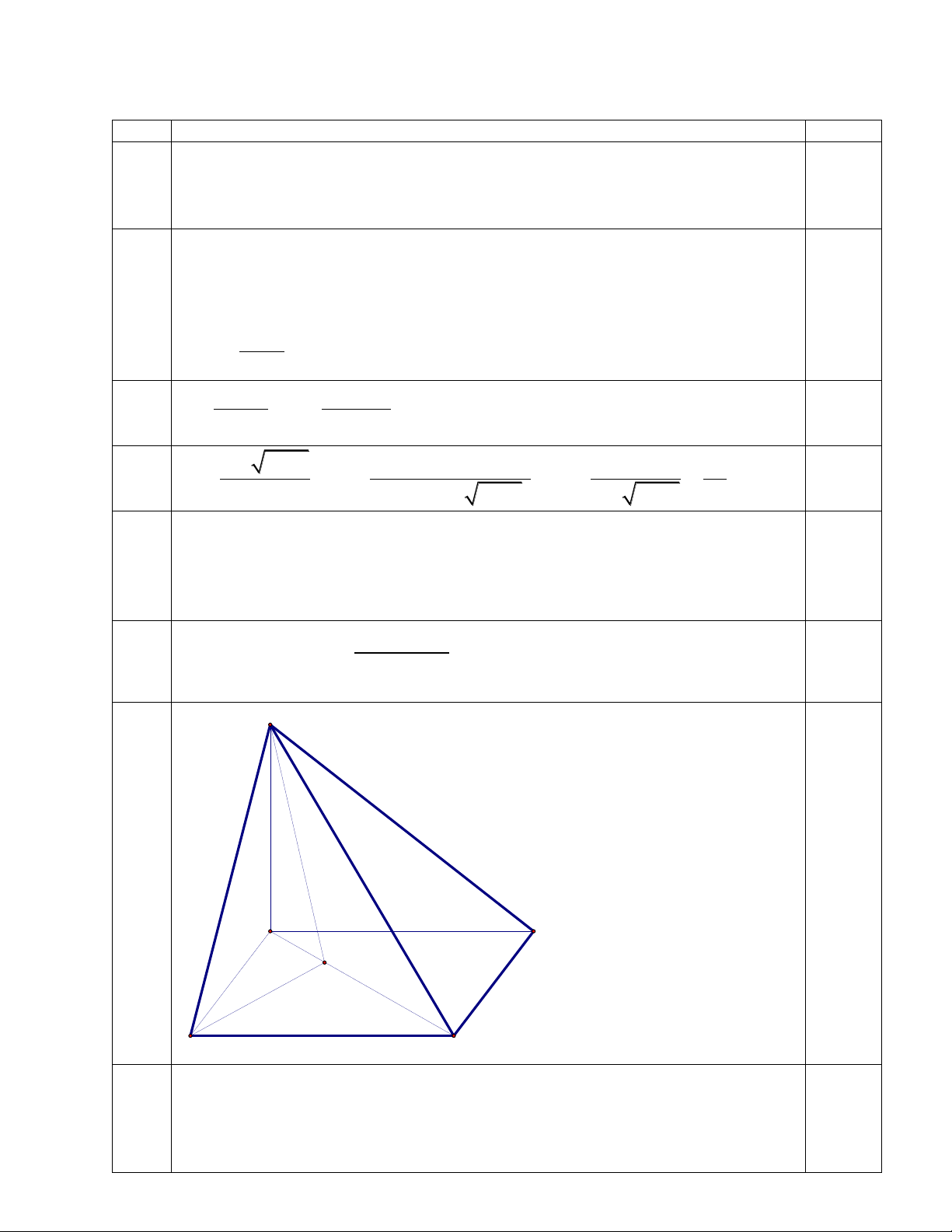
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB  , a AD  2 , a
SA  3a và SA  (ABC ) D .
a) Chứng minh rằng CD  (SA )
D ;CB  (SAB) .
b) Gọi H là hình chiếu vuông góc của B trên AC. Chứng minh rằng BH  S . C
c) Tính tan với  là góc giữa SB và SAC  .
Câu 7:(1,0 điểm). u  1, u  4 Cho dãy số u
u được xác định như sau: 1 2  với *
n  N . Tính lim n . n  u
 2u  u 1  2 n n2 n 1  n
-----------------HẾT---------------------
Học sinh không được sử dụng tài liệu. CBCT không giải thích gì thêm.
Họ và tên học sinh:…………………………..Lớp:………….Số báo danh:……………….
Chữ ký của giáo viên:………………………………….
SỞ GD-ĐT QUẢNG TRỊ ĐỀ KIỂM TRA HỌC KỲ II NĂM HỌC 2020-2021
TRƯỜNG THPT THỊ XÃ QUẢNG TRỊ Môn: Toán Lớp: 11
Thời gian làm bài: 90 phút, không kể thời gian giao đề Đề KT chính thức (Đề có 01 tran g) Mã đề:112
Câu 1:(1,0điểm). Cho cấp số cộng biết u  5;u  7 . Tính số hạng đầu và công sai của cấp số 2 3 cộng đó.
Câu 2:(1,0điểm). Cho cấp số nhân biết u  u  6 và u  u  12 . Tính u và S của cấp số 1 2 2 3 5 6 nhân đó.
Câu 3:(2,0điểm). Tính các giới hạn sau: 5n  4 3  x  6 a) lim lim n  . b) 1 x 3  x  . 3
Câu 4:(1,0 điểm). Chứng ming rằng phương trình 7 2
11x  3x  2021x  2020  0 có ít nhất một
nghiệm thuộc khoảng  1  ;  1 .
Câu 5: (1,0 điểm). 2
 x  5x  6  ; khi x  2
Cho hàm số: f (x)   x  2
m  2; khi x  2
Tìm m để hàm số đã cho liên tục tại x  2.
Câu 6:(3,0 điểm).
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB  , a AD  2 , a
SC  3a và SC  (ABC ) D .
a) Chứng minh rằng AD  (SC )
D ; AB  (SCB)
b) Gọi H là hình chiếu vuông góc của B trên AC. Chứng minh rằng BH  S . A
c) Tính tan với  là góc giữa SB và SAC  .
Câu 7:(1,0 điểm). u   2, u  5 Cho dãy số u
u được xác định như sau: 1 2  với *
n  N . Tính lim n . n  u
 2u  u 1  2 n n2 n 1  n
-----------------HẾT---------------------
Học sinh không được sử dụng tài liệu. CBCT không giải thích gì thêm.
Họ và tên học sinh:…………………………..Lớp:………….Số báo danh:……………….
Chữ ký của giáo viên:………………………………….
SỞ GD&ĐT QUẢNG TRỊ
ĐÁP ÁN KT HỌC KỲ II NĂM HỌC 2020 - 2021 TRƯỜNG THPT TXQT MÔN TOÁN KHỐI 11 Mã đề 111 Câu Lời giải Điểm C1.
Ta có u  3;u  5  d  u  u  5  3  2 0.5đ 2 3 3 2 1.0đ
u  u  d  3  2  1 0.5đ 1 2
Vậy u  1;d  2 1 C2. u   u  3 u  (1 q)  3 q  2 1.0đ Ta có 1 2 1      0.5đ u  u  6
u q(1 q)  6 u  1    2 3 1 1 4
u  u q  16 0.25đ 5 1 6 1 q S  u  63 0.25đ 6 1 1 q C3a. 4n  5 4  5 / n 1.0đ   lim lim 4 1.0đ n 1 1  1 / n C3b. 3  x  7 2  x 1  1  1.0đ lim  lim  lim  0.5đ x2 x  2
x2 (x  2)(3  x  7) x2 3  x  7 6 0.5đ C4. Xét 7 2
f (x)  11x  3x  2020x  2021 liên tục trên R 0.5đ 1.0đ f(1).f(-1)=-4049.13<0 0.5đ Vậy phương trình 7 2
11x  3x  2020x  2021  0 có ít nhất một nghiệm thuộc khoảng  1  ;  1 . C5. 2 x  5x  6 1.0đ
Ta có lim f (x)  lim  lim(x  2) 1 0.5đ x 3  x 3  x 3 x  3  0.5đ
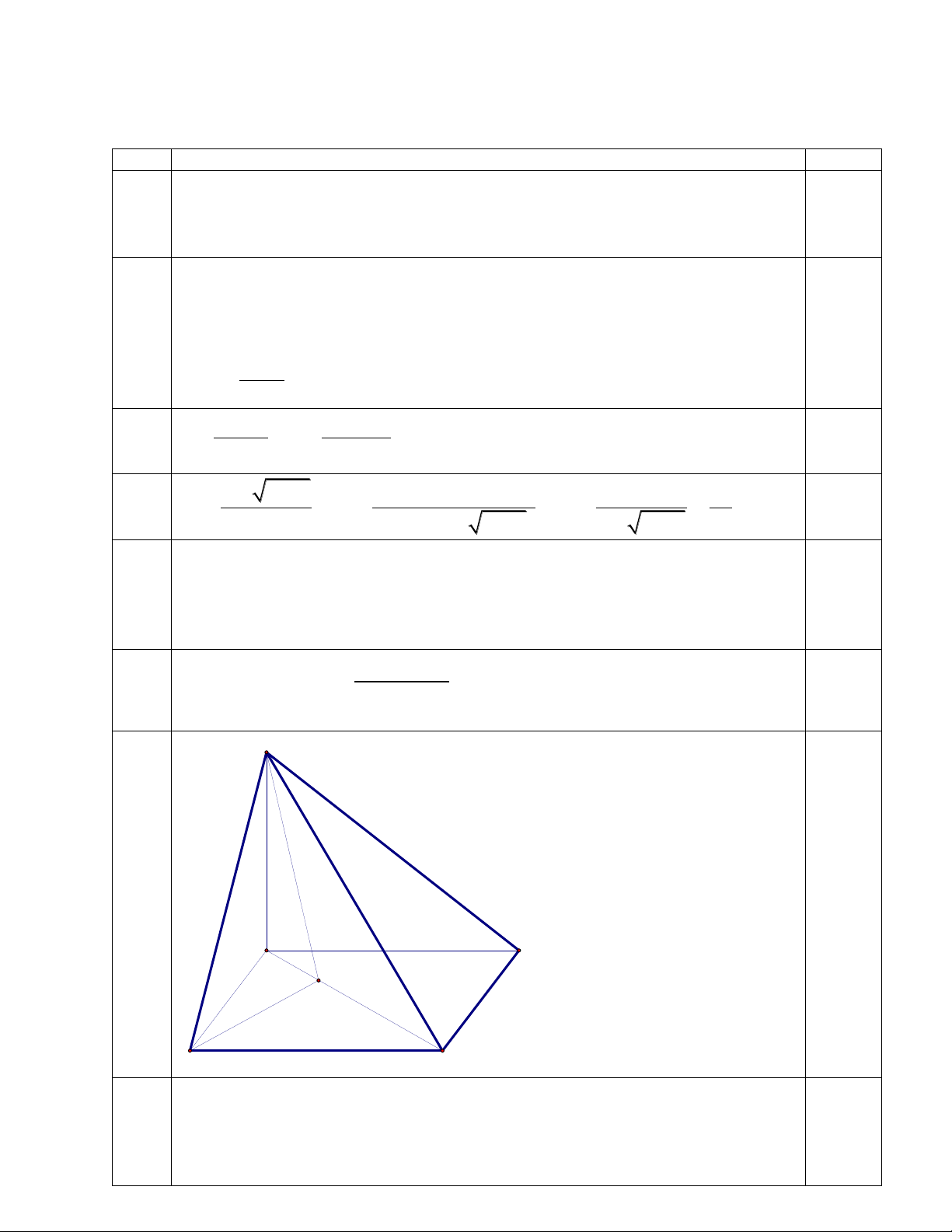
f(x) liên tục tại x = 3 khi m + 2 = 1=>m = -1 S A D H B C C6a. + Ta có: 1.0đ C  D  S ( A gt) 
 CD  (SAD) 0.5đ C  D  AD 0.5đ C  B  S ( A gt)   CB  (SAB) C  B  AB C6b. + Ta có: 0.5đ 1.0đ BH  S ( A gt)   BH  SC 0.5đ BH  AC C6c.
Ta có SH là hình chiếu của SB trên (SAC) và tam giác SBH vuông tại H nên góc 1.0đ
giữa SB và (SAC) là   B  SH . Mà S  AB có 0.25đ 2 A . B BC 2a 2a 5 2 2
SB  SA  AB  a 10 , BH    0.25đ 2 2 AB  BC a 5 5 a 230 2 2
 SH  SB  BH  0.25đ 5 0.25đ     B  SH  HB 46 tan tan   HS 23 C7. Ta có * u
u  u u 1, n N Đặt v  u  u  v  v 1 suy ra n2 n 1  n 1  n n n 1  n n 1  n 1.0đ 0.25đ
(v ) là CSC có : v  u  u  3;d  1 n 1 2 1
nên v  v  (n 1)d  2  n (1) n 1
Từ (1) ta được u u  u u  u u
... u u  v  v ... v  v 0.25đ n 1 n n 1  n 1  n2 2 1 n 1  n2 2 1 v  v n  4 n 1 n 1  1  n      1  2 2
n  4n   1  0.25đ u  1 n 2 u n  n   u 1 n  4  1 2 1 lim  lim  . Vậy lim n  . 0.25đ 2 2 n 2n 2 2 n 2
SỞ GD&ĐT QUẢNG TRỊ
ĐÁP ÁN KT HỌC KỲ II NĂM HỌC 2020 - 2021 TRƯỜNG THPT TXQT MÔN TOÁN KHỐI 11 Mã đề 112 Câu Lời giải Điểm C1.
Ta có u  5;u  7  d  u  u  7  5  2 0.5đ 2 3 3 2 1.0đ 0.5đ
u  u  d  5  2  3 1 2
Vậy u  3;d  2 1 C2. u   u  6 u  (1 q)  6 q  2 1.0đ Ta có 1 2 1      0.5đ u  u  12
u q(1 q)  12 u  2    2 3 1 1 4 u  u q  32 0.25đ 5 1 6 1 q S  u 126 0.25đ 6 1 1 q C3a. 5n  4 5  4 / n 1.0đ   lim lim 5 n 1 1  1.0đ 1 / n C3b. 3  x  6 3  x 1  1  1.0đ lim  lim  lim  0.5đ x 3  x  3 x 3
 (x  3)(3  x  6) x 3  3  x  6 6 0.5đ C4. Xét 7 2
f (x)  11x  3x  2021x  2020 liên tục trên R 0.5đ 1.0đ f(1).f(-1) = -60735<0 0.5đ Vậy phương trình 7 2
11x  3x  2021x  2020  0 có ít nhất một nghiệm thuộc khoảng  1  ;  1 . C5. 2 x  5x  6 1.0đ
Ta có lim f (x)  lim  lim(x  3)  1  0.5đ x2 x2 x2 x  2 0.5đ
f(x) liên tục tại x = 3 khi m + 2 = -1=>m = -3 S C D H B A C6a. + Ta có: 1.0đ
AD  SC(gt)   AD  (SCD) 0.5đ AD  CD 0.5đ
AB  SC(gt)   AB  (SCB) AB  CB C6b. + Ta có: 0.5đ 1.0đ
BH  SC(gt)   BH  SA 0.5đ BH  AC C6c.
Ta có SH là hình chiếu của SB trên (SAC) và tam giác SBH vuông tại H nên góc 1.0đ
giữa SB và (SAC) là   B  SH . Mà S  CB có 0.25đ 2 A . B BC 2a 2a 5 2 2
SB  SC  CB  a 13 , BH    0.25đ 2 2 AB  BC a 5 5 a 305 2 2
 SH  SB  BH  0.25đ 5 0.25đ     B
 SH  BH 2 61 tan tan   HS 61 C7. Ta có * u
u  u u 1, n N Đặt         v u u v v 1   suy ra 1.0đ n 2 n 1 n 1 n n n 1 n n 1 n 0.25đ
(v ) là CSC có : v  u  u  3;d  1 n 1 2 1
nên v  v  (n 1)d  2  n (1) n 1
Từ (1) ta được u u  u u  u u
... u u  v  v ... v  v 0.25đ n 1 n n 1  n 1  n2 2 1 n 1  n2 2 1 v  v n  4 n 1 n 1  1  n      1  2 2
n  4n   1  0.25đ u   2 n 2 u n  n   u 1 n  4  1 4 1 lim  lim  . Vậy lim n  . 0.25đ 2 2 n 2n 2 2 n 2