Đề thi học kỳ 2 Toán 11 năm 2023 – 2024 trường THPT Nguyễn Thị Minh Khai – TP HCM

Xin giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 11 đề kiểm tra cuối học kỳ 2 môn Toán 11 năm học 2023 – 2024 trường THPT Nguyễn Thị Minh Khai, thành phố Hồ Chí Minh; đề thi gồm 01 trang, hình thức tự luận với 07 bài toán, thời gian làm bài 90 phút, có đáp án và hướng dẫn chấm điểm. Mời bạn đọc đón xem!

43 22 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề HK2 Toán 11

Môn: Toán 11

Thông tin:

4 trang 6 tháng trước

Tác giả:

Profile M. Hậu
ĐÁP ÁN & BIỂU ĐIỂM (Toán 11Đề 1)
Bài 1: Giải các phương trình sau:
1đ
Câu 1a:
2
2
2
2 8
x
x x
0.5đ
2
3 2
2 2
2 2 5 6 0 .
6
x
x x
x
x x
x
0.25x2
Câu 1b:
1 1
3 3
7
log ( 6) logx
x
0.5đ
ĐK:
6
x
PT
2
7 (n)
7
6 6 7 0 .
1 (l)
x
x x x
x
x
0.25x2
Bài 2:
2 1
6.4 13.6 2.3 0
x x x
1đ
BPT
2
2 3
1
2 2
3 2
6 13 6 0 .
3 3
2 2
3 3
x
x x
x
x
x
0.25x4
Bài 3: 1đ
Câu 3a: Tính đạo hàm của hàm số:
5
1
log
x x
x
y e
0.5đ
5 5
1 1
log log
5
2
1 1 1 1
' log .
ln 5
2
x x x x
x x
y x x e e
x x
x
x
0.25x2
Câu 3b: Tính đạo hàm cấp hai của hàm số:
2 cos
y x x
0.5đ
' 2 sin 1,
y x
'' 2 cos .
y x
0.25x2
Bài 4: Cho hàm số
2 1
3
x
y f x
x
có đồ thị
C
. Viết phương trình tiếp tuyến
của đồ thị
C
biết
song song với đường thẳng
: 7 9.
D y x
1đ
2
7
' '
3
y f x
x
; Gọi
0
x
là hoành độ tiếp điểm.
0.25
Vì tiếp tuyến
song song với đường thẳng
: 7 9
D y x
nên
0
' 7
f x
2
0
0
2
0
0
2
7
7 3 1 .
4
3
x
x
x
x
0.25
Với
0
2
x
:
0 0 0
: ' 5 7 2 7 9
y f x f x x x x x
(loại).
0.25
Với
0
4
x
:
0 0 0
: ' 9 7 4 7 37
y f x f x x x x x
(nhận).
0.25
Bài 5: Có
2
hộp bút chì màu. Hộp thứ nhất có
5
bút chì màu đỏ và
7
bút chì màu xanh. Hộp thứ
hai có
8
bút chì màu đỏ và
4
bút chì màu xanh. Chọn ngẫu nhiên mỗi hộp một cây bút chì. Tính
xác suất để chọn được
1
cây bút chì màu đỏ và
1
cây bút chì màu xanh.
1đ
1 1
12 12
C C 144.
n
Xét các biến cố:
H
: " Chọn được
1
cây bút chì màu đỏ và
1
cây bút chì màu xanh "
A
: " Chọn được
1
bút đỏ ở hộp
1
và
1
bút xanh ở hộp
2
"
;
45
1 1
C C 20.
n A
B
: " Chọn được
1
bút đỏ ở hộp
2
và
1
bút xanh ở hộp
1
";
1 1
8 7
56.
n B C C
0.25x3
Khi đó
H A B
. Do hai biến cố
A
và
B
xung khắc nên
( )
19
P P( ) P( ) .
76
1
6
4
3
4
n A n B
H A B
n
0.25
Bài 6: Một chiếc máy có
2
động cơ I và II hoạt động độc lập với nhau. Xác suất để động cơ I chạy
tốt và động cơ II chạy tốt lần lượt là
0,8
và
0,7
. Tính xác suất để cả hai động cơ đều chạy không
tốt.
1đ
Xét các biến cố sau:
A
: “Động cơ I chạy tốt”;
.
P
,
P
0, 8; 0 2
A A
B
: “Động cơ II chạy tốt”;
.
P
,
P
0,7; 0 3
B B
0.25x2
C
: “Cả hai động cơ đều chạy không tốt”. Khi đó:
C A B
,
,
A B
là hai biến cố độc lập nên:
.
P
0
P
, 6
P 0C A B
0.25x2
Bài 7: Cho hình chóp
.
S ABC
có đáy
ABC
là tam giác cân tại
B
,
SA ABC
,
AB a
,
120
ABC
,
3
2
a
SA . Gọi
I
là trung điểm của
AC
.
4đ
Câu 7a: Chứng minh rằng:
.
BI SAC
1đ
Tam giác
ABC
cân tại
B
có
I
là trung điểm của
AC
(1)
BI AC
SA ABC
BI SA
(1), (2)
.
BI SAC
0.25x4
Câu 7b: Tính thể tích khối chóp
. .
S ABC
1đ
2
1 1 3
sin sin120 .
2 2 4
ABC
a
S BA BC ABC a a
2 3
.
1 1 3 3 3
.
3 3 4 2 8
S ABC ABC
a a a
V S SA
0.25x4
Câu 7c: Tính góc giữa hai mặt phẳng
SBI
và
.
ABC
1đ
, ,
SBI ABC BI
BI SAC
SBI ABC SI AC SIA
SAC SBI SI
SAC ABC AC
(do
SA ABC SA AI
)
0.25x2
3
sin 60 .
2
a
AI AB
3
2
tan 3 60 .
3
2
a
SA
SIA SIA
AI
a
Vậy
, 60 .
SBI ABC
0.25x2
Câu 7d: Trong
ABC
, lấy điểm
K
sao cho
3
2
CK AB
 
. Gọi
H
là hình chiếu vuông góc của
A
lên
SK
,
L
là điểm thuộc cạnh
SC
thỏa
3
4
SL SC
. Tính khoảng cách từ điểm
C
đến
.
AHL
1đ
Ta có:
2 2 0
3 3
; 2 3, 2 cos 30 ;
2 2
CK a AC AI a AK AC CK AC CK a
2 2 2
.
AK CK AC AK KC
mà
( )
SA CK SA ABC
nên
.
CK SAK CK KH
0.25
2 2
2
2 2 2
3
.
4
SH SA SA SL
SH SK SA HL KC
SK SC
SK SA AK
0.25
, , .
CK AHL d C AHL d K AHL
0.25
KH AH
HK AHL
KH HL CK HK
2 2
1 1 3
, .
4 4 4
a
d K AHL KH SK SA AK
0.25
HẾT
| 1/4
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

ĐÁP ÁN & BIỂU ĐIỂM (Toán 11Đề 1)
Bài 1: Giải các phương trình sau: 1đ Câu 1a: 2 x 2  x 2 2  8 x 0.5đ  2  x  x  x 32 x 1 2  2 2 2 x 5x 6 0         .  x  6 0.25x2  7 Câu 1b: log (x  6)  log 1 1 x 0.5đ 3 3 ĐK: x  6 7 x  7 (n) 0.25x2 PT  2 x 6 x 6x 7 0         . x x  1 (l)  Bài 2: x x 2x 1  6.4  13.6  2.3  0 1đ 2 x   3 2    2 x     2 x      3 2 x  1 BPT  6 13      6 0    0.25x4       x . 3 3     x  1 2   2     3 3  Bài 3: 1đ 1 x log x
Câu 3a: Tính đạo hàm của hàm số: 5 x y e    0.5đ   1 1   x  log 1   5 x  x  lo    1 1 1 5 g '     log x x  x y x x e          0.25x2    e . 5 2 x   x 2 x x ln 5
Câu 3b: Tính đạo hàm cấp hai của hàm số: y  2 cosx  x 0.5đ y '  2
 sinx 1, y '  2cosx. 0.25x2 x 
Bài 4: Cho hàm số y  f x 2 1 
có đồ thị C . Viết phương trình tiếp tuyến  của đồ thị x  3 1đ C biết  
 song song với đường thẳng D: y  7x  9. y  f x 7 ' ' 
; Gọi x là hoành độ tiếp điểm.  0.25 x  32 0 Vì tiếp tuyến  
 song song với đường thẳngD : y  7x  9 nên 7 x  2  f 'x  7 7 x 3 1        . 0.25 2  0 2 0 0    x   x  4 3   0 0  Với x  2 :  
 : y  f x  f ' x  x x  5
  7 x  2  7x  9 (loại). 0.25 0   0  0    0 Với x  4 :  
 : y  f x  f ' x  x x  9  7 x  4  7x  37 (nhận). 0.25 0   0  0    0
Bài 5: Có 2 hộp bút chì màu. Hộp thứ nhất có 5 bút chì màu đỏ và 7 bút chì màu xanh. Hộp thứ
hai có 8 bút chì màu đỏ và 4 bút chì màu xanh. Chọn ngẫu nhiên mỗi hộp một cây bút chì. Tính 1đ
xác suất để chọn được 1 cây bút chì màu đỏ và 1 cây bút chì màu xanh. n   1 1   C  C  144. 12 12 Xét các biến cố:
H : " Chọn được 1 cây bút chì màu đỏ và 1 cây bút chì màu xanh " 0.25x3
A : " Chọn được 1 bút đỏ ở hộp 1 và 1 bút xanh ở hộp 2 " ; n   1 1 A  C  C  20. 5 4
B : " Chọn được 1 bút đỏ ở hộp 2 và 1 bút xanh ở hộp 1"; n B 1 1  C C  56. 8 7
Khi đó H  A  B . Do hai biến cố A và B xung khắc nên   H  n   A n(B) 76 19 P  P( ) A  P(B)    0.25 n   .  144 36
Bài 6: Một chiếc máy có 2 động cơ I và II hoạt động độc lập với nhau. Xác suất để động cơ I chạy
tốt và động cơ II chạy tốt lần lượt là 0,8 và 0,7 . Tính xác suất để cả hai động cơ đều chạy không 1đ tốt. Xét các biến cố sau:
A: “Động cơ I chạy tốt”; P  A  0,8;P  A  ,02. 0.25x2
B : “Động cơ II chạy tốt”; PB  0,7;PB  ,0 .3
C : “Cả hai động cơ đều chạy không tốt”. Khi đó: C  A  B , ,
A B là hai biến cố độc lập nên: 0.25x2 PC  P  A  PB  ,00 .6
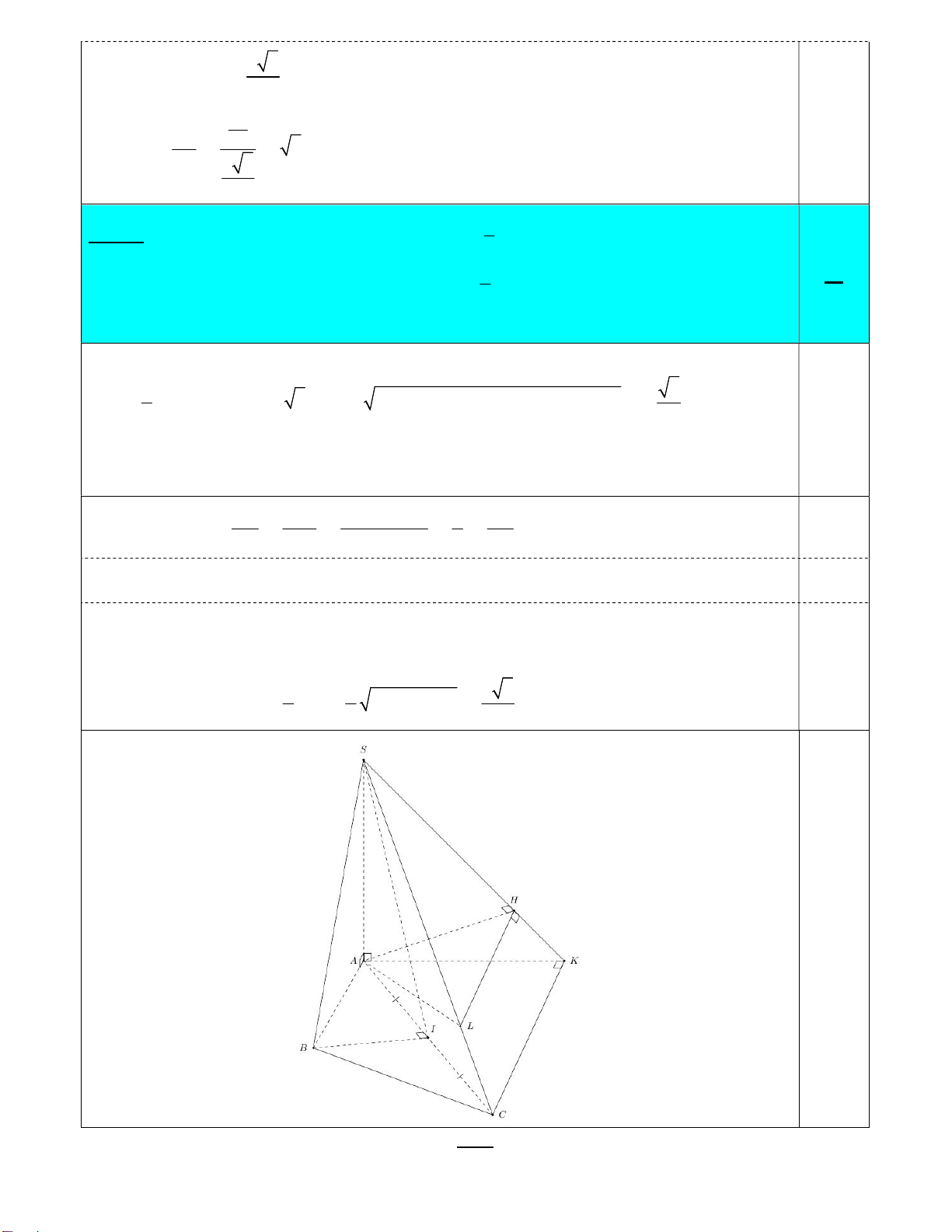
Bài 7: Cho hình chóp S.ABC có đáy ABC là tam giác cân tại B , SA  ABC, AB  a ,  4đ ABC  120 3a , SA 
. Gọi I là trung điểm của AC . 2
Câu 7a: Chứng minh rằng: BI  SAC . 1đ
Tam giác ABC cân tại B có I là trung điểm của AC  BI  AC (1) SA  ABC  BI  SA (2) 0.25x4
(1), (2)  BI  SAC.
Câu 7b: Tính thể tích khối chóp S.ABC. 1đ  2 1 1 a 3 S
 BA BC  sinABC  a a sin120  . ABC 2 2 4 0.25x4 2 3 1 1 a 3 3a a 3 V  S  SA     . S.ABC 3 ABC 3 4 2 8
Câu 7c: Tính góc giữa hai mặt phẳng SBI  và ABC. 1đ
SBIABC BI B  I   SAC 
(do SA  ABC  SA  AI ) 0.25x2     SBI ABC   SI AC   , ,  SIA SAC SBI  SI SAC  ABC AC a 3 AI  AB  sin60  . 2 3a 0.25x2  SA 2  tanSIA  
 3  SIA  60. Vậy SBI ABC  ,  60. AI a 3 2  3 
Câu 7d: Trong ABC , lấy điểm K sao cho CK   AB . Gọi H là hình chiếu vuông góc của 2 A 3 1đ
lên SK , L là điểm thuộc cạnh SC thỏa SL  SC . Tính khoảng cách từ điểm C đến 4 AHL. Ta có: 3 2 2 0 3
CK  a;AC  2AI  a 3,AK  AC CK  2AC CK  cos 30  a ; 2 2 0.25 2 2 2
AK CK  AC  AK  KC.
mà SA  CK (SA  ABC ) nên CK SAK  CK  KH. 2 2 2 SH SA SA 3 SL SH SK  SA       HL  KC. 0.25 2 2 2 SK SK SA  AK 4 SC
 CK  AHL  dC,AHL  dK,AHL . 0.25 K  H  AH    K  H  HL  CK  HK HK AHL 0.25  d K AHL 1 1 2 2 a 3 ,  KH  SK  SA  AK  . 4 4 4 HẾT
Document Outline

  • 11
  • dap-an-kthkii-toan-11-23-24de-1_234202415