Đề thi học kỳ 2 Toán 11 năm học 2019 – 2020 sở GD&ĐT Quảng Nam
Sáng thứ Tư ngày 08 tháng 07 năm 2020, sở Giáo dục và Đào tạo tỉnh Quảng Nam tổ chức kỳ thi kiểm tra khảo sát chất lượng môn Toán đối với học sinh khối 11 trong giai đoạn học kỳ 2 (HK2) năm học 2019 – 2020.
Chủ đề: Đề HK2 Toán 11 391 tài liệu
Môn: Toán 11 3.3 K tài liệu
Tác giả:
Preview text:
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KIỂM TRA HỌC KỲ II NĂM HỌC 2019-2020 QUẢNG NAM
Môn: TOÁN – Lớp 11
Thời gian: 60 phút (không kể thời gian giao đề) ĐỀ CHÍNH THỨC
(Đề gồm có 02 trang) MÃ ĐỀ 101
A/ TRẮC NGHIỆM: (5,0 điểm)
Câu 1: Cho hình lập phương ABC .
D A' B'C ' D' (minh họa như A B
hình bên). Khẳng định nào sau đây sai ? C D
A. AB ⊥ B . C
B. AB ⊥ CC '. B'
C. AB ⊥ B' D'. D. AB ⊥ B'C '. A' D' C'
Câu 2: Cho hình chóp S.ABCD có SA ⊥ (ABCD) (minh họa S
như hình bên). Khi đó góc tạo bởi đường thẳng SB và mặt phẳng ( ABC )
D bằng góc nào sau đây ? A. SAB. B. SC . A D C. SD . A D. . SBA A B C
Câu 3: Tìm đạo hàm của hàm số y = 5 − 4 x (với x 0 ). 4 2 4 2 A. y ' = − . B. y ' = − . C. y ' = . D. y ' = . x x x x
Câu 4: Cho hai hàm số u = u(x), v = v(x) có đạo hàm tại điểm x thuộc khoảng xác định. Mệnh
đề nào sau đây sai ? / u
u 'v − uv '
A. (uv)' = u 'v + uv ' . B. =
( v = v ( x) 0 ). v v
C. (u + v)' = u '+ v ' .
D. (u − v)' = u '− v '. 4
Câu 5: Tìm đạo hàm của hàm số y = x +
(với x 0 ). x 1 4 4 4 A. y ' = 1 − . B. y ' = 1 − . C. y ' = 1− . D. y ' = 1 + . 2 x 2 x x 2 x
Câu 6: Hàm số nào sau đây không liên tục tại x =1 ? 1 A. y = 2 . B. 2
y = x − x + 1 . C. y = y = x . x − . D. sin 1
Câu 7: Tìm mệnh đề sai trong các mệnh đề sau. 1 A. lim n q = + (q>1) . B. lim = 0 . n 1 1
C. limc = c ( c là hằng số). D. * lim = (k ) . k n k
Câu 8: Tìm đạo hàm của hàm số y = sin 2x .
A. y ' = 2 cos 2x .
B. y ' = − cos 2x . C. y ' = 2 − cos2x .
D. y ' = cos 2x . Trang 1/2 – Mã đề 101
Câu 9: Cho hình chóp đều S.ABCD (minh họa như hình bên). S
Khẳng định nào sau đây đúng ?
A. (SBC) ⊥ ( ABCD). B. (SAC) ⊥ ( ABCD).
C. (SAB) ⊥ ( ABCD). D. (SAD) ⊥ ( ABC ) D . A B D C
Câu 10: Cho hàm số y = 2x − 3. Tính y '(3) .
A. y '(3) = 3.
B. y '(3) = 6 .
C. y '(3) = 0 .
D. y '(3) = 2 . x Câu 11: Tính lim . 2 x→2 (x − 2) A. 0. B. − C. 1. D. + .
Câu 12: Cho hình hộp ABC .
D EFGH (minh họa như hình bên). A B
Hãy chọn khẳng định đúng trong các khẳng định sau. C D
A. AG = AB + AD + AE. B. AG = AD + AC + AE. F E
C. AG = AB + AC + AE. D. AG = AB + AD + AC. H G Câu 13: Tính 2
lim(x + 3x +1) . x 1 → A. 5. B. +. C. 1. D. 0. 3
Câu 14: Tính lim(1 + ) . n A. 4. B. 1. C. 3. D. +.
Câu 15: Tìm đạo hàm của hàm số y = 2cos x .
A. y ' = −sin x . B. y ' = 2 − sin x .
C. y ' = 2sin x .
D. y ' = sin x .
B/ TỰ LUẬN: (5,0 điểm)
Bài 1 (1,5 điểm). Tính các giới hạn sau: n 2 x − 3x + 2 a. lim . b. lim 2n + 5 x→2 x − . 2
Bài 2 (1,5 điểm). Cho hàm số 3 y = f ( )
x = x − 5x + 4 có đồ thị (C ).
a. Tính đạo hàm của hàm số trên.
b. Viết phương trình tiếp tuyến của đồ thị (C ) tại điểm M (2;2) .
Bài 3 (2,0 điểm). Cho hình chóp S.ABC có đáy là tam giác vuông tại B, cạnh bên SA vuông góc
với mặt phẳng ( ABC).
a. Chứng minh BC ⊥ (SAB).
b. Gọi ( ) là mặt phẳng qua A và vuông góc với SC . Tính diện tích thiết diện tạo bởi mặt
phẳng () và hình chóp, biết AB = a, BC = a 3 đồng thời góc tạo bởi hai mặt phẳng (SBC) và (ABC) bằng 0 45 .
=================Hết=================
Họ và tên:……………….......…………………..SBD: …….......………….
Chú ý: Học sinh không được sử dụng tài liệu. Giám thị coi thi không giải thích gì thêm. Trang 2/2 – Mã đề 101
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KIỂM TRA HỌC KỲ II NĂM HỌC 2019-2020 QUẢNG NAM
Môn: TOÁN – Lớp 11
Thời gian: 60 phút (không kể thời gian giao đề) ĐỀ CHÍNH THỨC MÃ ĐỀ 102
(Đề gồm có 02 trang)
A/ TRẮC NGHIỆM: (5,0 điểm) 9
Câu 1: Tìm đạo hàm của hàm số y = x +
(với x 0 ). x 1 9 9 9 A. y ' = 1 − . B. y ' = 1 + . C. y ' = 1− . D. y ' = 1 − . 2 x 2 x x 2 x
Câu 2: Cho hàm số y = 5x − 2 . Tính y '(2) .
A. y '(2) = 8 .
B. y '(2) = 0 .
C. y '(2) = 5 .
D. y '(2) = 10 .
Câu 3: Tìm đạo hàm của hàm số y = cos 3x . A. y ' = 3 − sin3x .
B. y ' = −sin 3x .
C. y ' = 3sin 3x .
D. y ' = sin 3x .
Câu 4: Hàm số nào sau đây không liên tục tại x = 3 ? 1 A. 2
y = x + 2x . B. y = y = x . D. y = 5 . x − . C. sin 3 Câu 5: Tính 2
lim(x + x −1) . x→2 A. -1. B. 6. C. 5. D. . +
Câu 6: Tìm đạo hàm của hàm số y = 3sin x .
A. y ' = 3cos x . B. y ' = 3 − cos x .
C. y ' = cos x .
D. y ' = − cos x . 1
Câu 7: Tính lim(2 + ) . n A. 1. B. +. C. 3. D. 2.
Câu 8: Tìm đạo hàm của hàm số y = 7 + 6 x (với x 0 ). 3 6 3 6 A. y ' = − . B. y ' = . C. y ' = . D. y ' = − . x x x x
Câu 9: Cho hai hàm số u = u(x), v = v(x) có đạo hàm tại điểm x thuộc khoảng xác định. Mệnh
đề nào sau đây sai ?
A. (u + v) ' = u '+ v ' .
B. (uv)' = u 'v + uv ' . / u
u 'v + uv '
C. (u − v)' = u '− v '. D. =
( v = v ( x) 0 ). 2 v v
Câu 10: Cho hình chóp đều S.ABCD (minh họa như hình bên). S
Khẳng định nào sau đây đúng ?
A. (SBD) ⊥ ( ABC )
D . B. (SAB) ⊥ ( ABCD). A
C. (SAD) ⊥ ( ABC )
D . D. (SBC) ⊥ ( ABCD). B D C Trang 1/2 – Mã đề 102
Câu 11: Cho hình chóp S.ABCD có SA ⊥ (ABCD) (minh họa như S
hình bên). Khi đó góc tạo bởi đường thẳng SC và mặt phẳng ( ABC )
D bằng góc nào sau đây ? D A. A SC . A B. SAC. C. SD . A D. . SBA B C x Câu 12: Tính lim . 2 x 1 → (x −1) A. . + B. 0. C. . − D. 1.
Câu 13: Tìm mệnh đề sai trong các mệnh đề sau. A. lim n q = + (q>1) . B. k * lim n = + (k ) . 1
C. limc = 0 ( c là hằng số). D. lim = 0 . n
Câu 14: Cho hình hộp ABC .
D EFGH (minh họa như hình bên). A B
Hãy chọn khẳng định đúng trong các khẳng định sau. C D
A. HB = HG + HE + H .
D B. HB = HG + HF + HE. F
C. HB = HE + HF + H .
D D. HB = HG + HF + H . D E H G
Câu 15: Cho hình lập phương ABC .
D A' B'C ' D' (minh họa như A B
hình bên). Khẳng định nào sau đây sai ? C D
A. AD ⊥ B' D'.
B. AD ⊥ C . D
C. AD ⊥ C ' D'.
D. AD ⊥ CC '. B' A' D' C'
B/ TỰ LUẬN: (5,0 điểm)
Bài 1 (1,5 điểm). Tính các giới hạn sau: 3n 2 x + 4x − 5 a. lim . b. lim n + 2 x 1 → x − . 1
Bài 2 (1,5 điểm). Cho hàm số 3
y = f (x) = x + 2x − 4 có đồ thị (C ).
a. Tính đạo hàm của hàm số trên.
b. Viết phương trình tiếp tuyến của đồ thị (C ) tại điểm N (1;− ) 1 .
Bài 3 (2,0 điểm). Cho hình chóp S.ABC có đáy là tam giác vuông tại C, cạnh bên SA vuông
góc với mặt phẳng ( ABC).
a. Chứng minh BC ⊥ (SAC ).
b. Gọi ( ) là mặt phẳng qua A và vuông góc với SB . Tính diện tích thiết diện tạo bởi
mặt phẳng () và hình chóp, biết AC = ,
a BC = 2a đồng thời góc tạo bởi hai mặt phẳng
(SBC) và (ABC) bằng 0 45 .
=================Hết=================
Họ và tên:……………….......…………………..SBD: …….......………….
Chú ý: Học sinh không được sử dụng tài liệu. Giám thị coi thi không giải thích gì thêm. Trang 2/2 – Mã đề 102
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KIỂM TRA HỌC KỲ II NĂM HỌC 2019-2020 QUẢNG NAM
Môn: TOÁN – Lớp 11
Thời gian: 60 phút (không kể thời gian giao đề) ĐỀ CHÍNH THỨC
(Đề gồm có 02 trang) MÃ ĐỀ 103
A/ TRẮC NGHIỆM: (5,0 điểm)
Câu 1: Hàm số nào sau đây không liên tục tại x = 2 ? 1 A. y = y = . C. 2
y = x + 3x .
D. y = sin x . x − . B. 3 2
Câu 2: Tìm đạo hàm của hàm số y = sin 4x .
A. y ' = − cos 4x .
B. y ' = cos 4x . C. y ' = 4 − cos4x .
D. y ' = 4 cos 4x .
Câu 3: Cho hình chóp đều S.ABCD (minh họa như hình bên). Khẳng S
định nào sau đây đúng ?
A. (SAD) ⊥ ( ABC )
D . B. (SAB) ⊥ ( ABCD). A
C. (SCD) ⊥ ( ABCD). D. (SAC) ⊥ ( ABCD). B D C
Câu 4: Cho hình lập phương ABC .
D A' B'C ' D' (minh họa như hình A B
bên). Khẳng định nào sau đây sai ? C D
A. CD ⊥ AA'.
B. CD ⊥ B' D'. B' A'
C. CD ⊥ A . D
D. CD ⊥ A' D'. D' C'
Câu 5: Cho hình chóp S.ABCD có SA ⊥ (ABCD) (minh họa như S
hình bên). Khi đó góc tạo bởi đường thẳng SD và mặt phẳng ( ABC )
D bằng góc nào sau đây ? D A. . SAD B. SD . A A C. SC . A D. . SBA B C
Câu 6: Tìm đạo hàm của hàm số y = 3cos x .
A. y ' = sin x .
B. y ' = −sin x . C. y ' = 3 − sin x .
D. y ' = 3sin x .
Câu 7: Cho hàm số y = 3x − 5 . Tính y '(4) .
A. y '(4) = 12 .
B. y '(4) = 0 .
C. y '(4) = 7 .
D. y '(4) = 3 . 5
Câu 8: Tìm đạo hàm của hàm số y = x +
(với x 0 ). x 5 5 1 5 A. y ' = 1 − . B. y ' = 1 + . C. y ' = 1 − . D. y ' = 1− . 2 x 2 x 2 x x x Câu 9: Tính lim 2 x→3 (x − . 3) A. 1. B. . + C. 0. D. . − Trang 1/2 – Mã đề 103
Câu 10: Cho hai hàm số u = u(x), v = v(x) có đạo hàm tại điểm x thuộc khoảng xác định. Mệnh
đề nào sau đây sai ? / u
u 'v − uv '
A. (uv)' = u 'v − uv ' . B. =
( v = v ( x) 0 ). 2 v v
C. (u + v)' = u '+ v '.
D. (u − v)' = u '− v '.
Câu 11: Tìm đạo hàm của hàm số y = 3 − 8 x (với x 0 ). 8 4 4 8 A. y ' = − . B. y ' = . C. y ' = − . D. y ' = . x x x x Câu 12: Tính 2
lim(x − x +1) . x→3 A. 7. B. 6. C. 1. D. . +
Câu 13: Tìm mệnh đề đúng trong các mệnh đề sau. 1 A. lim = 0 .
B. limc = 0 (c là hằng số). n 1 1 C. * lim = (k ) . D. lim n q = 0 (q>1) . k n k
Câu 14: Cho hình hộp ABC .
D EFGH (minh họa như hình bên). Hãy A B
chọn khẳng định đúng trong các khẳng định sau. C D
A. DF = DA + DB + DC. B. DF = DA + DB + DH. F E
C. DF = DA + DC + DH. D. DF = DB + DC + DH. H G 2
Câu 15: Tính lim(3 + ) . n A. 2. B. 3. C. 5. D. . +
B/ TỰ LUẬN: (5,0 điểm)
Bài 1 (1,5 điểm). Tính các giới hạn sau: 2n 2 x − 4x + 3 a. lim . b. lim n −1 x→3 x − . 3
Bài 2 (1,5 điểm). Cho hàm số 3 y = f ( )
x = x − 6x + 5 có đồ thị (C ).
a. Tính đạo hàm của hàm số trên.
b. Viết phương trình tiếp tuyến của đồ thị (C ) tại điểm K (2; ) 1 .
Bài 3 (2,0 điểm). Cho hình chóp S.ABC có đáy là tam giác vuông tại B, cạnh bên SA vuông góc
với mặt phẳng ( ABC).
a. Chứng minh BC ⊥ (SAB).
b. Gọi ( ) là mặt phẳng qua A và vuông góc với SC . Tính diện tích thiết diện tạo bởi mặt
phẳng () và hình chóp, biết AB = a, BC = a 6 đồng thời góc tạo bởi hai mặt phẳng (SBC) và (ABC) bằng 0 45 .
=================Hết=================
Họ và tên:……………….......…………………..SBD: …….......………….
Chú ý: Học sinh không được sử dụng tài liệu. Giám thị coi thi không giải thích gì thêm. Trang 2/2 – Mã đề 103
SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐÁP ÁN ĐỀ KIỂM TRA HỌC KỲ II QUẢNG NAM
MÔN TOÁN 11 – NĂM HỌC 2019-2020
Thời gian làm bài: 60 phút (Không kể thời gian phát đề)
A. Phần trắc nghiệm: (5,0 điểm) Câu Mã 101 Mã 102 Mã 103 Mã 104 Mã 105 Mã 106 1 C D A A B A 2 D C D A D B 3 B A D A D B 4 B B B A B D 5 B C B B A C 6 C A C A D B 7 D D D A A D 8 A C A D A D 9 B D B D C D 10 D A A B A C 11 D A C D B D 12 A A A A B B 13 A C A C B A 14 B A C A A D 15 B A B B C D
B. Phần tự luận: (5,0 điểm)
Gồm các mã đề 101; 104. Câu Nội dung Điểm 1
Tính các giới hạn sau: (1,5 điểm) n
a. lim 2n 5 n n lim lim 2n 5 5 0.25 n 2 n 1 lim 0.25 5 2 n 1 = 2 0.25
(thiếu bước 1 nhưng đúng bước 2, 3 thì vẫn được điểm tối đa) 2 x 3x 2 b. lim x2 x 2 2 x 3x 2
(x 1)(x 2) lim lim x 2 x 2 x 2 x 0.25 2 Trang 1/9 = lim(x 1) 0.25 x 2 = 1 0.25 2 Cho hàm số 3 y f ( )
x x 5x 4 có đồ thị (C ).
(1,5 điểm) a. Tính đạo hàm của hàm số trên. f x 2 ' 3x 5 0.75
(đạo hàm đúng mỗi số hạng thì được 0.25)
b. Viết phương trình tiếp tuyến của đồ thị C tại điểm M 2;2 .
Ta có: f '2 7 . 0.25
Phương trình tiếp tuyến cần tìm là y 7x 12. 0.5
(Viết đúng công thức thì được 0.25) 3
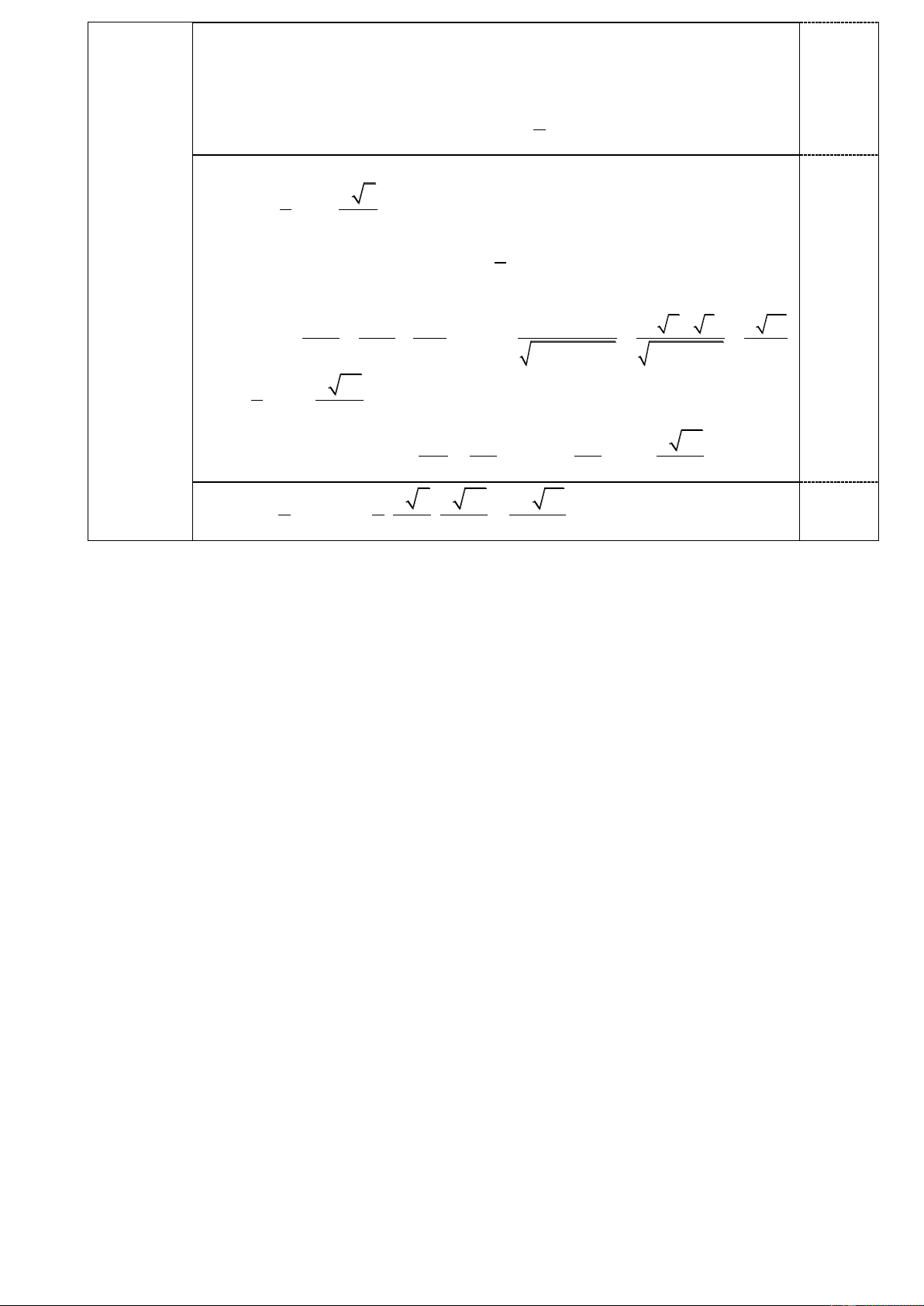
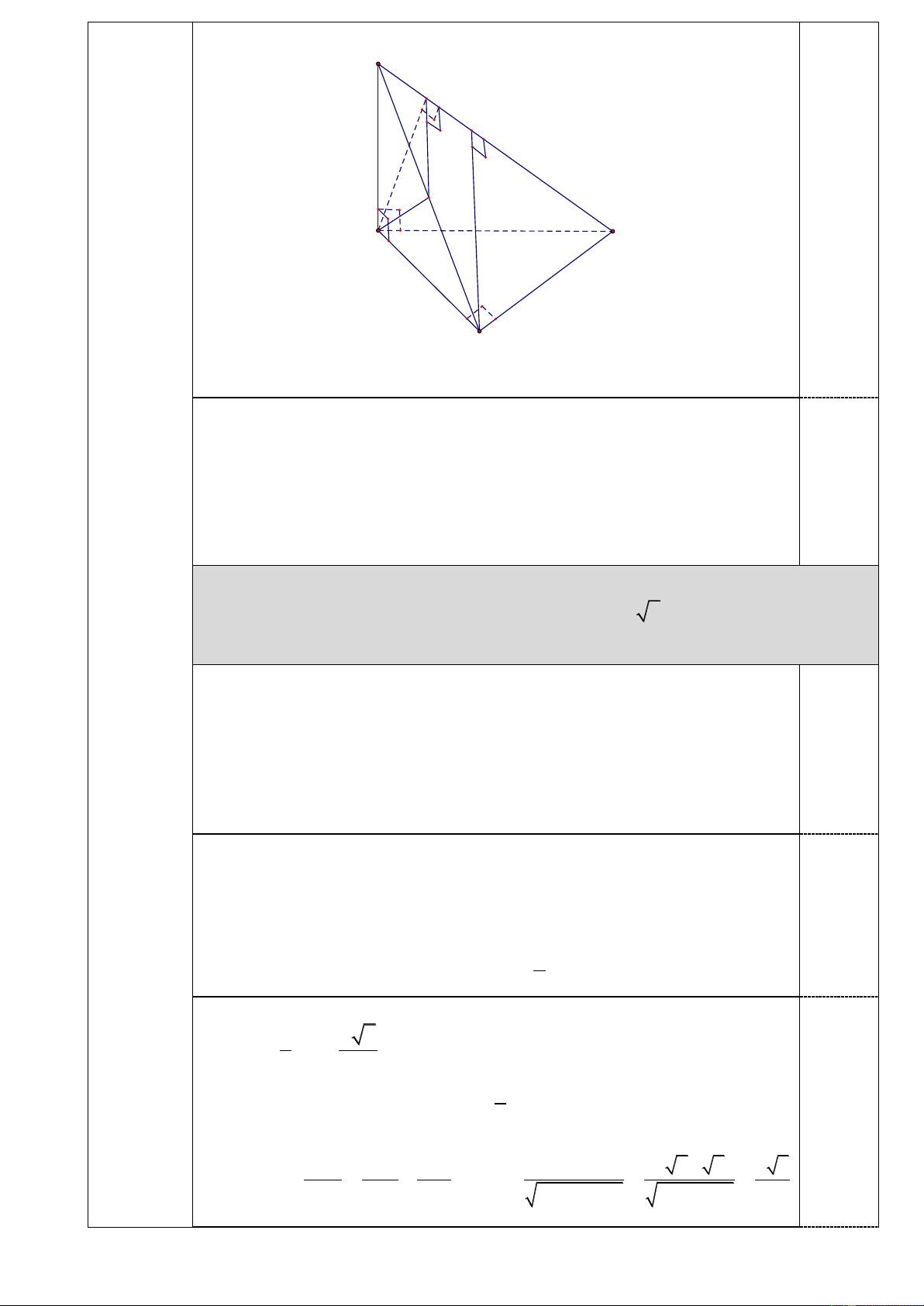
Cho hình chóp S.ABC có đáy là tam giác vuông tại B, cạnh bên SA vuông góc
(2,0 điểm) với mặt phẳng ABC .
a. Chứng minh BC SAB. S E K F A C B
Hình vẽ phục vụ đến câu a, đúng tất cả các nét ở 6 cạnh: 0.25 đ
BC AB (gt) (1) 0.25
SA (ABC) BC SA BC (2) 0.25 A ,
B SA (SAB) (3)
Từ (1),(2),(3) BC SAB. 0.25
(Nói BC SA mà không giải thích thì trừ 0.25 đ; thiếu ý (3): A , B SA (SA )
B ) vẫn cho điểm tối đa).
b. Gọi ( ) là mặt phẳng qua A và vuông góc với SC . Tính diện tích thiết diện tạo
bởi mặt phẳng () và hình chóp, biết AB ,
a BC a 3 đồng thời góc tạo bởi hai
mặt phẳng SBC và ABC bằng 0 45 . (
SBC) (ABC) BC
(SAB) BC(cmt)
(SAB)(ABC) A ,
B (SAB) (SBC) SB
SBC ABC SB AB 0 ( ),( ) , SBA 45 . 0.25
(Học sinh thiếu giải thích thì vẫn được 0.25)
Giả sử () cắt SC,SB lần lượt tại E, F . Trang 2/9
SC () SC AF
Mặt khác: theo cm trên, BC (SA )
B BC AF
AF (SBC) AF SB, AF FE
Diện tích thiết diện cần tìm 1 S AF. AEF FE . 0.25 2 Ta có S
AB vuông cân tại A và AF SB suy ra F là trung điểm SB 1 a 2
AF SB 2 2 Kẻ 1
BK SC BK / /FE FE BK 2 S BC vuông tại B, 1 1 1 BS.BC a 2.a 3 a 30 BK SC BK . 2 2 2 2 2 2 2 BK BC BS 5 BS BC 2a 3a 1 a 30 FE BK 0.25 2 10 (Hoặc EF SF SF a S EF ∽ S 30 BC EF .BC ) BC SC SC 10 2 1 1 a 2 a 30 a 15 S AF.FE . . AEF (đvdt). 0.25 2 2 2 10 20 Trang 3/9
Gồm các mã đề 102; 105. Câu Nội dung Điểm 1
Tính các giới hạn sau: (1,5 điểm) 3n a. lim n 2 3n 3n lim lim 0.25 n 2 2 n1 2 3 lim 0.25 2 1 n = 3 0.25
(thiếu bước 1 nhưng đúng bước 2, 3 thì vẫn được điểm tối đa) 2 x 4x 5 b. lim x 1 x 1 2 x 4x 5
(x 1)(x 5) lim lim x 1 x 1 x 1 x 0.25 1
= lim(x 5) 0.25 x 1 = 6 0.25 2 Cho hàm số 3 y f ( )
x x 2x 4 có đồ thị (C ).
(1,5 điểm) a. Tính đạo hàm của hàm số trên. f x 2 ' 3x 2 0.75
(đạo hàm đúng mỗi số hạng thì được 0.25)
b. Viết phương trình tiếp tuyến của đồ thị C tại điểm N 1; 1 . Ta có: f ' 1 5 . 0.25
Phương trình tiếp tuyến cần tìm là y 5x 6. 0.5
(Viết đúng công thức thì được 0.25) 3
Cho hình chóp S.ABC có đáy là tam giác vuông tại C, cạnh bên SA vuông góc với
(2,0 điểm) mặt phẳng ABC.
a. Chứng minh BC SAC. Trang 4/9 S E K F A B C
Hình vẽ phục vụ đến câu a, đúng tất cả các nét ở 6 cạnh: 0.25 đ
BC AC (gt) (1) 0.25
SA (ABC) BC SA BC (2) 0.25
AC, SA (SAC) (3)
Từ (1),(2),(3) BC SAC. 0.25
(Nói BC SA mà không giải thích thì trừ 0.25 đ; thiếu ý (3):
AC, SA (SAC) ) vẫn cho điểm tối đa).
b. Gọi ( ) là mặt phẳng qua A và vuông góc với SB . Tính diện tích thiết diện tạo
bởi mặt phẳng () và hình chóp, biết AC ,
a BC 2a đồng thời góc tạo bởi hai
mặt phẳng SBC và ABC bằng 0 45 . (
SBC) (ABC) BC
(SAC) BC(cmt)
(SAC)(ABC) AC,(SAC)(SBC) SC
SBC ABC SC AC 0 ( ),( ) , SCA 45 . 0.25
(Học sinh thiếu giải thích thì vẫn được 0.25)
Giả sử () cắt S ,
B SC lần lượt tại E, F .
SB () SB AF
Mặt khác: theo cm trên, BC (SAC) BC AF
AF (SBC) AF SC, AF FE
Diện tích thiết diện cần tìm 1 S AF. 0.25 AEF FE 2 Ta có S
AC vuông cân tại A và AF SC suy ra F là trung điểm SC 1 a 2
AF SC 2 2 Kẻ 1
CK SB CK / /FE FE CK 2 S BC vuông tại C, 1 1 1 CS.CB a 2.2a 2a 3 CK SB CK . 2 2 2 2 2 2 2 CK CB CS 3 CS CB 2a 4a Trang 5/9 1 a 3 0.25 FE CK 2 3 (Hoặc EF SF SF a S EF ∽ S 3 CB EF .BC ) BC SB SB 3 2 1 1 a 2 a 3 a 6 S AF.FE . . AEF (đvdt). 0.25 2 2 2 3 12 Trang 6/9
Gồm các mã đề 103; 106. Câu Nội dung Điểm 1
Tính các giới hạn sau: (1,5 điểm) 2n a. lim n 1 2n 2n l im lim n 1 1 0.25 n1 n 2 lim 1 0.25 1 n = 2 0.25
(thiếu bước 1 nhưng đúng bước 2, 3 thì vẫn được điểm tối đa) 2 x 4x 3 b. lim x3 x 3 2 x 4x 3
(x 1)(x 3) lim lim x 3 x 3 x 3 x 0.25 3 = lim(x 1) 0.25 x 3 = 2 0.25 2 Cho hàm số 3 y f ( )
x x 6x 5 có đồ thị (C ).
(1,5 điểm) a. Tính đạo hàm của hàm số trên. f x 2 ' 3x 6 0.75
(đạo hàm đúng mỗi số hạng thì được 0.25)
b. Viết phương trình tiếp tuyến của đồ thị C tại điểm K 2; 1 .
Ta có: f '2 6 0.25
Phương trình tiếp tuyến cần tìm là y 6x 11. 0.5
(Viết đúng công thức thì được 0.25) 3
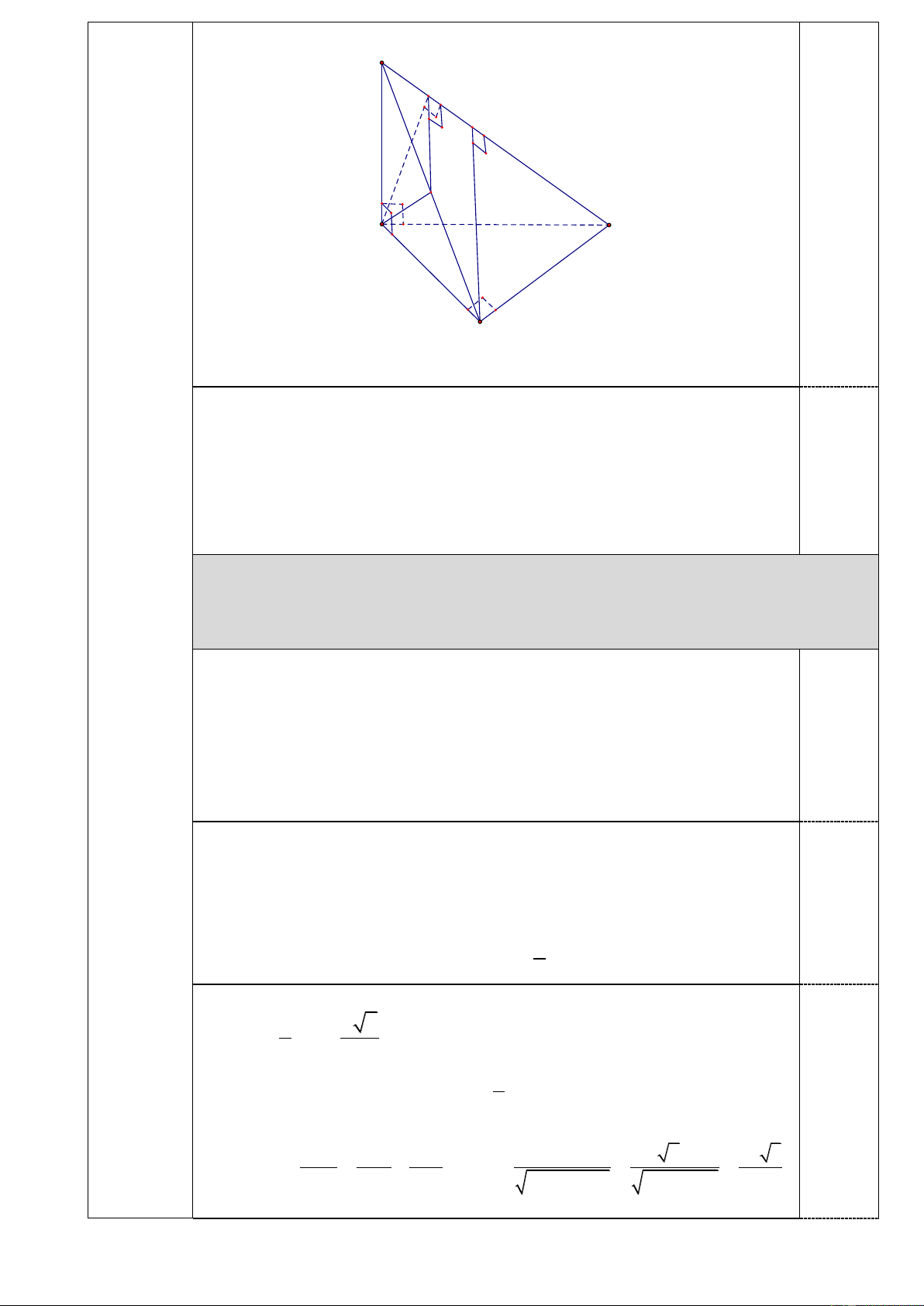
Cho hình chóp S.ABC có đáy là tam giác vuông tại B, cạnh bên SA vuông góc với
(2,0 điểm) mặt phẳng ABC.
a. Chứng minh BC SAB. Trang 7/9 S E K F A C B
Hình vẽ phục vụ đến câu a, đúng tất cả các nét ở 6 cạnh: 0.25 đ
BC AB (gt) (1) 0.25
SA (ABC) BC SA BC (2) 0.25 A ,
B SA (SAB) (3)
Từ (1),(2),(3) BC SAB. 0.25
(Nói BC SA mà không giải thích thì trừ 0.25 đ; thiếu ý (3): A , B SA (SA )
B ) vẫn cho điểm tối đa).
b. Gọi ( ) là mặt phẳng qua A và vuông góc với SC . Tính diện tích thiết diện tạo
bởi mặt phẳng () và hình chóp, biết AB ,
a BC a 6 đồng thời góc tạo bởi hai
mặt phẳng SBC và ABC bằng 0 45 . (
SBC) (ABC) BC
(SAB) BC(cmt)
(SAB)(ABC) A ,
B (SAB) (SBC) SB
SBC ABC SB AB 0 ( ),( ) , SBA 45 . 0.25
(Học sinh thiếu giải thích thì vẫn được 0.25)
Giả sử () cắt SC,SB lần lượt tại E, F .
SC () SC AF
Mặt khác: theo cm trên, BC (SA )
B BC AF
AF (SBC) AF S , B AF FE
Diện tích thiết diện cần tìm 1 S AF. 0.25 AEF FE . 2 Ta có S
AB vuông cân tại A và AF SB suy ra F là trung điểm SB 1 a 2
AF SB 2 2 Kẻ 1
BK SC BK / /FE FE BK 2 S BC vuông tại B, 1 1 1 BS.BC a 2.a 6 a 6 BK SC BK . 2 2 2 2 2 2 2 BK BC BS 2 BS BC 2a 6a Trang 8/9 1 a 6 0.25 FE BK 2 4 (Hoặc EF SF SF a S EF ∽ S 6 BC EF .BC ) BC SC SC 4 2 1 1 a 2 a 6 a 3 S AF.FE . . AEF (đvdt). 0.25 2 2 2 4 8
Ghi chú: - Học sinh giải cách khác đúng thì được điểm tối đa tương ứng.
- Tổ Toán mỗi trường cần thảo luận kỹ HDC trước khi tiến hành chấm.
--------------------------------Hết-------------------------------- Trang 9/9
Document Outline
- Ma de 101
- Ma de 102
- Ma de 103
- Dap an cac ma de