SỞ GDĐT PHÚ YÊN
ĐỀ KIỂM TRA HỌC KÌ II (2019-2020)
TRƯỜNG THPT NGÔ GIA TỰ
Môn: TOÁN - Khối 11 Mã đề thi: 132
Thời gian làm bài: 90 phút.
Họ, tên thí sinh:..................................................................... SBD: .............................
I. PHẦN TRẮC NGHIỆM (7điểm - 35 câu)
Câu 1: Trong các giới hạn sau, giới hạn nào bằng 1? 3 n+3 n 3 4 2 A. 2n + 3n − 4 lim . B. 3 + 5.2 − + lim . C. (5n +1)(n − 3) lim D. 9n n 2 lim . 2 3n + 5 4n + 3n 5 2n + n −1 3n +1 2 x −
Câu 2: Tính giới hạn 9 lim , kết quả là: x→3 x − 3 A. 1. B. 0 C. 3. D. 6 . Câu 3: Hàm số: x −1 y = có đạo hàm là: x A. 2 ' − x y − − = B. 1 y ' = . C. 1 ' x y = . D. 2 ' x y = . 2 2x x −1 2 2x x −1 2 x x −1 2x x −1  mx + 9 −3 Câu 4: Cho hàm số  , x ≠ 0 f (x) =  x
. Hàm số đã cho liên tục tại x = 0 khi 0 n , x = 0
A. m = 3n .
B. m = n .
C. m = 6n .
D. m = 9n
Câu 5: Hệ số góc của tiếp tuyến của đường cong 3 2
y = x − 4x − 7x + 5 tại điểm có hoành độ x = 1 − bằng: 0 A. 8 . B. 4 . C. 4 − . D. 6 .
Câu 6: Cho hình chóp S.ABC có SB ⊥ ( ABC), tam giác ABC S
vuông tại B . Khẳng định nào dưới đây là đúng ?
A. Góc giữa SC và mặt phẳng SAB là góc  SBC.
B. Góc giữa AC và mặt phẳng SAB là góc  CB . A C B
C. Góc giữa SA và mặt phẳng ABC là góc  AS . B
D. Góc giữa AC và mặt phẳng SBC là góc  AC . B A Câu 7: Hàm số: 3x y = có đạo hàm là: x + 2 A. 5 y ' − = . B. 6 y ' = . C. 3 y ' = . D. 5 y ' = (x + 2)2 (x + 2)2 x + 2 (x + 2)2
Câu 8: Cho hàm số y = f (x) = xcos x . Giá trị f ' π   bằng: 6    A. 6 3 + π B. 3 −1 C. 3 +1 D. 6 3 − π 12 2 2 12
Câu 9: Hàm số y = sin 5x có đạo hàm là:
A. y ' = −cos5x B. y ' = 5 − cos5x
C. y ' = 5cos5x
D. y ' = cos5x
Câu 10: Hàm số f (x) = 3x + 2 có đạo hàm là:
Trang 1/4 - Mã đề thi 132 A. 1 y ' = . B. 3 y ' = . C. 1 y ' = . D. 3 y ' = . 2 3x + 2 2 3x + 2 3x + 2 3x + 2 4 3 Câu 11: Hàm số: x x y = −
+ x + 2020 có đạo hàm là: 2 3 A. 3
y ' = x − x +1. B. 3
y ' = 8x − 3x . C. 3 2
y ' = 2x − x +1. D. 3 2
y ' = 2x − x
Câu 12: Hàm số y = tan x có đạo hàm là: − − A. 1 y ' = B. 1 y ' = C. 1 y ' = D. 1 y ' = 2 cos x 2 sin x 2 cos x 2 sin x 2 x +
Câu 13: Tính giới hạn 3 2 lim x , kết quả là: 2 x→+∞ 4x −1 A. 1 − B. 3 − . C. 3 . D. 2 . 2 4 2 3 3 + + +
Câu 14: Tính giới hạn x 1 2x 5 lim , kết quả là: x→−∞ 3x + 4 3 3 3 A. 2 −1 . B. 1 . C. 1+ 2 D. 1+ 5 . 3 3 3 3
Câu 15: Hàm số nào sau đây liên tục tại x =1. 0 2 A. 3x − 2 y x − = .
B. y = x −1 . C. 1 y = .
D. y = x − 3 x −1 x − 2 4 3
Câu 16: Cho hàm số: y = f (x) 3x − 2x + 7 = . Giá trị f '(− ) 1 bằng: x A. 6 . B. 20 . C. 8 . D. 6 − .
Câu 17: Hàm số: y = ( x − )4 5 1 có đạo hàm là:
A. y = ( x − )3
' 9 5 1 . B. y = ( x − )3 ' 5 5 1
C. y = ( x − )3
' 20 5 1 . D. y = ( x − )3 ' 4 5 1 .
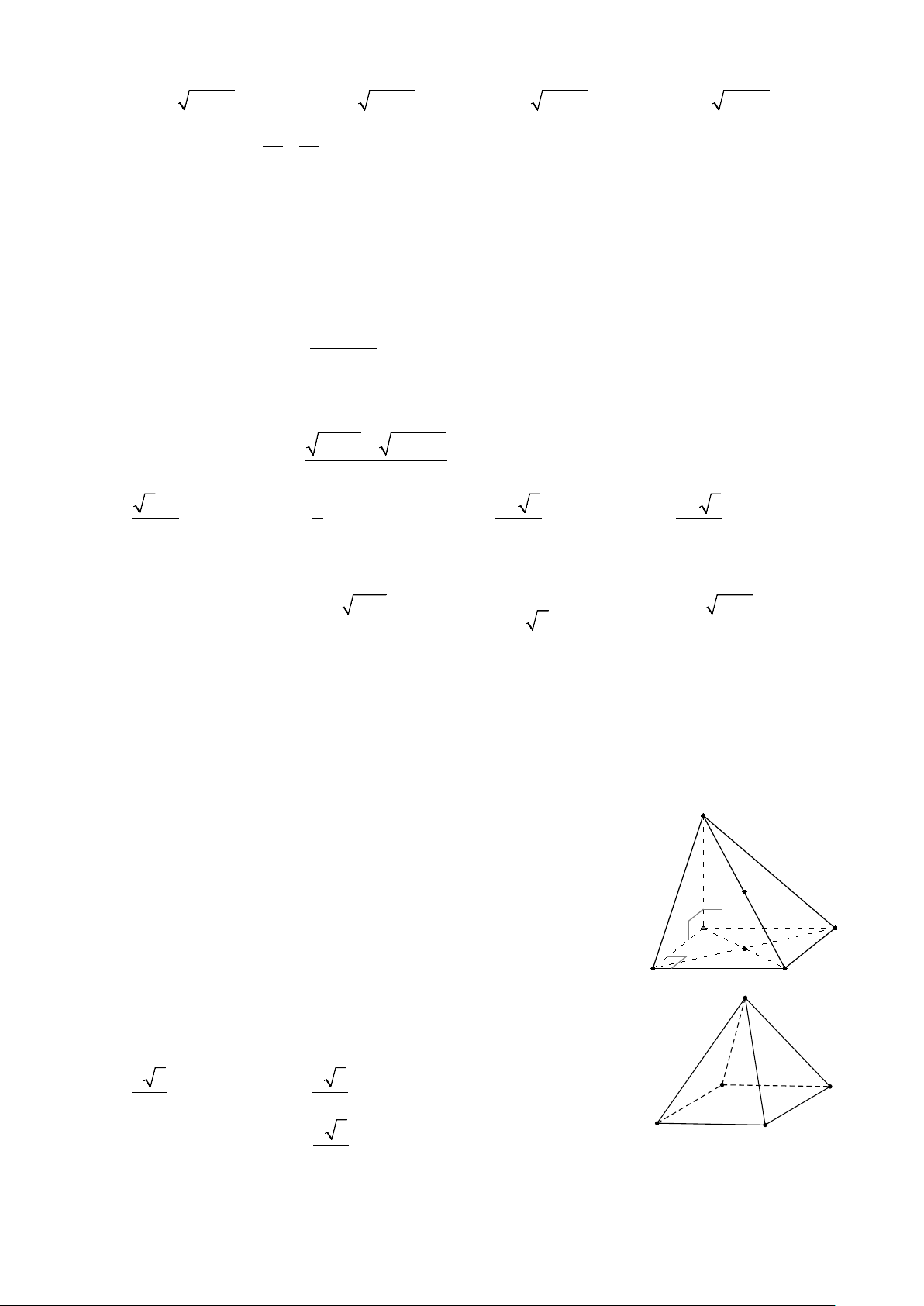
Câu 18: Cho hình chóp S.ABCD có đáy ABCD là hình vuông S
tâm O, SA ⊥ ( ABCD) gọi I là trung điểm của cạnh SC . Khẳng
định nào sau đây là sai?
A. IO ⊥ (ABCD) I
B. BD ⊥ SC D
C. Mặt phẳng(SBD)là mặt phẳng trung trực của đoạn AC. A O
D. Mặt phẳng(SAC) là mặt phẳng trung trực của đoạn B . D B C Câu 19: S
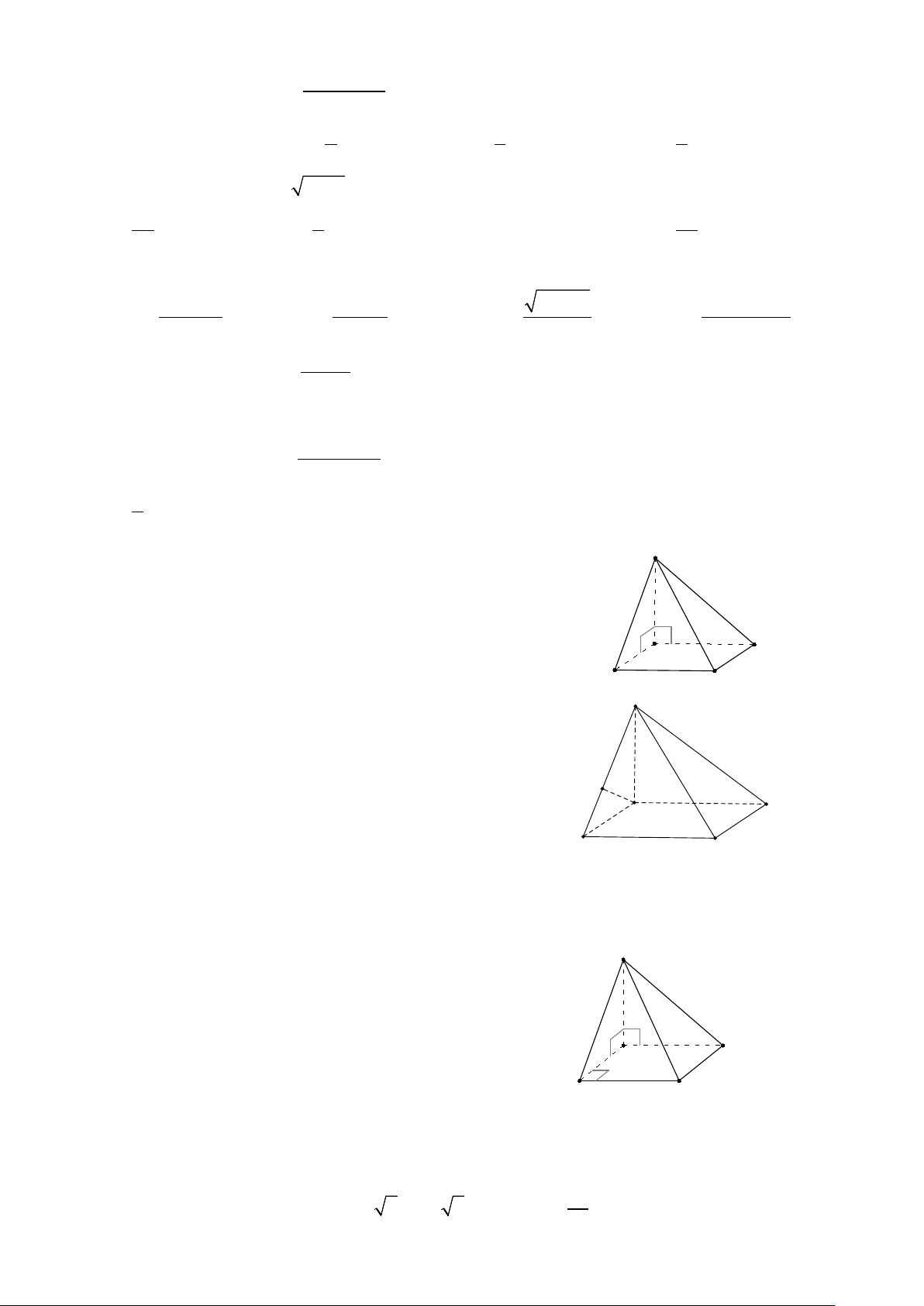
Cho hình chóp S.ABCD có đáy hình vuông a ,
SA = SB = SC = SD = a . Khoảng cách giữa hai đường thẳng chéo
nhau SA và BC bằng: A D A. a 6 B. a 2 3 2 B C. a D. a 6 C 6
Trang 2/4 - Mã đề thi 132 2 + −
Câu 20: Tính giới hạn 5n n 4 lim , kết quả là: 2 3n +1 A. 0 B. 5 − C. 1 . D. 5 . 2 3 3
Câu 21: Cho hàm số y = 3x −1 . Gía trị của 3 y .y '' bằng: A. 9 − . B. 3 . C. 1 − − . D. 3 . 4 2 2
Câu 22: Trong các giới hạn sau, giới hạn nào bằng 0 ? 3 2 2 3 A. 2 lim − n . B. 3 + lim n − n . C. 4n 3 lim . D. 2n + 5n − 4 lim 2 3n + 5n 2 n + 2 2n +1 4 3n +1 3x − 7
Câu 23: Tính giới hạn lim , kết quả là: x 1− → x −1 A. 7 B. +∞ . C. 3. D. −∞ . 2 x + x −
Câu 24: Tính giới hạn 3 4 lim , kết quả là: x→0 5x +1 A. 1 . B. 4 − . C. 4 D. 0 . 5
Câu 25: Cho hình chóp S.ABCD có đáy ABCD là hình bình S
hành, SA ⊥ ( ABCD) . Góc giữa đường thẳng SB và mặt
phẳng (ABCD) bằng góc nào sau đây: A.  SAB B.  SBA D A C.  ASB D.  SBC B C
Câu 26: Cho hình chóp S.ABCD có đáy là hình chữ nhật, S
SA ⊥ ( ABCD) . Gọi H là hình chiếu của điểm A lên
đường thẳng SB . Khẳng định nào sau đây là đúng?
A. AH ⊥ (SBC) B. AH ⊥ (SCD) H D A
C. AH ⊥ (SAD) D. AH ⊥ (SAB) B C
Câu 27: Hàm số y = cos x + 3sin x có đạo hàm là:
A. y ' = sin x − 3cos x
B. y ' = −sin x + cos x
C. y ' = 3cos x − sin x
D. y ' = sin x + 3cos x
Câu 28: Cho hình chóp S.ABCD có đáy ABCD là hình S
vuông cạnh a , SA ⊥ ( ABCD) và SA = a . Tính góc giữa
đường thẳng SB và mặt phẳng(ABCD) kết quả là: A. 0 30 B. 0 90 D C. 0 45 D. 0 60 A B C Câu 29: Hàm số: 3 2
y = x − x + 5x −1 có đạo hàm là: A. 2
y ' = 3x − 2x + 5 B. 2
y ' = 3x − x + 5. C. 2
y ' = 3x − 2x + 4 . D. 2
y ' = x − 2x −1. 2  π 
Câu 30: Cho hàm số y = f (x) = sin x − cos x . Giá trị f ' bằng: 16   
Trang 3/4 - Mã đề thi 132 A. 2 B. 0 C. 2 D. 2 2 π π
Câu 31: Hàm số nào sau đây có đạo hàm là y ' = 2(3x −1) ? A. 2 y = (3x −1) . B. 2
y = 3x − 2x + 7. C. 3
y = 2x − 2x + 5. D. 2
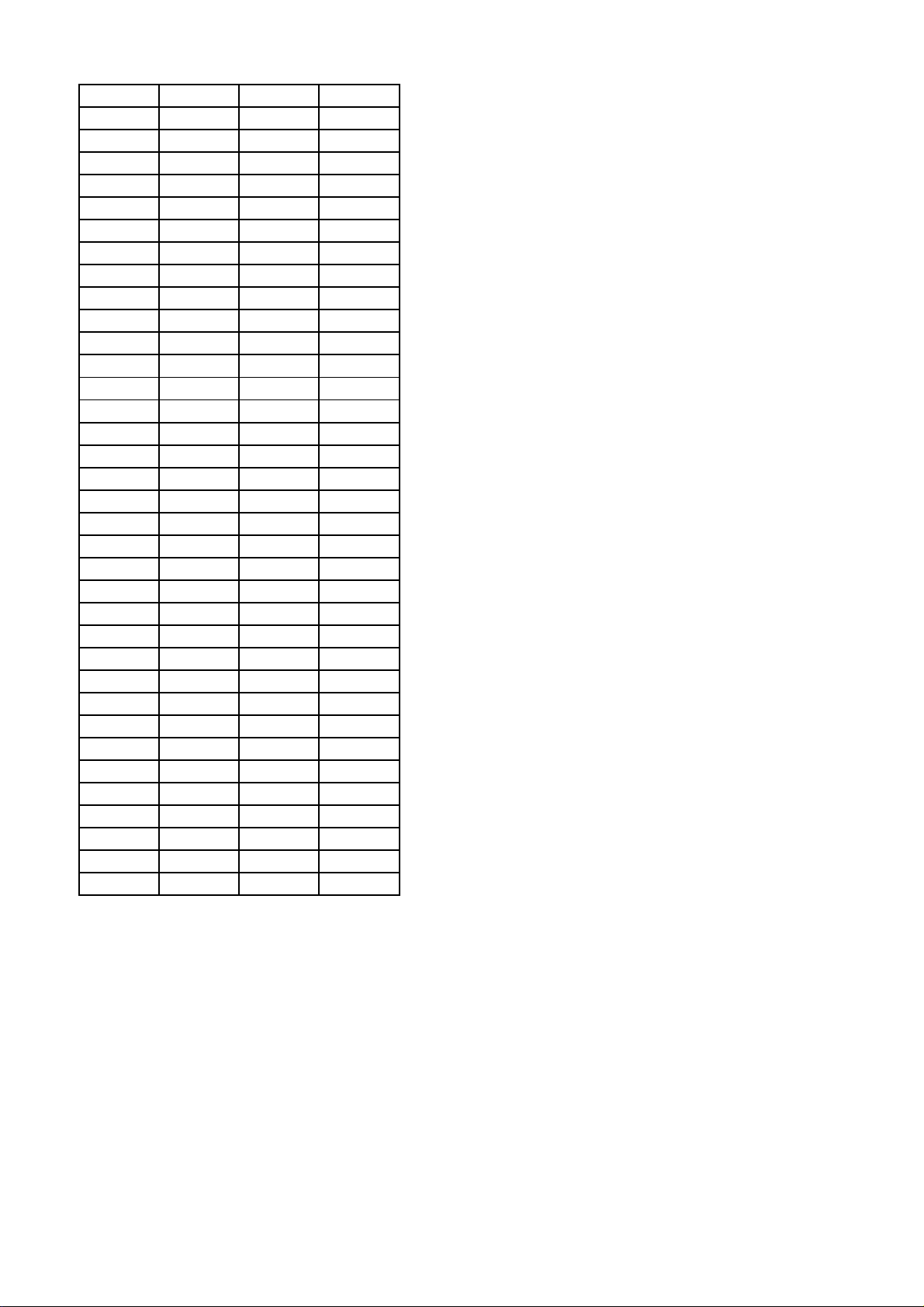
y = 6x − 2x +1 Câu 32: S
Cho hình chóp S.ABCD có đáy ABCD là hình vuông
tâmO , SA ⊥ ( ABCD). Khẳng định nào sau đây là sai ?
A. Góc giữa hai mặt phẳng (SBC) và ( ABCD) là  SBA.
B. Góc giữa hai mặt phẳng (SAC) và ( ABCD) bằng 900 D A
C. Góc giữa hai mặt phẳng (SBD) và ( ABCD) là  SOA O B C
D. Góc giữa hai mặt phẳng (SAD) và ( ABCD) là  SDA
Câu 33: Cho hình chóp S.ABCD có SA ⊥ ( ABCD) ), đáy ABCD là hình chữ nhật.
Biết SA = a, AD = 2a, AB = a 3. Khoảng cách từ điểm A đến mặt phẳng(SCD) bằng: A. 3a 7 B. 3a 2 C. 2a 5 D. a 3 7 2 5 2
Câu 34: Cho hình chóp S.ABCD có đáy là hình chữ nhật, S
SA ⊥ ( ABCD) . Tam giác nào sau đây không phải là tam giác vuông? A. S ∆ AB B. S ∆ BD D C. SC ∆ D D. S ∆ BC A B C
Câu 35: Cho hình chóp S.ABC có SA = SB = SC và tam giác ABC vuông tại B . Kẽ
SH ⊥ ( ABC) tại H . Khẳng định nào sau đây là đúng?
A. H trùng với trung điểm của đoạn AC .
B. H trùng với điểm B .
C. H trùng với trọng tâm của tam giác ABC . D. H trùng với trung điểm của đoạn BC .
-----------------------------------------------
II. PHẦN TỰ LUẬN (3 điểm) 2
Bài 1: Tính giới hạn : 4x + 5x + 2 lim + = x A . x→+∞ 7x − 3
Bài 2: Tính đạo hàm của hàm số: 4 3
y = x − 5x + 6 x + 2020 .  2 6 − 7x + 8  (x < 2)
Bài 3: Tìm a để hàm số 2 2x −9x +10 f (x) = 
liên tục tại x = 2 .  3 2 43 ax − 2a x + (x ≥ 2)  3
Bài 4: Viết phương trình tiếp tuyến với đường cong y = (x − 2) 2x + 4 biết hệ số góc của tiếp tuyến bằng 1.
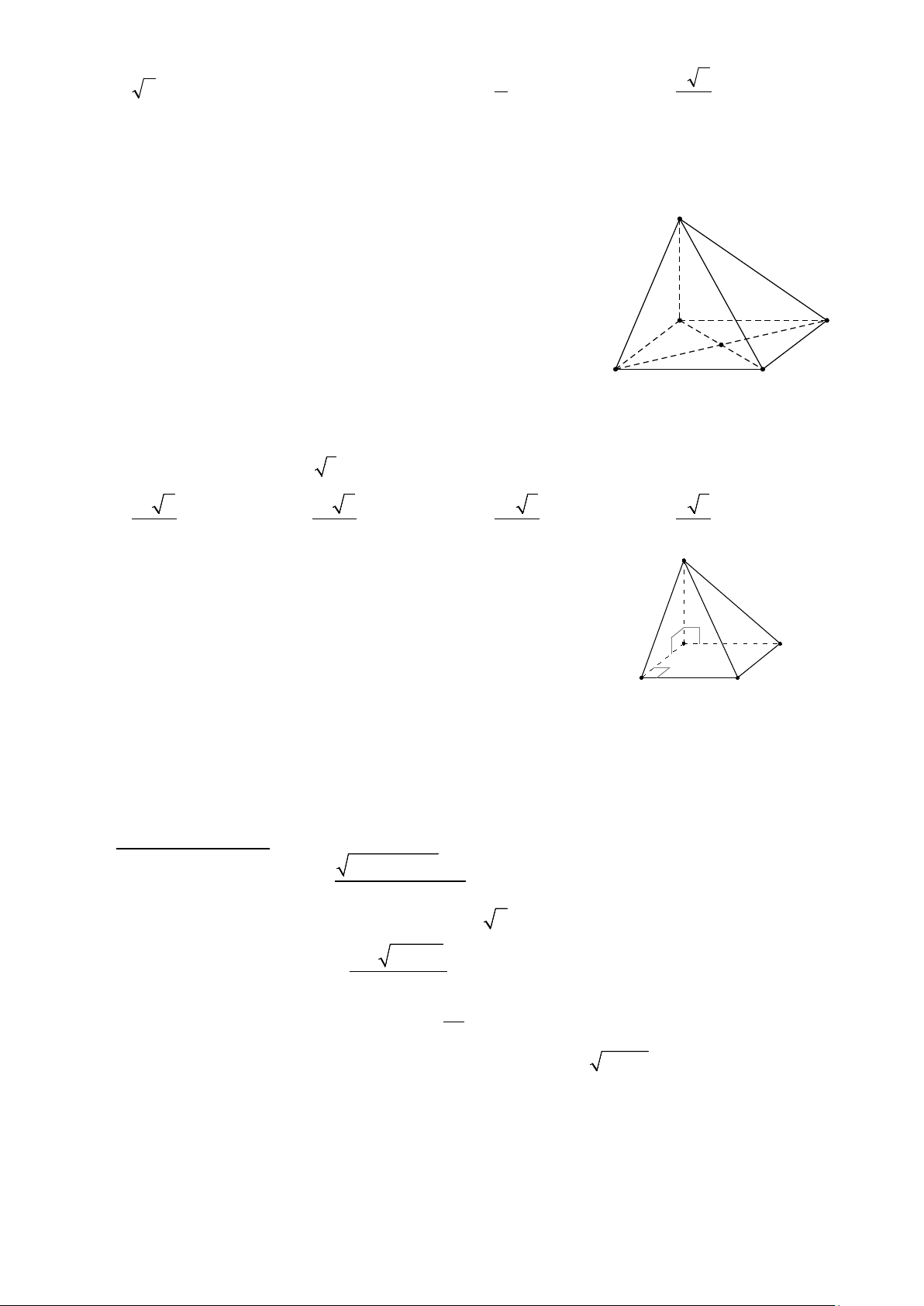
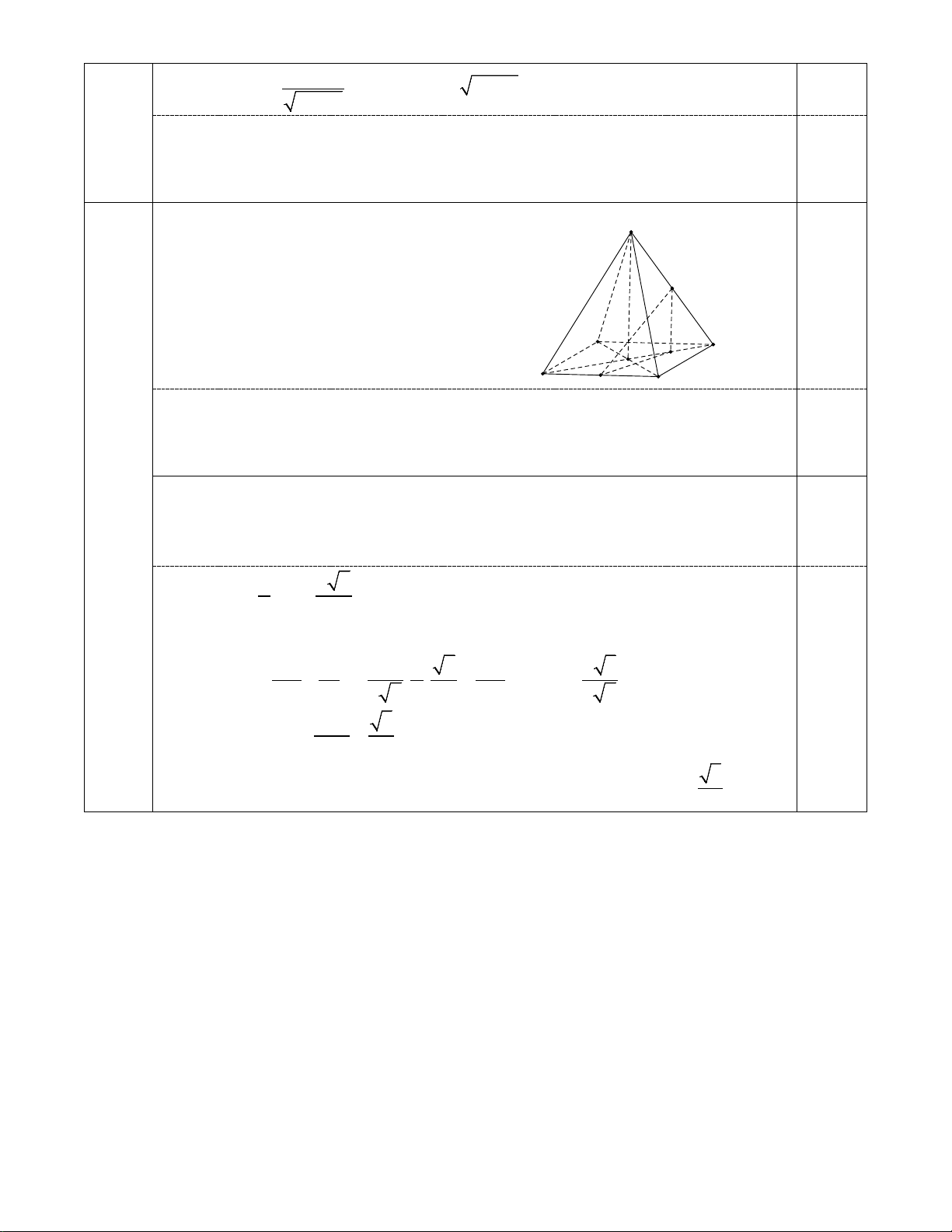
Bài 5: Cho hình chóp S.ABCD có đáy là hình vuông tâm O và SO ⊥ ( ABCD) .
a) Chứng minh rằng AC ⊥ (SBD), BD ⊥ (SAC).
b) Gọi M , N lần lượt là trung điểm của các cạnh BC , SD , biết SA = AD = a , tính góc
giữa đường thẳng MN và mặt phẳng (ABCD) .
Trang 4/4 - Mã đề thi 132 mamon made cautron dapan K11 132 1 D K11 132 2 D K11 132 3 A K11 132 4 C K11 132 5 B K11 132 6 D K11 132 7 B K11 132 8 D K11 132 9 C K11 132 10 B K11 132 11 C K11 132 12 A K11 132 13 C K11 132 14 A K11 132 15 C K11 132 16 A K11 132 17 C K11 132 18 C K11 132 19 A K11 132 20 D K11 132 21 A K11 132 22 D K11 132 23 B K11 132 24 B K11 132 25 B K11 132 26 A K11 132 27 C K11 132 28 C K11 132 29 A K11 132 30 D K11 132 31 B K11 132 32 D K11 132 33 C K11 132 34 B K11 132 35 A
ĐÁP ÁN ĐỀ THI HỌC KÌ II - TOÁN 11 ( NĂM HỌC 2019-2020) II. PHẦN TỰ LUẬN BÀI ĐÁP ÁN ĐIỂM Tính 5 2 2 x 4 + + + x 2 4x + 5x + 2 = lim + x = lim x x A x→+∞ 7x − 3 x→+∞  3 x7  − 0,25 x    1 5 2 4 + + +1 2 x x 3 A = lim = x→+∞ 3 7 7 0,25 − x
* Nếu chỉ bấm máy tính ghi đúng kết quả thì được 0,25đ
Tính đạo hàm của hàm số: 4 3
y = x − 5x + 6 x + 2020 . 3 2 1 3 2 3
y ' = 4x − 5.3x + 6 = 4x −15x + . 2 2 x x 0, 5
* Nếu chỉ tính đúng đến 3 2 1
y ' = 4x − 5.3x + 6 vẫn được 0,5đ 2 x  2 6 − 7x + 8  (x < 2)
Tìm a để hàm số 2 2x −9x +10 f (x) = 
liên tục tại x = 2 .  3 2 43 ax − 2a x + (x ≥ 2)   3 2 2 Ta có 6 − 7x + 8 28 − 7 lim ( ) = lim = lim x f x . − − 2 x 2
x 2 2x − 9x +10 x 2− → → →
(x − 2)(2x −5)( 2 6 + 7x + 8) 7 − (2 + x) 7 = lim = 0,25 3 x 2− → ( x − )( 2 − x + ) 3 2 5 6 7 8 2 43
lim f (x) = f (2) = 8a − 4a + x 2+ → 3
Hàm số đã cho liên tục tại
x = 2 khi và chỉ khi: 2 43 7
lim f (x) = lim f (x) = f (2) ⇔ 8a − 4a + = x 2− x 2+ → → 3 3 a = 1 − 2
⇔ 4a −8a −12 = 0 ⇔  a = 3
Vậy giá trị cần tìm là 0,25 a = 1, − a = 3 .
Viết phương trình tiếp tuyến với đường cong y = (x − 2) 2x + 4 biết hệ số
góc của tiếp tuyến bằng 1. 4
Ta có y = x + + (x − ) 1 2x + 4 + x − 2 3x + 2 ' 2 4 2 = = 2x + 4 2x + 4 2x + 4 0,25 1 Theo gt 3x + 2 k =
= 1 ⇔ 3x + 2 = 2x + 4 2x + 4 3  x + 2 ≥ 0 ⇔ 
⇔ x = 0 ⇒ y = 4 − 2 9  x +10x = 0 0,25
Vậy phương trình tiếp tuyến cần tìm là ∆ : y = x − 4 S
a) Chứng minh rằng AC ⊥ (SBD), BD ⊥ (SAC). N
a) Theo gt SO ⊥ ( ABCD) ⇒ SO ⊥ AC,SO ⊂ (SBD)
Tứ giác ABCD là hình vuông nên BD ⊥ AC A D O
Vậy AC ⊥ (SBD). H B 0,25 M C
Tương tự SO ⊥ BD,SO ⊂ (SAC)
Tứ giác ABCD là hình vuông nên AC ⊥ BD
Vậy BD ⊥ (SAC) 0,25
b) SA = AD = a , tính góc giữa đường thẳng MN và mặt phẳng(ABCD) . 5
Gọi H là trung điểm của đoạnOD ta có NH / /SO nên NH ⊥ ( ABCD) tại H
Suy ra góc giữa đường thẳng MN và mặt phẳng (ABCD) bằng  NMH . 0,25 Ta có 1 a 2 NH = SO = 2 4 2 2 2 ∆ = + −  BMH :MH BH BM
2BH.BM.cos MBH 2 2 2 2 9a a 3a a 2 5a a 5 MH = + − 2 . . = ⇒ MH = 8 4 2 2 2 2 8 2 2 Khi đó  HN 5 tan NMH = = HM 5
Vậy góc giữa đường thẳng MN và mặt phẳng (ABCD) bằng 5 arctan . 0,25 5 2 3
Document Outline

• THI HK2 K11_K11_132
• THI HK2 K11_K11_dapancacmade
  • Table1
• ĐÁP ÁN TOÁN 11hk2 2020