SỞ GD&ĐT QUẢNG TRỊ
ĐỀ KIỂM TRA HỌC KỲ II NĂM HỌC:2019 – 2020
TRƯỜNG THPT THỊ XÃ QUẢNG TRỊ
Môn: Toán 11 - Mã đề: 01 ĐỀ CHÍNH THỨC
(Thời gian làm bài: 90 phút) (Đề có 01 trang) ĐỀ 01
Câu 1: (2.0điểm). Tính các giới hạn sau: n 1 a) lim . n  3 2 x  2x  3 b) lim . x 3  x  3
Câu 2: (1.0 điểm).
 x  x  2  khi x  2
Cho hàm số: f (x)   x  2
m khi x  2
Tìm m để hàm số liên tục tại x  2 .
Câu 3: (2.0 điểm). Cho hàm số 3 2
f (x)  2x  6x  6x  2019 .
a) Tính f '(1) .
b) Giải bất phương trình f '(x 1)  6 .
Câu 4: (1.0 điểm). 2x  1 Cho hàm số y  có đồ thị là (C). x  1
Viết phương trình tiếp tuyến của (C) tại điểm có hoành độ x  -2.
Câu 5: (3.0 điểm).
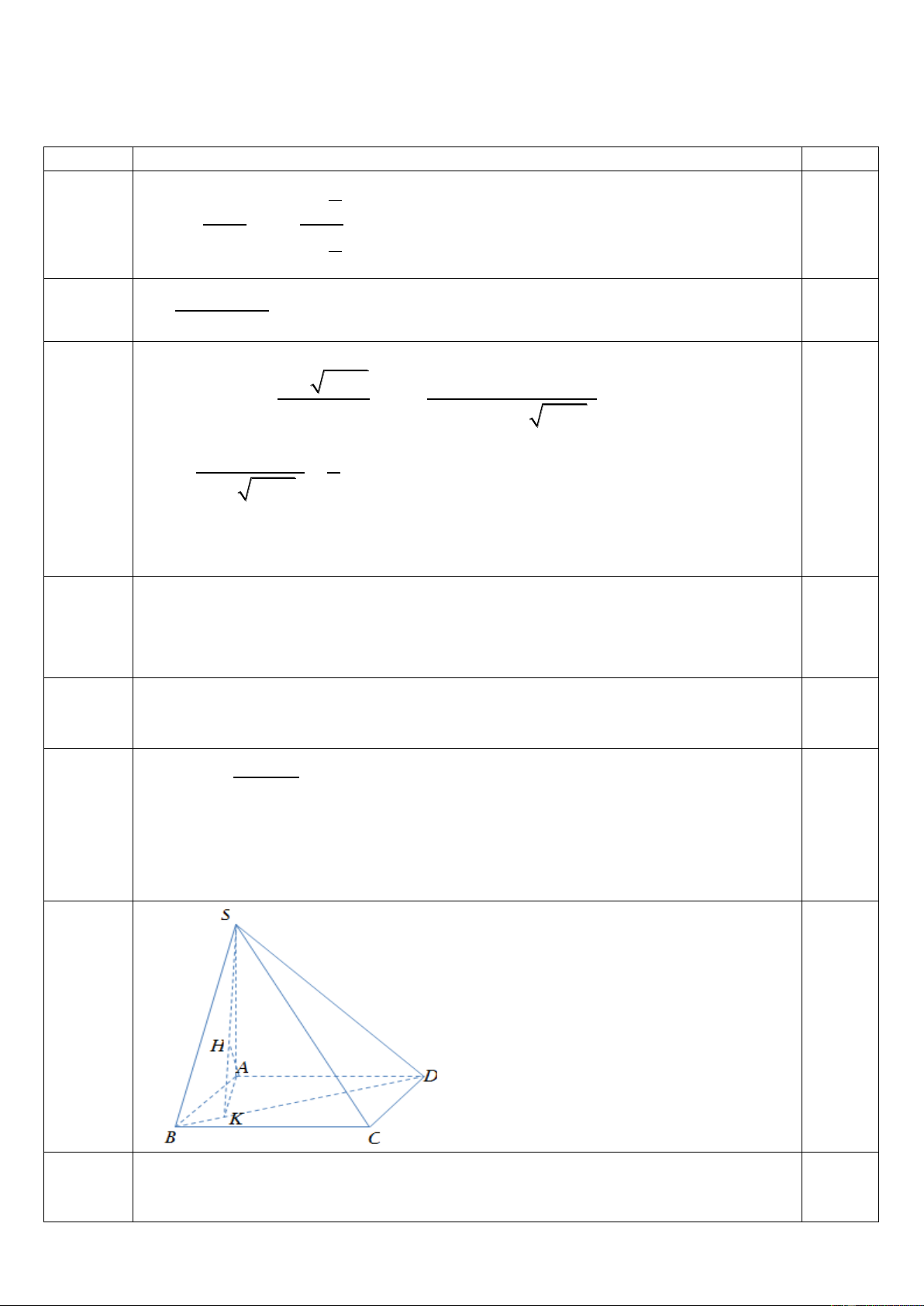
Cho hình chóp SABCD có đáy ABCD là hình chữ nhật có cạnh AB  , a AD  a 3 , SA  (ABC )
D , SA  a .
a) Chứng minh BC  SAB và CD  SAD.
b) Tính tan với  là góc giữa SC và  ABCD .
c) Gọi H là trực tâm tam giác SBD . Chứng minh AH  (SB ) D .
Câu 6: (1.0 điểm). Cho hàm số 3 2
f (x)  x  3x  9x 1có đồ thị (H).
Tiếp tuyến của (H) tại ( A ;
a f (a)) cắt (H) tại B( ; b f ( )
b ),b  a , tính b theo a.
-------------------------------- Hết ------------------------------
Họ và tên:.. ... ... ... ... ... . ..... ... ... ... ... ... ... ... ... ... ...... SBD.. ... ... ... ... ... ... ....Lớp............. SỞ GD&ĐT QUẢNG TRỊ
ĐỀ KIỂM TRA HỌC KỲ II NĂM HỌC:2019 – 2020
TRƯỜNG THPT THỊ XÃ QUẢNG TRỊ
Môn: Toán 11 - Mã đề: 02 ĐỀ CHÍNH THỨC
(Thời gian làm bài: 90 phút) (Đề có 01 trang) ĐỀ 02
Câu 1: (2.0điểm). Tính các giới hạn sau: n  2 a) lim . n  4 2 x  3x  4 b) lim . x4 x  4
Câu 2: (1.0 điểm).
 x  2x  3  khi x  3
Cho hàm số: f (x)   x  3
m khi x  3
Tìm m để hàm số liên tục tại x  3.
Câu 3: (2.0 điểm). Cho hàm số 3 2
f (x)  2x  6x  6x  2020 .
a) Tính f '(2) .
b) Giải bất phương trình f '(x  2)  6 .
Câu 4: (1.0 điểm). 2x  1 Cho hàm số y  có đồ thị là (C). x  2
Viết phương trình tiếp tuyến của (C) tại điểm có hoành độ x  -1.
Câu 5: (3.0 điểm).
Cho hình chóp SABCD có đáy ABCD là hình chữ nhật có cạnh AB  a 3, AD  a , SA  (ABC )
D , SA  2a .
a) Chứng minh BC  SAB và CD  SAD.
b) Tính tan với  là góc giữa SD và  ABCD .
c) Gọi H là trực tâm tam giác SBD . Chứng minh AH  (SB ) D .
Câu 6: (1.0 điểm). Cho hàm số 3 2
f (x)  x  3x  9x  2 có đồ thị (H).
Tiếp tuyến của (H) tại ( A ;
a f (a)) cắt (H) tại B( ; b f ( )
b ),b  a , tính b theo a.
-------------------------------- Hết ------------------------------
Họ và tên:.. ... ... ... ... ... . ..... ... ... ... ... ... ... ... ... ... ...... SBD.. ... ... ... ... ... ... ....Lớp.... ... ...
SỞ GD&ĐT QUẢNG TRỊ
ĐÁP ÁN THI HỌC KỲ II NĂM HỌC 2019 - 2020 TRƯỜNG THPT TXQT MÔN TOÁN KHỐI 11 Mã đề: 01 Câu Lời giải Điểm C1a. 1  1đ 1 n  1 0.5 lim  lim n 1 n  3 3 1  0.5 n C1b. 2 x  2x  3 0.5đ 1.0đ lim  lim(x 1)  4 0.5đ x 3  x 3 (x  3)  C2. Ta có f(2) = m 0.25đ 1.0đ 2 x  x  2 (x  x  2)
lim f (x)  lim  lim    x2 x2 x  x2 2
x  2x  x  2 0.25đ x  1 3  lim  
x2  x  x  2 4 0.25đ
lim f (x)  m  x 2 
f(x) liên tục tại x = 2  m =3/4 0.25 C3a. 3 2
f (x)  2x  6x  6x  2019 1.0đ 0.5đ 2
 f '(x)  6x 12x  6  f '(1)  0 0.5đ C3b. 2
f '(x 1)  6  6(x 1) 12(x 1)  0 0.5đ 1.0đ 0.5đ
0  x 1  2  1  x  3 C4. 1 0.25đ 1.0đ Ta có y  '  . x  2 1
x  -2  y  3 0.25đ y ' 2    1 0.25đ
Vây phương trình tiếp tuyến là: y  
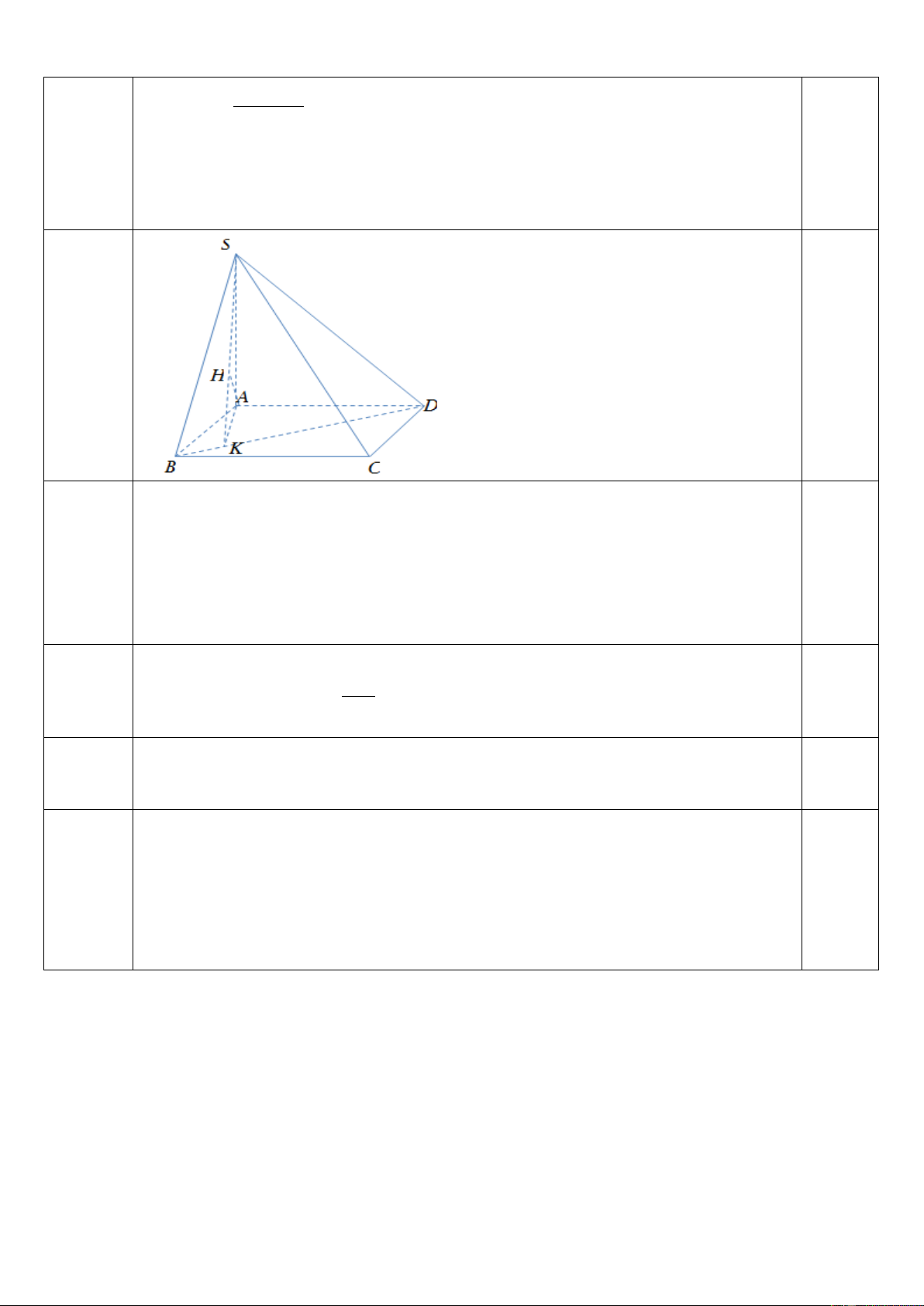
1 x  2  3  y  x  5 0.25 C5a. + Ta có: 1.0đ
BC  AB(gt) 0.5đ 
 BC  (SAB) BC  SA
DC  AD(gt) 0.5đ + 
 DC  (SAD) DC  SA C5b.
AC là hình chiếu của SC lên (ABCD) nên góc giữa Sc và (ABCD) là góc SCA 0.5đ 1.0đ     SCA SA 1 tan tan   0.5đ AC 2 C5c.
Ta có SH  BD, SA  BD  BD  (SAH)  BD  AH(1) 0.5 1.0đ
SB  DH, SB  AD  SB  (ADH)  SB  AH(2) 0.25 Từ (1) và (2) => đpcm 0.25 C6.
Phương trình tiếp tuyến tại A(a;f(a)) là 1.0đ 2 3 2
y  (3a  6a  9)(x  )
a  a  3a  9a 1(d) 0.25
Phương trình hòanh độ giao điểm của (d) và (H) 2 3 2 3 2
(3a  6a  9)(x  a)  a  3a  9a  x  3x  9x 0.25  x  a 2
 (x  a) (x  2a  3)  0   0.5
x  3 2a  b
SỞ GD&ĐT QUẢNG TRỊ
ĐÁP ÁN THI HỌC KỲ II NĂM HỌC 2019 - 2020 TRƯỜNG THPT TXQT MÔN TOÁN KHỐI 11 Mã đề: 02 Câu Lời giải Điểm C1a. 2  1đ 1 n  2 0.5 lim  lim n 1 n  4 4 1  0.5 n C1b. 2 x  3x  4 0.5đ 1.0đ lim  lim(x 1)  5 0.5đ x4 x4 (x  4) C2. Ta có f(3) = m 0.25đ 1.0đ 2 x  2x  3 (x  2x  3)
lim f (x)  lim  lim    x2 x 3  x  x 3 3 
x 3x  2x 3 0.25đ x  1 2  lim   x 3 
x 2x3 3 0.25đ
lim f (x)  m  x 3 
f(x) liên tục tại x = 3  m =2/3 0.25 C3a. 3 2
f (x)  2x  6x  6x  2020 1.0đ 0.5đ 2
 f '(x)  6x 12x  6  f '(2)  6 0.5đ C3b. 2
f '(x  2)  6  6(x  2) 12(x  2)  0 0.5đ 1.0đ 0.5đ
0  x  2  2  2  x  4 C4. 3 0.25đ 1.0đ Ta có y  '  . x  22
x  -1  y  1 0.25đ y '  1  3 0.25đ
Vậy phương trình tiếp tuyến là: y  3 x  
1  3  y  3x  6 0.25 C5a. + Ta có: 1.0đ
BC  AB(gt) 
 BC  (SAB) BC  SA 0.5đ
DC  AD(gt) + 
 DC  (SAD)  DC  SA 0.5đ C5b.
AD là hình chiếu của SD lên (ABCD) nên góc giữa SD và (ABCD) là góc SDA 0.5đ 1.0đ  SA
tan  tan SCA   2 0.5đ AD C5c.
Ta có SH  BD, SA  BD  BD  (SAH)  BD  AH(1) 0.5 1.0đ
SB  DH, SB  AD  SB  (ADH)  SB  AH(2) 0.25 Từ (1) và (2) => đpcm 0.25 C6.
Phương trình tiếp tuyến tại A(a;f(a)) là 1.0đ 2 3 2
y  (3a  6a  9)(x  )
a  a  3a  9a  2(d) 0.25
Phương trình hòanh độ giao điểm của (d) và (H) 2 3 2 3 2
(3a  6a  9)(x  a)  a  3a  9a  x  3x  9x 0.25  x  a 2
 (x  a) (x  2a  3)  0   0.5 x  3   2a  b