Đề thi học kỳ 2 Toán 9 năm 2019 – 2020 phòng GD&ĐT Hoàng Mai – Hà Nội

PHÒNG GIÁO DỤC
ĐỀ KIỂM TRA HỌC KÌ 2 QUẬN HOÀNG MAI NĂM HỌC 2019-2020 MÔN: Toán
Thời gian làm bài : 90 phút
Ngày thi 04 tháng 6 năm 2020 Câu I. (2 điểm): x −1 x 2 x − 4
Cho hai biểu thức A = và B = −
với x  0; x  4 x + 2 x + 2 x − 4
1. Tính giá trị biểu thức A khi x = 9. x − 2 2. Chứng minh B = . x + 2
3. Đặt P = A: B . Tìm các giá trị của x để 2P = 2 x +1.
Câu II. (2,5 điểm):
1. Quãng đường AB dài 6km . Một người đi xe đạp từ A đến B với vận tốc không đổi. Khi từ B trở về
A người đó giảm vận tốc 3km / h so với lúc đi từ A đến B . Biết thời gian lúc đi ít hơn thời gian lúc về
là 6 phút. Tính vận tốc của người đi xe đạp khi đi từ A đến B . 4cm
2. Một hộp sữa hình trụ có chiều cao 12cm, bán kính đáy là 4cm như hình
vẽ bên. Tính diện tích vật liệu cần dùng để tạo nên vỏ hộp sữa đó (không tính phần ghép nối). 12cm Câu III. (2 điểm): (  x − )
1 ( y + 2) = xy − 6
1. Giải hệ phương trình : (   x + 2 
)( y −3) = xy +1 2. Cho phương trình : 2 2
x − 2mx + m + m −1 = 0 với m là tham số
a) Giải phương trình với m = 3 −
b) Tìm m để phương trình có hai nghiệm phân biệt x ; x sao cho 2 2 x + x = 3− x x . 1 2 1 2 1 2
Câu IV. (3,0 điểm):
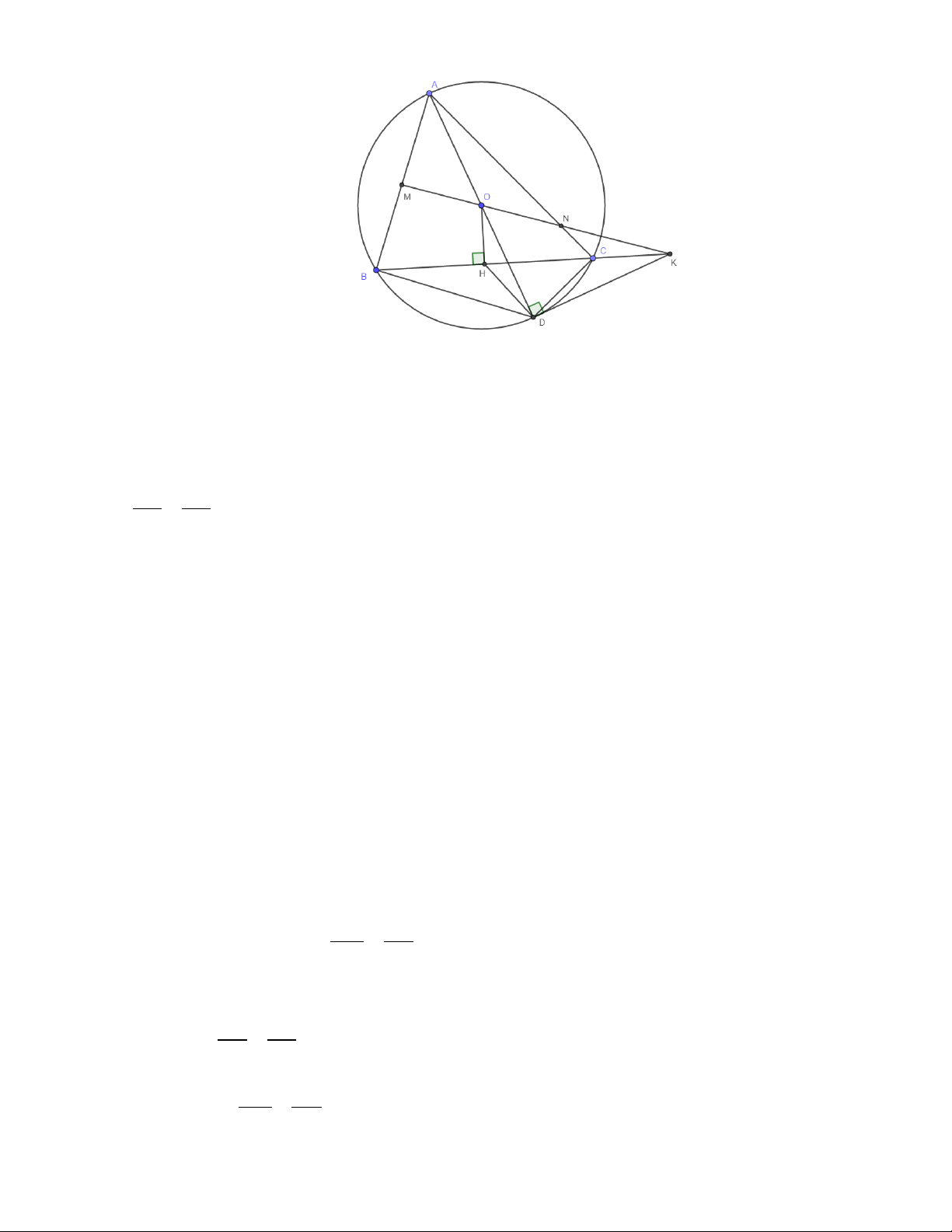
Cho tam giác ABC nhọn ( AB  AC) nội tiếp đường tròn (O) . Kẻ đường kính AD của đường tròn (O) .
Tiếp tuyến tại điểm D của đường tròn (O) cắt đường thẳng BC tại điểm K . Tia KO cắt AB tại điểm
M , cắt AC tại điểm N . Gọi H là trung điểm của đoạn thẳng BC
1) Chứng minh CBD = CDK và 2 KD = K . B KC
2) Chứng minh tứ giác OHDK nội tiếp và AON = BHD
3) Chứng minh OM = ON
Bài V.(0,5 điểm): Cho ,
a b R thỏa mãn 2 2
a − ab + b = a + b . = +
Tìm GTLN và GTNN của P 505a 505b ---HẾT--- HƯỚNG DẪN Câu I. (2 điểm): x −1 x 2 x − 4
Cho hai biểu thức A = và B = −
với x  0; x  4 x + 2 x + 2 x − 4
1. Tính giá trị biểu thức A khi x = 9. x − 2 2. Chứng minh B = . x + 2
3. Đặt P = A: B . Tìm các giá trị của x để 2P = 2 x +1. Hướng dẫn = = 3 −1 2 1. Khi x = 9 thì x 9 3 suy ra A = = 3 + 2 5 x 2( x − 2) x 2 x − 2 2. B = − = − = x + 2
( x −2).( x +2) x +2 ( x +2) x +2 3. P = A : B x −1 x − 2 x −1 x + 2 x −1 P = : = . = x + 2 x + 2 x + 2 x − 2 x − 2 x −1
2P = 2 x +1  2.
= 2 x +1  2( x − ) 1 = (2 x + ) 1 .( x − 2) x − 2 x = 0 (TMÐK)  x = 0 2x 5 x 0    − =   25  2 x −5 = 0 x = (TMÐK )  4
Câu II. (2,5 điểm):
1. Quãng đường AB dài 6km . Một người đi xe đạp từ A đến B với vận tốc không đổi. Khi từ B trở về
A người đó giảm vận tốc 3km / h so với lúc đi từ A đến B . Biết thời gian lúc đi ít hơn thời gian lúc về
là 6 phút. Tính vận tốc của người đi xe đạp khi đi từ A đến B .
2. Một hộp sữa hình trụ có chiều cao 12cm, bán kính đáy là 4cm như hình vẽ bên. Tính diện tích vật liệu
cần dùng để tạo nên vỏ hộp sữa đó (không tính phần ghép nối). Hướng dẫn
1. Gọi vận tốc của người đi xe đạp khi đi từ A đến B là x (km/h), x 3.
Vận tốc của người đi xe đạp khi đi từ B về A là x 3 (km/h) 6
Thời gian người đó đi từ A đến B là (h) x 6
Thời gian người đó đi từ B về A là (h) x 3 1
Vì thời gian lúc đi ít hơn thời gian lúc về là 6 phút
(h) nên ta có phương trình: 10 6 6 1 x 3 x 10 10.6x 10.6(x 3) ( x x 3) 2 60x 60x 180 x 3x 2 x 3x 180 0 (x 15)(x 12) 0 x 15 (TM ) x 12 (KTM )
Vậy vận tốc của người đi xe đạp khi đi từ A đến B là 15 km/h.
2. Diện tích vật liệu cần dùng chính là diện tích toàn phần của hình trụ có chiều cao 12cm, bán kính đáy
là 4cm . Do đó, diện tích vật liệu cần dùng là: 2 2 2
S = 2 rh + 2 r = 2.4.12 + 2.4 = 402,124(cm ) Câu III. (2 điểm). (  x − )
1 ( y + 2) = xy − 6
1. Giải hệ phương trình : (   x + 2 
)( y −3) = xy +1 2. Cho phương trình : 2 2
x − 2mx + m + m −1 = 0 với m là tham số
a) Giải phương trình với m = 3 −
b) Tìm m để phương trình có hai nghiệm phân biệt x ; x sao cho 2 2 x + x = 3− x x . 1 2 1 2 1 2 Hướng dẫn (  x − )
1 ( y + 2) = xy − 6
1. Giải hệ phương trình : (   x + 2 
)( y −3) = xy +1
 xy + 2x − y − 2 = xy − 6
 2x − y = −4
4x − 2y = −8  x = −1 x = −1         
xy − 3x + 2y − 6 = xy +1  3 − x + 2y = 7  3 − x + 2y = 7 4x − 2 y = 8 −   y = 2 Vậy ( , x y) = ( 1
− ,2) là nghiệm của hệ phương trình.
2. a) Giải phương trình với m = 3 − . Thay m = 3
− vào phương trình ta có : 2
x + 6x + 5 = 0 ( (a =1,b = 6, c = 5) vì a − b + c = 0 nên phương trình có 2 x = 1 − nghiệm phân biệt :  x = 5 − x = 1 − Vậy với m = 3
− thì phương trình có 2 nghiệm phân biệt  x = 5 −
b) Để phương trình có 2 nghiệm phân biệt thì :  = (b )2 ' ' − ac  0  m − +1 0  m 1
 x + x = 2m
Với m 1 áp dụng viet ta có : 1 2  2
x .x = m + m −1  1 2 Theo bài ra ta có : 2 2
x + x = 3 − x .x 1 2 1 2
 (x + x )2 − x .x −3 = 0 1 2 1 2 2
 3m − m − 2 = 0(a + b + c = 0)  m = 1(l)   2 −  m = (t / m)  3 2 − Vậy m =
thì phương trình có 2 nghiệm x , x thỏa mãn 2 2
x + x = 3 − x .x x 1 2 1 2 3 1 2
Câu IV. (3,0 điểm):
Cho tam giác ABC nhọn ( AB  AC) nội tiếp đường tròn (O) . Kẻ đường kính AD của đường tròn (O) .
Tiếp tuyến tại điểm D của đường tròn (O) cắt đường thẳng BC tại điểm K . Tia KO cắt AB tại điểm
M , cắt AC tại điểm N . Gọi H là trung điểm của đoạn thẳng BC
1) Chứng minh CBD = CDK và 2 KD = K . B KC
2) Chứng minh tứ giác OHDK nội tiếp và AON = BHD
3) Chứng minh OM = ON Hướng dẫn
1) Xét (O) có CDK là góc tạo bởi tia tiếp tuyến DK và dây cung chắn CD ; CBD là góc nội tiếp chắn
CD  CDK = CBD Xét K  DC và K
 BD có: K chung; KDC = KBD (cmt)  K  DC ~ K  BD (g.g) KD KC 2  =  KD = K . B KC KB KD
2) Xét (O) : H là trung điểm của dây BC 0
 OH ⊥ BC  OHK = 90  H  đường tròn đường kính OK Mà 0
KDO = 90 (do DK là tiếp tuyến của (O) )  D đường tròn đường kính OK
Vậy tứ giác OHDK nội tiếp đường tròn đường kính OK
 DHK = DOK (2 góc nội tiếp cùng chắn DK của đường tròn ngoại tiếpOHDK )  BHD = AON ( 0 0
=180 − DHK =180 − DOK )
3) Có MOA = DOK (đối đỉnh); DOK = DHC (chứng minh câu 2)  MOA = DHC Xét A  MO và C
 DH có: MOA = DHC (cmt); MAO = DCH (2 góc nội tiếp cùng chắn BD của (O) )  OM AO A  MO ~ C  DH (g.g)  = (1) HD CH Xét và B
 DH có: AON = BHD (chứng minh câu 2); NAO = DBH (2 góc nội tiếp cùng chắn CD của ( ON AO O) ) (g.g)  = (2)  A  NO ~ B  DH Mà (3) HD BH OM ON Từ (1) (2) (3)  =
 OM = ON (đpcm) HD HD
Bài V.(0,5 điểm): Cho ,
a b R thỏa mãn 2 2
a − ab + b = a + b . = +
Tìm GTLN và GTNN của P
505a 505b Hướng dẫn 2 (a + b) Ta có: 2 2
(a − b)  0  ,
a b  R  (a + ) b
 4ab  ab  a  ,b R 4 2 2 + + Khi đó, (a b) (a b) 2 2 2 2
a − ab + b = (a + b) − 3ab  (a + b) − 3 = 4 4 2 2 + Đặ (a ) b t
t: t = a + b 2 2
 a − ab + b = a + b   t 
 t(t − 4)  0  0  t  4 4 4
Ta có : P = 505a + 505b = 505(a + ) b = 505t
Từ điều kiện 0  t  4  0  505.t  505.4  0  P  2020 a = b Vậy, MinP = 0    a = b = 0 t  = a + b = 0 a = b MaxP = 2020    a = b = 2. t  = a + b = 4 ---HẾT---