Đề thi học kỳ 2 Toán 9 năm 2020 – 2021 phòng GD&ĐT Cầu Giấy – Hà Nội

ỦY BAN NHÂN DÂN QUẬN CẦU GIẤY
ĐỀ KIỂM TRA CHẤT LƯỢNG HỌC KÌ II
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
LỚP 9 NĂM HỌC 2020 - 2021 Môn: TOÁN
Thời gian làm bài 120 phút 2 x 4 x
Câu I (2,0 điểm). Cho biểu thức: A  và B   với x  0 và x  4 x  2 x  2 x  4
1) Tính giá trị biểu thức A khi x  9 . x 2) Chứng minh: B  . x  2 3x 3) Tìm x để A  B  . x  2
Câu II (2,0 điểm). Giải bài toán bằng cách lập phương trình hoặc hệ phương trình
Trong kì thi tuyển sinh vào 10, hai trường A và B có tất cả 750 học sinh dự thi. Trong số học sinh
trường A dự thi có 80% học sinh trúng tuyển, còn trong số học sinh trường B dự thi có 70% học sinh
trúng tuyển. Biết tổng số học sinh trúng tuyển của cả hai trường là 560 học sinh. Tính số học sinh dự thi mỗi trường? Câu III (2,0 điểm).  2  y 1  4 x  y
1. Giải hệ phương trình sau  . 1   3 y 1  5   x  y 2. Cho Parabol P 2
: y  x và đường thẳng d  y  m   2 : 2
1 x  m  2m (m là tham số)
a) Tìm tọa độ giao điểm của Parabol P và đường thẳng d  khi m  2;
b) Tìm m để đường thẳng d  và Parabol P cắt nhau tại hai điểm phân biệt có hoành độ x ; x 1 2 đối nhau.
Câu IV (3,5 điểm). Cho nửa đường tròn (O;R) đường kính AB và điểm M thuộc nửa đường tròn đó (M khác A,
B). Trên dây BM lấy điểm N (N khác B và M), tia AN cắt nửa đường tròn (O) tại điểm thứ hai là P.
Tia AM và tia BP cắt nhau tại Q.
1) Chứng minh : Bốn điểm M, N, P, Q cùng thuộc một đường tròn.
2) Chứng minh : MAB và MNQ đồng dạng.
3) Chứng minh MO là tiếp tuyến của đường tròn ngoại tiếp tam giác MNQ .
4) Dựng hình bình hành ANBC . Chứng minh QB  QC.sin  QPM . 1
Câu V (0,5 điểm). Tìm giá trị nhỏ nhất của biểu thức 2 2
P  2x  2xy  y  3x   2 x  2  2021 x ---HẾT---
NHÓM TOÁN THCS HÀ NỘI https://www.facebook.com/groups/650500558651229/ HƯỚNG DẪN 2 x 4 x
Câu I (2,0 điểm). Cho biểu thức: A  và B   với x  0 và x  4 . x  2 x  2 x  4
1) Tính giá trị biểu thức A khi x  9 . x 2) Chứng minh: B  . x  2 3x 3) Tìm x để A  B  . x  2 Hướng dẫn 2 1) Ta có : A  ĐKXĐ: x  0 và x  4 x  2 2 2
Thay x  9 (thỏa mãn) vào biểu thức A ta có: A    2 9  2 3  2
Kết luận: Với x  9 thì giá trị biểu thức A là 2 x 4 x 2) Ta có: B   ĐKXĐ: x  0 và x  4 x  2 x  4 x 4 x B  
x  2  x  2 x  2 x  x  2  4 x B   x  2 x  2 x  x  2 x B    x  2 x  2 x  2 x Kết luận: B  với x  0 và x  4 x  2 3x 2 x 3x 3) A  B     ĐKXĐ: x  0 và x  4 x  2 x  2 x  2 x  2 2  x  3x   0 x  2
 x  1 3 x 2   0 x  2  x 1  0  x 1  x 1 (t / m)      3  x  2  0 3 x  2  x
Kết luận: Với x  1thì thỏa mãn đề bài.
Câu II (2,0 điểm). Giải bài toán bằng cách lập phương trình hoặc hệ phương trình
Trong kì thi tuyển sinh vào 10, hai trường A và B có tất cả 750 học sinh dự thi. Trong số học sinh
trường A dự thi có 80% học sinh trúng tuyển, còn trong số học sinh trường B dự thi có 70% học sinh
trúng tuyển. Biết tổng số học sinh trúng tuyển của cả hai trường là 560 học sinh. Tính số học sinh dự thi mỗi trường? Hướng dẫn
Gọi số học sinh dự tuyển của trường A là x (đơn vị: học sinh), (x; y *   , x;y< 560)
số học sinh dự tuyển của trường B là y (đơn vị: học sinh)
Vì tổng số học sinh dự thi của hai trường là 750 học sinh nên ta có phương trình
NHÓM TOÁN THCS HÀ NỘI https://www.facebook.com/groups/650500558651229/ x + y = 750 (1) 4
Số học sinh trúng tuyển của trường A là 80%.x = x (học sinh) 5 7
Số học sinh trúng tuyển của trường B là 70%.y = y (học sinh) 10
Vì tổng số học sinh trúng tuyển của cả hai trường là 560 học sinh nên ta có phương trình 4 7 x  y  560 5 10  8x  7y  5600 (2)
Từ (1) và (2) ta có hệ phương trình x  y  750 8x   7y  5600 7x  7y  5250   8x   7y  5600 x  y  750  x 350 y  400  
(thỏa mãn điều kiện của ẩn) x  350
Vậy số học sinh dự thi của trường A là 350 học sinh
Số học sinh dự thi của trường B là 400 học sinh. Câu III (2,0 điểm).  2  y 1  4 x  y
1. Giải hệ phương trình sau  . 1   3 y 1  5   x  y 2. Cho Parabol P 2
: y  x và đường thẳng d  y  m   2 : 2
1 x  m  2m (m là tham số)
a) Tìm tọa độ giao điểm của Parabol P và đường thẳng d  khi m  2;
b) Tìm m để đường thẳng d  và Parabol P cắt nhau tại hai điểm phân biệt có hoành độ x ; x 1 2 đối nhau. Hướng dẫn
1. Điều kiện: x  y; y  1 1 Đặt  ; a
y 1  b (điều kiện a  0;b  0) x  y 2a  b  4 6a  3b  12 7a  7 a  1(tm)
Khi đó hệ phương trình đã cho có dạng        a  3b  5 a  3b  5 b  4  2a b  2(tm)  1 a 1 1  x  y 1 x  3 1 x  4(tm) Với   x  y        b   2   y 1  4  y  3  y  3(tm) y 1  2  x  4
Vậy hệ phương trình đã cho có nghiệm  . y  3
2. Xét phương trình hoành độ điểm chung 2 x  m   2 2
x  m  m  x  m   2 2 1 2 2 1 x  m  2m  0  1
a) Với m  2 phương trình (1) có dạng x  0 2 x  22   2 2
1 x  2  2.2  0  x  2x  0  x  x  2  0  .  x  2
NHÓM TOÁN THCS HÀ NỘI https://www.facebook.com/groups/650500558651229/ - Với 2
x  0  y  0  0  A0;0 - Với 2
x  2  y  2  4  B2;4
Vậy khi m  2 thì P cắt d  tại hai điểm phân biệt A0;0; B2;4
b) Tính   b  ac    m   2 2     2 m  m 2 2 ' ' 1 2
 m  2m 1 m  2m 1  0
Do  '  0 nên phương trình (1) luôn có hai nghiệm phân biệt x ; x với mọi . m 1 2
Suy ra đường thẳng d  luôn cắt Parabol P tại hai điểm phân biệt có hoành độ x ; x với mọi . m 1 2 x  x  2m  2
Khi đó theo hệ thức Viet ta có 1 2  2 x x  m  2m  1 2
Để đường thẳng d  cắt Parabol P tại hai điểm phân biệt có hoành độ đối nhau
 x  x  0  2m  2  0  m 1(tm) 1 2
Vậy m  1 thì đường thẳng d  luôn cắt Parabol P tại hai điểm phân biệt có hoành độ đối nhau.
Câu IV (3,5 điểm). Cho nửa đường tròn (O;R) đường kính AB và điểm M thuộc nửa đường tròn đó (M khác A,
B). Trên dây BM lấy điểm N (N khác B và M), tia AN cắt nửa đường tròn (O) tại điểm thứ hai là P.
Tia AM và tia BP cắt nhau tại Q.
1) Chứng minh : Bốn điểm M, N, P, Q cùng thuộc một đường tròn.
2) Chứng minh : MAB và MNQ đồng dạng.
3) Chứng minh MO là tiếp tuyến của đường tròn ngoại tiếp tam giác MNQ .
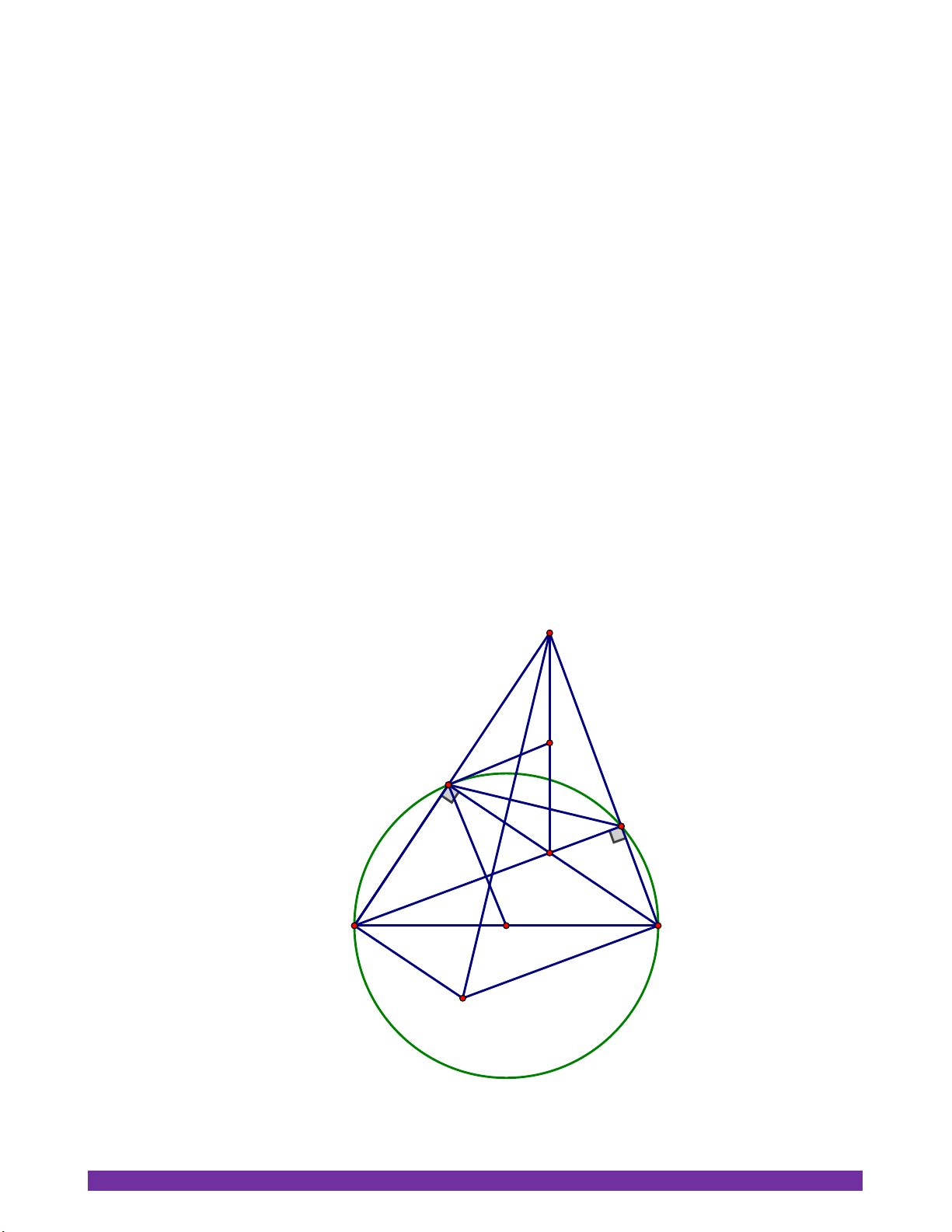
4) Dựng hình bình hành ANBC . Chứng minh QB  QC.sin  QPM . Hướng dẫn Q I M P N A B O C
1) Xét nửa đường tròn  ; O R ta có:  0
AMB = 90 (góc nội tiếp chắn nửa đường tròn)
NHÓM TOÁN THCS HÀ NỘI https://www.facebook.com/groups/650500558651229/   0 BMQ = 90 hay  0 NMQ = 90  0
APD = 90 (góc nội tiếp chắn nửa đường tròn)   0 APQ = 90 hay  0 NPQ = 90 Xét tứ giác MNPQ ta có:  0 NMQ  0 = 90 ; NPQ  90   NMQ  0 0 0 + NPQ = 90 +90 =180 Mà  NMQ ; 
NPQ là hai góc ở vị trí đối nhau
Suy ra, tứ giác MNPQ nội tiếp đường tròn
Vậy, 4 điểm M , N , P,Q cùng thuộc một đường tròn.
2) Xét tứ giác MNPQ nội tiếp đường tròn ta có:  MQN = 
NPM ( góc nội tiếp cùng chắn cung MN ) Hay  MQN = APM Mà  APM = 
ABM (Góc nội tiếp cùng chắn cung AM trong O )   MQN   ABM
Xét tam giác MAB và MNQ ta có:  ABM   o NMQ  90  MQN   ABM cmt   M  AB  M  NQg.g
3) Gọi I là trung điểm của QN 1
Xét MNQ vuông tại M  NI  IQ  QN 2
Suy ra, I là tâm đường tròn ngoại tiếp MNQ Xét O ta có: OM  OB  R  M  OB cân tại O   OMB   OBM
Xét I  ta có: MI  IN  M  IN cân tại I   IMN   INM  IMO   IMN   NMO =  IMN   MBO =  IMN   MBA =  INM   o MQN  90 Hay MI  MO
Vây, MO là tiếp tuyến của đường tròn ngoại tiếp tam giác MNQ tại M .
4) Vì tứ giác ANBC là hình bình hành nên
AN / /BC mà AN  BQ  CB  BQ hay  o CBQ  90
AC / /BN mà BN  AQ  AC  AQ hay  o CAQ  90 Xét tứ giác AQBC ta có :  CBQ   o o o CAQ  90  90  180 Mà  CB ; Q 
CAQ ở hai vị trí đối nhau
Suy ra, tứ giác AQBC nội tiếp một đường tròn   QCB  
QAB (góc nội tiếp cùng chắn cung QB ) Mà  QAB   MNQ   QPM
NHÓM TOÁN THCS HÀ NỘI https://www.facebook.com/groups/650500558651229/   QPM   QCB
Xét tam giác QCB vuông tại B ta có: QB sin  QCB 
(tỉ số lượng giác của góc nhọn) QC  QB  QC.sin  QCB  QC.Sin QPM (đpcm) 1
Câu V (0,5 điểm). Tìm giá trị nhỏ nhất của biểu thức 2 2
P  2x  2xy  y  3x   2 x  2  2021 x Hướng dẫn ĐKXĐ: x  2 Ta có: 1 2 2
P  2x  2xy  y  3x   2 x  2  2021 x 1 2 2 2
 x  2xy  y  x  4x  4  x   2 x  2  2017 x x 1 3x 2 2
 (x  y)  (x  2)     2 x  2  2017 4 x 4 Do 2 (x  y)  0 , 2
(x  2)  0 , 2 x  2  0 , x  2 . x 1 3x x 1 3.2 Suy ra P     2017  2 .   2017  2019,5. 4 x 4 4 x 4
Dấu "  " xảy ra khi x  y  2. ---HẾT---
NHÓM TOÁN THCS HÀ NỘI https://www.facebook.com/groups/650500558651229/
Document Outline

• de-thi-hoc-ky-2-toan-9-nam-2020-2021-phong-gddt-cau-giay-ha-noi
• 05.ĐỀ HK2 LỚP 9 PGD CẦU GIẤY- GV TOÁN HÀ NỘI 2021