Đề thi học kỳ I năm 2017-2018 môn toán 9 Sở GD Quảng Nam (có lời giải)
Tổng hợp Đề thi học kỳ I năm 2017-2018 môn toán 9 Sở GD Quảng Nam (có lời giải) rất hay và bổ ích giúp bạn đạt điểm cao. Các bạn tham khảo và ôn tập để chuẩn bị thật tốt cho kỳ thi tốt nghiệp sắp đến nhé. Mời bạn đọc đón xem.
Preview text:
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KIỂM TRA HỌC KỲ I NĂM HỌC 2017-2018 QUẢNG NAM
Môn: TOÁN – LỚP 9
Thời gian: 90 phút (không kể thời gian giao đề) ĐỀ CHÍ NH THỨC
Bài 1 (2,0 điểm):
a) Với giá trị nào của x thì 6 x xác định? b) Thực hiện tính: 1 A = 60 : 15 ; B = 2 (2 5) 4 ; C = 2 2 3
Bài 2 (1,5 điểm): 1 1
a 2 a 1 Cho biểu thức P .
với a 0 và a 1.
a 1 a a a 1
a) Rút gọn biểu thức P.
b) Tính giá trị của P khi a 2 3 5 3 5 10 2 .
Bài 3 (2,0 điểm):
a) Tìm điều kiện của m để hàm số y (m 3)x 4 là hàm số bậc nhất.
b) Vẽ đồ thị hàm số y 2x 3
c) Tìm m để đồ thị hàm số y (m 3)x 4 cắt đồ thị hàm số y 2x 3 tại
điểm có hoành độ bằng 1.
Bài 4 (2,0 điểm):
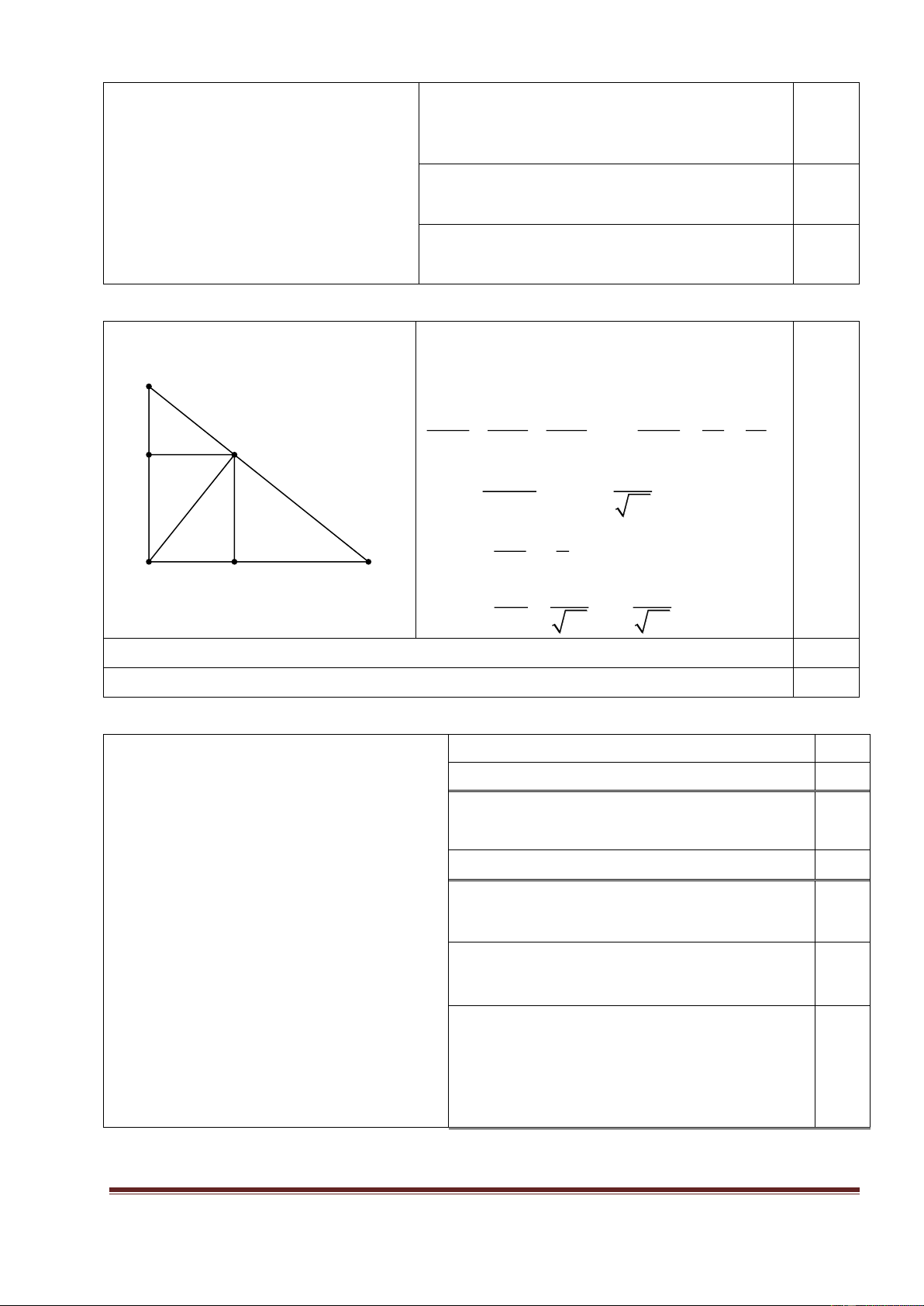
Vẽ tam giác ABC vuông tại A có AB = 4cm; AC = 5cm và AH là đường cao.
a) Tính độ dài đoạn thẳng AH.
b) Tính các tỉ số lượng giác: tanB , sin C .
c) Gọi E là hình chiếu của H trên AB và F là hình chiếu của H trên AC. Chứng minh AE.AB = AF.AC
Bài 5 (2,5 điểm):
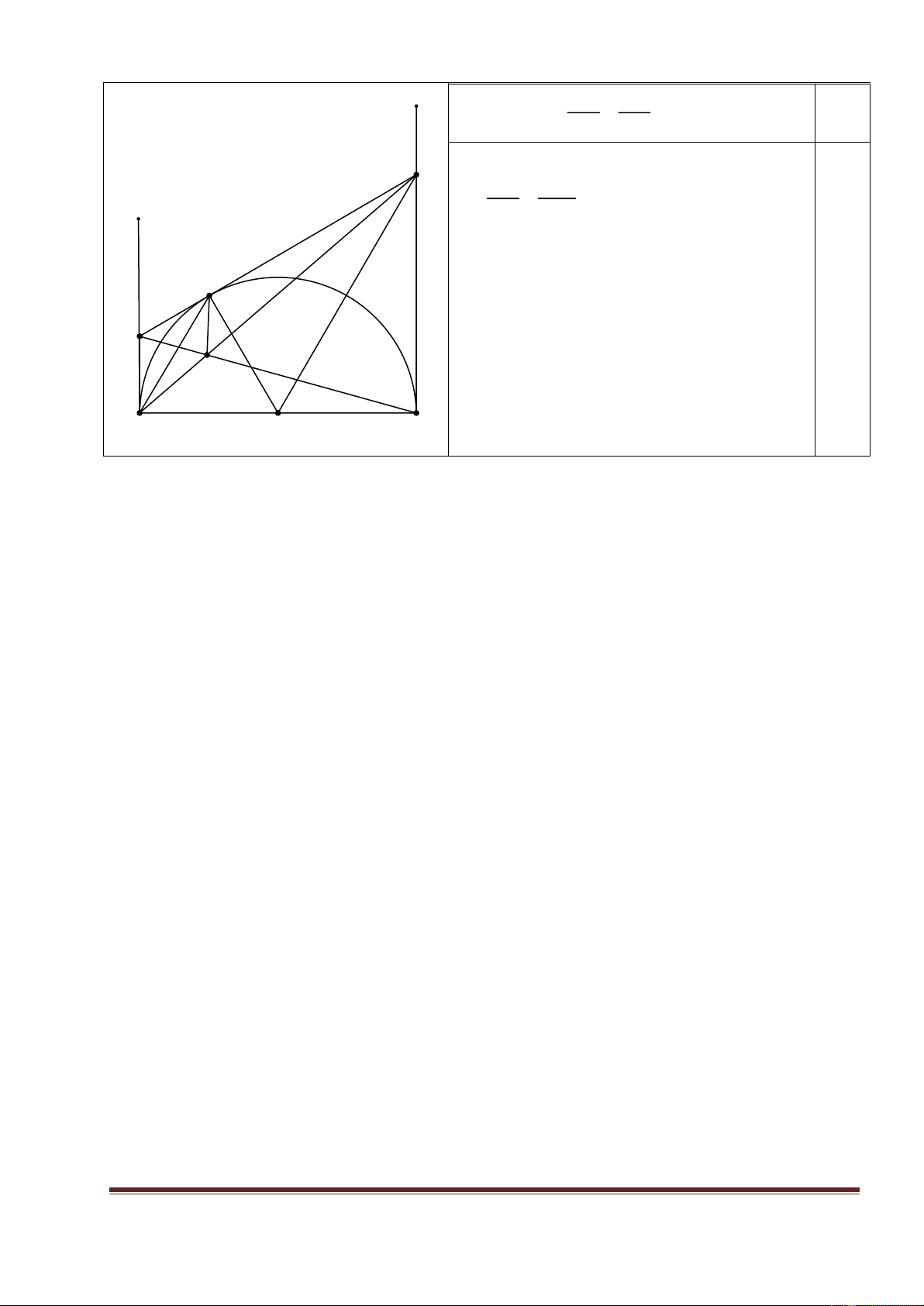
Cho nửa đường tròn tâm O có đường kính AB. Gọi Ax, By là các tia vuông
góc với AB (Ax, By và nửa đường tròn thuộc cùng một nửa mặt phẳng bờ AB). Gọi
M là điểm bất kì thuộc nửa đường tròn (M khác A và B). Đường thẳng qua M vuông
góc với OM cắt Ax tại C và cắt By tại D. a) Chứng minh CA = CM.
b) Chứng minh MOB = 2. MAO , từ đó suy ra AM song song với OD.
c) Gọi N là giao điểm của AD và BC. Chứng minh đường thẳng MN vuông
góc với đường thẳng AB. Trang 1 ===== HẾT =====
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KIỂM TRA HỌC KỲ I NĂM HỌC 2017-2018 QUẢNG NAM
HƯỚNG DẪN CHẤM MÔN TOÁN 9
Bài 1 (2,0 điểm):
a) 6 x xác định khi 6 + x ≥ 0 0,25 x ≥ 6 0,25
A= 60 : 15 = 60 :15 (hoặc 4 ) 0,25 = 4 2 0,25 B = 2
(2 5) 4 = 2 5 4 (hoặc 5 2 4 ) 0,25 = 5 2 2 5 0,25 1 2 3 C = 2 =
2 (hoặc = 3 2 2 ) 0,25 2 3 2 3 2 3 2 3 = 2 3 2 2 3 2 0,25 3
Bài 2 (1,5 điểm): a 1 a 2 a 1 a 2 a 1 P 0,50 a a . 1 a 1 a a 1 a 2 1 a 1 a a 0,50 a a 1 a a
a 2 3 5. 3 5. 3 5. 2 5 1 = 4 3 5. 2 5 1 0,25 5
a 4 6 2 5. 5 1 4 5 1 5 1 16 . Tính được P = 0,25 4
Bài 3 (2,0 điểm):
Để y (m 3)x 4 là hàm số bậc nhất 0,25 thì m 3 0 m 3 0,25
Xác định được tọa độ hai điểm thuộc đồ 0,50
thị hàm số (Ví dụ: A(0; -3) và B(2;1)).
Vẽ đồ thị hàm số y = 2x-3: Trang 2
- Vẽ hệ trục tọa độ.
- Biểu diễn hai điểm trên hệ trục tọa độ. 0,25
- Vẽ đường thẳng qua hai điểm. 0,25
Gọi C(x0; y0) là tọa độ giao điểm. Có: 0,25 x 0 =1 y 2.1 3 1 0
y (m 3)x 4 qua C(1; -1) có: 0,25 1
m 3 4 m 2. Bài 4 (2,0 điểm):
Hình vẽ: phục vụ câu a), b) 0,25 phục vụ câu c) 0,25 B Có: 1 1 1 1 1 1 = + thay: 0,25 H 2 2 2 AH AB AC 2 2 2 AH 4 5 E 2 2 4 .5 20 2 AH = AH= (3.12) 0,25 2 2 4 +5 41 AC 5 tanB = = ( = 1.25 ) 0,25 C F AB 4 A AH 20 4 sinC = : 5 ( 0.62 ) 0,25 AC 41 41
AHB vuông tại H có HE là đường cao nên AE. AB = AH2 0,25
Tương tự có AF.AC = AH2 AE. AB = AF.AC (cùng bằng AH2) 0,25 Bài 5 (2,5 điểm):
Hình vẽ: phục vụ câu a) 0,25
Chỉ yêu cầu phục vụ câu b) 0,25
CM MO CM là tiếp tuyến của (O) 0,25
CA AO CA là tiếp tuyến của (O). 0,25
CM = CA (T.chất 2 tt cắt nhau). 0,25
OMA cân tại O do OM = OA 0,25 MAO AMO
Mà MOB MAO AMO (góc ngoài) 0,25 MOB = 2 MAO
Lí luận được BD là tiếp tuyến của (O)
OD là phân giác của MOB 0,25
MOB 2 DOB MAO DOB AM // OD Trang 3 NC AC y AC// BD = 0,25 NB BD D Mà AC= MC và BD = MD NC MC = MN//BD MN AB NB MD x M 0,25 C N A O B
Học sinh giải cách khác đúng, tổ chấm thảo luận, thống nhất cho điểm phù hợp. ===== HẾT==== Trang 4