Đề thi học sinh giỏi cấp huyện Toán 9 năm 2018 – 2019 phòng GD&ĐT Hoài Nhơn – Bình Định

Đề ôn thi HSG 9
Tel: 0905.884.951 – 0929.484.951 UBND HUYỆN HOÀI NHƠN
ĐỀ THI HỌC SINH GIỎI CẤP HUYỆN
PHÒNG GIÁO DỤC & ĐÀO TẠO
Năm học 2018 – 2019 Môn: TOÁN 9
Đề chính thức Ngày thi: 01/12/2018
Thời gian làm bài: 150 phút (không kể thời gian phát đề)
Bài 1. (4.0 điểm) 2  3  6  8  4
a) Thu gọn biểu thức: A  . 2  3  4 2 b) Cho x 
. Tính giá trị của biểu thức B    x  x  x  x 2018 2 3 4 1 2 . 1 1  2 1 1 2 1 1 c) Cho 3 3
x  3  2 2  3 2 2 và 3 3
y  17 12 2  17 12 2 . Tính giá trị của biểu thức: 3 3
C  x  y 3x  y 2018 .
Bài 2. (4.0 điểm)
a) Tìm các số nguyên dương có hai chữ số, biết số đó là bội của tích hai chữ số của chính số đó.  1 1 1 1 
b) Chứng minh rằng số tự nhiên A  1.2.3.....2017.2018. 1      ...      chia hết cho  2 3 2017 2018 2019 .
Bài 3. (5.0 điểm) 2 2 2
3.1. Cho a, b, c là các số thực dương thỏa mãn điều kiện 2 2 2
a  b  c  a b b  c  c a
a) Tính a  b  c , biết rằng ab  bc  ca  9 .
b) Chứng minh rằng: Nếu c  a, c  b thì c  a b .
3.2. Cho ba số dương x, y, z thỏa mãn 2019 2019 2019 x  y  z
 3 . Tìm giá trị lớn nhất của biểu thức: 2 2 2
E  x  y  z .
Bài 4. (4.0 điểm) Cho tam giác đều ABC có cạnh bằng a . Hai điểm M , N lần lượt di động trên AM AN
hai đoạn thẳng AB, AC sao cho 
1. Đặt AM  x và AN  y . Chứng minh rằng: MB NC a) 2 2 2
MN  x  y  xy .
b) MN  a  x  y .
c) MN luôn tiếp xúc với đường tròn nội tiếp tam giác ABC .
Bài 5. (3.0 điểm) Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn O , gọi M là trung điểm
của cạnh BC , H là trực tâm của tam giác ABC và K là hình chiếu vuông góc của A trên cạnh KM
BC . Tính diện tích của tam giác ABC , biết OM  HK  và AM  30 cm. 4
----------  HẾT  ----------
Trường THCS Đào Duy Từ
Năm học 2018 – 2019 GV: Lê Hồng Quốc
" Đi rồi sẽ đến " Trang 1 Đề ôn thi HSG 9
Tel: 0905.884.951 – 0929.484.951 ĐÁP ÁN THAM KHẢO
Bài 1. (4.0 điểm) 2  3  6  8  4
a) Thu gọn biểu thức: A  . 2  3  4 Lời giải. 2  3  4  2      2  3  4 2 3 6 8 4  Ta có: A    1 2 . 2  3  4 2  3  4 2 b) Cho x 
. Tính giá trị của biểu thức B    x  x  x  x 2018 2 3 4 1 2 . 1 1  2 1 1 2 1 1 Lời giải. 2 2 Ta có: x  
 2. Thay x  2 vào biểu 1 1 2  2 1 1 2 1 1
 21 1 21 1 2018 2 3 4 2018   2018
thức, ta được: B  1
 2 2  2  2  2 
 12 2 22 2 4    1  1  .   c) Cho 3 3
x  3  2 2  3 2 2 và 3 3
y  17 12 2  17 12 2 . Tính giá trị của biểu thức: 3 3
C  x  y 3x  y 2018 . Lời giải. ● Ta có 3
x   32 2  32 2 3 3 3
 32 2 3.x 32 2  6 3x và 3
y   17 12 2  1722 2 3 3 3
17 12 2 3.y 1712 2  34  3y
● Cộng vế theo vế, ta được: 3 3 3 3
x  y  40  3x  3y  x  y 3x  y 2018  2058 .
 Vậy C  2058 khi 3 3
x  3  2 2  3 2 2 và 3 3
y  17 12 2  17 12 2 .
Bài 2. (4.0 điểm)
a) Tìm các số nguyên dương có hai chữ số, biết số đó là bội của tích hai chữ số của chính số đó. Lời giải.
Gọi số cần tìm là ab , theo đề, ta có 10a  b  . k .
a b . (Trong đó: 1  a, b  9 và , a b, k    ). 10 10 10 10 1 Suy ra b  
. Vì 1  b  9  1   9   k  10. k.a 1 1 1 9 a k  k  a a a 1  0 1   k  10  9 a 1 5 5    Từ  
 k   ;2; ;5;10  . 1    a  3 2  1  0 : k      a a  1  a   3  1 5  . a 3k   5  3  8    ● Nếu k     
k  (không thỏa) hoặc k   2 (thỏa)  ab  36 . a 3 b    6  3     b   6 b   6   
Trường THCS Đào Duy Từ
Năm học 2018 – 2019 GV: Lê Hồng Quốc
" Đi rồi sẽ đến " Trang 2 Đề ôn thi HSG 9
Tel: 0905.884.951 – 0929.484.951 a     1 a  k   1 . 2  1   ● Nếu k   2     k   3 (thỏa)  ab 15 . a b    5   b   5  a  1  a   2  1 5  . a 2k   5  2  7    ● Nếu k     
k  (không thỏa) hoặc k   3 (thỏa)  ab  24 . a 2 b    4  2     b   4 b   4    a     1 a  k   1 . 5  1   ● Nếu k   5     k   6 (thỏa)  ab  12 . a b    2   b   2  a     1 a  k   1 . 10  1   ● Nếu k  10     k  11 (thỏa)  ab  11. a b    1   b  1 
Vậy ab  11;12;15;24;36 .  1 1 1 1 
b) Chứng minh rằng số tự nhiên A  1.2.3.....2017.2018. 1      ...      chia hết cho  2 3 2017 2018 2019 . Lời giải.  1 1 1 
Ta có B  1.2.3..... . n 1      ...       
là số tự nhiên. Thật vậy  2 3 n 
● Với n  1 thì B  1       đúng.
● Với n  2 thì B  3       đúng.  1 1 1  ● Giả sử  
 đúng khi n  k , nghĩa là B 1.2.3.....k. 1      ...      .  2 3 k    ● Cần chứng minh  
 đúng khi n  k 1, nghĩa là B  k   1 1 1 1.2.3..... 1 . 1      ...      .  2 3 k 1  1 1 1   1 1 1 
Ta có 1.2.3.....k   1 . 1      ...     1.2.3..... 1      ...   .k   1 1.2.3.....k  .  2 3 k 1  2 3 k    1 1 1  1  .2.3..... 1      ...       2 3 k   Có k  1    B    . 1  .2.3.....k      1 1 1  Vậy 1.2.3..... . n 1      ...     là số tự nhiên.  2 3 n   1 1 1   1 1 
Suy ra, với n  2k thì 1.2.3.....2k. 1      ...      
và 1.2.....k. 1  
...  là các số tự nhiên  2 3 2k   2 k   1 1 1       ...   .k  
1 k  2.....2k 
cũng là các số tự nhiên.
k 1 k  2 2k   1 1  ● Áp dụng các chứng minh ta có: 1.2.....1009. 1     ...     và  2 1009   1 1 1      ...   .1010.1011.....2018 
cũng là các số tự nhiên. 1010 1011 2018
Trường THCS Đào Duy Từ
Năm học 2018 – 2019 GV: Lê Hồng Quốc
" Đi rồi sẽ đến " Trang 3 Đề ôn thi HSG 9
Tel: 0905.884.951 – 0929.484.951 1  0113  Ta có  
1010.1011.....1342.....20182019 1  342673   1 1   1.2.....1009. 1     ...  
.1010.1011.....1342.....20182019  .  2 1009  3  3  Và  
1.2.3.....673.....10092019 6  73673   1 1 1   1.2.....1009.    ...   .1010.1011.....20182019  . 1010 1011 2018  1 1 1 1 
 Vậy số tự nhiên A  1.2.3.....2017.2018. 1      ...      chia hết cho 2019 .  2 3 2017 2018
Bài 3. (5.0 điểm) 2 2 2
3.1. Cho a, b, c là các số thực dương thỏa mãn điều kiện 2 2 2
a  b  c  a b b  c  c a
a) Tính a  b  c , biết rằng ab  bc  ca  9 . Lời giải. 2 2 2 Từ 2 2 2
a  b  c  a b b  c  c a 2 2 2 
 a  b  c  2ab bc  ca 4ab bc  ca.
Mà ab  bc  ca  9 nên a  b  c2
a, b, c0
 36   a  b  c  6 .
b) Chứng minh rằng: Nếu c  a, c  b thì c  a b . Lời giải. 2 2 2 2 Ta có 2 2 2
a  b  c  a b b c  c a  c a b  4ab .
Không mất tính tổng quát, giả sử: c  a  b . Khi đó, ta có:
c a b  2b 1 2   c a b 2 4ab 4b        .
c  a  b  2b  2  ●  
1  c a b  0 
c  a b . ●  
1  c  a b  2
 b  c a b  0  
 , mà c a  0 suy ra    vô lí.
 Vậy: nếu c  a, c  b thì c  a b .
3.2. Cho ba số dương x, y, z thỏa mãn 2019 2019 2019 x  y  z
 3 . Tìm giá trị lớn nhất của biểu thức: 2 2 2
E  x  y  z . Lời giải. Cách 1.
● Áp dụng bất đẳng thức COSI ta có các đánh giá sau:  2019 2019 2  x  x
111...1 2019x

. Dấu "  " xảy ra khi x  1 . 2017 so 1  2019 2019 2  y  y
111...1 2019 y

. Dấu "  " xảy ra khi y  1 . 2017 so 1  2019 2019 2  z  z
111...1 2019z

. Dấu "  " xảy ra khi z  1 . 2017 so 1 ● Khi đó:  2019 2019 2019 x  y  z    2 2 2
x  y  z  2019 2019 2019 x y z 3 2 2 2 6 6051 2019 
 x  y  z  3 .
Dấu "  " xảy ra khi x  y  z  1 .
 Vậy E đạt giá trị lớn nhất bằng 3 khi x  y  z  1 . Cách 2.
● Áp dụng bất đẳng thức COSI ta có các đánh giá sau:
Trường THCS Đào Duy Từ
Năm học 2018 – 2019 GV: Lê Hồng Quốc
" Đi rồi sẽ đến " Trang 4 Đề ôn thi HSG 9
Tel: 0905.884.951 – 0929.484.951  2019 3  x
111...1 673x
 ; 2019 3 y
111...1 673y
 và 2019 3 z
111...1 673z
 672 so 1 672 so 1 672 so 1  2019  x
111...1 2019x
 ; 2019 y
111...1 2019 y
 và 2019 z
111...1 2019z
 2018 so 1 2018 so 1 2018 so 1 ● Khi đó:   2019 2019 2019 x  y  z    3 3 3
x  y  z  2019 2019 2019 x y z 3 3 3 3 2016 673 
 x  y  z  3 .
Dấu "  " xảy ra khi x  y  z  1 .   2019 2019 2019 x  y  z
 6054  2019x  y  z 2019 2019 2019 x  y z 3 
 x  y  z  3 .
Dấu "  " xảy ra khi x  y  z  1 . COSI ● Suy ra 3 3 3
 x  x  y  y  z  z   2 2 2
x  y  z  2 2 2 6 2 
 x  y  z  3 . 3 x  x  Dấu "  " xảy ra khi 3
y  y 
 x  y  z 1  .  3 z  z 
 Vậy E đạt giá trị lớn nhất bằng 3 khi x  y  z  1 .
Cách 3. (Sử dụng BĐT HOLDER)
● Áp dụng bất đẳng thức HOLDER, ta có
x  y  z x  y  z 
x  y  z 2019 2019 2019 2019 2019 2019 2019 2017 2 2 2 3 2019 2019 2019 x y z   
x  y  z 2019 3 2019 2 2 2 2 2 2 3 
3  x  y  z .
Dấu bằng xảy ra khi x  y  z  1 .
 Vậy E đạt giá trị lớn nhất bằng 3 khi x  y  z  1 .
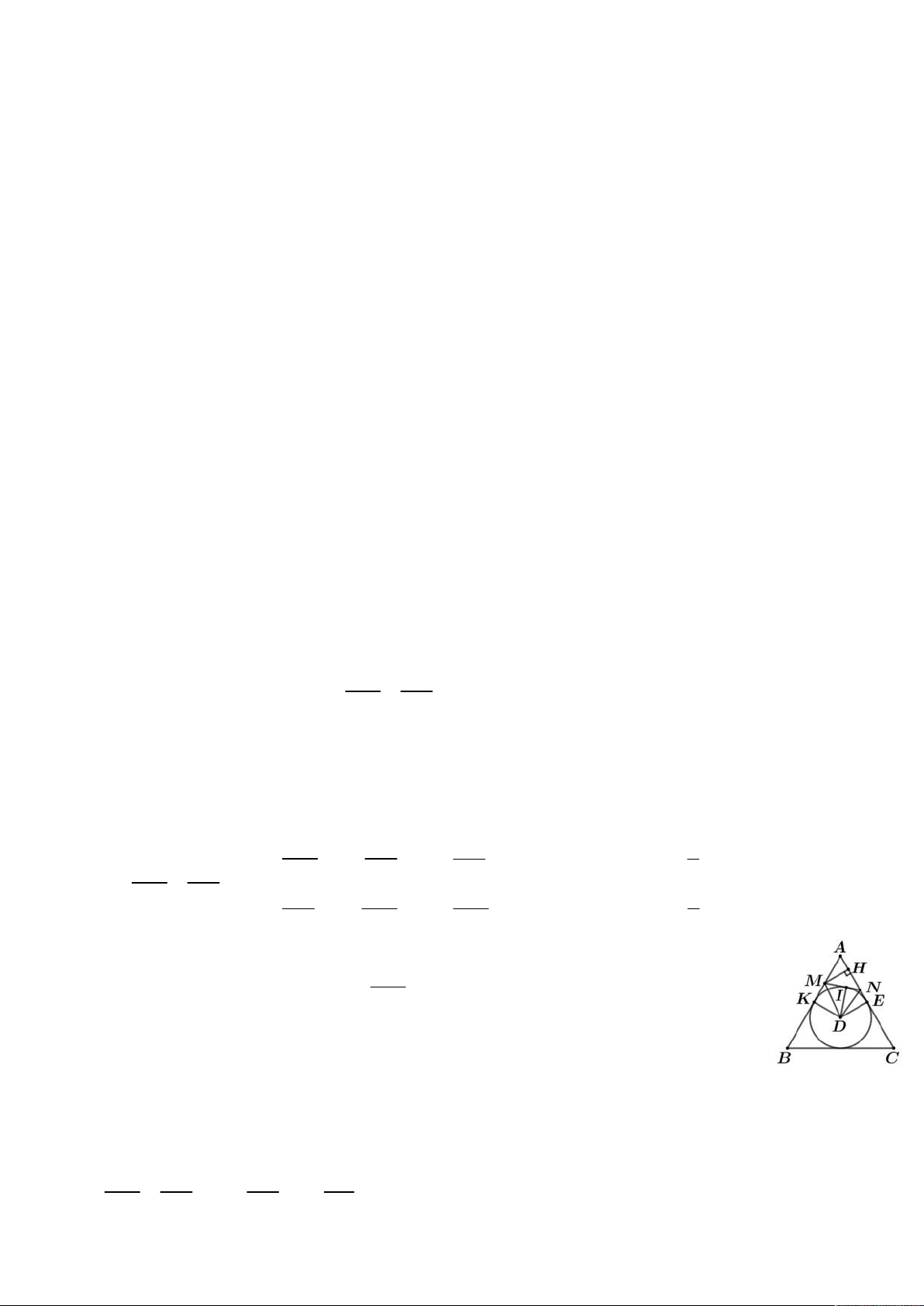
Bài 4. (4.0 điểm) Cho tam giác đều ABC có cạnh bằng a . Hai điểm M , N lần lượt di động trên AM AN
hai đoạn thẳng AB, AC sao cho 
1. Đặt AM  x và AN  y . Chứng minh rằng: MB NC a) 2 2 2
MN  x  y  xy .
b) MN  a  x  y .
c) MN luôn tiếp xúc với đường tròn nội tiếp tam giác ABC . Lời giải. AM AN AN  a  1  1 x      AM AN  
x  a  x MB NC  NC   2 ● Vì  1        
 x  y  a . MB NC  AN AM  AM
y  a  y  a     1  1     y   NC MB  MB  2
Không mất tính tổng quát ta giả sử AM  AN . Kẻ MH  AC như hình vẽ bên. AM
Khi đó, ta có AH  AM .cos 60  . 2
a) Áp dụng định lí PYTAGO, ta có:        2 2 2 2 2 2 MN MH HN AM AH AN AH 2 2 2 2
 AM  AN 2AN.AH  AM  AN  AM .AN  x  y  xy  x  y2 2 2 3xy .  2 Vậy 2 2 2
MN  x  y  xy  x  y 3xy   1 b) Theo đề, ta có: AM AN AB AC   1  1 1 1 MB NC MB NC
Trường THCS Đào Duy Từ
Năm học 2018 – 2019 GV: Lê Hồng Quốc
" Đi rồi sẽ đến " Trang 5 Đề ôn thi HSG 9
Tel: 0905.884.951 – 0929.484.951 a a 2  
  a ax  y 2 2 3
 a  3a 3ax  y3xy 2 
a 2ax  y 3xy 2 a  x a  y 2 2 2 Thay 2 vào   1 ta được: 2
MN  x  y  a x  y 2
 a  x  y  ax  y 2 2 2
 a  a  x  y
 Vậy MN  a  x  y  a  x  y (vì x  y  a ).
c) Gọi K , E lần lượt là trung điểm của AB, AC .
D là tâm đường tròn nội tiếp A  BC . a 3 a a
Kẻ DI  MN I  MN  . Khi đó ta dễ dàng tính được: DK  DE  ; MK 
 x; NE   y . 6 2 2 a a
Ta có KM  NE 
 x   y  MN và 2  ax ay 3xy  aa  x  y. 2 2 KD.MK KE.NE AH .AN ● S  2S S S S  DK.AK    D  MN AK  D M  KD N  ED AMN  2 2 2 2 DK .MN AH .AN a 3 a 3  AK    
a  x  y x 3y DK . .  2 4 12 12 4 3 3 a 3 DK .MN 2 
a aa x  y3xy 
ax ay 3xy
.a  x  y    12  . 12 12 2 DI .MN DK.MN  Do đó  
 DI  DK . Suy ra DI là bán kính đường tròn nội tiếp, mà 2 2 MN  DI 
 MN là tiếp tuyến của đường tròn.
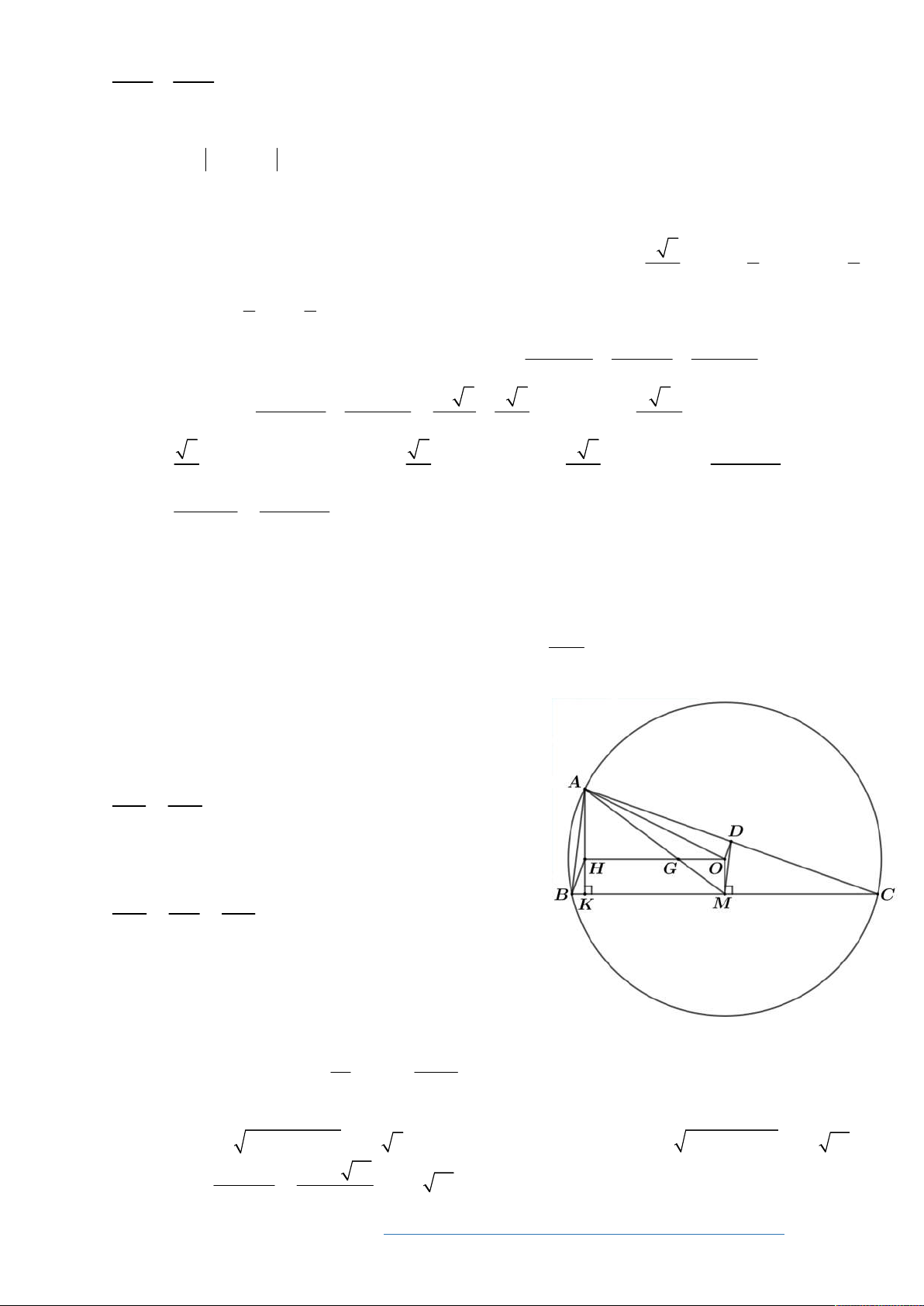
Bài 5. (3.0 điểm) Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn O , gọi M là trung điểm
của cạnh BC , H là trực tâm của tam giác ABC và K là hình chiếu vuông góc của A trên cạnh KM
BC . Tính diện tích của tam giác ABC , biết OM  HK  và AM  30 cm. 4 Lời giải.
● Gọi D là trung điểm của AC .
Ta chứng minh được AHB  MOD (3 cặp cạnh song song) AH AB    2 
 HG  2OG . OM MD
● Gọi G là giao điểm của AM và OH . Ta chứng minh được AG  H  MG 
O  g  g AG HG AH     2 
 AH  2OM . GM GO OM
● Dễ dàng chứng minh được tứ giác IMKH là hình
chữ nhật (hình bình hành có 1 góc vuông).
 HO  KM 
 HO  4OM , suy ra 3OG  4OM .
● Áp dụng định lý PYTAGO trong tam giác vuông OGM , ta có: 2 16 AM 2 2 2 2 2
OM OG  GM  OM  OM 
 5OM  AM  OM  6 cm . 9 9
Khi đó OH  24 cm; AH  12 cm; AK  18 cm . Ta có 2 2
OC  OA  OH  AH  12 5 , từ đó tính được 2 2
BC  2MC  2 OC OM  12 19 . AK .BC 18.12 19  Vậy S    108 19  . ABC  2 cm  2 2
Mọi sự góp ý, xin nhắn tin đến https://www.facebook.com/lehong.quoc.12
Trường THCS Đào Duy Từ
Năm học 2018 – 2019 GV: Lê Hồng Quốc
" Đi rồi sẽ đến " Trang 6