Đề thi học sinh giỏi cấp tỉnh Toán 12 năm 2018 – 2019 sở GD&ĐT Bến Tre

NHÓM TOÁN VD – VDC
SỞ GD&ĐT BẾN TRE
ĐỀ THI HỌC SINH GIỎI CẤP TỈNH LỚP 12 ĐỀ CHÍNH THỨC NĂM HỌC 2018 - 2019
MÔN: TOÁN – Hệ : THPT Ngày thi : 27/02/2019 Thời gian: 180 phút
Họ và tên: .......................................................................................... SBD: ................................................. . NHÓM Câu 1 (8 điểm).           TO
a) Giải phương trình: 2.sin 2x 6.sin x 1     .  4   4  Á      N
 y 2. x 2 x y 0 
b) Giải hệ phương trình:  với , x y  . VD
 x 1. y   1   y  3   2
1 x  y  3x  – x 1 VDC
c) Cho hàm số y 
có đồ thị C . Viết phương trình tiếp tuyến d  của đồ thị C biết 2x 1
d  cắt trục Ox , Oy lần lượt tại A, B sao cho AB  10.OA (với O là gốc tọa độ). Câu 2 (4 điểm). 1
a) Bạn An có đồng xu mà khi tung có xác suất xuất hiện mặt ngửa là
và bạn Bình có đồng xu 3 2
mà khi tung có xác suất xuất hiện mặt ngửa là
. Hai bạn An và Bình lần lượt chơi trò chơi tung 5
đồng xu của mình đến khi có người được mặt ngửa ai được mặt ngửa trước thì thắng. Các lần tung là độ p
c lập với nhau và bạn An chơi trước. Xác suất bạn An thắng là
trong đó p và q là các số NHÓM q
nguyên tố cùng nhau, tìm q  p . n  1 
b) Tìm hệ số của số hạng chứa 2
x trong khai triển nhi thức x 
biết rằng n là số nguyên TO   4  2 x  Á dương thỏ  a: 1 2 3
C  C  C 
 n  C  nC  n . n n n   n 1 2 3 ... 1 n 64 N n n VD Câu 3 (4 điểm). –     VDC
a) Trong không gian cho 4 điểm , A ,
B C, D thỏa mãn AB 3, BC 7, D C 11, DA 9 . Tính AC.BD .
b) Cho các số thực không âm , a , b c thỏa mãn 2 2 2
a  b  c  3b  0 . Tìm giá trị nhỏ nhất của 1 4 8 biểu thức P     . a  2 1
b  22 c 32 Câu 4 (4 điểm).
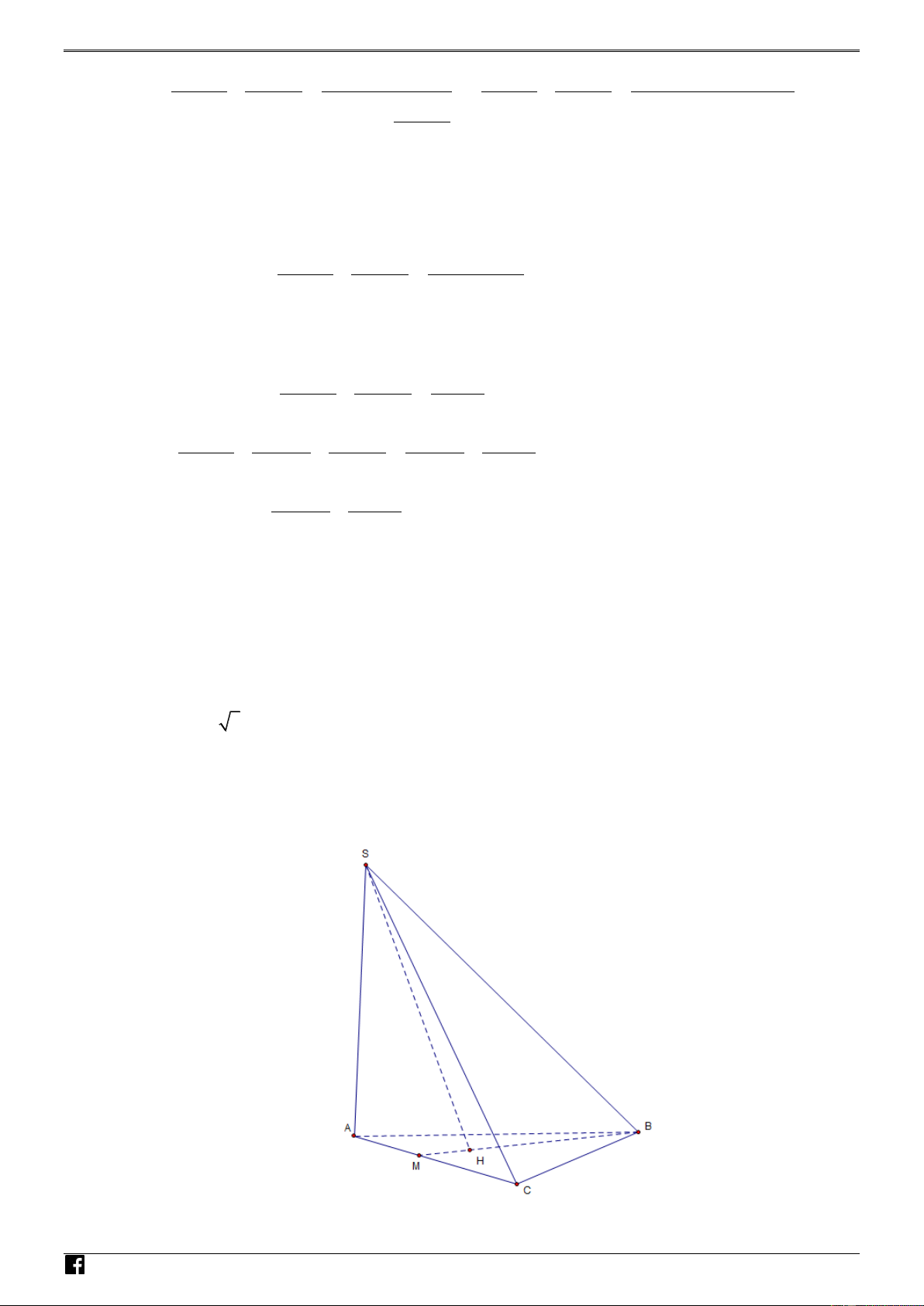
Cho hình chóp S.ABC , có SA vuông góc với mặt phẳng  ABC  , SA  2a và tam giác ABC
vuông tại C với AB  2a BAC  30 . Gọi M là điểm di động trên cạnh AC , đặt AM  , x
0 x  a 3. Tính khoảng cách từ S đến BM theo a và x. Tìm các giá trị của xđể khoảng cách này lớn nhất. ----- HẾT -----
https://www.facebook.com/groups/toanvd.vdc Trang 1 NHÓM TOÁN VD – VDC
SỞ GD&ĐT BẾN TRE
HƯỚNG DẪN GIẢI ĐỀ THI HỌC SINH GIỎI ĐỀ CHÍNH THỨC CẤP TỈNH LỚP 12 NĂM HỌC 2018 - 2019 Câu 1 (8 điểm).           NHÓM
a) Giải phương trình: 2.sin 2x 6.sin x 1     .  4   4  
 y  2. x  2  x y  0 
b) Giải hệ phương trình:  với , x y  . 2 TO
 x 1. y   1   y  3 
1 x  y3x Á x 1 N
c) Cho hàm số y 
có đồ thị C . Viết phương trình tiếp tuyến d  của đồ thị C biết 2x 1 VD
d  cắt trục Ox , Oy lần lượt tại A, B sao cho AB  10.OA (với O là gốc tọa độ). – Lời giải VDC       a) Ta có: 2.sin 2x   6.sin x 
1  sin 2x  cos 2x  3.    
sin x cos x1 0  4   4    x  x2   2 2 sin cos
sin x  cos x  3 sin x  cos x  0  sin x  cos x2sin x  3  0   x   k      4 sin x   0    
sin x  cos x  0  4       
 x   k2 . 2sin x  3  0   3 3 sin x   2  2 x   k2  3   2 NHÓM
Vậy phương trình có 3 họ nghiệm là: x 
 k , x   k2 , x 
 k2 , với k  . 4 3 3 
 y  2. x  2  x y  0   1  TO
b) Giải hệ phương trình:  .
 x 1. y   1   y  3   2
1 x  y  3x  2 Á N x  1 VD 
* Điều kiện:  y  0 . –  2     x y 3x 0 VDC 2
a  x  2 1 x  a 2 - Đặt    . 2 b   y  0   y  b Khi đó   1 trở thành:  2
b  a b 2 2
a  2  0  abb  a  2b  a  0
 b  aab  2  0  a  b do ab  2  0
 x  2  y  y  x  2 .
- Thay vào phương trình 2 ta được phương trình:
x   x      x    2 1. 2 1 1 . 1
x  2x  2 
 x    x     x     x 2 1. 1 1 1 1 . 1 1 1 3 .
- Nếu x  1 thì 3 vô nghiệm.
https://www.facebook.com/groups/toanvd.vdc Trang 2 NHÓM TOÁN VD – VDC
- Với x  1, xét hàm số: f t   t  2
. 1 1 t  trên 0; . 2 t
Có: f t  2 1 1 t   0, t
 0; , do đó hàm số f t đồng biến trên 0; 2 1 t   x 
3  f  x 1  f x   0 2 1 
x 1  x 1  x  3x  0   x  3  (do x  1) x  3 NHÓM
Vậy hệ có nghiệm duy nhất  ; x y  3;5 .   c) TXĐ: 1 \   . TO 2  Á 3 Ta có: y  . N 2x  2 1 VD
- Giả sử tiếp tuyến d  của C cắt Ox , Oy lần lượt tại A và B thỏa mãn AB  10.OA . –
Khi đó tam giác OAB vuông tại O và có AB  10.OA  OB  3.OA VDC OB  tan OAB   3  k  3
 , với k là hệ số góc của tiếp tuyến d  OA 3  2x 1 1 x 1  y  3    3
  2x 1 1     2  2 2x   1 2x 1  1  x  0 M 1;2   là các tiếp điểm. M  0;  1
Vậy có 2 tiếp tuyến d  thỏa mãn yêu cầu bài toán là : y  3
 x  5 và y  3  x 1. Câu 2 (4 điểm). NHÓM 1
a) Bạn An có đồng xu mà khi tung có xác suất xuất hiện mặt ngửa là
và bạn Bình có đồng xu 3 2
mà khi tung có xác suất xuất hiện mặt ngửa là
. Hai bạn An và Bình lần lượt chơi trò chơi tung TO 5
đồng xu của mình đến khi có người được mặt ngửa ai được mặt ngửa trước thì thắng. Các lần tung Á N là độ p
c lập với nhau và bạn An chơi trước. Xác suất bạn An thắng là
trong đó p và q là các số VD q
nguyên tố cùng nhau, tìm q  p . – n VDC  1 
b) Tìm hệ số của số hạng chứa 2
x trong khai triển nhi thức x  
 biết rằng n là số nguyên 4  2 x  dương thỏ  a: 1 2 3
C  C  C 
 n  C  nC  n . n n n   n 1 2 3 ... 1 n 64 n n Lời giải
a) Giả sử ở lần gieo thứ n bạn An thắng cuộc, khi đó ở n 1lần gieo trước bạn An đều chỉ gieo ra
mặt sấp và bạn Bình chỉ gieo được n 1 lần đều có kết quả là mặt sấp. n 1  n 1  n 1   2  1  3  1  2 
Xác suất để có được điều đó ở lần gieo thứ n là .        .  3  3  5  3  5 
Do đó, điều kiện thuận lợi để bạn An thắng là 2 n p 1  2 2 2        1 1 5  1    ... ...          . q 3   5   5   5    3 2 9  1 5
https://www.facebook.com/groups/toanvd.vdc Trang 3 NHÓM TOÁN VD – VDC
Suy ra q  p  9  5  4 . n n n n
b) Ta xét khai triển 1 x k k
 C x . Lấy đạo hàm 2 vế ta được: n1 x 1 k k 1  kC x  . n n k 0 k 1    Chọn 1 2 3
x   C  C  C 
 n  C  nC  n n n n   n 1 n n 1 1 2 3 ... 1 .2 n n Do đó 1 2 3 C C C n C  nC n n         
 n  n  . n n n   n 1 n n 1 2 3 ... 1 64 2 64 7 n n NHÓM Tiếp tục khai triển 7 k    7 k k   1   1   1 k k   1 k k  k k k x   C x   C x x   C x   . 7   7 7 7 7 7 7 3 7 2 4 4 TO     7   7 4 4  2 x        k  2 x k  2 k  2 0 0 0 Á N  Do đó để 3k 7
tìm được số hạng chứa 2
x thì ta cần tìm k để  2  k  5 . VD 4 – 75  1  21 5 VDC
Vậy hệ số của số hạng chứa 2 x là C    . 7  2  4 Câu 3 (4 điểm).
a) Trong không gian cho 4 điểm , A ,
B C, D thỏa mãn AB  3, BC  7, D C 11, DA  9 . Tính AC.BD .
b) Cho các số thực không âm , a , b c thỏa mãn 2 2 2
a  b  c  3b  0 . Tìm giá trị nhỏ nhất của 1 4 8 biểu thức P     . a  2 1
b  22 c 32 Lời giải a) Ta có 2 2 2 2
AB  BC  CD  DA   AB  BC AB  BC  CD  DACD  DA  NHÓM
  AB  BC AC CD  DACA  AC AB  BC CD  DA  2AC.DB 1
Do đó AC.BD   9  49 121  81  0 . TO 2 b) Cách 1: Á N Áp dụng BĐT A-G: 2 2 2 a 1  2 ; a b  4  4 ; b c 1  2c VD suy ra 2 2 2
2a  4b  2c  6  a  b  c  2a  b  2c  6  
1 . Dấu "  " xảy ra khi và chỉ khi – a  c 1 . VDC b   2  1 1  1 1 8 2 Ta lại có với ,
x y là các số thực dương:  x  y   8      , dấu "  " xảy 2 2 2 2  x y  x y x  y2
ra khi và chỉ khi x  y . Do đó 1 1 8 8 8 64 256 P        a  2 2 1  b  c 32 2  b  c 32 2  b 
2a b  2c 102 1 a   2 a   c  5        2   2   2  a  c 1 Kết hợp  
1 suy ra P  1. Vậy min P 1   . b   2 Cách 2: Ta có: 2 2 2
a  b  c  3b  0 2 2 2
 b 3b  a
 c  0  0  b  3.
https://www.facebook.com/groups/toanvd.vdc Trang 4 NHÓM TOÁN VD – VDC 1 8 9 1 8 18 Ta có         1 . a  2 1 c 32 2 2 2 2 2         a   c 3 a 1 c 3 2a 4a c 6c 11 2       1  2 Lại có a   2 4 2 a   1 và c   2 6 3 c   1 2 2 2
 a  a  c  c   a   2 a   2  c   2 2 4 6 11 2 2 1 3 c   1 11 2 2 2 2 NHÓM
 2a  4a  c  6c 11 4a  4c 16 2 . 1 8 9 Từ   1 và 2 ta có   3  . a  2 1 c 32 2 2 2a  2c  8 TO Lại có từ giả thiết 2 2 2
a  b  c  3b  0 2 2 2
 a b  c  3b 2 2 2
 a  c b  4  3b  4 mà Á 2 b  4  4b 2 2 2 2
 a  c  4b  3b  4  a  c  4b 2 2
 2a  2c  8 2b 4 . N VD 1 8 9
Từ 3 và 4 ta có   a  2 1
c 32 16 2b – VDC 1 4 8 4 9  P       . a  2 1
b  22 c 32 b  22 16 2b 4 9
Xét hàm số f b      với 0 b 3 . b  22 16  2b a  c 1
Ta có min f b  1 khi b  2  P  f b  min f b  1và min P  1   b    0;3 b    0;3 b   2 Câu 4 (4 điểm).
Cho hình chóp S.ABC , có SA vuông góc với mặt phẳng  ABC  , SA  2a và tam giác ABC
vuông tại C với AB  2a BAC  30 . Gọi M là điểm di động trên cạnh AC , đặt AM  , x NHÓM
0 x  a 3. Tính khoảng cách từ S đến BM theo a và x. Tìm các giá trị của xđể khoảng cách này lớn nhất. TO Lời giải Á Cách 1 N VD – VDC
https://www.facebook.com/groups/toanvd.vdc Trang 5 NHÓM TOÁN VD – VDC
Gọi H là hình chiếu vuông góc của S trên BM . Suy ra BM  SAH  . BC.AM . a x Ta có M  AH M
 BC  AH   . 2 2 BM
4a  x  2xa 3 2 2
5x  8xa 3 16a hình 2 2
 SH  SA  AH  a 2 2
x  2xa 3  4a NHÓM Cách 2 Ta có 2 2 2 2 SM 
SA  AM  4a  x , 2 2
SB  SA  AB  2a 2,
SM  SB  BM 2 2 2 2
BM  BA  AM  2A .
B AM cos BAM  4a  x  2xa 3, p  TO 2 Á
Diện tích tam giác SBM là S
 p p  SB p  MB p  SM SBM     N VD a 2 2 
5x  8xa 3 16a 2 – 1 VDC
Gọi H là hình chiếu vuông góc của S trên BM . Ta có S  SH.BM SBM 2 2S 2 2
5x  8xa 3 16a 2 2
5x  8xa 3 16a SBM  SH   a
 d S, BM   SH  a BM 2 2
x  2xa 3  4a 2 2 x  2xa 3  . 4a Cách 3 Ta có BC  , a AC  a 3 .
Chọn hệ trục tọa độ Oxyz sao cho C 0;0;0, B  ;
a 0; 0, A0;a 3;0, S 0;a 3;2a
Do H thuộc AC , AM  x nên M 0;a 3  ; x 0 Ta có MB   ;
a x  a 3; 0 , BS   ; a a 3; 2a . NHÓM MB BS     2 2 , 2ax  2a 3; 2  a ; xa . MB, BS  
5x  8xa 3 16a TO
Khoảng cách từ S đến BM là d S, BM  2 2   a . 2 2 MB
x  2xa 3  4a Á N VD
* Tìm các giá trị của x để khoảng cách này lớn nhất. –
5x  8xa 3 16a
Xét hàm số f  x 2 2 
0 x  a 3 VDC 2 2
x  2xa 3  4a x  0   2 2
2a 3x  8xa  f x  
, f  x  0  4 3a 
. Có f 0  4, f  3  7.    
x  2xa 3  4a 2 2 2 x 0; a 3     3 ----- HẾT -----
https://www.facebook.com/groups/toanvd.vdc Trang 6