Đề thi học sinh giỏi cấp tỉnh Toán THCS năm 2023 – 2024 sở GD&ĐT Đắk Lắk

1
HSG TOAN 9 NAM HOC 2023-2024 DAK LAK
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KÌ THI CHỌN HỌC SINH GIỎI CẤP TỈNH TỈNH ĐẮK LẮK NĂM HỌC 2023-2024 …ĐỀ
Môn: TOÁN - THCS CHÍNH THỨC…
Thời gian: 150 phút (không kể giao đề)
(Đề thi có 01 trang) Ngày thi: 26/3/2024
Bài 1. (4,0 điểm)
1. Tính giá trị của biểu thức 2
A x  2x  ,
23 với x  3 5 2 3  3 5 2 3
2. Trong mặt phẳng Ox ,
y cho đường thẳng d : y m2x  m ,
1 (m là tham số) và Parabol P 1 : 2
y  x . Chứng minh rằng với mọi số thực m đường thẳng d luôn cắt Parabol Ptại hai 2 điểm phân biệt.
Bài 2. (4,0 điểm)
1. Cho các số thực a,b,c thoả mãn 2a 3b  6c  .
0 Chứng minh rằng phương trình 2
ax  bx c  0
luôn có hai nghiệm phân biệt x , x . Tìm giá trị nhỏ nhất của x  x . 1 2 1 2  2 y  2 2
x  3y  4x 3xy  2  0
2. Giải hệ phương trình: 
 y x1  2
x  y  3  2  0
Bài 3. (4,0 điểm)
ab2 4a
1. Cho a,b là hai số nguyên dương thoả mãn
là số tự nhiên. Chứng minh rằng nếu b ab
là số lẻ thì a là số chính phương.
2. Tìm tất cả các tam giác vuông có độ dài các cạnh là các số nguyên dương và số đo chu vi bằng số đo diện tích.
Bài 4. (4,0 điểm)
Cho tứ giác ABCD nội tiếp đường tròn O, Gọi P là điểm chính giữa của cung CD không
chứa hai điểm A và .
B Tia AP cắt đường thẳng BC tại E. Tia BP cắt đường thẳng AD tại F.
1. Gọi M , N lần lượt là giao điểm của PA, PB với .
CD Chứng minh rằng bốn điểm A, B, M , N
cùng nằm trên một đường tròn và đường thẳng OP vuông góc với . EF 2  EF  PE PF 2. Chứng minh    .  AB  PA PB EF AB AF BE PE PA PF PB 3. Chứng minh        . AB EF BE AF PA PE PB PF
Bài 5. (2,0 điểm)
Trong hình tròn bán kính 46cm, người ta đặt 2024 điểm phân biệt. Chứng minh rằng tồn tại
một hình tròn có bán kính bằng1 ,
cm mà không chứa điểm nào trong 2024 điểm đã cho.
Bài 6. (2,0 điểm)
Cho các số thực dương x, y, .
z Tìm giá trị nhỏ nhất của biểu thức: x3 y3 z3 1 P     x2  y2 y2  z2 z2  x2
x  y  z ------ HẾT ------
Thí sinh không được sử dụng tài liệu và máy tính cầm tay
GV Vu Van Hoang To KHTN 1 HAU LOC * THANH HOA 2
HSG TOAN 9 NAM HOC 2023-2024 DAK LAK
Cán bộ coi thi không giải thích gì thêm
Họ và tên thí sinh: ……………………………………………………. Số báo danh: ……………………
Họ tên và chữ kí. Cán bộ coi thi thứ nhất: …………………………………………………………….....
Cán bộ coi thi thứ hai: …………………………………………………………………
HỌC TOÁN THẦY HOẰNG HƯỚNG DẪN CHẤM
ĐỀ THI CHỌN HỌC SINH GIỎI TOÁN 9 CẤP TỈNH SỞ GD&ĐT ĐẮK LẮC
Năm học 2023 – 2024
(Đây không phải là đáp án chính thức của SGD Tỉnh Đắc Lắk)
Bài 1. (4,0 điểm)
1. Tính giá trị của biểu thức 2
A x  2x  ,
23 với x  3 5 2 3  3 5 2 3
2. Trong mặt phẳng Ox ,
y cho đường thẳng d : y m  2 x  m ,
1 (m là tham số) và Parabol P 1 : 2
y  x . Chứng minh rằng với mọi số thực m đường thẳng d luôn cắt Parabol Ptại hai 2 điểm phân biệt. BÀI Ý NỘI DUNG ĐÁP ÁN ĐIỂM 1. 1. Đặ 0,5
t m 3 5 2 3 và n  3 5 2 3  x m n (4,0 điểm) 2 2
m  n 6 Ta thấy 
do đó x2 m2 n22mn  2 mn  3   1  3 1 2 x  6  2 3   1  4 2 3 0,5
 x 42 3  3 1 0,5
Thay vào ta có: A42 3  2 3   1  23 25 0,5
2. Gọi x; ylà giao điểm của Pvà d . Khi đó x, y thoả mãn 0,5  y  1 2 x  2
ym2xm1
Xét phương trình hoành độ giao điểm của  1 0,5
Pvà d : 2
x m2x  m1 2  x2  
2 m  2x   2 m   1  0 I 
Ta có: 'm22   2 m  1 Do 'm   1 2  5  '  , 0  . m 0,5
nên phương trình (I) luôn có 2 nghiệm phân biệt với mọi m.
Do đó P luôn cắt dtại hai điểm phân biệt với mọi m. 0,5
GV Vu Van Hoang To KHTN 2 HAU LOC * THANH HOA 3
HSG TOAN 9 NAM HOC 2023-2024 DAK LAK
Bài 2. (4,0 điểm)
1. Cho các số thực a,b,c thoả mãn a  0và 2a 3b  6c  .
0 Chứng minh rằng phương trình 2
ax  bx c  0 luôn có hai nghiệm phân biệt x , x . Tìm giá trị nhỏ nhất của x  x . 1 2 1 2  2 y  2 2
x  3y  4x 3xy  2  0
2. Giải hệ phương trình: 
 y x1  2
x  y  3  2  0 BÀI Ý NỘI DUNG ĐÁP ÁN ĐIỂM 2. 1. Ta có: a 2  b 3  c 6 0 a 2   b 3  c 6 0,5 (4,0 điểm)
Với a0, phương trình 2
ax  bx c  0 là phương trình bậc hai. Có 2 2 2
b 4acb 4acb 2c 3b6c 2 2
b 6bc12c
Ta thấy  b3c2 2 4c 0,5
Do a  0, nên b,c không đồng thời bằng 0.
Khi đó b3c2 4 2
c 0;b  c  0
  0; b  c 0
Chứng tỏ rằng phương trình luôn có hai nghiệm phân biệt x , x . 1 2  Theo hệ thức Vi b c 0,5
-ét, ta có: x  x  và x .x  1 2 a 1 2 a Khi đó 2 9 x  x 9 x  x 1 2  1 2 2   9b 36ac
2a  6c 36ac a  6c 9 x  x 36x x   3 1 2  2 2  2  2 1 2 2 2 2 a a a a6c2 0,5 Do 3  ,
3 mọi a,b,c 2 a 2 1
nên 9 x  x
3 x  x  1 2 1 2 3 1 a  c 6
Vậy Min x  x   
hay a  b  c 6 1 2 3 2a  b 3  c 6  0 2.
y  x 1 0 0,5
Với x, yR, sao cho   * 2
x  y 30  2 y  2 2
x  3y  4x 3xy  2  0
Hệ phương trình đã cho 
 y x1  2
x  y  3  2  0   2 y  2xy  2 x   1   2
x  xy  x 3x  3y 3  0 
 y x1  2
x  y 3  2 0 
 x y  
1 2x  y  2  0 
 y x1  2
x  y  3  2  0 x y  1 0
2x y 20    a hoặc  b
 y  x1  x2  y  3 20
 y  x1  x2  y  3 20
Xét hệ (a), thay y  x 1
 vào y  x 1 2
 x  y 3 20, ta được: 0,5 2
x  x  4  2 2
 x  x 0 x  ; 0 x 1.
GV Vu Van Hoang To KHTN 3 HAU LOC * THANH HOA 4
HSG TOAN 9 NAM HOC 2023-2024 DAK LAK
Khi đó, tương ứng: y  ; 1 y 0
Xét hệ (b), thay y  2x2 vào y  x 1 2
 x  y 3 20, ta được: 0,5 x 1 2
 x 2x 5 2  2
x  x 2 x 1. 2
x  2x  5 0  x  1 x x 1   2 2
x  2x  50  x 1  0  x 1 
Khi đó, tương ứng: y 0
(do x 1 x x 1  2 2
x  2x  5  0 ) x 0 x 1 0,5 Ta thấy 2 cặp  ;  đều thoả mãn
y 1 y 0
Tóm lại hệ có 2 nghiệm là:  ; x y   ;0 1, ;1  0 
Bài 3. (4,0 điểm)
ab2 4a
1. Cho a,b là hai số nguyên dương thoả mãn
là số tự nhiên. Chứng minh rằng nếu b ab
là số lẻ thì a là số chính phương.
2. Tìm tất cả các tam giác vuông có độ dài các cạnh là các số nguyên dương và số đo chu vi bằng số đo diện tích. BÀI NỘI DUNG ĐÁP ÁN ĐIỂM 3. 1. ab2  0,5 Với 4a a, *
bN . Đặt M  (4,0 điểm) ab a   xd
Gọi d UCLNa,b  ;  *
d, x, yN , với UC  LN ; x y ; 1 b   yd
Khi b lẻ thì y và d đều lẻ.
ab2 4a dxdy2 4dx dx y2 4x Do đó M    ab dxdy dxy
Vì M N* nêndx  y2  4xd 4xd , do d lẻ nên 4  d  xd
Do đó x  dz  * , zN  0,5
d dz  y2  4dz dz y2   4z * M   , mà M N 2 d yz dyz
nên dz  y2  4zz  y2  z  
1 , vì y lẻ nên z lẻ.
Cũng do: x  dz  *
, zN  xz   2 mà UC  LN ; x y ; 1 0,5 nên UCL  N ; dz y 1  UCL  N d ; z 1    3 Do đó, từ   1 ,  2 và   3  z 1  0,5 Với z 1 2
thì x  d và a  d . Vậy a là số chính phương
2. Gọi a,b,c là độ dài các cạnh của tam giác cần tìm (với a b c ). 0,5  2 a  2 b  2  c  2 a  2 b  2 c   Khi đó ta có: 1   1 
a bc  bc  
4 a  b  c 2bc 2  2
GV Vu Van Hoang To KHTN 4 HAU LOC * THANH HOA 5
HSG TOAN 9 NAM HOC 2023-2024 DAK LAK Từ (1) và (2) ta có: 2 a  
4 a bcbc2
abcabc  4 0
do : a b  c 0 nên(I )  a b c  40 0,5
 a  4b  c (3)
Từ (2) và (3) ta được: b  4 c   4 8 I  Với * ,
b cN xét các trường hợp ta có: 0,5  ;bc  ; 12  5 , 12 ; 5 , ;8  6 , ; 6  8  Lần lượt tính được: 0,5   a  10 ; 13
, chú ý b  c  a  b  c
Tóm lại, các tam giác vuông thoả mãn bài ra là:    13 ; 12 ; 5 ,  ; 6 10 ; 8 
Bài 4. (6,0 điểm)
Cho tứ giác ABCD nội tiếp đường tròn O, Gọi P là điểm chính giữa của cung CD không
chứa hai điểm A và .
B Tia AP cắt đường thẳng BC tại E. Tia BP cắt đường thẳng AD tại F.
1. Gọi M , N lần lượt là giao điểm của PA, PB với .
CD Chứng minh rằng bốn điểm A, B, M , N
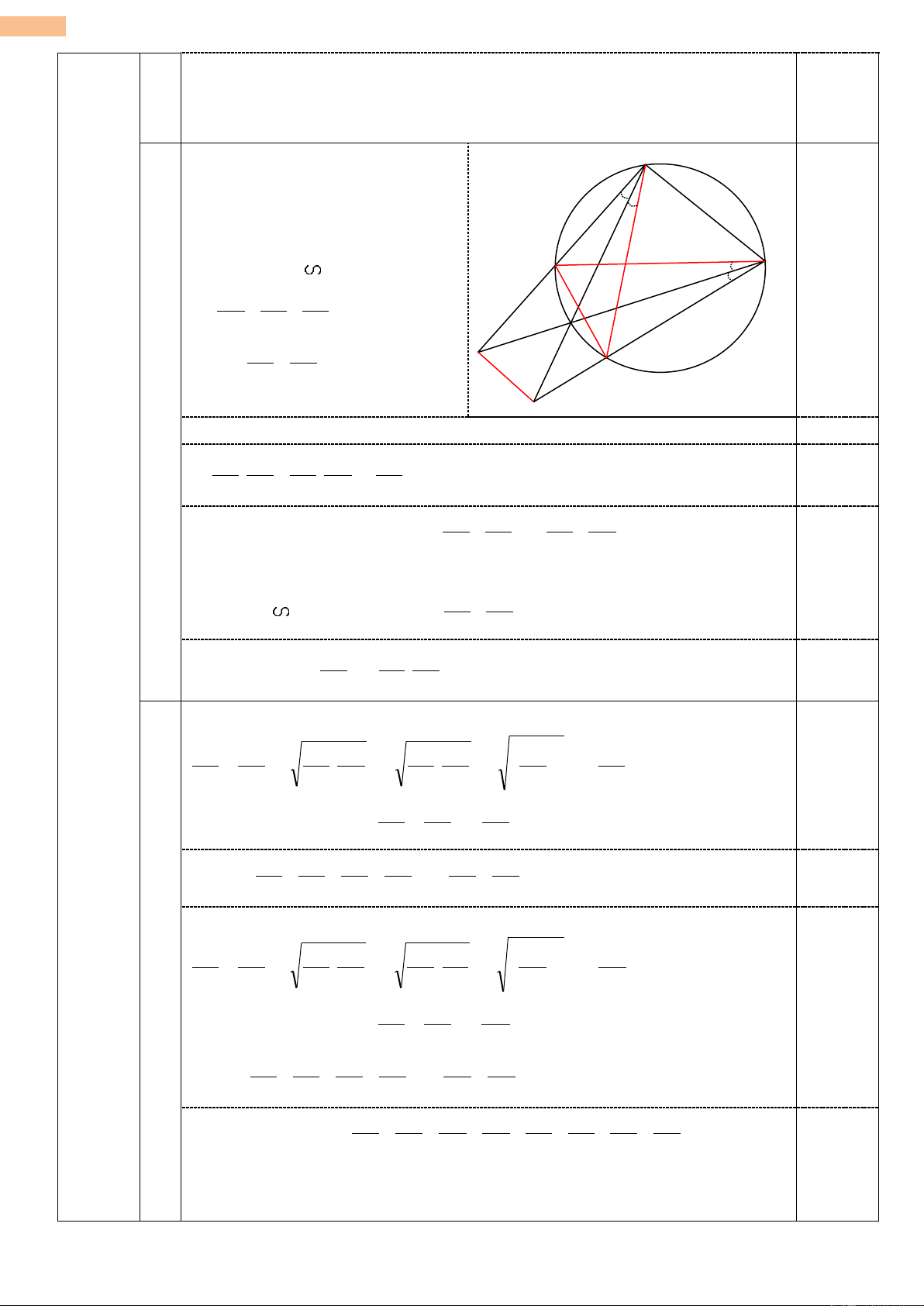
cùng nằm trên một đường tròn và đường thẳng OP vuông góc với . EF 2  EF  PE PF 2. Chứng minh    .  AB  PA PB EF AB AF BE PE PA PF PB 3. Chứng minh        . AB EF BE AF PA PE PB PF BÀI Ý NỘI DUNG ĐÁP ÁN ĐIỂM 4. 1. 𝑠đ𝐵𝐶 ̆ +𝑠đ𝐷𝑃 ̆ Ta có: 𝐵𝑁𝐶 ̂ =   0,5
1 , góc có đỉnh bên ngoài đường tròn O (6,0 điểm) 2 Lại có: 1 𝑠đ𝐵𝐶 ̆ +𝑠đ𝐶𝑃 ̆ 𝐵𝐴𝑀 ̂ = 𝑠đ𝐵𝑃 ̆ =  
2 , góc nội tiếp của O 2 2 mà 𝑠đ𝐷𝑃 ̆ = 𝑠đ𝐶𝑃
̆ (do P là điểm chính giữa của cung CD) nên 𝐵𝑁𝐶 ̂ = 𝐵𝐴𝑀 ̂
Xét tứ giác ABNM có: 𝐵𝑁𝐶 ̂ = 𝐵𝐴𝑀
̂ (chứng minh trên), do đó: 0,5 𝐵𝐴𝑀 ̂ + 𝐵𝑁𝑀 ̂ = 𝐵𝑁𝐶 ̂ + 𝐵𝑁𝑀 ̂ = 1800
Do đó ABNM là tứ giác nội tiếp (tổng hai góc đối bằng 0 180 ) Chú ý: Từ 𝐵𝑁𝐶 ̂ = 𝐵𝐴𝑀
̂ , có thể kết luận: “ ABNM là tứ giác nội tiếp” theo dấu
hiệu tứ giác có góc ngoài tại 1 đỉnh bằng góc trong của đỉnh đối diện.
Xét đường tròn O, có: 𝐷𝐴𝑃 ̂ = 𝑃𝐵𝐶
̂ (2 góc nội tiếp, và 𝐷𝑃 ̆ = 𝐶𝑃 ̆ ) 0,5 hay 𝐹𝐴𝐸 ̂ = 𝐹𝐵𝐸 ̂
do đó ABEF là tứ giác nội tiếp (tứ giác có 2 đỉnh kề nhau cùng nhìn đoạn
thẳng nối 2 đỉnh còn lại dưới góc không đổi) khi đó 𝐵𝐴𝐹 ̂ + 𝐴𝐹𝐸 ̂ = 1800 lại có: 𝐴𝐷𝐶 ̂ + 𝐴𝐵𝐶
̂ = 1800 (do ABNM là tứ giác nội tiếp) do đó 𝐴𝐷𝐶 ̂ = 𝐴𝐹𝐸
̂, lại đồng vị nên 𝐷𝐶 ∥ 𝐹𝐸 (1)
GV Vu Van Hoang To KHTN 5 HAU LOC * THANH HOA 6
HSG TOAN 9 NAM HOC 2023-2024 DAK LAK Do 𝑠đ𝐷𝑃 ̆ = 𝑠đ𝐶𝑃
̆ nên 𝐷𝑃 = 𝐶𝑃 mà 𝐷𝑂 = 𝐶𝑂 nên OP là đường trung 0,5 trực của .
CD Do đó OPCD   2 Từ   1 và  
2  OP  FE 2. A 0,5  Ta thấy 𝐹𝐴𝑃 ̂ = 𝑃𝐵𝐸 ̂ (2 góc nội tiếp, 𝐷𝑃 ̆ = 𝐶𝑃 ̆ ) kết hợp 𝐴𝑃𝐹 ̂ = 𝐵𝑃𝐸 ̂ (đối đỉnh) Do đó: D B
∆𝑃𝐸𝐵 ∆𝑃𝐹𝐴  g.g     PE PB EB /     *  M P  PF PA FA  N F / Do đó PE PF    C PB PA  E  2 0,5
 PE PF PE PF  PE  .  .     1 PA PB PB PA  PB  Mặt khác: PE PB PE PF 0,5 PFE  và P  AB , có:  (vì  ); PF PA PB PA kết hợp 𝐸𝑃𝐹 ̂ = 𝐴𝑃𝐵 ̂ (đối đỉnh)  PE EF P  FE PAB  (c.g.c) nên  2 PB AB 2 0,5 Từ    EF  PE PF 1 và 2    .  AB  PA PB
3. Theo bất đẳng thức AM  GM, ta có: 0,5 2 PE PF PE PF PE PF  FE  FE  2 . 2 . 2    . 2 PA PB PA PB PB PA  AB  AB
Chứng minh tương tự: PA PB AB   . 2 PE PF EF Do đó: PE PA PF PB  EF AB      0,5 . 2   I  PA PE PB PF  AB EF  Mặt khác, ta lại có: 0,5 2 PE PB PE PB PE PB  BE  BE  2 . 2 . 2    . 2 (theo   * ) PA PF PA PF PF PA  AF  AF
Chứng minh tương tự: PA PF AF   . 2 PE PB EB Do đó PE PA PF PB  AF BE      . 2   II  PA PE PB PF  BE AF  EF AB AF BE PE PA PF PB 0,5
Từ I và II suy ra:        . AB EF BE AF PA PE PB PF
Dấu “=” xảy ra khi và chỉ khi PA PB PE  PF ,
tức là: ABEF là hình chữ nhật , còn ABCD là hình vuông.
GV Vu Van Hoang To KHTN 6 HAU LOC * THANH HOA 7
HSG TOAN 9 NAM HOC 2023-2024 DAK LAK
Bài 5. (2,0 điểm)
Trong hình tròn bán kính 46cm, người ta đặt 2024 điểm phân biệt. Chứng minh rằng tồn tại
một hình tròn có bán kính bằng 1 ,
cm mà không chứa điểm nào trong 2024 điểm đã cho. BÀI NỘI DUNG ĐÁP ÁN ĐIỂM 5.
Ta biết hình tròn bán kính ,
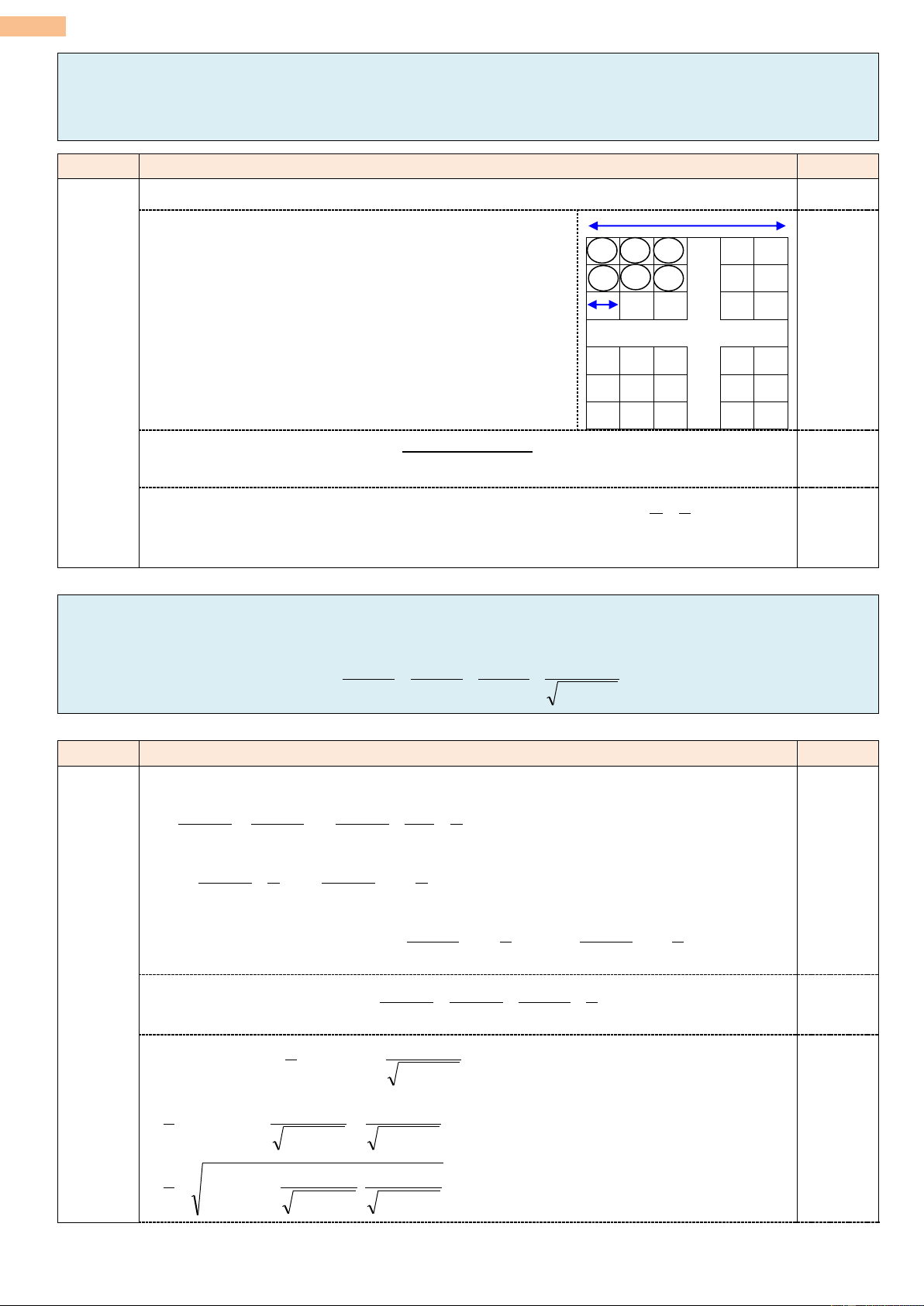
R sẽ nội tiếp được trong hình vuông cạnh 2 . R 0,5
(2,0 điểm) Do đó hình tròn bán kính 46cm, nội tiếp trong hình 0,5 92 cm vuông cạnh 92 . cm Ta chia hình vuông cạnh 92 ,
cm thành 46  46  2116
hình vuông nhỏ (cạnh cm 2 ). 2 cm
Vì 2116  2024 tức là số hình vuông nhỏ nhiều hơn ...
số điểm phân biệt đã cho.
Do đó theo nguyên lí Dirichlet có 1 hình vuông nhỏ (cạnh d  cm 2 ) không 0,5
chứa bất kì điểm nào trong 2024 điểm đã cho. Nghĩa là luôn có (tồ d 2 0,5
n tại) một hình tròn, có bán kính bằng R   1cm mà 2 2
không chứa bất kì điểm nào trong 2024 điểm đã cho.
Bài 6. (2,0 điểm)
Cho các số thực dương x, y, .
z Tìm giá trị nhỏ nhất của biểu thức: x3 y3 z3 1 P     x2  y2 y2  z2 z2  x2
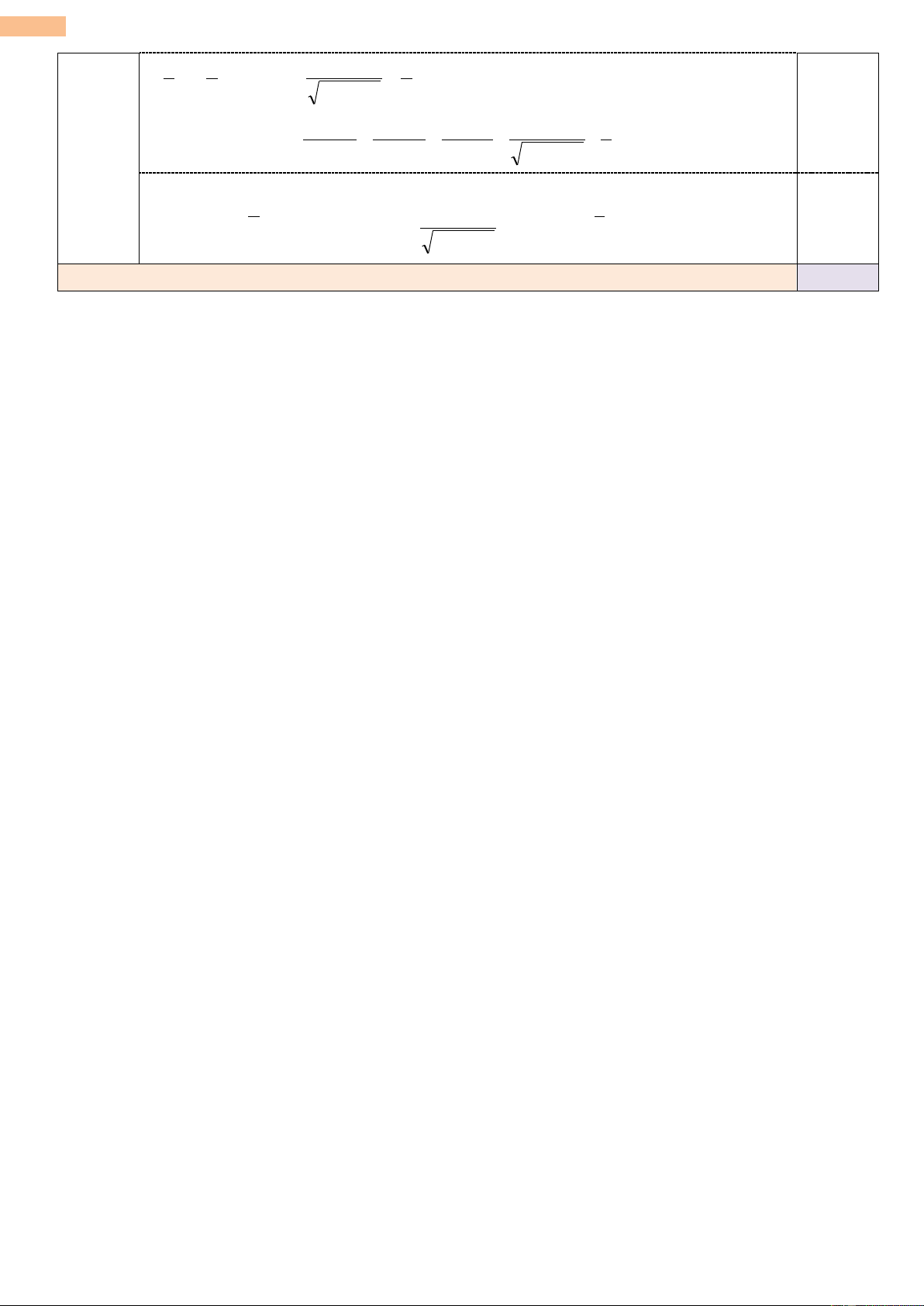
x  y  z BÀI NỘI DUNG ĐÁP ÁN ĐIỂM 6. Với , x y, z  . 0 Ta có: 0,5 (2,0 điểm) 3 2 2 2 x xy xy xy y x   mà   2 2 2 2 2 2 x  y x  y x  y 2xy 2 3 3 x y x y  x   , nên  x   1. 2 2 x  y 2 2 2 x  y 2 3 y z 3 z x
Chứng minh tương tự, ta được:  y  2;  z  3 2 2 y  và   z 2 2 2 y  z 2 3 3 3 0,5 Từ (1), (2) và (3) suy ra: x y z 1 P   
 x  y  z I  x2  y2 y2  z2 z2  x2 2 Mặt khác, ta có: 1 0,5 x  1 y  z 2
x  y  z  1    1 1
x  y  z     2 
x  y  z
x  y  z  1 1 1  .   3 3 x y z. . 2
x  y  z
x  y  z
GV Vu Van Hoang To KHTN 7 HAU LOC * THANH HOA 8
HSG TOAN 9 NAM HOC 2023-2024 DAK LAK 3   1 1 3
x  y  z  II 2 2
x  y  z 2 3 3 3 x y z 1 3
Từ I và II   P      2 2 2 2 2 2 x  y y  z z  x
x  y  z 2
x  y; y  z; z  x 0,5  Vậy 3 1
Min P  ; đạt   1
 x  y  z  . 2
x  y  z  3  
x  y  z TỔNG ĐIỂM 20 HẾT HƯỚNG DẪN
GV Vu Van Hoang To KHTN 8 HAU LOC * THANH HOA
Document Outline

• de-hoc-sinh-gioi-cap-tinh-toan-thcs-nam-2023-2024-so-gddt-dak-lak
• dethi&dapanHSGtoan9.CAPTINHdaklaknh2024