Đề thi Học sinh giỏi lớp 9 cấp tỉnh năm 2016-2017 Sở GD Quảng Nam (có lời giải)

SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI HỌC SINH GIỎI LỚP 9 CẤP TỈNH QUẢNG NAM
Năm học 2016 – 2017 Môn thi : TOÁN
Thời gian: 150 phút (không kể thời gian giao đề) ĐỀ CHÍNH THỨC Ngày thi : 10/4/2017
Câu 1. (5,0 điểm)  x  4
2x  5 x 1   x 1  1
a) Cho biểu thức P     x x  2    
 với x  0 và x  . 2x  3 x  2 4x 1   2 x  4
Rút gọn biểu thức P và tìm x để 3 P  . 2
b) Cho ba số thực dương a, b, c thỏa ab  bc  ca  3ab .
c Tìm giá trị nhỏ nhất của biểu 3 3 3 a b c thức A    2 2 2 c  a a  b b  . c
Câu 2. (4,0 điểm) a) Giải phương trình 2
x  1 x  1 x  2  0 . 2
xy  2x  4y  1 
b) Giải hệ phương trình  2 3 2
x y  2xy  4x  3y  2
Câu 3. (4,0 điểm)
a) Tìm tất cả các cặp số nguyên dương ( , a )
b thỏa mãn đẳng thức: 3 3 2 2
a  b  3(a  b )  3(a  b)  (a 1)(b 1)  25 .
b) Cho hai số nguyên a và b thỏa 2 2
24a 1  b . Chứng minh rằng chỉ có một số a hoặc b chia hết cho 5.
Câu 4. (2,5 điểm)
Cho tam giác nhọn ABC cân tại A và nội tiếp trong đường tròn (O) đường kính AK; lấy
điểm I thuộc cung nhỏ AB của đường tròn (O) (I khác A, B). Gọi M là giao điểm của IK và
BC, đường trung trực của đoạn thẳng IM cắt AB và AC lần lượt tại D và E. Chứng minh tứ
giác ADME là hình bình hành.
Câu 5. (4,5 điểm)
Cho tam giác nhọn ABC (AB nội tiếp trong đường tròn (O) và có trực tâm là H.
Gọi D, E, F lần lượt là các chân đường cao vẽ từ A, B, C của tam giác ABC.
a) Gọi K là giao điểm của hai đường thẳng EF và BC, gọi L là giao điểm của đường
thẳng AK và đường tròn (O) (L khác A). Chứng minh HL vuông góc với AK.
b) Lấy điểm M thuộc cung nhỏ BC của đường tròn (O) (M khác B, C). Gọi N và P lần
lượt là hai điểm đối xứng của điểm M qua hai đường thẳng AB và AC. Chứng minh ba điểm
N, H, P thẳng hàng.
–––––––––––– Hết ––––––––––––
Thí sinh không được sử dụng tài liệu. Giám thị không giải thích gì thêm.
Họ và tên thí sinh: …..…………………………………….; Số báo danh: ………………….. Page 1
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI HỌC SINH GIỎI LỚP 9 CẤP TỈNH QUẢNG NAM
NĂM HỌC 2016 – 2017 HƯỚNG DẪN CHẤM Môn: TOÁN
(Hướng dẫn chấm thi này có 08 trang) Câu Đáp án Điểm Câu 1  x  x  x    x 
(5,0 đ) Cho biểu thức 4 2 5 1 1 P     x x  2    
 với x  0 và 2x  3 x  2 4x 1   2 x  3,0 1 3 x 
. Rút gọn biểu thức P và tìm x để P  . 4 2 2  x  4 2x  5 x 1
  2x  4 x  x x  2  P        
(2 x 1)( x  2)
(2 x 1)(2 x 1) 2 x     0,75
(mỗi ý trong khai triển được 0,25 điểm)  x  2 2x  5 x 1
 (2 x 1)(x x  2)       0,5 2 x 1
(2 x 1)(2 x 1) 2 x      2 x 1
 (2 x 1)(x x  2)      0,5
(2 x 1)(2 x 1) 2 x     x x  2  0,25 2 x
+ Với x  0 , ta có: 3
x x  2  x x 11  3. x x.1.1  x x  2  3 x 0,5 x x  2 3 x 3 Suy ra P   hay P 
( dấu bằng xảy ra khi x 1). 0,25 2 x 2 x 2 3 Do đó, để P  thì x 1. 0,25 2
Hoặc trình bày cách khác: 3 x x  2 3 0,25
+ Với x  0 , ta có: P  
  x x  3 x  2  0 (*) 2 2 x 2
Đặt t  x, t  0 . 0,25 Khi đó (*) trở thành: 3
t  3t  2  0 2
 (t 1) (t  2)  0 0,25 Vì 2
t  2  0, (t 1)  0 nên 2
(t 1) (t  2)  0  t 1  0  t  1 hay x 1. 0,25
b) Cho ba số thực dương a, b, c thỏa: ab  bc  ca  3abc . Tìm giá trị nhỏ nhất 3 3 3 a b c 2,0
của biểu thức A    2 2 2 c  a a  b b  . c Page 2 1 1 1
Cách 1: heo đề : ab  bc  ca  3abc     3 a b c 3 3 a
(a  ac)  ac ac 0,25   a  2 2 2 c  a c  a c  a ac 1 c 1 2
c  a  2a c   c  2 c  0,5 a 2 4 3 a c 1 Suy ra  a  2 c  . 0,25 a 4 3 b a 1 3 c b 1 Tương tự :  b   c  2 a  , b 4 2 b  . 0,25 c 4 3 3 Suy ra A 
(a  b  c)  0,25 4 4  
Dùng BĐT Cô Si chứng minh được: a  b  c 1 1 1    9   0,25  a b c 
 a  b  c3  9  a  b  c  3 3 Suy ra A 
, dấu bằng xảy ra khi a  b  c 1. 2 0,25 3 Vậy min A 
khi a  b  c 1. 2 1 1 1
Cách 2 :Ta có: ab  bc  ca  3abc     3 a b c 0,25 1 1 1
x, y, z  0
Đặt x  , y  , z  , khi đó:  . a b c
x  y  z  3 x y z
Biểu thức A được viết lại: A    2 2 2 0,25
y(x  y )
z( y  z )
x(z  x ) 2 2 x
(x  y )  y 1 y Ta có :    ; 2 2 2
y(x  y )
y(x  y ) y x  y 0,25 y 1 x 1 1 mà 2
x  y  2 y x     2 x  nên y 2 x 2 y(x  ; y ) y 2 x 1 1 1 1  1  x 1 1  1  mà  .2 1.  1   nên   1   2 x 4 x 4  x  2
y(x  y ) y 4  x  0,25
(dấu bằng xảy ra khi x  y  1 )   Tương tự y 1 1 1 z 1 1  1  :   1   ,   1   2
z( y  z ) z 4  y  2
x(z  x ) x 4  z  0,25 3  1 1 1  3 Suy ra A       . 4  x y z  4  
Dùng BĐT Cô Si chứng minh được:  x  y  z  1 1 1    9   . 0,25  x y z   1 1 1  1 1 1  3    9     3  
(vì z  y  z  3 ). 0,25  x y z  x y z Page 3 3
Do đó A  , dấu bằng xảy ra khi x  y  z  1 hay a  b  c 1. 2 0,25 3 Vậy min A 
khi a  b  c 1. 2
Câu 2 a) Giải phương trình 2
x  1 x  1 x  2  0 2,0 (4,0 đ) Cách 1: Điề 0,25 u kiện: 1   x 1. Khi đó ta có: 2
x  1 x  1 x  2  0 0,25    x   x 2 2 2 1 1  (2  x ) 2 2 2
 2 1 x  2  (2  x ) (1) Đặt 2
t  1 x , t  0 . Phương trình (1) trở thành: 0,25 2 2
2t  2  (t  1) 4 2
 t  2t  2t 1 0 0,25 2
 (t 1) (t 1)(t 1)  2t  0   (2) 0,5 Vì t  0 nên 2
(t 1)(t 1)  2t  0. 0,25
Do đó phương trình (2) có nghiệm duy nhất là t 1.
+ Với t 1 x  0(thỏa).
Vậy phương trình đã cho có một nghiệm duy nhất là x  0 . 0,25 Cách 2: + Điều kiện: 1   x 1. 0,25 2 2
x  1 x  1 x  2  0  1 x  1 x  2  x (*) 2 2    0,25 + Đặ t 2
t t  1 x  1 x, t  0 . Suy ra 2 2 2
t  2  2 1 x  
 1  2  x  2 
Khi đó phương trình (*) trở thành: 4 2 3 2 0,5
t  4t  4t  8  0  (t  2)(t  2t  4)  0 (*) + vì 2 2
t  2  2 1  x  2 và t  0 nên t  2 . 0,25 Do đó 3 2
t  2t  4  2 2  4  4  0 . Suy ra phương trì 0,5
nh (*) có nghiệm duy nhất là t  2.
+ Với t  2  x  0 (thỏa). 0,25
Vậy phương trình đã cho có một nghiệm duy nhất là x  0 . Cách 3: + Điều kiện: 1   x 1. 0,25
Đặt 1 x  a, 1 x  b ( , a b  0) . Suy ra: 2 2
a  b  2 (1) 0,5 + Hơn nữa: 2 2 2 2
1 x  a b  2  x  a b 1 . 0,25
+ Phương trình đã cho trở thành: 2 2
a  b  a b 1 (2) Page 4 2 2
a  b  2 ab 1
Từ (1) và (2) ta cố hệ:    0,5 2 2
a  b  a b 1 a  b  2 a  1    x  0 0,5 b   1 2
xy  2x  4y  1 
b) Giải hệ phương trình  2,0 2 3 2
x y  2xy  4x  3y  2 Cách 1: 2
xy  2x  4y  1  2
xy  (2x 1)  4y    (*) 0,25 2 3 2
x y  2xy  4x  3y  2 2 2
(x y  2xy 1)y  2(2x 1)  2  y
(lưu ý: không nhất thiết biến đối đưa vế phải của pt thứ hai về 2 y , có thể 3y ) 2x 1  0 1
- Xét y  0 thay vào hệ (*) ta được:   x    2  (2x 1)  0 2  1 0,25 x   Suy ra 
2 là một nghiệm của hệ. y  0
- Xét y  0 , hệ phương trình (*) tương đương với hệ:  2x 1  2x 1 xy   4 (xy 1)   5   y y      (**) 0,25  2x 1  2x 1  2 2  2
x y  2xy 1 2  2  (xy 1)  2  2       y       y   a  b  5 Đặ 2x 1
t a  xy 1, b 
; khi đó hệ phương trình (**) trở thành:  (***) 0,25 2 2
a  2b  2
a  2 a  4
+ Giải hệ (***) tìm được:  ,  . 0,25 b   3 b   9   2x 1      3  xy 1 2 x 1    x   a  2     3  x  1  2 * Với  ta có 2x 1     hoặc  0,25 b   3  3   2x 1 y  1 2   y y  y     3  3   2x 1        xy 1 4 x 5    a  4    9  * Với  ta có  2x 1   (vô nghiệm) 0,25 b   9  9   2x  1  y y   9   3 1    x x   x  1  2
Vậy hệ phương trình đã cho có ba nghiệm:  2 ,  ,  . 0,25  y  1 2   y  0 y    3 Page 5 Cách 2: 2 2
xy  2x  4y  1 
xy  (2x 1)  4y    0,25 2 3 2 2 3 2
x y  2xy  4x  3y  2
x y  2xy  (4x  2)  3  y 2
2xy  (4x  2)  8y 2 3 2  
 x y  xy  5y  0 0,25 2 3 2
x y  2xy  (4x  2)  3  y  y  0   xy  1  0,5 xy  5   1
+ Với y  0 . Suy ra được ( ; x y)  ( ;0) . 0,25 2 3 2
+ Với xy  1. Suy ra được ( ;
x y)  (1;1) hoặc ( ;
x y)  ( ;  ) . 0,25 2 3 + Với xy  5
 . Trường hợp này không tồn tại cặp ( ; x y) . 0,25   3 1    x x   x  1  2
Vậy hệ phương trình đã cho có ba nghiệm:  2 ,  ,  . 0,25  y  1 2   y  0 y    3
Câu 3 a) Tìm tất cả các cặp số nguyên dương ( , a )
b thỏa mãn đẳng thức: (4,0 đ) 2,0 3 3 2 2
a  b  3(a  b )  3(a  b)  (a 1)(b 1)  25 . 3 3 2 2
a  b  3(a  b )  3(a  b)  (a 1)(b 1)  25 3 2 3 2
 (a  3a  3a 1)  (b  3b  3b 1)  (a 1)(b 1)  25 0,5 3 3
 (a 1)  (b 1)  (a 1)(b 1)  25 (*)
Đặt x  a 1, y  b 1(x, y  Z; x, y  2) . Khi đó 0,25 (*) trở thành: 3 3 2 2
x  y  xy  25  (x  y)(x  xy  y )  xy  25 (**)
+ Từ (**) suy ra x  y  x  y  1 , mà 2 2
x  xy  y  0 nên: 0,25 2 2 2 2
x  xy  y  xy  25  x  y  25  x  4 (1).
+ Hơn nữa: x  y và x, y  2 nên xy  6 . 0,25 Suy ra 3 3 3
x  y  xy  25  31  x  31  x  3 (2)
Từ (1) và (2) suy ra: x  4 . Do x  y và y  2 nên y 2;  3 . 0,25 x  4 a  3 + Thử lại, chỉ có  thỏa (**). Suy ra  là cặp số cần tìm. 0,5  y  3 b  2
b) Cho hai số nguyên a và b thỏa: 2 2
24a 1  b . Chứng minh rằng chỉ có một 2,0
số a hoặc b chia hết cho 5. Cách 1: 0,25 2 2 2 2 2 2 2
24a 1  b  25a 1  a  b  a  b  1(mod 5) (1)
a  0, 1, 2(mod 5) Ta có:  0,5 b   0, 1, 2(mod 5) Page 6 2 a  0,1,4(mod5)   (2) 0,5 2 b   0,1,4(mod5) 2 a  0(mod5) 2 a 1(mod5) Từ (1) và (2) suy ra:  hoặc  . 0,5 2 b  1(mod5) 2 b   0(mod5)
Suy ra chỉ một số a hoặc b chia hết cho 5. 0,25 Cách 2: 2 2 2 2 2 2 2 0,25
24a 1  b  25a 1  a  b  a  b  5.k 1 (1) n
 Z  n  5l  r l Z,r 0;1;2;3;  4  0,5 2 2
 n  5l  r  2
l  Z , r  0;1;4 (2) 1 1 1 1   0,5 2
a  5k 1 2 a  5k Từ (1) và (2) suy ra: 1  hoặc 1  0,5 2 b  5k  2 b  5k 1 2  2
Suy ra chỉ một số a hoặc b chia hết cho 5. 0,25 Cách 3: 2 2 2 2
24a 1  b  24a  b  1
 không chia hết cho 5 nên a và b không đồng 0,25 thời chia hết cho 5.
+ Giả sử a và b đều không chia hết cho 5. 4  
Theo định lý Fermat ta có a 1(mod 5) 2 2 2 2   0,5
(a  b )(a  b )  0(mod 5) 4 b  1(mod5) Nếu 2 2
a  b  0(mod 5) thì 2 2 2
25a 1  a  b  0(mod 5) ( vô lí). 0,25 Suy ra 2 2
a  b  0(mod 5) 2 2 2
 23a 1  b  a  0(mod5) (*) 0,25
Vì a không chia hết cho 5 nên a  1  , 2(  mod 5) . 0,25 Với 2 2 a  1
 (mod5)  a 1(mod5)  23a 1  1
 (mod5) ( trái với (*)) 0,25 Với 2 2 a  2
 (mod5)  a  4(mod5)  23a 1  3(mod5) ( trái với (*)) 0,25
Vậy điều giả sử là sai. Từ đó suy ra điều cần chứng minh.
Câu 4 Cho tam giác nhọn ABC cân tại A và nội tiếp trong đường tròn (O) đường
(2,5 đ) kính AK; lấy điểm I thuộc cung nhỏ AB của đường tròn (O) (I khác A, B). Gọi 2,5
M là giao điểm của IK và BC, đường trung trực của đoạn thẳng IM cắt AB và
AC lần lượt tại D và E. Chứng minh tứ giác ADME là hình bình hành. Page 7 A 1 2 E I O 1 / D 1 N 2 F / 1 1 // // B M C K
(Không có hình vẽ không chấm bài)
+ Gọi N là trung điểm của IM, F là giao điểm của DE và IB. 0,5
+ Ta có: I  A  A  F  C  F  B 1 1 2 1 1 2 1
Suy ra tứ giác BFDM nội tiếp trong đường tròn. 0,25
 DMB  F  C 1 1 0,5
Suy ra DM // AC hay DM // AE (1)
AED  EDM  EDI . Suy ra AEDI là hình thang cân. 0,5
(Hoặc tứ giác BFDM và BIAC nội tiếp nên FDM  IAE ;
FDM  FDI  DIA  DIA  IAE . Suy ra AEDI là hình thang cân.)
Suy ra ADE  IED  DEM nên AD//EM (2) 0,5
Từ (1) và (2) suy ra tứ giác ADME là hình bình hành. 0,25 Cách khác:
+ Gọi N là trung điểm của IM, F là giao điểm của DE và IB. 0,5
+ Ta có: I  A  A  F  C  tứ giác BFEC nội tiếp trong đường tròn. 1 1 2 1 1
Suy ra FBC  AED (1). 0,25
+ Mặt khác F  C  F  B  tứ giác BFDM nội tiếp trong đường tròn. 1 1 2 1 0,5
Suy ra FBC  MDE (2).
Từ (1) và (2) suy ra AED  MDE  AE//DM (*) 0,25
Hơn nữa AED  MDE  AED  IDE 0,25
Mà DE//IA. Do đó tứ giác AEDI là hình thang cân.
Suy ra ADE  IED ; mà IED  DEM nên ADE  DEM  AD//EM (**) 0,25
Từ (*) và (**) suy ra tứ giác ADME là hình bình hành.
Câu 5 Cho tam giác nhọn ABC (AB
(4,5 đ) là H. Gọi D, E, F lần lượt là các chân đường cao vẽ từ A, B, C của tam giác ABC. Page 8
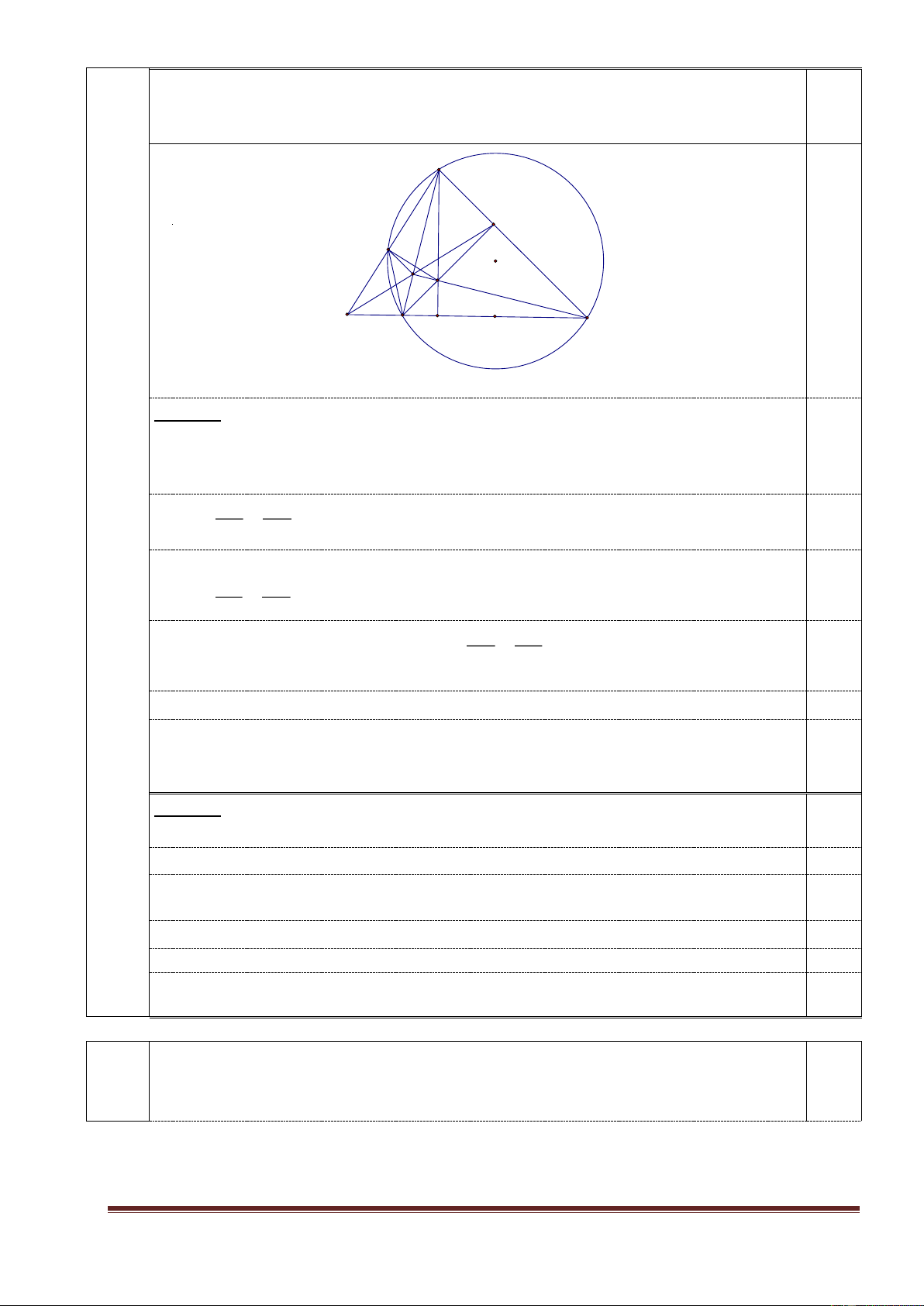
a) Gọi K là giao điểm của hai đường thẳng EF và BC, gọi L là giao điểm của
đường thẳng AK và đường tròn (O) (L khác A). Chứng minh HL vuông góc với 2,5 AK. A E L O F H K B D C
(Không có hình vẽ không chấm bài) Cách 1:
+ Xét hai tam giác K  BF và K  EC có: 0,5
K chung, KBF  KEC (vì cùng bù với FBC ) Suy ra K  BF và K
 EC đồng dạng. KB KF Suy ra:   K .
B KC  KF.KE (1) 0,25 KE KC + Tương tự: K  BL và K
 AC đồng dạng. KB KL 0,5 Suy ra:   . KB KC  . KL KA (2) KA KC KF KL
Từ (1) và (2) suy ra: KF.KE  K . L KA  
; hơn nữa FKL  AKE . KA KE 0,5 Suy ra K  FL và K
 AE đồng dạng.
Suy ra KFL  KAE . 0,25
Do đó 4 điểm A, L, F, E cùng nằm trên đường tròn.
Mà A, E, F nằm trên đường tròn đường kính AH nên L cũng nằm trên đường tròn 0,5
đường kính AH. Vậy HL vuông góc với AK. Cách 2:
+ Hạ HL’ vuông góc AK tại L’. Ta đi chứng minh L’ thuộc đường tròn (O). 0,25
+ 5 điểm A, L’, F, H, E cùng nằm trên đường tròn đường kính AH. 0,5
+ Chứng minh được K  FL' và K
 AE đồng dạng.  0,5
KL'.KA  KF.KE .
Tương tự chứng minh được: KF.KE  K . B KC 0,5
Suy ra KL'.KA  K . B KC . 0,25
Chứng minh được AL’BC nội tiếp. Suy ra L’ trùng L. 0,5
Vậy HL vuông góc với AK.
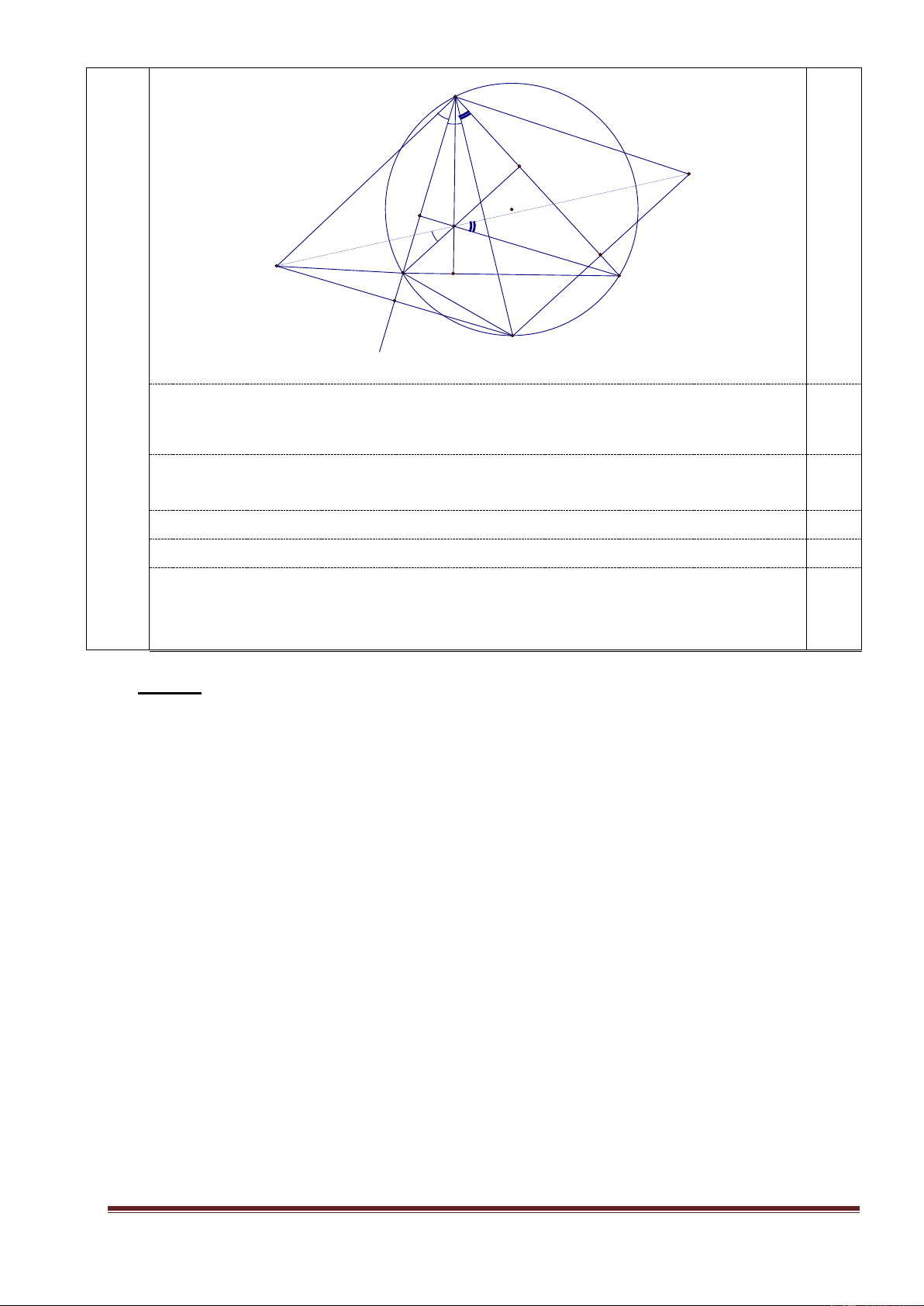
b) Lấy điểm M thuộc cung nhỏ BC của đường tròn (O) (M khác B, C). Gọi N
và P lần lượt là hai điểm đối xứng của điểm M qua hai đường thẳng AB và AC. 2,0
Chứng minh ba điểm N, H, P thẳng hàng. Page 9 A E P O F H N D C B M
(Không có hình vẽ không chấm bài)
ANB  AMB + Ta có: 
 ANB  ACB 0,25
AMB  ACB
+ Tứ giác DHEC nội tiếp nên 0
ACB  AHB  180 . Suy ra 0
ANB  AHB  180 . Do đó 0,5
tứ giác AHBN nội tiếp trong đường tròn.
Suy ra NHB  NAB . Mà NAB  MAB nên NHB  MAB 0,25
+ Tương tự ta cũng chứng minh được: CHP  MAC . 0,5
+ Suy ra NHB  BHC  CHP  MAB  BHC  MAC  (MAB  MAC)  BHC 0
 BAC  BHC  BAC  FHE 180 0,5
Suy ra N, H và P thẳng hàng.
Ghi chú: Nếu học sinh có cách giải khác đúng thì Ban Giám khảo thảo luận và thống nhất thang
điểm cho phù hợp với Hướng dẫn chấm. Page 10