Đề thi học sinh giỏi lớp 9 cấp tỉnh năm 2020-2021 Sở GD Quảng Nam (có đáp án và lời giải chi tiết)

SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI HỌC SINH GIỎI LỚP 9 CẤP TỈNH QUẢNG NAM NĂM HỌC 2020 - 2021 Môn thi : Toán ĐỀ CHÍNH THỨC Thời gian
: 150 phút (không kể thời gian giao đề)
(Đề thi có 01 trang)
Ngày thi : 10/4/2021
Câu 1. (4,0 điểm)
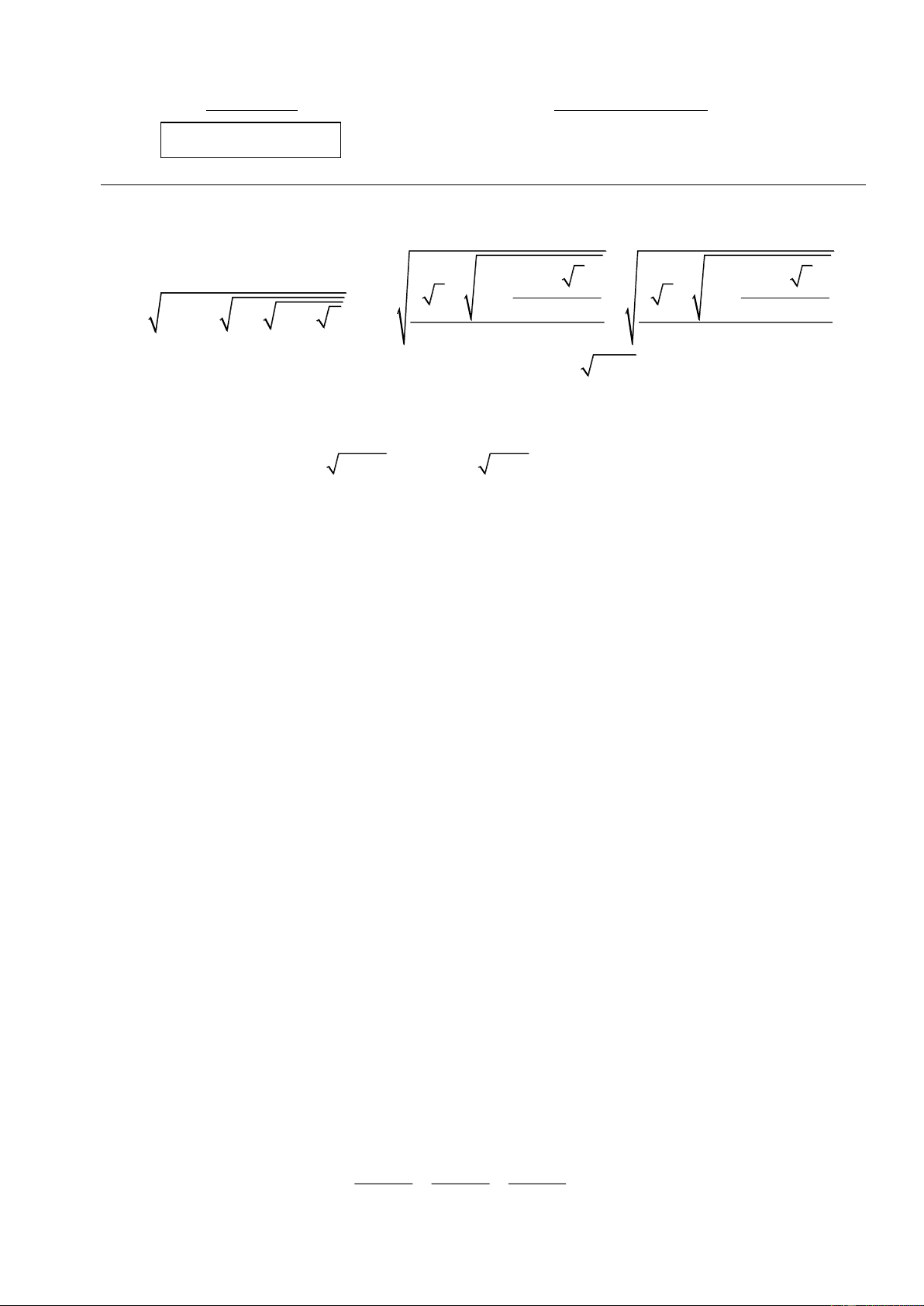
a) Rút gọn các biểu thức sau: 44  33 44  33     3 2 3 12 3 2 3 12
A  13  30 4  9  4 2 ; 27 27 B   . 2 2
b) Tìm giá trị của tham số m để phương trình (x 1  ) 2x 1
 mxm0 có hai nghiệm phân biệt.
Câu 2. (4,0 điểm)
a) Giải phương trình 4 3  2x  3x 1 4 4  x. 2 2
x  y  xy  4y 1 0
b) Giải hệ phương trình  . 2 2 3
 x  y(x  y) 10y  3  0
Câu 3. (2,5 điểm)
Cho hình vuông ABCD có tâm O và cạnh bằng 6cm , điểm M nằm trên cạnh BC.
a) Khi BM  2cm , hạ OK vuông góc với AM tại K. Tính độ dài đoạn thẳng OK.
b) Khi điểm M thay đổi trên cạnh BC (M không trùng B và C), điểm N thay đổi trên cạnh CD sao cho 0
MAN  45 , E là giao điểm của AN và BD. Chứng minh tam giác AEM
vuông cân và đường thẳng MN luôn tiếp xúc với một đường tròn cố định.
Câu 4. (4,5 điểm)
Cho hai đường tròn (O ; R) và (O ' ; r) tiếp xúc ngoài tại A (R  r). Dựng lần lượt hai tiếp tuyến O ,
B O'C của hai đường tròn (O ' ; r) , (O ; R) sao cho hai tiếp điểm , B C nằm
cùng phía đối với đường thẳng OO'. Từ B vẽ đường thẳng vuông góc với OO' cắt O'C tại
K , từ C vẽ đường thẳng vuông góc với OO' cắt OB tại H.
a) Gọi D là giao điểm của OB và O' .
C Chứng minh D . O BO'  C .
O DO' và DA là tia
phân giác của góc ODO '.
b) Đường thẳng AH cắt đường tròn (O ; R) tại E (E khác A). Chứng minh tứ giác OABE nội tiếp đường tròn.
c) Đường thẳng AK cắt đường tròn (O ' ; r) tại F (F khác A), L là giao điểm của BC và
EF. Chứng minh BF song song với CE và 3 điểm , A ,
D L thẳng hàng.
Câu 5. (5,0 điểm)
a) Tìm tất cả các cặp số nguyên ( ,
x y) thỏa mãn đẳng thức 3 3 2 2
x  y  3x  3y  3xy  6x  0 .
b) Cho ba số thực dương x, y, z thỏa mãn xyz  1. Tìm giá trị lớn nhất của biểu thức 1 1 1 A     x  2 yz y  2zx z  2xy Trang 1
---------- HẾT ----------
Họ và tên thí sinh: ……………………………… Phòng thi: ……… Số báo danh: …….......
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI HỌC SINH GIỎI LỚP 9 CẤP TỈNH QUẢNG NAM Năm học 2020 - 2021
HƯỚNG DẪN CHẤM VÀ ĐÁP ÁN Môn: TOÁN
(Hướng dẫn chấm này có 06 trang) Câu Đáp án Điểm
a) Rút gọn các biểu thức sau: A  13  30 4  9  4 2 , 3 3 4(4  3) 4(4  3) 2,5 2 3  12  2 3  12  3 3 27 27 B   . 2 2
Ta có A  13  30 4  9  4 2 2  13 30 4  (2 2 1) 0,25
 13 30 3 2 2  13 30( 2 1) 0,5 2
 43 30 2  (5  3 2)  5  3 2 0,5 3 3 4(4  3) 4(4  3) 2 3  12  2 3  12  3 3 Đặt 27 27 a  , b  0,25 2 2 Suy ra 3 3
a  b  2 3 . 3  4(4  3)  12  1  2   Câu 1 3 27   4  3 0,25   (4,5 đ) . a b 4 3 3 3 3
a  b  2 3  (a  ) b  3a ( b a  ) b  2 3 3  (a  )
b  (4  3)(a  ) b  2 3 0,25 3  (a  ) b  4(a  ) b  3(a  )
b  2 3  0  (a  b  2) (a  b)(a  b  2)  3   0   0,25
 a b  2 ( vì a  0, b  0 ). Vậy B  2 . 0,25
b) Tìm giá trị của tham số m để phương trình (x 1  ) 2x 1
 mxm0 có hai 1,5 nghiệm phân biệt. 1 Điều kiện: x  0,25 2 x 1  (thoa) (x 1  ) 2x 1
 mxm0(x 1  )( 2x 1   ) m   0,5  2x 1  m m0  2 2x 1
 m m 1  0,25 x   2 m0  m0
+ Phương trình đã cho có hai nghiệm phân biệt khi 2 m 1    0,5 1  m1  2 Trang 2
a) Giải phương trình 4 3  2x  3x 1 4 4  x 2,0 3   2x  0 Điều kiện: 3     x  4 0,25 4  x  0 2
4 3  2x  3x 1 4 4  x  4( 3  2x  4  x)  3x 1(*) 0,25
Do 3  2x  4  x  0 vô nghiệm nên pt(*) tương đương với phương trình 0,25
4( 3 2x  4  x)( 3 2x  4  x)  (3x 1)( 3 2x  4  x) 3x 1  0
 4(3x 1)  (3x 1)( 3 2x  4 x)   0,5
 3 2x  4  x  4  1
3x 1  0  x  (thỏa mãn) 3 0,25
3 2x  4 x  4  2 (3 2x)(4 x)  9 x x  3 2 
 9x  38x  33  0  11  (thỏa mãn) 0,25 x   9
Vậy phương trình đã cho có 3 nghiệm 1 11 x  , x  , x  3 . 0,25 3 9 2 2
x  y  xy  4y 1 0
b) Giải hệ phương trình  2,0 2 2 3
 x  y(x  y) 10y  3  0 Câu 2 (4,0 đ) 2 2 2        x y xy 4 y 1 0 (
 x 1)  y(x  y)  4  y    (*) 0,25 2 2 2 2 3
 x  y(x  y) 10y 3  0 3
 (x 1)  y(x  y)  1  0y
- Nhận xét y  0 không thỏa hệ. 0,25
- Khi y  0 : Hệ phương trình (*) tương đương với hệ: 2  x 1 
 (x  y)  4 y   (**) 2   x 1 2 3
  (x  y)  10     y    2  a  b  4  Đặt x 1  
a, x  y  b , khi đó hệ (**) trở thành:  0,5 y 2 3
 a b  10       
+ Giải hệ trên tìm được: a 2 a 3  ,  0,25 b   2 b  1 2  x 1 a  2    2  x  1 x   +    y   hoặc 3  b   2  y  1  y  5  x  y  2       0,5 2 3 17  3 17 x 1 x     x a  3    3    + 2    2 y   hoặc  b  1   5   17  5   17 x  y 1 y   y    2  2 Trang 3 2 2 2 2         x y xy 4 y 1 0
x 1  y  xy  4y Lưu ý:    2 2 2 2 3
 x  y(x  y) 10y  3  0 3
 (x 1)  y(x  y) 10  0 Thay 2 2
x 1  y  xy  4y vào phương trình thứ hai. Trang 4
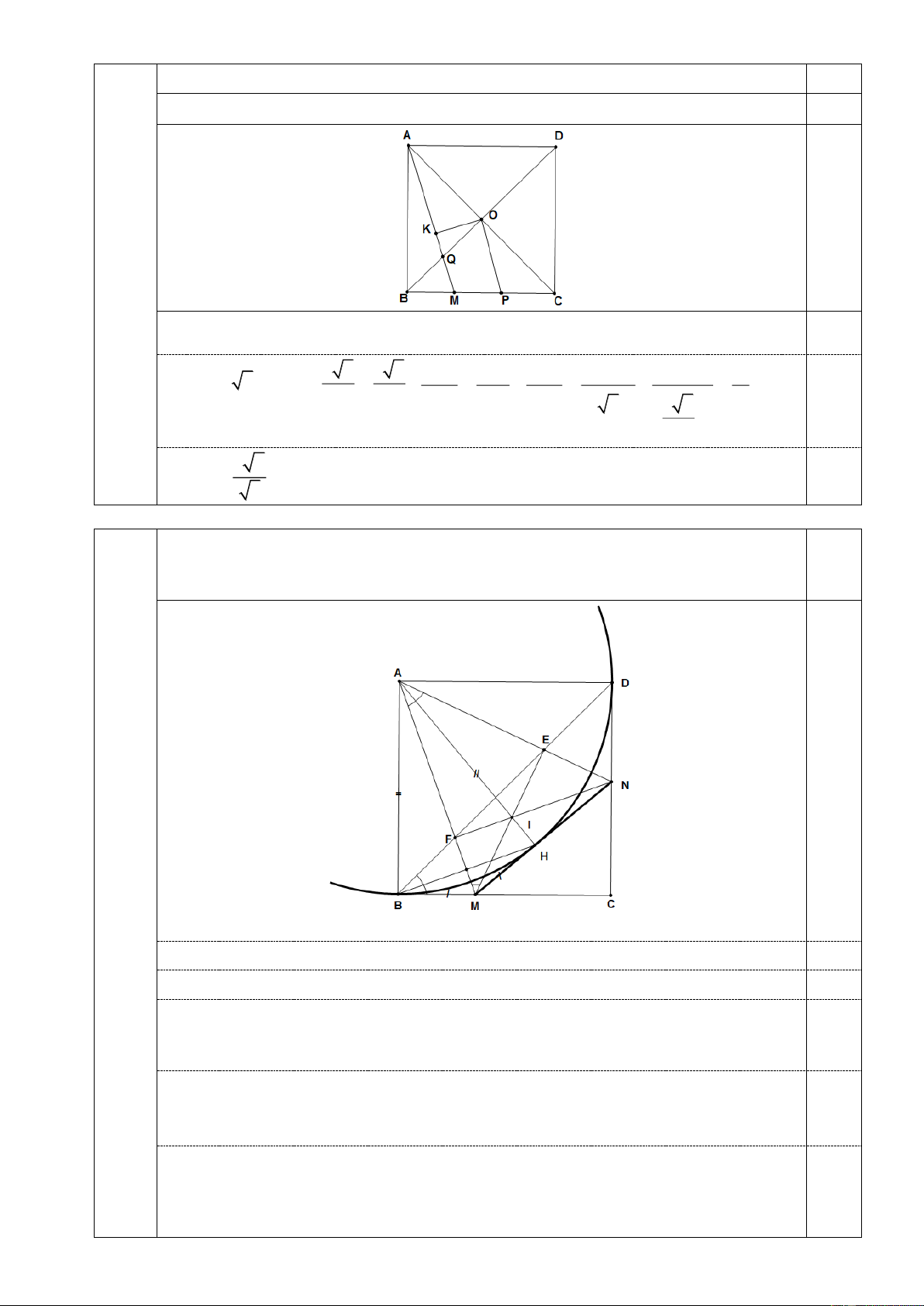
Câu 3 Cho hình vuông ABCD có tâm O và cạnh bằng 6 cm , điểm M nằm trên cạnh BC. 2,5
(2,5 đ) a) Khi BM  2cm, hạ OK vuông góc với AM tại K. Tính độ dài đoạn thẳng OK. 1,0
+ Gọi Q là giao điểm của AM và BD, P là trung điểm của MC. Suy ra OP//AM. 0,25
+ Trong tam giác OBP có MB = MP và MQ//OP. Suy ra Q là trung điểm của OB. 6 2 3 2 1 1 1 1 1 5
+ BD  6 2  OQ   ,      4 2 2 2 2 OK OA OQ 3 22 2 18  3 2  0,5   2   3 2  OK  0,25 5
b) Khi điểm M thay đổi trên cạnh BC (M không trùng B và C), điểm N thay đổi trên cạnh CD sao cho 0
MAN  45 , E là giao điểm của AN và BD. Chứng minh tam giác 1,5
AEM vuông cân và đường thẳng MN luôn tiếp xúc với một đường tròn cố định. 0,25
(Không có hình không chấm điểm) + 0
MAN  MBE  45 . Suy ra tứ giác ABME nội tiếp. 0,25 Mà 0
ABM  90 nên 0
AEM  90 . Vậy tam giác AEM vuông cân tại E. 0,25
+ Gọi F là giao điểm của AM và BD. Tương tự suy ra 0 AFN  90
+ Gọi I là giao điểm của EM và FN, H là giao điểm của AI và MN. Suy ra AH vuông 0,25 góc với MN.
+ Xét hai tam giác vuông ABM và AHM có: AM chung; 0,25 + AMB  AE ,
B AEB  AMH (vì tứ giác MNEF nội tiếp). Do đó AMB  AMH
Suy ra hai tam giác vuông ABM và AHM bằng nhau.
Suy ra AH  AB  6 cm (không đổi). Do đó 0,25
MN luôn cách A một khoảng cách bằng 6 cm.
Suy ra MN luôn tiếp xúc với đường tròn tâm A, bán kính bằng 6 cm. Trang 5
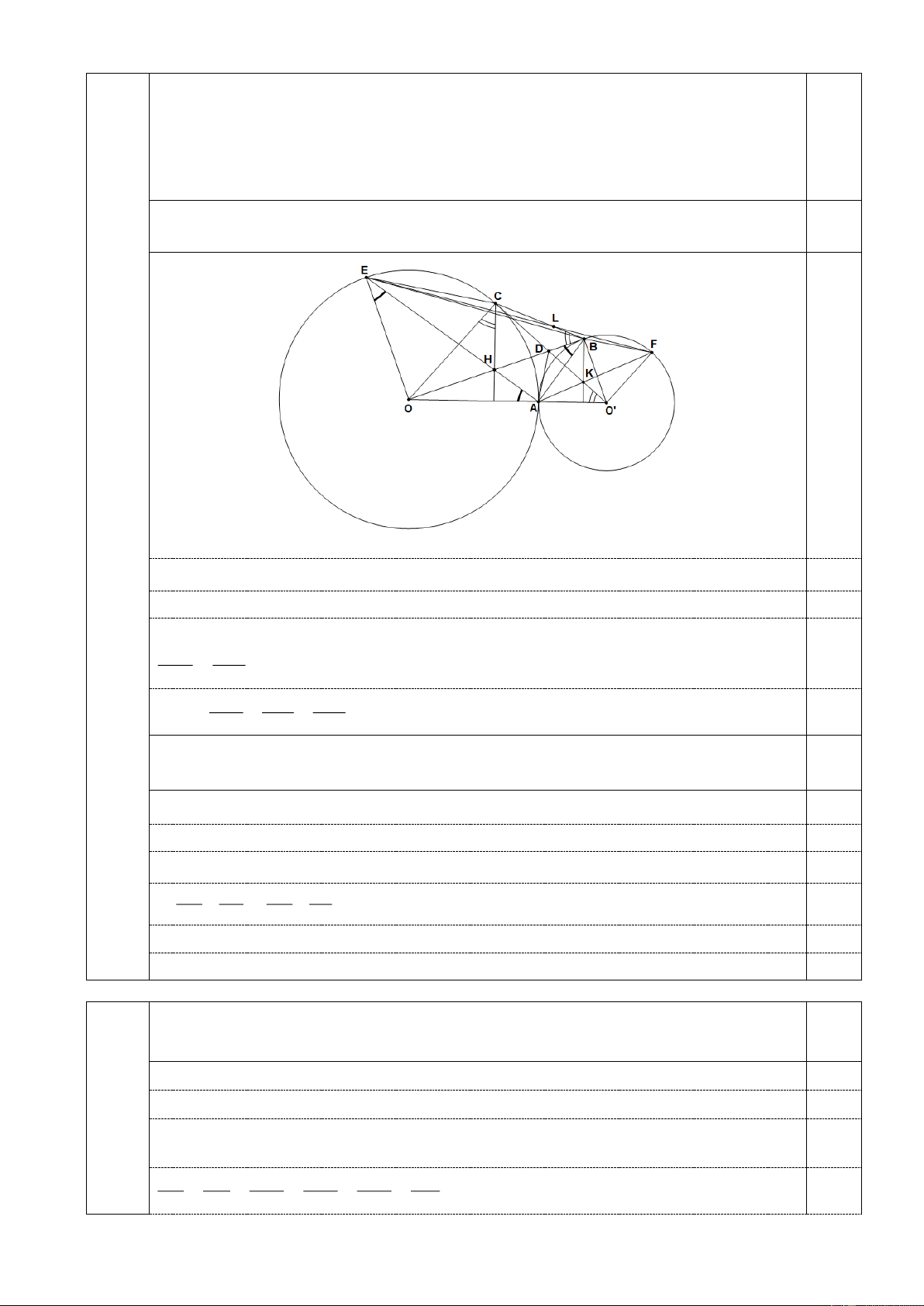
Câu 4 Cho hai đường tròn (O ; R) và (O ' ; r) tiếp xúc ngoài tại A (R  r) . Dựng lần
(4,5 đ) lượt hai tiếp tuyến OB, O'C của hai đường tròn (O ' ; r), (O ; R) sao cho hai
tiếp điểm B, C nằm cùng phía đối với đường thẳng OO'. Từ B vẽ đường thẳng 4,5
vuông góc với OO' cắt O'C tại K , từ C vẽ đường thẳng vuông góc với OO' cắt OB tại H .
a) Gọi D là giao điểm của OB và O'C . Chứng minh D . O BO'  C .
O DO' và 1,5
DA là tia phân giác của góc ODO ' . 0,25
(Không có hình vẽ không chấm)
Xét hai tam giác ODC và O'DB có: ODC  O' DB ; 0,25
+ Tứ giác OO'BC nội tiếp đường tròn đường kính OO' nên DOC  DO 'B . 0,25
Suy ra hai tam giác ODC và O'DB đồng dạng, do đó: DO CO   0,25 D . O BO '  C . O DO ' DO ' BO ' DO CO AO Ta có:  
. Suy ra DA là tia phân giác của góc ODO ' . 0,5 DO ' BO ' AO '
b) Đường thẳng AH cắt đường tròn (O ; R) tại E (E khác A). Chứng minh tứ giác 1,5
OABE nội tiếp đường tròn.
+ OCH  OO 'C (Cùng phụ với O 'CH ) 0,25
+ OO'C  OBC (Cùng chắn cung OC ) 0,25
Suy ra OCH  OBC . Suy ra hai tam giác OCH, OBC đồng dạng 0,25 OC OB OA OB     . 0,25 OH OC OH OA
Suy ra hai tam giác OH , A OAB đồng dạng. 0,25
 OAH  OBA hay OEA  OBA. Vậy tứ giác OABE nội tiếp trong đường tròn. 0,25
c) Đường thẳng AK cắt đường tròn (O ' ;r) tại F (F khác A), L là giao điểm của BC 1,5
và EF. Chứng minh BF song song với CE và 3 điểm , A ,
D L thẳng hàng. 0 0 0
EOB  EAB  180  OAE  O ' AB  180  OBA  O ' BA  90 0,5 Mà 0
OBO '  90 nên OE // O’B . Tương tự O’F // OC. Suy ra EOC  BO ' F 0,25
Lại có: hai tam giác EOC và BO’F là hai tam giác cân. Suy ra ECO  BFO' 0,25
Hơn nữa OE // O’B nên BF// EC ( lưu ý O’B //OE) LC EC OE OA OC DC      0,25 LB BF O ' B O ' A O ' B DB Trang 6
Suy ra DL là tia phân giác của góc BDC . Suy ra ,
A D, L thẳng hàng. 0,25 Câu 5
a) Tìm tất cả các cặp số nguyên (x, y) thỏa mãn đẳng thức 3,0 3 3 2 2
x  y  3x  3y  3xy  6x  0 . 3 3 2 2
x  y  3x  3y  3xy  6x  0 3 2 3 2 
(x  3x  3x 1)  ( y  3y  3y 1)  3xy  3x  3y  0 3 3
 (x 1)  (y 1)  3(x 1)(y 1)  3  0 0,5
  x   y  3 ( 1) (
1)  3(x 1)( y 1)(x 1)  ( y 1)3(x 1)( y 1) 3  0
Đặt a  (x 1)  ( y 1), b  (x 1)( y 1) Khi đó ta có: 3 0,25
a  3ab  3b  3  0 3
 a  3  3b(a 1) Suy ra 3 3
a  3  (a 1)  4 (a 1)  4 (a 1)   0,25 + Với 32 a 1  4   a  5   b  (không thỏa) 0,25 3 + Với 11 a 1  1   a  2   b  (không thỏa) 0,25 3 + Với 1
a 1  2  a  1  b   (không thỏa) 0,25 3
+ Với a 1  1  a  0  b  1
 . Tìm được (x, y)  (0,0); (x, y)  ( 2  , 2) 0,5
+ Với a 1 4  a  3b  2. Tìm được (x, y)  (0,3); (x, y)  (1, 2) 0,5 + Với a 1 2   a  3
 b  5 (không tồn tại x, y) 0,25
b) Cho ba số thực dương ,
x y, z thỏa mãn xyz  1 . Tìm giá trị lớn nhất của biểu thức 1 1 1 2,0 A     x  2 yz y  2zx z  2xy 1 1 1 x y z Ta có: A       2 2 2 0,25 x  2 yz y  2zx z  2xy x  2 y  2 z  2 x x 1  1  2 2
x  2  (x 1) 1  2x 1    1   2 x  2 2x 1 2  2x 1    0,5   Tương tự y 1 1 z 1 1 :  1 ,  1     2 2 y  2 2 
2 y 1  z  2 2  2z 1  3 1  1 1 1  Suy ra A       0,25 2
2  2x 1 2y 1 2z 1 Đặt a b c x  , y  , z 
(a,b, c  0). b c a 0,25 1 1 1 b c a      2x 1 2 y 1 2z 1 2a  b 2b  c 2c  a 2 2 2 2 b c a
(a  b  c)     1 2 2 2 2 2 2 2ab  b 2bc  c 2ca  a
2ab  b  2bc  c  2ca  a 0,5 2 2 2 2  
(Chứng minh được BĐT: m n k (m n k)   
(với các số dương) : 0,25) x y z
x  y  z 3 1 Suy ra A 
 .1  1 (Dấu bằng xảy ra khi a  b  c hay x  y  z  1) 2 2 0,25
Vậy giá trị lớn nhất của A bằng 1. Trang 7 Nhận xét: Đặt 3 3 3
x  a , y  b , z  x (a, ,
b c  0, abc  1) 1 1 1 abc abc abc      3 3 3 2x 1 2 y 1 2z 1 2a  abc 2b  abc 2c  abc bc ca ab 2 2 2    (bc) (ca) (ab)    2 2 2 2a  bc 2b  ca 2c  ab 2 2 2 2.c . a ab  (bc) 2.a . b bc  (ca) 2.b . c ca  (ab) 2
(bc  ca  ab)  2 2 2 2.c .
a ab  (bc)  2.a .
b bc  (ca)  2.b . c ca  (ab) 2
(bc  ca  ab)  1 2
(bc  ca  ab)
Ghi chú: Nếu học sinh có cách giải khác đúng thì Ban Giám khảo thảo luận và thống nhất thang
điểm cho phù hợp với Hướng dẫn chấm. Trang 8