Đề thi học sinh giỏi môn Toán 12 năm học 2017 – 2018 trường THPT Đan Phượng – Hà Nội

SỞ GD VÀ ĐT HÀ NỘI
ĐỀ THI HỌC SINH GIỎI MÔN TOÁN
TRƯỜNG THPT ĐAN PHƯỢNG
LỚP 12 – Năm học 2017-2018
Thời gian làm bài: 180 phút.
(Đề thi gồm 01 trang)
Họ tên thí sinh ….…………................................ Số báo danh …………
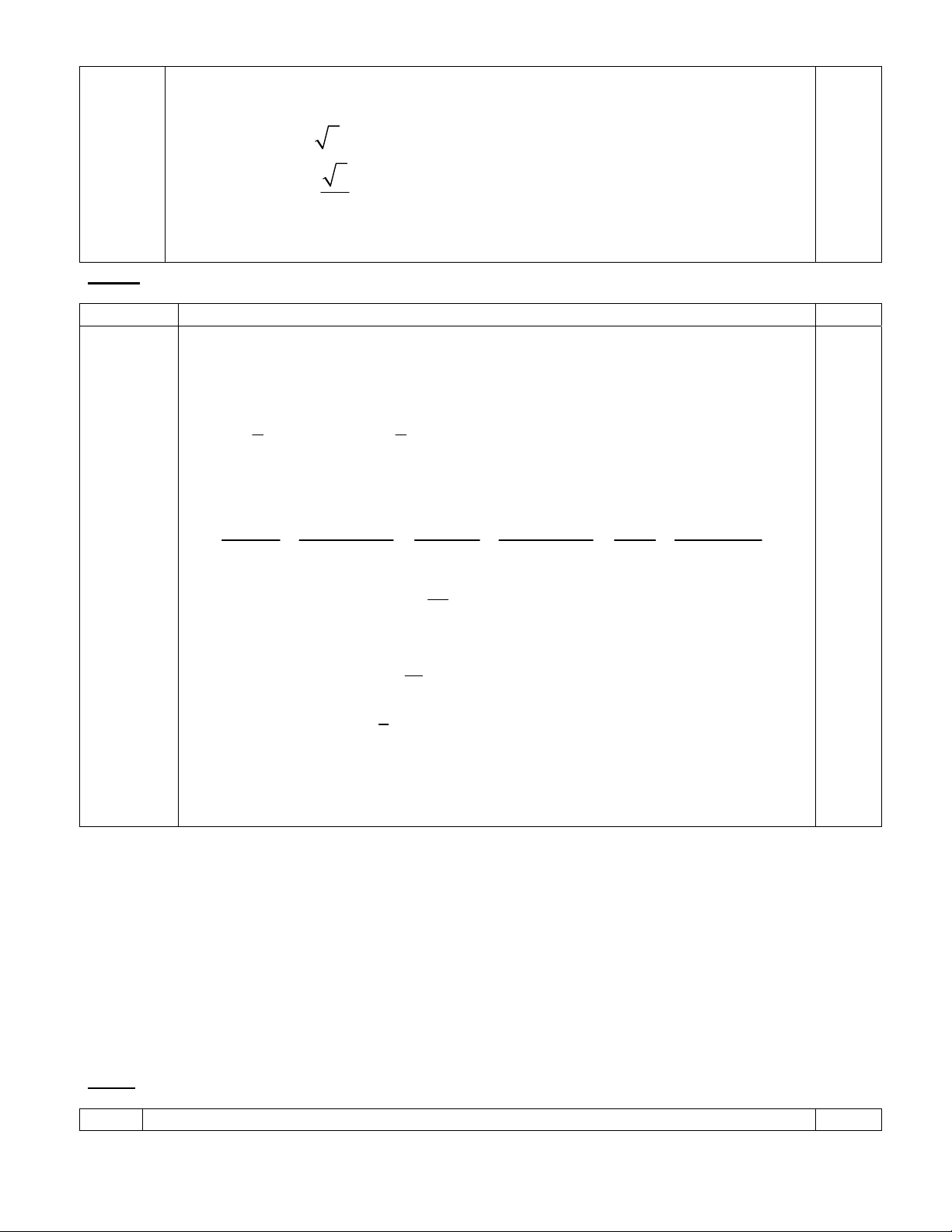
Câu 1 (5.0 điểm) x 1
1. Cho hàm số: y  2(x 1) (C)
Tìm những điểm M trên (C) sao cho tiếp tuyến với (C) tại M tạo với hai trục tọa độ một tam giác có trọng
tâm nằm trên đường thẳng 4x + y = 0.
2. Cho hàm số y = x3 – 3(m+1)x – 2 với m là tham số. Tìm các giá trị của m để đồ thị hàm số cắt trục Ox tại một điểm.
Câu 2 (4.0 điểm) 2
  x  2 x  6  6  y
1.Giải hệ phương trình sau :  ( x R ). x  2 2
y  2  y 1. x  4x  5 2.Giải phương trình sau: 2 3 4 2
x  3x 1 
x  x 1 ( x R ). 3
Câu 3 (3.0 điểm)Cho ,
x y, z là các số thực dương thỏa mãn  2 2 2
5 x  y  z   9xy  2yz  zx x 1
Tìm giá trị lớn nhất của biểu thức: P   2 2 y  z
x  y  z3
Câu 4 (3.0 điểm) 2 u 
 3u  n 1, n 1, n  N
1.Tìm số hạng tổng quát của dãy số (u n 1  n n ) xác định bởi :  . u   2  1
2. Tính u1 + u2+…. + u2017.
Câu 5 (5.0 điểm)
1. Cho tam giác ABC vuông tại A, D là một điểm nằm trong tam giác ABC sao cho CD = CA. M là một điểm 1 trên cạnh AB sao cho  
BDM  ACD , N là giao điểm của MD và đường cao AH của tam giác ABC. Chứng 2 minh DM = DN.
2. Cho tam giác ABC cân tại A có AB=AC=a, góc BAC = 1200. Điểm S thay đổi trong không gian nhưng luôn
nằm về 1 phía của mặt phẳng (ABC) và AS= a, góc SAB= 600. Gọi H là hình chiếu của S trên mặt phẳng (ABC)
a) Chứng minh rằng H thuộc đường thẳng cố định.
b) Chứng minh rằng khi độ dài SH lớn nhất thì hai mặt phẳng (SAB) và (ABC) vuông góc với nhau và khi đó
tính độ dài SC. …………….Hết………………..
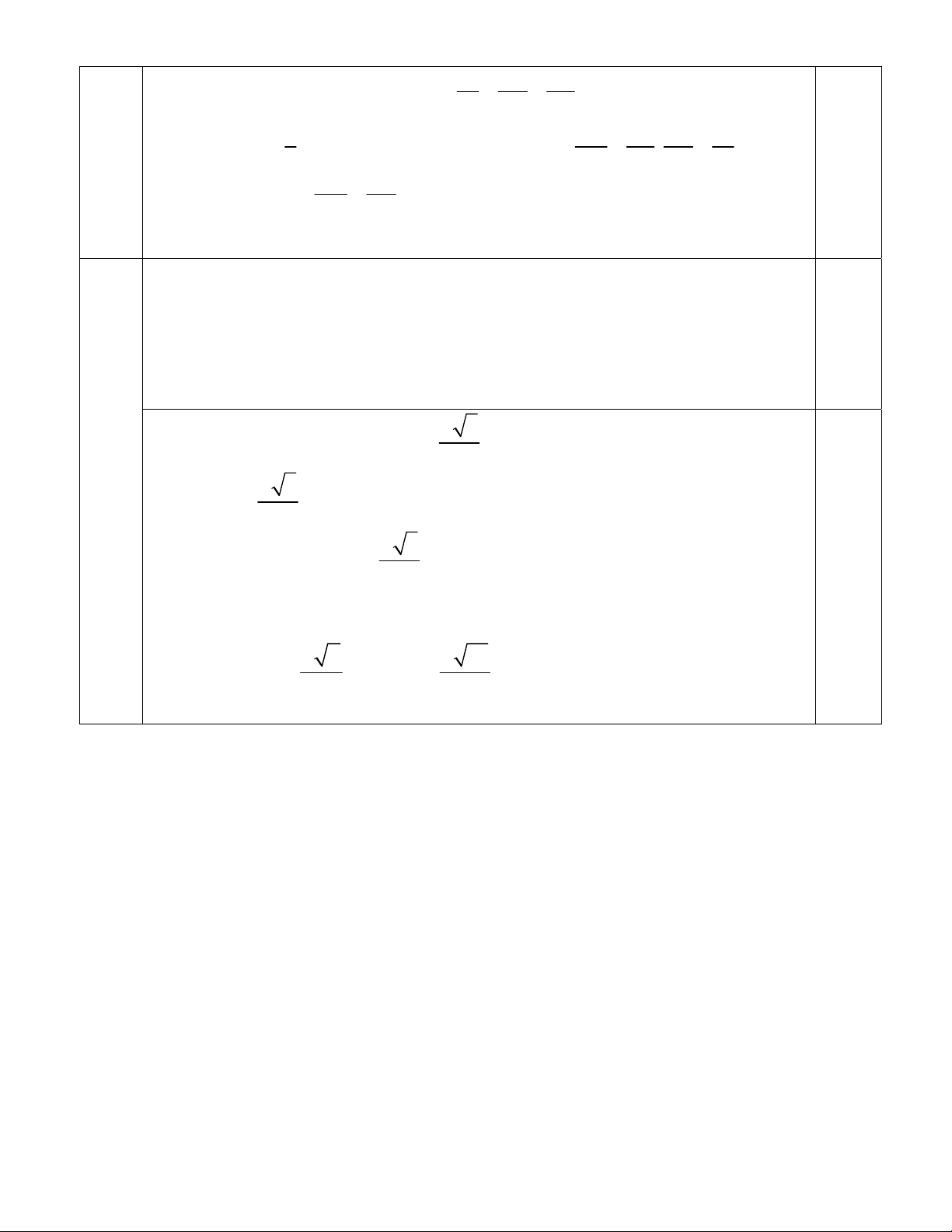
Đáp án bài thi chọn HSG Toán 12 (2017-2018) Câu 1( 5.0 điểm): Câu Nội dung Điểm 1 .1 x 1 Gọi M( 0 x ;
) (C) là điểm cần tìm (x 0 0  -1) 2(x 1) 0
Gọi  tiếp tuyến với (C) tại M ta có phương trình.  x 1 1 x 1 : ' 0
y  f (x )(x  x )  0  y  (x  x )  1.0đ 0 0 2(x 1) x  2 0 1 2(x 1) 0 0 0 2 x  2x 1 2 x  2x 1 Gọi A = ox  A( 0 0  ;0) B = oy  B(0; 0 0 ). 2 2 2(x 1) 0
Khi đó  tạo với hai trục tọa độ  OAB có trọng tâm là: 2 2
 x  2x 1 x  2x 1 G( 0 0 0 0   ; . 2  6 6(x 1)  0  1.0đ 2 2
x  2x 1 x  2x 1
Do G đường thẳng:4x + y = 0  0 0 0 0 4.    0 2 6 6(x 1) 0  1 4  (vì A, B  O nên 2
x  2x 1  0 ) x  2 1 0 0 0  1  1 x 1  x    0  0 2 2     1.0đ 1 3 x 1     x   0 0  2  2 1 1 3 3 3 5
Với x    M ( ; ) ; với x    M ( ; ) . 0 2 2 2 0 2 2 2 1.2
Xét phương trình hoành độ giao điểm của đồ thị hàm số và trục Ox 3 x  3x  2 3 x  3m   1 x  2  0 (1)   3m (2) x 0.5đ
( vì x = 0 không là nghiệm của phương trình (1) ) 3 x  3x  2 Xét hàm số f x  , x   \   0 . x 0.5đ 3   2x  2 f ' x  ; f '(x)  0  x  1  2 x Bảng biến thiên: x  1 0  f 'x  0 + + 0.5đ f x    0 
Đồ thị hàm số cắt trục Ox tại một điểm duy nhất  pt (2) có nghiệm duy nhất.
Từ bảng biến thiên kết luận m  0 . 0.5đ Câu 2( 4.0 điểm): Câu Nội dung Điểm 1 ( 2.5đ)
Điều kiện : y  2; x  6 x  2 2
y  2  y 1. x  4x  5 y  2 x  22 1 Từ (2) :   . y 1 x  2 y  2 x  22 1   . 0.5đ y 1 x  22  y   1 1 x  22 1   . . y 1 x 22 t 1  1  1
Xét hàm số f (t) 
t  0  f '(t)   1 '    0 . Chứng tỏ t  t    2 1 2t 1 t 0.5đ hàm số nghịch biến
Để f  x  2 (
2 )  f  y  
1 chỉ xảy ra khi : y    x  2 1 2 . Thay vào (1) ta được phương trình :   t   x   t    x    0.5đ 1   x  2 2 0 2 0
2  2x  2 x  6  7  0     2 2 t
  2t t 8  7
2t t 8  7 t
0  t  x  2  7  
0  t  x  2  7
0  t  x  2  7        2
4t t  8    2 7  t 2 4 3 2 t
  4t  46t  49  0 t   1   3 2
t  3t  49t  49  0
+/ Trường hợp : t=1 hay x-2=1 suy ra x=3 và y+1=1 hay y=0 . Vậy nghiệm hệ là (x;y)=(3;0) 0.5đ +/ Trường hợp :
f t  t  t  t 
  f t  t  t   t  2 3 2 2 ( ) 3 49 49 0 '( ) 3 6 49 3 1  52  0 t   0; 7   
Hàm số nghịch biến và f(0)= -49<0 chứng tỏ f(t)<0 với mọi t  0; 7  0.5đ   . Phương trình vô nghiệm . 4 2 4 2 2
x  x 1 x  2 x 1 x 2(1.5đ) 2 2
 (x  x 1)(x  x 1) 0.5đ 2
u  (x  x 1) Khi đó đặt 2
v  (x  x 1) thì 2 2 2
x  3x12u  v 0.5đ Ta có phương trình: 2 2
6u  3uv  3v  0 3 u  v 0.5đ 3 Giải ra được x = 1 Câu 3 ( 3.0 điểm): Câu Nội dung Điểm
Từ điều kiện: 5x2 + 5(y2 + z2) = 9x(y + z) + 18yz 0.5đ
 5x2 - 9x(y + z) = 18yz - 5(y2 + z2) Áp dụng BĐT Côsi ta có: 1 1
yz  y  z2 ;y  z  y  z2 2 2
 18yz - 5(y2 + z2)  2(y + z)2. 4 2 0.5đ
Do đó: 5x2 - 9x(y + z)  2(y + z)2  [x - 2(y + z)](5x + y + z)  0 0.5đ  x  2(y + z) x 1 2x 1 4 1 P       2 2 y  z
x  y  z3 y  z2 x  y  z3 y  z 27y  z3 0.5đ 1
Đặt y + z = t > 0, ta có: P  4t - 3 t 27 0.5đ Xét hàm  P  16.  1 y  z   Vậy MaxP = 16 khi 12  1 0.5đ x   3 Câu 4( 3.0 điểm): Câu Nội dung Điểm 1
Đặt g(n) = an2 + bn + c và v
n = un + g(n) ( a, b, c Î R) với vn+1 = 3vn .
Khi đó : vn+1 = 3vn  un+1 + g(n+1) = 3(un + g(n))
 3un + n2 + 1 + g(n+1) = 3un + 3g(n) 0.5đ
 n2 + 1 + a(n+1) 2 + b(n+1) + c = 3an2 + 3bn + 3c
 (a + 1)n2 + (2a + b)n + 1+ a + b + c = 3an2 + 3bn + 3c a 1  3a  1 1
Nên : 2a  b  3b  a = ; b = ; c = 1. 0.5đ 2 2 1
  a b  c  3c  1 1
Do đó ta được : g(n) = n2 + n + 1 . 2 2 1 1 1 1 0.5đ
Như vậy vn = un + n2 + n + 1  un = vn – ( n2 + n + 1) 2 2 2 2 2 u 
 3u  n 1, n 1, n  N
v  3v , n  1 thì n 1  n   n 1 n  . u   2 
v  u  g(1)  4 1  1 1
Suy ra : vn = 3n – 1.v1 = 4.3n – 1 . 1 1 1 0.5đ
Vậy : un = 4.3n – 1 – n2 – n – 1 = 4.3n – 1 – (n2 + n + 2) . 2 2 2 ( n n 1) Ta có +) 1 + 2 + … + n = 2 n n n 0.5đ +) 2 2 2 ( 1)(2 1) 1 2 . . n       6
+) 4(30 + 31 + 32 +…. + 3n – 1) 3n 1 = 4 0.5đ 3 1 Thay n= 2017 Câu 5( 5.0 điểm): Câu Nội dung Điểm
1(2đ) Vẽ đường tròn (C;CA) cắt đường thẳng BD tại E ( E ≠ D), khi đó BA là tiếp tuyến của
đường tròn. Ta có BD.BE = BA2 ( do BDA BAE), BH.BC = BA2 suy ra BH.BC = 0.5đ BD.BE  BD BC  BH BE BDH BCE (c.g.c) 0.5đ   
BHD  BEC  tứ giác DHCE nội tiếp       
BHD  BEC  CDE  CHE  AHD  AHE.
Do AH  BC nên HA, HB tương ứng là đường phân giác trong và phân giác ngoài của 0.5đ góc  DHE 0.5đ ID HD BD
Gọi I là giao điểm của AH và BE suy ra   (*) IE HE BE 1 MD BD DN DI giả thiết   
MDB  ACD  AEB nên MN // AE. Do đó  ,  . 2 AE BE AE IE MD DN Kết hợp với (*) ta có   DM  DN. AE AE
a) Tam giác SAB đều nên S thuộc mặt phẳng trung trực (P) của AB 0.5đ
2( 3đ) Mặt phẳng (P) cố định và (P) vuông góc với (ABC)
Gọi d là giao tuyến của mp(ABC) và mp(P) thì d là đường thẳng cố định
H là hình chiếu của S nên H thuộc d 0.5đ KL a 3
b)Gọi I là trung điểm của AB thì SI = 2 a 3 0.5đ SH  SI = 2 a 3
SH đạt giá trị lớn nhất bằng 2 khi H trùng I. 0.5đ
Khi đó SH vuông góc với mặt phẳng (ABC) nên (ABC) vuông góc với (SAB) a 7 a 10 CI  ; SC  Tính được 2 2 1.0đ