30 trang 38 lượt tải

Đề thi học sinh giỏi tỉnh Toán 12 năm 2021 – 2022 sở GD&ĐT Bắc Ninh

Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 12 đề thi chọn học sinh giỏi cấp tỉnh môn Toán lớp 12 năm học 2021 – 2022 sở Giáo dục và Đào tạo UBND tỉnh Bắc Ninh; đề thi được biên soạn theo dạng đề 100% trắc nghiệm

Chủ đề: Đề thi Toán 12 1.2 K tài liệu

Môn: Toán 12 3.9 K tài liệu

Tác giả:

Nguyễn Vân

1 năm trước

Danh sách Quiz

Trang 1

Câu 1. Trong không gian

Oxyz

, cho điểm





1; 2;0

A  và mặt phẳng





: 2 2 3 0

P x y z

   

. Mặt phẳng





: 2 0

x by cz d



   

(với

, ,b c d





) đi qua điểm

, song song với trục

và vuông góc

với





. Khi đó, giá trị

b c d

 

bằng

. B.

. C.

. D.

Lời giải

Chọn A

Ta có mặt phẳng





có 1 vectơ pháp tuyến





2; 2;1

n  



Trục

có 1 vectơ chỉ phương





0;1;0

j 



Suy ra

   

, 1;0;2 / / 1;0; 2

n j n

 

   

 

  

Mặt phẳng







vuông góc với mặt phẳng





và song song với trục

nên nhận vectơ





1;0; 2

 



là vectơ pháp tuyến, mặt phẳng







đi qua điểm

nên có phương trình













1. 1 0. 2 2. 0 0 2 1 0 2 4 2 0

x y z x z x z

             

Do đó

0; 4; 2

b c d

    

. Vậy

b c d

  

Câu 2. Thiết diện qua trục của hình nón





là tam giác vuông cân có cạnh góc vuông bằng

. Tính

diện tích toàn phần của hình nón









1 2 2





 . B.





2 2





 . C.





2 1

S a



 

. D.





2 1





 .

Lời giải

Chọn D

Ta có tam giác

SAB

vuông cân tại S có

SA SB a

 

Suy ra

2 2

AB SA SB a R    

Diện tích xung quanh hình nón





là

2 2

. .

2 2

a a

S Rl a



 

  

Diện tích mặt đáy hình nón





là

S R



 

Vậy diện tích toàn phần của hình nón là





2 1

d xq

S S S





   .

UBND TỈNH BẮC NINH

SỞ GIÁO DỤC VÀ ĐÀO TẠO

Đề thi gồm có 08 trang

ĐỀ THI CHỌN HỌC SINH GIỎI CẤP TỈNH

NĂM HỌC 2021 - 2022

MÔN TOÁN - LỚP 12

Thời gian làm bài: 90 phút (không kể thời gian giao đề)

Trang 2

Câu 3. Tìm tất cả các giá trị thực của tham số

để hàm số





log 2 4

y x mx

  

có tập xác định là





. B.



. C.







 



. D.

2 2

  

Lời giải

Chọn D

Điều kiện

1 0

2 4 0, 2 2

4 0

x mx x m





          

 



 

 





Vậy

2 2

  

Câu 4. Cho hàm số





y f x



là hàm số có đạo hàm cấp hai liên tục trên



. Gọi





là đồ thị của hàm

số đã cho. Tiếp tuyến với đồ thị





tại các điểm có hoành độ

1; 0

x x

  

lần lượt tạo với trục

hoành góc

0 0

30 ;45

. Tiếp tuyến với đồ thị





tại các điểm có hoành độ

1; 2

x x

 

lần lượt song

song với đường thẳng

: 2 1

 

d y x

và vuông góc với đường thẳng

: +5



d y x

Tính

     

 

0 2

1 1

3 . d 4 . d



   

 

 

I f x f x x f x f x x

. B.



. C.



. D.



Lời giải

Chọn D

 Từ giả thiết, ta có:

       

0 0

1 tan 30 ; 0 tan 45 1; 1 2; 2 1

f f f f

   

           

 Đặt









t f x dt f x d

 

  

 TH1:

       

1 ; 0 1; 1 2; 2 1

f f f f

   

     

, ta có

     

 

0 2 1 1

1 1 2

3 . d 4 . d 3 d 4 d 14



   

     

   

I f x f x x f x f x x t t t t

 TH2:

       

1 ; 0 1; 1 2; 2 1

f f f f

   

      

, ta có

     

 

0 2 1 1

1 1 2

3 . d 4 . d 3 d 4 d 14

 



   

     

   

I f x f x x f x f x x t t t t

 TH3:

       

1 ; 0 1; 1 2; 2 1

f f f f

   

      

, ta có

     

 

0 2 1 1

1 1 2

3 . d 4 . d 3 d 4 d 14



   

     

   

I f x f x x f x f x x t t t t

 TH4:

       

1 ; 0 1; 1 2; 2 1

f f f f

   

       

, ta có

Trang 3

     

 

0 2 1 1

1 1 2

3 . d 4 . d 3 d 4 d 14

 



   

     

   

I f x f x x f x f x x t t t t

 Vậy

     

 

0 2

1 1

3 . x 4 . x 14I f x f x d f x f x d



   

   

 

Câu 5. Cho hàm số

 

f x

xác định và có đạo hàm trên



Biết

 

f x



có bảng xét dấu như sau:

Hàm số

 

2 y f x x

nghịch biến trên khoảng nào dưới đây?

 

2;1

. B.

 

4; 3 

. C.

 

2; 1 

. D.

 

0;1

Lời giải

Chọn C

 Ta có:

 

2 2 2

 

  y x f x x

 Hàm số nghịch biến khi

 

2 2 0

2 2

2 0

3 1

2 30

3 1

2 2 0

2 0

3 <1

1 2 <3

  



  



  

















   















 















 



   

     











   

 











 









 















 

  











x x

f x x

x x

x xy

f x x

x x

Câu 6. Cho hàm số

 

y f x

và

 

y g x

có đạo hàm liên tục trên

 

0;1

thỏa mãn

       

1 1

0 0

x 2022; x 2023f x g x d f x g x d

 

 

 

Giá trị của biểu thức

       

1 1 0 0f g f g

bằng

1

. B.

. C.

4045

. D.

4046

Lời giải

Chọn C

 Đặt

 

u g x du g x d

dv f x d v f x



  

 



 



 

 

 

 Ta có:

           

1 1

0 0

x xf x g x d f x g x f x g x d

 

 

 

               

2022 1 1 0 0 2023 1 1 0 0 4045f g f g f g f g      

Câu 7. Cho hàm số

ln 2

ln 1

m x







(

là tham số thực). Gọi

là giá trị của

để

 

min max 2

y y 

Khẳng định nào dưới đây đúng?

0 10

 

. B.

 

. C.

6 11

 

. D.

0 2

 

Lời giải

Trang 4

Chọn C

Ta có

       

 

   

2 2 2

ln 1 ln 2

ln 2 ln 1 ln 1 ln 2

ln 1 ln 1 ln 1

x m x

m x x x m x

x x

x x x x

  

 

    





  

  

TH1: Nếu

2 0 2

m m

    

Khi đó

 

 

 

0 1; min 1 2

ln 1

y x e y y

x x





       



 

 

max

y y e



  .

Suy ra

 

min max 2 2 2 2 8 10

y y m m



          

(thỏa mãn).

TH2: Nếu

2 0 2

m m

    

Khi đó

 

 

 

0 1; max 1 2

ln 1

y x e y y

x x





       



 

 

min

y y e



  .

Suy ra

 

min max 2 2 2 2 8 10

y y m m



          

(không thỏa mãn).

Vậy



. Suy ra khẳng định đúng là

6 11

 

Câu 8. Cho biểu thức

P x x x

  

với



Khẳng định nào dưới đây đúng?

P x



. B.

P x



. C.

P x



. D.

P x



Lời giải

Chọn B

Ta có

1 1 1 1 1

3 2 3

6 6

P x x x x x

 

  

 

Câu 9. Cho hàm số





f x

có đạo hàm liên tục trên



, thoà mãn





6 1



và

   

 

6 d 10

x f x f x x



  



. Khi đó

 

3 d

xf x x







bằng

. B.

. C.



. D.



Lời giải

Chọn A

Với

 

3 d

I xf x x



 



Đặt

d d

x t

t x

 



  







Đổi cận: Khi

3 0

x t

   

;

3 6

x t

  

Ta có

           

6 6 6 6

0 0 0 0

3 d 3 d d 3 d

I t f t t x f x x xf x x f x x

     

   

Mặt khác

   

 

   

6 6 6

2 2

0 0 0

6 d 10 d 6 d 10

x f x f x x x f x x f x x

 

      

  

Trang 5

   

6 6

0 0

d 3 d 5

x f x x f x x



   

 

   

6 6

0 0

d 5 3 d

x f x x f x x



    

 

Suy ra

       

6 6 6 6

0 0 0 0

d 3 d d d 5

I xf x x f x x xf x x x f x x



     

   

   

6 6

0 0

1 1

2 d d 5

2 2

xf x x x f x x



   

 

   

2 + d 5

xf x x f x x

 

 

  

 

 

 



 

d 5

x f x x

 



 

  

 

 

 



   

5 18 6 0 5 13

x f x f

       

Vậy



Câu 10. Biết





F x e x

 

là một nguyên hàm của hàm số





f x

trên



. Khi đó





2 d

f x x



bằng

2 2

e x C

 

. B.

2 2

e x C

 

. C.

2 4

e x C

 

. D.

2 2

e x C

 

Lời giải

Chọn A

Xét





2 d

I f x x





Đặt

2 d d

t x x t

  

. Khi đó

 

1 1

2 2

I f t t e t C

   



Kết luận:

 

2 2

2 d 4

I f x x e x C

   



Câu 11. Cho

0, 0

a b

 

và



thỏa mãn

3ln 7ln 0

a b

 

. Khi đó





log

a b

bằng

. B.



. C.



. B.

Lời giải

Chọn A

Ta có:

3ln 7 ln 0 ln ln

a b a b

    

Xét

 

1 7 1

ln ln ln ln

3 3 3

log 3

1 7

ln ln

2 3

a b b b

a b

b b

  

   

 



 

 

 

Kết luận:





log 3

a b



Câu 12. Cho hàm số

2021

2022

y x x

 

. Có bao nhiêu giá trị nguyên của

để









f x f x



. B.

. C.

. D.

Lời giải

Chọn C

Xét hàm số:

2021 2020

2022 2021 2022 0,y x x y x y x

 

        





Hàm số

2021

2022

y x x

 

luôn đồng biến trên











2 2

22 22 0 22

f x f x x x x

      

Trang 6

 

1;2;3;4;...;21x 

Kết luận: Có

giá trị nguyên.

Câu 13. Cho khối chóp tứ giác đều có cạnh đáy bằng

, cạnh bên bằng

. Tính thể tích của khối chóp đã

cho.



. B.



. C.



. D.



Lời giải

Chọn B

Giả sử có hình chóp đều

.S ABCD

và

AB a

3SA a

Gọi

là đường cao của hình chóp, với

tâm của

ABCD

Vì

.S ABCD

là hình chóp đều nên

ABCD

là hình vuông có cạnh

2AB a AC a  

Xét tam giác vuông

SOA

có

2 2 2

SA SO OA 

 

2 2

2 2 2

AC a a

SO SA a

 

     

 

 

SO 

Thể tích khối chóp

.S ABCD

là:

1 1 34 34

. . .

3 3 2 6

ABCD

a a

V S SO a  

Câu 14. Cho

5 3

1I x x dx 



. Nếu đặt

1t x 

thì

 

2 2

I t t dt 



. B.

 

2 2

2 1I t t dt 



. C.

 

2 2

I t t dt 



. D.

 

2 2

2 1I t t dt 



Lời giải

Chọn A

Ta có

1 1

5 3 3 3 2

0 0

1 1 .

I x x dx x x x dx

   

 

Đặt

3 2 3 3 2

1 1 1t x t x x t       

   

3 2 2

d x d t x dx tdt     

Với

0 1x t  

; và với

1 0x t  

Khi đó

   

0 1

2 2 2

1 0

2 2

1 . 1

3 3

I t t t dt t t dt

 

    

 

 

 

Câu 15. Cho hình chóp

.S ABC

có

 

SA ABC

, tam giác

ABC

vuông tại

2AC a

6AB a

Tính thể tích khối chóp

.S ABC

biết

3SC a

14a

. B.

. C.

. D.

2 42

Trang 7

Lời giải

Chọn B

Trong tam giác

ABC

có

2 2

BC AB AC a

  

Trong tam giác

SAC

có

2 2

SA SC AC a

   .

Thể tích khối chóp

S ABC

là

1 1 1 1 1 14

. . . . 7. . 2.2

3 3 2 3 2 3

S ABC ABC

V SA S SA CACB a a a



   

Câu 16. Trong không gian với hệ tọa độ

Oxyz

, cho mặt phẳng





: 2 3 7 0

P x y z

   

và hai đường

thẳng

3 2 2

2 1 4

x y z

  

 

 

1 1 2

3 2 3

x y z

  

 

. Đường thẳng vuông góc với mặt

phẳng





và cắt cả hai đường thẳng

và

có phương trình là

5 1 2

1 2 3

x y z

  

 

. B.

7 6

1 2 3

x y z

 

 

4 3 1

1 2 3

x y z

  

 

. D.

3 2 2

1 2 3

x y z

  

 

Lời giải

Chọn A

Lấy





3 2 ; 2 ; 2 4

A t t t d d

       

và





1 3 ; 1 2 ; 2 3

B t t t d d

  

      

, suy ra





2 3 2 ;1 2 ;4 3 4

AB t t t t t t

  

      



Đường thẳng

nhận



làm véc-tơ chỉ phương.

Đường thẳng vuông góc với mặt phẳng nên





n k AB k

 

 

. Khi đó

2 3 2 1 2 4 3 4

1 2 3

t t t t t t

 

  



     

  





 



Do đó

qua





5; 1;2

A  

và nhận véc-tơ





1;2;3

n 



làm véc-tơ chỉ phương có phương

trình

5 1 2

1 2 3

x y z

  

 

Câu 17. Cho hàm số





f x

có đạo hàm trên





2;5

thỏa mãn





f x









2;5

x 









0 3;4

f x x



  

. Mệnh đề nào dưới đây sai?

A. Hàm số





f x

đồng biến trên khoảng





2;5

B. Hàm số





f x

đồng biến trên khoảng





4;5









10 13

f f .

Trang 8

D. Hàm số





f x

đồng biến trên khoảng





2;3

Lời giải

Chọn A

Ta có:





f x









2;5

x 









0 3;4

f x x



  

nên tồn tại vô số điểm





3;4

x 

để





f x





Vậy hàm số





f x

không đồng biến trên khoảng





2;5

Câu 18. Một vật

, có dạng khối nón có chiều cao bằng

40 cm

. Người ta cắt vật

bằng một mặt

phẳng song song với mặt đáy của nó để được một khối nón nhỏ

có thể tích bằng

thể tích

. Tính chiều cao

của khối nón

20 cm

. B.

10cm

. C.

5cm

. D.

40cm

Lời giải

Chọn A

Ta có:

2 2

1 1

h r

 

nên

2 2

1 1

. .

1 1

8 2

. .

r h

k k

V r h

r h



 

     

 

 

Khi đó

2 1

20cm

h h 

Câu 19. Quay xung quanh truc

hình phẳng giới hạn bởi đồ thị hàm số





2 1 ln

y x x

  , trục

và đường thẳng



ta thu được khối tròn xoay có thể tích bằng

 

2 1 ln

x xdx





. B.

 

2 1 ln

x xdx







. C.

 

2 1 ln

x xdx







. D.

 

2 1 ln

x xdx







Lời giải

Chọn C

 Xét phương trình hoành độ giao điểm:





2 1 ln 0,

x x

 

ĐK

ln 0 1

x x





 



  



2 1 0

ln 0



 







   











 Thể tích khố trong xoay quay quanh

là:

 

2 1 ln .

V x xdx



 



Câu 20. Trong không gian với hệ tọa độ

Oxyz

, cho tam giác

ABC

có













4;2;3 , 1; 2;3 , 1;2;3

A B C .

Tâm đường tròn nội tiếp tam giác

ABC

là điểm:

1 1 3

; ;

2 6 4

 

 

 

. B.

3; ;3

 

 

 

. C.





2;1;3

I . D.

3;1;

 

 

 

Trang 9

Lời giải

Chọn C

 Gọi





; ;

I I I

I x y z

là tâm đường tròn nội tiếp tam giác

ABC

Ta có

5, 3, 4

AB AC BC

  

Tọa độ tâm

được tính theo công thức:

 

. . .

4.4 3.1 5.1

4 3 5

4.2 3. 2 5.2

. . .

4 3 5

. . .

4.3 3.3 5.3

4 3 5

A B c

BC x CA x AB x

BC CA AB

BC y CA y AB y

BC CA AB

BC z CA z AB z

BC CA AB

 



  



   



  

 



  



   



 



  



   



 Vậy tọa độ điểm





2;1;3

Câu 21: Ban đầu ta có một tam giác đều cạnh bằng 3 (hình 1). Tiếp đó ta chia mỗi cạnh của tam giác thành

ba đoạn bằng nhau và thay mỗi đoạn ở giữa bằng hai đoạn bằng nó sao cho chúng tạo với đoạn bỏ

đi một tam giác đều về phía bên ngoài để được hình như hình 2.

Quay hình 2 xung quanh trục

ta được một khối tròn xoay có thể tích bằng

5 3



. B.

9 3



. C.

5 3



. D.

5 3



Lời giải

Chọn C

Ta đánh dấu các điểm như hình vẽ. Do tính chất đối xứng nên thể tích cần tìm của khối tròn xoay

bài ra bằng 2 lần thể tích của đường gấp khúc

ABDGI

quay quanh trục

. Đường gấp khúc này

khi quay quanh

tạo ra 1 khối nón có



và đường cao

h 

, 1 khối nón cụt có chiều cao

Trang 10

h 

, hai đáy

1 2

3 2

, 1

2 3

r HD r IG HD

    

nên ta có thể tích lần lượt tính theo công thức

 

2 2 2

1 2 1 2 1 2

. . ,

3 3

V r h V r r rr



    

Ta được

1 2

5 3

V V



 

. Từ đó ta có được thể tích khối tròn xoay cần tìm là

5 3





Câu 22: Biết rằng phương trình





3 2 3 9

5 5 5

3log log log 125

x x x

 

có nghiệm duy nhất

3 3 3

a b c

 

 với

, ,

a b c

là các số nguyên dương đôi một phân biệt. Giá trị của tích

abc

bằng

A. 9. B. 12. C. 7. D. 8.

Lời giải

Chọn D

Ta có





3 2 3 9 3 2

3 3

5 5 5 5 5 5 5

3log log log 125 3log 9log 9log 3 0 log 4 2 1

x x x x x x x

          

3 3

4 2 1

 

 

nên

4; 2; 1 8

a b c abc

    

Câu 23. Gọi

là tập hợp các giá trị nguyên của

để phương trình





1 2

9 4 2 1 3 3 .3 1 0

x x

m x x m



      

có nghiệm duy nhất. Tổng các phần tử của

bằng



. B.

. C.

. D.



Lời giải

Chọn D

Ta có:





1 2

9 4 2 1 3 3 .3 1 0

x x

m x x m



      







3 3 4. 1 3 3 0

x x

m x m

 

     

Nhận xét: Nếu

là nghiệm của phương trình đã cho thì

 

cũng là nghiệm của phương

trình đã cho.

Do đó điều kiện cần để phương trình đã cho có nghiệm duy nhất là

0 0

x x

  



 

Thay

 

vào phương trình đã cho ta được

 

1 3 3 . 1 0

m m

   









 



Điều kiện đủ:



Với



: Phương trình đã cho có dạng:





9 4. 1 6 .3 1 0

x x



    







3 1 4. 1.3 0

x x



   





Dễ thấy

2, 1

x x

   

và



là nghiệm của phương trình









không thỏa mãn.



Với

 

: Phương trình đã cho có dạng:





9 2 4. 1 3 .3 1 0

x x



    







3 1 8. 1.3 0

x x



   



 



 

thỏa mãn.

Do đó





 

. Vậy tổng các phần tử của

bằng



Câu 24. Cho hàm số





3 2

f x ax bx cx d

   

có đồ thị





. Đồ thị hàm số





y f x





được cho như hình

vẽ.

Trang 11

Biết rằng đường thẳng

y x

cắt đồ thị

 

tạo thành hai phần hình phẳng có diện tích bằng

nhau. Giá trị

a b c d  

bằng

. B.

5

. C.

. D.

6

Lời giải

Chọn B

Ta có:

 

3 2f x ax bx c



  

Từ hình vẽ suy ra

 

0 0

1 3



 













 







3 2 3

b a

a b c

 











   











 











 

3 6f x x x



 



 

6 6f x x



 

và

 

3 2

3f x x x d  

 

0f x







6 6 0x  



1x 



Điểm uốn của đồ thị

 

là điểm

 

1; 2I d 

Điều kiện cần: Đường thẳng

y x

cắt đồ thị

 

tạo thành hai phần hình phẳng có diện tích

bằng nhau khi đường thẳng

y x

đi qua điểm uốn

 

1; 2I d 

của đồ thị

 



2 1d  



3d 

Điều kiện đủ: Với

3d 



 

3 2

3 3f x x x  

Phương trình hoành độ giao điểm của đường thẳng

và đồ thị

 

là:

3 2

3 3x x x  



3 2

3 3 0x x x   



 













Đường thẳng

y x

cắt đồ thị

 

tạo thành hai phần hình phẳng có diện tích lần lượt là:

 

1 1

3 2

1 1

d 3 3 d 4S f x x x x x x x

 

       

 

 

Trang 12

 

3 3

3 2

1 1

d 3 3 d 4

S x f x x x x x x

       

 

 

 

Vậy



;

 

;



;





a b c d

    

Câu 25. Biết

4 1

d ln 2 1 ln 3

2 5 3

x a c

x x x C

b b

x x



    

 



với

, ,

a b c

là các số nguyên dương và

a c

b b

là

các phân số tối giản. Tính

2 3

S a b c

  



. B.



. C.



. D.



Lời giải

Chọn A

Ta có

  

4 1 4 1

2 1 3

2 5 3

x x

 



 

 

, gọi

A B

là hai số thực thỏa mãn

  

4 1

2 1 3 2 1 3

x A B

x x x x



 

   

Khi đó ta có:

2 4

3 1 13

A B







 







 

  











Suy ra

4 1 2 1 13 1 1 13

d d d ln 2 1 ln 3

7 2 1 7 3 7 7

2 5 3

x x x x x C

x x



   

      

   

 

 

   

  

Do đó,

1, 7, 13

a b c

  

nên

2 3 36

S a b c

   

Câu 26. Cho các số thực

x y

thỏa mãn





     

3 2

8 4 8 64

log log 1 log 2 log 1

x x x x y y

       

. Có bao

nhiêu giá trị nguyên của tham số





10;10

a   để biểu thức

P y a

  



có giá trị nhỏ nhất

bằng

. B.

. C.

. D.

Lời giải

Chọn D

Điều kiện:

3 2

1 0

2 0

1 0

x x x



  







 





 

 

 





 



Với điều kiện trên ta có:

 

     

3 2

2 2 2 2

1 1 1 1

log log 1 log 2 log 1

3 2 3 6

x x x x y y

       





 

   

3 2

2 2

log log 2 1

x x x

y y

 

   







 

   

3 2

2 1

x x x

y y

 

   



   

2 2

1 2 1

1 1

x x

y y

x x

   

     

   

 

   

(*).

Trang 13

Xét hàm số

   

3 2

1 2f t t t t t t    

trên khoảng

 

0; 

Ta có

   

3 4 1 0, 0;f t t t t



        .

Khi đó (*)

 

2 2 2

1 1 1

x x x

f f y y y

x x x

 

        

 

  

 

x x

P a

   



Đặt





với

 

0;x   

thì ta có

 

0;u   

Xét hàm

 

4 1g u u u a    ,

   

2 4 0 2g u u g u u

 

     

Ta có bảng biến thiên

Khi đó,

 

P g u

có giá trị nhỏ nhất bằng

khi và chỉ khi

 

5 0 5 *a a   

Mặt khác:

 

 

10;10

a Z







 



Từ (*) và (**) suy ra

 

10; 9;...;5a   

Vậy có

giá trị nguyên của

thỏa mãn yêu cầu bài toán.

Câu 27. Xác định

để phương trình

   

2 2

2log ( 1) log ( 1)

m m

x mx

 

  

có nghiệm .







 



. B.

1m 

. C.

1m 

. D.

1 1m  

Lời giải

Chọn D

   

2 2

2log ( 1) log ( 1)

m m

x mx

 

  

   

2 2

log ( 1) log ( 1)

m m

x mx

 

   

2 2

1 0

1 ( 1)

mx x

 







  



2 2

1 2 1

mx x x









   













 





Đặt

( ) 1 , 1f x x

   

ta có

( ) 0; 1f x x

   

Vậy

1 1m  



( )

f x

( )

f x



Trang 14

Câu 28. Tìm số hạng chứa

trong khai triển

 

1 2x x 

380x

. B.

540x

. C.

1900x

. D.

160x

Lời giải

Chọn A

Ta có:

 

2 2 3 20

0 1 2 3 20

1 2 ...x x a a x a x a x a x       

 

1 2x x 

   

20 20

0 0

1 1 2 ( 1) 2

i i i j j j

i j

x x C x C x

 

    

 

Do đó, số hạng chứa

trong khai triển là:

a x

     

3 2

0 3 3 3 3 0 3 1 2 2 3 2 1 3

20 20 20 20 20 20 20 20

. .2 . . 1 . . . 1 . .2 . . 1 . .2.C C x C C x C C x C C x      

380x

Câu 29. Cho hàm số

 

f x

liên tục trên đoạn

 

0;1

thỏa mãn

 

 

2 2

4 . 3 1 4 1 3 , 0;1 .x f x f x x x x x      

Tính tích phân

 

d .I f x x



Lời giải

Chọn C

Ta có:

 

 

2 2

4 . 3 1 4 1 3 , 0;1 .x f x f x x x x x      

 

1 1 1 1

2 2

0 0 0 0

4 . d 3 1 d 4 1 d 3 dx f x x f x x x x x x x     

   

   

 

1 1 1 1

2 2 2 2

0 0 0 0

2. d 3 1 d 1 2 1 d 1 3 df x x f x x x x x x        

   

   

 

1 1

2 3

0 0

2 d 3 d 1 2

f t t f u u x x

 

     

 

 

 

   

1 1

0 0

4 4 10 2

5 d .0 2.1 .1 2.0 d

3 3 3 3

f x x f x x

   

         

   

   

 

Vậy

 

I f x x 



Câu 30. Cho hàm số

 

y f x

có đạo hàm trên



và

 

1 1.f 

Đồ thị hàm số

 

y f x





như hình vẽ sau

Có bao nhiêu số nguyên dương

để hàm số

 

4 sin cos 2y f x x a  

nghịch biến trên

0; ?



 

 

 

B. Vô số. C.

Lời giải

Trang 15

Chọn C

Xét hàm số

   

4 sin cos 2g x f x x a  

trên khoảng



 

 

 

Ta có

     

4cos . 4sin .cos 4cos sing x x f x x x x f x x

  

   

 

 

cos 0, 0;

x x



 

  

 

 

nên

   

0 sing x f x x

 

  

(vô nghiệm vì trên khoảng



 

 

 

thấy đồ thị hàm

siny x

nằm phía trên đồ thị

 

f x



)

Bảng biến thiên

Dựa vào bảng biến thiên, để hàm số đã cho nghịch biến trên khoảng



 

 

 

thì

 

0 4 1 1 0 3 0 3

g f a a a



 

         

 

 

Mà

a



nên

 

1;2;3a 

Vậy có

giá trị nguyên dương của

thỏa mãn yêu cầu bài toán.

Câu 31: Cho hàm số

 

y f x

thỏa mãn

   

2 2, 2 2f f   

và có bảng biến thiên như hình vẽ sau.

Có bao nhiêu số tự nhiên

để bất phương trình

 

f f x m 

có nghiệm trên đoạn

 

1;1

. B.

. C.

. D.

Lời giải

Chọn C

Xét hàm số

 

y f f x 

trên đoạn

 

1;1

ta có:

Trang 16













 

' ' . '

' 0

y f x f f x

f x

f f x

  

 

 



 







 

' 0 1

f x x

f x

f f x f x

f x

   





      



 



 





 

2; 1 ( )

1 1;1

1;2 ( )

x x L

f x x x

x x L

   



    



 



 





  

 

5 5 2

2; 1 ( )

1 1;1

1;2 ( )

x x L

f x x x x x

x x L

   



      



 



Ta có bảng biến thiên như sau:

Từ bảng biến thiên ta thấy bất phương trình









f f x m

 

có nghiệm trên đoạn





1;1 2

  

Mà

là số tự nhiên nên





0;1;2

m

Câu 32: Cho hình chóp

O ABC

có

, ,

OA OB OC

đôi một vuông góc với nhau. Gọi

, ,

  

lần lượt là góc

tạo bởi các đường thẳng

, ,

OA OB OC

với mặt phẳng





ABC

. Giá trị nhỏ nhất của biểu thức













2 2 2

3 cot 3 cot 3 cot

  

   

bằng

. B.

125

. C.

125 3

. D.

48 3

Lời giải

Chọn B

Gọi

là trực tâm của tam giác

ABC

. Ta có:

Trang 17

là hình chiếu vuông góc của

trên mặt phẳng

 

ABC

2 2 2 2

1 1 1 1

OH OA OB OC

  

Khi đó

 



; ;OAH OBH OCH

  

  

Suy ra

2 2 2

sin ;sin ;sin sin sin sin 1

OH OH OH OH OH OH

OA OB OC OA OB OC

     

         

Đặt

2 2 2

sin ;sin ;sin 1 3

x y z x y z xyz xyz

  

         

Ta có:

   

2 2 2

3 cot 3 cot 3 cot

1 1 1

2 2 2

sin sin sin

1 1 1

2 2 2

x y z

  

   

  

 

   

   

 

  

 

   

   

 

   

   

 

Mặt khác:

 

5 5

3 3 3

1 1 1 1 1 1 1 1 1

2 1 1 5 ;2 5 ;2 5

3 3 3 27 27 27

125 125

x x x x x y y z z

xyz

          

  

Dấu bằng xảy ra khi

x y z  

Câu 33: Cho hàm số

 

f x

liên tục trên



và có đồ thị như hình bên dưới

Tính tổng tất cả các giá trị thực của tham số

để

 

 

1;1

max 8 4 4 1 5f x x m



    

20.

3.

10.

7.

Lời giải

Chọn C

Xét hàm số

 





8 4 4 1g x f x x m    

trên đoạn

 

1;1

Trang 18

Điều kiện:

8 4 4 0 1 2

x x x

      

 





2 1

. 2 2 1

g x f x x

x x

 

 

    

  

Cho

 





2 1 0

2 2 1 0

g x

f x x

  







 



    





 

1 5

2 2 1 1

1 5

2 2 1 2

x n

x x

x n

x x

x k























      









    













Ta có:









1 1 8

g f m m

     

 

1 5

1 2

g f m m

 



   

 

 

 

2 4

g f m m

 

   

 

 





2 8

g m

 

Suy ra

 

1;2

max ( ) 8 ; min ( ) 2

g x m g x m



   

Để

 





1;1

max 8 4 4 1 5

f x x m



    

8 5

5 2

2 5

5 8



  







 



 







 



 

  











 







Vậy





3 7 10

     



Chú ý: Công thức nhanh

 

 

1;1

8 2 8 ( 2)

max 5

m m m m

g x



      

 

Câu 34: Cho hình chóp

S ABC

có đáy

ABC

là tam giác đều cạnh





SA ABC

 , góc giữa đường

thẳng

và mặt phẳng





ABC

bằng

. Khoảng cách giữa hai đường thẳng

và SB

bằng

2 .

Lời giải

Chọn A

Trang 19

Ta có:

 









 



, , 60SB ABC SB AB SBA  

Dựng hình thoi

ACBE

 

;

; ;

/ /

AC SB

AC SBE A SEB

AC SEB d d d   

Kẻ

AK EB

và

AH SK

. Từ đó suy ra

 

;A SEB

AH SEB d AH  

Ta có:

.tan60 3SA AB a 

và

AK 

2 2

. 15

AK AS

AH a

AK AS

 



Câu 35: Cho hàm số

3 2

3 2y ax bx cx d   

( là các hằng số,

0a 

) có đồ thị như hình vẽ. Hàm

số

     

4 3 2

3 2 2022

y x a b x b c x d c x d        

nghịch biến trên khoảng nào sau đây?

 

2; 

. B.

 

1;2

. C.

 

;0

. D.

 

0;2

Lời giải

Chọn B

Xét hàm số

3 2

3 2y ax bx cx d   

3 6 2y ax bx c



   

Từ đồ thị hàm số suy ra đồ thị đi qua các điểm

   

0;1 , 2; 3A B 

nên

1 1

8 12 4 3 2 3 1

d d

a b c d a b c

 

 



 

        

 

(1)

Từ đồ thị hàm số suy ra hàm số có hai điểm cực trị là

0, 2 0x x y



   

có hai nghiệm là 0 và

12 12 0

a b









 



(2)

Từ (1) và (2) suy ra







 













, , ,

a b c d

Trang 20

Ta có

       

4 3 2

3 2 2022

y g x x a b x b c x d c x d         

     

3 2 3

3 2 3 2 6 1g x ax a b x b c x d c x x



          

     

0 ; 2,5 0,16; 2,3g x x



     

Do đó hàm số

     

4 3 2

3 2 2022

y x a b x b c x d c x d        

nghịch biến trên khoảng

 

1;2

Câu 36: Cho hình lăng trụ tam giác đều

.ABC A B C

  

có

AB a

, góc giữa hai mặt phẳng

 

A BC



và

 

ABC

bằng

60

. Gọi

là trọng tâm tam giác

A BC



. Thể tích của khối cầu ngoại tiếp tứ diện

GABC

bằng bao nhiêu?

343

1296



. B.

108



. C.

343

432



. D.

343

5184



Lời giải

Chọn A

Gọi

là trung điểm của

và

là trọng tâm tam giác

ABC

. Khi đó góc giữa hai mặt phẳng

 

A BC



và

 

ABC

là



60AMA





  

Ta có tan

3 3 1

tan 3.

2 2 3 2

AA a a a

AA GH AA





 

      

Khi đó

2 2

4 3

a a a

AG GH AH    



bán kính mặt cầu ngoại tiếp tứ diện

GABC

là

2 2

7 .2 7

2 12.2 12

AG a a

GH a

  



Thể tích khối cầu ngoại tiếp tứ diện

GABC

là

4 4 7

3 3 12

V R

 

 

  

 

 

343

1296



Câu 37.

Trong không gian với hệ tọa độ

Oxyz

, cho hai mặt cầu

   

2 2

: 4 16   S x y z

   

2 2

: 4 36   S x y z

và điểm

 

4;0;0A

. Đường thẳng



di động nhưng luôn tiếp xúc với

 

, đồng thời cắt

 

tại hai điểm

,B C

phân biệt. Tam giác

ABC

có diện tích lớn nhất bằng bao

nhiêu?

24 5

. B.

. C.

28 5

. D.

Lời giải

Trang 21

Chọn A

Ta có

 

có tâm

 

4;0;0I

và bán kính

4R

 

có tâm

 

4;0;0I

và bán kính

6R

Lại có

8IA

nên điểm

nằm ngoài hai mặt cầu

   

1 2

,S S

Gọi

là tiếp điểm của



và





, ta có

IH BC

mà

là dây cung của





nên

là trung

điểm của

Ta có

2 2 2 2

2 1

2 4 5     BC BH IB IH R R

Tam giác

ABC

có diện tích

   

, . 2 5. ,

 S d A BC BC d A BC

Do đó tam giác

ABC

có diện tích lớn nhất khi và chi khi

 

,d A BC

lớn nhất.

Xét hai trường hợp sau:

Trường hợp 1: Điểm

không thuộc mặt phẳng

 

BCI

Ta có

 

,  d A BC AH

2 2 2 2 2 2

2 . .cos 8 4 4 5      AI IH AI IH AIH AI IH

Trường hợp 2: Điểm

thuộc mặt phẳng

 

BCI

Ta có

 

, 12   d A BC AH AI IH

Suy ra

 

max , 12 max 2 5.12 24 5



   

ABC

d A BC S

Vậy tam giác

ABC

có diện tích lớn nhất bằng

24 5

Câu 38.

Cho hàm số

       

1 2 3 ... 2021    f x x x x x x

Có tất cả bao nhiêu giá trị nguyên của tham

số

thuộc đoạn

 

18;20

để phương trình

   



f x m f x

có

2022

nghiệm phân biệt?

. B.

. C.

Lời giải

Chọn D

Ta có

   

 

. *



  

f x

f x m f x m

f x

Đặt

 





f x

g x

f x

, phương trình

 

trở thành

 

g x m

Ta có

              

1 2 ... 2021 2 ... 2021 ... 1 ... 2020



          f x x x x x x x x x x

 

1 1 1 1

...

1 2 2021

     

  

g x

x x x x

Trang 22

 

     

 

2 2 2

1 1 1 1

... 0, 0;1;2;...;2021

1 2 2021



        

  

g x x

x x x

Bảng biến thiên của hàm





g x

Từ bảng biến thiên suy ra phương trình







g x m

có

2022

nghiệm khi và chỉ khi



m .

nguyên thuộc đoạn





18;20



nên có

giá trị

thỏa mãn bài toán.

Câu 39. Cho dãy số





thỏa mãn

1 1

1, 2 ,

n n

u u u n



   



. Với mỗi

n



ta đặt

 

n k

v n k u



  



Hỏi trong dãy





có bao nhiêu số hạng là số nguyên dương có bốn chữ số?

. B.

. C.

. D.

Lời giải

Chọn C

Ta được





là một cấp số nhân công bội

2, 1 2

q u u



   









1 2 3 2 1

1 . 2 . ... 3. 2.

 

        

n n n n

v nu n u n u u u u









2 3 2 1

1 .2 2 .2 ... 3.2 2.2 2 (1)

  

         

n n n

v n n n





2 3 2 1

2 .2 1 .2 ... 4.2 3.2 2.2 2 (2)

  

        

n n n n

v n n

 

1 2

2 2 ... 2 2. 2.2 2

1 2



            



n n

v n n n

Hàm





2.2 2

f x x

  

đồng biến trên









1; 1000 9999

    f n

Do vậy





9;10;11;12

n

Câu 40. Có bao nhiêu gía trị nguyên của tham số

để phương trình

 





3 3 3

sin 2 cos 2 2 2cos 1 2cos 2 3 2cos 2

x x x m x m x m

        

có đúng một nghiệm

trên



 





 

. B.

. C.

. D.

Lời giải

Chọn B

 





 

3 3 3

3 3 3 3

sin 2 cos2 2 2cos 1 2cos 2 3 2cos 2

2sin sin 2 2cos 2 2cos 2 2cos 2

x x x m x m x m

        

         

Hàm số





f t t t

 

đồng biến trên



 





3 3

sin 2cos 2 sin 2cos 2 sin 0 0;

f x f x m x x m x x



 

 

          



 



 

 

Trang 23

2 3 3 2

sin 2cos 2 1 2cos cos

x x m m x x

        

Xét hàm số

3 2

2cos cosy x x 

trên



 





 

 

sin 0

' 2sin .cos . 3cos 1 cos 0

2cos

;

2 3

y x x x x x



 















      



 

 



 



 



 



BBT

Từ BBT ta có, phương trình đã cho có đúng 1 nghiệm khi và chỉ khi

 

1 0 1

4; 3; 2; 1

1 28

1 3 4

27 27

m m

    

 

 

      

 

       

 

Câu 41. Cho khối chóp tam giác đều

SABC

có cạnh đáy bằng

. Gọi

,M N

là trung điểm của

,SB SC

tính thể tích của khối chóp

.S ABC

biết

CM BN

. B.

. C.

. D.

Lời giải

Chọn B

Khối chóp

SABC

đều nên

SA SB SC x  

Gọi

là trọng tâm

ABC

 

SO ABC 

; Do

2 3

AB OC  

Xét tam giác cân

SBC

có

SB SC x 

BN CM G 

G

là trọng tâm tam giác

SBC

SG BC I 

là trung điểm

Ta có

GA GB GC  

  

2 2 2

3 3 3

SI BN CM

  

  

  

 

SI BN CM SI BN CM     

     

2 2 2

SI BN CM  

( do

CM BN

)

2 2 2

2.SC IC BN  

Trang 24

Có

2 2 2

2 4

SB BC SC



 

nên

2 2

1 4 10

x x x     

2 2

SO SC OC  

. Diện tích

ABC

2 3

S  

Thể tích khối chóp bằng

1 26 26

. 3.

3 3 3

V  

Câu 42. Cho tập hợp

 

1;2;...;20A 

. Chọn ngẫu nhiên bốn số khác nhau từ tập

. Xác suất để bốn số được

chọn ra không có hai số nào là hai số nguyên liên tiếp là

. B.

. C.

364

969

. D.

284

285

Lời giải

Chọn A

Gọi

là biến cố: ” bốn số được chọn ra không có hai số nào là hai số nguyên liên tiếp”.

Ta có:

 

.n C 

Gọi bốn số được chọn là :

 

, , ,a b c d a b c d  

Có:

1 1 1 2 3 17.

a b

b c a b c d

c d







 



          





 









Do đó có:

cách chọn bộ bốn số

 

, , ,a b c d a b c d  

Vậy:

 

n A

P A

n C

  



Câu 43: Cho hình chóp

.S ABCD

, đáy

ABCD

là hình vuông cạnh bằng

2SA 

vuông góc với mặt

phẳng

 

ABCD

;

hai điểm thay đổi nằm trên hai cạnh

sao cho

   

SMC SNC

Tính tổng

2 2

1 1

AN AM

 

khi thể tích khối chóp

.S AMCN

đạt giá trị lớn nhất.

2 3





. B.

2T 

. C.

T 

. D.

T 

Lời giải

Chọn D

Tọa độ hóa với

O A

Ox AB

Oy AD

Oz AS

Trang 25



, ta có





0;0;2

S ;





0;0;0

A ;





2;0;0

B ;





0;2;0





2;2;0

 C .

Đặt



AM x

;



AN y









, 0;2

x y









;0;0 ; 0; ;0



M x N y

Do đó

 

;0; 2

0; ; 2

2;2; 2



 



 





 







SM x

SN y

 

; 4;2 4;2

; 4 2 ; 4; 2



 

  

  





 

    



 



 



 



SMC

SNC

n SM SC x x

n SN SC y y

Ta có









SMC SNC

 

     

8 2

4 4 2 4 2 4 4 0 2 8

y x xy xy x y y



          



8 2

2 2 1

y x



    











4 2 2

AMCN ABCD BMC DCN

S S S S x y x y

         

Do đó

 

1 2 2 8 2 2 8

. .

3 3 3 2 3 2

SAMCD AMCN

x x

V SA S x y x

x x

 

 

 

     

 

 

 

Xét hàm

 

 

2 8

; 1;2

3 2

 



 

 



 

f x x

 

2 4 8

3 ( 2)

 



 



x x

f x







 

f x

4 8 0

   

x x

 

2 2 3



  





  





x l

Lập BBT ta được

 













0;2

Max 1 2 2

  

f x f f

Vậy

MaxV 2

 













 



















SAMCN

2 2 2 2

1 1 1 1 5

     

AM AN x y

Câu 44: Cho hàm số trùng phương

4 2

y ax bx c

  

có đồ thị như hình vẽ. Hỏi đồ thị hàm số









4 3 2

2 4 8

2 3

x x x x

f x f x

  



 

 

 

có tổng cộng bao nhiêu tiệm cận đứng?

. B.

. C.

. D.

Lời giải

Chọn C









4 3 2

2 4 8

2 3

x x x x

f x f x

  



 

 

 

















2 2

2 3

 



 

 

 

x x x

f x f x

Trang 26

Ta có:

   

2 3 0

 

  

 

f x f x

 











 





f x

 



 







  







 



x m m

x n n

Dựa vào đồ thị ta thấy các nghiệm

0; 2x x

  

là các nghiệm kép và đa thức

   

2 3f x f x

 

 

 

có bậc là 8 nên

   

      

2 2

 



   

x x x

a x x x x m x n

Vậy hàm số có các tiệm cận đứng là

0; 2; ;

   

x x x m x n

Câu 45. Cho parabol

 

: 6  P y x

cắt trục hoành tại hai điểm phân biệt

,A B

và đường thẳng

: d y a

 

0 6 a

. Xét parabol

 

đi qua hai điểm

,A B

và có đỉnh thuộc đường thẳng

y a

. Gọi

là diện tích hình phẳng giới hạn bởi

 

và

;

là diện tích hình phẳng giới hạn bởi

 

và

trục hoành (tham khảo hình vẽ)

Nếu

1 2

S S

thì giá trị của biểu thức

3 2

12 108  T a a a

bằng

218

. B.

219

. C.

216

. D.

217

Lời giải

Chọn C

Phương trình hoành độ giao điểm của

 

và trục hoành:

6 0



 

   









Phương trình hoành độ giao điểm của

 

và đường thẳng



  

   



 





x a

Trang 27

Diện tích

 

   

2 6 2 6 6 6

3 3



 

          

 

 



S x a dx a x a a

 

có dạng:

 y mx a

Điểm

 

6;0 0 .6

      

A P m a m

Vậy

 

2 2

6 6

     

a a

y x a x

Diện tích

 

2. 6

  



S x dx

4 6



* Theo giả thiết, ta có:

 

1 2

4 4 6

6 6

3 3

    

S S a a

 

6 6  a a

3 2

12 108 216 0     a a a

Vậy

3 2

12 108 216   T a a a

Câu 46. Có bao nhiêu số nguyên

để phương trình

4 2 1 2 2



   

x x x

có hai nghiệm phân biệt?

. B.

. C.

. D.

Lời giải

Chọn A

 

4 2 1 2 2 2 1 2 2



       

x x x x x

m m

 

2 2 4 2.2 1

2 4 4.2 1

2 4 1

2 2 4 2.2 1



   



   



 



   

    



x x x

x x

x x x

(1)

Đặt

2 0 

 

2 4 1

2 1



   





   



m t t

m t

(2)

* Đồ thị của hai hàm số

4 1  y t t

và

1  y t

trên

 

0;

* Phương trình hoành độ giao điểm của hai đồ thị

 

: 4 1  P y t t

và

 

: 1  P y t

trên

 

0;

là:

2 2 2

4 1 1 2 4 2 0 1 2             t t t t t t y

 

 P

tiếp xúc với

 

tại

 

1; 2A

* Phương trình

4 2 1 2 2



   

x x x

có hai nghiệm phân biệt

 

2

có hai nghiệm phân biệt

Trang 28

1 1

1 2 1

2 2



   

  





 



  







 

0;1 m

Vậy có hai số nguyên

thỏa yêu cầu bài toán.

Câu 47. Có bao nhiêu giá trị nguyên của tham số

để hàm số

   

2 1 3 2 siny m x m x   

nghịch biến

trên



. B.

. C. Vô số. D.

Lời giải

Chọn D

     

2 1 3 2 2 1 3 2 cosy m x m y m m x



        

Hàm số

   

2 1 3 2 siny m x m x   

nghịch biến trên





0,y x



  





   

2 1 3 2 cos 0, 1m m x x     



Đặt

 

cos 1 1t x t   

 

có dạng

 

 

2 1 3 2 0, 1;1m m t t      



   

 

2 1 3 2 . 1 0

2 1 3 2 .1 0

m m

    





   









 







 





m   

nguyên nên

 

3; 2; 1m   

Vậy có

giá trị nguyên của

thỏa mãn yêu cầu bài toán.

Câu 48. Cho lăng trụ đứng

.ABC A B C

  

có đáy

ABC

là tam giác vuông tại

, 3B AC a

. Góc



30ACB  

, góc giữa đường thẳng



và mặt phẳng

 

ABC

bằng

60

. Tính bán kính mặt cầu

ngoại tiếp tứ diện

A ABC



. B.

. C.

. B.

Lời giải

Chọn B

Gọi

, ,M H I

lần lượt là trung điểm của

, ,AA AC A C

 

Góc giữa

đường thẳng



và mặt phẳng

 

ABC

là đường thẳng



và mặt phẳng



60BAB



 



tan .

AA BBB BA AB



 





Trang 29

Tam giác

A C



là tam giác vuông tại

 

2 2

3 21

2 2

a a

A A C A AC aA

 

     





 





Tam giác

ABC

vuông tại

và



ACB

 

nên ta có



sin .sin 30

AB a

ACB AB AC

    



cos .cos30

BC a

ACB BC AC

    

Tam giác

ABC

là tam giác vuông tại

B HB HA HC   

Tam giác

ABC

là tam giác vuông tại





. .

IHA IHB IHC c g c IA IB IC

       





Tam giác

AA C

là tam giác vuông tại

 

2 4

C a

A IC IA I

A   





Từ









1 , 2



là tâm mặt cầu ngoại tiếp tứ diện



, bán kính

R IA 

Câu 49. Cho hàm số





3 2

f x ax bx cx d

   

(

, , ,

a b c d

là hằng số,



) và

   

4 3

2021

a d a b

g x x x a b d x

a b

 

   

     

   



   

Biết đồ thị của hàm số





f x

như hình vẽ.

Hỏi hàm số









2 2

1 1

y f x g x

   

có bao nhiêu cực trị?

. B.

. C.

. D.

Lời giải

Chọn D

Xét hàm số:





3 2

f x ax bx cx d

   

Ta có:





3 2

f x ax bx c



  

Dựa vào đồ thị hàm số





f x

, ta có:





0 4

f d

 

;









2 , 0

f x mx x m



  

 

2 2 2

2 3 2 2 3 2

m a

mx x ax bx c mx mx ax bx c b m







            









 

3 2

f x x mx

   

 

2 0 4 4 0 3

f m m

      

   

3 2 4 3

3 4; 2021

f x x x g x x x      

Trang 30









2 3 2

3 6 ; 6 3

f x x x g x x x

 

    

















2 2 2 3

1 1 6 1 6 6

y f x g x x x x

 

  

        

 

 



Cho

0 0

y x



  

Kết luận: Hàm số









2 2

1 1

y f x g x

   

có

cực trị.

Câu 50. Có tất cả bao nhiêugiá trị nguyên của tham số để phương trình





3 3

log log

x m x m

  

có

nghiệm trên khoảng

 

 

 

. B.

. C.

. D.

Lời giải

Chọn D

Xét phương trình





3 3

log log

x m x m

  

trên khoảng

 

 

 

Điều kiện:





3 3

log 0 min log 1

x m m x

 



 

 

     

Ta có:





3 3 3

log log log 3

x m

x m x m x m



     

log

3 3

log 3 log 3 3

x m x m

x x x m x x m

 

         

Xét hàm số









3 ; 3 ln3 1 0,

t t

g x t g x t



     









3 3 3

log log log

g x g x m x x m x x m

        

Xét hàm số

     

1 1

log ; 1; 0

ln 3 ln3

f x x x f x f x x

 

      

Bảng biến thiên

Dựa vào bảng biến thiên, ta có:





6; 5; 4; 3; 2; 1

      

Kết luận: Có tất cả

giá trị nguyên.

____________________

HẾT ____________________

Bấm Tải xuống để xem toàn bộ.

Preview text:

UBND TỈNH BẮC NINH
ĐỀ THI CHỌN HỌC SINH GIỎI CẤP TỈNH
SỞ GIÁO DỤC VÀ ĐÀO TẠO NĂM HỌC 2021 - 2022 MÔN TOÁN - LỚP 12
Đề thi gồm có 08 trang
Thời gian làm bài: 90 phút (không kể thời gian giao đề)
Câu 1. Trong không gian Oxyz , cho điểm A1;2;0 và mặt phẳng P : 2x  2y  z  3  0 . Mặt phẳng
 : 2x by  cz  d  0 (với b,c,d ) đi qua điểm A, song song với trục Oy và vuông góc
với P . Khi đó, giá trị b  c  d bằng A. 2 . B. 0 . C. 4 . D. 8 . Lời giải Chọn A 
Ta có mặt phẳng P có 1 vectơ pháp tuyến n  2;2;  1 . P 
Trục Oy có 1 vectơ chỉ phương j  0;1;0 .   
Suy ra n , j  1;0;2 / /n  1;0;2 . P   
Mặt phẳng   vuông góc với mặt phẳng P và song song với trục Oy nên nhận vectơ
n  1;0;2 là vectơ pháp tuyến, mặt phẳng  đi qua điểm A nên có phương trình 1. x  
1  0. y  2  2. z  0  0  x  2z 1  0  2x  4z  2  0 . Do đó b  0;c  4  ;d  2
 . Vậy b  c  d  2.
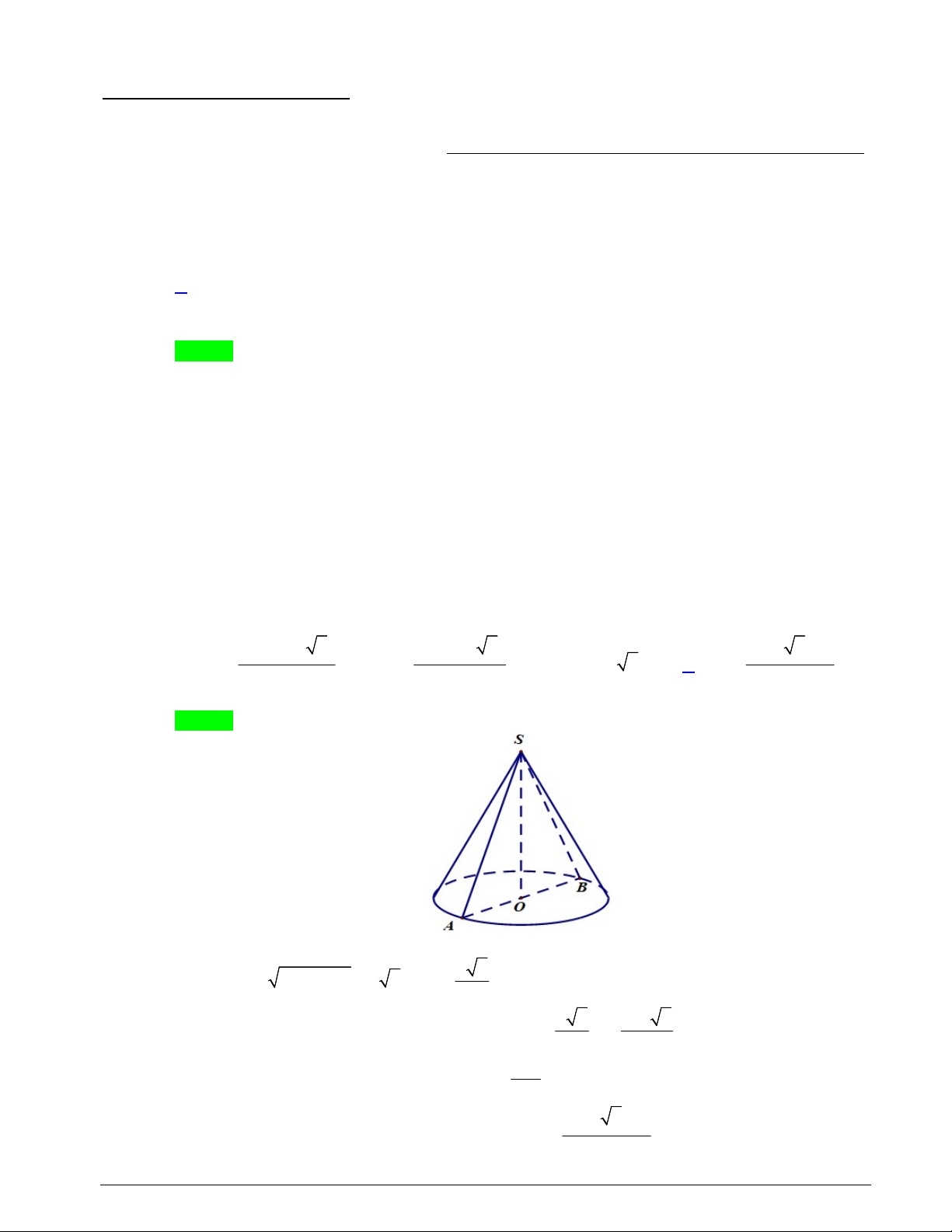
Câu 2. Thiết diện qua trục của hình nón  N  là tam giác vuông cân có cạnh góc vuông bằng a . Tính
diện tích toàn phần của hình nón  N  . 2  a 1 2 2 2  a 2 2 2  a  2  1 A. S  . B. S  . C. 2 S   a  . D. S  . xq  2 1 xq 2 xq 2 xq 2 Lời giải Chọn D
Ta có tam giác SAB vuông cân tại S có SA  SB  a . a 2 Suy ra 2 2
AB  SA  SB  a 2  R  . 2 2 a 2  a 2
Diện tích xung quanh hình nón  N  là S   Rl  . .a  . xq 2 2 2  a
Diện tích mặt đáy hình nón  N  là 2 S   R  . d 2 2 a  2  1
Vậy diện tích toàn phần của hình nón là S  S  S  . d xq 2 Trang 1
Câu 3. Tìm tất cả các giá trị thực của tham số m để hàm số y   2
log x  2mx  4 có tập xác định là  . m  2 A. m  2 . B. m  2 . C.  . D. 2  m  2 . m  2 Lời giải Chọn D a  0 1   0 Điều kiện 2 x  2mx  4  0, x         2  m  2 . 2   0 m  4  0 Vậy 2  m  2 .
Câu 4. Cho hàm số y  f  x là hàm số có đạo hàm cấp hai liên tục trên  . Gọi C là đồ thị của hàm
số đã cho. Tiếp tuyến với đồ thị C tại các điểm có hoành độ x  1; x  0 lần lượt tạo với trục hoành góc 0 0
30 ;45 . Tiếp tuyến với đồ thị C tại các điểm có hoành độ x 1; x  2 lần lượt song
song với đường thẳng d : y  2x 1 và vuông góc với đường thẳng d : y  x+5 . 1 2 0 2 Tính I  3 f 
 x.f  xdx 4 f x3.f  xdx 1 1 1 37 A. . B.  . C. 5  8. D. 14 . 2 12 Lời giải Chọn D 3
 Từ giả thiết, ta có: f   0 1   tan 30   ; f 0 0   tan 45  1  ; f   1  2; f 2  1  . 3
 Đặt t  f  x  dt  f   x x d . 3  TH1: f   1 
; f 0 1; f   1  2; f 2  1  , ta có 3 0 2 1 1 I  3 f 
 x.f  xdx 4 f x3.f  x 3 dx  3 tdt  4 t dt  1  4   1 1 3 2 3 3  TH2: f   1  ; f 0  1  ; f   1  2; f 2  1  , ta có 3 0 2 1 1 I  3 f 
 x.f  xdx 4 f x3.f  x 3 dx  3 tdt  4 t dt  1  4   1 1 3 2 3 3  TH3: f   1  
; f 0  1; f   1  2; f 2  1  , ta có 3 0 2 1 1  I  3 f 
 x.f  xdx 4 f x3.f  x 3 dx  3 tdt  4 t dt  1  4   1 1 3 2  3 3  TH4: f   1   ; f 0  1  ; f   1  2; f 2  1  , ta có 3 Trang 2 0 2 1 1  I  3 f 
 x.f  xdx 4 f x3.f  x 3 dx  3 d t t  4 t dt  1  4   1 1 3 2  3 0 2  Vậy I  3 f 
 x.f  xdx 4 f x3.f  x x d  1  4 1  1
Câu 5. Cho hàm số f  x xác định và có đạo hàm trên  . Biết f  x có bảng xét dấu như sau: Hàm số y  f  2
x  2x nghịch biến trên khoảng nào dưới đây? A.  2  ;  1 . B.  4  ;  3 . C.  2  ;  1 . D. 0;  1 . Lời giải Chọn C
 Ta có: y   x   f  2 2 2 x  2x
 Hàm số nghịch biến khi x  1  x  1 2x  2  0      f  x x x  x  x 2     2 2 2    2 0  x y    1 2  0  
 x  2x  3  x  3   x  1   . 2x  2  0   3  x  1   x x f      1    1 2 x  2x  0   2  1   x  2x<3 3  x<1
Câu 6. Cho hàm số y  f  x và y  g  x có đạo hàm liên tục trên 0;  1 , thỏa mãn 1 1 f 
 xgxdx  2022; f
 xgxdx  2023. Giá trị của biểu thức f  1g 1 f 0g0bằng 0 0 A. 1  . B. 1. C. 4045 . D. 4046 . Lời giải Chọn C u  g  x du  g  x x d  Đặt    . dv  f   xdx v  f  x 1 1  Ta có: f 
 xg xdx  f xgx1  f  x gx x d 0 0 0  2022  f   1 g  
1  f 0 g 0  2023  f   1 g  
1  f 0 g 0  4045 m ln x  2 Câu 7. Cho hàm số y 
( m là tham số thực). Gọi m là giá trị của m để min y  max y  2 . ln x 1 0 1;e 1;e
Khẳng định nào dưới đây đúng? A. 0  m  10 . B. m  2  . C. 6  m  11. D. 0  m  2 . 0 0 0 0 Lời giải Trang 3 Chọn C Ta có m 1
mln x 2 ln x 1 ln x 1     mln x  2
ln x  1 mln x  2 m  2 x x y    . ln x  2 1 ln x  2 1 x ln x  2 1
TH1: Nếu m  2  0  m  2  .  Khi đó m  2 m 2 y   0 x
  1;e  min y  y 1  2 , max y  y e  . 2     x ln x   1;  1 e 1;e 2 m  2
Suy ra min y  max y  2  2 
 2  m  2  8  m  10 (thỏa mãn). 1;e 1;e 2
TH2: Nếu m  2  0  m  2  .  Khi đó m  2 m 2 y   0 x
  1;e  max y  y 1  2 , min y  y e  . 2     x ln x   1;  1 e 1;e 2 m  2
Suy ra min y  max y  2  2 
 2  m  2  8  m  10 (không thỏa mãn). 1;e 1;e 2
Vậy m 10 . Suy ra khẳng định đúng là 6  m  11. 0 0 1 1 Câu 8. Cho biểu thức 2 3 6
P  x  x  x với x  0. Khẳng định nào dưới đây đúng? 7 11 5 A. 6 P  x . B. P  x . C. 6 P  x . D. 6 P  x . Lời giải Chọn B 1 1 1 1 1 1   Ta có 2 3 6 2 3 6 P  x  x  x  x  x . Câu 9. Cho hàm số
f x có đạo hàm liên tục trên  , thoà mãn f 6 1 và 6 3
 2x  f x6 f xdx 10. Khi đó xf  x 3dx bằng 0 3  A. 13 . B. 26 . C. 1  3. D. 2  6. Lời giải Chọn A 3 Với I  xf  x3dx. 3  x  t  3 Đặt t  x  3   . dt  dx Đổi cận: Khi x  3
  t  0 ; x  3  t  6 . 6 6 6 6
Ta có I  t 3 f tdt  x 3 f xdx  xf  xdx 3 f  xdx . 0 0 0 0 6 6 6
Mặt khác  2x  f x6 f x 2 dx  10  x  f   xdx  6 f  xdx 10 0 0 0 Trang 4 6 6 1 6 6 2  1 x  f   xdx  3 f  xdx  5 2  x  f   xdx 5  3  f  xdx. 2 2 0 0 0 0 6 6 6 6 Suy ra I  xf  xdx 3 f  xdx  xf  x 1 2 dx  x  f   xdx 5 2 0 0 0 0 6 6 1 6    1 2xf  x 1 2 dx  x  f   xdx 5   2xf  x 2 +x  f  x dx     5 2 2 2 0 0  0  6 1   6 1 2   x  f  x    dx 2  
  5  x  f  x  5 18 f 6  0  5  13 . 2  2 0  0 Vậy I 13. Câu 10. Biết F  x x 2
 e  2x là một nguyên hàm của hàm số f x trên  . Khi đó f 2xdx  bằng 1 1 A. 2x 2 e  4x  C . B. 2 x 2 e  2x  C . C. x 2 2e  4x  C . D. 2x 2 e  8x  C . 2 2 Lời giải Chọn A Xét I  f  2xdx 1 1 1
Đặt t  2x  dx  dt . Khi đó I  f  t t 2 dt  e  t  C . 2 2 2 1 Kết luận: I  f  2x 2 x 2 dx  e  4x  C . 2
Câu 11. Cho a  0, b  0 và ab  1 thỏa mãn 3ln a  7ln b  0 . Khi đó  3 log a b bằng ab  1 1 A. 3. B.  . C. 3  . B. . 3 3 Lời giải Chọn A 7
Ta có: 3ln a  7 ln b  0  ln a   ln b 3 1 7 1 3 ln a b ln a  ln b  ln b  ln b Xét a b     . ab  3    3 3 3 log  ab 3 1  a b 1  7 ln ln ln    ln b  ln b 2   2  3  Kết luận:  3 log a b   3. ab Câu 12. Cho hàm số 2021 y  x
 2022x . Có bao nhiêu giá trị nguyên của x để f  x  f  2 22 x  ? A. 20 . B. 23. C. 21 . D. 22 . Lời giải Chọn C Xét hàm số: 2021 2020 y  x  2022x  y  2021x
 2022  y  0,x   .  Hàm số 2021 y  x
 2022x luôn đồng biến trên  .  f  x  f  2 x  2 22
 22x  x  0  x  22 . Trang 5  x 1;2;3;4;...;2  1 .
Kết luận: Có 21 giá trị nguyên.
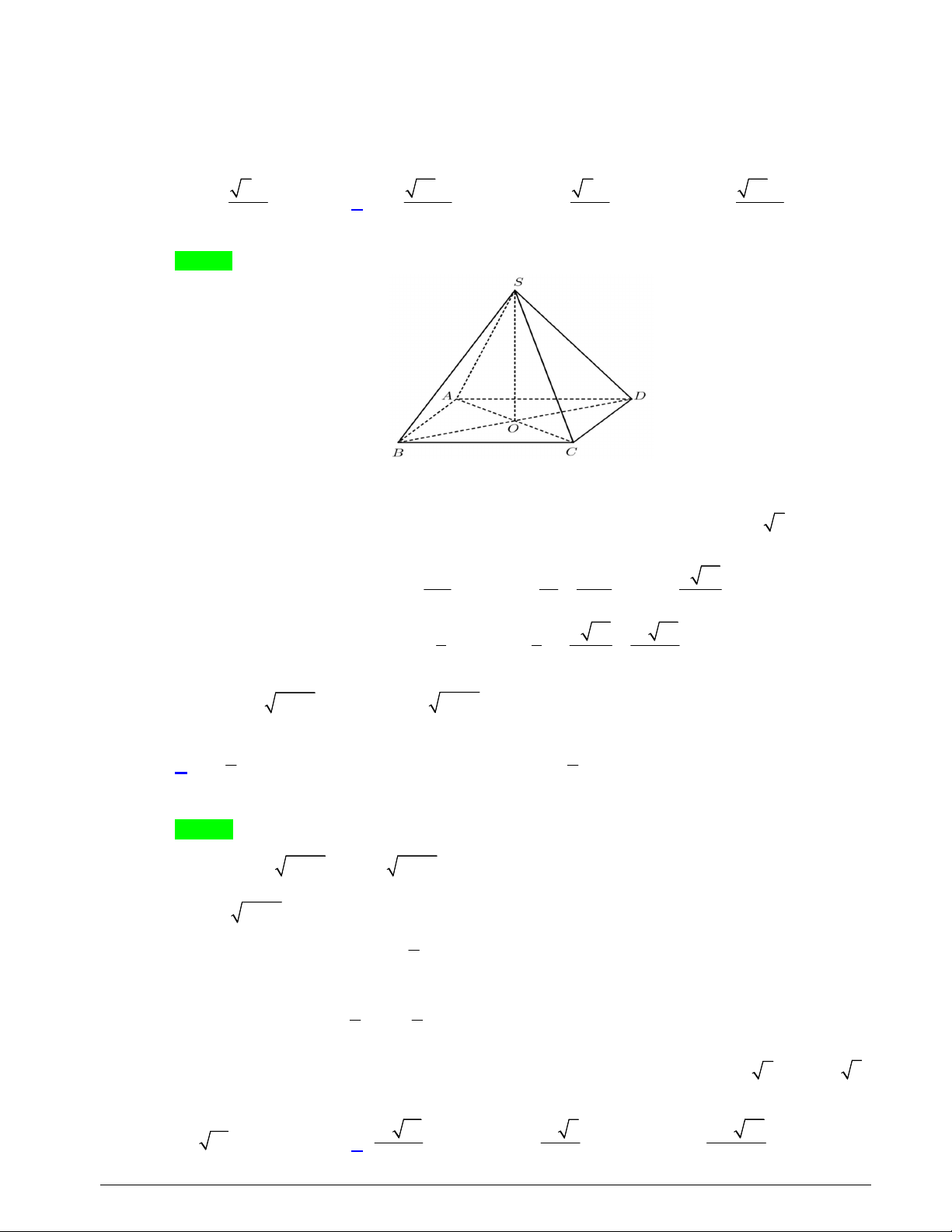
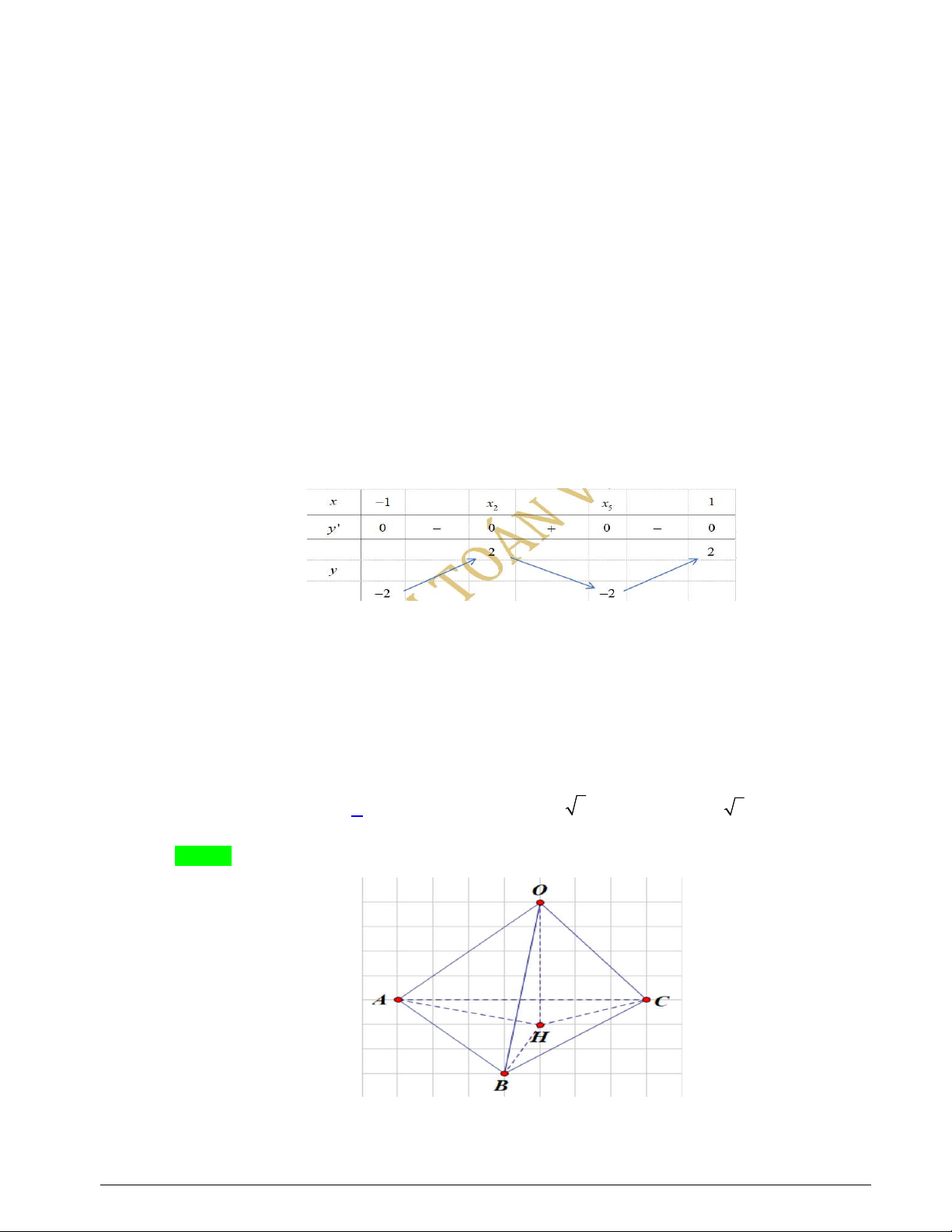
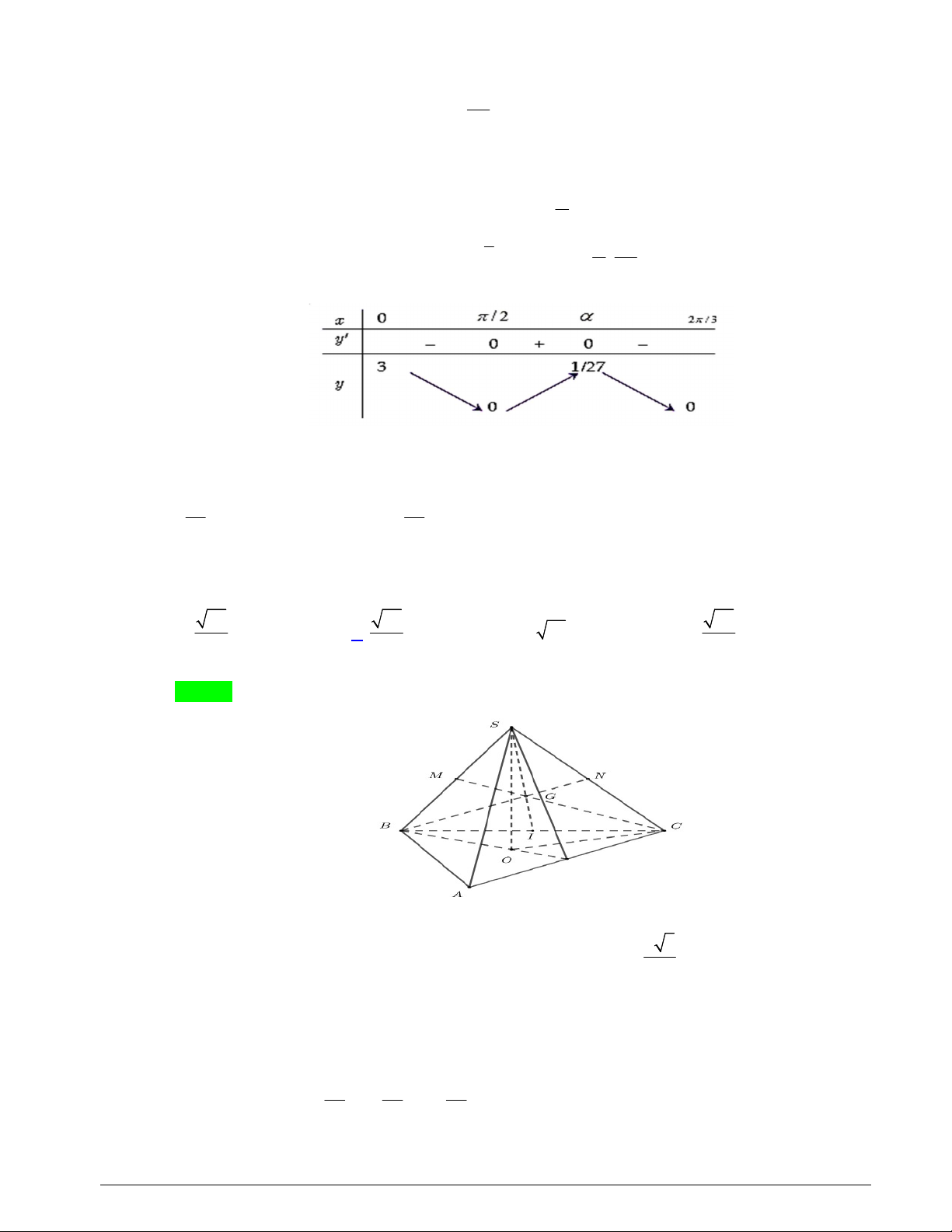
Câu 13. Cho khối chóp tứ giác đều có cạnh đáy bằng a , cạnh bên bằng 3a . Tính thể tích của khối chóp đã cho. 3 2a 3 34a 3 2a 3 34a A. V  . B. V  . C. V  . D. V  . 2 6 6 2 Lời giải Chọn B
Giả sử có hình chóp đều S.ABCD và AB  a , SA  3a .
Gọi SO là đường cao của hình chóp, với O tâm của ABCD .
Vì S.ABCD là hình chóp đều nên ABCD là hình vuông có cạnh AB  a  AC  a 2 . Xét tam giác vuông SOA có 2 2 2 a 34 2 2 2  AC  a 17a
SA  SO  OA  SO  SA   3a2 2 2      SO  .  2  2 2 2 3 1 1 a 34 a 34
Thể tích khối chóp S.ABCD là: 2 V  S .SO  .a .  . 3 ABCD 3 2 6 1 Câu 14. Cho 5 3 I  x 1  x dx  . Nếu đặt 3 t  1 x thì 0 1 2 1 1 2 1 A. 2 I  t   2 1 t dt . B. 2 I  2 t   2 1 t dt . C. 2 I  t  2t   1dt . D. 2 I  2 t  2t   1dt . 3 3 0 0 0 0 Lời giải Chọn A 1 1 Ta có 5 3 3 3 2
I  x 1  x dx  x 1 x .x dx   . 0 0 Đặt 3 2 3 3 2
t  1  x  t  1  x  x  1 t  d  2 3 x   d  2 1 t  2  x dx   tdt . 3
Với x  0  t  1; và với x  1  t  0 . 0 1  2  2 Khi đó I    2 1  t  2 t.  t dt  t     2 1  t dt .  3  3 1 0
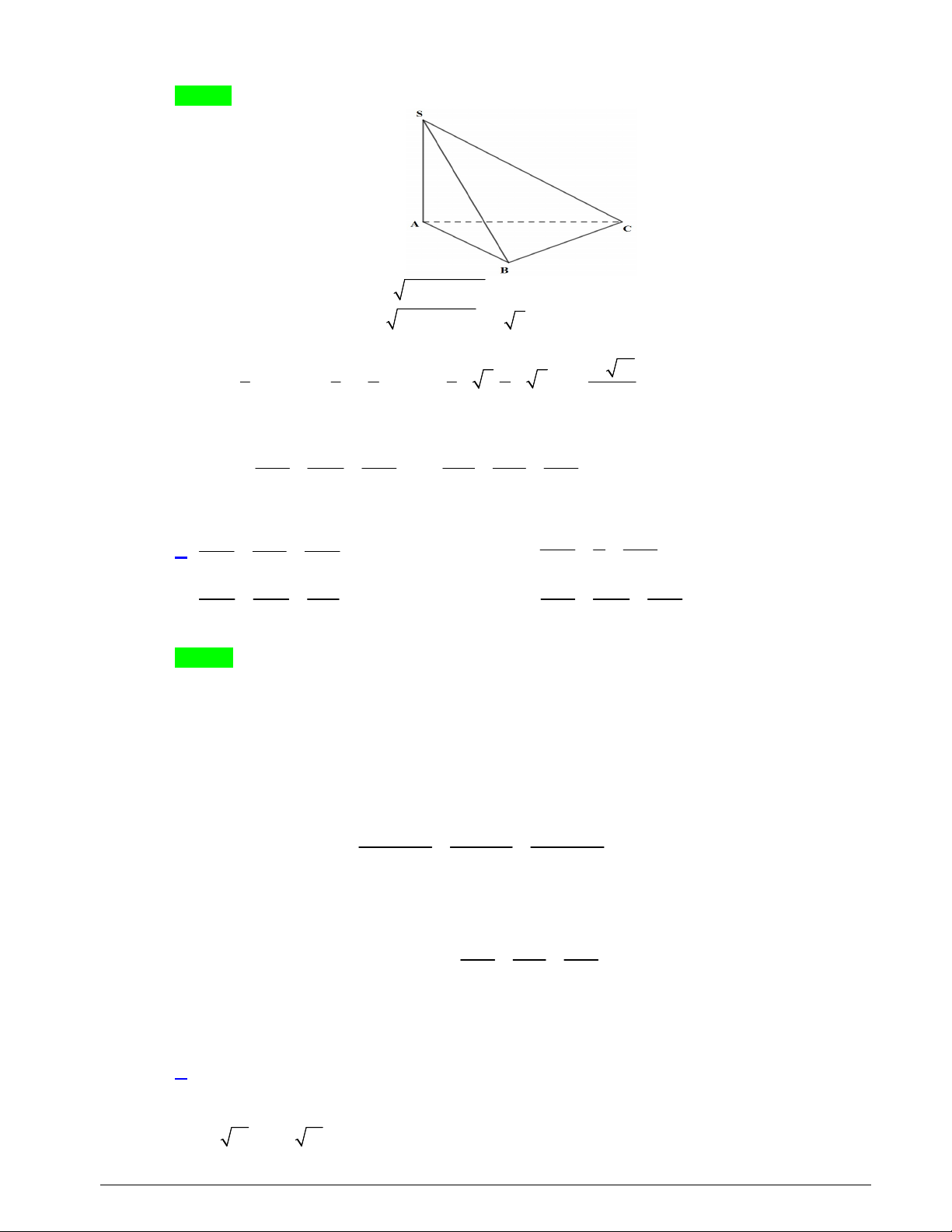
Câu 15. Cho hình chóp S.ABC có SA   ABC , tam giác ABC vuông tại C , AC  a 2 , AB  a 6 .
Tính thể tích khối chóp S.ABC biết SC  3a . 3 a 14 3 a 6 3 2a 42 A. 3 14a . B. . C. . D. . 3 3 3 Trang 6 Lời giải Chọn B Trong tam giác ABC có 2 2 BC  AB  AC  2a . Trong tam giác SAC có 2 2 SA  SC  AC  a 7 .
Thể tích khối chóp S.ABC là 3 1 1 1 1 1 a 14 V  S . A S  S . A C . A CB  .a 7. .a 2.2a  . S. ABC 3 A  BC 3 2 3 2 3
Câu 16. Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng P : x  2y  3z  7  0 và hai đường thẳng x  3 y  2 z  2 x 1 y 1 z  2 d :   , d :  
. Đường thẳng vuông góc với mặt 1 2 1 4 2 3 2 3
phẳng P và cắt cả hai đường thẳng d và d có phương trình là 1 2    x  7 y z  6 A. x 5 y 1 z 2   . B.   . 1 2 3 1 2 3 x  4 y  3 z 1 x  3 y  2 z  2 C.   . D.   . 1 2 3 1 2 3 Lời giải Chọn A Lấy
A3  2t; 2  t; 2  4t   d  d và
B 1 3t ; 1 2t ; 2  3t  d  d , suy ra 1 2 
AB  2  3t  2t;1 2t  t;4  3t  4t . 
Đường thẳng d nhận AB làm véc-tơ chỉ phương.  
Đường thẳng vuông góc với mặt phẳng nên n  k AB k  0 . Khi đó P  2  3t  2t 1 2t  t 4  3t  4t t  1     1 2 3 t  2 
Do đó d qua A5;1;2 và nhận véc-tơ n  1;2;3 làm véc-tơ chỉ phương có phương P  trình x  5 y 1 z  2 d :   . 1 2 3
Câu 17. Cho hàm số f  x có đạo hàm trên 2;5 thỏa mãn f  x  0 , x 2;5 ,
f  x  0  x 3;4 . Mệnh đề nào dưới đây sai?
A. Hàm số f  x đồng biến trên khoảng 2;5 .
B. Hàm số f  x đồng biến trên khoảng 4;5 .
C. f  10  f  13 . Trang 7
D. Hàm số f  x đồng biến trên khoảng 2;3 . Lời giải Chọn A
Ta có: f  x  0 , x
 2;5 , f x  0  x 3;4 nên tồn tại vô số điểm x 3;4 để f  x  0
Vậy hàm số f  x không đồng biến trên khoảng 2;5 .
Câu 18. Một vật N , có dạng khối nón có chiều cao bằng 40 cm . Người ta cắt vật N bằng một mặt 1 1
phẳng song song với mặt đáy của nó để được một khối nón nhỏ N có thể tích bằng 1 2 8
thể tích N . Tính chiều cao h của khối nón N . 1 2 A. 20 cm . B. 10cm . C. 5cm. D. 40cm . Lời giải Chọn A 1 2 2 .r .h V 2 2   N r h 1 1 3 Ta có: h r 2 2 3 2 2   k nên 2 
   .  k   k  . h r V 1 2 r h 8 2   1 1 1 N 1 1 .r .h 1 1 3 1 Khi đó h  h  20cm . 2 1 2
Câu 19. Quay xung quanh truc Ox hình phẳng giới hạn bởi đồ thị hàm số y  2x   1 ln x , trục Ox ,
và đường thẳng x  2 ta thu được khối tròn xoay có thể tích bằng 2 2 2 2 A. 2x   2 1 ln xdx . B.  2x   2 1 ln xdx . C.  2x   2 1 ln xdx . D.  2x   2 1 ln xdx . 1 1 1 1 2 2 Lời giải Chọn C
 Xét phương trình hoành độ giao điểm:  x  0 2x   1 ln x  0, ĐK   x 1. ln x  0  x 1  1 2x 1  0 x      2  x  1 ln x  0  x 1 2
 Thể tích khố trong xoay quay quanh Ox là: V   2x   2 1 ln xd . x 1
Câu 20. Trong không gian với hệ tọa độ Oxyz , cho tam giác ABC có A4;2;3, B1; 2  ;3,C 1;2;  3 .
Tâm đường tròn nội tiếp tam giác ABC là điểm:  1 1 3   2   9  A. I ; ;  . B. I 3; ;3   . C. I 2;1;3 . D. I 3;1;   .  2 6 4   3   2  Trang 8 Lời giải Chọn C
 Gọi I  x ; y ; z là tâm đường tròn nội tiếp tam giác ABC . I I I 
Ta có AB  5, AC  3, BC  4  BC.x  C . A x  A . B x 4.4  3.1 5.1 A B c x    2  I BC  CA  AB 4  3  5   BC.y  C . A y  A . B y 4.2  3.   A B c  2 5.2
Tọa độ tâm I được tính theo công thức: y   1 I BC  CA  AB 4  3  5   BC.z  C . A z  A . B z 4.3  3.3  5.3 A B c z    3  I BC  CA  AB 4  3  5 
 Vậy tọa độ điểm I 2;1;3 .
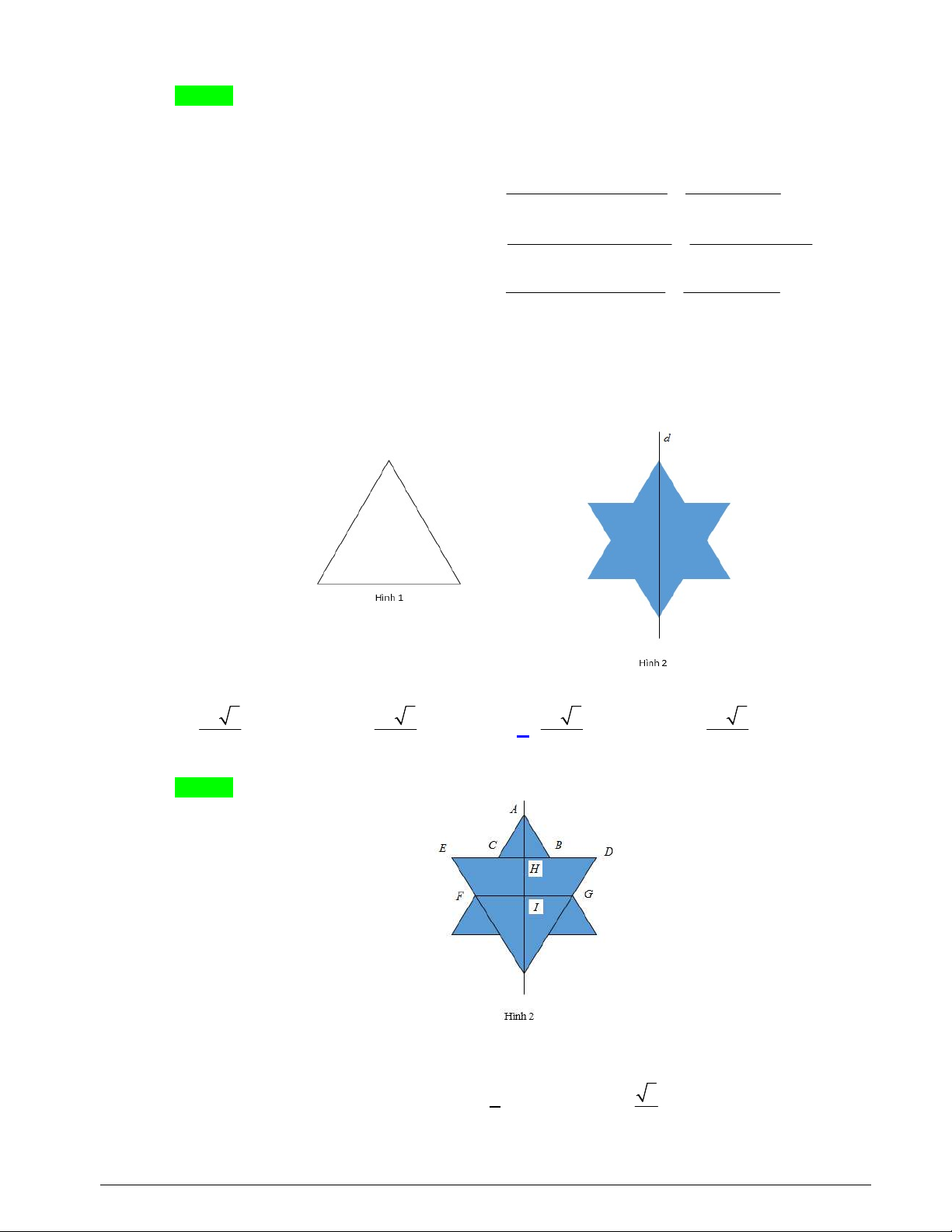
Câu 21: Ban đầu ta có một tam giác đều cạnh bằng 3 (hình 1). Tiếp đó ta chia mỗi cạnh của tam giác thành
ba đoạn bằng nhau và thay mỗi đoạn ở giữa bằng hai đoạn bằng nó sao cho chúng tạo với đoạn bỏ
đi một tam giác đều về phía bên ngoài để được hình như hình 2.
Quay hình 2 xung quanh trục d ta được một khối tròn xoay có thể tích bằng 5 3 9 3 5 3 5 3 A. . B. . C. . D. . 2 8 3 6 Lời giải Chọn C
Ta đánh dấu các điểm như hình vẽ. Do tính chất đối xứng nên thể tích cần tìm của khối tròn xoay
bài ra bằng 2 lần thể tích của đường gấp khúc ABDGI quay quanh trục d . Đường gấp khúc này 1 3
khi quay quanh d tạo ra 1 khối nón có r  và đường cao h 
, 1 khối nón cụt có chiều cao 2 2 Trang 9 3 3 2 h 
, hai đáy r  HD  , r  IG  HD  1 nên ta có thể tích lần lượt tính theo công thức 1 2 1 2 2 3 1 h  2 V  .  r .h, V   2 2 r  r  r r . 1 2 1 2 1 2  3 3 5 3 5 3 Ta được V V 
. Từ đó ta có được thể tích khối tròn xoay cần tìm là V  . 1 2 6 3
Câu 22: Biết rằng phương trình 3 2 3 3log x  log x  log  9 125x có nghiệm duy nhất 3 3 3 5 a b c x    với 5 5 5 
a,b, c là các số nguyên dương đôi một phân biệt. Giá trị của tích abc bằng A. 9. B. 12. C. 7. D. 8. Lời giải Chọn D Ta có 3 2 3 3log x  log x  log  9 125x  3 2 3 3
 3log x  9log x  9log x  3  0  log x  4  2 1 5 5 5 5 5 5 5 3 3 4  2 1 x 5   
nên a  4;b  2;c  1  abc  8.
Câu 23. Gọi S là tập hợp các giá trị nguyên của m để phương trình x 1 9    4 2 4  2 1  3  3.3x m x x m 1  0
có nghiệm duy nhất. Tổng các phần tử của S bằng A. 1. B. 1. C. 2 . D. 2 . Lời giải Chọn D Ta có: x 1 9    4 2 4  2 1  3  3.3x m x x m 1  0  x2 3
 3x  m4. x 1 3m3  0 .
Nhận xét: Nếu x là nghiệm của phương trình đã cho thì x  2 cũng là nghiệm của phương 0 0 trình đã cho.
Do đó điều kiện cần để phương trình đã cho có nghiệm duy nhất là x  x  2  x  1  . 0 0 0 m  1 Thay x  1
 vào phương trình đã cho ta được  m m   1 1 3 3 . 1  0  . 0  3 m  2  Điều kiện đủ:
 Với m  1: Phương trình đã cho có dạng: x 1
9   4. 1  6.3x x 1  0   x  2 1 3 1  4. 1.3x x  0   1
Dễ thấy x  2, x  1 và x  0 là nghiệm của phương trình   1 .
 m 1 không thỏa mãn.
 Với m  2 : Phương trình đã cho có dạng: x 1
9   24. 1 3.3x x 1  0   x  2 1 3 1  8. 1.3x x  0  x  1.  m  2 thỏa mãn. Do đó S   
2 . Vậy tổng các phần tử của S bằng 2 . Câu 24. Cho hàm số   3 2
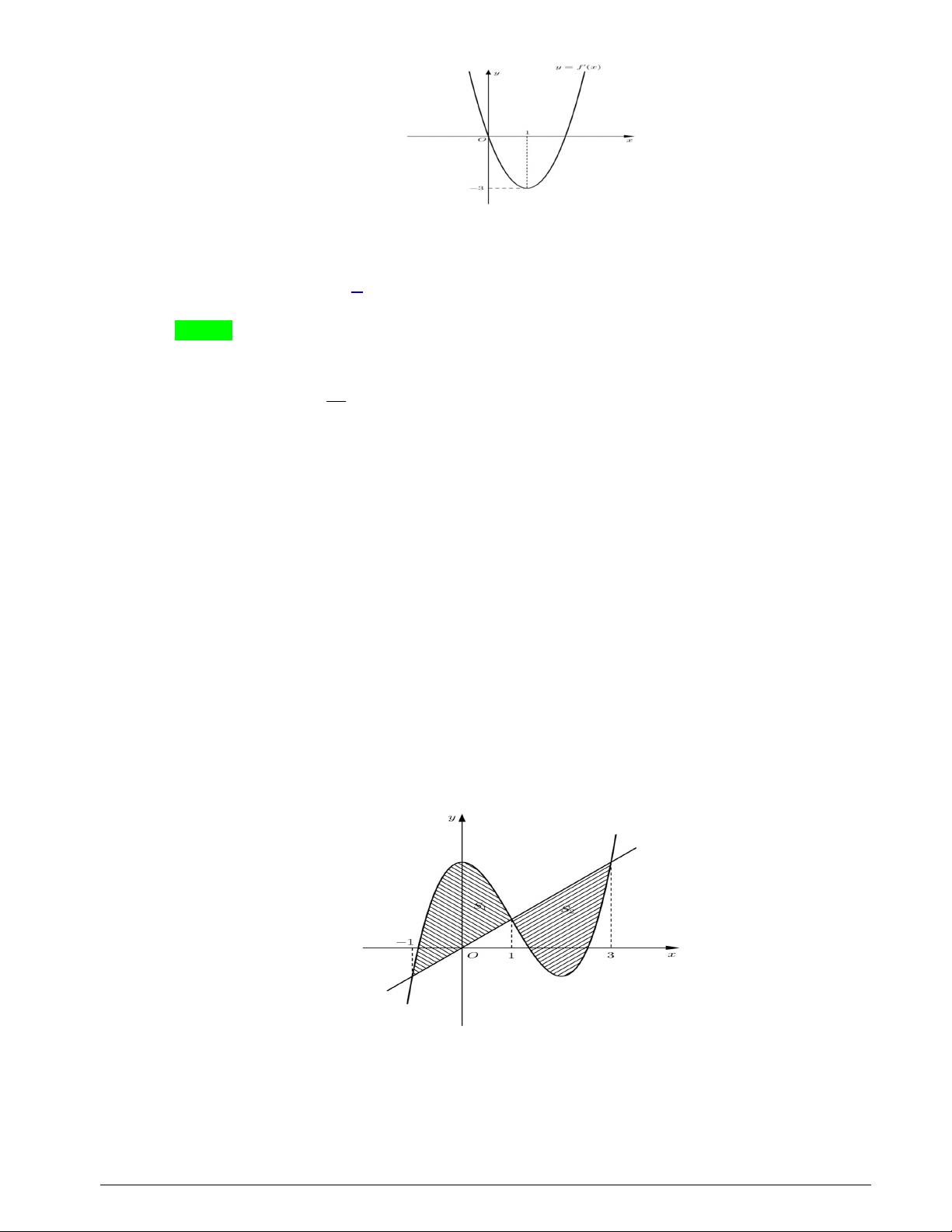
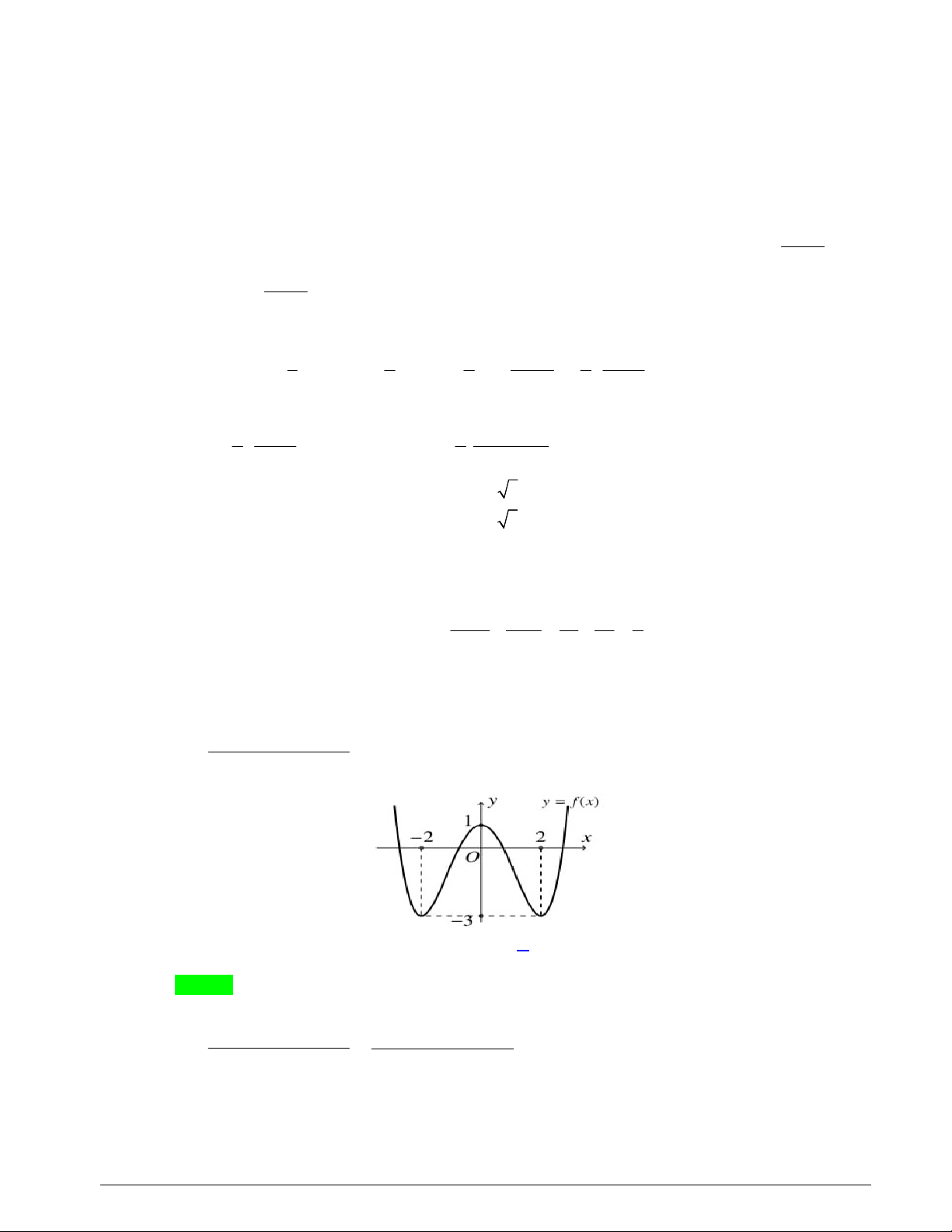
f x  ax  bx  cx  d có đồ thị C. Đồ thị hàm số y  f  x được cho như hình vẽ. Trang 10
Biết rằng đường thẳng d : y  x cắt đồ thị C tạo thành hai phần hình phẳng có diện tích bằng
nhau. Giá trị a  b  c  d bằng A. 6 . B. 5 . C. 1. D. 6 . Lời giải Chọn B Ta có: f  x 2  3ax  2bx  c .  b  1  3a b   3a a 1   
Từ hình vẽ suy ra  f 0  0  c  0  b   3     f   1  3   3a  2b  c  3   c  0    f  x 2
 3x  6x  f  x  6x  6 và f x 3 2  x 3x  d .
f  x  0  6x  6  0  x  1 Điểm uốn của đồ thị C là điểm I 1;d  2 .
Điều kiện cần: Đường thẳng d : y  x cắt đồ thị C tạo thành hai phần hình phẳng có diện tích
bằng nhau khi đường thẳng d : y  x đi qua điểm uốn I 1;d  2 của đồ thị C .
 d  2  1  d  3.
Điều kiện đủ: Với d  3  f  x 3 2  x  3x  3.
Phương trình hoành độ giao điểm của đường thẳng d và đồ thị C là: x  1  3 2 x  3x  3  x  3 2
x  3x  x  3  0  x 1  x  3 
Đường thẳng d : y  x cắt đồ thị C tạo thành hai phần hình phẳng có diện tích lần lượt là: 1 1 S   f   x xdx     3 2
x  3x  x  3 dx  4 . 1  1 1 Trang 11 3 3 S  x  f  xdx    3 2
x  3x  x  3 dx  4 . 2  1 1
Vậy a  1; b  3 ; c  0 ; d  3  a  b  c  d  5 . 4x 1 a c a c Câu 25. Biết
dx  ln 2x 1  ln x  3  C  với a, ,
b c là các số nguyên dương và , là 2 2x  5x  3 b b b b
các phân số tối giản. Tính S  2a  3b  c . A. S  36 . B. S  34 . C. S  32 . D. S  38. Lời giải Chọn A 4x 1 4x 1 Ta có  , gọi , A B là hai số thực thỏa mãn 2 2x  5x  3 2x   1  x  3 4x 1 A B    . 2x  
1  x  3 2x 1 x  3  2 A  A  2B  4  Khi đó ta có: 7    . 3  A  B  1  13 B   7 4x 1 2  1  13  1  1 13 Suy ra dx  dx  dx  ln 2x 1  ln x  3  C    . 2     2x  5x  3 7  2x 1 7  x  3  7 7
Do đó, a  1,b  7,c  13 nên S  2a  3b  c  36 .
Câu 26. Cho các số thực , x y thỏa mãn log  3 2
x  x  x  log x 1  log y  2  log y 1 . Có bao 8  4   8   64   4x
nhiêu giá trị nguyên của tham số a 10;10 để biểu thức P  y 
 a có giá trị nhỏ nhất x 1 bằng 0 . A. 6 . B. 15 . C. 1. D. 16 . Lời giải Chọn D 3 2 x  x  x  0  x 1  0 x  0 Điều kiện:    . y  2  0  y  1 y 1 0
Với điều kiện trên ta có: 1  3 2 1 1 1 log         2 x x x log2 x  1 log2  y 2 log2  y  1 3 2 3 6 x  x  x2 3 2  log
 log  y  22 y 1 2 3 2   x   1 x  x  x2 3 2 
  y  22  y   1 x  3 1 2 2 2  x   x          y  2 1 2  y   1 (*). x 1 x 1     Trang 12
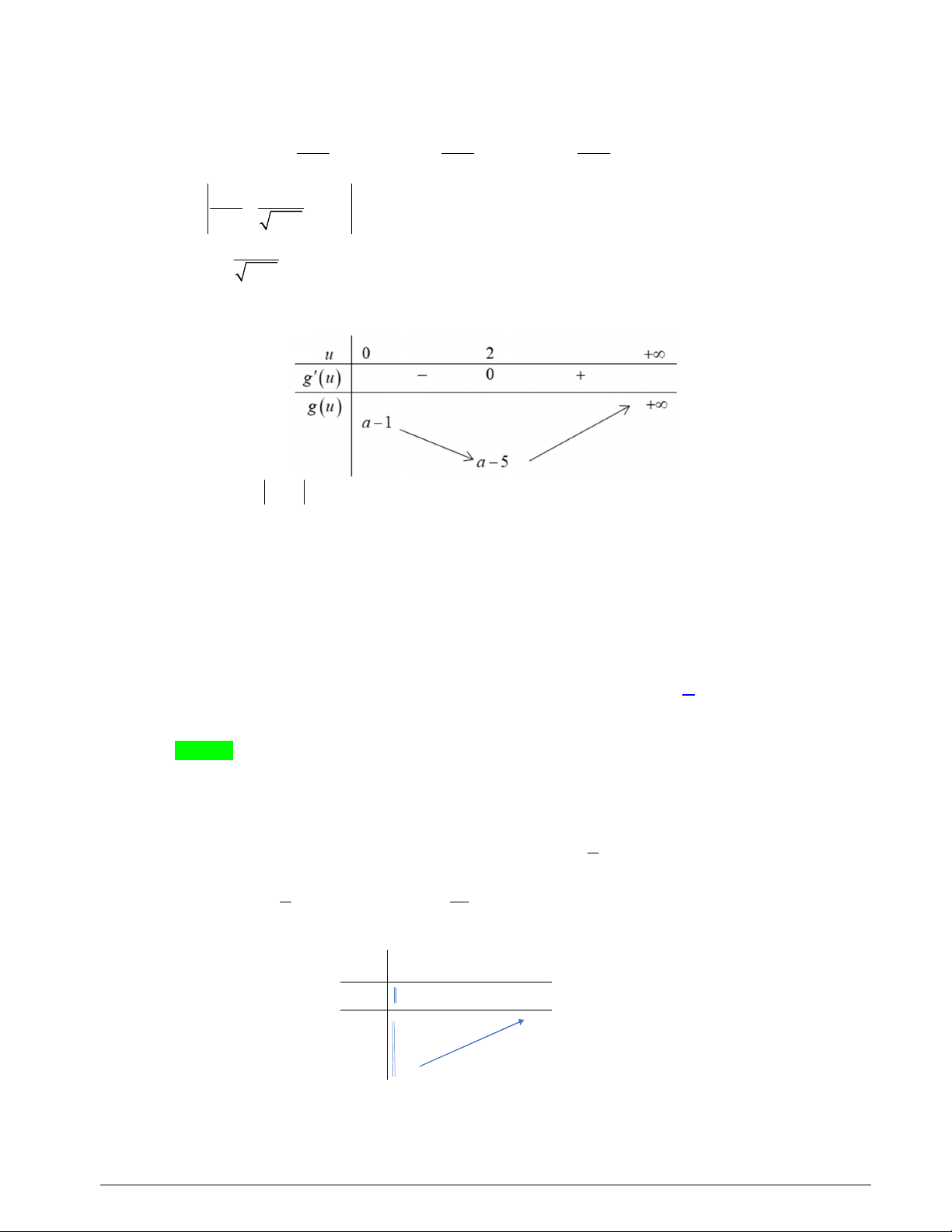
Xét hàm số f t   t t  2 3 2
1  t  2t  t trên khoảng 0;  . Ta có f t 2  3t  4t 1  0, t  0;  . 2 2 2  x  x x Khi đó (*)  f    f  y   1   y 1  y  1. x 1 x 1 x 1   2 x 4x P    a 1 x 1 x 1 x Đặt u 
với x  0;  thì ta có u 0;  . x 1 Xét hàm g u 2
 u  4u  a 1, gu  2u  4  gu  0  u  2 Ta có bảng biến thiên
Khi đó, P  g u có giá trị nhỏ nhất bằng 0 khi và chỉ khi a  5  0  a  5* .  a  Z Mặt khác:  a   10;10**
Từ (*) và (**) suy ra a  1  0; 9  ;...;  5
Vậy có 16 giá trị nguyên của a thỏa mãn yêu cầu bài toán.
Câu 27. Xác định m để phương trình 2 2 log (x 1)  log (mx 1) có nghiệm . 2 m 2  2m2 m  1 A.  . B. m 1. C. m 1. D. 1   m 1. m  1  Lời giải Chọn D 2 2 log 2 2  (x 1)  log (mx 1)  log (x 1)  log (mx 1) 2 m 2  2 m 2  2 m 2  2 m 2    x 1  0 x  1 x 1        2 2 2 mx 1  (x 1) 2 2 mx 1  x  2x 1 m  1  x Đặt 2 2
f (x)  1 ,x  1 ta có ' f (x)   0;x  1. x 2 x x 1  ' f ( ) x + 1 f ( ) x 1 Vậy 1  m  1 Trang 13
Câu 28. Tìm số hạng chứa 3
x trong khai triển   x  x 20 2 1 2 . A. 3 380x . B. 3 540x . C. 3 1900x . D. 3 160x . Lời giải Chọn A Ta có: *)1 x  2x 20 2 2 3 20
 a  a x  a x  a x  ...  a x 0 1 2 3 20 *)   x  x 20 2 1 2  1 x 1 2x 20 20 20 20 i  C (1)i i j x C 2j j x 20 20 i0 j0 Do đó, số hạng chứa 3 x trong khai triển là: 3 a x  C .C .2 .x  C . 1 
.C .x  C . 1 .C .2 .x  C . 1 .C .2.x = 3 380x . 20 20 20  3 20 20   20 20  2 0 3 3 3 3 0 3 1 2 2 3 2 1 3 3 20
Câu 29. Cho hàm số f  x liên tục trên đoạn 0;  1 thỏa mãn x f  2 x   f   x 2 4 . 3 1  4x 1 x  3 x, x  0;  1 . 1 Tính tích phân I  f  xd .x 0 1 1 2 5 A. . B. . C. . D. . 6 4 3 6 Lời giải Chọn C Ta có: x f  2 x   f   x 2 4 . 3 1  4x 1 x  3 x, x  0;  1 . 1 1 1 1  4 . x f   2xdx 3f  1 x 2 dx  4x 1 x dx  3 x dx   0 0 0 0 1  2. f  x dx  1 1 1 2 2  3 f  1 xd1 x 2   2 1 x d   2 1 x   3 x dx  0 0 0 0 1 1 1    f  t t  f  u 4 2 d 3 du    1 x 3 2 3  2 x 3    0 0 0 1 1      f  x 4 4 10 x         f  x 2 5 d .0 2.1 .1 2.0 dx      .  3   3  3 3 0 0 1 2 Vậy I  f  xdx   . 3 0
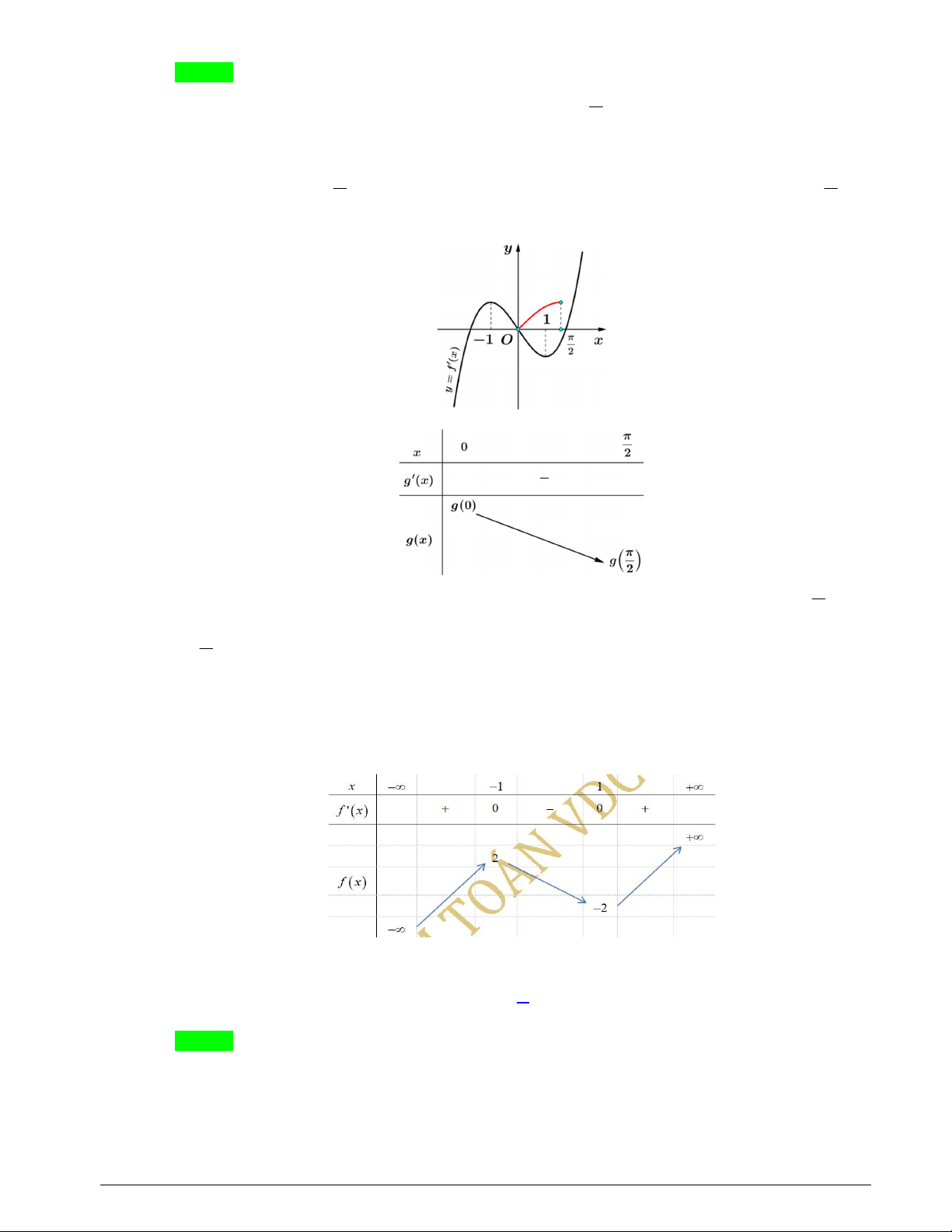
Câu 30. Cho hàm số y  f  x có đạo hàm trên  và f  
1  1. Đồ thị hàm số y  f  x như hình vẽ sau   
Có bao nhiêu số nguyên dương a để hàm số y  4 f sin x  cos 2x  a nghịch biến trên 0; ?    2  A. 2. B. Vô số. C. 3. D. 5. Lời giải Trang 14 Chọn C   
Xét hàm số g  x  4 f sin x  cos 2x  a trên khoảng 0;    2  Ta có g x  4cos . x f  x  4sin .
x cos x  4 cos x  f  x  sin x         Do cos x  0, x   0; 
 nên g x  0  f  x  sin x (vô nghiệm vì trên khoảng 0;   ta  2   2 
thấy đồ thị hàm y  sin x nằm phía trên đồ thị f  x ) Bảng biến thiên   
Dựa vào bảng biến thiên, để hàm số đã cho nghịch biến trên khoảng 0;   thì  2     g  0  4 f  
 1 1 a  0  3 a  0  a  3  2  Mà *
a   nên a 1;2;  3
Vậy có 3 giá trị nguyên dương của a thỏa mãn yêu cầu bài toán.
Câu 31: Cho hàm số y  f  x thỏa mãn f  2
   2, f 2  2 và có bảng biến thiên như hình vẽ sau.
Có bao nhiêu số tự nhiên m để bất phương trình f  f  x  m có nghiệm trên đoạn 1;  1 ? A. 2. B. 1. C. 3 . D. 4 . Lời giải Chọn C
Xét hàm số y  f  f  x trên đoạn  1  ;  1 ta có: Trang 15
y '   f ' x. f ' f x  f ' x  0 y '  0   f '   f  x  0 f ' x  0  x  1   
f  f x    f  x f  x 1 ' 0  1    f x 1  x  x  2; 1 (L) 1    f  x  1  x  x  1  ;1 2     x  x  1;2 (L)  3    x  x  2  ; 1  (L) 4   
f  x  1  x  x  1;1 x  x 5   5 2    x  x  1; 2 (L)  6  
Ta có bảng biến thiên như sau:
Từ bảng biến thiên ta thấy bất phương trình f  f  x  m có nghiệm trên đoạn  1  ;  1  m  2
Mà m là số tự nhiên nên m 0;1;  2 Câu 32: Cho hình chóp . O ABC có O ,
A OB,OC đôi một vuông góc với nhau. Gọi ,  , lần lượt là góc
tạo bởi các đường thẳng O ,
A OB,OC với mặt phẳng  ABC  . Giá trị nhỏ nhất của biểu thức M   2    2    2 3 cot 3 cot 3  cot   bằng A. 48 . B. 125 . C. 125 3 . D. 48 3 . Lời giải Chọn B
Gọi H là trực tâm của tam giác ABC . Ta có: Trang 16
+) H là hình chiếu vuông góc của
trên mặt phẳng  ABC . O 1 1 1 1 +)    . 2 2 2 2 OH OA OB OC Khi đó    OAH ;    OBH ;   OCH . 2 2 2 OH OH OH OH OH OH Suy ra 2 2 2 sin  ;sin   ;sin  
 sin   sin   sin      1. 2 2 2 OA OB OC OA OB OC 1 Đặt 2 2 2 3
sin   x;sin   y;sin   z  x  y  z  1  3 xyz  xyz  . 27 Ta có: M   2 3  cot   2 3  cot   2 3  cot    1  1  1   2  2  2   2  2  2   sin   sin   sin    1  1   1   2  2  2       x  y  z  Mặt khác: 1 1 1 1 1 1 1 1 1 5 2   11    5 ; 2   55 5 ; 2   5 3 3 3 x 3x 3x 3x 27x y 27 y z 27z 1  M  1255  125 27  xyz3 3 Dấu bằng xảy ra khi 1 x  y  z  . 3
Câu 33: Cho hàm số f x liên tục trên  và có đồ thị như hình bên dưới
Tính tổng tất cả các giá trị thực của tham số m để max f        2 8 4x 4x 1 m 5 1;1    A. 20. B. 3  . C. 1  0. D. 7  . Lời giải Chọn C
Xét hàm số g  x  f  2 8  4x  4x   1  m trên đoạn  1  ;  1 Trang 17 Điều kiện: 2
8  4x  4x  0  1  x  2 .   g x 2x 1  . f  2 2 x  x  2 1 2  x  x  2  1 x   2  1 x     1 5  2  x 1  0 2 x   n  Cho g x  0   2 2
 2 x  x  2 1  1    f    2 2 x  x  2   1  0   1 5 2 2    2 1  2 x   n x x  2     1 x  k   2 Ta có: g   1  f   1  m  8  m 1 5  g    f   1  m  2  m  2     1  g  f   2 m  4 m  2  g 2  8  m Suy ra max g(x)  8  ; m min g(x)  2  m . 1;2 1;2  8  m  5    5   2  m  m  3  Để max f          .   2 8 4x 4x 1 m 5 1;1     2  m  5 m    7  5   8  m  Vậy m  3    7    1  0.
m  8  m  2  m  8  (m  2)
Chú ý: Công thức nhanh max g  x   5.  1  ;  1 2
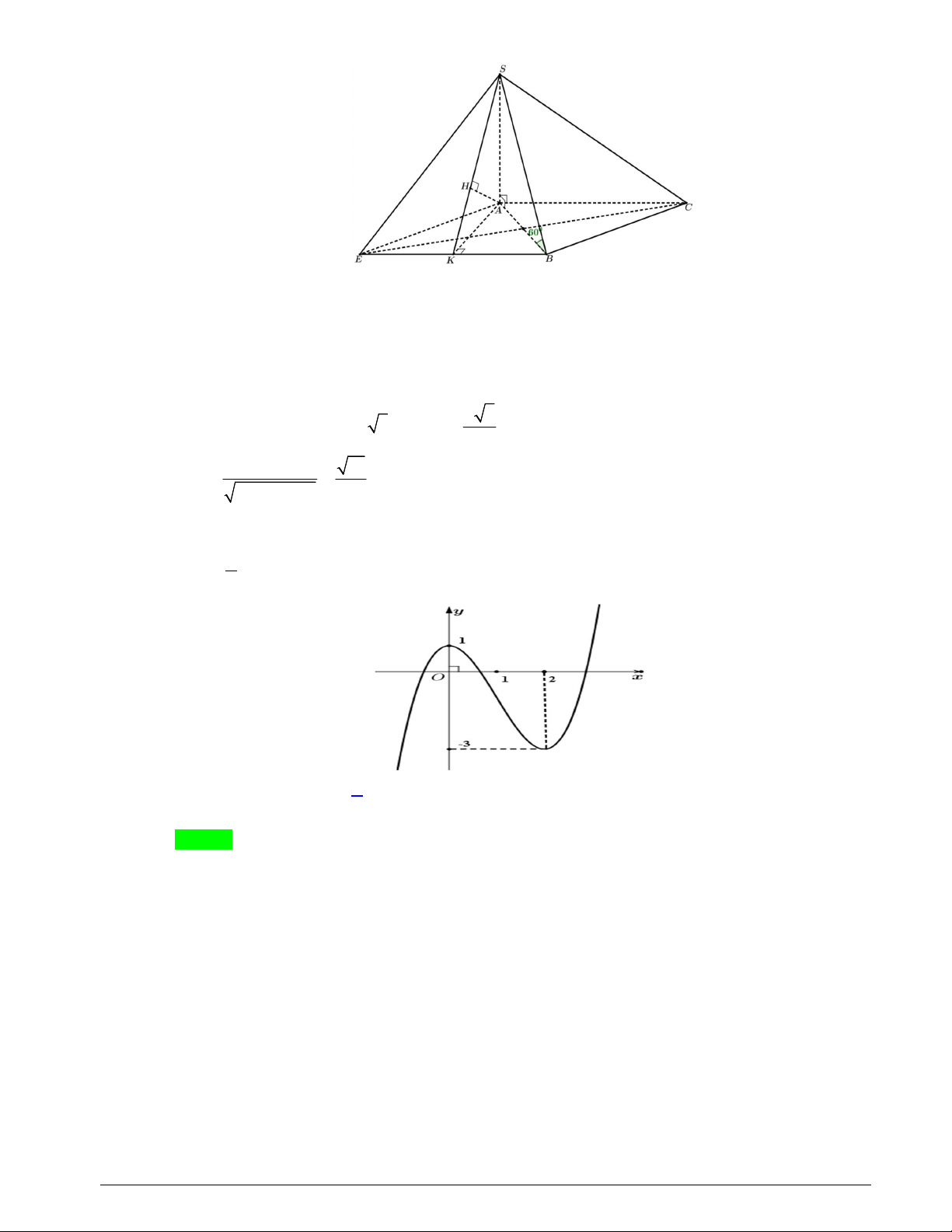
Câu 34: Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, SA   ABC , góc giữa đường
thẳng SB và mặt phẳng  ABC bằng 0
60 . Khoảng cách giữa hai đường thẳng AC và SB bằng a 15 a 2 a 7 A. . B. . C. . D. 2 . a 5 2 7 Lời giải Chọn A Trang 18 Ta có: SB  ABC      SB AB  0 , , SBA  60
Dựng hình thoi ACBE  AC / / SEB  d  d  d AC;SB AC;SBE A;SEB
Kẻ AK  EB và AH  SK . Từ đó suy ra AH  SEB  d  AH . ; A SEB a 3 Ta có: 0 SA  A . B tan 60  a 3 và AK  2 AK.AS 15 AH   a . 2 2 AK  AS 5 Câu 35: Cho hàm số 3 2
y  ax  3bx  2cx  d ( a, ,
b c, d là các hằng số, a  0 ) có đồ thị như hình vẽ. Hàm a số 4 y  x  a  b 3 x   b  c 2 3
x  d  2c x  d  2022 nghịch biến trên khoảng nào sau đây? 4 A. 2;  . B. 1;2 . C.  ;  0 . D. 0;2 . Lời giải Chọn B Xét hàm số 3 2 y  ax  3bx  2cx  d 2
 y  3ax  6bx  2c .
Từ đồ thị hàm số suy ra đồ thị đi qua các điểm A0;  1 , B 2; 3   nên d  1 d  1    (1) 8
 a 12b  4c  d  3 2a  3b  c  1 
Từ đồ thị hàm số suy ra hàm số có hai điểm cực trị là x  0, x  2  y  0 có hai nghiệm là 0 và c  0 2   (2) 1  2a 12b  0 a 1 b    1  Từ (1) và (2) suy ra  c  0  d 1 Trang 19 a Ta có y  g  x 4  x  a  b 3 x   b  c 2 3
x  d  2c x  d  2022 4  gx 3  ax  a  b 2 x   b  c 3 3 2 3
x  d  2c  x  6x 1
g x  0  x  ;
  2,5  0,16; 2,3 a Do đó hàm số 4 y  x  a  b 3 x   b  c 2 3
x  d  2c x  d  2022 nghịch biến trên khoảng 4 1;2 .
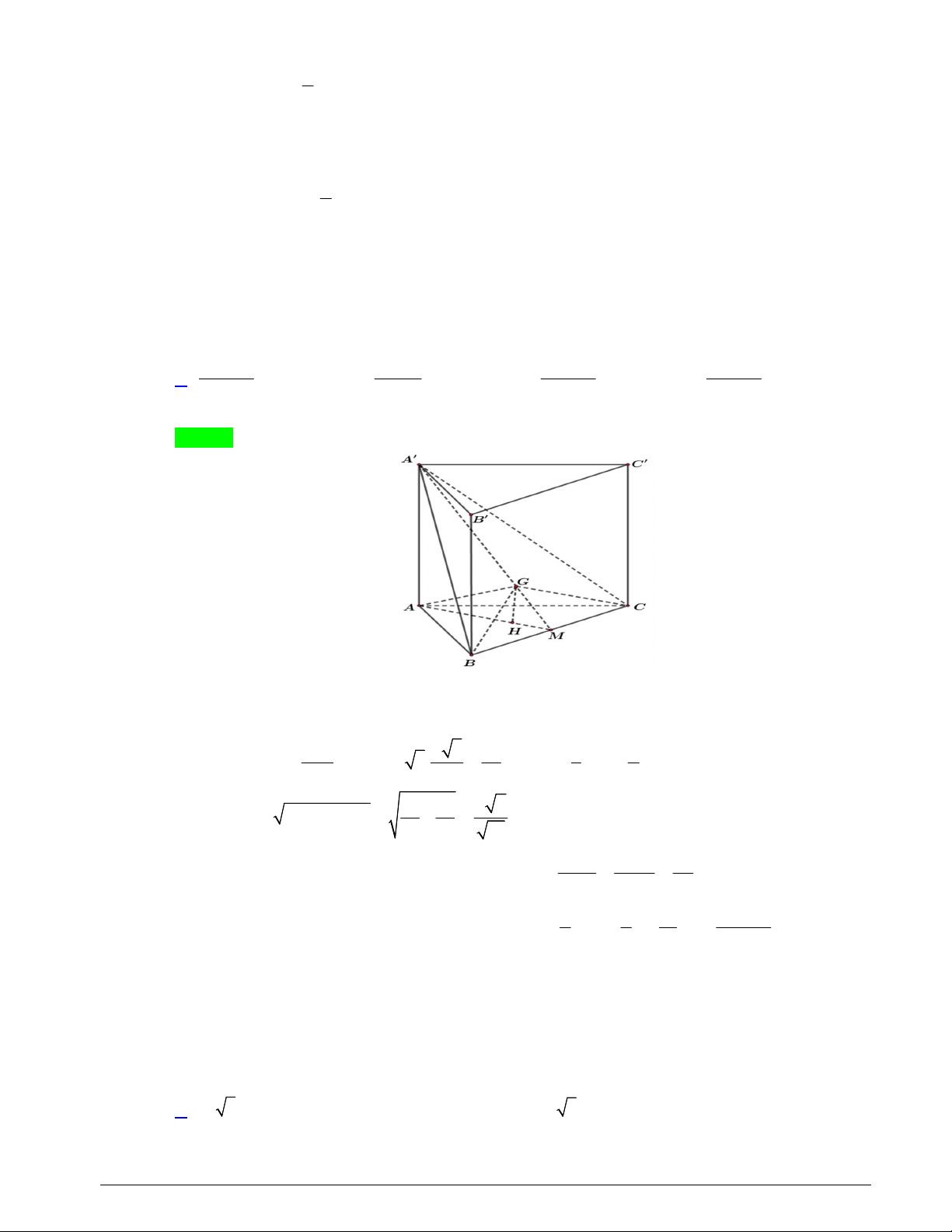
Câu 36: Cho hình lăng trụ tam giác đều ABC.AB C
  có AB  a , góc giữa hai mặt phẳng  ABC  và
 ABCbằng 60. Gọi G là trọng tâm tam giác ABC . Thể tích của khối cầu ngoại tiếp tứ diện GABC bằng bao nhiêu? 3 343 a 3 49 a 3 343 a 3 343 a A. . B. . C. . D. . 1296 108 432 5184 Lời giải Chọn A
Gọi M là trung điểm của BC và H là trọng tâm tam giác ABC . Khi đó góc giữa hai mặt phẳng
 ABC và  ABC là    AMA  60 . AA a 3 3a 1 a Ta có tan tan   AA  3.   GH  AA  . AM 2 2 3 2 2 2 a a a Khi đó 2 2 7 AG  GH  AH    4 3 12 2 2  AG 7a .2 7a
bán kính mặt cầu ngoại tiếp tứ diện GABC là R    2GH 12.2a 12 3 3   4 4 7 343 a
Thể tích khối cầu ngoại tiếp tứ diện GABC là 3 V  R      .    . 3 3 12  1296
Câu 37. Trong không gian với hệ tọa độ Oxyz , cho hai mặt cầu S  : x  42 2 2  y  z 16 , 1 S :x42 2 2
 y  z  36 và điểm A4;0;0 . Đường thẳng  2
di động nhưng luôn tiếp xúc với
S , đồng thời cắt S tại hai điểm , B C 2  1 
phân biệt. Tam giác ABC có diện tích lớn nhất bằng bao nhiêu? A. 24 5 . B. 48 . C. 28 5 . D. 72 . Lời giải Trang 20 Chọn A Ta có S có tâm I  4
 ;0;0 và bán kính R  4 . S I 4
 ;0;0 và bán kính R  6 . 2  1  1 có tâm   2
Lại có IA  8 nên điểm A nằm ngoài hai mặt cầu S , S . 1   2 
Gọi H là tiếp điểm của  và S , ta có IH  BC mà BC là dây cung của S2  1  nên H là trung điểm của BC . Ta có 2 2 2 2
BC  2BH  IB  IH  R  R  4 5 . 2 1 1
Tam giác ABC có diện tích S  d  , A BC.BC  2 5.d  , A BC  . 2
Do đó tam giác ABC có diện tích lớn nhất khi và chi khi d  , A BC lớn nhất. Xét hai trường hợp sau:
Trường hợp 1: Điểm A không thuộc mặt phẳng BCI  Ta có d  , A BC   AH  2 2 2 2 2 2
AI  IH  2AI.IH.cos AIH  AI  IH  8  4  4 5 .
Trường hợp 2: Điểm A thuộc mặt phẳng BCI  Ta có d  ,
A BC   AH  AI  IH 12. Suy ra max d  , A BC 12  max S  2 5.12  24 5  . ABC
Vậy tam giác ABC có diện tích lớn nhất bằng 24 5 .
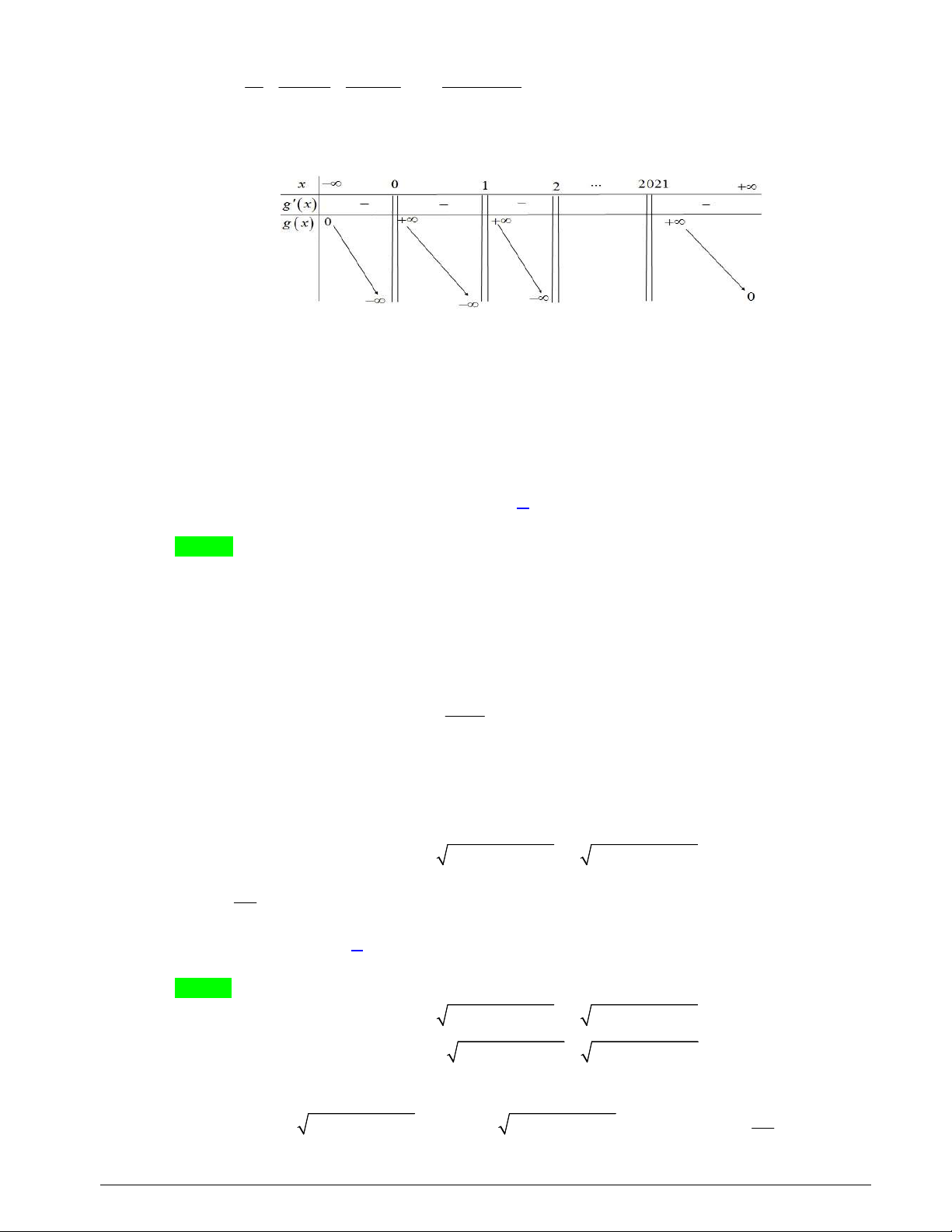
Câu 38. Cho hàm số f  x  x x  
1  x  2x 3... x  202 
1 Có tất cả bao nhiêu giá trị nguyên của tham số m thuộc đoạn  1  8;2 
0 để phương trình f  x  .
m f x có 2022 nghiệm phân biệt? A. 39. B. 18. C. 20 . D. 38. Lời giải Chọn D f  x Ta có f  x  . m f  x    . f  x  m  * f  x Đặt g  x   
, phương trình * trở thành g  x  m . f x
Ta có f  x   x  
1 x  2...x  202 
1  xx  2...x  202  1 ... x x   1 ... x  2020  g x 1 1 1 1    ... . x x 1 x  2 x  2021 Trang 21 gx 1 1 1 1     .. 
 0,x 0;1;2;. .;2021 . 2 2 2 2   x x 1 x 2 x202 1
Bảng biến thiên của hàm g  x .
Từ bảng biến thiên suy ra phương trình g  x  m có 2022 nghiệm khi và chỉ khi m  0 .
Do m nguyên thuộc đoạn  1
 8;20 nên có38 giá trị m thỏa mãn bài toán. n
Câu 39. Cho dãy số u thỏa mãn * u  1,u  2u , n    . Với mỗi *
n   ta đặt v   n  k  u . n   1 n  1 n 1  n k k 1 
Hỏi trong dãy v có bao nhiêu số hạng là số nguyên dương có bốn chữ số? n  A. 6 . B. 9. C. 4 . D. 12 . Lời giải Chọn C
Ta được u là một cấp số nhân công bội 1 q 2,u 1 u 2n     . n  1 n
v  nu  n 1 .u  n  2 .u  ...  3.u  2.u  u n 1   2   3 n2 n 1  n v n n n n     2 n3 n2 n 1 1 .2 2 .2 ... 3.2 2.2 2            (1) v n n n   2 n3 n2 n 1 2 .2 1 .2 ... 4.2 3.2 2.2           2n (2) n  v  n  n n n  n 1 2 2
2  2  ... 2     2.  2.2n   2 1 2 Hàm    2.2x f x
 x  2 đồng biến trên 1;  1000  f n  9999 Do vậy n 9;10;11;1  2 . Câu 40. Có bao nhiêu gía trị nguyên của tham số m để phương trình x   x   3 x  m   3 3 sin 2 cos 2 2 2 cos 1
2cos x  m  2  3 2cos x  m  2 có đúng một nghiệm  2  trên 0;   ?  3  A. 1. B. 4 . C. 3. D. 2 . Lời giải Chọn B
sin x 2  cos 2x  2 3 2cos x  m   3 3
1 2cos x  m  2  3 2cos x  m  2 3  2sin x  sin x  2 3 2cos x  m  2 3 3
2cos x  m  2  2 cos x  m  2 Hàm số f t  3
 2t  t đồng biến trên       f sin x  f  2 3 2cos x  m  2  3
 sin x  2cos x  m  2 sin x  0 x   0;      3  Trang 22 2 3 3 2
 sin x  2cos x  m  2  m 1  2cos x  cos x .  2  Xét hàm số 3 2
y  2cos x  cos x trên 0;   .  3    x  0 sin x  0     y '  2  sin . x cos . x 3cos x   1  cos x  0  x    2  1  cos x      2   3 x    ;     2 3  BBT
Từ BBT ta có, phương trình đã cho có đúng 1 nghiệm khi và chỉ khi m 1  0 m  1  1  
28  m 4;  3;  2;   1 .   m 1  3 4  m    27  27
Câu 41. Cho khối chóp tam giác đều SABC có cạnh đáy bằng 2 . Gọi M , N là trung điểm của SB, SC .
tính thể tích của khối chóp S.ABC biết CM  BN . 26 26 26 A. . B. . C. 26 . D. . 6 3 2 Lời giải Chọn B
Khối chóp SABC đều nên SA  SB  SC  x . 2 3 Gọi O là trọng tâm A
 BC  SO   ABC ; Do AB  2  OC  . 3
Xét tam giác cân SBC có SB  SC  x .
BN CM  G  G là trọng tâm tam giác SBC .
SG  BC  I , I là trung điểm BC . Ta có
     
       2 2 2 2 GA  GB  GC  SI  BN 
CM  SI  BN  CM  SI  BN  CM 2 3 3 3 2 2 2
 SI  BN  CM ( do CM  BN ) 2 2 2  SC  IC  2.BN Trang 23 2 2 2 SB  BC SC 2 x Có 2 BN   nên 2 2 x 1  x  4   x  10 2 4 2 26 3 2 2 SO  SC  OC  . Diện tích A  BC : 2 S  2  3 3 4 1 26 26
Thể tích khối chóp bằngV  . 3.  . 3 3 3
Câu 42. Cho tập hợp A  1;2;...;2 
0 . Chọn ngẫu nhiên bốn số khác nhau từ tập A . Xác suất để bốn số được
chọn ra không có hai số nào là hai số nguyên liên tiếp là 28 1 364 284 A. . B. . C. . D. . 57 5 969 285 Lời giải Chọn A
Gọi A là biến cố: ” bốn số được chọn ra không có hai số nào là hai số nguyên liên tiếp”. Ta có: n 4  C . 20
Gọi bốn số được chọn là : a,b,c, d a  b  c  d  . 1   a a 1 b  Có: b
 1 c 1  a  b 1 c  2  d  3  17. c 1 d  d  20  Do đó có: 4
C cách chọn bộ bốn số a,b,c, d a  b  c  d  . 17 4 n A C 28 Vậy: P  A   17    n  . 4 C 57 20
Câu 43: Cho hình chóp S.ABCD , đáy ABCD là hình vuông cạnh bằng 2 , SA  2 vuông góc với mặt
phẳng  ABCD ; M , N hai điểm thay đổi nằm trên hai cạnh AB , AD sao cho SMC  SNC  . 1 1 Tính tổng T  
khi thể tích khối chóp S.AMCN đạt giá trị lớn nhất. 2 2 AN AM 2  3 13 5 A. T  . B. T  2 . C. T  . D. T  . 4 9 4 Lời giải Chọn D
Tọa độ hóa với O  A, Ox  AB , Oy  AD , Oz  AS . Trang 24
Do SA  2 , ta có S 0;0;2 ; A0;0;0 ; B 2;0;0 ; D0;2;0  C 2;2;0 .
Đặt AM  x ; AN  y x, y 0;2  M  ; x 0;0; N 0; y;0 .  SM   ;x0; 2         n  SM ;SC  x x SMC 4;2  4;2       Do đó SN  0; y; 2       .  n  SN; SC  y y SNC 4 2 ;4;2  SC  2;2; 2           x
Ta có SMC  SNC     y   x    xy   xy   x  y 8 2 4 4 2 4 2 4 4 0 2  8  y  . x  2 8  2x Do y  2   2  x  1. x  2 S  S  S  S
 4  2  x  2  y  x  y . AMCN ABCD BMC DCN  2 1 2 2  8  2x  2  8  x  Do đó V  .S . A S  x  y  x   SAMCD AMCN       3 3 3  x  2  3  x  2  Xét hàm 2 2 2 x  4x  8 f  x 2  8  x   
; x 1;2  f  x  . 3  x  2  2 3 (x  2) x  2  2 3  f x  0 2
 x  4x 8  0   . x  2  2 3  l
Lập BBT ta được Max f  x  f   1  f 2  2 . 0;2 x 1  y  2 1 1 1 1 5 Vậy MaxV  2   T      . SAMCN x  2 2 2 2 2 AM AN x y 4  y 1
Câu 44: Cho hàm số trùng phương 4 2
y  ax bx c có đồ thị như hình vẽ. Hỏi đồ thị hàm số 4 3 2 x 2x 4x 8x y 
có tổng cộng bao nhiêu tiệm cận đứng?
 f x 2 2 f x3   A. 2 . B. 3. C. 4 . D. 5. Lời giải Chọn C 4 3 2 x 2x 4x 8x xx  22 x2 y  
 f x 2 2 f x3 2    f x 2  f x3 Trang 25 x  mm2   x  0 f x1 
Ta có:  f x 2  2 f x3 0        x  nn  2  f x 3  x2 x 2  
Dựa vào đồ thị ta thấy các nghiệm x  0; x  2
 là các nghiệm kép và đa thức 2  xx 2 x  2 f  x 2  2 f 
x3 có bậc là 8 nên y  a x x 22 x22 2 2 xmxn
Vậy hàm số có các tiệm cận đứng là x  0; x  2; x  ; m x  n . Câu 45. Cho parabol P  2
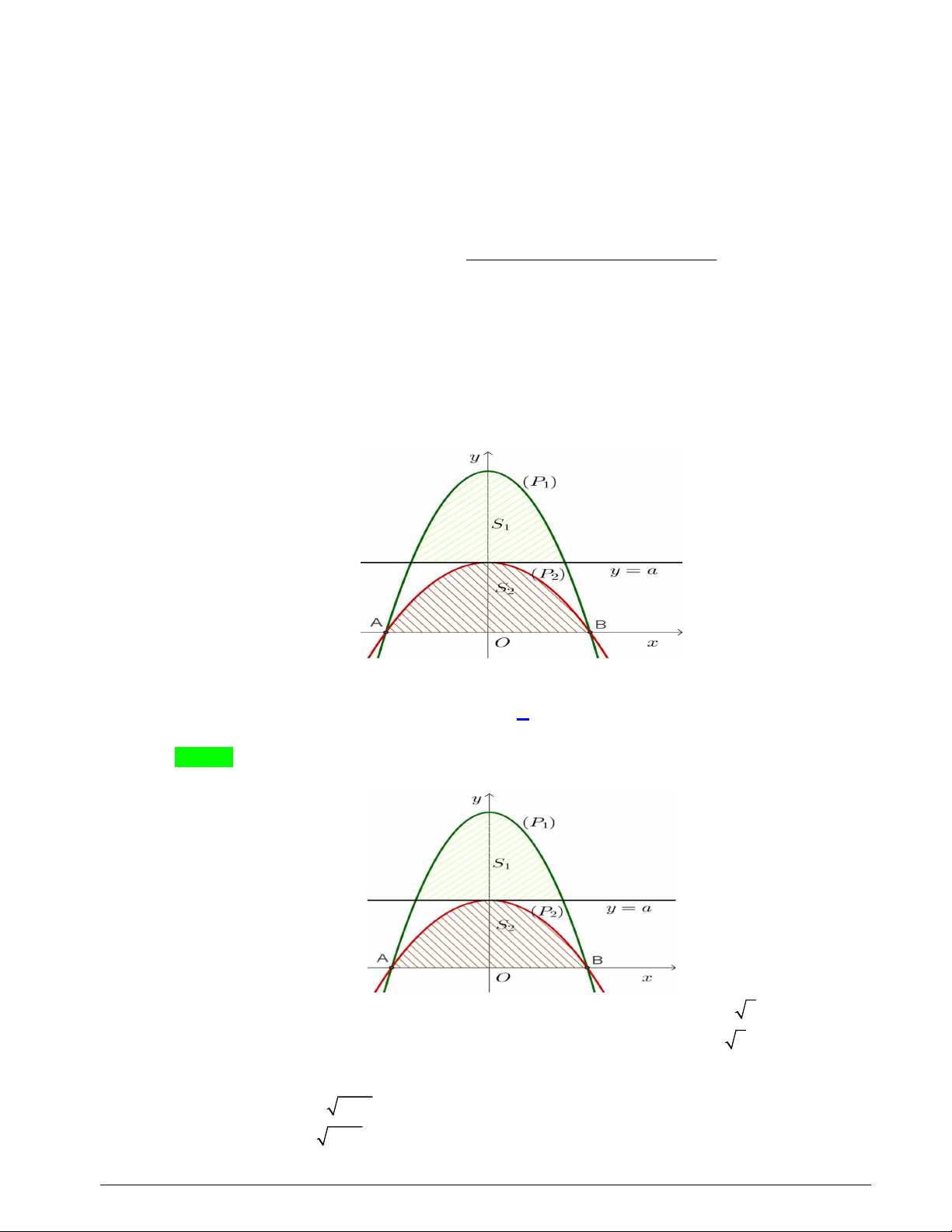
: y  x  6 cắt trục hoành tại hai điểm phân biệt ,
A B và đường thẳng d : y  a 1
0  a  6 . Xét parabol P đi qua hai điểm ,
A B và có đỉnh thuộc đường thẳng y  a . Gọi S 2  1
là diện tích hình phẳng giới hạn bởi P và d ; S là diện tích hình phẳng giới hạn bởi P và 2  1  2
trục hoành (tham khảo hình vẽ)
Nếu S  S thì giá trị của biểu thức 3 2 T  a 12a 108a bằng 1 2 A. 218 . B. 219 . C. 216 . D. 217 . Lời giải Chọn C x   6
Phương trình hoành độ giao điểm của P và trục hoành: 2 x  6  0   1  x  6
Phương trình hoành độ giao điểm của P và đường thẳng d : 1  x   6  a 2 x  6  a   x  6  a Trang 26 6a 3 6a  x  4 Diện tích S  2  2 x  6  a dx  2   6  a x  6  a 6  a 1        0  3  3 0 * P có dạng: 2 y  mx  a 2  Điểm  6;0  0  .6     a A P m a m 2  6 a a Vậy 2 y   x  a   2 x  6 6 6 a 6 4 6
Diện tích S  2.   2 x  6 dx  a 2  0 6 3 4 4 6 * Theo giả thiết, ta có:   6  6   a S S a a 1 2   3 3    a3 2 6  6a 3 2
 a 12a 108a  216  0 Vậy 3 2
T  a 12a 108a  216 .
Câu 46. Có bao nhiêu số nguyên m để phương trình x x 1 4 2  
1  2 2x  m có hai nghiệm phân biệt? A. 2 . B. 3 . C. 5 . D. 4 . Lời giải Chọn A x x    x    x  2 1 4 2 1 2 2 2 1  2 2x m  m
22x  m  4x  2.2x 1 2m  4x  4.2x 1     (1) 2 x x x x  2  m  4   2.2 1 2m  4  1 Đặt  2x t  0 , 2    2  m  t  4t 1 1   (2) 2  2  m  t 1
* Đồ thị của hai hàm số 2 y  t  4t 1 và 2
y  t 1 trên 0;
* Phương trình hoành độ giao điểm của hai đồ thị P  2
: y  t  4t 1 và P : y  t 1 trên 2  2 1 0; là: 2 2 2
t  4t 1  t 1  2t  4t  2  0  t  1 y  2 
 P tiếp xúc với P tại A1;2 2  1  * Phương trình x x 1 4 2  
1  2 2x  m có hai nghiệm phân biệt  2có hai nghiệm phân biệt Trang 27  1 1  1   2m  1   m      2 2  2  m  2   m  1  m 0;  1 .
Vậy có hai số nguyên m thỏa yêu cầu bài toán.
Câu 47. Có bao nhiêu giá trị nguyên của tham số m để hàm số y  2m  
1 x  3m  2sin x nghịch biến trên  ? A. 1. B. 2 . C. Vô số. D. 3 . Lời giải Chọn D y  2m  
1 x  3m  2  y  2m 1 3m  2cos x . Hàm số y  2m  
1 x  3m  2sin x nghịch biến trên   y  0, x
    2m 13m  2cos x  0, x     1 Đặt t  cos x  1   t   1 .
 1 có dạng 2m13m 2t  0, t   1  ;  1 2m 1  1 
3m 2. 1  0     m    5  1 3  m   . 2m 1  3m 2.1 0  5 m  3 Do m nguyên nên m 3  ; 2;  1 .
Vậy có 3 giá trị nguyên của m thỏa mãn yêu cầu bài toán.
Câu 48. Cho lăng trụ đứng ABC.AB C
  có đáy ABC là tam giác vuông tại B, AC  a 3 . Góc 
ACB  30 , góc giữa đường thẳng AB và mặt phẳng  ABC bằng 60 . Tính bán kính mặt cầu
ngoại tiếp tứ diện AABC a 21 a 21 3a a 21 A. . B. . C. . B. . 2 4 4 8 Lời giải Chọn B
Gọi M , H , I lần lượt là trung điểm của AA , AC, AC .
Góc giữa đường thẳng AB và mặt phẳng  ABC là đường thẳng AB và mặt phẳng  BAB  60 .   BB   3a AA tan BAB .AB  . 2 Trang 28 2 2  3a  a 21
Tam giác AAC là tam giác vuông tại 2 2 A  A C   AA  AC    a 3    2  2
Tam giác ABC vuông tại B và  ACB  30 nên ta có  AB a 3 sin ACB   AB  AC.sin 30  AC 2  BC 3a cos ACB   BC  AC.cos30  . AC 2 a 3
Tam giác ABC là tam giác vuông tại B  HB  HA  HC  . 2
Tam giác ABC là tam giác vuông tại I  HA  I  HB  I
 HC  .cg.c  IA  IB  IC   1 A C  a 21
Tam giác AA 'C là tam giác vuông tại A  IC  IA  IA   2 2 4 a 21 Từ  
1 ,2  I là tâm mặt cầu ngoại tiếp tứ diện AABC , bán kính R  IA  . 4 Câu 49. Cho hàm số   3 2
f x  ax  bx  cx  d ( a, ,
b c, d là hằng số, a  0 ) và       g  x a d a b 4 3  x  x     
a b  d  x  2021  a  b   2 
Biết đồ thị của hàm số f x như hình vẽ. Hỏi hàm số y  f  2  x  g  2 1
1 x  có bao nhiêu cực trị? A. 2 . B. 3 . C. 0 . D.1. Lời giải Chọn D Xét hàm số:   3 2
f x  ax  bx  cx  d Ta có: f x 2  3ax  2bx  c
Dựa vào đồ thị hàm số f  x , ta có: f 0  d  4 ; f  x  mx x  2,m  0 . m  3a   mx x  2 2 2 2
 3ax  2bx  c  mx  2mx  3ax  2bx  c  b  m c  0   m f  x m 3 2  x  mx  4 , f   8 2  0 
 4m  4  0  m  3. 3 3  f x 3 3 2  x  3x  4; g x 4 3  x  x  2021 2 Trang 29  f x 2  x  x gx 3 2 3 6 ;  6x  3x x    y 
 f 1x g 1x   x 6 1x 2 2 2 2 3  6  6x  2 1 x   Cho y  0  x  0
Kết luận: Hàm số y  f  2  x  g  2 1 1 x  có 1cực trị.
Câu 50. Có tất cả bao nhiêugiá trị nguyên của tham số để phương trình log log x  m  x  m có 3  3   1  nghiệm trên khoảng ;9   ?  3  A. 4 . B. 5 . C. 7 . D. 6 . Lời giải Chọn D  1 
Xét phương trình log log x  m  x  m trên khoảng ;9 3  3     3 
Điều kiện: log x  m  0  m  min log x  1  3  3   1  x ;9    3  Ta có: log log log 3x m x m x m x m        3  3  3 xm log3  log     3  log  3 x    3xm x x x m x x m 3 3
Xét hàm số    3t  ;    3t g x t g x ln 3 1  0, t 
 g log x  g x  m  log x  x  m  log x  x  m 3    3 3 Xét hàm số f  x 1 1  log x  ; x f  x  1; f  x  0  x  3     x ln 3 ln 3 Bảng biến thiên
Dựa vào bảng biến thiên, ta có: m 6  ; 5  ; 4  ; 3  ; 2  ;  1 .
Kết luận: Có tất cả 6 giá trị nguyên.
____________________ HẾT ____________________ Trang 30

Đề thi học sinh giỏi tỉnh Toán 12 năm 2021 – 2022 sở GD&ĐT Bắc Ninh

Tài liệu liên quan:

Đề thi thử tốt nghiệp THPT 2025 môn Toán trường Lê Thánh Tông – TP HCM

Bộ đề tham khảo tốt nghiệp THPT 2025 môn Toán sở GD&ĐT Bắc Giang

Đề thi thử HSG Toán 12 lần 2 năm 2024 – 2025 trường THPT Nguyễn Bính – Nam Định

Đề kiểm tra chất lượng Toán 12 tháng 10 năm 2024 trường THPT Quế Võ 1 – Bắc Ninh

Đề khảo sát lần 1 Toán 12 năm 2024 – 2025 trường THPT Văn Giang – Hưng Yên