Đề thi học sinh giỏi tỉnh Toán 12 THPT năm 2019 – 2020 sở GD&ĐT Gia Lai

NHÓM TOÁN VD – VDC ĐỀ THI HSG TOÁN
SỞ GD&ĐT GIA LAI
KỲ THI CHỌN HSG LỚP 12 ĐỀ CHÍNH THỨC NĂM HỌC 2019 - 2020 (Đề thi có 01 trang) MÔN: TOÁN –THPT N HÓM Thời gian: 180 phút TOÁ ĐỀ BÀI N
Câu 1: ( 2,0 điểm) Cho hàm số 3 2
y = x − 3mx + 3 có đồ thị (C ) . Tìm tất cả các giá trị thực của V D
tham số m để đường thẳng d : y = x cắt đồ thị (C) tại ba điểm phân biệt có hoành độ – V
lập thành cấp số cộng. DC
Câu 2: (4.0 điểm)
a) Giải phương trình sau trên tập số thực ( 2 2 x + ) 1
x −1 + 8 = (5 + 4 x −1) x 2  + 2 2 − x y x 2020 2019 = 1  2 ( )
b) Giải hệ phương trình trên tập số thực y + 2020   2
y + 2x 3x −1 = 9 y − 3  (2)
Câu 3: (2,0 điểm) 2 Tìm hệ số của  1  10 3n
x trong khai triển f ( x) 2 = x + x +1 
 ( x + 2) với n là số tự nhiên  4  thỏa mãn 3 n−2 A + C =14n n n Câu 4: A C
(2,0 điểm) Cho tam giác ABC có sin A + sin C = 2sin B và 2 3 tan + tan = . Chứng 2 2 3 minh
rằng tam giác ABC đều. u  = 2 1 
Câu 5: (2,0 điểm) Cho dãy số (un) xác định bởi  4u − 3 n u = , n ∀ ≥1 n 1 +  3u − 2  n 1 1 1 + + ... + − − − Tính u 1 u 2 u 1 1 1 A = lim n là một CSN. 2 n
Câu 6: (2,0 điểm) Trong mặt phẳng với hệ tọa độ Oxy , cho hình chữ nhật ABCD . Gọi H là hình
chiếu vuông góc của B lên AC , M và N lần lượt là trung điểm của BH và AH . Trên
cạnh CD lấy điểm K sao cho tứ giác MNCK là hình bình hành. Biết  9 2  M ;   , K (9;2) ,
điểm B thuộc đường thẳng d : 2x − y + 2 = 0 và điểm C thuộc  1 5 5 
d : x − y − 5 = 0 và hoành
độ đỉnh C lớn hơn 4 . Tìm tọa độ các đỉnh của hình 2 chữ nhật ABCD .
Câu 7: (2,0 điểm). Cho tứ diện ABCD có thể tích V . Gọi I là điểm thuộc miền trong của tứ diện
ABCD , các đường thẳng AI , BI , CI , DI lần lượt cắt các mặt phẳng
https://www.facebook.com/groups/toanvd.vdc Trang 1
NHÓM TOÁN VD – VDC ĐỀ THI HSG TOÁN
(BCD) , ( ACD), (ABD), ( ABC) tại các điểm M , N , P , Q thỏa mãn AI MI CI DI = = = . Biết a V
= V , với a,b ∗
∈  và a tối giản. Tính S = a + b . IBCD N MI NI PI QI b b HÓM
Câu 8: (4,0 điểm) Cho hai số thực dương a , b thỏa mãn ab − = ( 4 4 8 2
3 a + b ) . Tìm giá trị lớn TOÁ nhất của biểu thức 1 1 ab P = + + . 2 2 2 2 1+ a 1+ b 1+ 3a b N V D
-----------HẾT----------- – VDC
https://www.facebook.com/groups/toanvd.vdc Trang 2
NHÓM TOÁN VD – VDC ĐỀ THI HSG TOÁN
SỞ GD&ĐT GIA LAI
KỲ THI CHỌN HSG LỚP 12 ĐỀ CHÍNH THỨC NĂM HỌC 2019 - 2020 (Đề thi có 01 trang) MÔN: TOÁN –THPT N HÓM Thời gian: 180 phút TOÁ HƯỚNG DẪN GIẢI N
Câu 1: ( 2,0 điểm) Cho hàm số 3 2
y = x − 3mx + 3 có đồ thị (C) . Tìm tất cả các giá trị thực của V D
tham số để đường thẳng
cắt đồ thị (C) tại ba điểm phân biệt có hoành độ m d : y = x – V
lập thành cấp số cộng. DC Lời giải
Ta có phương trình hoành độ 3 2 3 2
x − 3mx + 3 = x ⇔ x − 3mx − x + 3 = 0 , (1)
Do phương trình (1) có ba nghiệm phân biệt x , x , x theo thứ tự lập thành cấp số 1 2 3 cộng suy ra
2x = x + x ,(2). 2 1 3
x + x + x = 3m 1 2 3 
Mặt khác theo định lí Vi-ét cho phương trình bậc ba ta có x x + x x + x x = 1 − . 1 2 2 3 3 1 x x x = 3 −  1 2 3
Thay (2) vào phương trình đầu tiên ta được x = m , mà x là nghiệm của phương 2 2  = trình (1) ta được m 1 3 2
− m − m + 3 = 0 ⇔  ⇔ m = 1. 2
2m + 2m + 3 = 0 x = 1 − 1 Thử lại với 
m = 1 ta được phương trình hoành độ 3 2
x − 3x − x + 3 = 0 ⇔ x = 1 dễ thấy 2  x = 3  3
ba nghiệm này lập thành cấp số cộng với công sai d = 2 .
Câu 2: (4.0 điểm)
a) Giải phương trình sau trên tập số thực ( 2 2 x + ) 1
x −1 + 8 = (5 + 4 x −1) x Lời giải Cách 1 Điều kiện x ≥ 1 PT ⇔ ( 2
2x + 2) x −1 + 8 = 5x + 4x x −1 ⇔ (x − )2 2 1
x −1 − 5( x − ) 1 + 3 = 0
Đặt t = x −1 (t ≥ 0), phương trình trở thành 5 2 2
2t − 5t + 3 = 0 ⇔ (t − ) ( 3 2 1
2t + 4t + 6t + 3) = 0 ⇔ t = 1 vì 3 2
2t + 4t + 6t + 3 > 0, t ∀ ≥ 0
⇒ x −1 =1⇔ x = 2 . Cách 2 Điều kiện x ≥ 1
https://www.facebook.com/groups/toanvd.vdc Trang 1
NHÓM TOÁN VD – VDC ĐỀ THI HSG TOÁN PT ⇔ ( 2
2x + 2) x −1 + 8 = 5x + 4x x −1 ⇔ ( 2
2x − 4x + 2) x −1 − 5x + 8 = 0 N 2 3 2 HÓM
⇔ (x − 2x + )
1 (2 x −1 − x) + x − 2x + x − 5x + 8 = 0 ⇔ ( 2 x − x + )( x − − x) 3 2 2 1 2 1
+ x − 2x − 4x + 8 = 0 TOÁ ( − − ⇔ − x + ) 2 4x 4 x x 2 1 . + (x − 2)2 2 (x + 2) = 0 N 2 x −1 + x V D
(x −2x + )1(x −2)2 2 2 – ⇔ −
+ ( x − 2) ( x + 2) = 0 V 2 x −1 + x DC  −x + x −  ⇔ ( x − ) 2 2 2 1 2  + x + 2 = 0  2 x −1 + x  2 2 ⇔ ( − ) − + − + + − + + 2 x
2x 1 2 ( x 2) x 1 x 2x x 2 . = 0 2 x −1 + x ( + − + −
⇔ x − )2 2(x 2) x 1 4x 1 2 . = 0 2 x −1 + x 2 ( x + 2) − + − ⇔ x 1 4x 1 x − 2 = 0 vì > 0, ∀ x > 1 2 x −1 + x ⇔ x = 2 (TM)
Vậy phương trình có nghiệm x = 2 . 2  + 2 2 − x y x 2020 2019 = 1  2 ( )
b) Giải hệ phương trình trên tập số thực y + 2020   2
y + 2x 3x −1 = 9 y − 3  (2) Lời giải  1 x ≥  − ≥  Điều kiện 3x 1 0  3  ⇔  . 9  y − 3 ≥ 0 1 y ≥  3 2 y 2 Từ (1) ta có + 2 2019 x 2020 =
⇔ 2019x x + 2020 = 2019y y + 2020 . (*) 2 ( 2 ) 2 2 2 ( ) 2019x y + 2020
Nếu x > y ⇒ VT(*) > VP(*). Ngược lại nếu x < y ⇒ VT(*) < VP(*).
Mặt khác với x = y ⇒ VT(*) = VP(*). Vậy x = .y
Thay x = y vào phương trình (2), ta có
x + 2x 3x −1 = 9x − 3 ⇔ (x + 3x −1)2 = (2 3x −1)2 2 (   ⇔ x − x − )(x + x − ) 1 3 1 3 3
1 = 0 ⇔ x − 3x −1 = 0 x ≥ .    3  3 ± 5 2
⇔ x − 3x +1 = 0 ⇔ x = . 2
https://www.facebook.com/groups/toanvd.vdc Trang 2
NHÓM TOÁN VD – VDC ĐỀ THI HSG TOÁN  + +   − − 
Kết luận: Hệ phương trình có hai nghiệm 3 5 3 5 3 5 3 5  ; ; ; .     2 2 2 2     N HÓM
Câu 3: (2,0 điểm) 2 Tìm hệ số của  1  10 3n
x trong khai triển f ( x) 2 = x + x +1 
 ( x + 2) với là số tự nhiên n TOÁ  4  n− N thỏa mãn 3 2 A + C =14n n n V D Lời giải – − n n n ! ! V Ta có 3 2 A + C =14n ⇔ + =14n, với ≥ ∈ D  . n n ( n 3, n
n − 3)! (n − 2)!.2! C −
⇔ n(n − )(n − ) n(n ) 1 1 2 + =14n 2 ⇔ 2(n − )
1 (n − 2) + n −1 = 28, vì n ≥ 3 . n = 5 (tm) 2 
⇔ 2n − 5n − 25 = 0 ⇔ 5  . n = − (l)  2 2 Với 2  1  1
n = 5 suy ra f ( x) = x + x +1   ( x + 2)15 =
(x +4x+4) (x+2)15 2 2  4  16 ⇔ f (x) 1 = (x + 2) 19 19 1 k 19 k = ∑C x − 2k . 19 16 16 k 1 = ⇒ số hạng tổng quát 1 k k 19 T = C 2 k x − . k 1 + 19 16 Cho 1
19 − k = 10 ⇒ k = 9 ta được số hạng chứa 10 x là 9 9 10 9 5 10 T = C 2 x = C 2 x . 10 19 19 16
Vậy hệ số của số hạng chứa 10 x là 9 5 C 2 = 2956096 . 19 Câu 4: A C
(2,0 điểm) Cho tam giác ABC có sin A + sin C = 2sin B và 2 3 tan + tan = . Chứng 2 2 3 minh
rằng tam giác ABC đều. Lời giải Vì A C B A C B A B C π + + + + = ⇒ sin = cos ;cos = sin . 2 2 2 2 Ta có A + C A − C B B A − C B
sin A + sin C = 2 sin B ⇔ 2 sin cos = 4sin cos ⇔ cos = 2sin ( ) 1 2 2 2 2 2 2 . A + C sin Và A C 2 3 2 3 2 B A C tan + tan = ⇔ = ⇔ 3cos = 2 3 cos cos 2 2 3 A C 3 2 2 2 cos cos 2 2 B A + C A − C B B A − C ⇔ 3 cos = cos + cos ⇔ 3 cos = sin + cos (2) . 2 2 2 2 2 2
https://www.facebook.com/groups/toanvd.vdc Trang 3
NHÓM TOÁN VD – VDC ĐỀ THI HSG TOÁN π Từ ( ) B B B 1 và (2) ta có 1 3 cos = 3sin ⇔ tan = ⇒ B = . 2 2 2 3 3 π A − C N
Thay B = vào ( )1 suy ra cos
= 1 ⇔ A − C = k4π ⇒ A = C . HÓM 3 2 Vậy tam giác π
ABC có A = C, B =
suy ra tam giác ABC đều. TOÁ 3 N u  = 2 1 V  D
Câu 5: (2,0 điểm) Cho dãy số (un) xác định bởi  4u − 3 n u = , n ∀ ≥1 – n 1 +  − V 3u 2  n DC 1 1 1 + + ... + u −1 u − 2 u −1 Tính 1 1 A = lim n là một CSN. 2 n Lời giải − 4u − 3 u 1 n u −1 n = −1 = n 1 + 3u − 2 3(u − + n )1 1 n
Đặt v = u −1 v 1 1 1 n ⇒ = ⇒ = + . Vậy ( 1 ) là 1 CSC = = n n v 3 d 3, 1 n 1 + 3v + 1 v v v v n n 1 + n n 1 1 =1+ 3(n − ) 1 = 3n − 2 vn Nên 1 = 3n − 2 u −1 n Ta có 1 1 1 + + ... +
= 3.1− 2 + 3.2 − 2 + ... + 3n − 2 u −1 u − 2 u −1 1 1 n
= 3.(1+ 2 + 3 + ...+ n) − 2n n( + n) 2 1 3n − n = 3. − 2n = 2 2 1 1 1 + + ... + 2 u −1 u − 2 u −1 3n − n 3 Do đó 1 1 A = lim n = lim = 2 2 n 2n 2
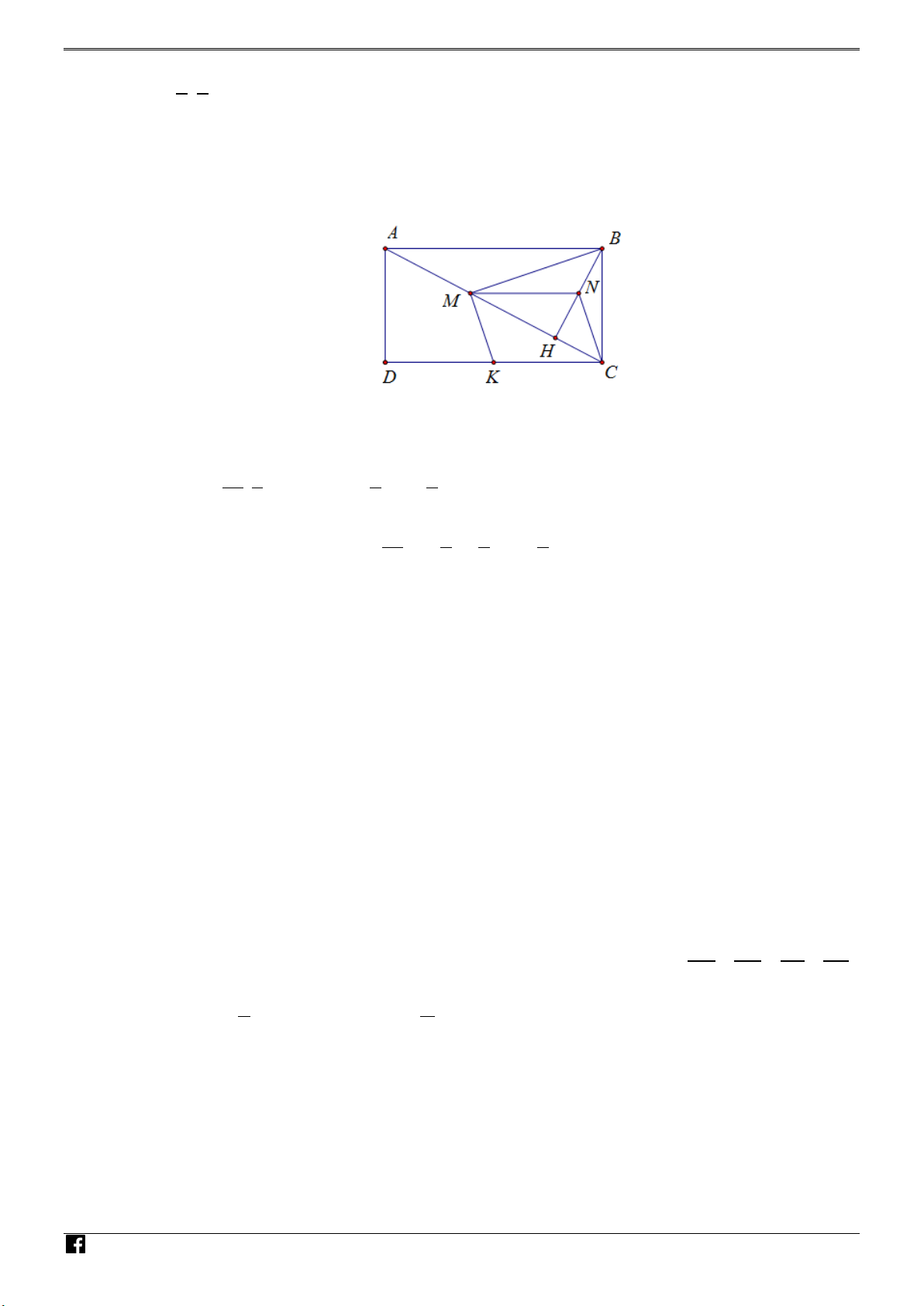
Câu 6: (2,0 điểm) Trong mặt phẳng với hệ tọa độ Oxy , cho hình chữ nhật ABCD . Gọi H là hình
chiếu vuông góc của B lên AC , M và N lần lượt là trung điểm của BH và AH . Trên
cạnh CD lấy điểm K sao cho tứ giác MNCK là hình bình hành. Biết
https://www.facebook.com/groups/toanvd.vdc Trang 4
NHÓM TOÁN VD – VDC ĐỀ THI HSG TOÁN  9 2  M ;   , K (9;2),
điểm B thuộc đường thẳng d : 2x − y + 2 = 0 và điểm C  5 5  1 N
thuộc d : x − y − 5 = 0 và hoành độ đỉnh 2
C lớn hơn 4 . Tìm tọa độ các đỉnh của HÓM
hình chữ nhật ABCD . Lời giải TOÁ N V D – VDC
B (b; 2b + 2) ; C (c;c − 5) , (c > 4) . Ta có MN // CK nên MN ⊥ BC , mà BH ⊥ AC nên N
là trực tâm tam giác MBC . Vậy CN ⊥ BM ⇒ MK ⊥ BM .       +) 36 8 MK = ;  ; 9 8
MB = b − ; 2b +   .  5 5   5 5 
  36  9  8  8 
MK ⊥ BM ⇒ MK.BM = 0 ⇔ b − + 2b + = 0    
⇔ b = 1 ⇒ B(1;4) . 5  5  5  5   
+) KC = (c − 9;c − 7); BC = (c −1;c −9).  
CK ⊥ CB ⇒ KC.BC = 0 ⇔ (c − 9)(c − )
1 + (c − 7)(c − 9) = 0 ⇔ (c − 9)(2c − 8) = 0 c = 9(NhËn) ⇔  . Vậy C (9;4) . c = 4  (Lo¹i)
+) K là trung điểm CD nên ta được D(9;0) .  − =  = +) Giả sử   x 1 0 x 1
A( x; y) , ta có BA = CD ⇔  ⇔  . Vậy A(1;0) . y − 4 = 4 − y = 0
Kết luận: A(1;0) , B(1;4) , C (9;4) , D(9;0) .
Câu 7: (2 điểm). Cho tứ diện ABCD có thể tích V . Gọi I là điểm thuộc miền trong của tứ diện
ABCD , các đường thẳng AI , BI , CI , DI lần lượt cắt các mặt phẳng ( BCD) ,
(ACD), (ABD), (ABC) tại các điểm M , N , P , Q thỏa mãn AI MI CI DI = = = . MI NI PI QI Biết a V
= V , với a,b ∗
∈ và a tối giản. Tính S = a +b . IBCD b b Lời giải
https://www.facebook.com/groups/toanvd.vdc Trang 5
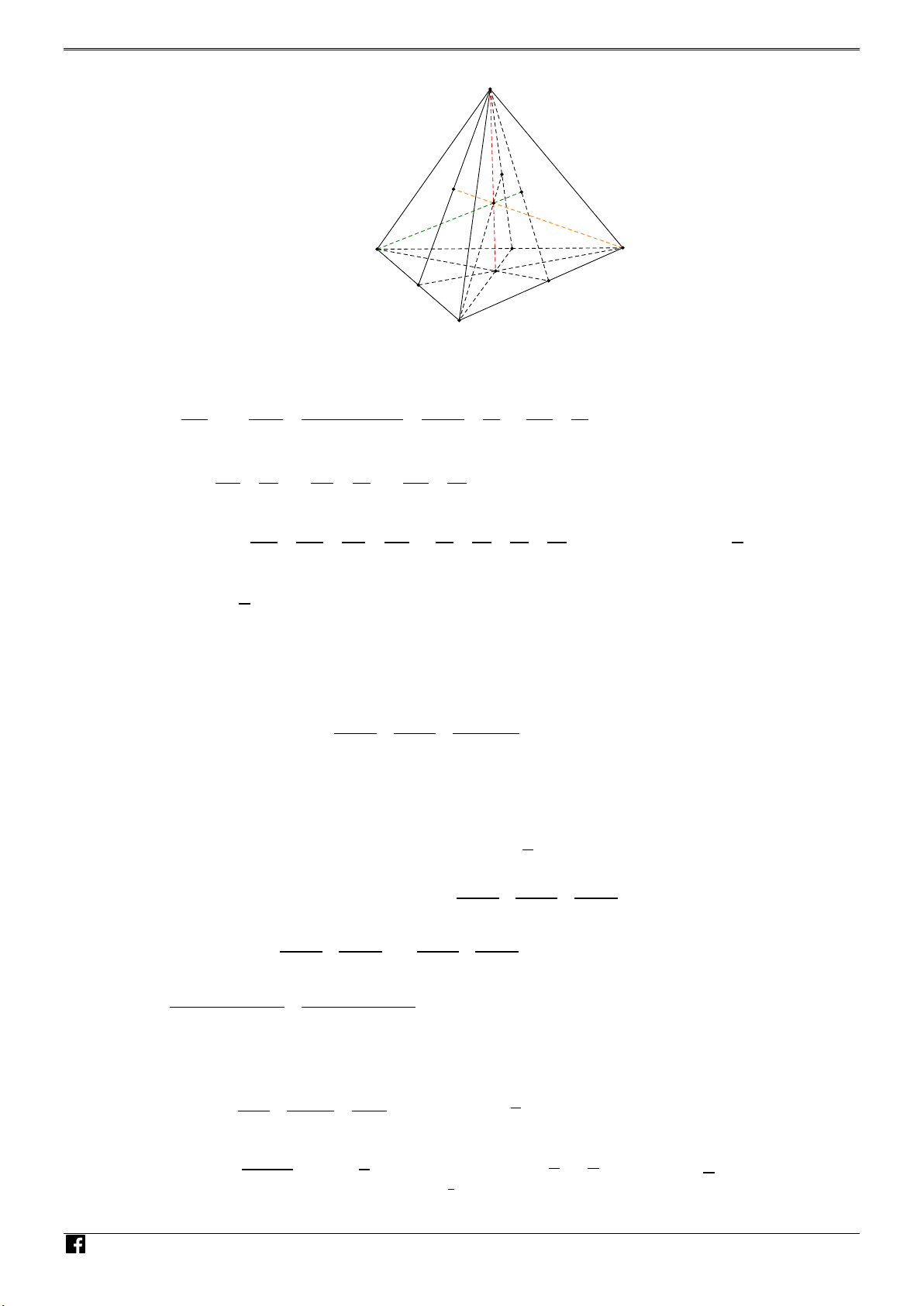
NHÓM TOÁN VD – VDC ĐỀ THI HSG TOÁN A N HÓM P Q N TOÁ I N B D V D M H – VD C C - Đặt V =V , V =V , V =V , V
=V , ta có: V =V +V +V +V IBCD 1 IACD 2 IABD 3 IABC 4 1 2 3 4 AI AM d ( , A ( BCD)) - Ta có: V V AI V +1 = = = = ⇒ = − . MI IM d ( ABCD I ( BCD)) 1 , V V MI V IBCD 1 1 - Tương tự: BI V CI V DI V = −1; = −1; = −1. NI V PI V QI V 2 3 4
- Theo giả thiết: AI MI CI DI V V V V 1 = = = ⇒ = = =
⇒ V = V = V = V = V . 1 2 3 4 MI NI PI QI V V V V 4 1 2 3 4  = Hay 1 a 1 V = V ⇒  . IBCD 4 b  = 4
Vậy S = a + b = 5.
Câu 8: (4,0 điểm) Cho hai số thực dương a, b thỏa mãn ab − = ( 4 4 8 2
3 a + b ) . Tìm giá trị lớn nhất của biểu thức 1 1 ab P = + + . 2 2 2 2 1+ a 1+ b 1+ 3a b Lời giải
Từ giả thiết suy ra ab − = ( 4 4 a + b ) 2 8 2 3 ≥ 6(ab) (1). AM −GM Đặt 1
ab = t, t > 0 . Từ (1) suy ra 2 3
− t + 4t −1 0  ⇔ t 1  (2). 3 Với 1 1 2
a, b > 0, ab 1  ta chứng minh được +  (3). 2 2 1+ a 1+ b 1+ ab     Thật vậy 1 1 1 1 (3) ⇔ − + − 0     2 2 1+ a
1+ ab  1+ b 1+ ab 
a(b − a)
b(a − b) ⇔ ( + 0  2 1+ a )(1+ ab) ( 2 1+ b )(1+ ab) 2
⇔ (a −b) (ab −1) 0  (đúng).   Khi đó, 2 t t + 2 P +  = f (t) với 1 t ∈ ;1   . 2 1+ t 1+ 3t t +1 3     1  7 Do ′ 1 1 f (t) = −
< 0,t ∈ ;1 nên Max f (t) = f =   . Suy ra, 7 P . 2   (1+ t) 3  1    ,1 3 4   4 3 
https://www.facebook.com/groups/toanvd.vdc Trang 6
NHÓM TOÁN VD – VDC ĐỀ THI HSG TOÁN
Vậy giá trị lớn nhất của P bằng 7 đạt được khi 3 a = b = . 4 3 N HÓM TOÁ N V D – VDC
https://www.facebook.com/groups/toanvd.vdc Trang 7
Document Outline

• 545
• ĐỀ BÀI
• HDG HSG TOAN 12 GIA LAI