



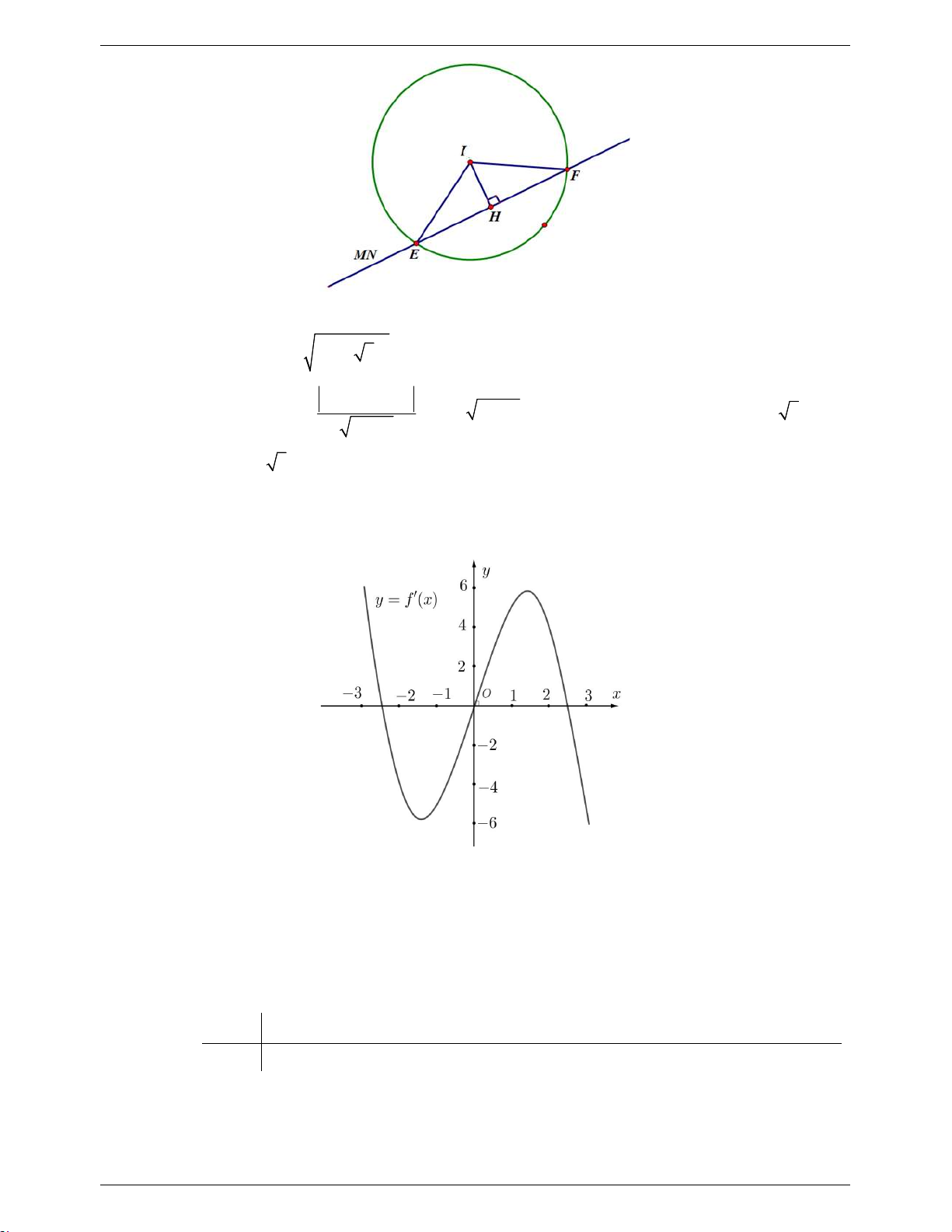

Preview text:
NHÓM TOÁN VDC&HSG THPT
ĐỀ THI HỌC SINH GIỎI 2020 - 2021
ĐỀ THI HỌC SINH GIỎI - SỞ KHÁNH HÒA NĂM HỌC 2020 – 2021 Môn: Toán 12
HỌC HỎI - CHIA SẺ KIẾN THỨC
Thời gian: 180 phút (Không kể thời gian phát đề)
LINK NHÓM: https://www.facebook.com/groups/1916660125164699 Câu 1. (6,0 điểm)
a) Giải các phương trình
1) 3 2 x x 1 1.
2) 3 sin 4x cos 4x 4sin 2x 1.
b) Một bài thi Đánh giá năng lực theo hình thức trắc nghiệm có 100 câu hỏi. Mỗi câu hỏi có 4
phương án trả lời, trong đó có 1 phương án đúng và 3 phương án sai. Với mỗi câu hỏi, người
làm bài thi chỉ được chọn một phương án, nếu chọn đúng được 1, 0 điểm, chọn sai bị trừ 0, 25
điểm. Một học sinh làm bài đủ 100 câu bằng cách: với mỗi câu hỏi, học sinh đó chọn ngẫu
nhiên một phương án. Tính xác suất để học sinh đó được 60 điểm.
Câu 2. (4,0 điểm) Cho hàm số 3 2 2
y 2x 3mx m có đồ thị C và đường thẳng 2 y 2x m m (m là tham số)
a) Tìm tất cả các giá trị của m để C cắt tại 3 điểm phân biệt , A , B C sao cho B là m trung điểm của AC .
b) Tìm tất cả các giá trị của m để đường thẳng đi qua 2 điểm cực trị của C cắt đường tròn m
C có phương trình x 2 y 2 1
1 4 tại 2 điểm E, F : EF 2 3 .
Câu 3. (4,0 điểm) Cho hàm số y f x xác định và liên tục trên . Hàm số y f x có đồ thị như hình dưới .
a. Tìm số điểm cực tiểu của hàm số y f x
b. xét chiều biến thiên của hàm số g x f x 2 2
1 4x 4x trên các khoảng ; 2 và 1; Câu 4. (4,0 điểm)
a) Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh 2a . Hình chiếu của S lên
ABC là điểm H thuộc cạnh AC sao cho HA 2HC , góc tạo bởi SB và mặt phẳng ABC bằng 0
30 . Tính thể tích khối chóp S.ABC và khoảng cách từ A đến SBC theo a .
b) Cho khối lăng trụ tam giác AB . C A B C
có thể tích là V . Gọi I và K lần lượt là trung điểm của AC và A B
; G là trọng tâm của tam giác BCC . Tính thể tích của khối tứ diện BIKG theo V
TÀI LIỆU ÔN THI HỌC SINH GIỎI Trang 1
NHÓM TOÁN VDC&HSG THPT
ĐỀ THI HỌC SINH GIỎI 2020 - 2021 Câu 5.
(2,0 điểm) Cho các số x, y 0 thỏa mãn
xy xy x y 2 2 1 2 x y 2xy 1 . Tính giá xy
trị lớn nhất của biểu thức P . x y
------------------------HẾT------------------------ Trang 2
TÀI LIỆU ÔN THU THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT
ĐỀ THI HỌC SINH GIỎI 2020 - 2021 HƯỚNG DẪN GIẢI Câu 1. (6,0 điểm)
a) Giải các phương trình
1) 3 2 x x 1 1.
2) 3 sin 4x cos 4x 4sin 2x 1.
b) Một bài thi Đánh giá năng lực theo hình thức trắc nghiệm có 100 câu hỏi. Mỗi câu hỏi có 4
phương án trả lời, trong đó có 1 phương án đúng và 3 phương án sai. Với mỗi câu hỏi, người
làm bài thi chỉ được chọn một phương án, nếu chọn đúng được 1, 0 điểm, chọn sai bị trừ 0, 25
điểm. Một học sinh làm bài đủ 100 câu bằng cách: với mỗi câu hỏi, học sinh đó chọn ngẫu
nhiên một phương án. Tính xác suất để học sinh đó được 60 điểm. Lời giải
GVSB: Nguyễn Minh Thành ; GVPB: Vân Vũ
a) Giải các phương trình
1) 3 2 x x 1 1. Điều kiện: x 1.
Đặt t x 1 t 0, khi đó 2 x t 1.
Phương trình trở thành 2t 3 2 3 2
1 t 1 1 t t 1 0 . 3
1 t1 t t 1 0 1 t 1 t 1 t2 3 3 3 0 . 3 t 1 1 t 0 t 1 t 0
thỏa mãn điều kiện t 0 . 1 t 1t 1 t 1t2 2 3 3 t 3
Với t 1 x 1 1 x 2 (thỏa mãn).
Với t 0 x 1 0 x 1 (thỏa mãn).
Với t 3 x 1 3 x 10 (thỏa mãn).
Vậy tập nghiệm của phương trình đã cho là S 1;2;1 0 .
2) 3 sin 4x cos 4x 4sin 2x 1.
Phương trình đã cho tương đương 2
2 3 sin 2x cos 2x 1 2sin 2x 4sin 2x 1 2sin 2x 3 cos 2x sin 2x 2 0 . sin 2 0 k x x , k 2 . cos 2x 1 6 x k ,k 12 k
Vậy tập nghiệm của phương trình đã cho là S ; k ,k, k. 2 12 b)
Gọi x là số câu trả lời đúng, y là số câu trả lời sai (với 0 x, y 100 và x, y ).
Vì có tất cả 100 câu hỏi, nếu chọn đúng được 1, 0 điểm, chọn sai bị trừ 0, 25 điểm và học x y 100 x 68
sinh đó đạt 60 điểm nên ta có hệ phương trình . x 0,25y 60 y 32
Mỗi câu hỏi có 4 phương án trả lời, trong đó có 1 phương án đúng và 3 phương án sai nên 1 3
xác suất để chọn được phương án đúng là và xác suất để chọn được phương án sai là . 4 4
TÀI LIỆU ÔN THI HỌC SINH GIỎI Trang 3
NHÓM TOÁN VDC&HSG THPT
ĐỀ THI HỌC SINH GIỎI 2020 - 2021
Vậy để học sinh đó đạt được 60 điểm chọn 32 câu sai và 68 câu đúng nên có xác suất là 68 32 1 3 32 C . 100 4 4 Câu 2. (4,0 điểm) Cho hàm số 3 2 2
y 2x 3mx m có đồ thị C và đường thẳng 2 y 2x m (m là tham m số)
a) Tìm tất cả các giá trị của m để C cắt tại 3 điểm phân biệt , A B,C sao cho B là m trung điểm của AC .
b) Tìm tất cả các giá trị của m để đường thẳng đi qua 2 điểm cực trị của C cắt đường tròn m
C có phương trình x 2 y 2 1
1 4 tại 2 điểm E, F : EF 2 3 . Lời giải
Tập xác định D .
a) Phương trình hoành độ giao điểm của C và là: 3 2 2 2 2x 3mx m 2x m m x 0 3 2
2x 3mx 2x 0 x 2
2x 3mx 2 0 * . 2 2x 3mx 2 0 1 Vì
1 có 2 nghiệm trái dấu nên * luôn có 3 nghiệm phân biệt m . 3m x x
Ta có: x 0 nên x , x là nghiệm của
1 nên theo định lý vi-et ta có: A C . B A C 2 x .x 1 A C x x 3m
Theo giả thiết B là trung điểm của AC nên A C x 0 m 0. 2 4 B
b) Tìm tất cả các giá trị của m để đường thẳng đi qua 2 điểm cực trị của C cắt đường tròn m
C có phương trình x 2 y 2 1
2 4 tại 2 điểm E, F : EF 2 3 . Lời giải x 0 Ta có 2
y 6x 6mx 6x x m ; y 0 . x m
Để hàm số có cực đại, cực tiểu thì m 0 .
Khi đó hai điểm cực trị của C là: M 2 0; m và N 3 2 ; m m m . m 2 x y m
Phương trình đường thẳng MN có dạng: 2 2 2 2
m x y m m x y m 0 . 3 m m
Đường tròn C có tâm I 1; 2 , bán kính R 2 . Trang 4
TÀI LIỆU ÔN THU THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT
ĐỀ THI HỌC SINH GIỎI 2020 - 2021
Gọi là H trung điểm của EF ta có tam giác IHE vuông tại H nên IH d I MN 2 2 , 2 3 1. 2 2 m .1 2 m Vậy d I, MN 4 4 4 4
1 m 1 2 m 1 4 m 3 m 3 . 4 m 1 Vậy 4
m 3 thoả mãn yêu cầu bài toán. Câu 3. (4,0 điểm)
Cho hàm số y f x xác định và liên tục trên . Hàm số y f x có đồ thị như hình dưới .
a) Tìm số điểm cực tiểu của hàm số y f x
b) Xét chiều biến thiên của hàm số g x f x 2 2
1 4x 4x trên các khoảng ; 2 và 1; Lời giải
a) Từ đồ thị ta có bảng xét dấu của f (x) như sau x x 0 x 1 2 f (x) + 0 - 0 + 0 -
Vậy f (x) có 3 điểm cực trị ( 2 điểm cực đại, 1 điểm cực tiểu)
b) Ta có g (x) 2f (2x 1) 8x 4 2 f (2x 1) 2(2x 1)
g (x) 0 f (2x 1) 2(2x 1)
TÀI LIỆU ÔN THI HỌC SINH GIỎI Trang 5
NHÓM TOÁN VDC&HSG THPT
ĐỀ THI HỌC SINH GIỎI 2020 - 2021
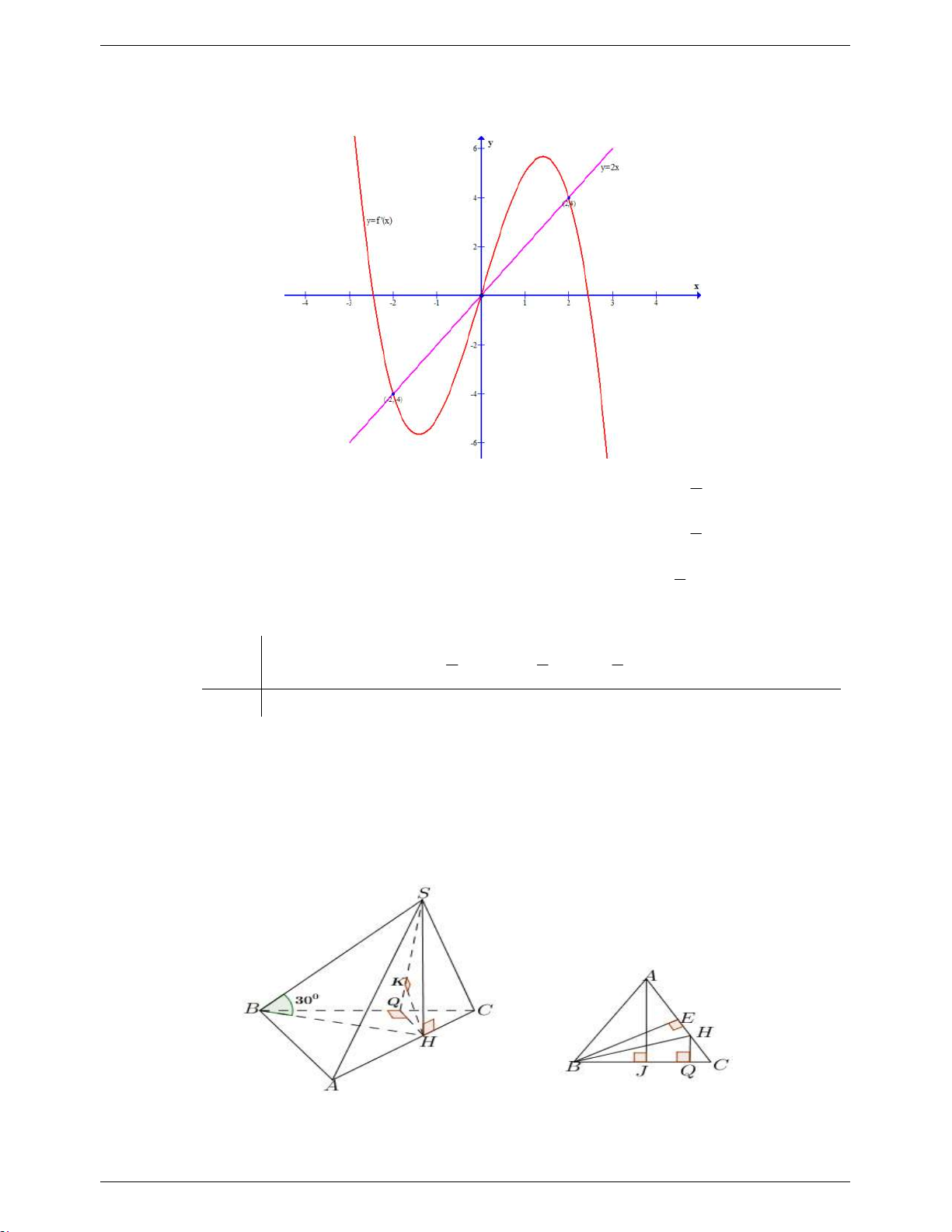
Đặt t 2x 1, phương trình trở thành f (t) 2t Ta có đồ thị sau : 3 x t 2 2 1
Từ đồ thị ta có f (t) 2t t 0 . Suy ra g (x) 0 x . t 2 2 1 x 2
Ta có bảng xét dấu của g (x) x 3 1 1 -2 1 2 2 2 g (x) + 0 - 0 + 0 -
Vậy hàm số g(x) đồng biến trên ( ; 2
) và nghịch biến trên (1; ) . Câu 4. (4,0 điểm)
a) Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh 2a . Hình chiếu của S lên
ABC là điểm H thuộc cạnh AC sao cho HA 2HC , góc tạo bởi SB và mặt phẳng ABC bằng 0
30 . Tính thể tích khối chóp S.ABC và khoảng cách từ A đến SBC theo a . Lời giải
Vì SH ABC SB ABC 0 , SBH 30 .
Gọi E là trung điểm AC . Khi đó ta có: Trang 6
TÀI LIỆU ÔN THU THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT
ĐỀ THI HỌC SINH GIỎI 2020 - 2021 2a 7 2 2 2 2
EC a BE BC EC a 3 BH BE EH . 3 SH 2a 21 Xét S BH ta có: 0 0 tan 30 SH tan30 .BH . BH 9 2 3 1 1 2a 21 4a 3 2a 7 Vậy thể tích V .SH.S . . . S.ABC 3 A BC 3 9 4 9
Gọi Q là hình chiếu của H lên cạnh BC . Khi đó ta có SH BC
BC SHQ BC SQ HQ BC .
Khi đó, nếu kẻ HK SQ HK SBC d H,SBC HK . Ta có, d ,
A SBC 3.d H, SBC 3HK . a 1 1 1 111 2a 777 Kẻ 1 3 AJ BC HQ AJ . Ta có: HK 3 3 2 2 2 2 HK HQ SH 28a 111 Suy ra d A SBC 6a 777 , 3HK . 111
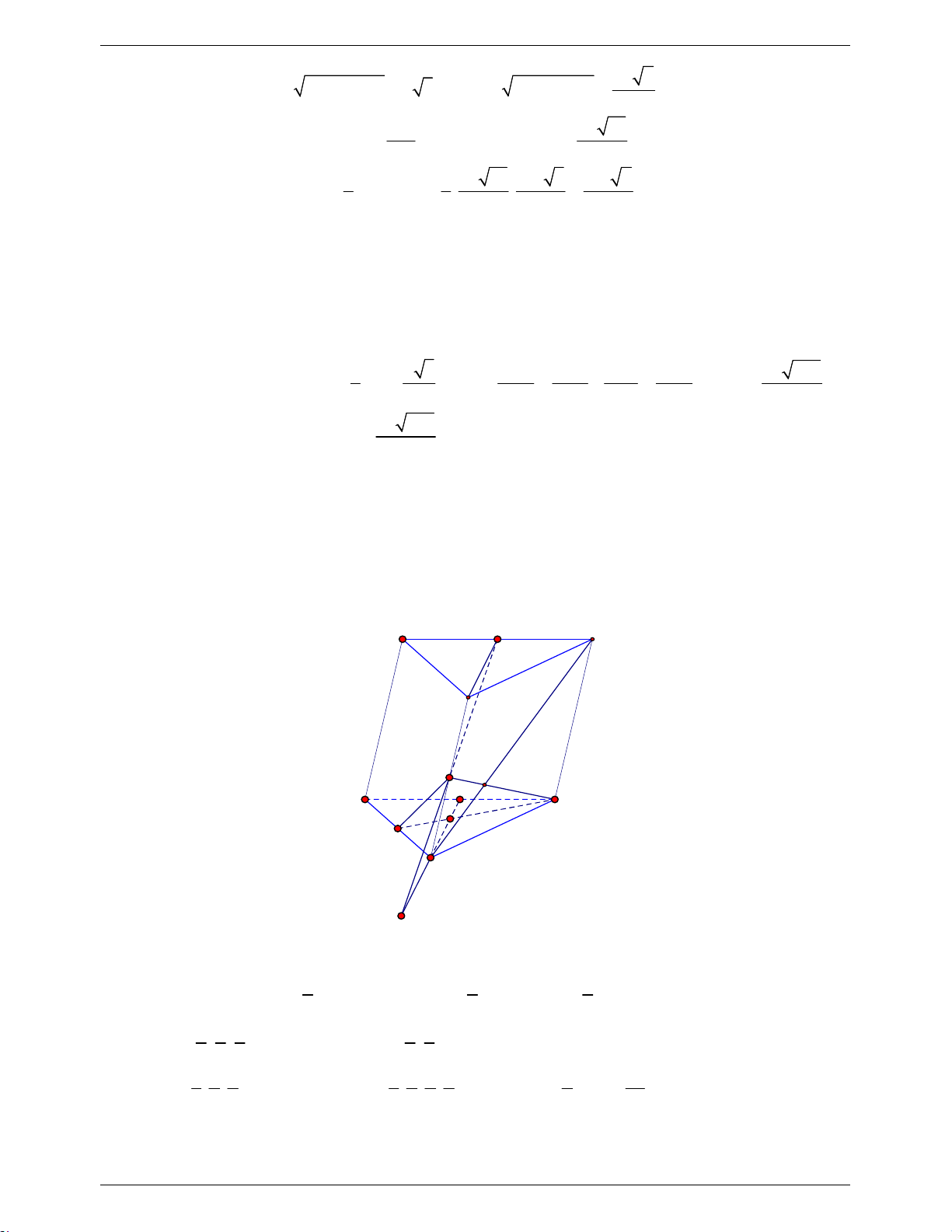
b) Cho khối lăng trụ tam giác ABC.A B C
có thể tích là V . Gọi I và K lần lượt là trung
điểm của AC và AB ; G là trọng tâm của tam giác BCC . Tính thể tích của khối tứ diện BIKG theo V Lời giải
GVSB: Nguyễn Thị Phương Hiền; GVPB: Bùi Văn Cảnh A' K B' C' M G J A B O I C H
Gọi H là giao điểm của KM với CO , (O là trọng tâm tam giác ABC ). 1 1 2 Ta có V d K BIG S d H BIM S KBIG , . BIG , . 3 3 3 BIM 1 2 5 d C BIM 2 5 . . . , .S . .V 3 3 2 BIM 3 2 CBIM 1 2 5 d M BIC 1 2 5 1 S d C ABC S V . BIC 1 5 . . . , . . . . , . 3 3 2 3 3 2 2 2 ABC 36
TÀI LIỆU ÔN THI HỌC SINH GIỎI Trang 7
NHÓM TOÁN VDC&HSG THPT
ĐỀ THI HỌC SINH GIỎI 2020 - 2021 Câu 5. (2,0 điểm)
Cho các số x, y 0 thỏa mãn
xy xy x y 2 2 1 2 x y 2xy
1 . Tính giá trị lớn nhất xy của biểu thức P . x y Lời giải Ta có :
xy xy x yx y xy xy xy xy x y3 2 2 1 2 2 1 1 1 1 x y
xy 3 xy x y3 1 1 x y.
Xét hàm số đặc trưng 3
f t t t , ta có f t 2 3t 1 0, t .
Suy ra hàm số f t đơn điệu tăng với mọi t .
Do đó phương trình f 1 xy f x y x y 1 xy .
Theo bất đẳng thức AM-GM cho bộ số ,
x y dương ta có x y 2xy 1 xy 2xy 1
1 xy 4xy xy . 3 xy xy 1 1 1 3 Ta có: P P P xy P . P . x y 2 xy 2 2 3 6 3 3
Vậy giá trị lớn nhất của biểu thức P là
đặt được khi x y . 6 3
------------------------HẾT------------------------ Trang 8
TÀI LIỆU ÔN THU THPT QUỐC GIA
Document Outline
- de-thi-hoc-sinh-gioi-tinh-toan-thpt-nam-2020-2021-so-gddt-khanh-hoa
- khanh hoa




