Đề thi học sinh giỏi Toán 12 cấp tỉnh năm 2020 – 2021 sở GD&ĐT Cà Mau

SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI CHỌN HỌC SINH GIỎI CẤP TỈNH THPT CÀ MAU MÔN TOÁN – LỚP 12 NĂM HỌC 2020 - 2021 TOANMATH.com
Thời gian làm bài: 180 phút (không kể thời gian phát đề)
Ngày thi: 04 tháng 10 năm 2020 Câu 1: (3,0 điểm)
Giải các phương trình sau:
a) cos 2x  5sin x  3 sin 2x  5 3 cos x  8  0 . b)  x   2
3 1 x  x 4  x  2x  6x  3. Câu 2: (3,0 điểm)
a) Cho hàm số y  f  x có đạo hàm trên  và có bảng xét dấu của f x như sau: x  3  1 1 8  f  x  0  0  0  0 
Tìm các điểm cực trị của hàm số g  x  f  2 x  2x. 2 x  3x
b) Tìm tất cả các giá trị của tham số m để hàm số y 
đồng biến trên 1; . x  m Câu 3: (3,0 điểm)
Trong mặt phẳng Oxy cho tam giác ABC có đỉnh A1;2 , đường trung tuyến và đường phân
giác trong hạ từ đỉnh B lần lượt có phương trình d : 2x  3y  2 , d : 9x  3y  16 . Tìm tọa độ 1
đỉnh C của tam giác ABC . Câu 4: (3,0 điểm)
Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O , cạnh a . Biết SA  SB  SC  a .
Đặt SD  x 0  x  a 3.
a) Tính số đo góc giữa đường thẳng SB và mặt phẳng  ABCD khi x  a .
b) Tính x theo a sao cho tích AC.SD lớn nhất. Câu 5: (3,0 điểm)
a. Cho đa giác đều có 24 đỉnh, chọn ngẫu nhiên 4 đỉnh của H  . Tính xác suất để 4 đỉnh
chọn được tạo thành một hình chữ nhật nhưng không phải là hình vuông.
b. Cho P  x    x  x 13 2 1 4 3
. Xác định hệ số của 3
x trong khai triển P  x theo lũy thừa của x . Câu 6: (3,0 điểm)
Cho dãy số u được xác định bởi u 1 và 2 u  3u  2  , n . n n  n  1 1 
a) Xác định số hạng tổng quát của dãy số u . n  b) Tính tổng 2 2 2 S  u  u  . . u . 1 2 2020 Câu 7: (2,0 điểm)
Cho hai số thực thay đổi x, y với x  0. Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức 2 xy P  . 2 2 2 2 (x  3y )(x  x 12 y )
____________________ HẾT ____________________ HƯỚNG DẪN GIẢI
Câu 1: Giải các phương trình sau:
a) cos 2x  5sin x  3 sin 2x  5 3 cos x  8  0 . b)  x   2
3 1 x  x 4  x  2x  6x  3. Lời giải
a) cos 2x  5sin x  3 sin 2x  5 3 cos x  8  0  5
 sin x  3cos x  3sin2x  cos2x 8  0  1 3  3 1  5 sin x  cos x   sin 2x  cos 2x  4  0  2 2  2 2          5  sin x   sin 2x   4  0      3   6     Đặt t  x   2x   2t  . 3 6 2   
Phương trình trở thành 5sin t  sin 2t   4  0   .  2 
 5sin t  cos2t  4  0 2
 2sin t  5sin t  3  0 sint 1     3  t 
 k2  x   k2 k  . sint  2 6  2 b)  x   2
3 1 x  x 4  x  2x  6x  3. Điều kiện: 1   x  4 .
PT   x    x    x   x  2 3 1 1 1 4  2x  6x x x  3 x x  3    2xx  3 1 x 1 1 4  x x x  3  0   1   1 1    2 2
 1 x 1 1 4  x   x  0 1   . x  3  1 x 11 1 1
Xét phương trình (2): Ta có     2 . 1   4  x 1 1 x 1 1 4  x x  1 Dấu bằng xảy ra khi 
(vô lí). Vậy phương trình (2) vô nghiệm. x  4
Vậy phương trình đã cho có hai nghiệm x  0 và x  3 . Câu 2:
a) Cho hàm số y  f  x có đạo hàm trên  và có bảng xét dấu của f x như sau: x  3  1 1 8  f  x  0  0  0  0 
Tìm các điểm cực trị của hàm số g  x  f  2 x  2x. Lời giải x  1  x  1 2 x  2x  3   x 1 BC
Ta có g x  2x  2 f  2 x  2x   2  0   x  2x  1    .  x 1 2 BC 2   x  2x  1   x  2  ; x  4 2 x  2x  8 
Vậy các điểm cực trị của hàm số g  x lần lượt là x  2; x  1; x  4 . 2 x  3x
b) Tìm tất cả các giá trị của tham số m để hàm số y 
đồng biến trên 1; . x  m Lời giải ĐK: x  m . 2 x  2mx  3m Ta có: y  . x  m2 y  x      2 0, 1; x  2mx 3m  0, x  1; *
Hàm số đồng biến trên 1;     . m  1; m  1 
*  min f x  0 với f x 2  x  2mx  3m . 1;
Đồ thị của hàm số f  x là parabol có toạ độ đỉnh I  2  ; m m  3m . BBT: x m 1  f  x 1 m
Dựa vào BBT, suy ra min f  x  0  1 m  0  m  1. 1;
Vậy 1  m  1 thoả mãn yêu cầu bài toán.
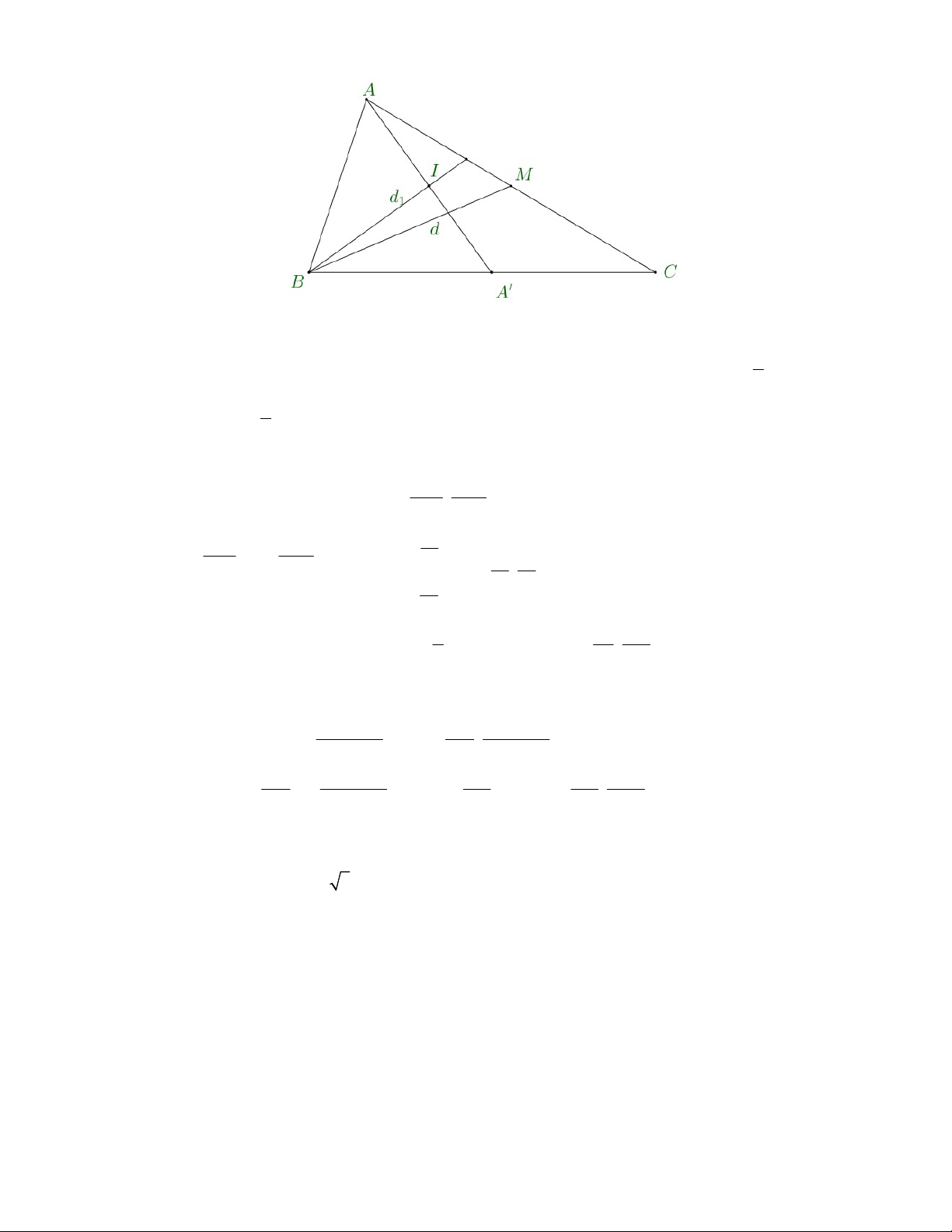
Câu 3: Trong mặt phẳng Oxy cho tam giác ABC có đỉnh A1;2 , đường trung tuyến và đường phân
giác trong hạ từ đỉnh B lần lượt có phương trình d : 2x  3y  2 , d : 9x  3y  16 . Tìm tọa độ 1
đỉnh C của tam giác ABC . Lời giải    x 2 2x  3y  2 
Ta có d  d  B nên toạ độ điểm B thoả hệ phương trình  . 1   2 9  x  3y  16 y   3  2  Do đó B 2;   .  3  Gọi A ;
a b là điểm đối xứng với A qua d  A  BC . 1 1 a 2  b   
Khi đó trung điểm của AA là I ; d  
và AA  u nên ta có hệ: 1  2 2  1 d  1 a   2  b   18 9  3  16 a        5 18 17    2   2     A ;   .  17  5 5  a 1 3   b 2  0 b   5  2    8  4  1
Đường thẳng BC đi qua điểm B 2;   nhận vectơ AB  ; 
 làm vectơ pháp tuyến nên  3   5 15 
có phương trình: 72x 123y  226  0 .
Gọi M là trung điểm của đoạn AC .  226  72t   t 1 472  72t  Do C  BC  C t;  M ;     .  123   2 123  t 1 472  72t 513  513 278  M  d  2.  3.  2  t  suy ra C ;  . 2 123 113  113 339  Câu 4:
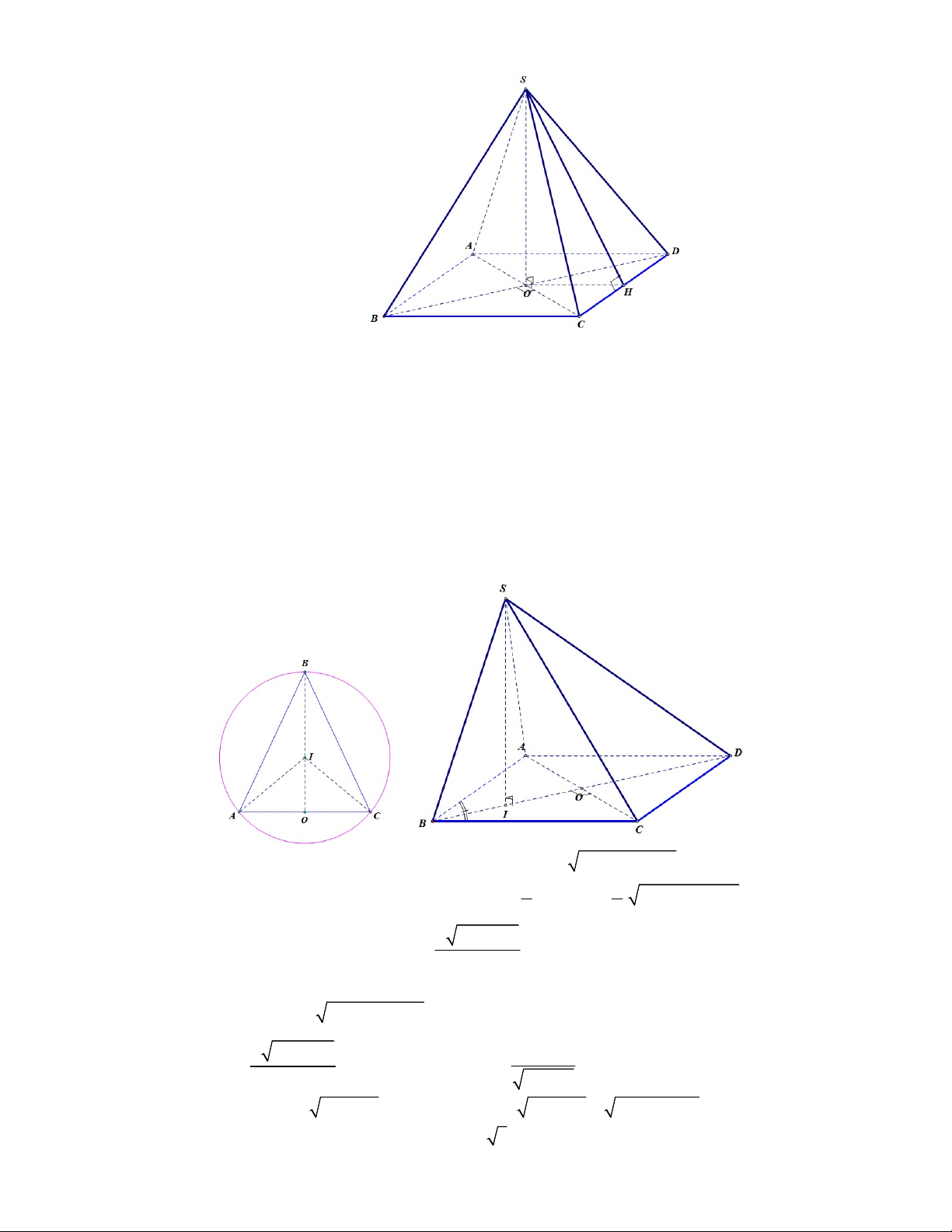
Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O , cạnh a . Biết SA  SB  SC  a .
Đặt SD  x 0  x  a 3.
a) Tính số đo góc giữa đường thẳng SB và mặt phẳng  ABCD khi x  a .
b) Tính x theo a sao cho tích AC.SD lớn nhất. Lời giải Cách 1: S x A A D O B D G B C C
a) Tính số đo góc giữa đường thẳng SB và mặt phẳng  ABCD khi x  a .
Gọi O là hình chiếu của S lên mặt phẳng  ABCD .
Ta có: SA  SB  SC  SD  a  OA  OB  OC  OD  ABCD là hình vuông. Xét tam giác vuông: a 2  BO 2 2 cos SBC      0 SBC  45 . SB a 2
b) Tính x theo a sao cho tích AC.SD lớn nhất.
Gọi G là tâm đường tròn ngoại tiếp tam giác ABC .
Do SA  SB  SC  SG   ABCD . AC  BD Ta có: 
 AC  SBD  AC  SO. AC  SG SOC  B
 OC (do SC  BC  a , OC chung).
SO  OB  OD  BSD vuông tại S . 2 2 a  x 2 2 2 BD  a  x  OD  . 2 2 2 2 2 a  x 3a  x 2 2 2 2 OA  AD  OD  a   . 4 4 2 2 3a  x 2 2  OA   AC  3a  x . 2 2 2 2 2 x  3a  x 3a Xét 2 2 AC.SD  . x 3a  x   . 2 2 2 3a a 3 a 6 Dấu "  " xảy ra khi 2 2 2 2 2
x  3a  x  2x  3a  x   x   . 2 2 2 Cách 2:
a) Tính số đo góc giữa đường thẳng SB và mặt phẳng  ABCD khi x  a .
Do SA  SB  SC  SD  a  SO   ABCD . Gọi H là trung điểm của CD suy ra
CD  SOH   CD  OH  ABCD là hình vuông.
Từ đó SBD vuông cân tại S , nên SB, ABCD    SBD  45 .
b) Tính x theo a sao cho tích AC.SD đạt giá trị lớn nhất.
Gọi I là hình chiếu vuông góc của S trên mặt phẳng  ABCD , do SA  SB  SC  a nên I là
tâm đường tròn ngoại tiếp tam giác ABC , dễ thấy I thuộc đường thẳng BO . Đặt 
ABC   . Ta có AC  2R sin . Suy ra 2 2 2 BO  a  R sin  . 1 1
Theo công thức tính diện tích tam giác ABC ta có: 2 2 2 2
.a .sin  . a  R .sin  .2R sin 2 2 2 2 a 4R a 2 2  a  R  2 2 2 4 a  R .sin   sin    . 2 2R
Mặt khác xét tam giác vuông SBI và tam giác vuông SID ta có:
SI  a  R  x   a  R   R2 2 2 2 2 2 2 2 2 sin . 2 2 a 4R a 2 a Thay sin  
vào rút gọn ta được R  . 2 2R 2 2 a  x Nên 2 2
AC  2R sin  3a  x . Từ đó 2 2 4 2 2
AC.SD  x 3a  x  x  3a x . Xét hàm số f  x 4 2 2
 x  3a x với 0  x  a 3. x  0 6 Có f  x 3 2 4x 6a x 0        6a 
do x 0; 3a nên ta nhận x  a . x   2  2  6  6
Lập bảng biến thiên ta được max f  x  f  a  . Vậy khi x 
a thì AC.SD đạt giá trị lớn    0; 3a 2   2 nhất. Câu 5:
a. Cho đa giác đều có 24 đỉnh, chọn ngẫu nhiên 4 đỉnh của H  . Tính xác suất để 4 đỉnh chọn
được tạo thành một hình chữ nhật nhưng không phải là hình vuông.
b. Cho P  x    x  x 13 2 1 4 3
. Xác định hệ số của 3
x trong khai triển P  x theo lũy thừa của x . Lời giải
a. Số phần tử của không gian mẫu là : 4 C . 24
Đa giác đều có 24 đỉnh thì có 12 đường chéo đi qua tâm nên số hình chữ nhật , kể cả hình vuông là : 2 C hình. 12
Ứng với 1 đường chéo thì có một đường chéo duy nhất để tạo thành hình vuông, nên số hình vuông là 6 .
Nên số hình chữ nhật cần tìm là 2 C  6 . 12 2 C  6 10
Vậy xác suất cần tìm là : 12  . 4 C 1771 24
b. P  x    x  x 13 2 1 4 3    x 13 2 1 4  3x  13 12 0 1 2 
  C 1 4x  C 1 4x .3x  ... 13   13  
   x13    x12 2 1 4 13 1 4
.3x  ...    x13    x12 2 1 4 39 1 4 .x  ... * Tìm hệ số của 3 x trong khai triển   13 1 4x : 1 4x 13 13 13   13 C .1  4 k k k x k  C .4k. kx . 13   13 k 0 k 0
Ta có k  3 nên hệ số của 3 x là : 3 3 C .4 . 13 * Tìm hệ số của 3
x trong khai triển   x12 2 1 4
.x tức là tìm hệ số của x trong khai triển   12 1 4x . 12 Ta có 1 4x12 12   12 C .1  4 m m m x m  C .4 .m m x . 12   12 k 0 k 0
Từ đó m 1 nên hệ số của 3 x là : 1 C .4 . 12 Vậy hệ số của 3
x trong khai triển P  x là : 3 3 1 C .4  39.C .4  20176 . 13 12 Câu 6:
Cho dãy số u được xác định bởi u 1 và 2 u  3u  2  , n . n n  n  1 1 
a) Xác định số hạng tổng quát của dãy số u . n  b) Tính tổng 2 2 2 S  u  u  . . u . 1 2 2020 Lời giải
a) Xác định số hạng tổng quát của dãy số u . n  Ta có: 2 2
u  3u  2  u 1  3 u  ,n . n n n n     2 1  1 1  v  2 Đặt 2 1 v  u 1 . n n  v  3  v ,n  n n  1 
Suy ra v là cấp số nhân với số hạng đầu v  2, công bội q  3 . n  1 n 1 v 2.3     ,n . n  n 1 u 2.3  1   
 ,n là số hạng tổng quát của dãy số u . n  n  b) Tính tổng 2 2 2 S  u  u  . . u . 1 2 2020 Ta có: 2 2 2 S  u  u  . . u  2 2 2019 1 3  3  . . 3  2020 . 1 2 2020  2020 1 3 2020  2.  2020  3  2021. 1 3 Vậy 2020 S  3  2021.
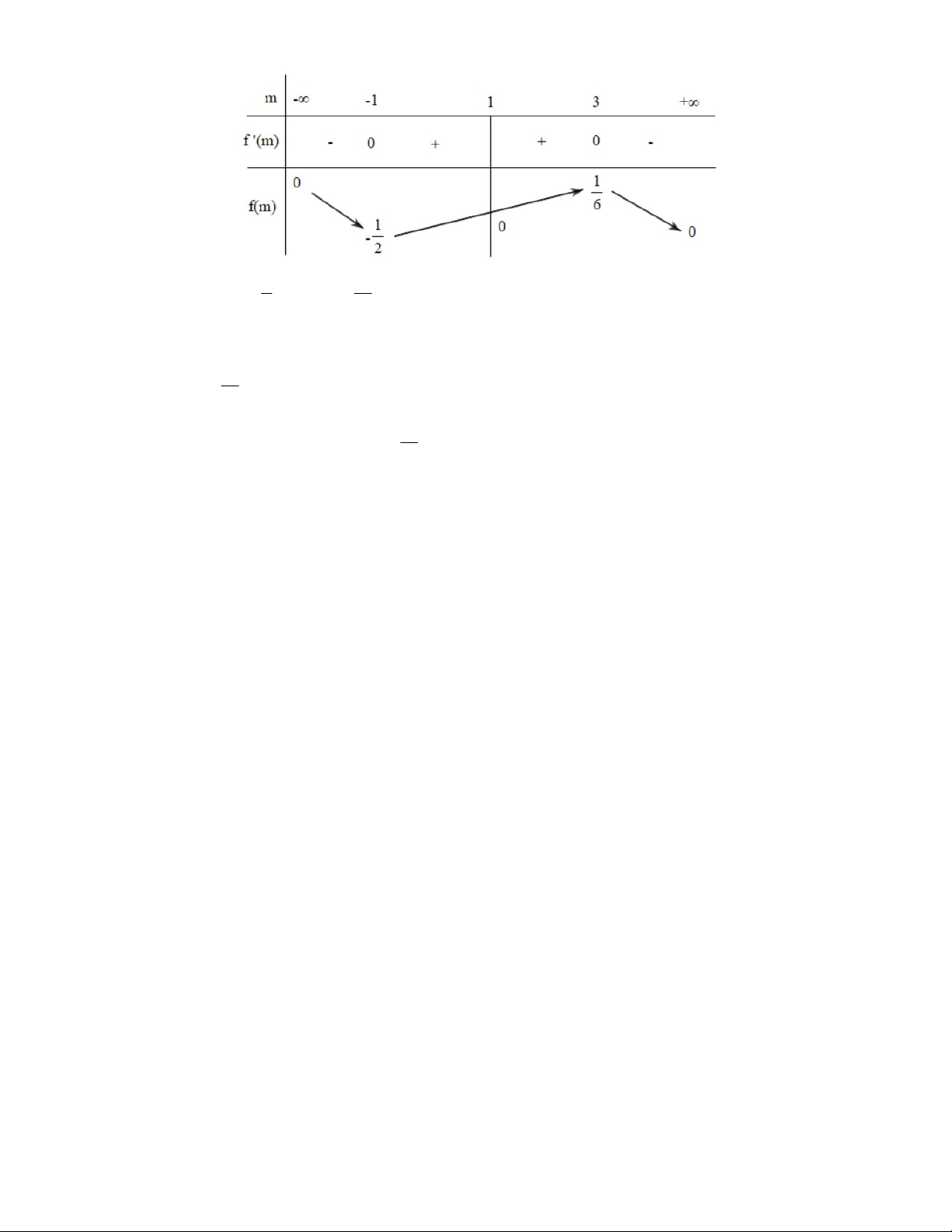
Câu 7: Cho hai số thực thay đổi x, y với x  0. Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức 2 xy P  . 2 2 2 2 (x  3y )(x  x 12 y ) Lời giải 2 y 2 xy 2 P  = x (do x  0 ) . 2 2 2 2 (x  3y )(x  x 12 y ) 2 2 y y (1 3 )(1 112 ) 2 2 x x y Đặt  t . x 2 2 2 2 2 t t (1 112t ) 1 112t 1 1 112t 1 Khi đó: P    .  . . 2 2 2 2 2 2 (1 3t )(1 112t ) (1 3t )(12t ) 12 1 3t 3 12t  4 Đặt 2 m  112t  1. 1 m 1 m 1 Khi đó P  .  3P   f (m) . 2 2 3 m  3 m  3 2 2 m  3  2m(m 1) m  2m  3 f '(m)    0 2 2 2 2 (m  3) (m  3) . m  1   m 3 1 1
 0  3P   0  P  . 6 18
+ P  0 , dấu "  "  m  1  y  0 . 1 + P  , dấu 2 2
"  "  m  3  2x  3y . 18 1 Vậy MinP  0  y  0 ; 2 2 MaxP   2x  3y . 18
____________________ HẾT ____________________