Đề thi học sinh giỏi Toán 12 cấp tỉnh năm 2020 – 2021 sở GD&ĐT Kon Tum

SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI CHỌN HỌC SINH GIỎI CẤP TỈNH KON TUM MÔN TOÁN – LỚP 12 NĂM HỌC 2020 - 2021 TOANMATH.com
Thời gian làm bài: 180 phút (không kể thời gian phát đề)
Đề thi gồm 01 trang + 05 bài toán tự luận
Câu 1. (2,5 điểm) Cho hàm số f  x 4 2 2
 x  2mx  m 1. Tìm m để đồ thị hàm số f x có ba điểm
cực trị và ba điểm đó cùng gốc tọa độ O lập thành tứ giác nội tiếp đường tròn. sin 3x  3 cos3x 1
Câu 2. (4,0 điểm) 1. Giải phương trình  0 với x    ;0. cos x x  3  x  y y   1  4  5y   1 2. Giải phương trình  .
 2x  2y  4  4  3x  2y  2y 1  2 Câu 3.
(5,0 điểm) 1. Một nhóm gồm 9 học sinh một lớp trong đó có ba bạn Việt, Nam và Hùng đi dự
đại hội Đoàn trường, ban tổ chức sắp xếp ngẫu nhiên 9 học sinh này ngồi vào một dãy ghế
được đánh số từ 1 đến 9. Tính xác suất để số ghế của bạn Hùng bằng trung bình cộng số ghế
của hai bạn Việt và Nam. u   2020  1 2. Cho dãy số u thỏa . n   2n 5n5  u   2
2n  6n  2u , n 1,2,3... n n 1   2nu  Tính lim n  . 2  n   Câu 4.
(6,0 điểm) Cho tứ diện ABCD có BC  AD  a, AC  BD  , b AB  CD  c .
1. Tính khoảng cách giữa hai đường thẳng AB và CD theo a, , b c .
2. Biết mặt phẳng  ABC vuông góc với mặt phẳng  ABD. Chứng minh rằng cos . A cos B  cos C ; với ,
A B,C là ký hiệu ba góc tương ứng với các đỉnh , A B,C của tam giác ABC .
3. Gọi S là diện tích toàn phần của tứ diện ABCD . Tìm giá trị lớn nhất của biểu thức 2 2 2 S S S   . 2 2 2 2 2 2 a b b c c a
Câu 5. (2,5 điểm) Cho các số thực dương a,b,c thỏa mãn 2 2 2
a  b  c  3 . Tìm giá trị nhỏ nhất của a  b  c 2 2 biều thức P   a  b 2 1  c  . 2 2 2 2 c  2ab a b c
------------------------- HẾT ------------------------- HƯỚNG DẪN GIẢI
Câu 1: Cho hàm số f  x 4 2 2
 x  2mx  m 1. Tìm m để đồ thị hàm số f x có ba điểm cực trị và
ba điểm đó cùng gốc tọa độ O lập thành tứ giác nội tiếp đường tròn. Lời giải f  x 3  4  x  4mx   2 4x x  m x  0 x  2 4 x  m  0   . 2 x  m
Để đồ thị hàm số có ba điểm cực trị thì : m  0 .
Ba điểm cực trị là A 2 0; m   1 ; B  m;  1 ; C  m;  1 .   BA 2
 m;m  ; BO m;  1 .
Để ba điểm A , B , C và gốc tọa độ O 0;0 tạo thành tứ giác nội tiếp khi và chỉ khi   B C 180   B 90   (do B   C ).   m  0  B . A BO  0 2  m  m  0   . m 1 Vậy m  1. sin 3x  3 cos3x 1
Câu 2.1: Giải phương trình  0 với x    ;0. cos x Lời giải
Trường hợp 1: sin 3x  0 . sin 3x  3 cos 3x 1     0 x   k   cos x  2   sin 3x  3 cos3x 1 1  sin 3x  3 cos3x 1 2   2 x   k      6 3  sin  3x  sin      3  6   2 x   k  18 3     13  Theo đề bài x  
 ;0 và x   k nên x ;  . 2  8 18 
Trường hợp 2: sin 3x  0 sin 3x  3 cos3x 1     0 x   k   cos x  2   sin 3x  3 cos3x 1 1
  sin 3x  3 cos3x 1 2    2 x   k 2     6 3  sin  3x  sin      3  6  2 x   k  18 3  5   11  Theo đề bài x  
 ;0 và x   k nên x ; ;  . 2  6 6 18  5   11   13 
Vậy nghiệm của phương trình trên là x   ; ; ; ;  .  6 6 18 8 18  x  3 
x  y y  1  45y   1
Câu 2.2: Giải phương trình  .
 2x  2y  4  4  3x  2y  2 y 1  2 Lời giải   x  y y   1  0 
Điều kiện: 2x  2y  4  0 . 2y 1 0  Ta có  
1   x  y  3  x  y y   1  4 y   1  0 .
Đặt u  x  y , v  y 1 u  0,v  0 . u  v Khi đó   1 trở thành 2 2 u  3uv  4v  0   . u  4v  vn
Với u  v ta có x  2 y 1, thay vào 2 ta được: 6y  2  2y 1  4y 1  0 .
Dễ dàng ta tìm được y  1  x  3 .
Vậy nghiệm của phương trình là 3;  1 .
Câu 3.1: Một nhóm gồm 9 học sinh một lớp trong đó có ba bạn Việt, Nam và Hùng đi dự đại hội Đoàn
trường, ban tổ chức sắp xếp ngẫu nhiên 9 học sinh này ngồi vào một dãy ghế được đánh số từ 1
đến 9. Tính xác suất để số ghế của bạn Hùng bằng trung bình cộng số ghế của hai bạn Việt và Nam. Lời giải
Số phần tử không gian mẫu n()  9!
Gọi A là biến cố mà số ghế của bạn Hùng bằng trung bình cộng số ghế của hai bạn Việt và Nam
Gọi số ghế của Hùng, Việt, Nam lần lượt là h, v, n v  n  , h v, n   Có h  mà  2  , h v, n    1;9
 v, n cùng lẻ hoặc cùng chẵn
Mỗi bộ v, n cùng lẻ hoặc cùng chẵn do 1 h duy nhất.
Các bộ v, n thõa mãn là ( Chưa xét hoán vị )
1;3;1;5;1;7;1;9;3;5;3;7;3;9
5;7;5;9;7;9;2;4;2;6;2;8 4;6;4;8;6;8  16 bộ v, n
 16.2!.1 cách xếp h,v, n thõa mãn
 n A  16.2!.  1 .6!  P A 16.2!.1.6! 4   . 9! 63 u   2020  1
Câu 3.2: Cho dãy số u thỏa . n   2n 5n5  u   2
2n  6n  2u , n 1,2,3... n n 1   2nu  Tính lim n  . 2  n   Lời giải n  5n  5 n  2 2 1  3n   1 1 Ta có u  u  u n 1  2 2 n  6n  2 n 2 2 n  3n   1 n n  2 1  3n   2 1 1 n  3n 1 n  2 1  3n   1 1  u  u 2 . 2 n  3n   1 n n 1  2 n   1  3n   1 2 1 1 2 2         2 n 1 3n  1 1   n  2 1  3n   1 1 n  2 1  3n   1 1 2    n 5n 5 u  ….  u  .404 n 1
2 n  2  3n  2 2 2 3 1 2 n       2n   2 2  1 32  1 1   2 n  3n 1 Vậy u  .404 . n n 1 2   2nu  Suy ra lim n    808. 2 n  
Câu 4: Cho tứ diện ABCD có BC  AD  a, AC  BD  , b AB  CD  c .
1. Tính khoảng cách giữa hai đường thẳng AB và CD theo a, , b c .
2. Biết mặt phẳng  ABC vuông góc với mặt phẳng  ABD. Chứng minh rằng cos . A cos B  cos C ; với ,
A B,C là ký hiệu ba góc tương ứng với các đỉnh , A B,C của tam giác ABC .
3. Gọi S là diện tích toàn phần của tứ diện ABCD . Tìm giá trị lớn nhất của biểu thức 2 2 2 S S S   . 2 2 2 2 2 2 a b b c c a Lời giải
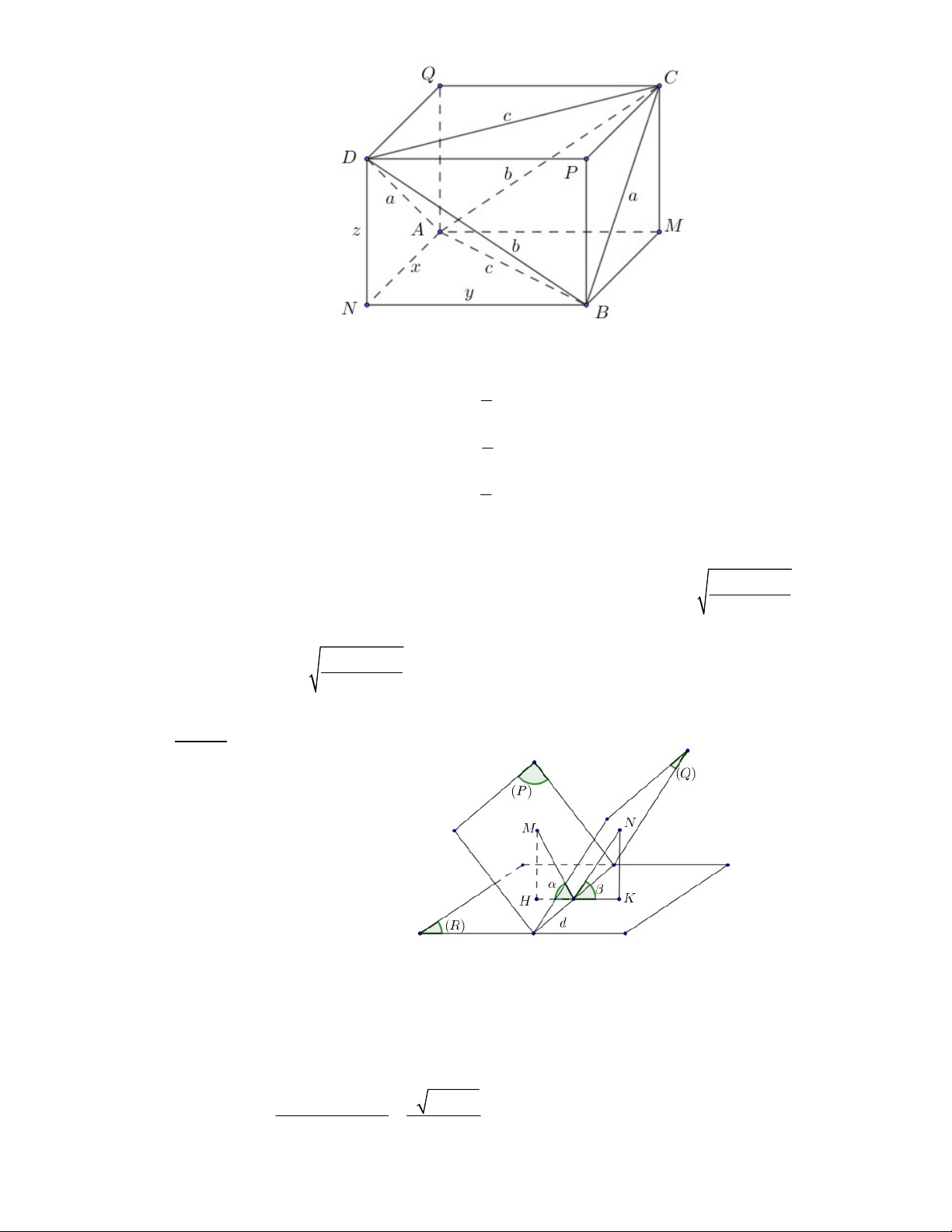
Dựng hình hộp chữ nhật AMBN.QCPD (tham khảo hình vẽ)
Gọi x, y, z lần lượt là ba kích thước của hình hộp chữ nhật AMBN.QCPD .  1 2 x    2 2 2 a  c  b  2 2 2  2 x  y  c    1 Theo giả thiết, ta có 2 2 2 2
 y  z  b   y   2 2 2 b  c  a  . 2  2 2 2  x  z  a   1 2 z    2 2 2 a  b  c   2
1. Tính khoảng cách giữa hai đường thẳng AB và CD theo a, , b c . AB   AMBN   a  b  c Ta có C  D  QCPD
 d  AB CD  d  AMBN  QCPD 2 2 2 , ,  z  .   AMBN   QCPD 2 // 2 2 2 a  b  c Vậy d  AB,CD  . 2 2. Chứng minh rằng cos . A cos B  cos C .
Cách 1: Sử dụng bổ đề sau:
P,R    
P,Q 180   
Nếu P Q  d  R và     .
Q,R     
P,Q    
Áp dụng vào bài toán như sau:
Gọi  ABD, AMBN   ; ABC, AMBN    . d D  AMBN  2 2 , z x  y Ta có tan     1 . d  N, AB xy d C  AMBN  2 2 , z x  y
Tương tự, cũng có tan    2 . d C, AB xy Từ  
1 và 2  tan  tan      .
Do  ABC   ABD      45        z x  y  2 2 2 2 2 2 2 2 2 a b c a c b b c a 2 2 2 2 2 2  x y  .c  . 2 2 2 2 2 2 2 2 2 2 2 2 a  b  c a  c  b b  c  a   . . 2ab 2ac 2bc  cosC  cos . A cos B (đpcm). Cách 2:
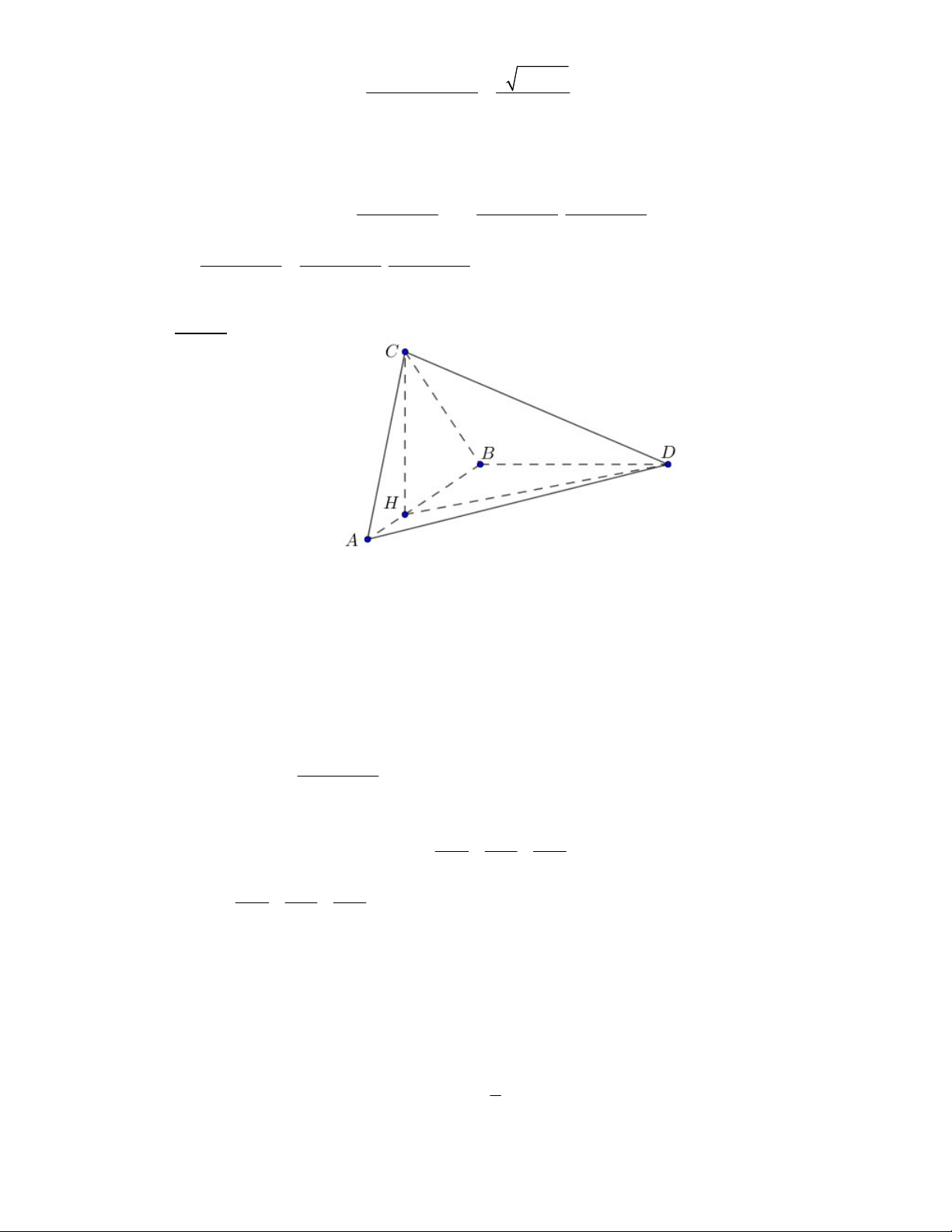
Dựng CH  AB vì  ABC    ABD  CH   ABD . Ta có CH  . a sin B ; BH  . a cos B .
Áp dụng định lý cosin trong tam giác BHD , ta có 2 2 2 DH  BH  BD  2BH.B . D cos  ABD 2 2 2 2
 DH  a cos B  b  2 . a cos . B . b cos A (vì  ABD   CAB ) 2 2 2 2
 DH  a cos B  b  2ab cos Acos B
Lại có CHD vuông tại H , nên 2 2 2 2 2 2
DH  CD  CH  CD  CH  DH 2 2 2 2 2 2
 c  a sin B  a cos B  b  2ab cos Acos B 2 2 2 a  b  c  cos . A cos B   cosC . 2ab Vậy cos C  cos . A cos B (đpcm). 2 2 2 S S S
3. Tìm giá trị lớn nhất của biểu thức   . 2 2 2 2 2 2 a b b c c a 2 2 2 S S S Đặt T    . 2 2 2 2 2 2 a b b c c a
Gọi R là bán kính đường tròn ngoại tiếp tam giác ABC, ta có a  2R sin A , b  2R sin B , c  2R sin C .
Tứ diện ABCD , có BC  AD  a, AC  BD  , b AB  CD  c 2  S  4.S  8R sin Asin B sin C . ABC Suy ra T   2 2 2
4 sin A  sin B  sin C .  1  Ta có T  4 2 2 2
sin A  sin B  sin C   4 1 cos 2A  cos 2B 2  sin C  2     T     A B  A B 2 4 1 cos cos  sin C     T    C  A B 2 4 2 cos .cos  cos C     T  4 2  cosC. 
cosA BcosA B  81cos AcosBcosC  9  1 (vì cos Acos B cos C  ). 8 Suy ra T  9 .
Vậy giá trị lớn nhất của biểu thức T bằng 9 , xảy ra khi A  BC đều.
Câu 5: Cho các số thực dương a,b,c thỏa mãn 2 2 2
a  b  c  3 . Tìm giá trị nhỏ nhất của biều thức a  b  c P   a  b 2 2 2 1  c  . 2 2 2 2 c  2ab a b c Lời giải Ta có 2 2 2 2
c  2ab  c  a  b  3. x  y  z
Dễ thấy x  y  z2   2 2 2 x  y  z  2 2 2 3  x  y  z  3 a  b  c 1 1 1 1 Từ đó suy ra P   a  b 2 1   c   2 2 2 2 2 2 3 a b a b c c 2 2 1 c  a  b  c      ab  c a b 3 3 3 2ab  bc  ca
 3P  a  b  c  a  b  c  abc 3 2 2 2 6 a b c 6 3 3 6 3  3P  3 abc  3 abc   3 abc  3 abc  3 abc abc 6 Đặt 6
t  abc ,0  t  1. Ta được 2 3P  3t  3t  . 2 t 6 Xét f t 2
 3t  3t  liên tục trên 0;1 và có 2 t  3t  6   4t 2 12  f t  3  6t    0,t  0;1 . 3 3   t t
nên f t nghịc biến trên 0;1 suy ra f t  f  
1  9  3  P  3 3 1.
Vậy giá trị nhỏ nhất của P là 3 3 1 đạt được khi a  b  c 1.
------------------------- HẾT -------------------------