Đề thi học sinh giỏi Toán 12 cấp tỉnh năm 2020 – 2021 sở GD&ĐT Lạng Sơn

SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI CHỌN HỌC SINH GIỎI CẤP TỈNH LẠNG SƠN MÔN TOÁN – LỚP 12 NĂM HỌC 2020 - 2021 TOANMATH.com
Thời gian làm bài: 180 phút (không kể thời gian phát đề)
Đề thi gồm 01 trang + 05 bài toán tự luận Câu 1. (4 điểm)
a) Tìm tất cả các giá trị của tham số m để hàm số 3 2 y  x  x   2 m   2 3 3 1 x  3m 1 có hai
điểm cực trị trái dấu. 1
b) Cho hàm số bậc ba y  f  x 3 2
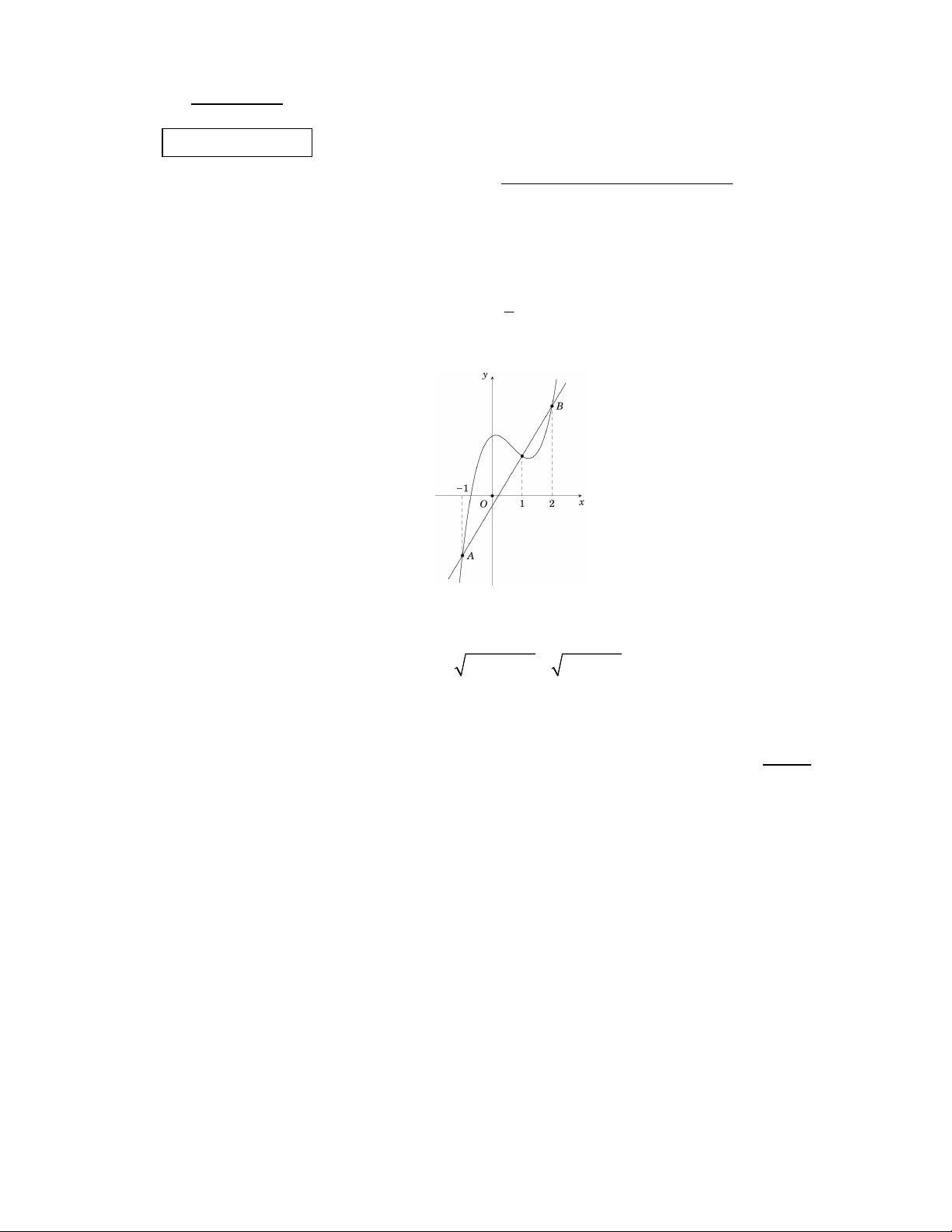
 ax  bx  x  c và đường thẳng y  g x có đồ thị như 3
trong hình vẽ bên và AB  5 . Giải phương trình f  x  g  x 2  x  2 . Câu 2. (6 điểm) 3 2 3
x  6x 13x  y  y 10
Giải hệ phương trình trong tập số thực  .
 2x  y  2  5  x  y  3  y  a) Giải phương trình  2  x x   2 1 sin cos
1 cos xsin x 1 sin 2x . b) Giải phương trình  2  x x   2 1 sin cos
1 cos xsin x 1 sin 2x .
Câu 3. (2,0 điểm) Gọi S là tập hợp các số có 5 chữ số đôi một khác nhau abcde với
a,b,c, d,e 1, 2,3,..., 
9 . Chọn ngẫu nhiên một số từ S , tính xác suất để số được chọn là số
chẵn và thỏa mãn a  b  c  d  e .
Câu 4. (2 điểm) Một khách sạn có 50 phòng. Hiện tại mỗi phòng cho thuê với giá 400 nghìn đồng một
ngày thì toàn bộ phòng được thuê hết. Biết rằng cứ mỗi lần tăng giá lên them 20 nghìn đồng thì
có thêm 2 phòng trống. Hỏi giám đốc phải chọn giá phòng mới là bao nhiêu để số tiền thu được
của khách sạn trong 1 ngày là lớn nhất. Câu 5.
(6 điểm) Cho hình lăng trụ tam giác đều ABC.A' B 'C ', ABC.A' B 'C ', M là trung điểm AA',
G là trọng tâm tam giác A' B 'C ' . a) Gọi I  MB ' A' ;
B J  MC ' A'C . Tính thể tích V . A'.B'C 'IJ
b) Tính khỏng cách giữa hai đường thẳng BC, MG .
c) Gọi là mặt phẳng qua và song song với . Tính tan góc tạo bởi mặt phẳng và P và  A'B'C '.
____________________ HẾT ____________________ 1 HƯỚNG DẪN GIẢI Câu 1. (4 điểm)
a) Tìm tất cả các giá trị của tham số m để hàm số 3 2 y  x  x   2 m   2 3 3 1 x  3m 1 có hai
điểm cực trị trái dấu. 1
b) Cho hàm số bậc ba y  f  x 3 2
 ax  bx  x  c và đường thẳng y  g x có đồ thị như 3
trong hình vẽ bên và AB  5 . Giải phương trình f  x  g  x 2  x  2 . Lời giải a) Ta có 2 y   x  x   2 m     2 2 3 6 3 1 3 x  2x  m   1 .
Gọi x , x là hai nghiệm của phương trình y  0  x , x là hai điểm cực trị 1 2 1 2 x  x  2
Theo định lý Vi-ét, ta có 1 2  . 2 x x  m 1  1 2
Hàm số có hai điểm cực trị trái dấu  phương trình y  0 có hai nghiệm trái dấu, nghĩa là m 1 2
x x  0  m 1 0  . 1 2  m  1 
b) Đặt g  x  mx  n (với m  0 ).  Ta có A 1
 ;m  n , B2;2m  n. Suy ra AB  3;3m . 16 4 Ta lại có 2 2
AB  5  9  9m  25  m   m  (vì m  0 ). 9 3 Do đó g  x 4  x  n . 3
Dựa vào đồ thị, ta thấy f  x  g  x  a 2
x  x    a 3 2 1 2 x  2x  x  2.
Mặt khác, ta lại có      3 2 f x
g x  ax  bx  x  c  n . b   2  a 
Đồng nhất hệ số, ta được a  1   f x  g x 3 2  x  2x  x  2 . 2a  c  n  Do đó 2 f  x  g  x 2  x  2  f  x  g x 2  x  2  0 3 2 2
 x  2x  x  2  x  2  0 x  0 3 2 x 3x x 0       . 3  13 x   2 Câu 2. (6 điểm) 3 2 3
x  6x 13x  y  y 10 a)
Giải hệ phương trình trong tập số thực  .
 2x  y  2  5  x  y  3  y  b) Giải phương trình  2  x x   2 1 sin cos
1 cos xsin x 1 sin 2x . Lời giải 3 2 3
x  6x 13x  y  y 10 a)  .
 2x  y  2  5  x  y  3  y 
Ta có x  x  x   x  a3 3 2 6 13  x  a 10 3 2 3 2 2 3
 x  6x 13x  x  3x a  3xa  a  x  a 10  a  2 Nên x  x  x  y  y   x  3 3 2 3   x   3 6 13 10 2
2  y  y , dễ thấy hàm số f t 3  t  t  f t 2
 3t 1  0 nên hàm số đồng biến trên  .
Suy ra ta được x  2  y .
Thay vào phương trình thứ hai ta được 7
3x  7  2x  5  x điều kiện 0  x  2
Khi đó phương trình đã cho được viết lại  3x 3  7  2x   1  3  x 3 x  3 7  2x 1    x  3  0 3x  3 7  2x 1 x  3   3 2  .  1  0 VN  3x  3 7  2x 1
Vậy nghiệm của hệ là  ; x y  3;  1 . b) Giải phương trình  2  x x   2 1 sin cos
1 cos xsin x 1 sin 2x .   x  x  x x  x  x   x  x2 sin cos sin cos sin cos sin cos 3   x    k   4
1sin xcosx sin xcosx     x    k x    k  4  4    sin x 1     x   k2   . 2 cos x 1   x  k2   
Câu 3. (2,0 điểm) Gọi S là tập hợp các số có 5 chữ số đôi một khác nhau abcde với
a,b,c, d,e 1, 2,3,..., 
9 . Chọn ngẫu nhiên một số từ S , tính xác suất để số được chọn là số
chẵn và thỏa mãn a  b  c  d  e . Lời giải
Lập số tự nhiên có 5 chữ số đôi một khác nhau từ các số 1, 2,3,..., 
9 là một chỉnh hợp chập 5 của 9 phần tử nên 5
n(S)  A  9.8.7.6.5  15120 . 9
Chọn ngẫu nhiên một số từ S có n  1  C  15120 . 15120
Gọi A là biến cố: “Số được chọn là số chẵn và thỏa mãn a  b  c  d  e ” TH1: e  6 : có 4
C  5 cách lập số thỏa mãn biến cố A. 5 TH2: e  8 : có 4
C  35 cách lập số thỏa mãn biến cố A. 7 40 1 Do đó: n( )
A  35  5  40 . Vậy P( ) A   . 15120 378
Câu 4. (2 điểm) Một khách sạn có 50 phòng. Hiện tại mỗi phòng cho thuê với giá 400 nghìn đồng một
ngày thì toàn bộ phòng được thuê hết. Biết rằng cứ mỗi lần tăng giá lên them 20 nghìn đồng thì
có thêm 2 phòng trống. Hỏi giám đốc phải chọn giá phòng mới là bao nhiêu để số tiền thu được
của khách sạn trong 1 ngày là lớn nhất. Lời giải
Gọi x (ngàn đồng) là giá phòng khác sạn cần đặt ra  x  400 . Giá chênh lệch sau khi tăng là x  400 x  400
x  400. Số phòng cho thuê giảm nếu giá tăng là 2.  . 20 10 x  400 x
Số phòng cho thuê với giá x là 50   90 
. Tổng doanh thu trong ngày là: 10 10 2    x  x f x  x 90   90x    . \  10  10
Bài toán trở thành tìm giá trị lớn nhất của hàm số f x với x  400 . x
Ta có: f ' x  90  , f ' x  0  x  450. 5
Mặc khác: max f  x  f 450  20250 . x   400;
Vậy nếu cho thuê với giá 450 ngàn thì sẽ có doanh thu cao nhất trong ngày 2.025.000 (đồng). Câu 5.
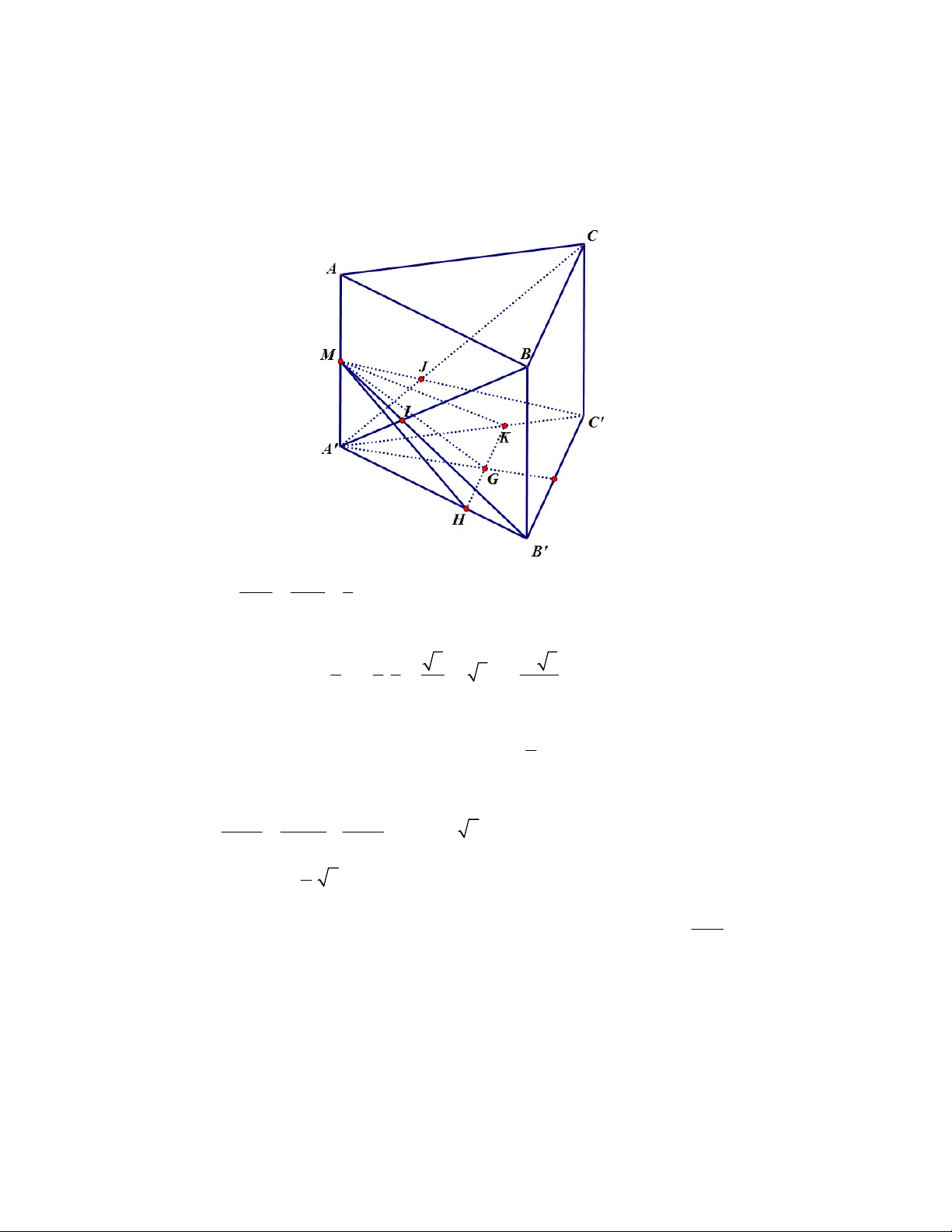
(6 điểm) Cho hình lăng trụ tam giác đều ABC.A' B 'C ', ABC.A' B 'C ', M là trung điểm AA',
G là trọng tâm tam giác A' B 'C ' . 4 a) Gọi I  MB ' A' ;
B J  MC ' A'C . Tính thể tích V . A'.B'C 'IJ
b) Tính khỏng cách giữa hai đường thẳng BC, MG .
c) Gọi là mặt phẳng qua và song song với . Tính tan góc tạo bởi mặt phẳng và P và  A'B'C '. Lời giải MI MJ 1 a) Ta có   . MB ' MC ' 3 Đặt V  V . MA'B'C ' 8 8 1 3 V  V V  V   . A B C IJ MA IJ  2 16 3 . .2. . 2 3 '. ' ' ' 9 9 3 4 9
b) Lấy H  A' B ', K  A'C ' sao cho HK / /BC và G  HK .
d BC MG  d BC MHK   d B MHK  5 , , ,  d  , A MHK  . 2
Có HK  MA'G , kẻ A'O  MG  A'O  MHK  . 1 1 1 Ta có    A'O  2 . 2 2 2 A'O A' M A'G  d BC MG 5 ,  . 2 . 2 MA
c) Góc tạo bởi mặt phẳng  P và  A' B 'C ' là  MGA' , ta có  ' tan MGA'  1. GA'
____________________ HẾT ____________________ 5