Đề thi học sinh giỏi Toán 12 cấp tỉnh năm 2020 – 2021 sở GD&ĐT Thái Nguyên

NHÓM TOÁN VD – VDC UBND TỈNH THÁI NGUYÊN
KỲ THI CHỌN HỌC SINH GIỎI TỈNH LỚP 12
SỞ GIÁO DỤC VÀ ĐÀO TẠO NĂM HỌC: 2020 – 2021 TOANMATH.com Môn thi: TOÁN Đề thi gồm có 01 trang
Thời gian làm bài: 180 phút (không kể thời gian giao đề) Câu 1. (6,0 điểm)
a) Tìm cực trị của hàm số 2 y  x  2 x  x 1 . b) Cho hàm số 7
y  x  m m   4 x  m  2 m  m   2 2 3 2 5
3 x  2020 . Tìm tất cả các giá trị thực
của tham số m để hàm số nghịch biến trên  . Câu 2. (6,0 điểm) 6x  4
a) Giải bất phương trình 2x  4  2 2  x  . 2 5 x 1  x  b) Giải phương trình 6 32 cos  sin3x    3sin x .  2  Câu 3. (3,0 điểm)
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB  3a , AD  3a 2 ,
SA   ABCD , SA  4a . Gọi M, N lần lượt là trung điểm của các cạnh SD và AD.
a) Tính góc giữa đường thẳng AC và mặt phẳng  BMN .
b) Mặt phẳng   đi qua hai điểm B , M và song song với AC . Biết mặt phẳng   cắt các cạnh
SA , SC lần lượt tại hai điểm E , F . Tính khoảng cách từ điểm C đến mặt phẳng  BEMF . Câu 4. (2,0 điểm)
Cho tam giác ABC có ba góc nhọn và AB  AC (tam giác ABC không cân ). Gọi O, I lần lượt
là tâm đường tròn ngoại tiếp, nội tiếp của tam giác ABC. AD (D BC) là đường phân giác trong của 
BAC. Đường thẳng AD cắt đường tròn O tại điểm E (E  ) A . Đường thẳng d đi
qua điểm I và vuông góc với AE cắt đường thẳng BC tại điểm K. Đường thẳng K , A KE cắt
đường tròn O lần lượt tại các điểm M , N (M  ;
A N  E). Đường thẳng ND, NI cắt đường
tròn O lần lượt tại các điểm P,Q(P  N;Q  N). Chứng minh rằng EQ là đường trung trực của đoạn thẳng M . P Câu 5. (2,0 điểm)  u  2020 Cho dãy số (u ) với 1 . n  2021 2020 u  u  2020u  u (*)  n 1 n n n
a) Chứng minh lim u   . n 2020 2020 2020  u u u  b) Tính 1 2 lim n     . u  2020 u  2020 u  2020  2 3 n 1   Trang 1 NHÓM TOÁN VD – VDC Câu 6. (1,0 điểm)
Cho x , y, z là các số thực dương thay đổi thỏa mãn: x  y  z  3. Chứng minh rằng:  2 2 2 x  y  z    2 2 2 2 2 2 3
2 x y  y z  z x   3.
____________________ HẾT ____________________ Trang 2 NHÓM TOÁN VD – VDC HƯỚNG DẪN GIẢI Câu 1:
a) Tìm cực trị của hàm số 2 y  x  2 x  x 1 . b) Cho hàm số 7
y  x  m m   4 x  m  2 m  m   2 2 3 2 5
3 x  2020 . Tìm tất cả các giá trị thực
của tham số m để hàm số nghịch biến trên  . Lời giải
a) Tìm cực trị của hàm số 2 y  x  2 x  x 1 . 2 y  x  2 x  x 1 TXĐ: D   . 2 2x 1 x  x 1  2x 1 y  1  . 2 2 x  x 1 x  x 1   2x   1  0 2 2
y  0  x  x 1  2x 1  0  x  x 1  2x   1   x  x 1   2x  2 2 1  1 x     2 2 3  x 3x  0  1 x     2 x  0 x  1   x  1  y  1. x ∞ 1 +∞ y' 0 + +∞ +∞ y 1
Vậy hàm số đạt cực tiểu tại x  1, y  1 CT . b) Cho hàm số 7
y  x  m m   4 x  m 2 m  m   2 2 3 2 5
3 x  2020 . Tìm tất cả các giá trị thực
của tham số m để hàm số nghịch biến trên  . 7
y  x  m m   4 x  m  2 m  m   2 2 3 2 5 3 x  2020 TXĐ: D   . 6
y   x  m m   3 x  m 2 7 4 2 3 2 2m  5m  3 x . 6
y    x  m m   3 x  m 2 0 7 4 2 3 2 2m  5m  3 x  0 5
 x  x  m m   2 x  m   2 7 4 2 3 2 2m  5m  3  0  x  0    . 5 7x  4m  2m 3 2x  2m   2
2m  5m  3  0   1 Trang 3 NHÓM TOÁN VD – VDC
Hàm số nghịch biến trên   y  0, x
   ( Dấu bằng xảy ra tại hữu hạn điểm).    1 có nghiệm bằng x  0  m 2 2 2m  5m  3  0 m  0   2m  5m  3  0   m  0   m  1  .  3 m   2 Thử lại:  Với m  0 : 7 y  x  2020 6  y  7  x  0 , x
    Hàm số nghịch biến trên  .  Với m  1: 7 4 y  x  x 6 3  y  7  x  4x . x  0 6 3 3 y 0 7x 4x 0 x  3 7x 4 0             3 196  . x    7 3 196 Đặt x   và x  0 . 1 7 2 x ∞ x1 x2 + ∞ y' 0 + 0 y 3  196 
Hàm số đồng biến trên   ;0   . 7    3  Với m  : 7 y  x  2020 6  y  7  x  0 , x
    Hàm số nghịch biến trên  . 2 3
Vậy m  0 , m  thì hàm số nghịch biến trên  . 2 Câu 2: 6x  4
a) Giải bất phương trình 2x  4  2 2  x  . 2 5 x 1  x  b) Giải phương trình 6 32 cos  sin3x    3sin x .  2  Lời giải
a) Điều kiện xác định: 2  x  2 . Trang 4 NHÓM TOÁN VD – VDC
Do 2x  4  2 2  x  0, 2;2 
 nên bất phương trình đã cho tương đương với bất 2x  4  42  x 6x  4 6x  4 6x  4 phương trình    2
2x  4  2 2  x 5 x 1 2
2x  4  2 2  x 5 x 1   x   2 6
4 5 x 1  2x  4  2 2  x   0 (*). 2 2
Ta có  2x  4  2 2  x    2x  4  2 4 2x   1 22x  4 42x  24
Suy ra 2x  4  2 2  x  24  5,x   2  ;2   Mặt khác 2 5 x 1  5, x    2  ;2   , do đó 2
5 x 1  2x  4  2 2  x  0,x   2  ;2   . 2
Do đó (*)  6x  4  0  x  . 3  2 
Đối chiếu với điều kiện ta được tập nghiệm của bất phương trình đã cho là: S  2  ;  .  3   x  b) Giải phương trình: 6 32cos  sin 3x  3sin x   .  2  3  x    x  Ta có 6 2 3 32 cos
 sin3x  3sin x  32cos   3sin x  4sin x      3sin x  2    2   4  x3 3 1 cos
 4sin x  0  1 cos x  sin x  sin x  cos x  1    x    k2    2    4 4 x   k2 sin x          2 k.  4  2  3  x     k2 x    k2  4 4 
Vậy phương trình đã cho có các nghiệm là x 
 k2; x    k2 k  . 2 Câu 3:
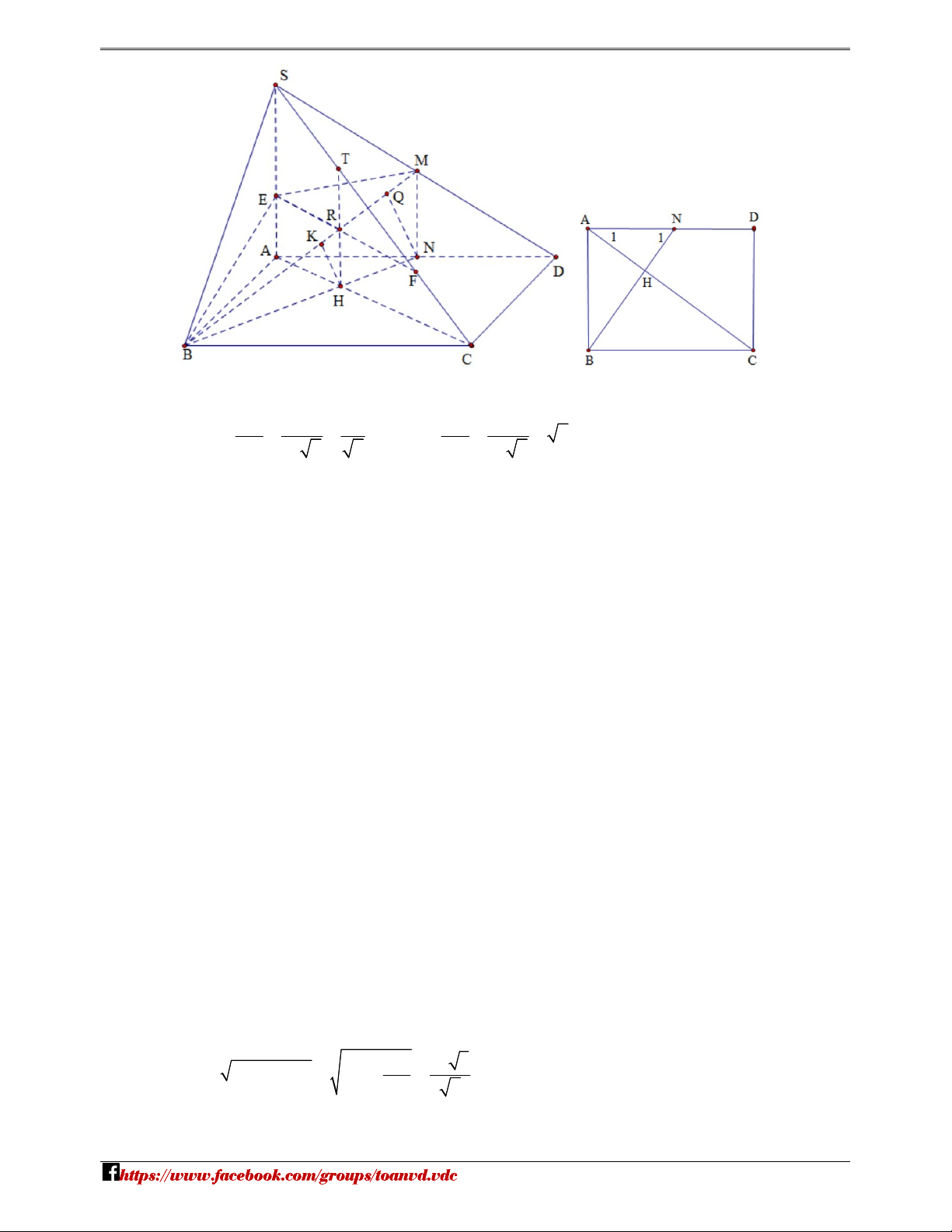
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB  3a , AD  3a 2 , SA   ABCD ,
SA  4a . Gọi M, N lần lượt là trung điểm của các cạnh SD và AD .
3. Tính góc giữa đường thẳng AC và mặt phẳng  BMN .
4. Mặt phẳng   đi qua hai điểm B , M và song song với AC . Biết mặt phẳng   cắt các cạnh
SA , SC lần lượt tại hai điểm E , F . Tính khoảng cách từ điểm C đến mặt phẳng  BEMF . Lời giải Trang 5 NHÓM TOÁN VD – VDC
1. Tính góc giữa đường thẳng AC và mặt phẳng  BMN .  DC 3a 1 AB 3 . a 2 tan A    ; tan  N    2 1 AD 3a 2 2 1 AN 3a 2  tan  A .tan  N  1   A   N  90   A   N  90  AC  BN . 1 1 1 1 1 1 AC  BN Ta có: 
 AC   BMN   A , C  BMN  90 . AC  MN  MN // SA
2. Mặt phẳng   đi qua hai điểm B , M và song song với AC . Biết mặt phẳng   cắt các
cạnh SA , SC lần lượt tại hai điểm E , F . Tính khoảng cách từ điểm C đến mặt phẳng BEMF .
Trong (SAC) qua H kẻ đường thẳng song song với SA cắt SC tại T.
Vì HT // MN (//SA)  T   .
Trong (BMN) gọi R  HT  EF .
Trong (SAC) qua R kẻ đường thẳng song song với AC cắt SA, SC theo thứ tự tại E, F.
    BEMF .
Kẻ HK  BM,NQ  BM  HK // NQ .
Vì  AC // EF , EF     d  ,
C    d H,  HK  BM Ta có:  HQ  EF  HQ  A , C AC // EF
 NQ  BEMF  d H,   HK  d  , C    HK 2 9a 3a 3 2 2 2 BN  AB  AN  9a   2 2 Trang 6 NHÓM TOÁN VD – VDC 2 AB 3a 2 2 AB  BH.BN  BH    a 6 BN 3 1 1 1 2 1 35      6a 3  NQ  2 2 2 2 2 2 NQ NB NM 27a 4a 108a 35 HK BH N . Q BH Ta có:   HK  NQ BN BN  d C   4a 3 ,  HK  . 35 Câu 4:
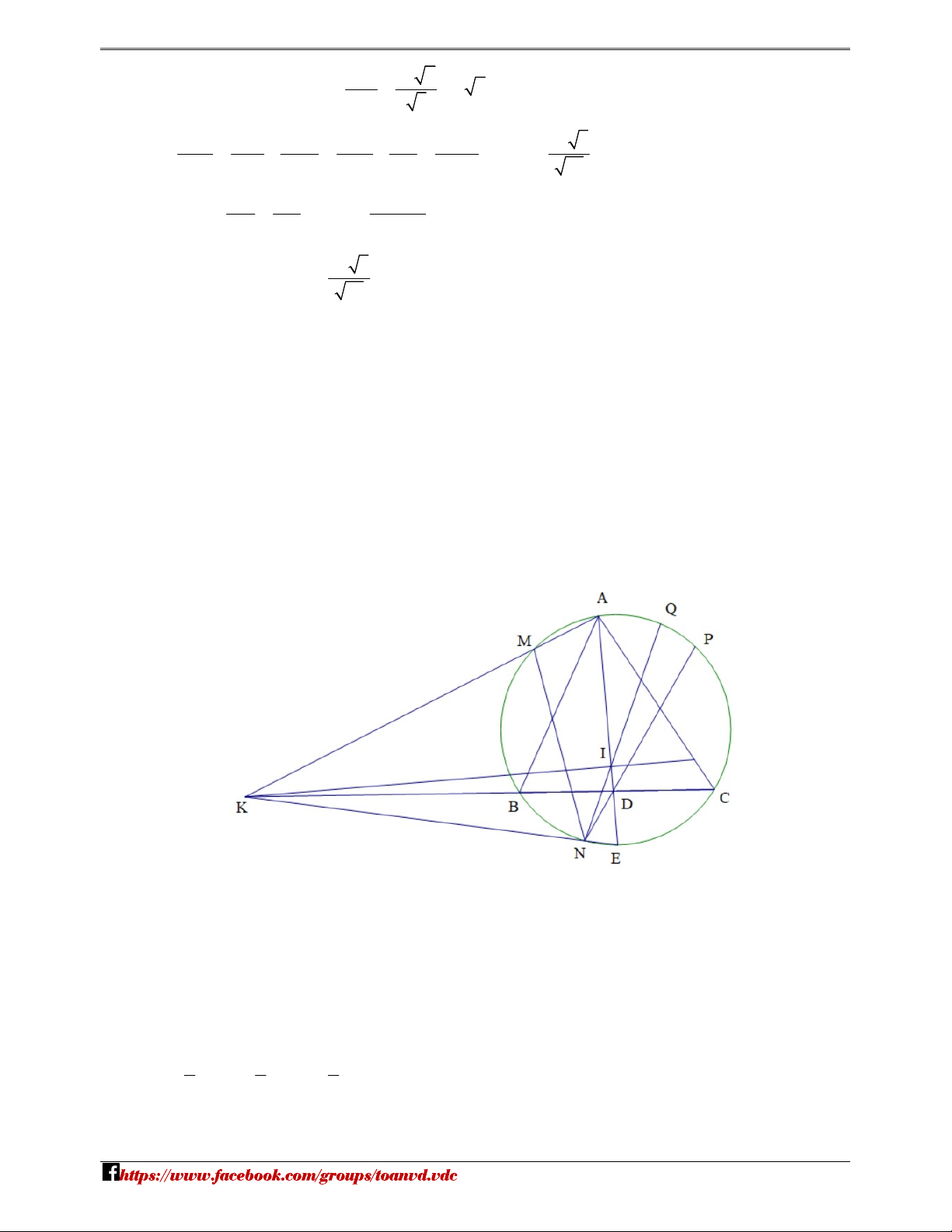
Cho tam giác ABC có ba góc nhọn và AB  AC (tam giác ABC không cân ). Gọi O, I lần lượt là tâm
đường tròn ngoại tiếp, nội tiếp của tam giác ABC. AD (D  BC) là đường phân giác trong của 
BAC. Đường thẳng AD cắt đường tròn O tại điểm E (E  )
A . Đường thẳng d đi qua điểm
I và vuông góc với AE cắt đường thẳng BC tại điểm K. Đường thẳng K , A KE cắt đường
tròn O lần lượt tại các điểm M , N (M  ;
A N  E). Đường thẳng N , D NI cắt đường tròn
O lần lượt tại các điểm P,Q(P  N;Q  N). Chứng minh rằng EQ là đường trung trực của đoạn thẳng M . P Lời giải
Từ bài toán, chú ý AB, AC  AI  NI là phân giác góc  BNC
 P là điểm chính giữa 
BAC  EQ là đường kính của O  IN  KE 2
 KM .KA  KN.KE  KI  IM  KA  IMKN nt KI    QNM   AKI 1 1 1 Có  BKN  sd CE  sd  BN  sd  NE   BAN 2 2 2  ADNK nt   AKD   AND Trang 7 NHÓM TOÁN VD – VDC Lại có  0 IKD    0 90 IDK  90   IAC   ACB 1  1 1 1 1 sd  1 QBE  sd  1 CE  sd  AE  sd  QBE  sd  BE  sd  AB  sd  AQ   ANQ 2 2 2 2 2 2 2   AKI   INQ   MNI  
INP  Q là điểm chính giữa MP Mà QE là đường kính
 EQ là đường trung trực của đoạn thẳng M . P  u  2020
Câu 5: Cho dãy số (u ) với  1 . n  2021 2020 u   u  2020u  u (*)  n 1 n n n 
c. Chứng minh lim u   . n 2020 2020 2020  u u u  d. Tính 1 2 lim n      . u 2020 u 2020 u  2020 2 3 n 1   Lời giải
a. Từ giả thiết dễ dàng suy ra u  0 với mọi n  1. Do đó ta có u  u  2020 với mọi n n 1  n
n  1. Hay ta có dãy (u ) đơn điệu tăng. Suy ra n limu    n limu  a  2020  n 
Giả sử limu  a  2020 . Qua giới hạn hai vế của (*) ta được n 2021 2020 a  a  2020a
a . Điều này tương đương a  0 hoặc a  2020 (Vô lý) Vậy lim u   . n
b. Từ điều kiện (*) ta có với mọi k  1 2021 2020 u  u  2020u u k 1  k k k 2020
 u (u  2020)  u u . k k k 1  k Từ đó suy ra 2020 2020 u u (u  2020) u u k k k k 1  k  
u  2020 (u  2020)(u  2020) (u  2020)(u  2020) k 1  k 1  k k 1  k 1 1   u  2020 u  2020 k k 1  2020 2020 2020  u u u  Suy ra 1 2 lim n      u 2020 u 2020 u  2020 2 3 n 1    1 1 1 1 1 1   lim        
u 2020 u 2020 u 2020 u 2020 u  2020 u  2020 1 2 2 3 n n 1   Trang 8 NHÓM TOÁN VD – VDC  1 1  1  lim      .
u  2020 u 2020 4040 1 n 1 
Câu 6: Cho x , y, z là các số thực dương thay đổi thỏa mãn: x  y  z  3. Chứng minh rằng:  2 2 2 x  y  z    2 2 2 2 2 2 3
2 x y  y z  z x   3. Lời giải
Vì x , y , z vai trò như nhau, không mất tính tổng quát giả sử x  y  z .
Suy ra x  y  z  3x  3  3x  x  1 * . Ta có  2 2 2 x  y  z    2 2 2 2 2 2 3
2 x y  y z  z x   3  3 2 2 2 x  y  z   2 2 2 2 2 2 2 x y  y z  z x  2  3  0  3x  3 2 2 y  z  2  2x  2 2 y  z  2 2  2y z  3  0
  y  z 3 2x  2y z  3x 3  0   y  z2 2 2 2 2 2 2  2 3  2x   2yz  2 3  2x  2 2 2
 2y z  3x  3  0  1
Áp dụng BĐT AM-GM cho 2 số dương y và z ta được: 2 2 2  y  z   3  x   3  x  yz     yz          2   2   2  2 4     x    x  VT 1  3  x2  3 3 2 3  2x   2   2 3  2x  2  2  3x  3  f   x  2   2  2 4  3  x   3  x 
Xét f x  3  x2  2 3  2x   2   2 3  2x  2  2  3x  3    2   2  1     3  x2 3 2x  1  3 x4 1  3x  3  3 x2 9 6 1 2 2 2 2 2
3  2x   x  x  3x  3   2 8 2  4 4 4  1     3  x2 9 3 3 1  x  x 
 3x  3  3 x2 3 2 2 . 1 x3x   1  3 x   1  x    1 2  4 2 4  2 4   
  x 3   x  x  x      x 3
   x x  x  x   3 1 9 6 3 1 3 1 1 3 17 13 1  1 x2 2 3 2  2 3  x 14x    1 8  8 8 Mà 2 3
 x 14x 1  3x1 x 11x 1 0 với x  0;  1 3 Vậy 1 x2  2 3x 14x   1  0 với x  0;  1 . 8
Từ đó suy ra f  x  0 với x  0;  1 , hay VT   1  0 với x  0;  1 .
Đẳng thức xảy ra khi x  y  z  1.
____________________ HẾT ____________________ Trang 9