Đề thi học sinh giỏi Toán 12 năm 2019 – 2020 trường Đồng Đậu – Vĩnh Phúc

TRƯỜNG THPT
ĐỀ THI CHỌN HỌC SINH GIỎI 12 NĂM HỌC 2019 - 2020 ĐỒNG ĐẬU MÔN: TOÁN
(Đề thi gồm 01 trang)
Thời gian: 180 phút (không kể thời gian giao đề)
Câu 1 (2,0 điểm) U U 1
a) Tìm tất cả các giá trị của tham số m để hàm số 3 y =
mx − (m − ) 2
1 x + 3(m − 2) x + 2019 3
đồng biến trên [2;+∞) . mx − m + 2 b) Cho hàm số y =
có đồ thị là (C). Tìm tất cả các giá trị của tham số m để đường x +1
thẳng d : y = 2x −1 cắt (C) tại hai điểm phân biệt A, B sao cho góc giữa hai đường thẳng OA, OB bằng 45° .
Câu 2 (2,0 điểm) U U
cos x (2sin x + ) 1
a) Giải phương trình lượng giác sau ( = . x + )( x − ) 3 sin 1 2 sin 1 2 2
x −4y +3 x y +3y +3 = 0
b) Giải hệ phương trình sau  (
x, y ∈ ) . 2 3
 x + 3x − y + 5 + 3x − 2 = 2  3a 6
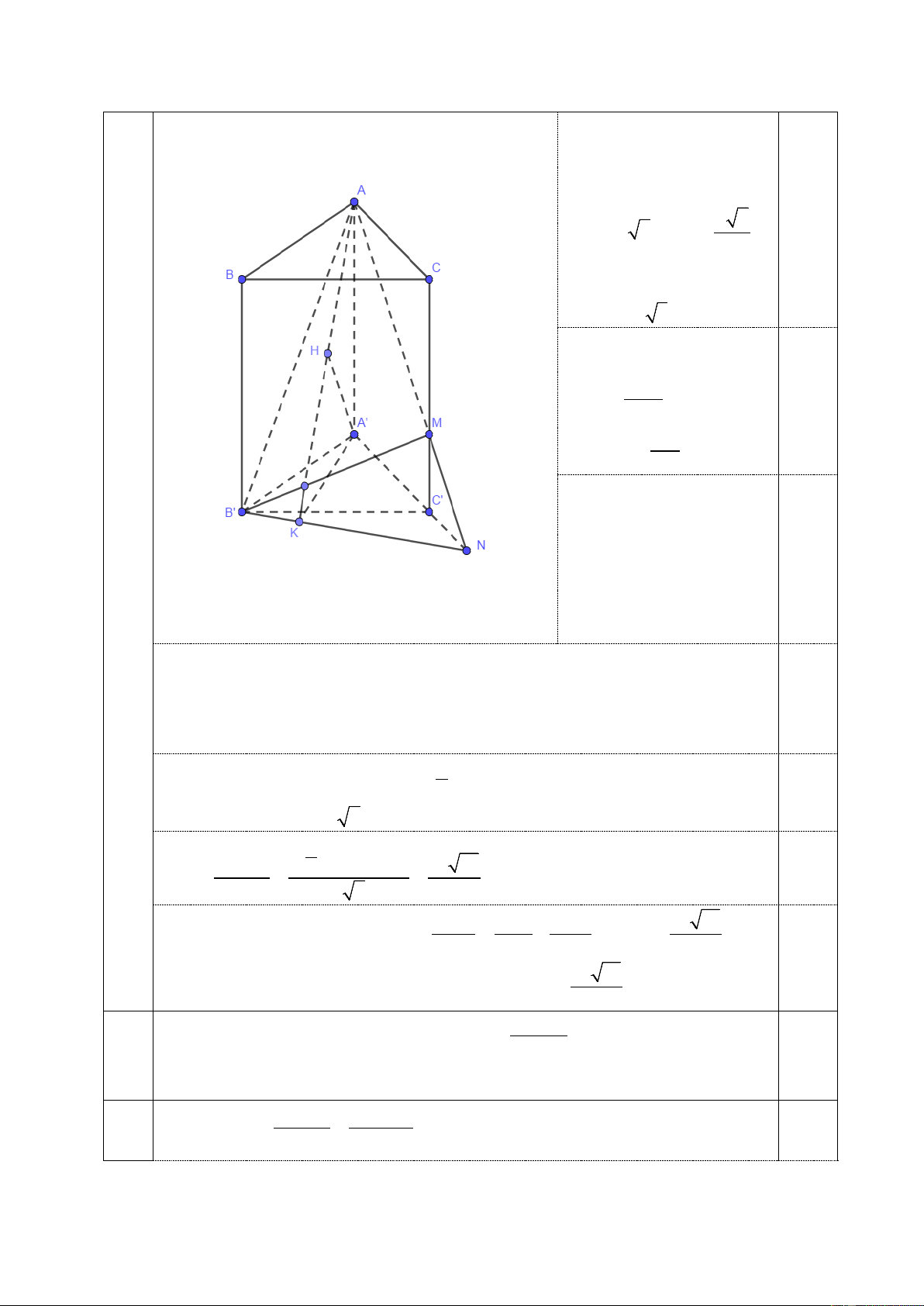
Câu 3 (2,0 điểm) Cho hình lăng trụ đứng ABC.A′B C
′ ′ có AB = a , AC = 2a , AA′ = U U 2   và góc 
BAC = 60° . Gọi M là điểm trên cạnh CC′ sao cho CM = 2MC′ .
a) Chứng minh rằng AM ⊥ B M ′ .
b) Tính khoảng cách từ đỉnh A′ đến mặt phẳng ( AB M ′ ) . 1
Câu 4 (1,0 điểm) Cho dãy số (u có số hạng tổng quát u = 1− , n ∈  . n ( * 2 ) n ) U U (n + ) 1
Tính lim (u u u u . 1 2 3 n )
Câu 5 (1,0 điểm) Cho đa giác lồi ( H ) có n đỉnh ( n ∈ , n > 4 ). Biết số các tam giác có ba U U
đỉnh là đỉnh của (H ) và không có cạnh nào là cạnh của (H ) gấp 5 lần số các tam giác có ba
đỉnh là đỉnh của (H ) và có đúng một cạnh là cạnh của (H ) . Xác định n.
Câu 6 (1,0 điểm) Trong mặt phẳng với hệ tọa độ Oxy, cho hình bình hành ABCD có phương U U
trình đường chéo AC là x − y +1 = 0 , điểm G (1;4) là trọng tâm tam giác ABC, điểm E (0; 3
− ) thuộc đường cao kẻ từ D của tam giác ACD. Tìm tọa độ các đỉnh của hình bình
hành đã cho, biết rằng diện tích tứ giác AGCD bằng 32 và đỉnh A có tung độ dương.
Câu 7 (1,0 điểm) Cho a,b, c > 0 và a + b + c = 3 . Chứng minh bất đẳng thức: U U 1 1 1 + + ≤ 1 2 2 2 a + b + c b + c + a c + a + b
--------------- HẾT --------------- TRƯỜ
HƯỚNG DẪN CHẤM THI CHỌN HỌC SINH GIỎI 12 NG THPT ĐỒNG ĐẬ
NĂM HỌC: 2019 - 2020 U MÔN: TOÁN
Thời gian: 180 phút (không kể thời gian giao đề)
I. Những lưu ý chung: U U
- Điểm toàn bài thi không làm tròn.
- Câu 3 học sinh không vẽ hình thì không cho điểm.
- Học sinh giải theo cách khác đáp án mà đúng vẫn cho điểm tối đa.
II. Đáp án và thang điểm: U U Câu Đáp án Điểm 1
a)Tìm tất cả các giá trị của tham số m để hàm số 1 1 3 y =
mx − (m − ) 2
1 x + 3(m − 2) x + 2019 đồng biến trên [2; +∞) . 3 Ycbt 2
⇔ y′ = mx − 2(m − )
1 x + 3(m − 2) ≥ 0, x ∀ ∈[2;+∞) 0,25 2 − x + 6 ⇔ 0,25 m ≥ = f x , x
∀ ∈ 2;+∞ ⇔ m ≥ max f x 2 ( ) [ ) ( ) − + [2;+∞) x 2x 3 2 ( 2 x − 6x + 3) x = 3+ 6 (tm) 0,25
Ta có: f ′( x) =
; f ′ x = 0 ⇔  2 ( ) ( 2x −2x+3) x = 3− 6  (ktm) 0,25 mx − m + 2 1 b) Cho hàm số y =
có đồ thị là (C). Tìm tất cả các giá trị của tham số x +1
m để đường thẳng d : y = 2x −1 cắt (C) tại hai điểm phân biệt A, B sao cho góc
giữa hai đường thẳng OA, OB bằng 45° . Phương trình hoành độ: 0,25 x = 1 mx − m + 2 2x 1 (x )
1 (2x 3 m) 0,( x ) 1  = − ⇔ − + − = ≠ − ⇔ m − 3 x +1 x =  2
Đường thẳng d cắt (C) tại hai điểm phân biệt A, B khi và chỉ khi m ≠ 1∧ m ≠ 5. 0,25 Khi đó,  −  A( ) m 3 1;1 , B ; m − 4   .  2 
Điều kiện để OA, OB tạo với nhau một góc 45° là: 0,25 2   m − 3 2  m − 3  . OA OB = . OA . OB cos 45° ⇔ + m − 4 = 2. . +   (m − 4)2 2 2  2  m = 3 0,25 2
⇔ m − 7m +12 = 0 ⇔  (tm) m = 4 2
cos x (2sin x + ) 1 1
a) Giải phương trình lượng giác sau ( = . x + )( x − ) 3 sin 1 2 sin 1 si  n x ≠ 1 − 0,25 ĐKXĐ: 
1 . Phương trình đã cho biến đổi thành: sin x ≠  2 x + x = ( 2 sin 2 cos
3 2 sin x + sin x − ) 1
⇔ sin 2x + cos x = 3 (sin x − cos 2x)  π   π  ⇔ 0,25
sin 2x + 3 cos 2x = 3 sin x − cos x ⇔ sin 2x + = sin x −      3   6   π π  π 0,25 2x + = x − + k2π x = − + k2π (ktm)   3 6 2 ⇔  ⇔  π 7π 5π 2π   2x + = −x + + k2π x = + k. (tm)  3 6  18 3 5π 2π 0,25
Vậy nghiệm của phương trình là: x = + k. , (k ∈ ) 18 3 2 2
x − 4y +3 x y +3y +3 = 0 1
b) Giải hệ phương trình sau  (
x, y ∈ ) . 2 3
 x + 3x − y + 5 + 3x − 2 = 2   ≥ 0,5 ĐK: y 0 
. Biến đổi phương trình đầu về dạng: 2
x + 3x − y + 5 ≥ 0  y  = 1 2 y y x + 3 2 4 − 3 −1 = 0 ⇔  ⇒ y = x + 3 2 2 x + 3 x + 3  y 1  = − l 2 ( )  x + 3 4 Thay 2
y = x + 3 vào phương trình thứ hai, ta được: 0,25 2  3
2x + 3 + 3x − 2 = 2 . Vế trái pt là hàm đồng biến trên ; +∞   mà x = 2 là 3  2  2  31
nghiệm nên nghiệm đó duy nhất. Suy ra: y = + 3 =   (tm)  3  9   0,25
Vậy, nghiệm của hệ là: ( x y) 2 31 ; = ;    3 9  3 2 Cho hình lăng trụ 3a 6
đứng ABC.A′B C
′ ′ có AB = a , AC = 2a , AA′ = và góc 2   
BAC = 60° . Gọi M là điểm trên cạnh CC′ sao cho CM = 2MC′ .
a) Chứng minh rằng AM ⊥ B M ′ .
b) Tính khoảng cách từ đỉnh A′ đến mặt phẳng ( AB M ′ ) . a) Chứng minh rằng 0,5 AM ⊥ B M
′ .  
Từ giả thiết CM = 2MC′ suy ra: a 6
CM = a 6, MC′ = 2 Áp dụng định lí cosin trong tam giác ABC ⇒ BC = a 3 .
Sử dụng Pitago, dễ dàng 0,25 tính được: 2 29a 2 2 2 AB′ = , AM = 10a 2 2 9a và 2 B M ′ = . 2 Từ đó suy ra: 0,25 2 2 2
AB′ = AM + B M ′ hay tam giác AB M ′ vuông tại M.
b) Tính khoảng cách từ đỉnh A′ đến mặt phẳng ( AB M
′ ) . Đặt N = AM ∩ A′C′, 0,25
gọi K là hình chiếu vuông góc của A′ lên B N
′ và H là hình chiếu vuông góc của B N
′ ⊥ AK ⇒ B N ′ ⊥ A′H
A′ lên AK. Ta có 
⇒ A′H ⊥ ( AB M ′ )
A′H ⊥ AK 1 0,25 Do NC ∆ M ′  A
∆ CM theo tỉ số k = nên dễ dàng suy ra: C N
′ = a và theo định 2 lí cosin suy ra: B N ′ = a 7 1 0,25 2. .3 a . a sin 60° 2.S ′ ′ 3a 21 A B N 2 A′K = = = B N ′ a 7 14 1 1 1 3a 10 0,25
Trong tam giác vuông AA′K ta có: = + ⇒ A′H = 2 2 2 A′H AA′ A′K 10 3a 10
Vậy khoảng cách từ A′ đến mặt phẳng ( AB M ′ ) bằng . 10 4 1 1
Cho dãy số (u có số hạng tổng quát u = 1− , n ∈  . n ( * 2 ) n ) (n + ) 1
Tính lim (u u u u . 1 2 3 n ) 1 n (n + 2) 0,25 Ta có: * u = 1− = n ∀ ∈  n (n + ) , 2 1 (n + )2 1 1.3 2.4 3.5 4.6 n (n + 2) 1 n + 2 0,5
Suy ra: u u u u =  = . 1 2 3 n 2 2 2 2 2 3 4 5 (n + )2 1 2 n +1 Do đó, ( 1 0,25 lim u u u u = 1 2 3 n ) 2 5
Cho đa giác lồi (H ) có n đỉnh ( n∈,n > 4 ). Biết số các tam giác có ba đỉnh là 1
đỉnh của (H ) và không có cạnh nào là cạnh của (H ) gấp 5 lần số các tam giác
có ba đỉnh là đỉnh của (H ) và có đúng một cạnh là cạnh của (H ) . Xác định n.
Số các tam giác có 3 đỉnh là đỉnh của (H) là: 3 C 0,25 n
Số các tam giác có 3 đỉnh là đỉnh của (H) và có đúng 2 cạnh là cạnh của (H) là: n 0,25
Số các tam giác có 3 đỉnh là đỉnh của (H) và có đúng 1 cạnh là cạnh của (H) là: 0,25 n (n − 4) Theo giả thiết, ta có: 0,25 n = 4(ktm) 3
C − n − n n − = n n − ⇔ n − n + = ⇔  n ( 4) 5 ( 4) 2 39 140 0 n = 35  (tm)
Vậy đa giác (H) có 35 đỉnh. 6
Trong mặt phẳng với hệ tọa độ Oxy, cho hình bình hành ABCD có phương trình 1
đường chéo AC là x − y +1 = 0 , điểm G (1;4) là trọng tâm tam giác ABC, điểm E (0; 3
− ) thuộc đường cao kẻ từ D của tam giác ACD. Tìm tọa độ các đỉnh của
hình bình hành đã cho, biết rằng diện tích tứ giác AGCD bằng 32 và đỉnh A có tung độ dương.
Vì DE ⊥ AC nên 0,25
DE : x + y + 3 = 0 ⇒ D (t; t − − 3) . Ta có, d (G AC ) 1 = d (B AC) 1 , ,
= d (D, AC) 3 3 1 2t + 4
t =1⇒ D(1; 4 − ) ⇔ 2 = ⇔  3 2 t = 5 − ⇒ D  ( 5; − 2)
Vì D và G nằm khác phía so với AC nên D (1; 4
− ) ⇒ B(1;8) ⇒ B : x =1 0,25
Vì A ∈ AC ⇒ A( ; a a + ) 1 . Từ gt S = 32 ⇒ S = 24 nên 0,25 AGCD ABD
a = 5 ⇒ A(5;6 1 )(tm) d ( ,
A B).DB = 24 ⇔ a −1 = 4 ⇒  2 a = 3 − ⇒ A  ( 3 − ; 2 − )(l)  
Từ AD = BC ⇒ C ( 3 − ; 2
− ) . Vậy tọa độ 4 đỉnh của hình bình hành là: 0,25 A(5;6), B ( 1;8), C ( 3 − ; 2 − ), D( 1; 4 − ) 7
Cho a, b, c > 0 và a + b + c = 3 . Chứng minh bất đẳng thức: 1 1 1 1 + + ≤ 1 2 2 2
a + b + c b + c + a c + a + b Đưa bất đẳ 1 1 1 0,25 ng thức về dạng: + + ≤ 1 2 2 2 a − a + 3 b − b + 3 c − c + 3 1 −x + 4 Ta chứng minh BĐT phụ: ≤ , x ∀ ∈ 0;3 . 2 ( ) x − x + 3 9 2
Thật vậy, ta có: BĐT phụ tương đương với: ( x − )
1 ( x − 3) ≤ 0 luôn đúng, x ∀ ∈(0;3).
Dấu bằng xảy ra khi x = 1 .
Vì a, b, c là ba số dương có tổng bằng 3 nên: 0 < a,b, c < 3. 0,25
Áp dụng BĐT phụ cho 3 số a, b, c: 1 −a + 4 1 b − + 4 1 −c + 4 ≤ ; ≤ ; ≤ . 2 2 2 a − a + 3 9 b − b + 3 9 c − c + 3 9
Cộng vế theo vế ba bất đẳng thức trên , ta có: 0,25 1 1 1
−(a + b + c) +12 + + ≤ =1 (đpcm) 2 2 2 a − a + 3 b − b + 3 c − c + 3 9
Dấu bằng xảy ra khi a = b = c = 1 . 0,25
--------------- HẾT ---------------
Document Outline

• DE-THI-HSG-12
• HUONG-DAN-CHAM-HSG-12