Đề thi học sinh giỏi Toán 12 năm 2020 – 2021 sở GD&ĐT Quảng Trị

UBND TỈNH QUẢNG TRỊ
KỲ THI CHỌN HỌC SINH GIỎI VĂN HÓA LỚP 12
SỞ GIÁO DỤC VÀ ĐÀO TẠO
Khóa ngày 06 tháng 10 năm 2020 ĐỀ CHÍNH THỨC Môn thi: TOÁN
Thời gian làm bài 180 phút (không kể thời gian giao đề)
Câu 1. (5,0 điểm)
1. Tìm tất các các điểm cực đại và điểm cực tiểu của hàm số y  cos x  sin . x
2. Tìm m để phương trình 4 2
2x  4x 1  2m  0 có đúng 5 nghiệm phân biệt.
Câu 2. (5,0 điểm) 1. Chứng minh rằng 1 2 1010 2019 C  2C  ... 1010C 1010.2 . 2020 2020 2020
2. Tìm tất cả các cặp số thực  ;
x y thỏa mãn xy  4 và
x  y2  20  x  yxy 8.
Câu 3. (6,0 điểm)
1. Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, tam giác SAB
vuông cân tại S và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Tính thể tích
của khối chóp S.ABC và khoảng cách giữa hai đường thẳng SB và AC theo . a
2. Cho tam giác ABC ngoại tiếp đường tròn (I ). Gọi M , D, E lần lượt là trung
điểm của BC, IB, IC; F, G lần lượt là tâm đường tròn ngoại tiếp các tam giác ABD
và ACE. Chứng minh rằng AM vuông góc F . G
Câu 4. (2,0 điểm)
Cho dãy số  x được xác định bởi x  2 và x  2  x , n  1. Chứng minh n  1 n 1  n
dãy số  x có giới hạn và tìm giới hạn đó. n 
Câu 5. (2,0 điểm)
Xét các số thực dương a,b,c có tổng bằng 3. Tìm giá trị nhỏ nhất của biểu thức
2b  c 2c  a 2a  b 18abc P     . a b c
ab  bc  ca
========== HẾT ==========
Thí sinh không được sử dụng máy tính cầm tay. HƯỚNG DẪN GIẢI
Câu 1.1. Tìm tất các các điểm cực đại và điểm cực tiểu của hàm số y  cos x  sin . x  
x    k2 
y '  sin x  cos x ; 4 y '  0   3 x   k2  4     3 
y ''  sin x  cos x ; y ''   k2   2  0; y ''  k2  2  0      4   4  3
Vậy các điểm cực đại của hàm số là: x 
 k2 ; Các điểm cực tiểu của hàm số là: 4 
x    k2 4
Câu 1. 2. Tìm m để phương trình 4 2
2x  4x 1  2m  0 có đúng 5 nghiệm phân biệt. 4 2 4 2
2x  4x 1  2m  0  2x  4x 1  2m .
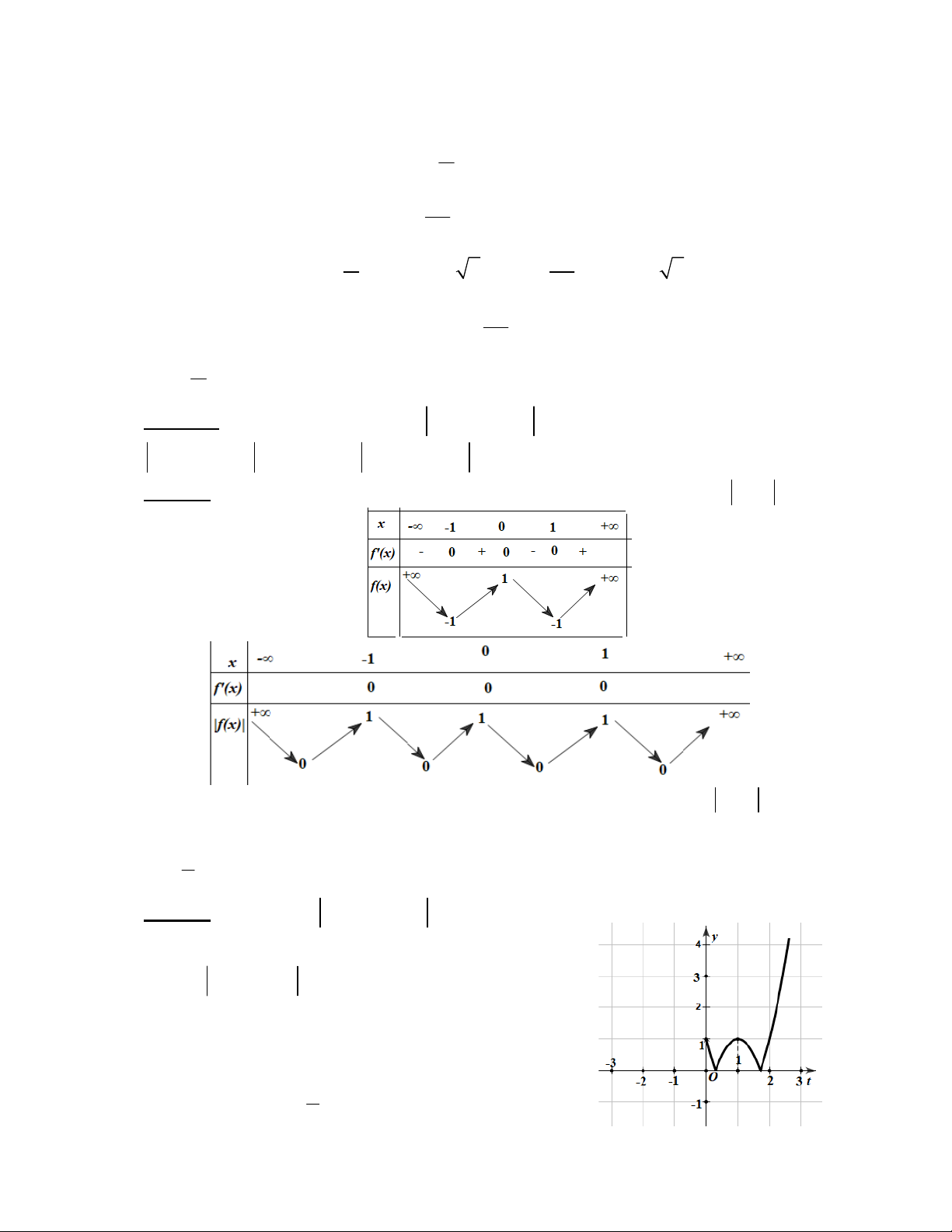
Cách 1: Xét hàm số 4 2
f (x)  2x  4x 1 có BBT của hàm số f (x) và f (x)
Số nghiệm của phương trình bằng số giao điểm cửa đồ thị hàm số f (x) và đường
thẳng y  m . Vậy phương trình đã cho có đúng 5 nghiệm phân biệt khi 2m 1 hay 1 m  . 2
Cách 2: (HS 10,11). 4 2
2x  4x 1  2m (1) . Đặt 2
t  x ,t  0 PTTT: 2
2t  4t 1  2m (2). Xét hàm số 2
f (t)  2t  4t 1 trên [0;) . | f (t) |có đồ thị
Biện luận các trường hợp số nghiệm của (2) và (1). 1
Từ đó kết luận m  . 2
Cách 3: Nhận thấy nếu x là nghiệm của (1) thì x cũng là nghiệm của pt (1). Do đó 0 0
nếu các nghiệm x  0 thì số nghiệm của phương trình (1) là số chẵn. Vậy đk cần để i 1
pt có 5 nghiệm là pt (1) có nghiệm x  0 , thế vào tìm được m  . Giải phương 0 2 1
trình khi m  và kết luận. 2
Câu 2.1. Chứng minh rằng 1 2 1010 2019 C  2C  ... 1010C 1010.2 . 2020 2020 2020
Cách 1: Ta có: n n  k ! ( 1)! k 1
k.C  k.  n  nC  n k  ! n  k  n 1 !
(k 1)!(n  k)!  1 0 C  2020C 2020 2019 2 1 2C  2020C ... 2020 2019 1010 1009 1010C  2020C . 2020 2019 VT  2020 0 1 1009 C  C  ...  C 2019 2019 2019  Xét 0 1 1009 1010 2019 2019 C  C  ...  C  C  ...  C  2 . Mà k n k C C   nên 2019 2019 2019 2019 2019 n n 2 0 1 1009 C  C  ...  C  2019  2 . 2019 2019 2019 Vậy VT  2020 0 1 1009 C  C  ...  C  2019 1010.2 . 2019 2019 2019 Cách 2: Xét 2020 0 1 2 2 2020 2020 (1 x)  C  xC  x C  ...  x C 2020 2020 2020 2020 Suy ra được: 2019 1 2 2019 2020 2020(1 x)  C  2xC  ...  2020x C 2020 2020 2020 1 2 1010 1011 2020 2019 C  2C  ... 1010C 1011C  ...  2020C  2020.2 2020 2020 2020 2020 2020 Ta có: n n n k ! ! ! nk 1 k.C k. n k n k C          n
k n  k  ( 1) ( 1) !
! (k 1)!(n  k)!
(n  k 1)!(k 1)! n Do đó: 1 2020 C  2020C 2020 2020 2 2019 2C  2019C 2020 2020 ... 1010 1011 1010C 1011C 2020 2020 Vậy: 1 2 1010 2019 C  2C  ... 1010C 1010.2 2020 2020 2020
Câu 2.2. Tìm tất cả các cặp số thực  ;
x y thỏa mãn xy  4 và
x  y2  20  x  yxy 8. Đặt 2
S  x  y; P  xy (S  4P) . Từ giả thiết ta có: 2
S  4P  S(P  8)  20  0 2
S  S(P  8)  4P  20  0 . Xét pt theo S. 2 2
  (P  8)  4( 4
 P  20)  P 16. Điều
kiện phương trình có nghiệm P  4 . Kết hợp điều kiện của giả thiết ta có P  4, P  4  .
P  4  S  2  (loại); P  4   S  6
 , x, y là 2 nghiệm của pt 2
X  6X  4  0 Vậy các cặp ;
x y: 3 13;3 13,3  13; 3   13.
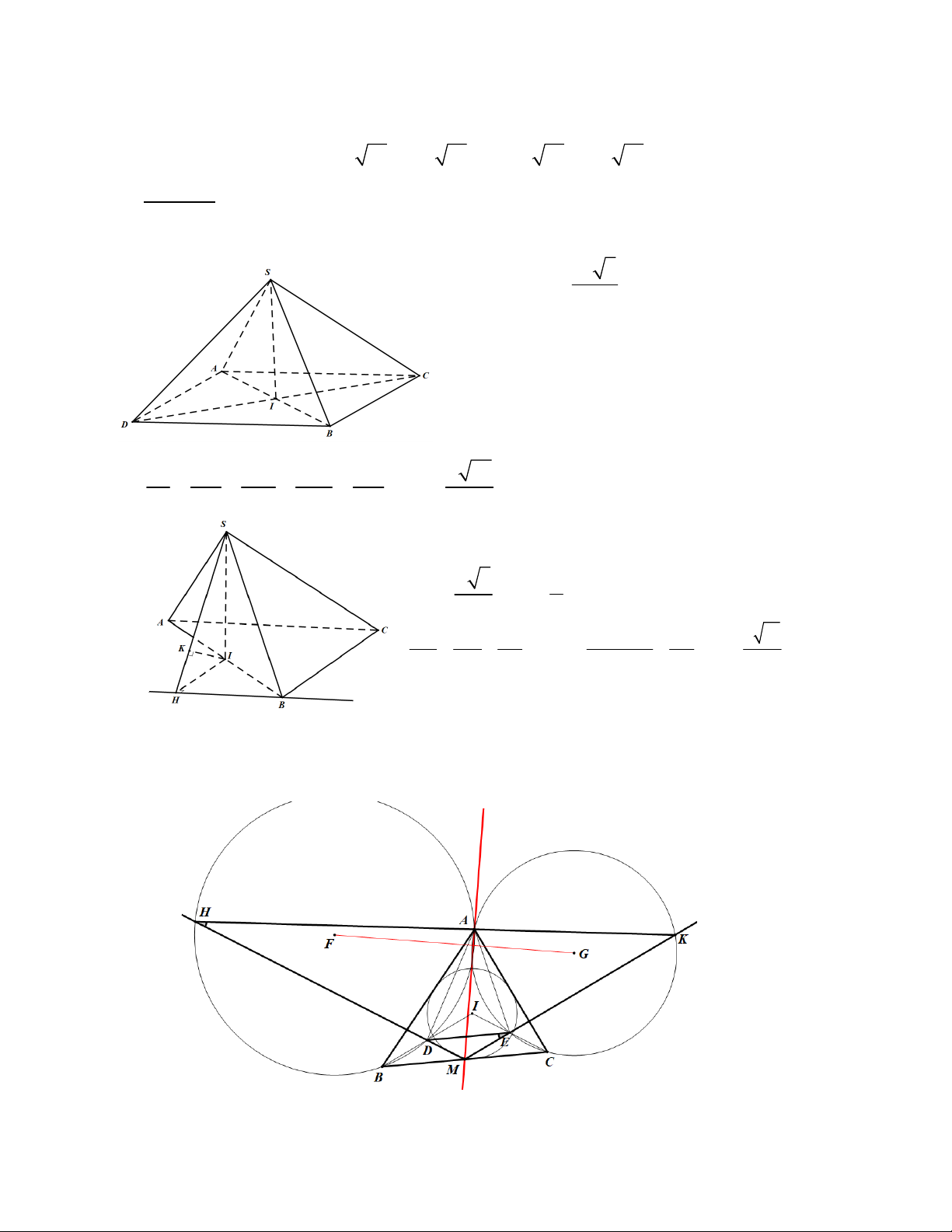
Câu 3.1. Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, tam giác SAB
vuông cân tại S và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Tính thể tích
của khối chóp S.ABC và khoảng cách giữa hai đường thẳng SB và AC theo . a 3 a 3 *Thể tích: V  . 24
*Khoảng cách giữa SB và AC :
Cách 1: Dựng D đối xứng với C qua I d(S , B A ) C  d( ,( AC SB )
D )  2d(I,(S ) BD )  2HK
ACBD là hình thoi, nên IB, ID, IS đôi một vuông góc. 1 1 1 1 28 a 21      d  . 2 2 2 2 2 d SI SB SD 3a 7
Cách 2: *Kẻ đt BD song song với AC. d(S , B A ) C  d( ,( AC SB )
D )  2d(I,(S ) BD )  2HK a 3 a HI  ; SI  4 2 2 2 2 1 1 1 2 IH .SI 3a a 21   IK   d   2 2 2 2 2 IK IH SI IH SI 28 7
Câu 3.2. Cho tam giác ABC ngoại tiếp đường tròn (I ). Gọi M , D, E lần lượt là
trung điểm của BC, I ,
B IC; F, G lần lượt là tâm đường tròn ngoại tiếp các tam giác
ABD và ACE. Chứng minh rằng AM vuông góc F . G
Gọi H là giao điểm thứ 2 của MD và đường tròn qua , A B, . D
Gọi K là giao điểm thứ 2 của ME và đường tròn qua , A C, E. Ta có:  1  1
AHM  B và   
AKM  C  EDM nên ,
A H , K thẳng hàng. 2 2
Tam giác MDE và MKH đồng dạng (Vì  
MED  MHK ). Suy ra ME.MK  M . D MH , hay
M nằm trên trục đẳng phương của hai đường tròn tâm F, G.
Suy ra AM  F .
G (Trục đẳng phương vuông góc với đường nối tâm)
Câu 4. (2,0 điểm)
Cho dãy số  x được xác định bởi x  2 và x  2  x , n  1. Chứng minh n  1 n 1  n
dãy số  x có giới hạn và tìm giới hạn đó. n 
HD: 0  x  2, n  1. n Ta có: x  x  x  x . n 1  n n2 n 1 
x  2 , x  2  2 , x  2  2  2 , như vậy x  x nên từ (*) ta suy ra 1 2 3 3 1 x
là dãy giảm. Cùng với tính bị chặn nên tồn tại lim x  . a 2n 1   2n 1  n
Từ x  x  x  x . Tương tự tồn tại lim x  . b 3 1 4 2 2n n
Từ hệ thức truy hồi ở giả thiết, chuyển qua giới hạn ta được:
a  2  b a 1    b   2  a b  1 Do lim x
 lim x 1 nên lim x 1. 2n 1  2n n n n n 1 x Cách 2: x 1  2  x 1 n  n 1  n 2  x 1 n 1 x 1  1 x . n 1  n 2  x 1 n 1 1
Do 0  x  2, n  1   q(0;1) n 2  x 1 n 2  2 1 2
 x 1  x 1.q  x 1.q  ...  x 1. n q n 1  n n 1  1 lim x
1  0  lim x 1 lim x 1 n 1  n 1  n
Cách 3: 0  x  2, n  1. n Đặt  
x  2cos ,  0; . Ta có   ; x  2cos n  n n 1 1 4 4     x
 2  x  2cos  2(1 cos )  2sin n  2cos n  n 1  n n 1  n   2  2 2     1    n            n 1  n 1   2 2  3 2 n  3  n n 1  1      1            . n 1     1     2   3   2  6   1 n    
 x  2cos       lim x 1. n  3 2 6 n     
Câu 5. (2,0 điểm)
Xét các số thực dương a,b,c có tổng bằng 3. Tìm giá trị nhỏ nhất của biểu thức
2b  c 2c  a 2a  b 18abc P     . a b c
ab  bc  ca 2b  c 2c  a 2a  b 18abc HD: P  1 1 1  3. a b c
ab  bc  ca
b  3 c  3 a  3 18abc      3 a b c
ab  bc  ca b c a  1 1 1  18  1 1 1  18     3     3  3        a b c  a b c 1 1 1   a b c 1 1 1      a b c a b c  1 1 1  18  3      .(1)  a b c 1 1 1    a b c 1 1 1 9 Ta có:     3 (2) a b c
a  b  c 1 1 1 18
Đặt t     3. Xét hàm f (t)  3t  trên [3;) a b c t
Ta có: f (t) 15  f (3) . (3)
Vậy min P 15 đạt được khi các đẳng thức (1), (2), (3) xảy ra. b c a   a b c  1 1 1
    3,hay a  b  c 1. a b c 
a  b  c   1 1 1  18  1 1 1   1 1 1  18 Cách 2: …..  3        2           a b c 1 1 1   a b c   a b c 1 1 1      a b c a b c  3  2 2.18 15. ….
========== HẾT ==========