
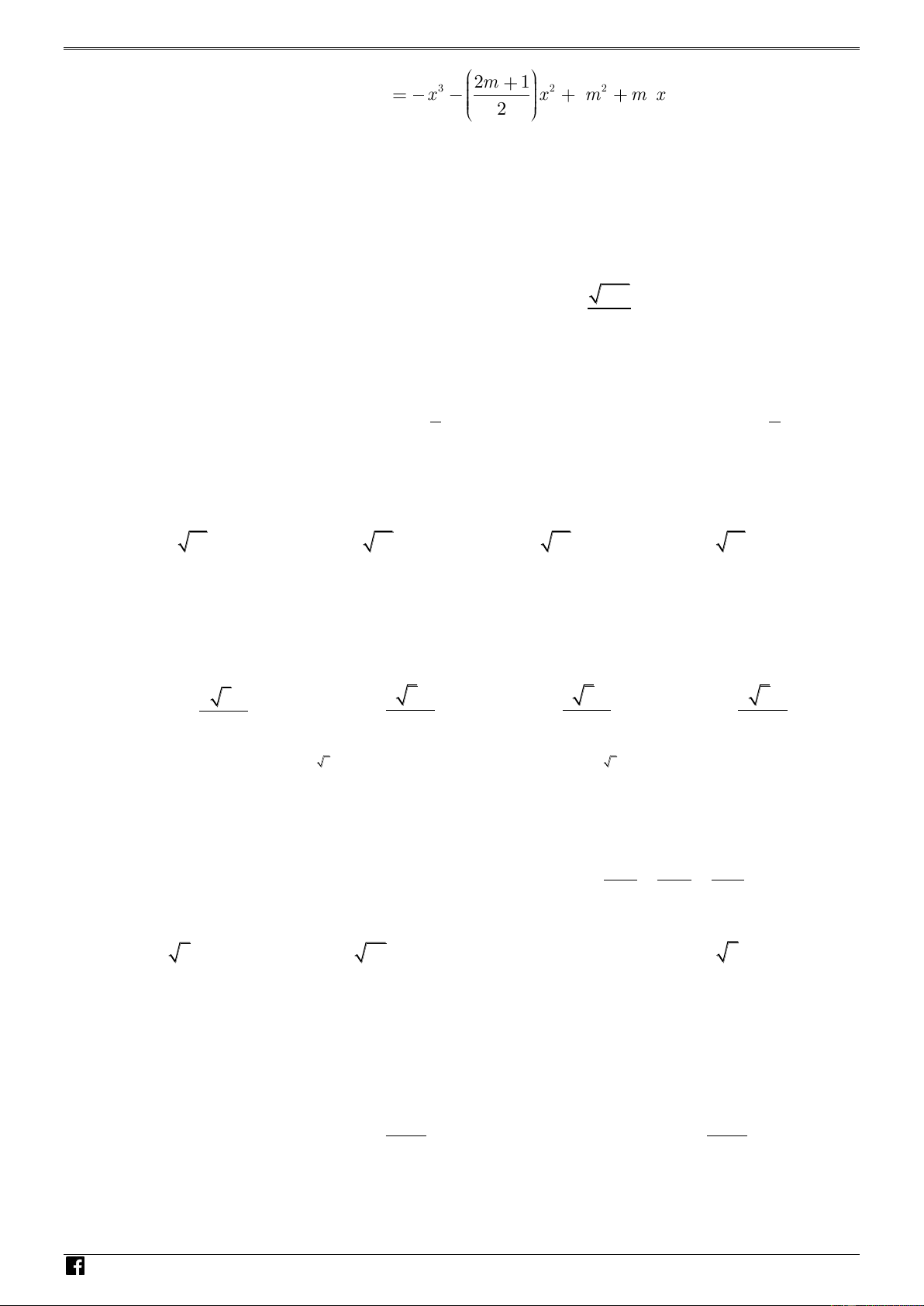











Preview text:
NHÓM TOÁN VD – VDC HSG QUẢNG NAM-2020
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI HỌC SINH GIỎI LỚP 12 THPT CẤP TỈNH QUẢNG NAM NĂM HỌC: 2019 - 2020 N Môn thi: TOÁN H
Thời gian làm bài: 90 phút (không kể thời gian phát đề) Ó M T .
Ngày thi: 10 tháng 06 năm 2020 O Á N V
Họ và tên: ……………………………………………… D
…………. SBD: ……………… – VDC 2 x 3 Câu 1. Hàm số y
nghịch biến trên khoảng nào dưới đây? x 1 A. (1; 3). B. ( ; 1). C. ( 3;1). D. (1; ). Câu 2.
Trong không gian Oxyz cho u (2; 1;1), v
( 3;4; 5). Số đo góc giữa hai vectơ u và v bằng A. 0 150 . B. 0 120 . C. 0 60 . D. 0 30 . Câu 3.
Cho khối chóp có chiều cao bằng 2a , đáy là hình thoi cạnh a và có một góc bằng 60 . Thể
tích của khối chóp đã cho bằng 3 a 3 3 a 3 3 a 3 A. 3 a 3 . B. . C. . D. . 3 2 6 Câu 4.
Điểm cực đại của hàm số 3
y x 3x 2 là N A. x 1 .
B. x 4 .
C. x 0 . D. x 1 . H Ó M T Câu 5.
Trong không gian Oxyz , giao tuyến của hai mặt phẳng P : x 2y 3z 0 , 4 1 0 O Q : x z
có một véc tơ chỉ phương là. Á N A. u 5; 2 ; 3 . B. u 5; 2; 3 . C. u 8;1; 2 . D. u 4; 1 ; 2 . 4 3 2 1 V D 3 1 – Câu 6. Nếu tích phân f x dx 6 thì f 2x 1 dx bằng VDC 1 0 A. 3 . B. 12 . C. 6 . D. 4 . Câu 7.
Giá trị lớn nhất của hàm số y 2 x x 1 bằng A. 3 . B. 3 . C. 0 . D. 2 . Câu 8.
Cho hình nón có bán kính đáy bằng 1, góc giữa đường sinh và trục của hình nón bằng 0 30 .
Diện tích xung quanh của hình nón đã cho bằng 4 3 2 3 A. . B. 3 . C. . D. 2 . 3 3 Câu 9.
Trong không gian Oxyz , điểm đối xứng với điểm M 4; 5 ;
3 qua trục Oz có tọa độ là
https://www.facebook.com/groups/toanvd.vdc Trang 1
NHÓM TOÁN VD – VDC HSG QUẢNG NAM-2020 A. 4; 5 ; 3 . B. 4 ;5;3. C. 4 ;5; 3 . D. 0;0;3 . 2 x 4 N
Câu 10. Tổng số đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số y là 3 2 H
x x 2x Ó M T A. 4 . B. 3 . C. 2 . D. 1. O
Câu 11. Bất phương trình log x 1 log
6x 5 có bao nhiêu nghiệm nguyên? 2 4 Á N A. 6 . B. 7 . C. 8 . D. 9 . V D 1 –
Câu 12. Họ tất cả nguyên hàm của hàm số f x là 2 VDC 4x 4x 1 1 1 1 1 A. C . B. C . C. C . D. C . 22x 1 2x 1 2x 1 22x 1
Câu 13. Số điểm cực trị của hàm số 2
y x sin x trong khoảng ;2 là A. 0 . B. 1. C. 2 . D. 3 . x x
Câu 14. Tích các nghiệm của phương trình 2 5 2 3
7 4 3 0 bằng A. 2 . B. 2 . C. 5 . D. 5 .
Câu 15. Cho khối trụ có chiều cao bằng bán kính đáy và có diện tích thiết diện qua trục của khối trụ
bằng 16 . Thể tích khối trụ đã cho bằng. 64 16 2 A. 64 . B. . C. 16 2 . D. . 3 3 N H 2 x 2 x Ó
Câu 16. Biết x 1 .e dx
a x b.e
C , với a, b là các số hữu tỉ. Giá trị của a b bằng. M T 5 O A. . B. 4 . C. 1 . D. 2 . Á 2 N V x
Câu 17. Biết phương trình 2 log x log
0 có hai nghiệm x , x với x x . Hiệu x x bằng D 9 3 27 1 2 1 2 2 1 – VDC 80 80 6560 6560 A. . B. . C. . D. . 3 27 27 729
Câu 18. Biết rằng tập nghiệm của bất phương trình 4x 8.6x 12.9x 0 là khoảng ;
a b . Giá trị của
b a bằng A. log 4 . B. log 4 . C. log 3 . D. log 3 . 2 2 2 2 3 3 3 3
Câu 19. Cho hình lập phương ABC . D A B C D
cạnh a . Thể tích khối cầu có tâm A và tiếp xúc với đường thẳng A C bằng 3 2 a 3 8 6 a 3 3 a A. . B. . C. . D. 3 6 a . 3 27 2
https://www.facebook.com/groups/toanvd.vdc Trang 2
NHÓM TOÁN VD – VDC HSG QUẢNG NAM-2020 4 Câu 20. Biết 2
x dx a b c với a, ,
b c là các số hữu tỉ. Giá trị của a b c bằng 3 N 41 25 13 5 H A. . B. . C. . D. . Ó 2 2 2 2 M T a O
Câu 21. Biết nghiệm dương nhỏ nhất của phương trình 21 3.cosxsinx cos2x là x , với a,b 0 Á b N
là các số nguyên dương và a 10 . Giá trị của a+b bằng V A. 23 B. 7 C. 11 D. 17 D – 2x 1 VDC
Câu 22. Tiếp tuyến đi qua điểm A 1
;0 của đồ thị hàm số y
C có phương trình là x 1 1 1 A. y x .
B. y x 1.
C. y 3x 3.
D. y x 1. 3 3
Câu 23. Cho phương trình 9x 2 1 .3x m
m 7 0 với m là tham số. Có bao nhiêu giá trị nguyên
của m để phương trình đã cho có 2 nghiệm thực phân biệt? A. 3 . B. 4 . C. 5 . D. Vô số.
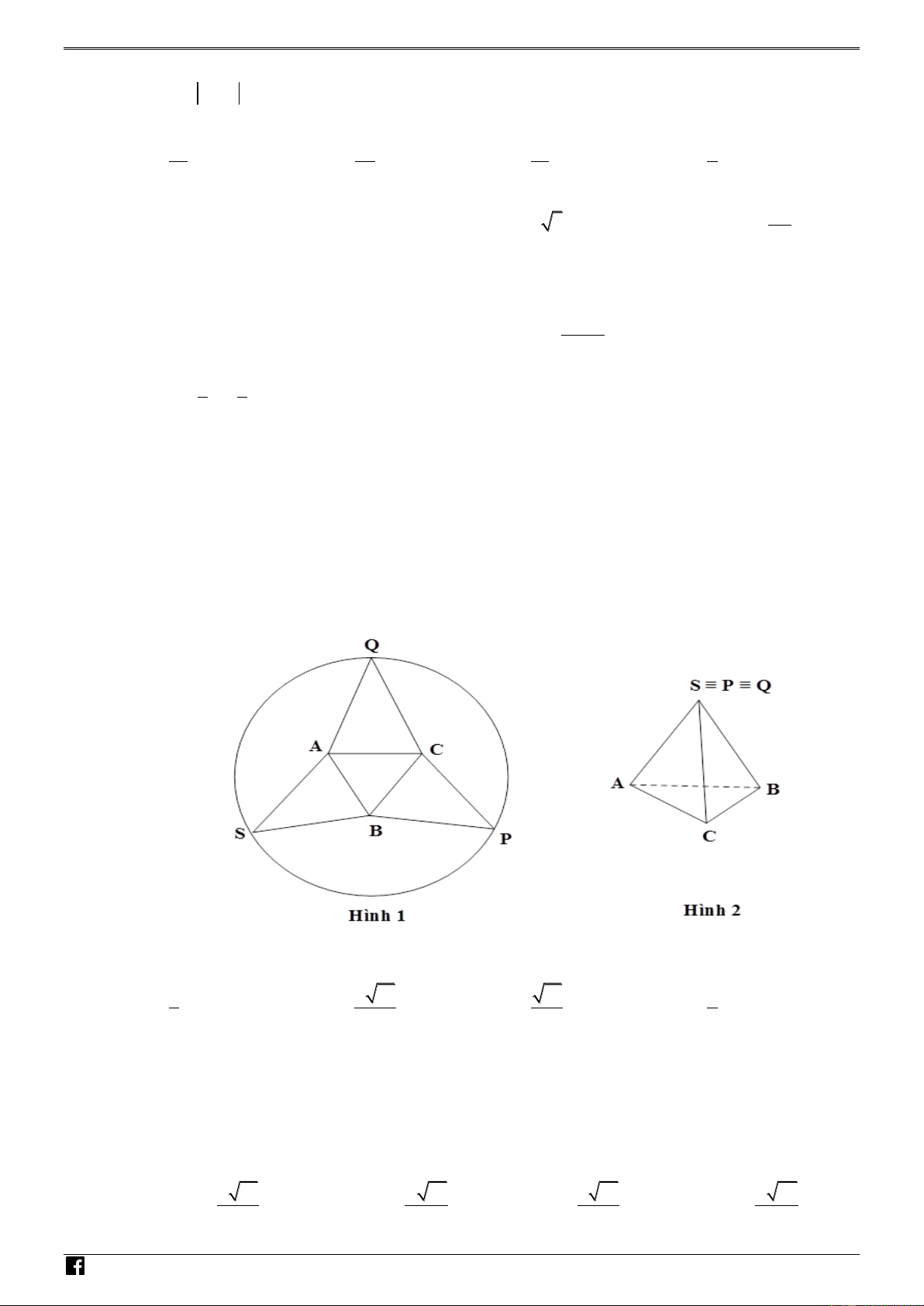
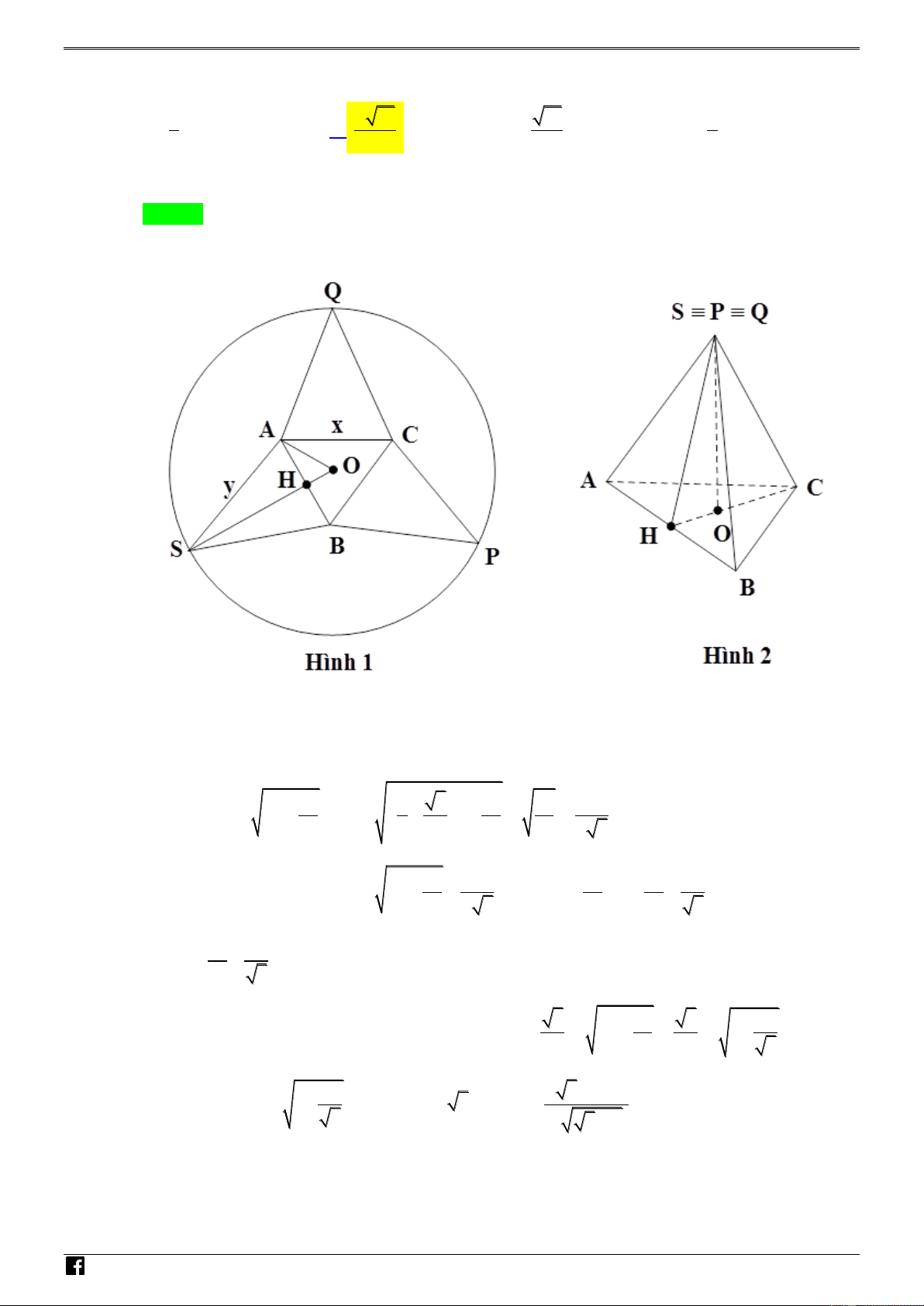
Câu 24. Cắt tấm bìa hình tròn có bán kính bằng 1 ( độ dày không đáng kể) theo đường gấp khúc
SAQCPBS như hình 1, sau đó gấp phần đa giác còn lại theo các đoạn AB , BC , CA sao cho các điểm S, ,
P Q trùng nhau để được hình chóp đều có đáy là tam giác ABC như hình 2. N H Ó M T O Á N V D – VDC
Giá trị lớn nhất của thể tích khối chóp SABC bằng 1 4 15 15 4 A. . B. . C. . D. 9 125 125 9
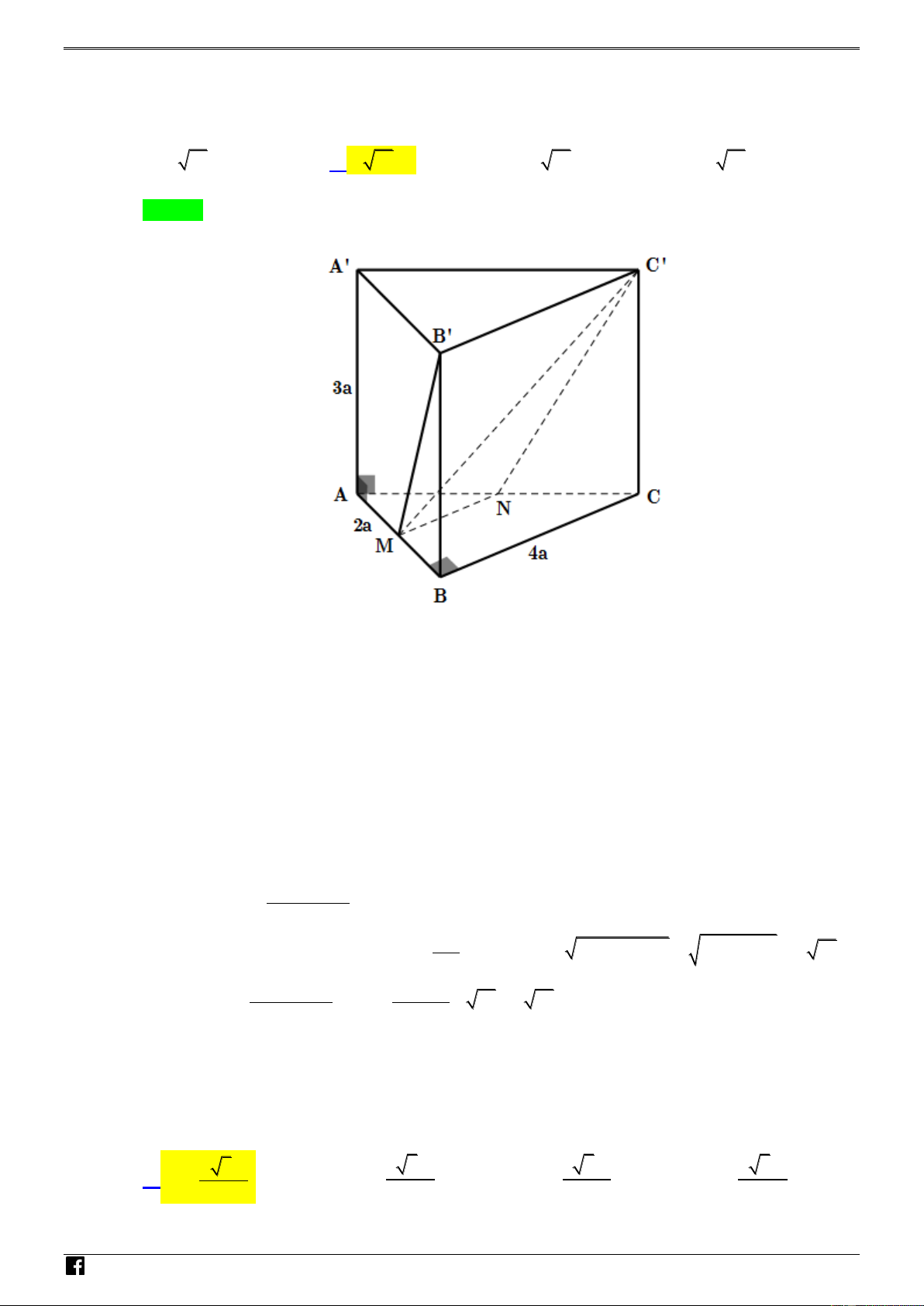
Câu 25. Cho lăng trụ tam giác đều ABC.A' B 'C ' có cạnh đáy bằng a và chiều cao bằng 3a . Một hình
trụ T có hai đáy nội tiếp tam giác ABC,A' B 'C ' . Gọi M là trung điểm cạnh BC . Đường
thẳng A' M cắt mặt xung quanh của hình trụ T tại N ( N khác M ). Tính độ dài đoạn thẳng MN . a 15 a 15 a 39 a 39 A. MN . B. MN . C. MN . D. MN . 3 6 3 6
https://www.facebook.com/groups/toanvd.vdc Trang 3
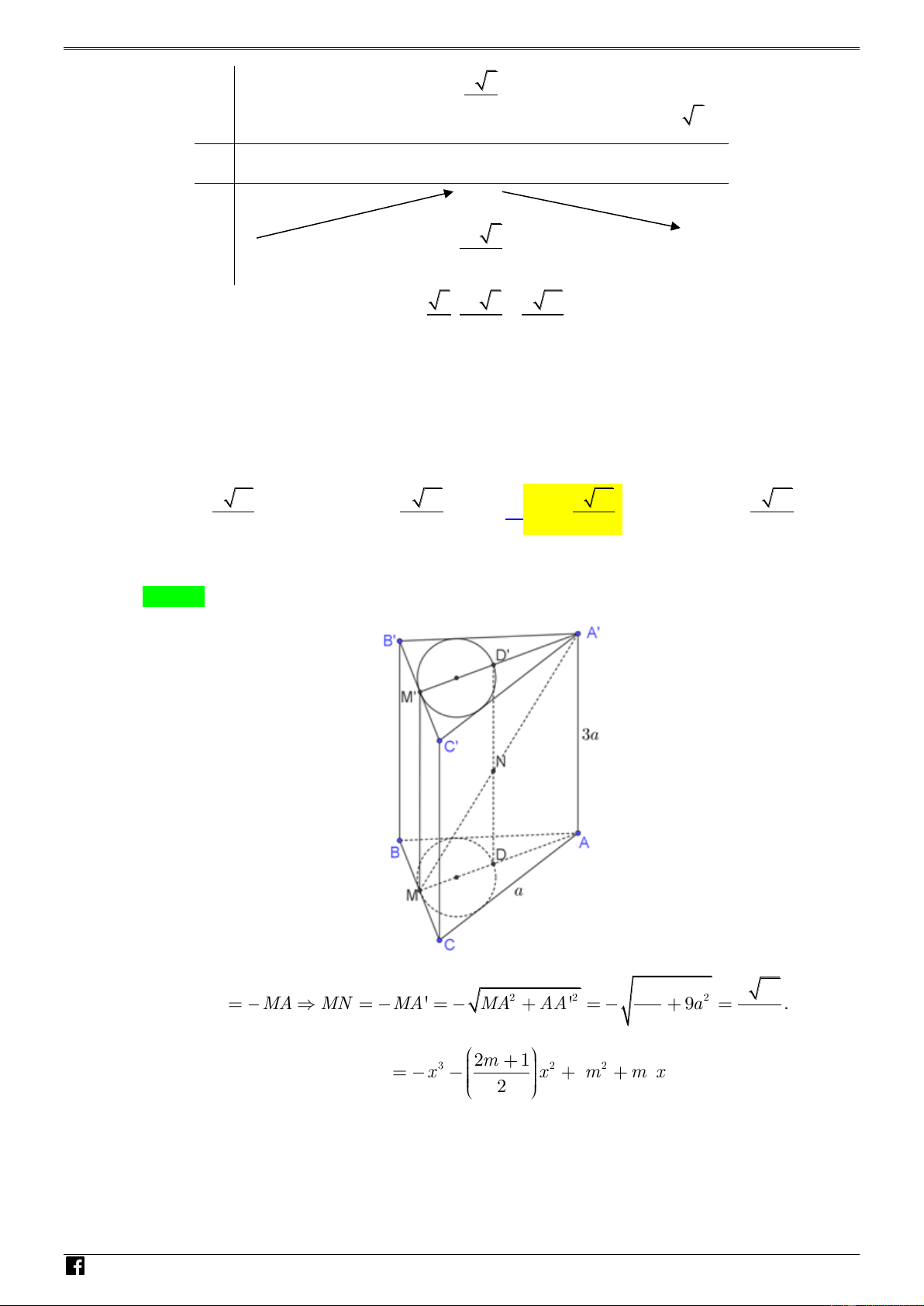
NHÓM TOÁN VD – VDC HSG QUẢNG NAM-2020 1 2m 1 Câu 26. Gọi C
là đồ thị của hàm số 3 2 2 y x x m
m x với m là tham số. Có m 3 2 N H
bao nhiêu điểm M sao cho tồn tại hai giá trị khác nhau m ,m mà M là điểm cực đại của đồ 1 2 Ó M T thị C
và là điểm cực tiểu của đồ thị C ? m m 1 2 O Á N A. 2 . B. 0 . C. 1. D. Vô số. V D ln x
Câu 27. Gọi H là hình phẳng giới hạn bởi đồ thị hàm số y
, trục hoành và đường thẳng – x VDC
x 2 . Biết thể tích của khối tròn xoay tạo thành khi quay hình H xung quanh trục hoành
bằng a b ln với a,b là các số hữu tỉ. Tính a 3b . 1 5
A. a 3b 2 .
B. a 3b .
C. a 3b 1 .
D. a 3b . 2 2
Câu 28. Cho lăng trụ đứng AB . C A B C
có đáy ABC là tam giác vuông tại B , AB 2a , BC 4a ,
AA 3a . Gọi M là trung điểm của cạnh AB . Diện tích thiết diện của lăng trụ AB . C A B C
khi cắt bới mặt phẳng MB C bằng A. 2 2 10a . B. 2 3 10a . C. 2 4 10a . D. 2 6 10a .
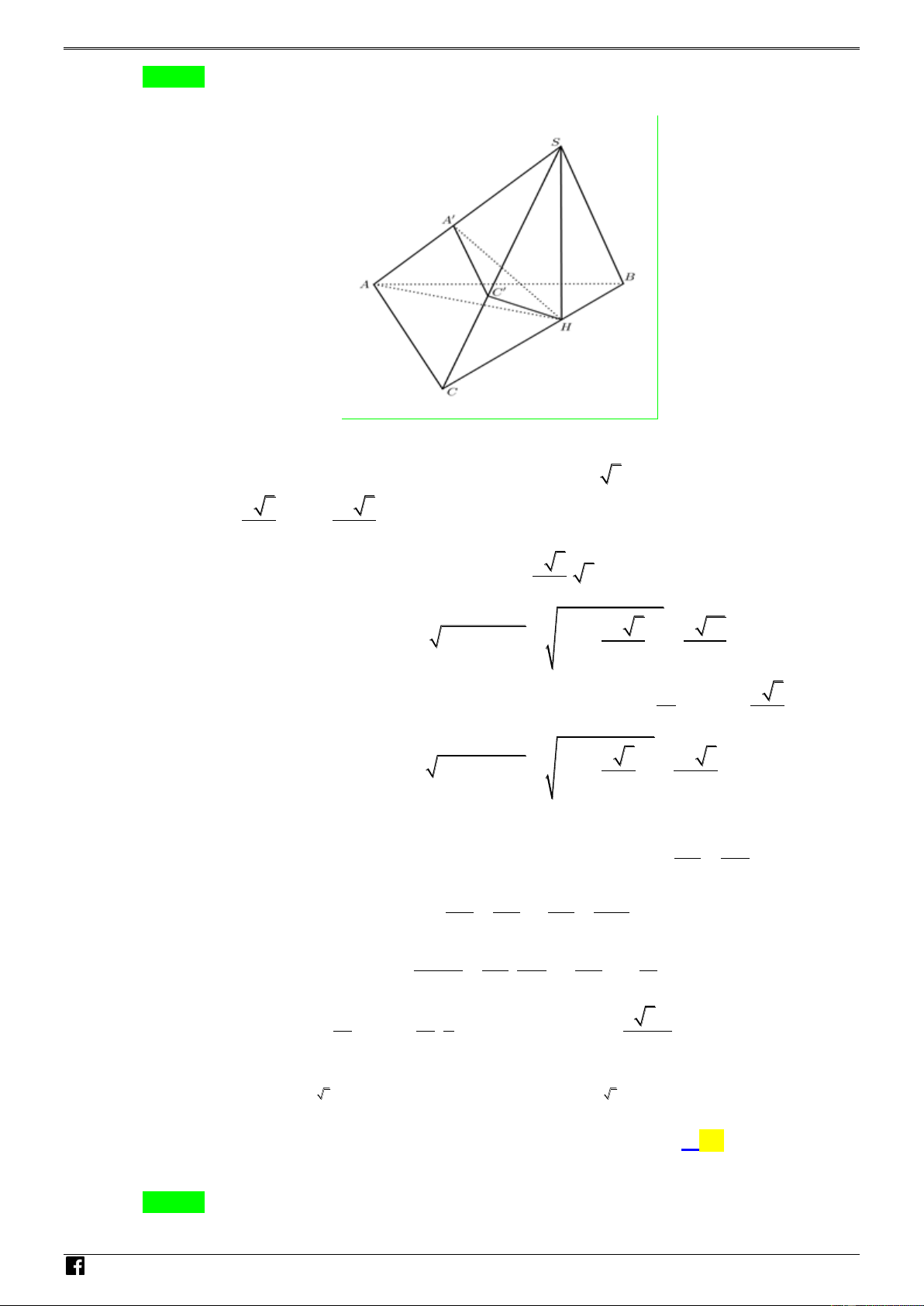
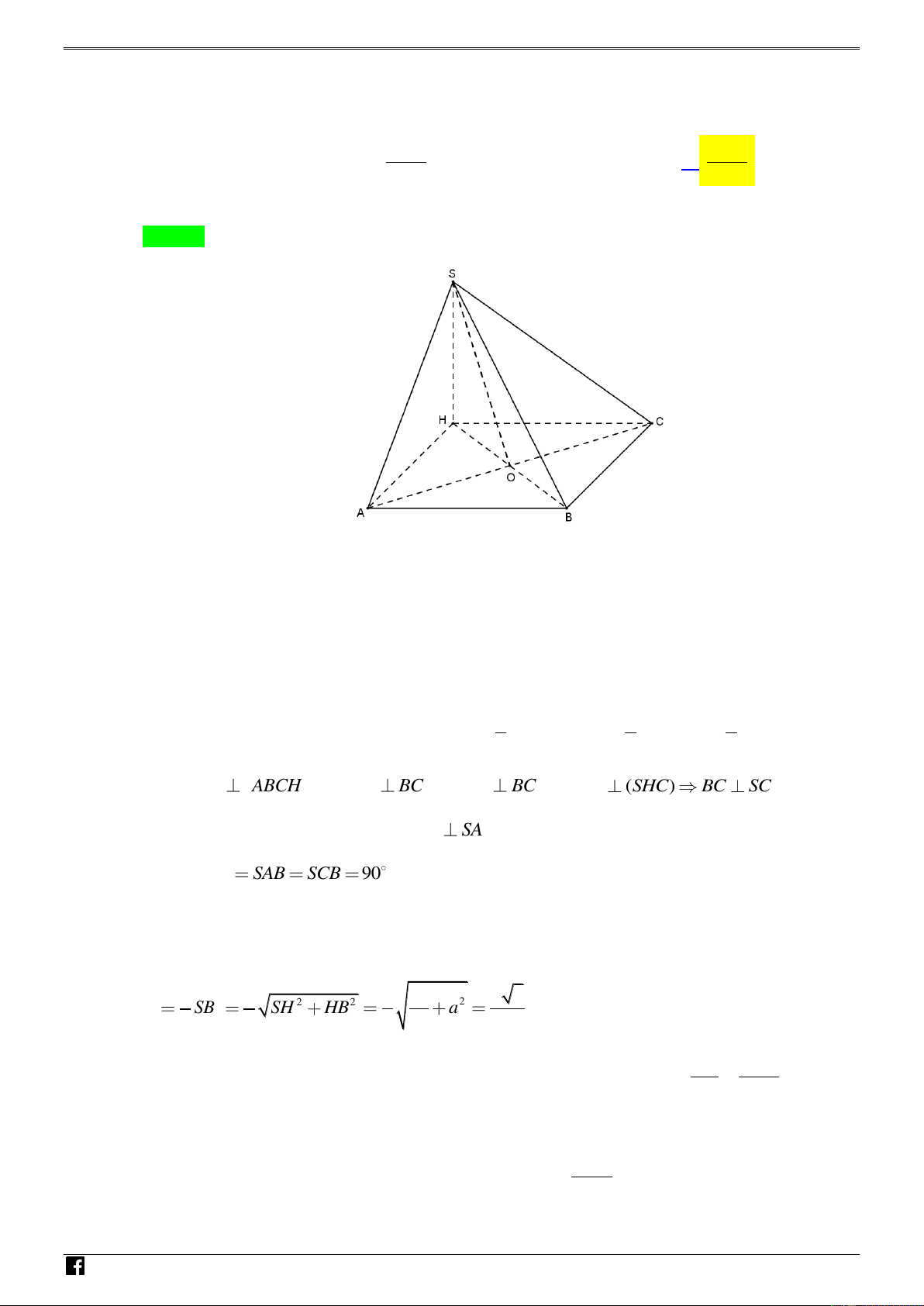
Câu 29. Cho hình chóp S.ABC có đáy ABC là tam giác cân với AB AC a và 0 BAC 120 . Hình
chiếu vuông góc của đỉnh S lên mặt phẳng ABC là điểm H thuộc cạnh BC với HC 2HB
. Góc giữa SB và mặt phẳng ABC bằng 0
60 . Mặt phẳng đi qua H và vuông góc với SA cắt các cạnh S ,
A SC lần lượt tại A ,
C . Tính thế tích V của khối chóp . B ACC A 3 3 3 3 7 3a 3 3a 3 3a 5 3a N A. V . B. V . C. V . D. V . H 192 64 100 108 Ó 2 2 M T
Câu 30. Cho phương trình log x
2m 3 x m m 6 log x 0 2 1
với m là tham số. Có 2 1
bao nhiêu giá trị nguyên của m để phương trình đã cho có đúng một nghiệm? O Á A. 7 . B. 4 . C. 5 . D. 6 . N V
Câu 31. Trong không gian Oxyz , cho hai mặt cầu S , S có điểm chung A1;2; 1, cùng tiếp xúc 2 1 D x 1 y 1 z 1 –
với mặt phẳng Oxy và đều có tâm thuộc đường thẳng d : . Khoảng cách 1 1 2 VDC
giữa hai tâm của hai mặt cầu S , S bằng 2 1 A. 6 . B. 46 . C. 4 . D. 2 6 .
Câu 32. Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B và AC a . Hình chiếu
vuông góc của đỉnh S lên mặt phẳng ABC là điểm H đối xứng với B qua AC . Góc giữa
hai mặt phẳng SAC và ABC bằng 45 . Diện tích mặt cầu ngoại tiếp hình chóp S.ABC bằng 2 2 a 2 5 a A. 2 2 a . B. V . C. 2 5 a . D. . 3 4
https://www.facebook.com/groups/toanvd.vdc Trang 4
NHÓM TOÁN VD – VDC HSG QUẢNG NAM-2020
Câu 33. Cho hàm số f x có đạo hàm liên tục, nhận giá trị dương trên đoạn 1;4, f
1 1, f 4 8và 4 x
x f x f x x f x 2 3 2 . . ' 2 , x 1;4. Tích phân dx bằng N f x 1 H Ó 1 3 2 M T A. . B. . C. . D. 2. 2 2 3 O Á
Câu 34. Đồ thị C của hàm số 3 2
y ax bx cx 3a và đồ thị C ' của hàm số 2
y 3ax 2bx c N V
,a ,bc ,a 0có đúng hai điểm chung khác nhau ,
A B và điểm A có hoành độ bằng 1. D –
Các tiếp tuyến của C và C ' tại điểm A trùng nhau; diện tích hình phẳng giới hạn bởi C VDC
và C ' bằng 1. Giá trị của a b c bằng A. 12. B. 17. C. 60. D. 45.
Câu 35. Chọn ngẫu nhiên đồng thời sáu số tự nhiên khác nhau thuộc đoạn [1;25]. Gọi A là biến cố
“Chọn được sáu số tự nhiên sao cho tổng bình phương của sáu số đó chia hết cho 3”. Xác suất
của biến cố A bằng 633 453 211 1803 A. . B. . C. . D. . 6325 6325 6325 6325
Câu 36. Cho bất phương trình 2
x (m 2019)x 2020m (x m 1) log
x 2020 với m là tham số. 2019
Có bao nhiêu giá trị nguyên của m để tập nghiệm của bất phương trình đã cho chứa trong
khoảng (1000;2020) ? A. 1018. B. 1019. C. 1020. D. 1021. N
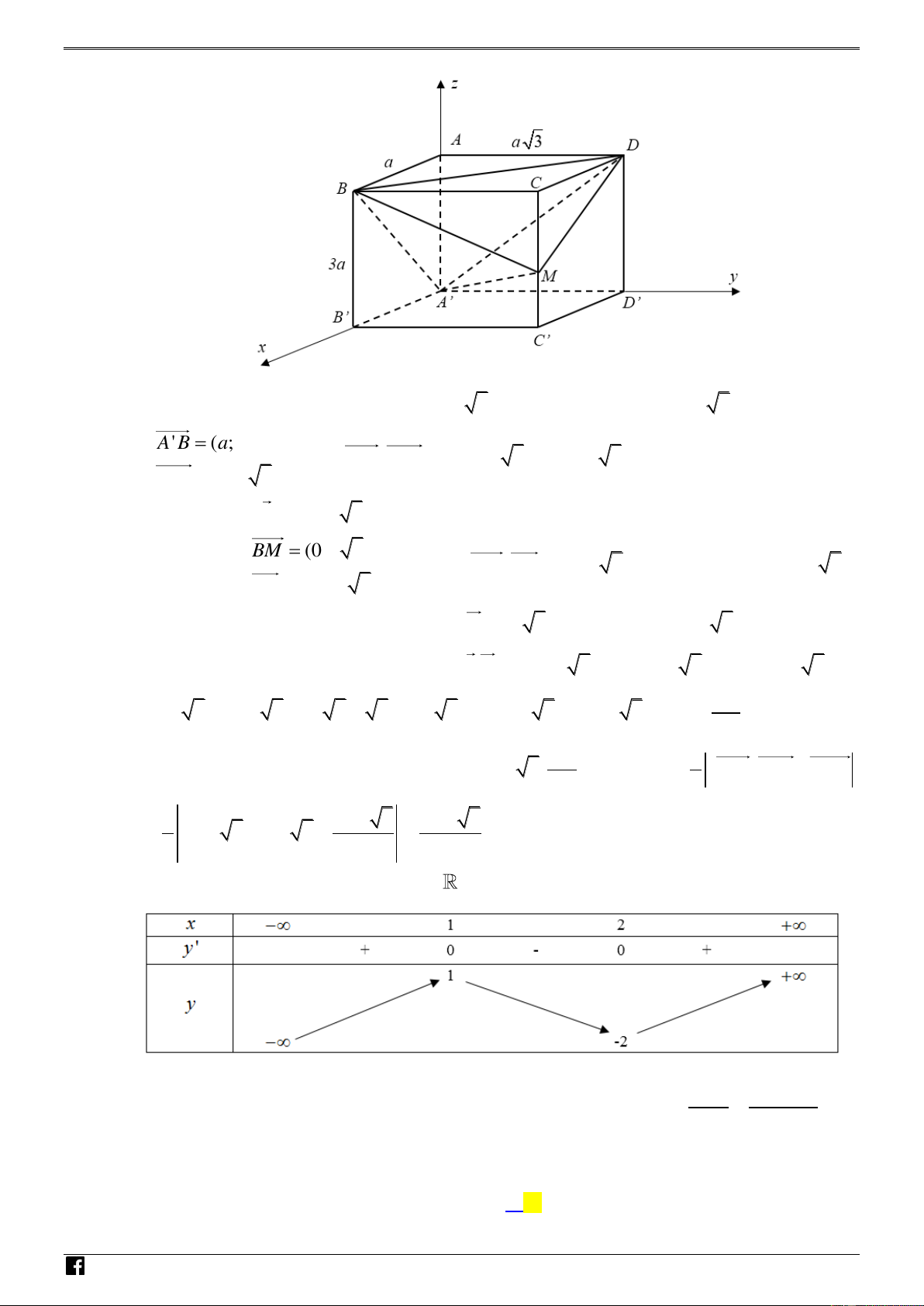
Câu 37. Cho hình hộp chữ nhật ABC .
D A' B'C ' D' có AB , a AD a 3, AA'
3a . Gọi M là điểm H
thuộc cạnh CC ' sao cho mp(MB )
D vuông góc với mp( A' B )
D . Thể tích khối tứ diện Ó M T A' BDM bằng O 3 13 3a 3 10a 3 100a 3 13 3a Á A. . B. . C. . D. . N 8 9 3 24 V D
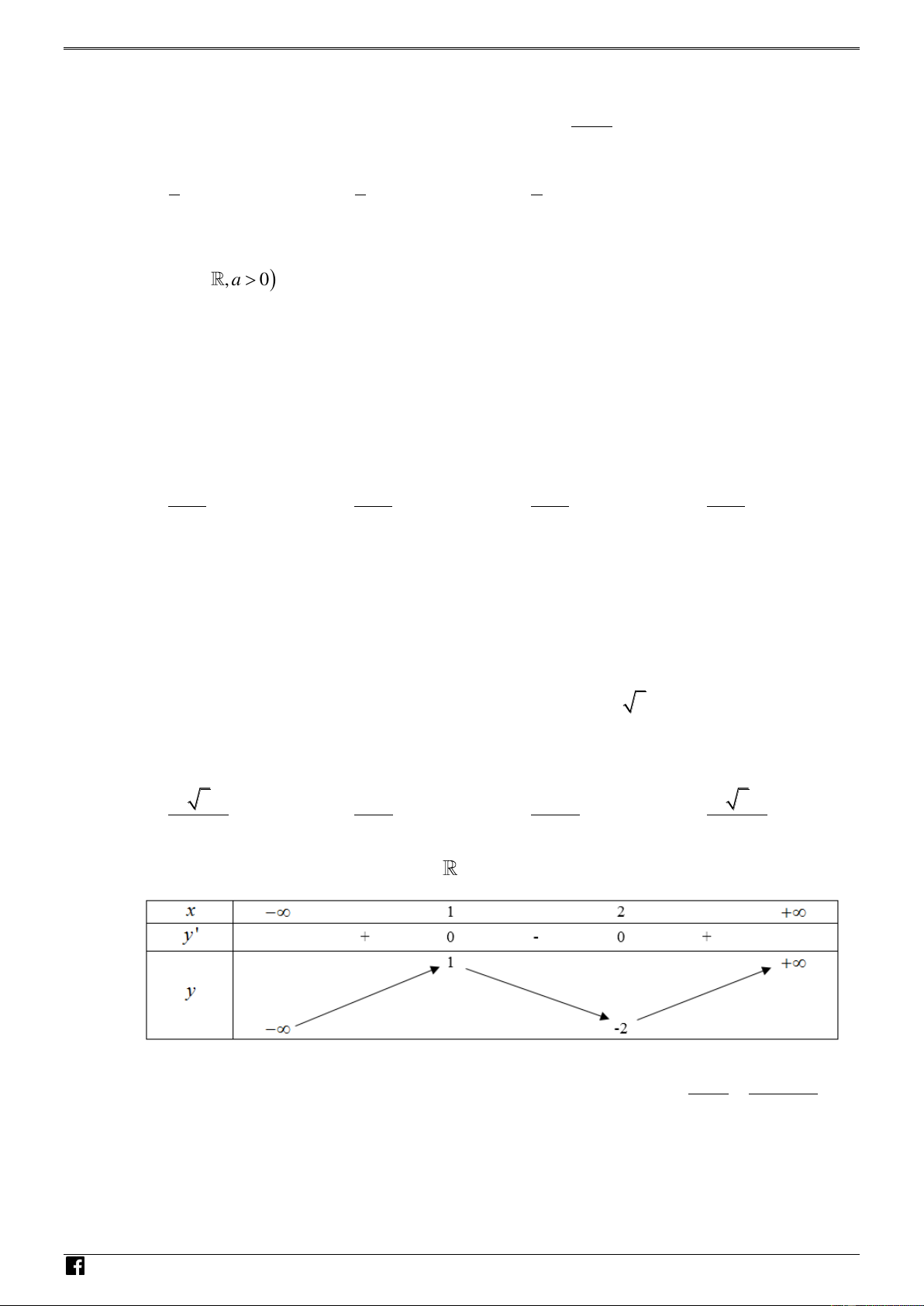
Câu 38. Cho hàm số y f (x) có đạo hàm trên
và có bảng biến thiên sau : – VDC 1 1
Gọi S là tập hợp tất cả các giá trị của tham số thực m để phương trình m f (x) f (x) 2
có đúng 3 nghiệm thực phân biệt. Hỏi tập S có bao nhiêu phần tử? A. 3. B. Vô số. C. 1. D. 2.
https://www.facebook.com/groups/toanvd.vdc Trang 5 NHÓM TOÁN VD – VDC HSG QUẢNG NAM-2020
Câu 39. Trong không gian Oxyz , cho hai điểm ,
A B theo thứ tự thay đổi trên các tia O , x Oy sao cho O .
AOB 9 . Điểm S thuộc mặt phẳng Ozx sao cho hai mặt phẳng SAB và SOB cùng N
tạo với mặt phẳng Oxy một góc 30o . Gọi ;
a 0;c là tọa độ điểm S . Tính giá trị của biểu H Ó thức 4 4
P a c trong trường hợp thể tích khối chóp S.OAB đạt giá trị lớn nhất. M T 10 40 40 45 O A. P . B. P . C. P . D. P . 3 81 9 8 Á N 2 2 V
Câu 40. Cho ba số thực dương ,
x y, z thỏa mãn x z y z 2 2
3z 4 . Giá trị lớn nhất của biểu D 3 3 3 –
x y z 4y x 2z z xy thức P bằng VDC xy 112 110 128 55 A. . B. . C. . D. . 27 27 27 27
-------------- HẾT --------------- N H Ó M T O Á N V D – VDC
https://www.facebook.com/groups/toanvd.vdc Trang 6
NHÓM TOÁN VD – VDC HSG QUẢNG NAM-2020 BẢNG ĐÁP ÁN 1A 2A 3B 4D 5C 6A 7A 8D 9B
10C 11B 12D 13A 14C 15C N H
16D 17D 18C 19B 20C 21A 22A 23A 24B 25C 26C 27C 28B 29A 30D Ó M T
31A 32D 33D 34C 35D 36D 37D 38C 39A 40A O Á N V
LỜI GIẢI CHI TIẾT D – 2 x 3 VDC Câu 1. Hàm số y
nghịch biến trên khoảng nào dưới đây? x 1 A. (1; 3). B. ( ; 1). C. ( 3;1). D. (1; ). Lời giải Chọn A 2 x 2x 3 y ' x 1, y ' 0 x 1; x 3 . 2 (x 1)
y ' 0 x ( 1
;3) \ {1}.Hàm số nghịch biến trên ( 1 ;1) và (1;3) . Câu 2.
Trong không gian Oxyz cho u (2; 1;1), v
( 3;4; 5). Số đo góc giữa hai vectơ u và v bằng A. 0 150 . B. 0 120 . C. 0 60 . D. 0 30 . Lời giải Chọn A N H Ó u.v 1 5 3 0 M T cos( , u v) ( , u v) 150 . u . v 6.5 2 2 O Á Câu 3.
Cho khối chóp có chiều cao bằng 2a , đáy là hình thoi cạnh a và có một góc bằng 60 . Thể N V
tích của khối chóp đã cho bằng D 3 3 3 – a 3 a 3 a 3 A. 3 a 3 . B. . C. . D. . VDC 3 2 6 Lời giải Chọn B 2 a 3 Diện tích hình thoi là 2
S a .sin 60 . 2 2 3 1 1 a 3 a 3
Thể tích của khối chóp là V Sh . .2a . 3 3 2 3 Câu 4.
Điểm cực đại của hàm số 3
y x 3x 2 là A. x 1 .
B. x 4 .
C. x 0 . D. x 1 .
https://www.facebook.com/groups/toanvd.vdc Trang 7
NHÓM TOÁN VD – VDC HSG QUẢNG NAM-2020 Lời giải Chọn D N TXĐ H D . Ó M T x 1 Ta có 2 y 3
x 3; y 0 . x 1 O Á N Bảng biến thiên V D – VDC
Dựa vào bảng biến thiên, hàm số đạt cực đại tại x 1 . Câu 5.
Trong không gian Oxyz , giao tuyến của hai mặt phẳng P : x 2y 3z 0 , Q : x
4z 1 0 có một véc tơ chỉ phương là. A. u 5; 2 ; 3 . B. u 5; 2; 3 . C. u 8;1; 2 . D. u 4; 1 ; 2 . 4 3 2 1 Lời giải Chọn C
Mặt P có một véc tơ pháp tuyến là n ; 1 ; 2 3 1 ; 1 0 4 N
Mặt Q có một véc tơ pháp tuyến là n ; ; 2 ; H Ó Gọi
là giao tuyến của hai mặt phẳng P và Q , và u là 1 véc tơ chỉ phương của ; khi M T n u n đó ta có 1 1 đường thẳng
có 1 véc tơ chỉ phương là O n u n Á 2 2 N 8 1 2 V u n , n ; ; u 1 2
3 . Suy ra u3 cũng là 1 véc tơ chỉ phương của . D 3 1 – Câu 6. Nếu tích phân f x dx 6 thì f 2x 1 dx bằng VDC 1 0 A. 3 . B. 12 . C. 6 . D. 4 . Lời giải Chọn A Đặ 1 t 2x 1 u dx
du ; đổi cận x 0 u 1 ; x 1 u 3. 2 1 3 3 3 Khi đó 1 1 1 1 f 2x 1 dx f u du f u du f x dx .6 3 . 2 2 2 2 0 1 1 1 Câu 7.
Giá trị lớn nhất của hàm số y 2 x x 1 bằng A. 3 . B. 3 . C. 0 . D. 2 .
https://www.facebook.com/groups/toanvd.vdc Trang 8
NHÓM TOÁN VD – VDC HSG QUẢNG NAM-2020 Lời giải Chọn A N H 2 x 0 x 2 Ó Hàm số có nghĩa x 1;2 x 1 0 x 1 M T O 1 1 1 1 Á
Ta có y 2 x x 1 0, x 1 ;2 . N 2 2 x 2 x 1
2 2 x 2 x 1 V D
Suy ra hàm số nghịch biến trên đoạn 1
;2 nên Max y y 1 3 . – VDC Câu 8.
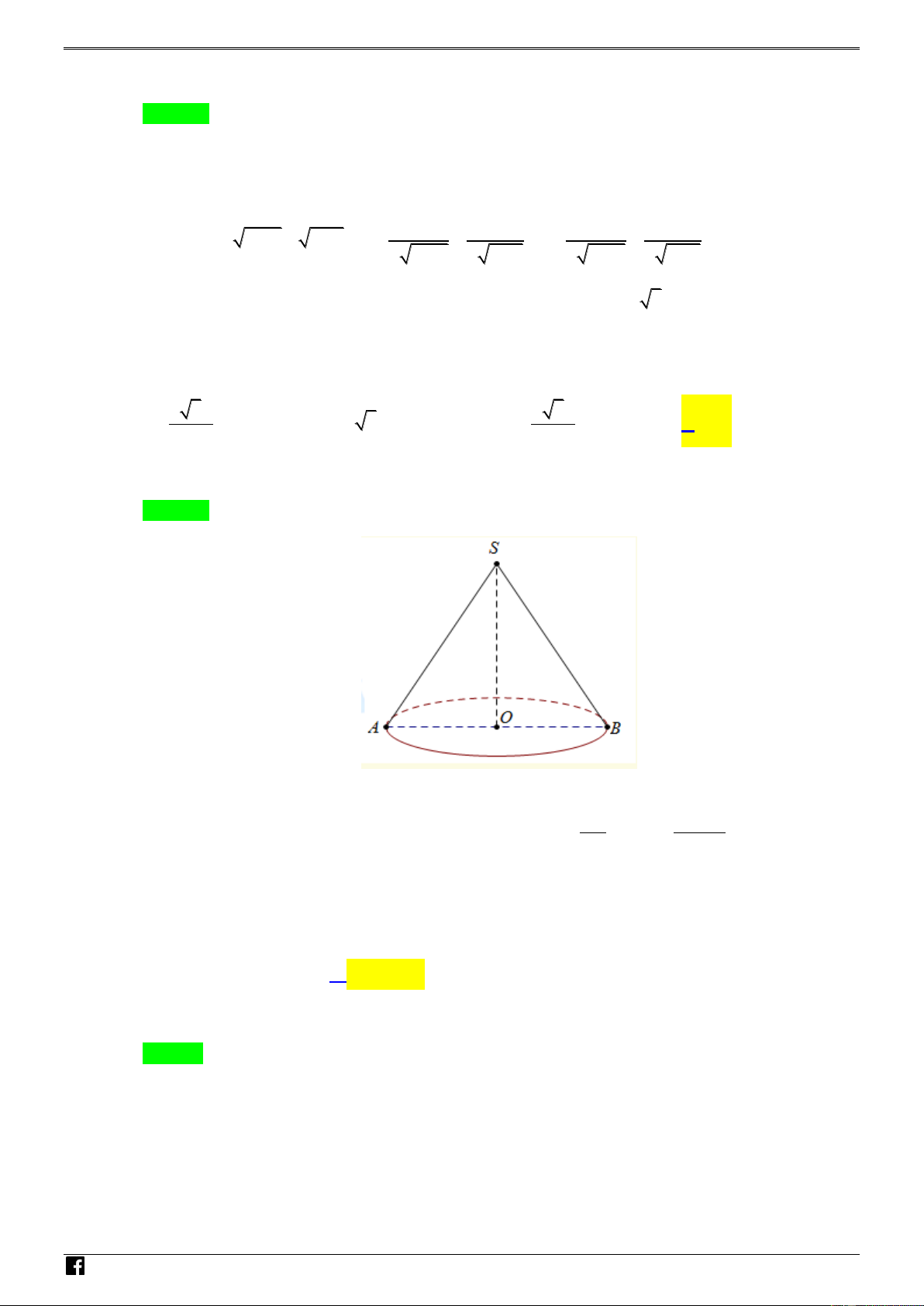
Cho hình nón có bán kính đáy bằng 1, góc giữa đường sinh và trục của hình nón bằng 0 30 .
Diện tích xung quanh của hình nón đã cho bằng 4 3 2 3 A. . B. 3 . C. . D. 2 . 3 3 Lời giải Chọn D N H Ó M T O Á OB OB N
Xét tam giác SOB ta có 0 0 OB 1, O
SB 30 sin 30 SB 2 . V 0 SB sin 30 D – Vậy ta có S
Rl .1.2 2 . xq VDC Câu 9.
Trong không gian Oxyz , điểm đối xứng với điểm M 4; 5 ;
3 qua trục Oz có tọa độ là A. 4; 5 ; 3 . B. 4 ;5;3. C. 4 ;5; 3 . D. 0;0;3 . Lời giải Chọn B
Hình chiếu của điểm M lên trục Oz là H 0;0;3 .
Gọi M là điểm đối xứng với điểm M qua trục Oz . Ta có H là trung điểm của MM nên suy ra H 4 ;5;3.
https://www.facebook.com/groups/toanvd.vdc Trang 9
NHÓM TOÁN VD – VDC HSG QUẢNG NAM-2020 2 x 4
Câu 10. Tổng số đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số y là 3 2
x x 2x N A. 4 . B. 3 . C. 2 . D. 1. H Ó M T Lời giải O Chọn C Á x 2 N V 2 x 2 D x 4 0 x 2 Hàm số xác định khi x 0 . – 2 x x x 2 0 x 2 VDC x 1 x 2
TXĐ: D ; 2 2; . 4 1 4 x 1 1 2 2 2 2 x 4 x x x 0 *) Ta có lim y lim lim lim 0 . 3 2 3 2 x
x x x 2 x x
x x 2 x x 1 2 1 1 2 x x
suy ra y 0là đường tiệm cận ngang của đồ thị hàm số.
*) Không tồn tại lim y, lim y, lim y, lim y x 0 x 0 x 1 x 1 Khi x 2
thì hàm số không xác định nên ta chỉ tìm lim y x 2 2 2 4 4 x x Ta có lim y lim lim x x x 2 2 2
x x 2 x 2
x x 1 x 2 N H Ó 2 x x 2 2 x M T lim lim x x 2 xx 1 x 2 O x x 1 x 2 2 2 Á N suy ra x 2
là đường tiệm cận đứng của đồ thị hàm số. V
Do đó tổng số đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số là 2 . D –
Câu 11. Bất phương trình log x 1 log
6x 5 có bao nhiêu nghiệm nguyên? 2 4 VDC A. 6 . B. 7 . C. 8 . D. 9 . Lời giải Chọn B x 1 0 Điều kiện x 1. 6x 5 0 2 Bất phương trình log x 1 log 6x 5 log x 1 log 6x 5 2 4 2 2 x 2 1 6x 5 2
x 8x 4 0 4 2 5 x 4 2 5 .
Kết hợp điều kiện 1 x 4 2 5 .
Vì x Z x 2;3;4;5;6;7; 8 .
https://www.facebook.com/groups/toanvd.vdc Trang 10
NHÓM TOÁN VD – VDC HSG QUẢNG NAM-2020 1
Câu 12. Họ tất cả nguyên hàm của hàm số f x là 2 4x 4x 1 N 1 1 1 1 H A. C . B. C . C. C . D. C . Ó 22x 1 2x 1 2x 1 22x 1 M T Lời giải O Á Chọn D N V 1 1 Ta có f
xdx dx C . D 2x 21 22x 1 – VDC
Câu 13. Số điểm cực trị của hàm số 2
y x sin x trong khoảng ;2 là A. 0 . B. 1. C. 2 . D. 3 . Lời giải Chọn A
y 1 sin 2x . y 0, x
;2 suy ra hàm số đồng biến trên ;2 .
Vậy hàm số không có cực trị trong khoảng ;2 . x x
Câu 14. Tích các nghiệm của phương trình 2 5 2 3
7 4 3 0 bằng A. 2 . B. 2 . C. 5 . D. 5 . N H Ó Lời giải M T Chọn C O x x Á 2 5 2 3 7 4 3 0 N V 2 x 5x 2 D 2 3 2 3 – VDC 2
x 5x 2 0.
Tổng các nghiệm của phương trình bậc hai 2
x 5x 2 0 bằng 5.
Câu 15. Cho khối trụ có chiều cao bằng bán kính đáy và có diện tích thiết diện qua trục của khối trụ
bằng 16 . Thể tích khối trụ đã cho bằng. 64 16 2 A. 64 . B. . C. 16 2 . D. . 3 3 Lời giải Chọn C Ta có: Từ đây ta suy ra.
Ta có: chiều cao h R
https://www.facebook.com/groups/toanvd.vdc Trang 11
NHÓM TOÁN VD – VDC HSG QUẢNG NAM-2020
Diện tích thiết diện qua trục S . h 2R 16 . h R 8 2
R 8 R 2 2 và h 2 2 N
Thể tích khối trụ: V R h 2 2 . . . 2 2 .2 2 16 2 H Ó Câu 16. Biết 2 x 2 x , với bằng. M T
x 1.e dx ax b.e C
a, b là các số hữu tỉ. Giá trị của a b O 5 Á A. . B. 4 . C. 1 . D. 2 . N 2 V D Lời giải – Chọn D VDC du dx u x 1 Đặt 1 2 x 2 x dv e dx v e 2
I x x 1 x 1 x 1 x 1 x 1 x 3 2 1 .e dx x 2 2 1 .e e dx x 2 2 2 1 .e
.e C e x C 2 2 2 4 2 2 1 3 Vậy a ;b 2 2 x
Câu 17. Biết phương trình 2 log x log
0 có hai nghiệm x , x với x x . Hiệu x x bằng 9 3 27 1 2 1 2 2 1 80 80 6560 6560 A. . B. . C. . D. . 3 27 27 729 Lời giải Chọn D N H
Điều kiện x 0 . Ó M T 2 x 1 2 log x log 0 log x
log x log 27 0 . O 9 3 3 3 3 27 2 Á N V 1 6 log x 6 x 3 1 D
log x 4log x 12 0 729 x , x 9 . 3 2 3 3 1 2 – log x 2 729 3 2 VDC x 3 9 1 6560
Do đó x x 9 . 2 1 729 729
Câu 18. Biết rằng tập nghiệm của bất phương trình 4x 8.6x 12.9x 0 là khoảng ;
a b . Giá trị của
b a bằng A. log 4 . B. log 4 . C. log 3 . D. log 3 . 2 2 2 2 3 3 3 3 Lời giải Chọn C
https://www.facebook.com/groups/toanvd.vdc Trang 12
NHÓM TOÁN VD – VDC HSG QUẢNG NAM-2020 2 x x x x x 2 2
Vì 9x 0 nên 4 8.6 12.9 0 8. 12 0 3 3 N x H 2 Ó 2 6 log 6 x log 2 2 2 3 M T 3 3 O 1
Suy ra a log 6, b log 2 b a log 2 log 6 log log 3 . Á 2 2 2 2 2 2 3 N 3 3 3 3 3 3 V D
Câu 19. Cho hình lập phương ABC .
D A B C D cạnh a . Thể tích khối cầu có tâm A và tiếp xúc với – đường thẳng A C bằng VDC 3 2 a 3 8 6 a 3 3 a A. . B. . C. . D. 3 6 a . 3 27 2 Lời giải Chọn B N H
Gọi H là hình chiếu vuông góc của A trên đường thẳng A C . Ó M T
Ta có ABCD là hình vuông cạnh a nên AC a 2 O Vì ABC .
D A B C D là hình lập phương nên AA
ABCD AA A C tam giác ACA Á N vuông tại A . V 1 1 1 3 a 6 D Do đó ta có AH 2 2 2 2 AH AA . AC 2a 3 – VDC a 6
Vì khối cầu tâm A và tiếp xúc với đường thẳng A C
nên có bán kính R AH . 3 3 4 8 6 a
Vậy thể tích khối cầu là 3 V R . 3 27 4 Câu 20. Biết 2
x dx a b c với a, ,
b c là các số hữu tỉ. Giá trị của a b c bằng 3 41 25 13 5 A. . B. . C. . D. . 2 2 2 2 Lời giải Chọn C
https://www.facebook.com/groups/toanvd.vdc Trang 13
NHÓM TOÁN VD – VDC HSG QUẢNG NAM-2020 4 4 4 Ta có x dx x dx x dx
xdx x dx 3 3 3 N 4 H 2 2 x x 25 2 Ó
x x 7 . M T 2 2 2 3 O Á N a 1 V 13 Từ đó suy ra b 7
a b c . D 2 – 25 c VDC 2 a
Câu 21. Biết nghiệm dương nhỏ nhất của phương trình 21 3.cosxsinx cos2x là x , với a,b 0 b
là các số nguyên dương và a 10 . Giá trị của a+b bằng A. 23 B. 7 C. 11 D. 17 Lời giải Chọn A Ta có:
21 3.cosxsinx cos2x 2sinx 3sin2x cos2x 3 1 sinx s in2x
cos2x s inx sin 2x 2 2 6 x k2 1 6 , k, l N 5 l2 H x 2 Ó 18 3 M T 1 1
Nếu x có dạng (1) thì: x k 2
2k 0 k k 0 0 O 6 6 12 Á 11 N Vì a<10 nên suy ra 1
12k 10 k k . V 12 D 11 1 – Vậy k
k nên không có giá trị k thỏa mãn. VDC 12 12 5
Nếu x có dạng (2) thì nghiệm dương nhỏ nhất của phương trình ứng với k=0.Hay x 0 0 18
Từ đây ta suy ra a=5;b=18. Vậy a+b=23. 2x 1
Câu 22. Tiếp tuyến đi qua điểm A 1
;0 của đồ thị hàm số y
C có phương trình là x 1 1 1 A. y x .
B. y x 1.
C. y 3x 3.
D. y x 1. 3 3 Lời giải Chọn A
https://www.facebook.com/groups/toanvd.vdc Trang 14
NHÓM TOÁN VD – VDC HSG QUẢNG NAM-2020
Đường thẳng đi qua A 1
;0 với hệ số góc k có phương trình y k x 1 x
k k tiếp xúc 2x 1 với (C) x k k x
k k x
1 2x 1 có nghiệm kép x 1 . N x 1 H Ó 2
kx 2xk
1 k 1 0 có nghiệm kép x 1 M T O k 0 k 0 Á 2 1 ' N
k
1 k k
1 1 3k 0 1 k V k 3 k 2 1
k 1 k 1 0 3 D – VDC Vậy tiếp tuyến đó là 1 1 y x . 3 3
Câu 23. Cho phương trình 9x 2 1 .3x m
m 7 0 với m là tham số. Có bao nhiêu giá trị nguyên
của m để phương trình đã cho có 2 nghiệm thực phân biệt? A. 3 . B. 4 . C. 5 . D.Vô số. Lời giải Chọn A Đặt 3x t
t 0 ta được phương trình 2t 2m
1 t m 7 0 1
Theo yêu cầu đề bài suy ra phương trình
1 phải có 2 nghiệm phân biệt cùng dương 2 0
m m 6 0 m ; 3 2;
S 0 2 m 1 0 m 1 7 m 3 N H P 0 m 7 0 m 7 Ó M T
Suy ra có 3 giá trị nguyên của tham số m là 6 ; 5 ; 4 . O Á
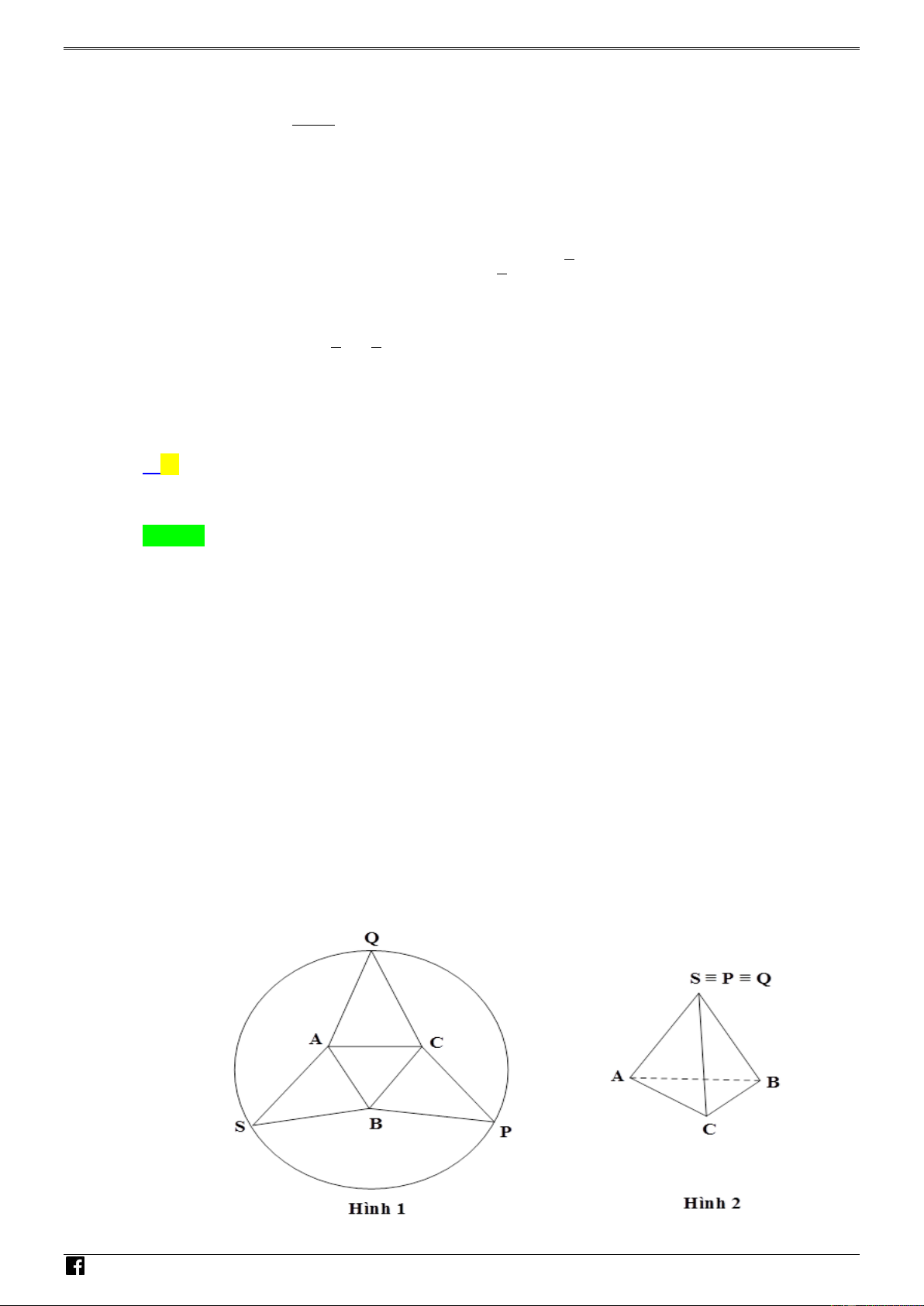
Câu 24. Cắt tấm bìa hình tròn có bán kính bằng 1 ( độ dày không đáng kể) theo đường gấp khúc N
SAQCPBS như hình 1, sau đó gấp phần đa giác còn lại theo các đoạn AB , BC , CA sao cho V D các điểm S, ,
P Q trùng nhau để được hình chóp đều có đáy là tam giác ABC như hình 2. – VDC
https://www.facebook.com/groups/toanvd.vdc Trang 15
NHÓM TOÁN VD – VDC HSG QUẢNG NAM-2020
Giá trị lớn nhất của thể tích khối chóp SABC bằng 1 4 15 15 4 A. . B. . C. . D. N 9 125 125 9 H Ó
Lời giải M T Chọn B O Á N V D – VDC N Đặt AB ;
x SA y x 0; y 0 H Ó M T
Ta có tâm O của hình tròn cũng là tâm của tam giác đều ABC và SO AB . 2 O 2 2 2 x 2 3 x x x Á Khi đó: 2 SH y ;OH x N 4 3 2 4 12 2 3 V D 2 2 2 – x x x x x 2 2
Mà SO 1 SH OH 1 y 1 y 1 VDC 4 2 3 4 12 3 2 x x 2 y 1 3 3 2 3 x 3 x
Mặt khác, ta có thể tích khối chóp đều SABC là 2 2 2 V x y x 1 12 3 12 3 x 2 4 3x 5x Xét hàm số 2 y x 1
ĐK: 0 x 3 . Có y 3 2 3 x BBT:
https://www.facebook.com/groups/toanvd.vdc Trang 16
NHÓM TOÁN VD – VDC HSG QUẢNG NAM-2020 4 3 x 0 5 3 N H y 0 Ó M T O y 48 5 Á N 125 V D 3 48 5 4 15 –
Vậy giá trị lớn nhất của thể tích bằng . VDC 12 125 125
Câu 25. Cho lăng trụ tam giác đều ABC.A' B 'C ' có cạnh đáy bằng a và chiều cao bằng 3a . Một hình
trụ T có hai đáy nội tiếp tam giác ABC,A' B 'C ' . Gọi M là trung điểm cạnh BC . Đường
thẳng A' M cắt mặt xung quanh của hình trụ T tại N ( N khác M ). Tính độ dài đoạn thẳng MN . a 15 a 15 a 39 a 39 A. MN . B. MN . C. MN . D. MN . 3 6 3 6 Lời giải Chọn C N H Ó M T O Á N V D – VDC 2 2 2 2 2 3a a 39 Ta có 2 2 2 MD MA MN MA' MA AA' 9a . 3 3 3 3 4 3 1 2m 1 Câu 26. Gọi C
là đồ thị của hàm số 3 2 2 y x x m
m x với m là tham số. Có m 3 2
bao nhiêu điểm M sao cho tồn tại hai giá trị khác nhau m ,m mà M là điểm cực đại của đồ 1 2 thị C
và là điểm cực tiểu của đồ thị C ? m m 1 2
https://www.facebook.com/groups/toanvd.vdc Trang 17
NHÓM TOÁN VD – VDC HSG QUẢNG NAM-2020 A. 2 . B. 0 . C. 1. D. Vô số. Lời giải N Chọn C H Ó M T 2 2m 1 m 1 x m 1 y O Ta có 2 2 y ' x 2m 1 x m m 0 6 . Á x m 1 1 N 3 2 y m m V 3 2 D – Giả sử M x ;y thỏa mãn yêu cầu bài toán, ta có hệ 0 0 VDC x m m 1 2 0 1 2 2m 1 m 1 1 3 1 2 2 2 2 m 1 m 1 2m 1 m 1 2 2 1 1 3 2 2 2 3 2 6 y m m 0 1 1 3 2 6 2 m 1 0 2 m 1 m 0 M 0;0 . 2m 1 2 1 1 1 2 m 1 2 3 2 6
Như vậy, có duy nhất điểm M
0;0 là điểm cực đại của đồ thị với m 0 và là điểm cực
tiểu của đồ thị với m 1. ln x
Câu 27. Gọi H là hình phẳng giới hạn bởi đồ thị hàm số y
, trục hoành và đường thẳng x N H
x 2 . Biết thể tích của khối tròn xoay tạo thành khi quay hình H xung quanh trục hoành Ó M T
bằng a b ln với a,b là các số hữu tỉ. Tính a 3b . 1 5 O
A. a 3b 2 .
B. a 3b .
C. a 3b 1 .
D. a 3b . Á 2 2 N V Lời giải D Chọn C – x 0 x 0 VDC
Xét phương trình ln x 0 ln x 0 x 1 x 1. x ln x 0 x 1
Thể tích của khối tròn xoay tạo thành khi quay hình H xung quanh trục hoành là 2 2 2 2 2 2 ln x ln x 1 1 1 V .dx .dx ln . x d ln x .d ln x 2 x x x x x 1 1 1 1 1 2 2 2 1 1 1 1 1 1 1 ln 2 . dx ln 2 .dx ln 2 2 2 x x 2 x 2 x 1 1 1 1 1 1 1 ln 2 1 ln 2 . 2 2 2 2 1 1 Vậy a ;b
. Suy ra a 3b 1 . 2 2
https://www.facebook.com/groups/toanvd.vdc Trang 18
NHÓM TOÁN VD – VDC HSG QUẢNG NAM-2020
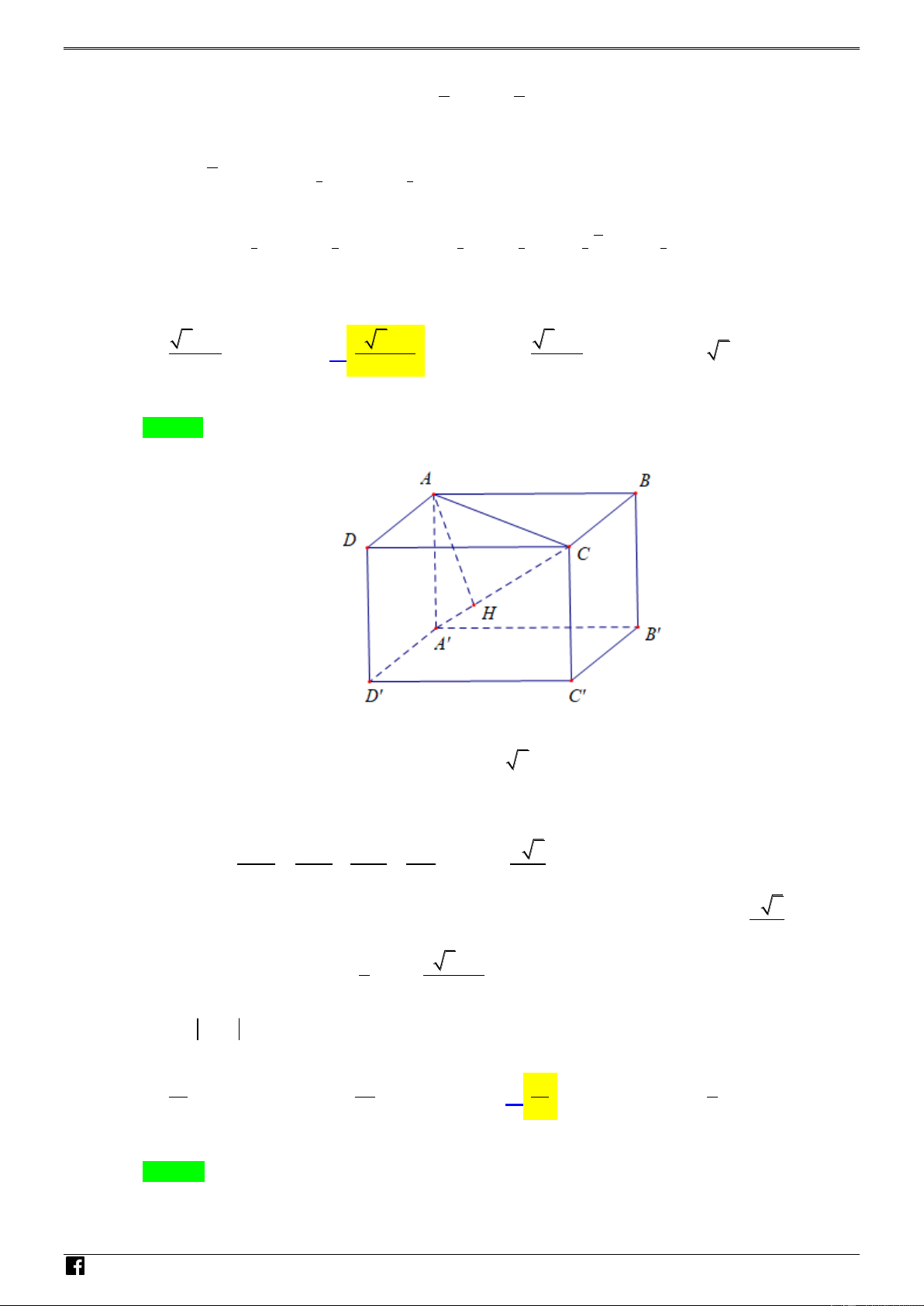
Câu 28. Cho lăng trụ đứng AB . C A B C
có đáy ABC là tam giác vuông tại B , AB 2a , BC 4a ,
AA 3a . Gọi M là trung điểm của cạnh AB . Diện tích thiết diện của lăng trụ AB . C A B C
khi cắt bới mặt phẳng MB C bằng N H A. 2 2 10a . B. 2 3 10a . C. 2 4 10a . D. 2 6 10a . Ó M T Lời giải Chọn B O Á N V D – VDC Ta có AB . C A B C
là lăng trụ đứng nên BC / /B C
mà M MB C ABC MB C
ABC MN / /BC nên N là trung điểm của AC . N Do đó MB C
ABC MN ; MB C ACC A NC; H Ó MB C A B C B C ; MB C ABB A B M M T
Suy ra thiết diện của lăng trụ AB . C A B C
khi cắt bới mặt phẳng MB C là hình thang O Á B C N M . N
Tam giác ABC vuông tại B nên BC AB và AB . C A B C
là lăng trụ đứng nên AA BC suy V D
ra BC AA B B
mà MN / /BC MN AA B B
MN B M . – MN B C VDC Suy ra S .B M . B C NM 2 BC Mặt khác ta có B C BC 4 ; a MN
2a ; MB BB BM a2 2 2 2 3
a a 10 . 2 MN B C 2a 4a Vậy 2 S .B M .a 10 3 10a . B C NM 2 2
Câu 29. Cho hình chóp S.ABC có đáy ABC là tam giác cân với AB AC a và 0 BAC 120 . Hình
chiếu vuông góc của đỉnh S lên mặt phẳng ABC là điểm H thuộc cạnh BC với HC 2HB
. Góc giữa SB và mặt phẳng ABC bằng 0
60 . Mặt phẳng đi qua H và vuông góc với SA cắt các cạnh S ,
A SC lần lượt tại A ,
C . Tính thế tích V của khối chóp . B ACC A 3 3 3 3 7 3a 3 3a 3 3a 5 3a A. V . B. V . C. V . D. V . 192 64 100 108 Lời giải
https://www.facebook.com/groups/toanvd.vdc Trang 19
NHÓM TOÁN VD – VDC HSG QUẢNG NAM-2020 Chọn A N H Ó M T O Á N V D – VDC
Do SH ABC nên góc giữa SB và mặt phẳng ABC bằng 0 SBH 60 Ta có 2 2 2 2 2
BC AB AC 2A . B A .
C cos120 3a BC a 3 khi đó a 3 2a 3 HB , HC . 3 3 a 3
Trong ta giác vuông SHB ta có 0 SH H . B tan 60 . 3 a 3 2 2a 3 a 21
Trong ta giác vuông SHC ta có 2 2 2 SC SH BC a 3 2 2 a a 3 2 2 2 0 N
Trong tam giác AHC ta có AH AC HC 2AC.HC.cos 30 AH 3 3 H Ó 2 M T a 3 2a 3
Trong ta giác vuông SHA ta có 2 2 2 SA AH SH a 3 3 O Á Khi đó 2 2 2
SA AC SC khi đó tam giác SAC vuông tại N A hay SA AC V SA SC D Do SA
HA C SA A C . Vậy A C
song song với AC , suy ra SA SC – 2 VDC Khi đó SA SH SA SH S A H
đồng dạng với S HA . 2 SH SA SA SA 4 V SA SC SH 9 Ta có V S .A C B V V . Mà . . B.ACC A S.ABC S.A C B V SA SC SA 16 S .ACB 3 Khi đó 9 7 1 7 3a 0 V V V . SH.A . B AC.sin120 . B.ACC A S .ABC S . 16 ABC 16 6 192
Câu 30. Cho phương trình 2 log
x 2m3 2
x m m 6 log x 0 2 1
với m là tham số. Có 2 1
bao nhiêu giá trị nguyên của m để phương trình đã cho có đúng một nghiệm? A. 7 . B. 4 . C. 5 . D. 6 . Lời giải Chọn D
https://www.facebook.com/groups/toanvd.vdc Trang 20
NHÓM TOÁN VD – VDC HSG QUẢNG NAM-2020 x 0 Ta có 2 log
x 2m 3 2
x m m 6 log x 0 2 1 2 1 2 x 2m3 2
x m m 6 x N x 0 H 2 2 Ó x 2 m
1 x m m 6 0 1 M T
Bài toán trở thành: Có bao nhiêu giá trị m nguyên đề phương trình (1) có đúng một nghiệm O dương Á N
TH1: Phương trình (1) có một nghiệm kép dương V 2 Ta có m 2
1 m m 6 7 m 0 m 7 . Nghệm kép: x 6 D –
TH1: Phương trình (1) có hai nghiệm trái dấu hay 2
m m 6 0 2
m 3. Vì m nguyên VDC nên m 1 ;0;1; 2
TH3:: Phương trình (1) có một nghiệm bằng 0 và một nghiệm dương m 3
Vì x 0 là nghiệm của (1) nên 2
m m 6 0 m 2 x 0
* Với m 3 phương trình (1) trở thành 2
x 4x 0 . Vậy m 3 (t/m) x 4 x 0 * Với m 2
phương trình (1) trở thành 2
x 6x 0 . Vậy m 2 (Loại) x 6
Vậy có 6 giá trị m nguyên.
Câu 31. Trong không gian Oxyz , cho hai mặt cầu S , S có điểm chung A1;2; 1 , cùng tiếp xúc 2 1 x 1 y 1 z 1
với mặt phẳng Oxy và đều có tâm thuộc đường thẳng d : . Khoảng cách 1 1 2 N
giữa hai tâm của hai mặt cầu S , S bằng 2 1 H Ó A. 6 . B. 46 . C. 4 . D. 2 6 . M T Lời giải O Á Chọn A N Gọi
AI d I , Oxy . V
I là điểm thuộc đường d thẳng thỏa mãn D x 1 t – VDC
Phương trình tham số d : y 1 t . z 1 2t
Tọa độ điểm I 1 t;1 t; 1
2td . Khi đó 2 2 2
AI d I,Oxy t
t 1 2t 1 2t .
t 0 I 1;1; 1 2 2 2
6t 2t 1 4t 4t 1 2t 2t 0 . t 1 I 2;0; 3
Do đó tọa độ tâm hai mặt cầu S , S là I 1;1; 1 , I 2;0; 3 hoặc ngược lại. 2 1 2 1
Vậy Khoảng cách giữa hai tâm của hai mặt cầu S , S là 2 2 2 1 1 2 6 . 2 1
Câu 32. Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B và AC a . Hình chiếu
vuông góc của đỉnh S lên mặt phẳng ABC là điểm H đối xứng với B qua AC . Góc giữa
https://www.facebook.com/groups/toanvd.vdc Trang 21
NHÓM TOÁN VD – VDC HSG QUẢNG NAM-2020
hai mặt phẳng SAC và ABC bằng 45 . Diện tích mặt cầu ngoại tiếp hình chóp S.ABC bằng N 2 2 a 2 5 a H A. 2 2 a . B. V . C. 2 5 a . D. . Ó 3 4 M T Lời giải O Á Chọn D N V D – VDC
Do điểm H đối xứng với B qua AC nên tứ giác ABCH là hình vuông.
Gọi O là giao điểm của AC và HB .
Ta có HO AC và SH AC nên AC SHO SO AC . Do đó góc giữa hai mặt phẳng
SAC và ABC bằng SOH 45 . N H 1 1 a
Trong tam giác SHO có SH H . O tan SOH AC.tan SOH . a tan 45 . Ó 2 2 2 M T Ta có: SH ABCH nên SH BC mà HC BC nên BC (SHC) BC SC . O Á N
Tương tự ta cũng chứng minh được AB SA . V D Do đó SHB SAB SCB 90 . – VDC
Suy ra các điểm S, , A ,
B C, H cùng thuộc mặt cầu đường kính SB .
Do đó bán kính mặt cầu ngoại tiếp hình chóp S.ABCH là 1 1 2 1 a a 5 R SB 2 2 SH HB 2 a . 2 2 2 4 4 2 2 5a 5 a
Vây diện tích mặt cầu ngoại tiếp hình chóp S.ABC bằng 2
S 4 R 4 . . 16 4
Câu 33. Cho hàm số f x có đạo hàm liên tục, nhận giá trị dương trên đoạn 1;4, f
1 1, f 4 8và 4 x
x f x f x x f x 2 3 2 . . ' 2 , x 1;4. Tích phân dx bằng f x 1
https://www.facebook.com/groups/toanvd.vdc Trang 22
NHÓM TOÁN VD – VDC HSG QUẢNG NAM-2020 1 3 2 A. . B. . C. . D. 2. 2 2 3 N Lời giải H Ó Chọn D M T 2 2
Ta có: x f x f x f x 3 2
x x f x f x xf x 4 2 . . ' 2 2 . . ' 2 x O Á N
2x . f x. f ' x 2xf x2 2 2
f x V 1 ' 1 4 2 D x x – VDC 2 f x 2 f x
Tích phân hai vế ta được ' 1
x C f x x x C . 2 2 x x 4 4 x
Thay x 4 C 0 . Vậy f x x x 2 x 2 1 x x 1
Câu 34. Đồ thị C của hàm số 3 2
y ax bx cx 3a và đồ thị C ' của hàm số 2
y 3ax 2bx c
,a ,bc ,a 0có đúng hai điểm chung khác nhau ,
A B và điểm A có hoành độ bằng 1.
Các tiếp tuyến của C và C ' tại điểm A trùng nhau; diện tích hình phẳng giới hạn bởi C
và C ' bằng 1. Giá trị của a b c bằng A.12. B.17. C. 60. D. 45. Lời giải Chọn C N H 3 2 2 Ó
Gọi f x ax bx cx 3 ;
a g x 3ax 2bx c M T
Ta có: f x g x có 1 nghiệm bằng 1 và f ' x g ' x có nghiệm bằng 1 O Á N c 3a V Do đó:
Diện tích hình phẳng giới hạn bởi C và C ' là b a D 1 – 2 VDC a x
x 1 dx 1 a 12 abc 60. 0
Câu 35. Chọn ngẫu nhiên đồng thời sáu số tự nhiên khác nhau thuộc đoạn [1;25]. Gọi A là biến cố
“Chọn được sáu số tự nhiên sao cho tổng bình phương của sáu số đó chia hết cho 3”. Xác suất
của biến cố A bằng 633 453 211 1803 A. . B. . C. . D. . 6325 6325 6325 6325 Lời giải Chọn D
Nhận xét: Số chính phương chia 3 luôn dư 0 hoặc dư 1. Thật vậy: Xét số chính phương 2
n (n N ) , ta có 3 trường hợp:
Trường hợp 1: n = 3k (k ∈ N):
https://www.facebook.com/groups/toanvd.vdc Trang 23
NHÓM TOÁN VD – VDC HSG QUẢNG NAM-2020 Khi đó: 2 2 n 9k 3
Trường hợp 2: n = 3k + 1 (k ∈ N): N Khi đó: 2 2 2
n (3k 1) 9k 6k 1chia 3 dư 1. H Ó
Trường hợp 3: n = 3k + 2 (k ∈ N) M T Khi đó: 2 2 2 2
n (3k 2) 9k 12k 4 (9k 12k 3) 1 chia 3 dư 1. O
Vậy, số chính phương chia 3 luôn dư 0 hoặc 1. Á N
Chia 25 số tự nhiên trong đoạn [1;25] thành 2 nhóm V
Nhóm 1: Gồm các số tự nhiên chia hết cho 3. Có 8 số tự nhiên thuộc nhóm 1. D
Nhóm 2: Gồm các số tự nhiên không chia hết cho 3. Có 17 số tự nhiên thuộc nhóm 2. – Để VDC
chọn được sáu số tự nhiên sao cho tổng bình phương của sáu số đó chia hết cho 3 thì chỉ có
thể thực hiện 1 trong 3 cách chọn:
Cách 1: Cả 6 số tự nhiên được chọn đều nằm trong nhóm 1
Cách 2: Cả 6 số tự nhiên được chọn đều nằm trong nhóm 2
Cách 3: Chọn 3 số tự nhiên trong nhóm 1 và 3 số tự nhiên trong nhóm 2.
Số phần tử không gian mẫu: n 6 C 177100 25
Xác suất của biến cố A: 6 6 3 3
C C C .C 1803 8 17 8 17 P A 177100 6325
Câu 36. Cho bất phương trình 2
x (m 2019)x 2020m (x m 1) log
x 2020 với m là tham số. 2019
Có bao nhiêu giá trị nguyên của m để tập nghiệm của bất phương trình đã cho chứa trong
khoảng (1000;2020) ? A. 1018. B. 1019. C. 1020. D. 1021. N H Lời giải Ó M T Chọn D O Theo bài ra: Á N 2 V
x (m 2019)x 2020m (x m 1) log x 2020 2019 D 2
x 2019x mx 2020m . x log x . m log x log x 2020 2019 2019 2019 – 2 VDC
m(x 2020 log
x) 2020 x 2019x . x log x log x 2019 2019 2019
m(x 2020 log
x) (x 2020 log
x) x(2020 x log x) 2019 2019 2019
m(x 2020 log
x) (x 2020 log x)(1 x) 2019 2019
Trường hợp 1: x 2020 log 0 2019x
Xét hàm số f (x) x 2020 log x : 2019 1 f '(x) 1 0 x (1000;2020) . x ln 2019
Do đó, f’(x) là hàm nghịch biến trên (1000;2020).
Mà f(2019) = 0 nên phương trình f(x) = 0 nhận nghiệm duy nhất x = 2019.
https://www.facebook.com/groups/toanvd.vdc Trang 24
NHÓM TOÁN VD – VDC HSG QUẢNG NAM-2020
Khi đó, bất phương trình trở thành:
0.m < 0.(1 – 2019) (Vô lý) N Như vậ H
y, x = 2019 không là nghiệm của bất phương trình đã cho. Ó M T
Trường hợp 2: x 2020 log x 0 2019 O
Vì hàm f(x) nghịch biến nên x < 2019. Á N V
Khi đó m 1 x x m 1 D
Mà tập nghiệm của bất phương trình chứa trong khoảng (1000;2019) nên – VDC
1000 m 1 2019 1001 m 2020
Trường hợp 2 có 1019 giá trị nguyên của m thỏa mãn bài toán.
Trường hợp 3: x 2020 log x 0 2019
Vì hàm f(x) nghịch biến nên x > 2019.
Khi đó m 1 x x m 1
Mà bất phương trình của tập nghiệm đã cho chứa trong khoảng (2019;2020) nên
2019 m 1 2020 2020 m 2021
Trường hợp 3 có 1 giá trị nguyên của tham số m thỏa mãn bài toán.
Trường hợp 4: m = 2020
Bất phương trình trở thành: 2020(x 2020 log
x) x 1 (x 2020 log ) x 2019 2019 N H Ó
*) Nếu x 2019 thì bất phương trình tương đương với 2020 x 1 x 2019 M T
Tập nghiệm của bất phương trình: S O Á N
*) Nếu x < 2019, chứng minh tương tự, ta được tập nghiệm của phương trình S V D
Vì tập rỗng cũng nằm trong (1000;2020) nên m = 2020 cũng thỏa mãn bài toán. – VDC
Vậy có tất cả 1021 giá trị nguyên m sao cho tập nghiệm của bất phương trình chứa trong khoảng (1000;2020).
Câu 37. Cho hình hộp chữ nhật ABC .
D A' B'C ' D' có AB ,
a AD a 3, AA' 3a . Gọi M là điểm
thuộc cạnh CC ' sao cho mp(MB )
D vuông góc với mp( A' B )
D . Thể tích khối tứ diện A' BDM bằng 3 13 3a 3 10a 3 100a 3 13 3a A. . B. . C. . D. . 8 9 3 24 Lời giải Chọn D
Chọn hệ trục tọa độ Oxyz như hình vẽ:
https://www.facebook.com/groups/toanvd.vdc Trang 25
NHÓM TOÁN VD – VDC HSG QUẢNG NAM-2020 N H Ó M T O Á N V D – VDC Ta có A'(0;0;0), ( B ; a 0;3a), ( D 0; a 3;3 ) a . Giả sử M ( ; a a 3; z ) , suy ra 0
A'B ( ; a 0;3a) A B A D 2 2 2 ' , ' 3 a 3; 3
a ;a 3 . Chọn véctơ pháp tuyến của
A'D (0;a 3;3a)
mp( A' B ) D là n ( 3 ; 3;1) .
BM (0;a 3;z 3a) Lại có 0
BM , BD 2
a 3(z 3a);a(z 3a);a 3 . 0 0 BD ( ; a a 3;0)
Chọn véctơ pháp tuyến của mp(MB )
D là n ' 3(z 3a);(3a z );a 3 . 0 0 Vì (A' B ) D (MB ) D .
n n' 0 3 3(z 3a) 3(3a z ) a 3 0 0 0 11a N
3 3z 9a 3 3a 3 3z a 3 0 4 3z 11a 3 z . 0 0 0 0 H 4 Ó M T 11a 1 Vậy M ; a a 3; V
A'B, A'D.A'M 4 A ' BDM 6 O Á 3 3 1 11a 3 13a 3 N 3 3 3
a 3 3a 3 V 6 4 24 D –
Câu 38. Cho hàm số y f (x) có đạo hàm trên
và có bảng biến thiên sau : VDC 1 1
Gọi S là tập hợp tất cả các giá trị của tham số thực m để phương trình m f (x) f (x) 2
có đúng 3 nghiệm thực phân biệt. Hỏi tập S có bao nhiêu phần tử? A. 3. B. Vô số. C. 1. D. 2.
https://www.facebook.com/groups/toanvd.vdc Trang 26
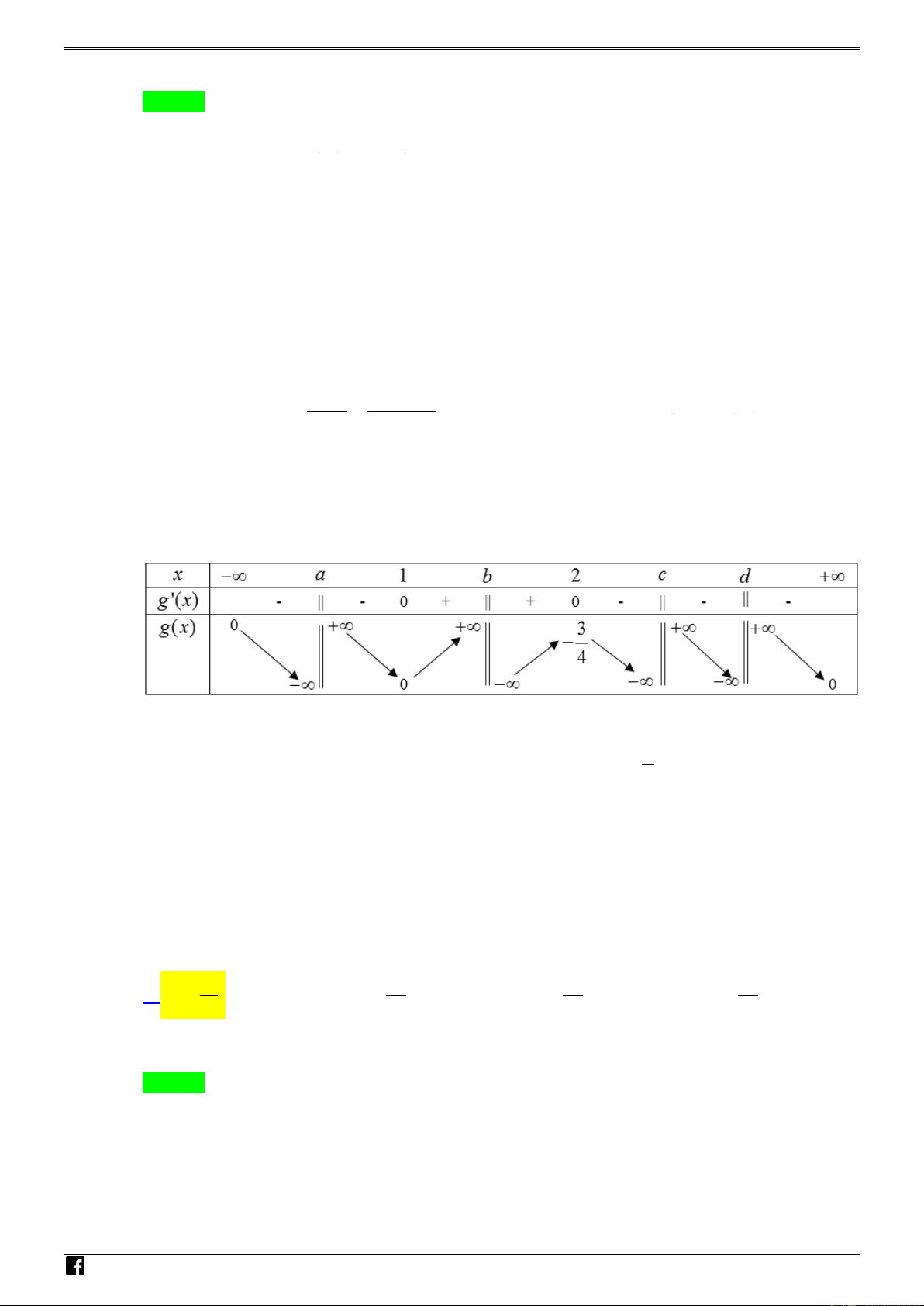
NHÓM TOÁN VD – VDC HSG QUẢNG NAM-2020 Lời giải Chọn C N 1 1 H Xét phương trình m Ó f (x) f (x) (1). 2 M T f (x) 0 O Điều kiện . Á f (x) 2 N V x a 1 D –
Ta có f (x) 0 x b (1; 2) ; f (x) 2 x d c VDC x c 2 1 1 1 1 Đặt g(x)
g '(x) f '(x) f (x) f (x) 2
f (x)2 f (x) 22 x 1
g '(x) 0 f '(x) 0 x 2 Bảng biến thiên: N H
Phương trình (1) có đúng 3 nghiệm thực phân biệt khi và chỉ khi đường thẳng y m có 3 điểm Ó M T 3
chung phân biệt với đồ thị hàm số y g(x) , khi và chỉ khi m . 4 O Á
Vậy có một giá trị của m thỏa mãn yêu cầu bài toán. N V
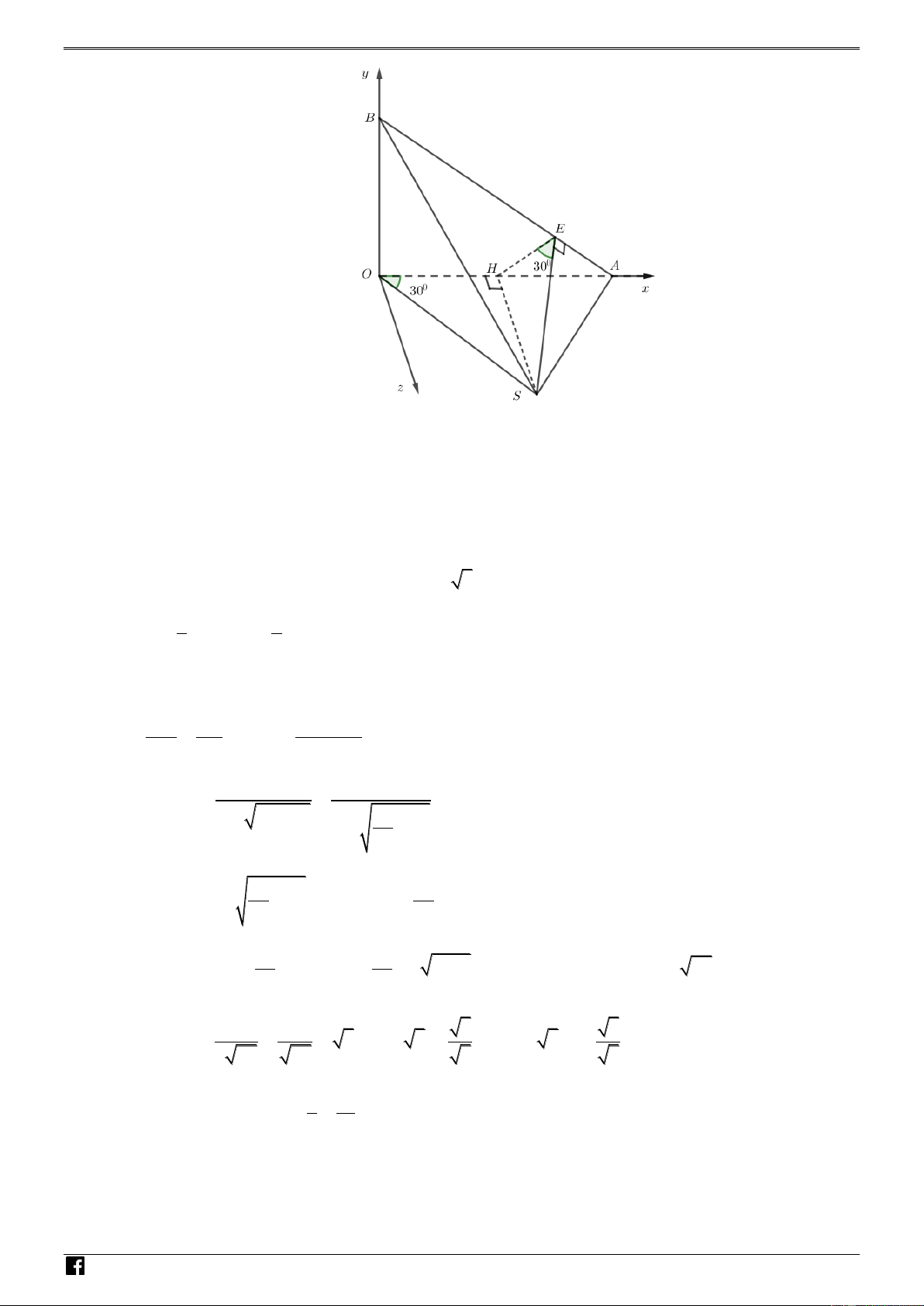
Câu 39. Trong không gian Oxyz , cho hai điểm ,
A B theo thứ tự thay đổi trên các tia O , x Oy sao cho D – O .
AOB 9 . Điểm S thuộc mặt phẳng Ozx sao cho hai mặt phẳng SAB và SOB cùng VDC
tạo với mặt phẳng Oxy một góc 30o . Gọi ;
a 0;c là tọa độ điểm S . Tính giá trị của biểu thức 4 4
P a c trong trường hợp thể tích khối chóp S.OAB đạt giá trị lớn nhất. 10 40 40 45 A. P . B. P . C. P . D. P . 3 81 9 8 Lời giải Chọn A
https://www.facebook.com/groups/toanvd.vdc Trang 27
NHÓM TOÁN VD – VDC HSG QUẢNG NAM-2020 N H Ó M T O Á N V D – VDC Ta có:
Hạ SH OA SOB,Oxy SOH
HE AB SAB,Oxy SEH 30o SOH SEH
HO HE SH 3 , suy ra BH là tia phân giác của góc OBA. 1 3 V S .SH SH V SH HO . OAB max max max 3 2 Đặt OA , x OB y , , x y 0 . x y 9 . N H OH OB O . A OB Ó OH
(Do BH là tia phân giác của góc OBA ). HA BA OB BA M T 9 9 O OH (Do . x y 9 ). Á 2 2 y x y 81 2 N y y 2 V y D – 81 81 VDC Xét A y
y A y2 2 2 y 2 2 y y 81 81 2 3 2 6 2 4 4
A 2Ay
Ay Ay
3 81A A 27.81.A A 3 27 2 2 y y 4 4 9 3 3 3 4 4 4 OH 3 S 3;0;
a 3; c . 4 4 3 27 27 3 3 1 10 Vậy 4 4
P a c 3 . 3 3
https://www.facebook.com/groups/toanvd.vdc Trang 28 NHÓM TOÁN VD – VDC HSG QUẢNG NAM-2020 2 2
Câu 40. Cho ba số thực dương ,
x y, z thỏa mãn x z y z 2 2
3z 4 . Giá trị lớn nhất của biểu 3
x y z 3
y x z 3 4 2 z xy thức P bằng N xy H Ó M T 112 110 128 55 A. . B. . C. . D. . 27 27 27 27 O Á Lời giải N V Chọn A D – 2 2 2 2 2 2 2 2 VDC Ta có:
x z 2y z 3z 4 x 2xz z 4y 4yz z 3z 4 2 2
x y z x y 2 2 2
z x y z x y 2 4 2 2 4 4 2 2 z 4 1 Khi đó:
x y z 4y x 2z z xy
x y x z 4 y x 8 z y z z xy 3 3 3 3 3 3 3 3 3 3 x 8y 2 2 3 P x 4y z xy xy xy
z x 2y 2 2
x 4 y 2xy 2
2z x 2y 3 z 4 z (Do 1 ). xy
x y xy
2z x 2y 2 2 4 2 2 3 1
z z 4 2xy
xy x y
2z x 2y 2 2 4 4 2 3
z z 4 N xy H Ó M T x y 2
z x 2y 2 2 2 3 3 2
z z 4 z z 4 . Dấu bằng xảy ra khi x 2y . xy O Á 2 N
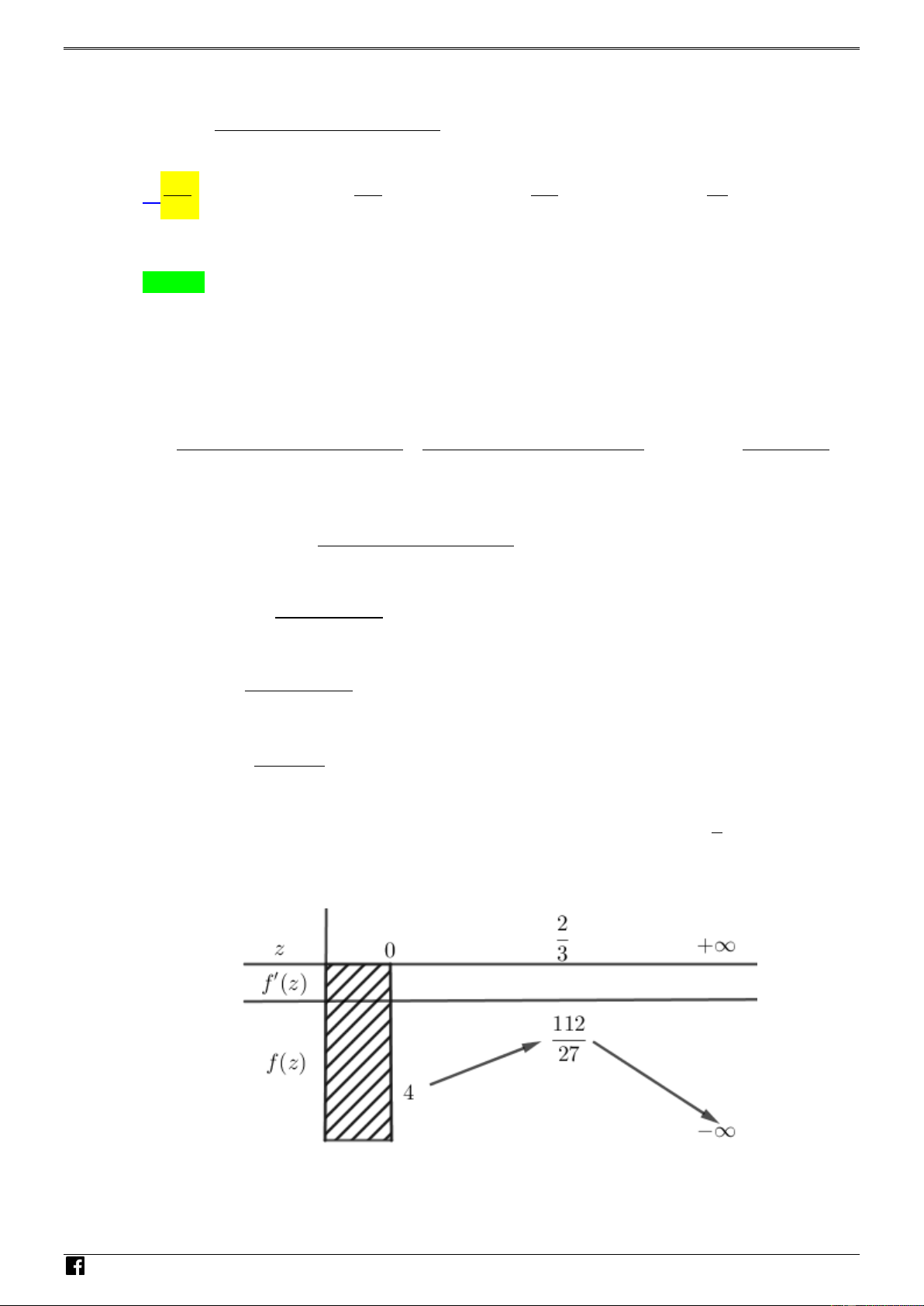
Xét hàm f z 3 2
z z 4 với z 0. Ta có f 'z 2 3
z 2z 0 z (do z 0). V 3 D – Bảng biến thiên: VDC
-------------- HẾT ---------------
https://www.facebook.com/groups/toanvd.vdc Trang 29