Đề thi học sinh giỏi Toán 9 cấp tỉnh năm 2017 – 2018 sở GD&ĐT Lai Châu

UBND TỈNH LAI CHÂU
KỲ THI CHỌN HỌC SINH GIỎI LỚP 9 CẤP TỈNH
SỞ GIÁO DỤC VÀ ĐÀO TẠO NĂM HỌC 2017-2018 Môn:
ĐỀ THI CHÍNH THỨC
(Đề thi có 01 trang)
Thời gian: 150 phút (không kể thời gian giao đề) Ngày thi: 22/4/2018
Câu 1 (3, 0 điểm
): Cho biểu thức 3 3    + + + 1 1 2 1 1 =  +  ⋅ + +  : x y x x y y A   với x > 0, 0 y > 3 3  x
y  x + y x y  x y + xy
a) Rút gọn biểu thức A.
b) Biết xy = 16. Tìm các giá trị của x, y để A có giá trị nhỏ nhất, tìm giá trị đó.
Câu 2 (4,0 điểm)
2.1. Tìm nghiệm nguyên của phương trình 3 2
x − 4x − xy + 5x + y + 3 = 0.
2.2. Tìm số tự nhiên n ≥ 1 sao cho tổng 1! + 2! + 3! + … + n! là một số chính phương .
Câu 3 ( 5,0 điểm)
3.1. Cho phương trình: 2 x − ( m + ) 2 2
1 x + m + m − 6 = 0 . Tìm m để phương trình có
2 nghiệm x , x thoả mãn 3 3 =50. 1 2 x − x 1 2
3.2. Giải phương trình 3x − 2 = 3− x −1. 2 2
x + y + 2(x + y) = 7
3.3. Giải hệ phương trình  .
y(y − 2x) − 2x =10
Câu 4 (6,0 điểm): Cho đường tròn tâm O đường kính AB. Vẽ dây cung CD vuông góc
với AB tại I (I nằm giữa A và O ). Lấy điểm E trên cung nhỏ BC ( E khác B và C ), AE
cắt CD tại F. Chứng minh:
a) Tứ giác BEFI là tứ giác nội tiếp đường tròn.
b) AE.AF = AC2.
c) Khi E chạy trên cung nhỏ BC thì tâm đường tròn ngoại tiếp ∆CEF luôn thuộc
một đường thẳng cố định.
Câu 5 ( 2,0 điểm): Choa,b,c là 3 số thực dương thỏa mãn ab +bc + ca = 3abc . Chứng minh rằng: a b c 3 + + ≤ . 2 2 2
a + bc b + ca c + ab 2
…………………..HẾT……………………
- Thí sinh không sử dụng tài liệu
- Cán bộ coi thi không giải thích gì thêm. Trang 1/1 UBND TỈNH LAI CHÂU
KỲ THI CHỌN HỌC SINH GIỎI LỚP 9 CẤP TỈNH
SỞ GIÁO DỤC VÀ ĐÀO TẠO NĂM HỌC 2017-2018
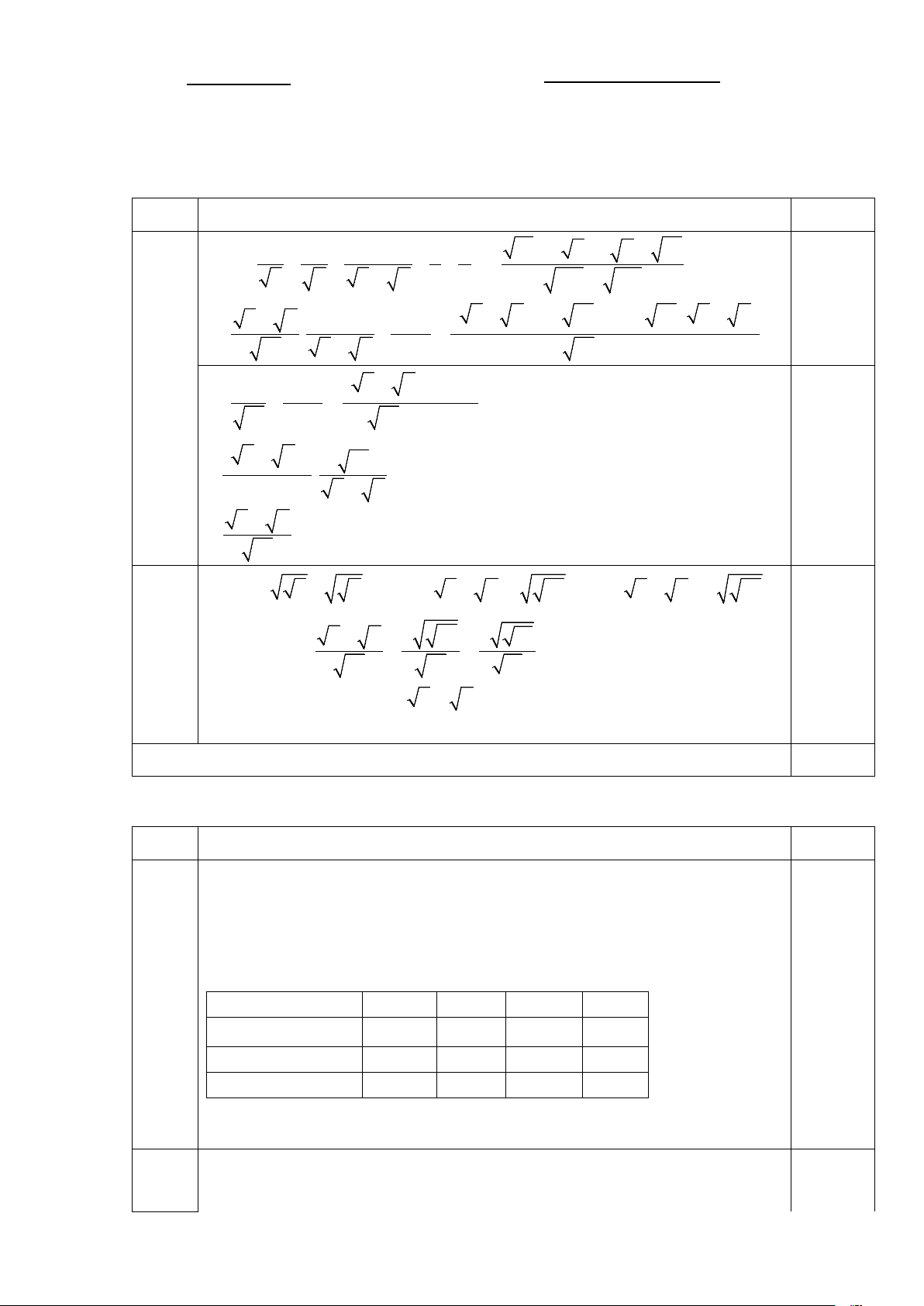
ĐÁP ÁN THANG ĐIỂM Môn: Toán Câu 1. ( 3,0 điểm) ý Nội dung Điểm 3 3  1 1  2 1 1  + + + =  + . + +  : x y x x y y A   3 3  x
y  x + y x y  x y + xy 0,5  +
+  ( x + y )( x - 2
xy + y)+ xy ( x + y x y x y ) = . +  :  xy x y xy  + xy (x +   y)  2
+  ( x + y )( x + y x y ) a = +  :  0,5 xy xy  xy (x +   y) ( x + y)2 = . xy . xy x + y 0,5 x + y = 0,5 xy
Ta có ( x − y )2 ≥ 0 ⇔ x + y -2 xy ≥ 0 ⇔ x + y ≥ 2 xy. 0, 25 x + y xy b Do đó 2 2 16 A = ≥ = = 1 0,5 xy xy 16
Vậy min A = 1 khi  x = y  ⇔ x = y = 4. 0,25 xy =16
Tổng điểm câu 1 3,0 Câu 2 ( điểm) ý Nội dung Điểm 3 2
x − x − xy + x + y + = ⇔ ( 3 4 5 3 0
x − 4x + 3x) + ( y − xy) + 2x − 2 = 5 − 0,25 ⇔ x(x − )
1 (x −3) − y(x − ) 1 + 2(x − ) 1 = 5 − 0,25 ⇔ (x − )( 2
1 x − 3x − y + 2) = 5 − 0,25
2.1 Ta có bảng kết quả sau x −1 1 5 − 5 1 − 2
x − 3x − y + 2 5 − 1 1 − 5 1,0 x 2 4 − 6 0 y 5 29 21 3 −
Vậy (x, y)∈ ({2;5),( 4; − 29),(6;2 ) 1 ,(0; 3 − )} 0,25
2.2 Với n = 1 thì 1! = 1 = 12 là số chính phương . 0,5
Với n = 2 thì 1! + 2! = 3 không là số chính phương 0,5 Trang 1/4
Với n = 3 thì 1! + 2! + 3! = 1+1.2+1.2.3 = 9 = 32 là số chính 0,5 phương
Với n ≥ 4 ta có 1! + 2! + 3! + 4! = 1+1.2+1.2.3+1.2.3.4 = 33 0,25
còn 5!; 6!; …; n! đều tận cùng bởi 0 do đó 1! + 2! + 3! + … + n!
có tận cùng bởi chữ số 3 nên nó không phải là số chính phương 0,25
Vậy có 2 số tự nhiên n thoả mãn đề bài là n = 1; n = 3
Tổng điểm câu 2 4,0 Câu 3 (5,0 điểm) ý Nội dung Điểm 3.1
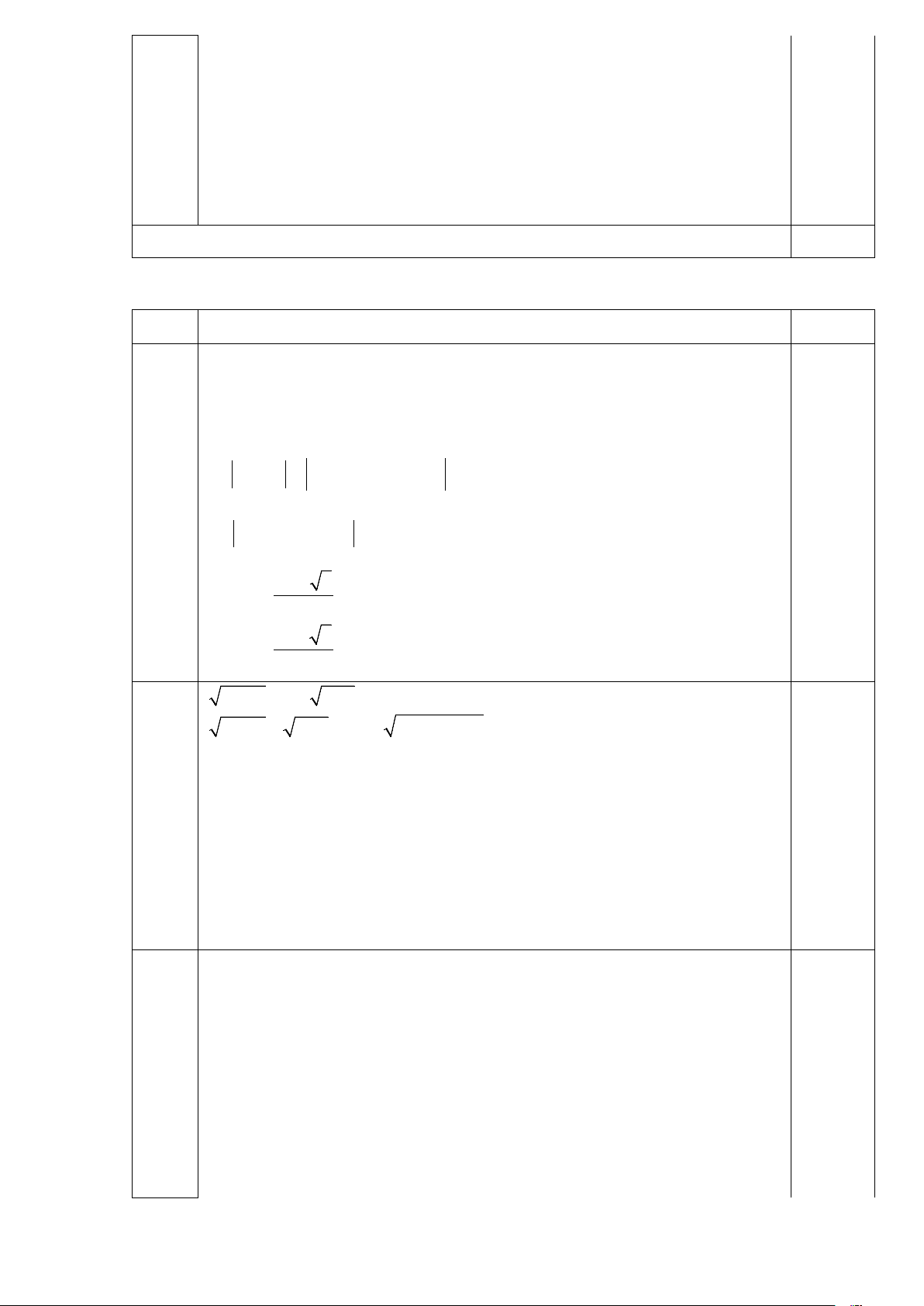
Ta có: ∆ = ( m + )2 − ( 2 2 1
4 m + m − 6) = 25 > 0 x = m − 2 0,5
⇒ Phương trình luôn có 2 nghiệm phân biệt x x 1 ⇒ 1, 2 x = m+  3 2 3 3
⇒ x − x = (m − 2)3 3 − (m + 3) = 50 1 2 0,5 2
m + m −1 = 0 2
⇔ 5(3m + 3m + 7) = 50 ⇔  0,5 2
3m + 3m +17 = 0 (VN)  1 − + 5 m = 2 ⇔   0,5 1 − − 5 m =  2 3.2
3x − 2 = 3− x −1 Điều kiện: x ≥1 0,25 2
3x − 2 + x −1 = 3 ⇔ 3x − 5x + 2 = 6 − 2x 1  ≤ x ≤ 3 ⇔  0,25 2 2 3
 x − 5x + 2 = 36 − 24x + 4x 1  ≤ x ≤ 3 ⇔  0,25 2
x −19x + 34 = 0 1  ≤ x ≤ 3 
⇔ x = 2 (TM ) 0,25  x = 17 (L) 2 2
x + y + 2(x + y) = 7 2 2
(x +1) + (y +1) = 9  ⇔ 
y(y − 2x) − 2x = 10 2 2
(y − x) − (x +1) = 9 0,5 2 2 Đặt a + b = 9
a = x +1, b = y +1⇒ b − a = y − x ⇒  2 2
(b − a) − a = 9 0,5 a = 0 2 2 2 2
⇒ a + b = (b − a) − a ⇔ a(a + 2b) = 0 ⇔  0,5 a = 2 − b
Với a = 0 ⇒ b = 3 ± ⇒ x = 1
− , y = 2 hoặc x = 1, − y = 4 − 0,25 Trang 2/4 3.3 Với 2 3 6 a = 2
− b ⇒ 5b = 9 ⇒ b = ± ⇒ a =  5 5 6 3 0,25 ⇒ x = 1 − − , y = 1 − + hoặc 6 3 x = 1 − + , y = 1 − − 5 5 5 5
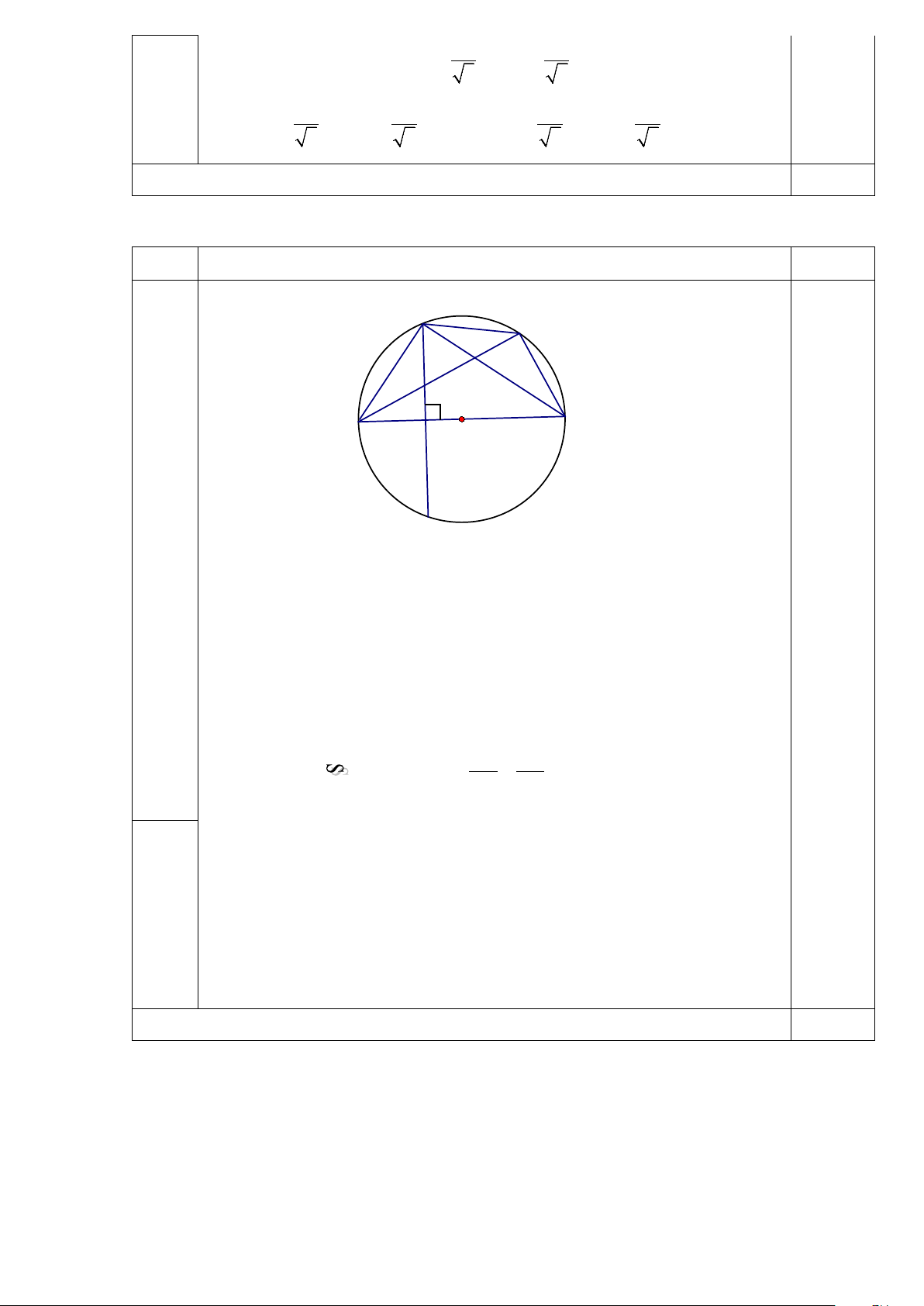
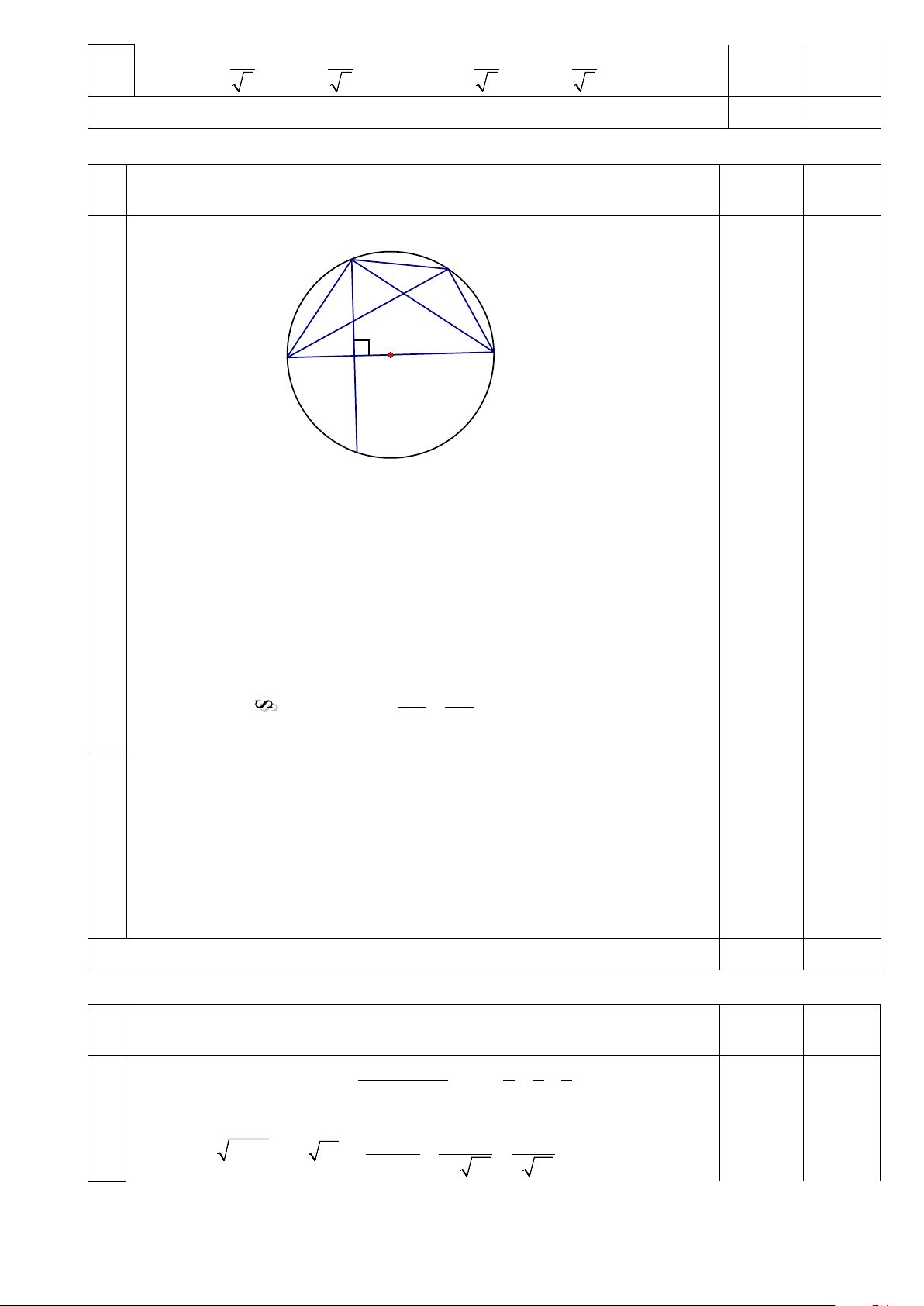
Tổng điểm câu 3 5,0 Câu 4 ( 6 điểm) ý Nội dung Điểm C E F B A 0,5 I O D
a) Tứ giác BEFI có:  0 BIF = 90 (gt) a  =  0
BEF BEA = 90 (góc nội tiếp chắn nửa đường tròn) 1,5
Suy ra tứ giác BEFI nội tiếp đường tròn đường kính BF
b) Vì AB ⊥ CD nên  =  AC AD, suy ra  =  ACF AEC .
Xét ∆ACF và ∆AEC có góc A chung và 1,0 b  =  ACF AEC .
Suy ra: ∆ACF với ∆AEC AC AE ⇒ = AF AC 1,0 2 ⇒ AE.AF = AC Theo câu b) ta có  = 
ACF AEC , suy ra AC là tiếp tuyến của đường
tròn ngoại tiếp ∆CEF (1). 1,0 c Mặt khác  0
ACB = 90 (góc nội tiếp chắn nửa đường tròn), suy ra
AC⊥ CB (2). Từ (1) và (2) suy ra CB chứa đường kính của đường
tròn ngoại tiếp ∆CEF, mà CB cố định nên tâm của đường tròn 1,0
ngoại tiếp ∆CEF thuộc CB cố định khi E thay đổi trên cung nhỏ BC
Tổng điểm câu 4 6 Câu 5 (2,0 điểm) Trang 3/4 ý Nội dung Điểm
Từ điều kiện đề bài ta có ab +bc + ca 1 1 1 = 3 ⇔ + + = 3 0,25 abc a b c
Áp dụng hai lần bất đẳng thức Côsi cho hai số dương, ta có: 2 2 a a 1
a + bc ≥ 2 a .bc = 2a bc ⇒ ≤ = 0,5 2
a + bc 2a bc 2 bc 1 1 1  1 1  1 1 1 1  1 1  a 1  1 1 . .  ≤ + ⇒ ≤ + ⇒ ≤ +     2 0,5
b c 2  b c 
2 b c 4  b c 
a bc 4  b c  +  Tương tự ta có: b 1  1 1  c 1  1 1  ;  ≤ + ≤ + 2 2 0,25
b ca 4  c a  c ab 4  a b  + +  a b c 1  1 1 1  3 ⇒ + + ≤ + + = (đpcm) 2 2 2 0,25 a bc b ca c
ab 2  a b c  + + +   2
Đẳng thức xảy ra khi a = b = c =1. 0,25
Tổng điểm câu 5 2,0
ĐIỂM TOÀN BÀI THI: Câu 1+2+3+4+5 20,0 Lưu ý:
- Điểm bài thi là tổng điểm của các câu thành phần. Thang điểm toàn bài
là 20,0 điểm, không được làm tròn (điểm lẻ từng ý trong một câu nhỏ nhất là
0,25) - Thí sinh làm bài bằng cách khác, lập luận chặt chẽ, logic, ra kết quả
đúng vẫn cho điểm tối đa.
……………………….Hết……………………… Trang 4/4 UBND TỈNH LAI CHÂU
KỲ THI CHỌN HỌC SINH GIỎI LỚP 9 CẤP TỈNH
SỞ GIÁO DỤC VÀ ĐÀO TẠO NĂM HỌC 2017-2018 PHIẾU CHẤM VÒNG 1 Môn: Toán
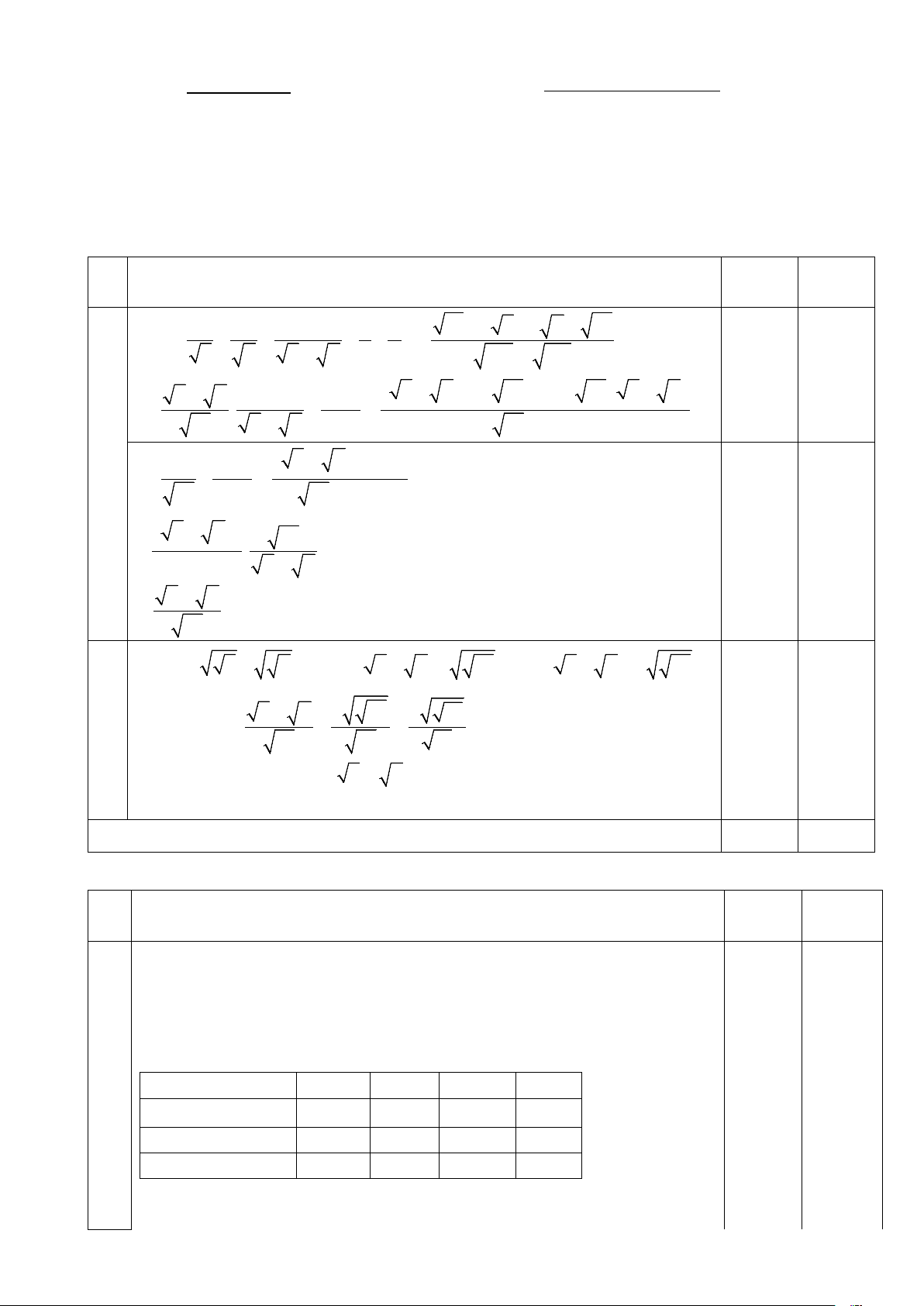
Mã túi………………. ………Số phách……….…….………..………………… Câu 1. ( 3,0 điểm) ý Nội dung Điểm Điểm chấm 3 3  1 1  2 1 1  + + + =  + . + +  : x y x x y y A   3 3  x
y  x + y x y  x y + xy 0,5  +
+  ( x + y )( x - 2
xy + y)+ xy ( x + y x y x y ) = . +  :  xy x y xy  + xy (x +   y)  2
+  ( x + y )( x + y x y ) a = +  :  0,5 xy xy  xy (x +   y) ( x + y)2 = . xy . xy x + y 0,5 x + y = 0,5 xy
Ta có ( x − y )2 ≥ 0 ⇔ x + y -2 xy ≥ 0 ⇔ x + y ≥ 2 xy. 0, 25 x + y xy b Do đó 2 2 16 A = ≥ = = 1 0,5 xy xy 16
Vậy min A = 1 khi  x = y  ⇔ x = y = 4. 0,25 xy =16
Tổng điểm câu 1 3,0 Câu 2 ( điểm) ý Nội dung Điểm Điểm chấm 3 2
x − x − xy + x + y + = ⇔ ( 3 4 5 3 0
x − 4x + 3x) + ( y − xy) + 2x − 2 = 5 − 0,25 ⇔ x(x − )
1 (x −3) − y(x − ) 1 + 2(x − ) 1 = 5 − 0,25 ⇔ (x − )( 2
1 x − 3x − y + 2) = 5 − 0,25
2.1 Ta có bảng kết quả sau x −1 1 5 − 5 1 − 2
x − 3x − y + 2 5 − 1 1 − 5 1,0 x 2 4 − 6 0 y 5 29 21 3 −
Vậy (x, y)∈ ({2;5),( 4; − 29),(6;2 ) 1 ,(0; 3 − )} 0,25 Trang 1/4
Với n = 1 thì 1! = 1 = 12 là số chính phương . 0,5
Với n = 2 thì 1! + 2! = 3 không là số chính phương 0,5
Với n = 3 thì 1! + 2! + 3! = 1+1.2+1.2.3 = 9 = 32 là số chính 0,5 2. phương
2 Với n ≥ 4 ta có 1! + 2! + 3! + 4! = 1+1.2+1.2.3+1.2.3.4 = 33 0,25
còn 5!; 6!; …; n! đều tận cùng bởi 0 do đó 1! + 2! + 3! + … + n!
có tận cùng bởi chữ số 3 nên nó không phải là số chính phương 0,25
Vậy có 2 số tự nhiên n thoả mãn đề bài là n = 1; n = 3
Tổng điểm câu 2 4,0 Câu 3 (5,0 điểm) ý Nội dung Điểm Điểm chấm
3.1 Ta có: ∆ = ( m+ )2 − ( 2 2 1
4 m + m − 6) = 25 > 0 x = m − 2 0,5
⇒ Phương trình luôn có 2 nghiệm phân biệt x x 1 ⇒ 1, 2 x = m+  3 2 3 3
⇒ x − x = (m − 2)3 3 − (m + 3) = 50 1 2 0,5 2
m + m −1 = 0 2
⇔ 5(3m + 3m + 7) = 50 ⇔  0,5 2
3m + 3m +17 = 0 (VN)  1 − + 5 m = 2 ⇔  0,5  1 − − 5 m =  2
3.2 3x − 2 = 3− x −1 Điều kiện: x ≥1 0,25 2
3x − 2 + x −1 = 3 ⇔ 3x − 5x + 2 = 6 − 2x 1  ≤ x ≤ 3 ⇔  0,25 2 2 3
 x − 5x + 2 = 36 − 24x + 4x 1  ≤ x ≤ 3 ⇔  0,25 2
x −19x + 34 = 0 1  ≤ x ≤ 3 
⇔ x = 2 (TM ) 0,25  x = 17 (L) 2 2
x + y + 2(x + y) = 7 2 2
(x +1) + (y +1) = 9  ⇔ 
y(y − 2x) − 2x =10 2 2
(y − x) − (x +1) = 9 0,5 2 2 Đặt a + b = 9
a = x +1, b = y +1⇒ b − a = y − x ⇒  2 2
(b − a) − a = 9 0,5 a = 0 2 2 2 2
⇒ a + b = (b − a) − a ⇔ a(a + 2b) = 0 ⇔  0,5 a = 2 − b
Với a = 0 ⇒ b = 3 ± ⇒ x = 1
− , y = 2 hoặc x = 1, − y = 4 − 0,25 3.3 Với 2 3 6 a = 2
− b ⇒ 5b = 9 ⇒ b = ± ⇒ a =  0,25 5 5 Trang 2/4 6 3 ⇒ x = 1 − − , y = 1 − + hoặc 6 3 x = 1 − + , y = 1 − − 5 5 5 5
Tổng điểm câu 3 5,0 Câu 4 ( 6 điểm) ý Nội dung Điểm Điểm chấm C E F B A 0,5 I O D
a) Tứ giác BEFI có:  0 BIF = 90 (gt) a  =  0
BEF BEA = 90 (góc nội tiếp chắn nửa đường tròn) 1,5
Suy ra tứ giác BEFI nội tiếp đường tròn đường kính BF
b) Vì AB ⊥ CD nên  =  AC AD, suy ra  =  ACF AEC .
Xét ∆ACF và ∆AEC có góc A chung và 1,0 b  =  ACF AEC .
Suy ra: ∆ACF với ∆AEC AC AE ⇒ = AF AC 1,0 2 ⇒ AE.AF = AC Theo câu b) ta có  = 
ACF AEC , suy ra AC là tiếp tuyến của đường
tròn ngoại tiếp ∆CEF (1). 1,0 c Mặt khác  0
ACB = 90 (góc nội tiếp chắn nửa đường tròn), suy ra
AC⊥ CB (2). Từ (1) và (2) suy ra CB chứa đường kính của đường
tròn ngoại tiếp ∆CEF, mà CB cố định nên tâm của đường tròn 1,0
ngoại tiếp ∆CEF thuộc CB cố định khi E thay đổi trên cung nhỏ BC
Tổng điểm câu 4 6 Câu 5 (2,0 điểm) ý Nội dung Điểm Điểm chấm
Từ điều kiện đề bài ta có ab +bc + ca 1 1 1 = 3 ⇔ + + = 3 0,25 abc a b c
Áp dụng hai lần bất đẳng thức Côsi cho hai số dương, ta có: 2 2 a a 1
a + bc ≥ 2 a .bc = 2a bc ⇒ ≤ = 0,5 2
a + bc 2a bc 2 bc Trang 3/4 1 1 1  1 1  1 1 1 1  1 1  a 1  1 1 . .  ≤ + ⇒ ≤ + ⇒ ≤ +     2 0,5
b c 2  b c 
2 b c 4  b c 
a bc 4  b c  +  Tương tự ta có: b 1  1 1  c 1  1 1  ;  ≤ + ≤ + 2 2 0,25
b ca 4  c a  c ab 4  a b  + +  a b c 1  1 1 1  3 ⇒ + + ≤ + + = (đpcm) 2 2 2 0,25 a bc b ca c
ab 2  a b c  + + +   2
Đẳng thức xảy ra khi a = b = c =1. 0,25
Tổng điểm câu 5 2,0
ĐIỂM TOÀN BÀI THI: Câu 1+2+3+4+5 20,0
Tổng điểm toàn bài: …………………………..điểm.
Bằng chữ: ……………………………………. ………………..
Lai Châu, ngày……………. tháng ………….năm 2018
CÁN BỘ CHẤM THI LẦN 1
(Ký, ghi rõ họ tên) Trang 4/4
Document Outline

• DE CHINH THUC
• DAP AN CHINH THUC
• PHIEU CHAM