Đề thi học sinh giỏi Toán 9 năm 2020 – 2021 phòng GD&ĐT thị xã Hoài Nhơn – Bình Định

HSG 9 – Tuyển chọn đề thi 2020 – 2021
: 0905.884.951 – 0929.484.951
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THI HỌC SINH GIỎI LỚP 9 THỊ XÃ HOÀI NHƠN
Năm học: 2020 – 2021
Môn: TOÁN – Ngày thi: 04/12/2020
Đề chính thức
Thời gian làm bài: 150 phút (không kể thời gian phát đề)
Bài 1. (4.5 điểm)
Rút gọn các biểu thức: a) A  5  3 29 12 5 . b) 3 3
B  70  4901  70  4901 . 1 1 1 1 c) C    ... . 2  2 3 2  2 3 4 3  3 4 100 99  99 100
Bài 2. (4.5 điểm) 2 2 a  b a) Cho *
a , b   . Tính giá trị của biểu thức: A 
, biết A có giá trị nguyên. ab
b) Cho ba số nguyên a , b , c và M  a  bb  c c  aabc . Chứng minh rằng:
" Nếu a  b  c   4 thì M  4 ".
c) Tìm số abcd biết abcd  3 và abc bda  650 .
Bài 3. (4.0 điểm) a) Giải phương trình: 2
4x  9 y 1  3x  6 xy .
b) Cho hai số dương x , y thỏa mãn: x  y  1 . Tìm giá trị nhỏ nhất của biểu thức: 2 2  1   1       A
x   y     .     x  y 
Bài 4. (3.0 điểm)
Cho nửa đường tròn tâm O đường kính AB . Gọi I là một điểm trên nửa đường tròn tâm
O ( I khác A và B ). Vẽ đường tròn tâm I tiếp xúc với AB tại H . Từ A và B vẽ hai tiếp
tuyến với đường tròn tâm I , tiếp xúc với đường tròn tâm I lần lượt tại C và D .
a) Chứng minh C , I , D thẳng hàng. 2 CD
b) Chứng minh AC.BD  . 4
Bài 5. (4.0 điểm)
a) Cho tam giác ABC có đường phân giác trong AD ( D thuộc BC ) sao cho BD  a và
CD  b (với a  b ). Tiếp tuyến tại A của đường tròn ngoại tiếp tam giác ABC cắt tia BC
tại M . Tính MA theo a và b .
b) Cho nửa đường tròn tâm O , đường kính AB  2R và M là một điểm thuộc nửa đường
tròn (khác A và B ). Tiếp tuyến của O tại M cắt các tiếp tuyến tại A và B của O lần
lượt tại các điểm C và D . Tìm giá trị nhỏ nhất của tổng diện tích của hai tam giác ACM và BDM .
----------  HẾT  ---------- GV: Lê Hồng Quốc
" Cần cù bù thông minh " Trang 1
HSG 9 – Tuyển chọn đề thi 2020 – 2021
: 0905.884.951 – 0929.484.951
ĐÁP ÁN THAM KHẢO – HSG TOÁN 9 THỊ XÃ HOÀI NHƠN – 2021
Bài 1. (4.5 điểm)
Rút gọn các biểu thức: a) A  5  3 29 12 5 . b) 3 3
B  70  4901  70  4901 . 1 1 1 1 c) C    ... . 2  2 3 2  2 3 4 3  3 4 100 99  99 100 a) Ta có: A          2 5 3 29 12 5 5 3 2 5 3  5  3 2 5  3     2 5 5 1  5  5 1  1 . b) Ta có: 3 B        3 3 3 140 3 70 4901 70 4901 .
70  4901  70  4901 3 3  B  B    B   B 
  B   2 3 140 0 125 3 15 0
5 B  5B  2  8  0 B  5 B 5  0     2   5 87  . 2 
B  5B  28  0   B      0 v« nghiÖm  2 4  Vậy B  5 . 1 1 n 1  n 1 1 c) Ta có:     . n   1 n  n n 1
n. n 1 n  n 1 n. n 1 n n 1 1 1 1 1 1 1 1 1 1 1 9
Áp dụng ta được: C       ...     . 1 2 2 3 3 4 98 99 99 100 10
Bài 2. (4.5 điểm) 2 2 a  b a) Cho *
a , b   . Tính giá trị của biểu thức: A 
, biết A có giá trị nguyên. ab
b) Cho ba số nguyên a , b , c và M  a  bb  c c  aabc . Chứng minh rằng:
" Nếu a  b  c   4 thì M  4 ".
c) Tìm số abcd biết abcd  3 và abc bda  650 . a   d.m 
a) Đặt d ­clna ,b, suy ra: 
; với m,n  1 và *
m , n , d   . b   d.n  2 2 2 2 2 2
d .m  d .n m  n Khi đó A   . 2 d . . m n . m n
Vì A có giá trị nguyên nên 2 2 2 m 
 n  m  n  m m   n 2 2   m  n  . m n  
, mà m,n  1    m  n . 2 2 2 m
 n  n  m  n  n   m  2 2 2 m  n 2m Vậy A    2 . 2 . m n m
b) Ta có: M  a  bb  c c  aabc       2 a b c
c ab  bc  ca  c abc GV: Lê Hồng Quốc
" Cần cù bù thông minh " Trang 2
HSG 9 – Tuyển chọn đề thi 2020 – 2021
: 0905.884.951 – 0929.484.951
           2  2 a b c ab bc ca a b c c
ab  bc  ca  c c abc
 a b  cab bc  ca2abc .
Vì a  b  c   4 nên trong ba số a , b , c phải có ít nhất một số chẵn   2abc  4 . Vậy M  4 .
c) Vì abc bda  650 mà 650 là số tròn chục nên c  a .
Suy ra ab bd  65  10a  b 10b d  65  10a  65  9b  d  74 (do b 1 ).
Lại có 10a  90  a  8; 9 . b  1  
Với a  8  9b  d  15  
. Khi đó abcd  8186  3 . Do đó trường hợp này loại. d   6  b   2  
Với a  9  9b  d  15  
. Khi đó abcd  9 297  3 . Do đó trường hợp này thỏa. d   7 
Vậy số cần tìm là: 9 297 .
Bài 3. (4.0 điểm) a) Giải phương trình: 2
4x  9 y 1  3x  6 xy .
b) Cho hai số dương x , y thỏa mãn: x  y  1 . Tìm giá trị nhỏ nhất của biểu thức: 2 2  1   1       A
x   y     .     x  y 
a) Điều kiện xy  0 . 1
 Trường hợp 1: x  0 , ta được phương trình: 9 y 1  0  y   . 9  
Do đó, trong trường hợp này phương trình có nghiệm là: x y 1 ;  0;     .  9 2  3  7
 Trường hợp 2: y  0 , ta được phương trình: 2
4x 1  3x  2x      0  (vô nghiệm).  4  4
Do đó, trong trường hợp này phương trình vô nghiệm.
 Trường hợp 3: x  0 , y  0 . Khi đó
x  y   x 
xy  x  x   y  xy  x 
  x    y  x 2 2 2 2 4 9 1 3 6 4 4 1 9 6 0 2 1 3  0   2x   2 1  0 2  x 1 0  1  1 Vì       x   và y  .
 3 y  x 2  3 y  x  0 2 0  18   
Do đó, trong trường hợp này phương trình có nghiệm là: x y 1 1 ;   ;   . 2 18
 Trường hợp 4: x  0 , y  0 . Khi đó
x  y   x 
xy  x  x   y  xy  x 
  x    y  x 2 2 2 2 4 9 1 3 6 4 4 1 9 6 0 2 1 3  0   2x   2 1  0 2  x 1 0   Vì        hệ này vô nghiệm. 
y  x 2 
3 y  x  0 3 0  
Do đó, trong trường hợp này phương trình vô nghiệm.    
 Vậy nghiệm của phương trình là: x y 1 1 1 ;   ; , 0;     . 2 18  9 GV: Lê Hồng Quốc
" Cần cù bù thông minh " Trang 3
HSG 9 – Tuyển chọn đề thi 2020 – 2021
: 0905.884.951 – 0929.484.951 1 1  1  b) Với  
x , y dương và x  y  1 , ta có: 2 2
P  x  y    4   2 2 x  y . 1    4 . 2 2  2 2   x y x y  
x  y2 xy 1  Ta có: 2 2 1 2 2 x  y 
 x  y  . 2 2 1 1
 Lại có:  x  y2 1  4xy , suy ra  4   16 . 2 2 xy x y 1 25 1
Do đó P  .116 4 
, đẳng thức xảy ra  x  y  . 2 2 2 25 1  Vậy P 
, xảy ra khi và chỉ khi x  y  . min 2 2
Bài 4. (3.0 điểm)
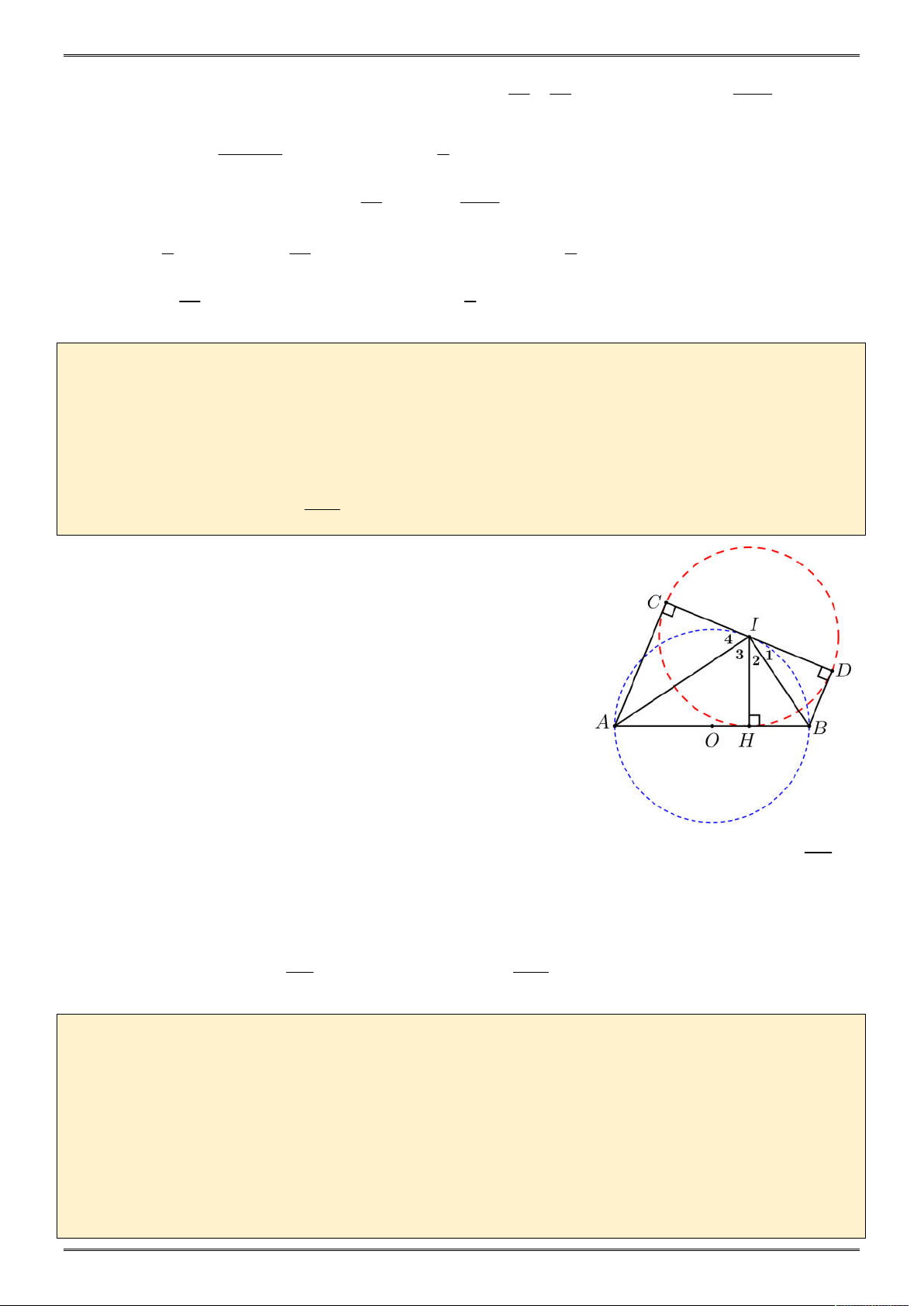
Cho nửa đường tròn tâm O đường kính AB . Gọi I là một điểm trên nửa đường tròn tâm
O ( I khác A và B ). Vẽ đường tròn tâm I tiếp xúc với AB tại H . Từ A và B vẽ hai tiếp
tuyến với đường tròn tâm I , tiếp xúc với đường tròn tâm I lần lượt tại C và D .
a) Chứng minh C , I , D thẳng hàng. 2 CD
b) Chứng minh AC.BD  . 4
a)  Vì BH , BD là tiếp tuyến của đường tròn I  nên IB là tia phân giác của  HID    I  I . 1 2
 Vì AC , AH là tiếp tuyến của đường tròn I  nên IA là tia phân giác của  CIH    I  I . 3 4  Vì A
 IB có AB là đường kính của đường tròn O và I
nằm trên đường tròn O    
 AIB  90  I  I  90 . 2 3 Do đó    
I  I  I  I  180 
 C , I , D thẳng hàng. 1 2 3 4
b)  Tam giác AIB vuông tại I có IH là đường cao nên 2 IH  H . A HB . CD
 Vì C , I , D thẳng hàng mà I là tâm của đường tròn nên CD là đường kính  IH  . 2
 Vì BH , BD là tiếp tuyến của đường tròn I  nên HB  BD .
 Vì AC , AH là tiếp tuyến của đường tròn I  nên HA  AC . 2 2 CD  CD  Do đó 2 IH  H . A HB    
  AC.BD  AC.BD   .  2  4
Bài 5. (4.0 điểm)
a) Cho tam giác ABC có đường phân giác trong AD ( D thuộc BC ) sao cho BD  a và
CD  b (với a  b ). Tiếp tuyến tại A của đường tròn ngoại tiếp tam giác ABC cắt tia BC
tại M . Tính MA theo a và b .
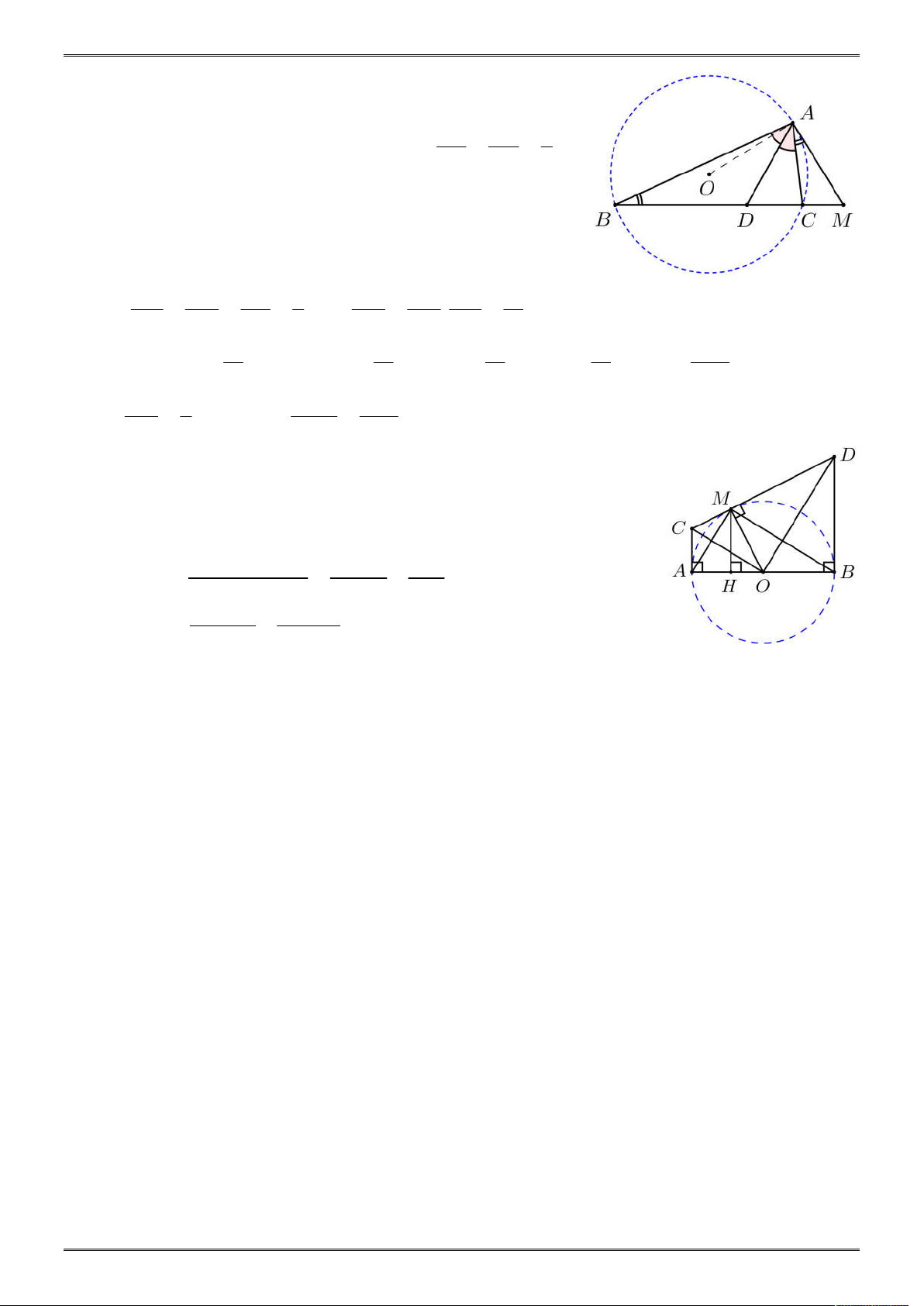
b) Cho nửa đường tròn tâm O , đường kính AB  2R và M là một điểm thuộc nửa đường
tròn (khác A và B ). Tiếp tuyến của O tại M cắt các tiếp tuyến tại A và B của O lần
lượt tại các điểm C và D . Tìm giá trị nhỏ nhất của tổng diện tích của hai tam giác ACM và BDM . GV: Lê Hồng Quốc
" Cần cù bù thông minh " Trang 4
HSG 9 – Tuyển chọn đề thi 2020 – 2021
: 0905.884.951 – 0929.484.951 a)  Ta có: 
MAC là góc tạo bởi tia tiếp tuyến và dây cung và 
ABC là góc nội tiếp cùng chắn một cung  
 MAC  ABC . AC DC b
 Vì AD là đường phân giác của ABC    . AB DB a
 Xét MAC và M  BA , ta có:  
MAC  ABC (chứng minh trên)  AMB chung. Do đó M  AC  M  BA (g - g) 2 MA MC AC b MC MC MA b Suy ra       .  2 MB MA AB a MB MA MB a 2 2 2 2 2 b b  b  b b    MC  MB.
 MC  a b.  MC 1  
  a b.  MC  . 2 2 2   2 a a  a  a a b MC b . a MC ab Ta có:    MA   . MA a b a b
b) Ta có: CA  CM và DB  DM (tính chất 2 tiếp tuyến cắt nhau).
Ta có: CD  CM  MD 
CD  AC  BD .
Kẻ MH  AB ( H  AB ), khi đó MH  MO  R .
Tứ ABDC là hình thang vuông nên CD  AB  2R . AC  BD 2 .AB CD.AB AB Ta có: 2 S     2R . ABDC 2 2 2 MH .AB MO.AB 2 S    R . MAB  2 2 Do đó 2 2 2 S S  S S
 2R  R  R . CAM  D  BM ABCD MAB 
Dấu "  " xảy ra khi H  O  M là điểm chính giữa cung AB . Vậy S S
đạt giá trị nhỏ nhất bằng 2
R khi M là điểm chính giữa cung AB . CAM  D  BM
----------  CHÚC CÁC EM MAY MẮN  ---------- GV: Lê Hồng Quốc
" Cần cù bù thông minh " Trang 5