Đề thi học sinh giỏi Toán 9 năm 2023 – 2024 phòng GD&ĐT Châu Đức – BR VT

UBND HUYỆN CHÂU ĐỨC
KỲ THI CHỌN HỌC SINH GIỎI LỚP 9 THCS
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
NĂM HỌC 2023 – 2024 - MÔN: TOÁN ĐỀ CHÍNH THỨC Ngày thi: 06/03/2024
Thời gian làm bài:150 phút
Bài 1. (6.0 điểm)  x + y x − y  
x + y + 2xy 
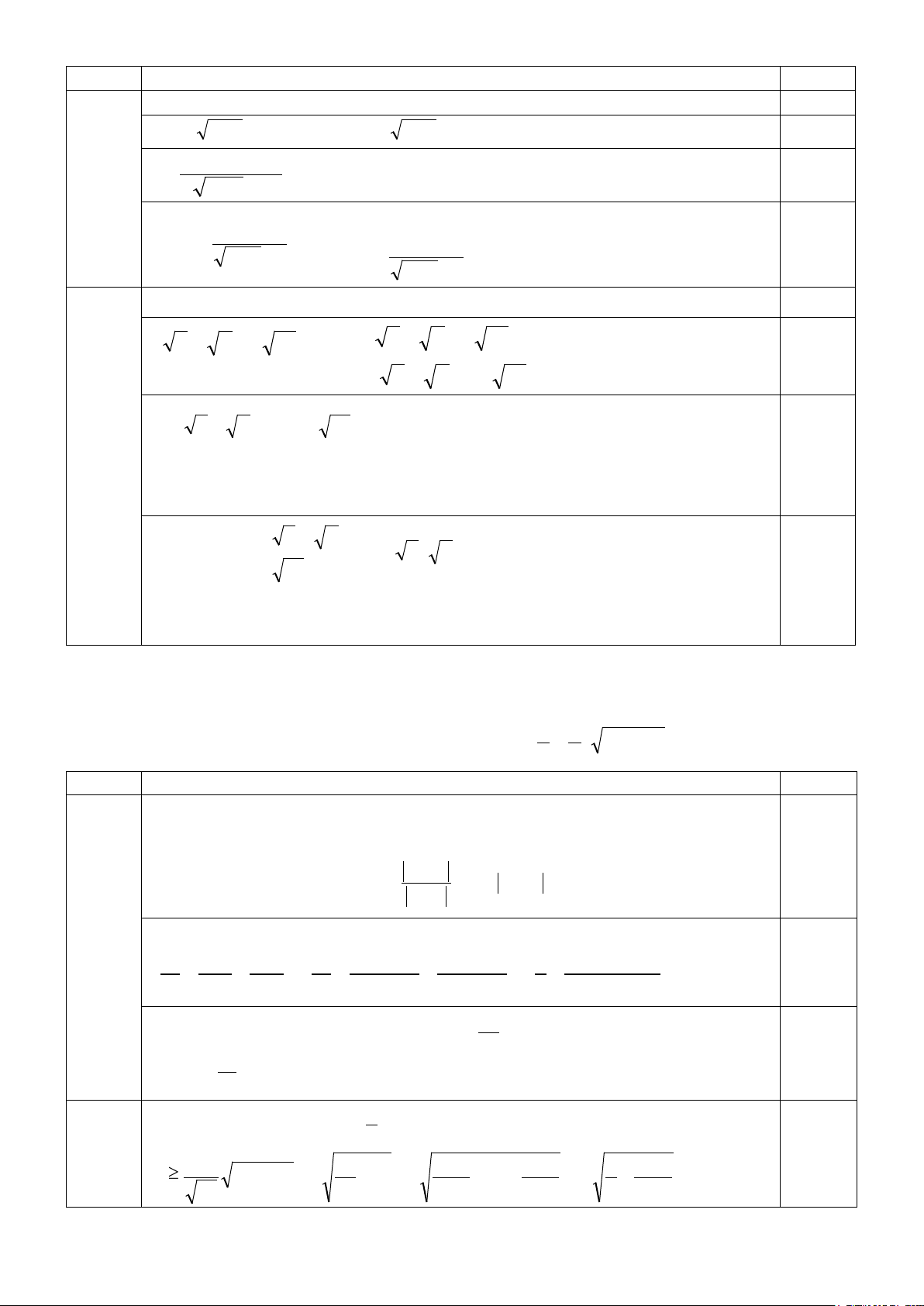
a) Rút gọn biểu thức P =  +   : 1+   với x ≥ ; 0 y ≥ ; 0 xy ≠ 1.  1− xy 1+ xy   1− xy 
b) Chứng minh rằng với n là số chẵn thì 3
A = n + 20n + 96 chia hết cho 48.
c) Tìm số tự nhiên có 2 chữ số sao cho tích của số đó với tổng các chữ số của nó bằng tổng lập
phương các chữ số của số đó.
Bài 2. (3.0 điểm)
a) Giải phương trình (x + )
1 x −1 + 5x =13. 
b) Giải hệ phương trình  x + y + 4 xy =16  . x + y = 10
Bài 3. (3.0 điểm)
a) Cho đường thẳng (d) : y = (m − 2)x + 2m −1 ( m là tham số). Tìm giá trị của m để khoảng
cách từ gốc toạ độ O đến đường thẳng (d) có giá trị bằng 2.  1 1  b) Cho x > ;
0 y > 0 và x + y ≤1. Tìm giá trị nhỏ nhất của 2 2 P = + 1+ x y  .  x y 
Bài 4. (5.0 điểm) Cho tam giác ABC nội tiếp đường tròn (O) và điểm D bất kì trên cạnh AB. Gọi
M và N lần lượt là trung điểm của các cạnh BC và CA. Gọi P và Q là các giao điểm của MN với
đường tròn (O) (điểm P thuộc cung nhỏ BC và điểm Q thuộc cung nhỏ CA). Gọi I là giao điểm
khác B của BC với đường tròn ngoại tiếp tam giác BDP. Gọi K là giao điểm của DI với AC.
a) Chứng minh tứ giác CIPK nội tiếp đường tròn.
b) Chứng minh PK .QC = QB.PD .
c) Gọi G là giao điểm khác P của AP với đường tròn ngoại tiếp tam giác BDP. Đường thẳng IG
cắt BA tại E. Chứng minh khi D di chuyển trên cạnh AB thì tỉ số AD không đổi. AE
Bài 5. (2.0 điểm) Cho tam giác ABC vuông tại A, tia phân giác của góc A cắt BC ở D. Gọi M, N
lần lượt là hình chiếu của 1
B, C lên đường thẳng AD. Chứng minh AD ≤ (BM + CN ). 2
--------Hết--------
Thí sinh không được sử dụng máy tính cầm tay. Giám thị coi thi không giải thích gì thêm.
Họ và tên thí sinh: …………………………….. Họ, tên chữ ký GT 1: ………………………………...
Số báo danh:…………………………………… Họ, tên chữ ký GT 2: ………………………………… UBND HUYỆN CHÂU ĐỨC
KỲ THI CHỌN HỌC SINH GIỎI LỚP 9 THCS
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
NĂM HỌC 2023 – 2024 - MÔN: TOÁN
HƯỚNG DẪN CHẤM MÔN TOÁN LỚP 9 I. Hướng dẫn chung:
1) Hướng dẫn chấm chỉ trình bày một cách giải với các ý cơ bản học sinh phải trình bày, nếu học sinh
giải theo cách khác mà đúng và đủ các bước thì vẫn cho điểm tối đa.
2) Điểm toàn bài là tổng điểm của các ý, các câu và không làm tròn.
II. Đáp án và thang điểm:
Bài 1. (6.0 điểm)  x + y x − y  a) Rút gọn biểu thức 
x + y + 2xy  P =  +   : 1+   với x > ; 0 y > ; 0 xy ≠ 1.  1− xy 1+ xy   1− xy 
b) Chứng minh rằng với n là số chẵn thì 3
A = n + 20n + 96 chia hết cho 48.
c) Tìm số tự nhiên có 2 chữ số sao cho tích của số đó với tổng các chữ số của nó bằng tổng lập phương
các chữ số của số đó. Câu
Nội dung trình bày Điểm a)
 x + x y + y + y x
x − x y − y + y x  (2.0đ)
1− xy + x + y + 2xy  P =  +    :   0.5  1− xy 1− xy   1− xy 
 2 x + 2y x  1+ x + y + xy  P =   :   0.5  1− xy   1− xy  2 x(1+ y) 1− xy 2 x P = . = 0.5x2 1− xy
(1+ x)(1+ y) 1+ x b)
Ta thấy 48 = 3.16 và (3;16) = 1 nên để chứng minh A chia hết cho 48 ta chứng (2.0đ) 0.5
minh A chia hết cho 3 và A chia hết cho 16. Ta có 3 3
n + 20n = n − n + 21n = (n − 1) n (n + 1) + 21n nên 3 n + 20n chia hết cho 3. 0.5
Do đó suy ra A chia hết cho 3.
Mặt khác do n là số chẵn, khi đó ta đặt n = 2k với k là một số tự nhiên. Từ đó ta có + = ( )3 3 3 + = + = ( 3 n 20n 2k 20.2k 8k 40k
8 k − k) + 48k = 8 (k − 1) k (k + 1) + 48k 0.5 Suy ra 3
n + 20n chia hết cho 16. Từ đó dẫn đến A chia hết cho 16.
Vậy A chia hết cho 48 với mọi n là số tự nhiên chẵn. 0.5 c)
Gọi số cần tìm là ab với a,b ∈ Ν;0 < a,b ≤ 9 (2.0đ) 0,5
Theo đề bài, ta có: ab(a + b) 3 3 = a + b
⇔ (10a + b)(a + b) = (a + b)( 2 2
a − ab + b ) ⇔ 10 2 2
a + b = a − ab + b 0,5
⇔ 10a + b = (a + b)2 − 3ab ⇔ 3a(3+ b) = (a + b)(a + b − ) 1
mà a + b và a + b −1nguyên tố cùng nhau.
a + b = a 3
a + b = 3 + b Do đó  Hoặc  0,5
a + b −1 = 3 + b
a + b −1 = a 3
Giải tìm được ab = 48và ab = 37 0,5
Bài 2. (3.0 điểm) 
a) Giải phương trình (x + )
1 x −1 + 5x =13
b) Giải hệ phương trình  x + y + 4 xy = 16  x + y =10 Câu Nội dung trình bày Điểm a) ĐK: x ≥ 1 0,5
(2.0đ) (x + )1 x −1 + 5x =13 ⇔ (x + )1( x −1 − )1+ (6x −12)= 0 0,5 (x + ) 1 (x − 2) ⇔ + ( 6 x − 2) = 0 0,5 x −1 +1 x − 2 = 0 (x − ) x +1 2 + 6   = 0  ⇔ x +1
⇔ x − 2 = 0 ⇔ x = 2 0,5  x −1 +1   + 6 = 0 (VN)  x −1 +1 b)
ĐK: x ≥ 0; y ≥ 0 0,5
(2.0đ)  x + y +4 xy =16  x + y +4 xy =16  ⇔ 0,5  2 x + y = 10
( x + y) −2 xy =10 S + 4P = 16 S + 4P = 16
Đặt x + y = S ≥ 0; xy = P ≥ 0 Suy ra:  ⇔   2 S − 2P = 10 2 2 S + S = 36 0,5 S = 4 S = − 5 , 4 ⇔   (Thỏa ĐK) Hoặc  (Không thỏa ĐK) P = 3 P = 125 , 5 S = 4  x + y = 4 Với  ⇒ 
⇒ x , y là nghiệm của phương trình P = 3  xy = 3 0,5 X = x x = 9 2 1 1  = 1
X − 4X + 3 = 0 ⇔ ⇒   hoặc  X = y y =1 2 3  = 9 
Bài 3. (3.0 điểm)
a) Cho đường thẳng(d ): y = (m − 2)x + 2m −1 (m là tham số). Tìm giá trị của m để khoảng cách từ gốc toạ
độ O đến đường thẳng (d) có giá trị bằng 2.   b) Cho x 1 1 > ;
0 y > 0 và x + y ≤1. Tìm giá trị nhỏ nhất của 2 2 P = + 1+ x y  .  x y  Câu Nội dung trình bày Điểm a)
* Với m = 2 ta có y = 3. Khi đó khoảng cách từ gốc toạ độ O đến đường thẳng (1.5đ)
(d) có giá trị bằng 3 (không thỏa mãn).
* Với m ≠ 2, gọi A và B thứ tự là giao điểm của đường thẳng (d) với trục hoành 0,25x2
và trục tung. Ta tính được: 1− 2m OA = ;OB = 2m −1 m − 2
Do khoảng cách từ O đến (d) có giá trị bằng 2 nên ta có: 2 2 1 1 1 1 (m − 2) 1 1 m − 4m + 5 = + ⇔ = + ⇔ = 0,5 2 2 2 2 2 OA OB 2
(1− 2m)2 (2m − )2 2 1 4 4m − 4m +1 2 2 19
⇔ 4m − 4m +1= 4m −16m + 20 ⇔ m = 12 19 0,5
Vậy m = 12 thì khoảng cách từ O đến (d) có giá trị bằng 2. b) 1
(1.5đ) Dự đoán điểm rơi là x = y = nên ta có: 2 0,5 P 2 1+ x2 y2 1 = 2 + xy 15 = 2 + xy 1 1 15 + ≥ . 2 + xy xy 16xy 16xy 2 16xy 1 1 15 15
Từ x + y ≤ 1 ⇔ 2 xy ≤ 1 ⇔ xy ≤ ⇔ ≥ 4 ⇔ ≥ 4 xy 16xy 4 0,5 => 1 15 P ≥ 2 + = 17 2 4 0,5
Vậy GTNN của P là 17 khi 1 x = y = 2
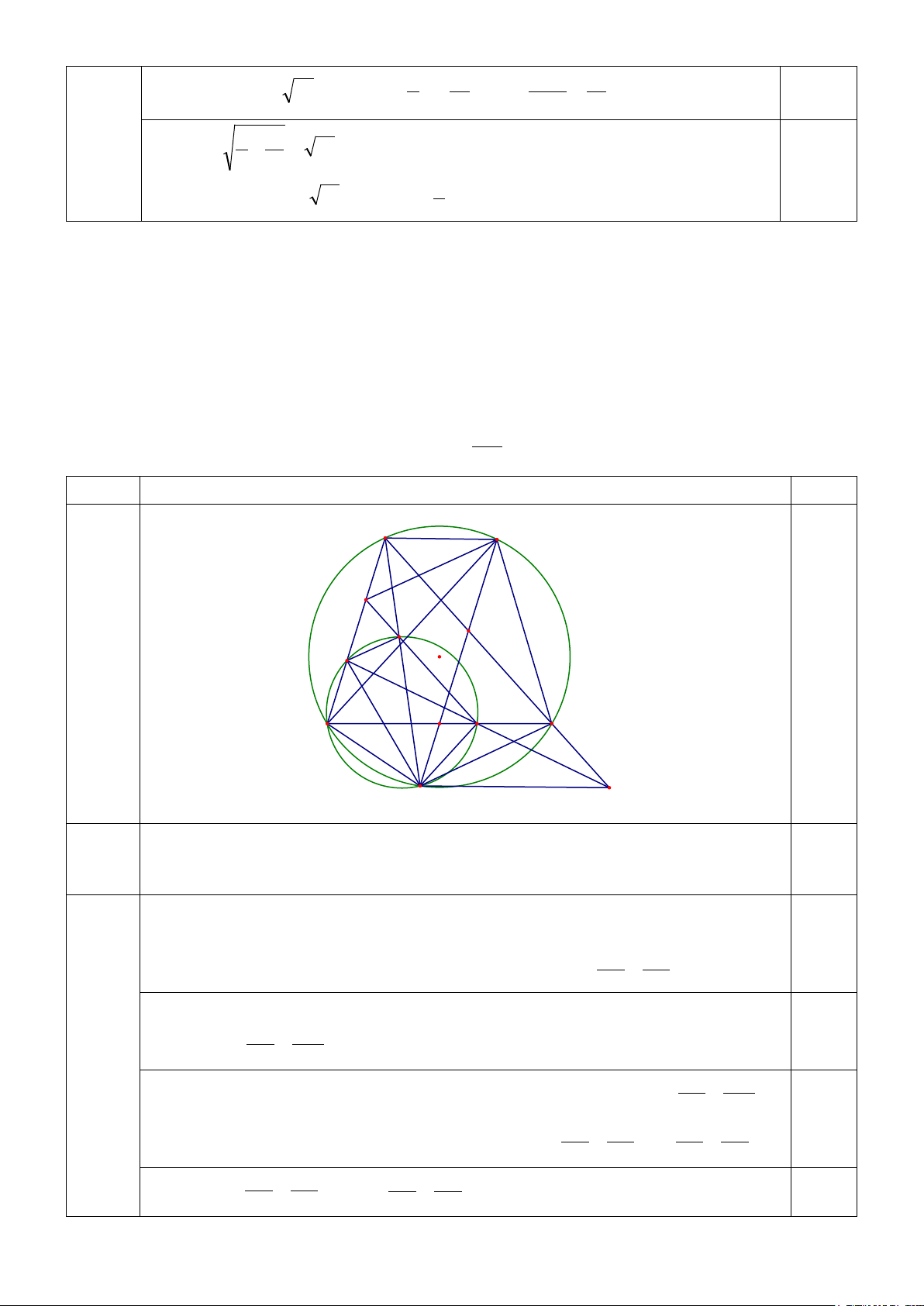
Bài 4. (5.0 điểm) Cho tam giác ABC nội tiếp đường tròn (O) và điểm D bất kì trên cạnh AB. Gọi M và N
lần lượt là trung điểm của các cạnh BC và CA. Gọi P và Q là các giao điểm của MN với đường tròn (O)
(điểm P thuộc cung nhỏ BC và điểm Q thuộc cung nhỏ CA). Gọi I là giao điểm khác B của BC với đường
tròn ngoại tiếp tam giác BDP. Gọi K là giao điểm của DI với AC.
a) Chứng minh tứ giác CIPK nội tiếp đường tròn.
b) Chứng minh PK .QC = QB.PD .
c) Gọi G là giao điểm khác P của AP với đường tròn ngoại tiếp tam giác BDP. Đường thẳng IG cắt BA tại
E. Chứng minh khi D di chuyển trên cạnh AB thì tỉ số AD không đổi. AE Câu Nội dung trình bày Điểm A Q E G N D O B C M I P K a)
Chứng minh tứ giác CIPK nội tiếp đường tròn.
(2.0đ) Ta có các tứ giác ABPC và BDIP nội tiếp đường tròn nên ta có 2,0 C
P ˆK = ˆP B A = ˆP B D = I P K
ˆ nên suy ra tứ giác CIPK nội tiếp đường tròn. b)
Chứng minh: PK QC . = QB PD .
(2.0đ) Do tứ giác BDIP và CIPK nội tiếp đường tròn nên ˆK D P = ˆC B P và K P ˆD = C P ˆB 0,5
nên hai tam giác BPC và DPK đồng dạng với nhau, suy ra PD PB = . PK PC
Tam giác MBP và MQC, có: ˆM B P = C ˆM Q và ˆM P B = C
Q ˆM nên đồng dạng với nhau, suy ra PB PM = . 0,5 QC CM
Chứng minh tương tự ta có hai tam giác BMQ và PMC đồng dạng nên PC PM = . QB BM 0,5
Mà M là trung điểm của BC hay MB = MC nên suy ra PB PC = hay PB QC = . QC QB PC QB Kết hợp với PD PB = ta được PD QC = hay PK QC . = QB PD . . PK PC PK QB 0,5 C) AD
(1.0đ) Chứng minh khi D di chuyển trên cạnh AB thì tỉ số không đổi. AE Ta có I B G ˆ = ˆG P B = ˆA P B = C
B ˆA nên suy ra IE // AC, do đó ta được ˆG E D = ˆC A B . 0,25 Lại có ˆG D E = B I Eˆ = C
A ˆB nên hai tam giác ABC và EGD đồng dạng với nhau, do đó suy ra ED AC = . DG BC
Mặt khác dễ thấy hai tam giác ADG và APB đồng dạng với nhau nên AD AP = . 0,25 DG PB
Đến đây ta suy ra được ED AD AC AP : = : hay ED AC PB . = . 0,25 DG DG BC PB AD BC.AP
Do tam giác ABC cố định nên suy ra P cũng là điểm cố định nên ED AC.PB = AD BC.AP không đổi hay AE DE AD 0,25 = 1− không đổi. Do vậy
có giá trị không đổi khi D thay AD AD AE đổi trên AB.
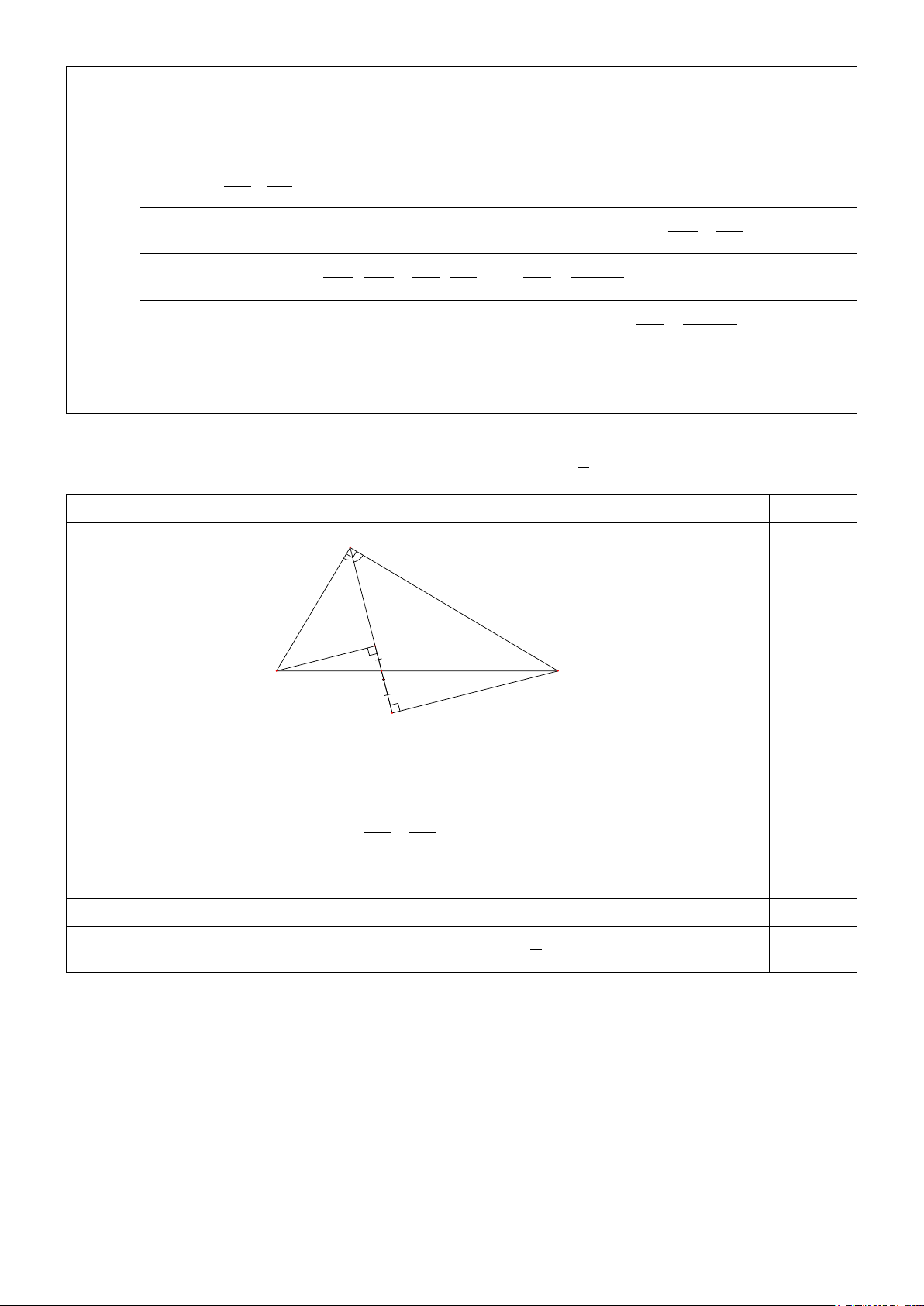
Bài 5. (2.0 điểm) Cho tam giác ABC vuông tại A, tia phân giác của góc A cắt BC ở D. Gọi M , N lần
lượt là hình chiếu của B, C lên đường thẳng AD . Chứng minh AD ≤ 1 (BM + CN). 2 Nội dung trình bày Điểm A M B D I C N
AD là phân giác của 0 ˆC A B ⇒ ˆB A D = 45 ⇒ A ∆ MB và A ∆ NC vuông cân
⇒ MA = MB; NA = NC ⇒ AM + AN = BM + CN . 0,5
Không mất tính tổng quát, giả sử AB ≤ AC .
Theo tính chất đường phân giác ta có: DB = AB ≤1. DC AC 0,5 Do B
∆ DM đồng dạng với C ∆ DN nên DM DB =
≤ 1 ⇒ DM ≤ DN DN DC
Gọi I là trung điểm của MN, khi đó AD ≤ AI và AM + AN = 2AI 0,5
Từ AD ≤ AI ⇒ . 2 AD ≤ .
2 AI = AM + AN = BM + CN ⇒ AD ≤ 1 (BM + CN ) 0,5 2