Đề thi học sinh giỏi Toán 9 năm 2023 – 2024 phòng GD&ĐT thành phố Bắc Ninh

UBND THÀNH PHỐ BẮC NINH
ĐỀ THI CHỌN HỌC SINH GIỎI CẤP THÀNH PHỐ
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO NĂM HỌC 2023 - 2024
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯ Môn: Toán lớp 9
Thời gian làm bài: 150 phút (không kể thời gian giao đề) ĐỀ CHÍNH THỨC
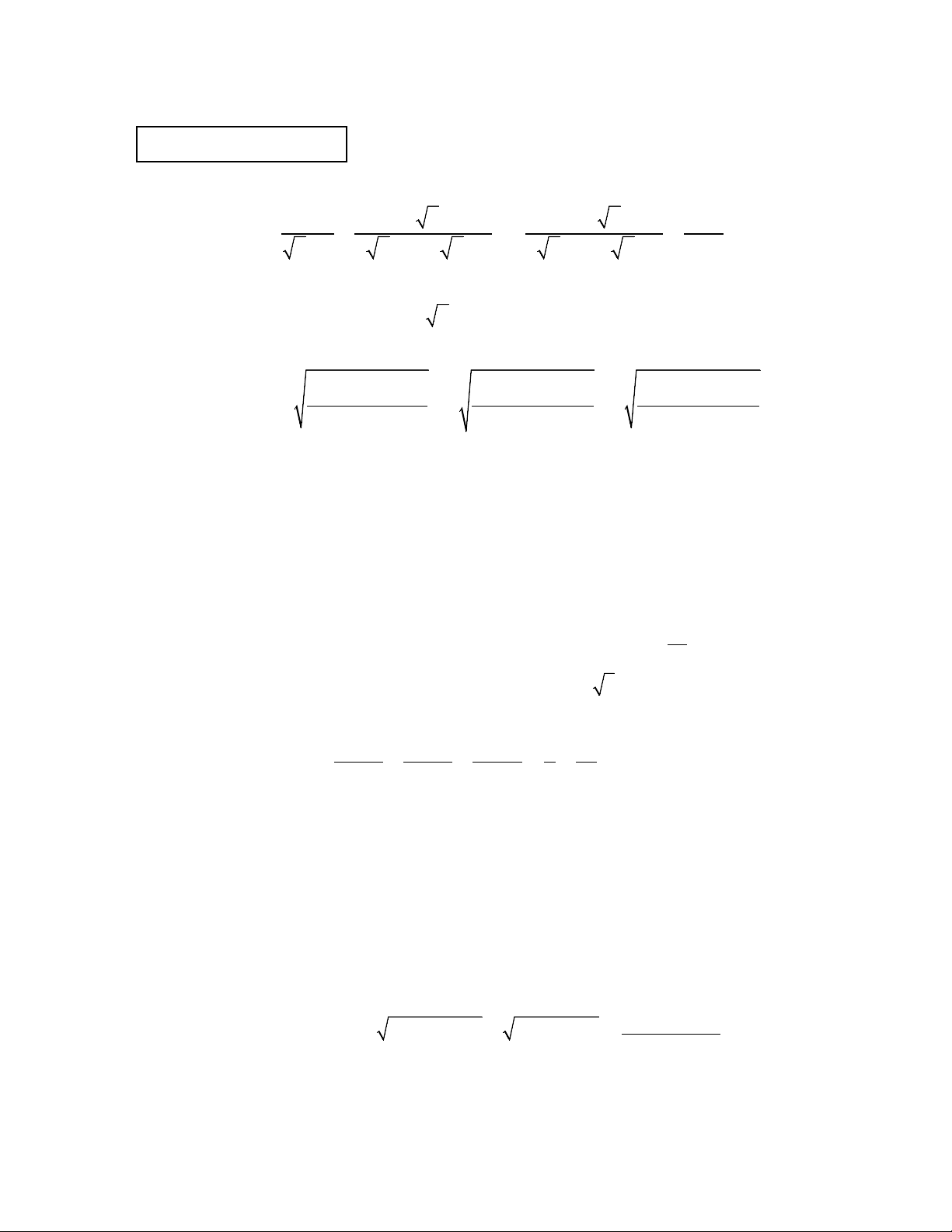
Câu 1 (5,0 điểm)     1. Cho hai biểu thức 1 2 x x + x 1 P =  −  :  +  với ≥ ≠ .  x 0;x 1
x − 1 x x − x + x − 1   x x + x + x +    1 x + 1 
a. Rút gọn biểu thức P .
b. Tìm tất cả các giá trị nguyên của x để P > x − 2.
2. Cho các số dương x, ,
y z thỏa mãn các điều kiện x + y + z = 2 và 2 2 2
x + y + z = 2 . ( 2 1 + y )( 2 1 + z ) ( 2 1 + z )( 2 1 + x ) ( 2 1 + x )( 2 1 + y )
Tính giá trị biểu thức: P = x + y + z . 2 2 2 1 + x 1 + y 1 + z
Câu 2 (4,0 điểm):
1. Tìm tất cả các cặp số nguyên (x;y) thoả mãn: 2 2 2x + y 4
+ x = 4 + 2xy . P
 = (x + 2023)5 + (2y − 2024)5 + (3z + 2025)5
2. Cho x;y;z là các số nguyên và  S
 = x + 2y + 3z + 2024 
Chứng minh rằng P chia hết cho 30 khi và chỉ khi S chia hết cho30 .
Câu 3 (3,0 điểm): 2 1. Cho đường thẳng x
(d) : y = mx − m + 2 (m là tham số) và parabol (P) : y =
. Đường thẳng (d) cắt (P) tại 2
hai điểm phân biệt (x ;y ) và (x ;y ). Chứng minh rằng y + y ≥ (2 2 − 1)(x + x ). 1 1 2 2 1 2 1 2
2. Cho ba số thực dương x, ,
y z thỏa mãn x + y + z = 3 . Chứng minh rằng: 3 3 3 x y z 1 2 + + ≥ +
xy + yz + zx 3 3 3 ( ) y + 8 z + 8 x + 8 9 27 .
Câu 4 (6,0 điểm): Cho tam giác nhọn ABC (AB < AC ) nội tiếp đường tròn (O). Các đường cao A ,
D BE,CF cắt nhau tại H . Tia AH cắt (O) tại K (K khác A ), tia KO cắt (O) tại M (M khác K ) và tia
MH cắt (O) tại P (P khác M ).
a) Chứng minh OD //MH và tứ giác AODP nội tiếp một đường tròn.
b) Gọi Q là giao điểm của PA và EF . Chứng minh AQ.AP = AH.AD và DQ ⊥ EF .
c) Tia PE và tia PF cắt đường tròn (O)lần lượt tại L và N ( ,
L N khác P ). Chứng minh LC = NB . 2
Câu 5 (2,0 điểm): 1. Giải phương trình + 2 2 8x 2x
6x + 2x + 1 − 2x + x + 1 = 2 3x + 3x + 4
2. Cho n là số lẻ. Chứng minh rằng từ (n − )2
1 + 1 số nguyên bất kì có thể chọn ra được n số sao cho tổng
của chúng chia hết cho n . ====== Hết ======
Họ và tên thí sinh :..................................................... Số báo danh:…….................... UBND THÀNH PHỐ BẮC NINH
HƯỚNG DẪN CHẤM ĐỀ THI HSG CẤP THÀNH PHỐ
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO NĂM HỌC 2023 - 2024
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯ Môn: Toán lớp 9 Câu Đáp án Điểm Cho hai biểu thức  1 2 x   x x 1  + P =  −  :  +
 với x ≥ 0;x ≠ 1. 1.1
 x − 1 x x − x + x − 1  x x + x + x +    1 x + 1  3,0
a. Rút gọn biểu thức P .
b. Tìm tất cả các giá trị nguyên của x để P > x − 2
ĐKXĐ: x ≥ 0;x ≠ 1  1 2 x   x x 1  + P =  −  :  + 
 x − 1 x x − x + x − 1  x x + x + x +    1 x + 1   x  x + − x  ( x +1 1 2 ) 1  = ( +  
x − )(x + ) :  ( x + )(x + ) x + 1 1 1 1 1    ( x − 1)2 2,0 x + 1
= ( x −1)(x +1). x +1 x − 1 = x +1 Vậy với x −
x ≥ 0;x ≠ 1 thì 1 P = . x + 1 x − 1
P > x − 2 ⇒
> x − 2 ⇔ x − 1 > x − x − 2 x + 1
⇔ x − 2 x − 1 < 0 ⇔ ( x − 1)2 < 2 ⇔ − 2 < x − 1 < 2
⇔ 1 − 2 < x < 1 + 2 1,0 Lại có x ≥ 0 x ∀ ≥ 0;x ≠ 1
Nên 0 ≤ x < 3 + 2 2
Mà x là số nguyên thỏa mãn x ≥ 0;x ≠ 1 Vậy x ∈ {0;2;3;4; } 5 .
Cho các số dương x, ,
y z thỏa mãn các điều kiện x + y + z = 2 và 2 2 2
x + y + z = 2 .
Tính giá trị biểu thức: 1.2 ( 2,0 2 1 + y )( 2 1 + z ) ( 2 1 + z )( 2 1 + x ) ( 2 1 + x )( 2 1 + y ) P = x + y + z 2 2 2 1 + x 1 + y 1 + z
Xét = (x + y + z )2 2 2 2 4
= x + y + z + 2xy + 2yz + 2zx Mà 2 2 2
x + y + z = 2 nên xy + yz + zx = 1 Khi đó ta có: 2 2
1 + x = xy + yz + zx + x = (x + z )(x + y) 2 2
1 + y = xy + yz + zx + y = (y + z )(y + x ) 2 2
1 + z = xy + yz + zx + z = (z + x )(z + y) 2,0 ( 2 1 + y )( 2 1 + z )
(y + z)(y + x)(z + x)(z + y) ⇒ x = x = x y + z 2 1 + x
(x + z)(x + y) ( ) ( 2 1 + z )( 2 1 + x ) 2 2 1 + x 1 + y Tương tự y
= y z + x ;z = z x + y 2 ( ) ( )( ) 2 ( ) 1 + y 1 + z
Do đó P = xy + xz + zx + zy + yz + yx = 2(xy + yz + zx ) = 2
2.1 Tìm tất cả các cặp số nguyên (x;y) thoả mãn: 2 2 2x + y 4 + x = 4 + 2xy 2,0
x + y + x = + xy ⇔ (x − y)2 + (x + )2 2 2 2 4 4 2 2 = 8 0,5 Do 2 2
x,y là các số nguyên nên (x − y) ;(x + 2) là các số chính phương không vượt quá
8 nên (x − y)2 ≤ 8 Mà ( − )2 2
x y là số chính phương nên (x − y) ∈ {0;1; } 4 1,0 Khi đó ta có (x + )2
2 ∈ {8;7; } , mà (x + 2)2 là số chính phương nên 4 (  = x + )2 x 0 2 = 4 ⇔  x = 4 −  Với x = 0 thì 2 y = 4 ⇔ y = 2 ±  + y = y  = − Với x = 4 − thì (− − y)2 4 2 2 4 = 4 ⇔  ⇔  4 + y = 2 − y = 6 − 0,5  
Vậy phương trình đã cho có các nghiệm nguyên là (0;2);(0; 2 − );( 4 − ; 2 − );( 4 − ; 6 − ). P
 = (x + 2023)5 + (2y − 2024)5 + (3z + 2025)5 Cho 2.2
x;y;z là các số nguyên và S = x + 2y + 3z + 2024 2,0 
Chứng minh rằng P chia hết cho 30 khi và chỉ khi S chia hết cho30 .
Đặt a = x + 2023;b = 2y − 2024;c = 3z + 2025 với a; ;
b c là các số nguyên. 5 5 5 P
 = a + b + c Khi đó ta có: 
S = a + b + c 0,5 
Xét − = ( 5 − ) + ( 5 − ) + ( 5 P S a a b b c − c)
Ta có chứng minh với mọi số nguyên m thì 5
m − m chia hết cho 30 Thật vậy: 5 4 2 2
m − m = m(m − 1) = m(m − 1)(m + 1) 2 2 2
= m(m − 1)(m − 4) + 5m(m − 1)
= m(m − 1)(m + 1)(m − 2)(m + 2) + 5m(m − 1)(m + 1)
Với mọi số nguyên m thì m;(m − 1);(m + 1);(m − 2);(m + 2) là 5 số nguyên liên
tiếp nên trong đó có một thừa số chia hết cho 2 ; một thừa số chia hết cho3 ; một thừa 1,0
số chia hết cho 5 mà 2;3;5 nguyên tố cùng nhau từng đôi một nên tích của chúng chia
hết cho 2.3.5 . Do đó m(m − 1)(m + 1)(m − 2)(m + 2) chia hết cho 30 .
Tương tự m(m − 1)(m + 1) chia hết cho 6 , mà (5,6) = 1 nên 5m(m − 1)(m + 1) chia hết cho 30 .
Vậy với mọi số nguyên m thì 5
m − m chia hết cho 30 .
Do đó − = ( 5 − ) + ( 5 − ) + ( 5 P S a a b b
c − c) chia hết cho 30 với a; ;bc là các số
nguyên. Suy ra P ≡ S (mod30) do đó P chia hết cho 30 khi và chỉ khi S chia hết 0,5 cho 30 . 2 Cho đường thẳng x
(d) : y = mx − m + 2 (m là tham số) và parabol (P) : y = . 2
3.1 Đường thẳng (d) cắt (P) tại hai điểm phân biệt (x ;y ) và (x ;y ). Chứng minh rằng 1,5 1 1 2 2
y + y ≥ (2 2 − 1)(x + x ). 1 2 1 2
Xét phương trình hoành độ giao điểm của (d)và (P) 2 x 2
= mx − m + 2 ⇔ x − 2mx + 2m − 4 = 0 2 0,5 Có 2 2 '
 = m − (2m − 4) = (m − 1) + 3 > 0 với mọi m , nên phương trình luôn có hai
nghiệm phân biệt. Vì vậy (d) luôn cắt (P) tại hai điểm phân biệt (x ;y ) và (x ;y ). 1 1 2 2
Theo định lý Vi-ét ta có x + x = 2 , m do đó 1 2 2
y + y = m(x + x ) − 2m + 4 = 2m − 2m + 4 . 1 2 1 2
Do đó ta cần chứng minh: 2
2m − 2m + 4 ≥ (2 2 − 1).2m 1,0 ⇔ m −
m + ≥ ⇔ (m − )2 2 2 2 2 0 2
≥ 0 luôn đúng với mọi m .
Nên suy ra y + y ≥ (2 2 − 1)(x + x ). 1 2 1 2
Cho ba số thực dương x, ,
y z thỏa mãn x + y + z = 3 . Chứng minh rằng: 3.2 3 3 3 x y z 1 2 1,5 + + ≥ +
xy + yz + zx 3 3 3 ( ) y + 8 z + 8 x + 8 9 27 .
Áp dụng bất đẳng thức AM-GM cho ba số dương, ta có: 3 2 3 2 x y + 2 y − 2y + 4 x
y + 2 y − 2y + 4 x + + ≥ 3.3 . . = 1,0 3 3 y + 8 27 27 y + 8 27 27 3 . 3 2 x
9x + y − y − 6 ⇒ ≥ . 3 y + 8 27 3 2 3 2 Tương tự ta có: y
9y + z − z − 6 z
9z + x − x − 6 ≥ ; ≥ . 3 3 z + 8 27 x + 8 27
Cộng theo vế ba bất đẳng thức ta được:
10 (x + y + z ) − ( 2 2 2 3 3 3 x + y + z x y z ) −18 + + ≥ 3 3 3 y + 8 z + 8 x + 8 27 − ( 2 2 2 12
x + y + z ) = 0,5 27
+ (x + y + z )2 − ( 2 2 2 3
x + y + z ) 1 2 = = +
(xy + yz + zx). 27 9 27
Đẳng thức xảy ra khi và chỉ khi x = y = z = 1.
Câu 4 (6,0 điểm): Cho tam giác nhọn ABC (AB < AC ) nội tiếp đường tròn (O). Các đường cao A ,
D BE,CF cắt nhau tại H . Tia AH cắt (O)tại K (K khác A ), tia KO
cắt (O) tại M (M khác K ) và tia MH cắt (O)tại P (P khác M ). 4
a) Chứng minh OD //MH và tứ giác AODP nội tiếp một đường tròn. 6,0
b) Gọi Q là giao điểm của PA và EF . Chứng minh AQ.AP = AH.AD và DQ ⊥ EF .
c) Tia PE và tia PF cắt đường tròn (O)lần lượt tại L và N ( ,
L N khác P ). Chứng minh LC = NB . Ta có    BCH BAK 90 ABC  = = ° −      1 
 ⇒ BCH = BCK
BCK = BAK = sdBK  2  1,5
Vì CB là phân giác của góc HCK mà CB ⊥ HK tại D nên CH ∆
K cân tại C .
Suy ra D là trung điểm của HK K ∆ MH có ,
O D lần lượt là trung điểm của KM và KH ⇒ OD là đường trung bình a của K
∆ MH , suy ra OD//HM . Vì  
OD//HM ⇒ DOK = PMK (2 góc đồng vị) Xét (O) có  
PMK = PAK (hai góc nội tiếp cùng chắn cung PK ) 1,0 và  1  1
PMK = POK nên    
PMK = KOD = POK = POD . 2 2 Suy ra   DOP = PAD .
Do đó tứ giác APDO nội tiếp một đường tròn.
Có tứ giác EFBC nội tiếp nên   
AFE = ACB = APB ⇒ FQPB nội tiếp
⇒ AF.AB = AQ.AP 1,0
Mà tứ giác BFHD nội tiếp ⇒ AF.AB = AH.AD
Do đó AQ.AP = AH.AD
Ta có AQ.AP = AH.AD nên QHDP nội tiếp   ⇒ ADQ = APH Mà  
APH = AKM (cùng chắn cung  AM )   ⇒ ADQ = AKM b Mà  
AKM = OAK (vì OA ∆
K cân tại O )  
⇒ ADQ = OAK ⇒ DQ//OA (1) 1,0
Vẽ tiếp tuyến Ax của đường tròn (O), suy ra Ax//EF
Mà Ax ⊥ OA nên EF ⊥ OA (2)
Từ (1) và (2)suy ra DQ ⊥ FE .
Kéo dài FE và BC cắt nhau tại T .
Dễ thấy EB và EC là các phân giác trong và ngoài tại đỉnh E của D ∆ ET . Suy ra CD BD TB DB = ⇒ = CT BT TC DC Xét BQ ∆
C có QD ⊥ QT và TB DB =
nên QD và QT lần lượt là phân giác trong c TC DC 1,5
và phân giác ngoài tại đỉnh Q của BQ ∆ C   ⇒ BQF = CQE .
Mặt khác, tứ giác PBFQ nội tiếp nên   BPN = BQF . Tương tự:   CPL = CQE Do đó    
BPN = CPL ⇒ BN = LC ⇒ BN = LC . 2
5.1 Giải phương trình + 2 2 8x 2x
6x + 2x + 1 − 2x + x + 1 = 1,0 2 3x + 3x + 4 2 + 2 2 8x 2x
6x + 2x + 1 − 2x + x + 1 = 2 3x + 3x + 4 2 2 4x + x 8x + 2x ⇔ − = 0 2 2 2
6x + 2x + 1 + 2x + x + 1 3x + 3x + 4 ⇔ (   2 x + x ) 1 2 4  −  = 0  2 2 2 
 6x + 2x + 1 + 2x + x + 1 3x + 3x + 4  2 4x + x = 0 0,5  ⇔ 1 2  = 2  2 2
 6x + 2x + 1 + 2x + x + 1 3x + 3x + 4 x  = 0 Với 2 4x x 0  + = ⇔ 1 x  = −  4 Với 1 2 = 2 2 2
6x + 2x + 1 + 2x + x + 1 3x + 3x + 4 ⇔ 2( 2 2
6x + 2x + 1 + 2x + x + 1) 2 = 3x + 3x + 4 2 2
⇔ x + x + 2 − 2 2x + x + 1 + 2( 2 2
x + x + 1 − 6x + 2x + 1) = 0 4 3 2 4 3 2
x + 2x − 3x
x + 2x − 3x ⇔ + 2 = 0 2 2 2 2
x + x + 2 + 2 2x + x + 1
x + x + 1 + 6x + 2x + 1 ⇔ (   4 3 2
x + x − x ) 1 2 2 3  +  = 0 (*)  2 2 2 2 
 x + x + 2 + 2 2x + x + 1 x + x + 1 + 6x + 2x + 1  2  1  7 Ta có 2 2 2
x + x + 2 = x +  + > 0 ⇒ x + x + 2 + 2 2x + x + 1 > 0 ;  2  4 0,5 2   2 1 3 2 2
x + x + 1 = x +  + > 0 ⇒ x + x + 1 + 6x + 2x + 1 > 0  2  4 Do đó 1 2 + > 0 2 2 2 2
x + x + 2 + 2 2x + x + 1
x + x + 1 + 6x + 2x + 1 x  = 0  Nên (*) 4 3 2 2
⇔ x + 2x − 3x = 0 ⇔ x (x − 1)(x + 3) = 0 ⇔ x  = 1 x  = 3 −   
Vậy phương trình có nghiệm 1 x ∈ − ; 3 − ;0;1  4 
5.2 Cho n là số lẻ. Chứng minh rằng từ (n − )2
1 + 1 số nguyên bất kì có thể chọn ra được 1,0
n số sao cho tổng của chúng chia hết cho n . Lấy (n − )2
1 + 1 số nguyên bất kì đã cho chia cho n , và xem xét số dư của chúng khi
chia n , ta có hai trường hợp sau:
Trường hợp 1: Chọn được n số a ;a ;a ;...;a khi chia cho n có đầy đủ n số dư là 1 2 3 n 0,1,2, , … n − 1. n n − 1 0,5
Khi đó a + a + a + ... + a ≡ 0 + 1 + 2 + ... + n − = n n ( 1) ( )(mod ) 1 2 3 2 n (n − 1) Ta có n − n là số lẻ nên 1 là số nguyên. Do đó ≡ 0(modn) 2 2
Hay a + a + a + ... + a ≡ 0(modn) 1 2 3 n
Trường hợp 2: Với (n − )2
1 + 1 số dư ở phép chia của (n − )2 1 + 1 số nguyên bất kì
cho n có nhiều nhất n − 1 loại số dư.
Khi đó theo nguyên lý Dirichlet có ít nhất n số có cùng số dư khi chia cho n (vì nếu
có tối đa n − 1 số có cùng số dư khi chia n thì số các số tối đa là 0,5
(n − )2 < (n − )2 1 1 + 1).
Giả sử n số đó là a ;a ;a ;...;a , chúng chia n có cùng số dư là k . 1 2 3 n
Khi đó a + a + a + ... + a ≡ nk ≡ 0(modn). 1 2 3 n