Đề thi học sinh giỏi Toán THPT cấp tỉnh năm 2019 – 2020 sở GD&ĐT Hậu Giang

SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI CHỌN HỌC SINH GIỎI CẤP TỈNH
TỈNH HẬU GIANG CÁC MÔN VĂN HÓA THPT NĂM HỌC 2019 – 2020
KHÓA NGÀY: 02/7/2020 MÔN: TOÁN ĐỀ CHÍNH THỨC
Thời gian làm bài: 180 phút (không kể thời gian phát đề)
(Đề thi gồm 01 trang) Câu I (3,0 điểm) 9  1 
1) Tìm số hạng không chứa x trong khai triển 2 2x  ,   với x  0. 4  x 
2) Trong đợt ứng phó đại dịch COVID – 19 vừa qua, ngành y tế của một tỉnh miền Tây đã chọn ngẫu
nhiên một tổ gồm 3 nhân viên trong 6 nhân viên y tế dự phòng của tỉnh và 16 nhân viên y tế của các trung
tâm y tế dự phòng cơ sở để thực hiện hành động chống dịch đột xuất. Tính xác suất để 3 nhân viên y tế được
chọn có cả nhân viên y tế của tỉnh và nhân viên y tế của cơ sở. Câu II (3,0 điểm) Giải phương trình 2 2
2x  7x  8  (x  2) 2x 11x 16, với x  . Câu III (5,0 điểm)
1) Cho hình chóp S.ABCD có đáy ABCD là hình vuông, SA vuông góc với mặt phẳng đáy,
SA  a 2, góc giữa đường thẳng SC và mặt phẳng đáy bằng 0
45 . Gọi M là trung điểm của cạnh . AB Tính
theo a khoảng cách h giữa hai đường thẳng DM và . SB
2) Trong mặt phẳng với hệ tọa độ Oxy, cho tứ giác ABCD nội tiếp trong đường tròn đường kính . BD
Gọi H, K lần lượt là hình chiếu vuông góc của điểm A trên các đường thẳng BC, BD và E là giao điểm
của hai đường thẳng HK và AC. Biết đường thẳng AC đi qua điểm M (3;2) và nhận n  (1; 1  ) làm vectơ
pháp tuyến. Tìm tọa độ các điểm E và ,
A biết điểm H (1;3), K(2; 2) và hoành độ điểm A lớn hơn 2. Câu IV (3,0 điểm) 2u Cho dãy số 1
(u ) được xác định bởi: u  và n * u  , n   . n 1  3 n 1 2u (3n 1)  1 n
a) Tìm u và số hạng tổng quát u của dãy số. 4 n 1 1 1 b) Tính S    
(tổng gồm n số hạng) theo . n u u u 1 2 n Câu V (3,0 điểm) Cho hàm số 3 2
f (x)  ax  bx  cx  d (với , a , b , c d  ) thỏa mãn '
f (0)  4, f (0)  0, f (2)  0 và ' f (2)  0.
a) Tìm hàm số f (x). b) Giả sử 2 (
h x)  f (x  2x  )
m . Tìm tất cả các giá trị thực của tham số m để phương trình ' h (x)  0
có 5 nghiệm phân biệt x , x , x , x , x thỏa mãn 4 4 4 4 4
x  x  x  x  x  229. 1 2 3 4 5 1 2 3 4 5 Câu VI (3,0 điểm) Cho hàm số 4 2
f (x)  x  2x  m 1 (với m là tham số thực). Tìm tất cả các giá trị của tham số m để
giá trị nhỏ nhất của hàm số g(x)  f (x) trên đoạn [0;2] bằng 2020.
………………………..HẾT………………………..
Thí sinh không được sử dụng tài liệu và máy tính cầm tay. Giám thị không giải thích gì thêm.
Họ và tên thí sinh:…………………………………………….Số báo danh:………………..
Chữ ký của giám thị 1: ……………………… Chữ ký của giám thị 2: …………………….
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI CHỌN HỌC SINH GIỎI CẤP TỈNH
TỈNH HẬU GIANG CÁC MÔN VĂN HÓA THPT NĂM HỌC 2019-2020
KHÓA NGÀY: 02/7/2020 MÔN: TOÁN ĐỀ CHÍNH THỨC
HƯỚNG DẪN CHẤM ĐỀ CHÍNH THỨC MÔN: TOÁN
(Hướng dẫn chấm gồm 06 trang) Câu Nội dung Điểm 9  
1) Tìm số hạng không chứa 1 x trong khai triển 2 2x  ,   với x  0. 1,0 4  x  k  
Số hạng tổng quát có dạng k k 1 2 9 k k 9k 186 C (2 )   C ( 1  ) .2 . k x x
, với 0  k  9, k  . 0,5 9   4 9  x 
Ứng với số hạng không chứa x, ta có 18 6k  0  k  3. Số hạng không chứa 0,5 x là 6 3 2  .C  5  376. 9
2) Trong đợt ứng phó đại dịch COVID – 19 vừa qua, ngành y tế của một tỉnh miền
Câu I Tây đã chọn ngẫu nhiên một tổ gồm 3 nhân viên trong 6 nhân viên y tế dự phòng của tỉnh và (3,0
điểm) 16 nhân viên y tế của các trung tâm y tế dự phòng cơ sở để thực hiện hành động chống dịch 2,0
đột xuất. Tính xác suất để 3 nhân viên y tế được chọn có cả nhân viên y tế của tỉnh và nhân viên y tế của cơ sở.
* Số phần tử của không gian mẫu là 3 ( n )   C 1540. 0,5 22
* Gọi A là biến cố cần tính xác suất.
Số phần tử của biến cố A là 2 2 ( n )
A  6.C 16.C  960. 16 6 1,0 n A * Xác suất cần tìm là ( ) 960 48 P( ) A    . n( )  1540 77 0,5 Giải phương trình 2 2
2x  7x  8  (x  2) 2x 11x 16, với x  . 3,0 Đặt 2
t  2x 11x 16. Điều kiện t  0. 0,5 Ta có 2 2
t  2x 11x 16
Phương trình đã cho trở thành 2
t  (x  2)t  4x  8  0. 0,5 Ta có 2 2 2
  (x  2)  4(4x 8)  x 12x 36  (x 6) .
x  2  x  6       x x   Câu Từ đó, ta có t x 2 hoặc 2 6 t 4. 0,5 2 2 II (3,0
* Với t  x  2, ta có điểm) x  2 2
2x 11x 16  x  2   2 2
2x 11x 16  x  4x  4 0,75 x  2  
 x  3 hoặc x  4. 2
x  7x 12  0
* Với t  4, ta có 2 2 2 0,5
2x 11x 16  4  2x 11x 16  16  2x 11x  0  x  0 hoặc 11 x  . 2  
Vậy, tập nghiệm của phương trình là 11 S  0; 3; 4; .  0,25 2 
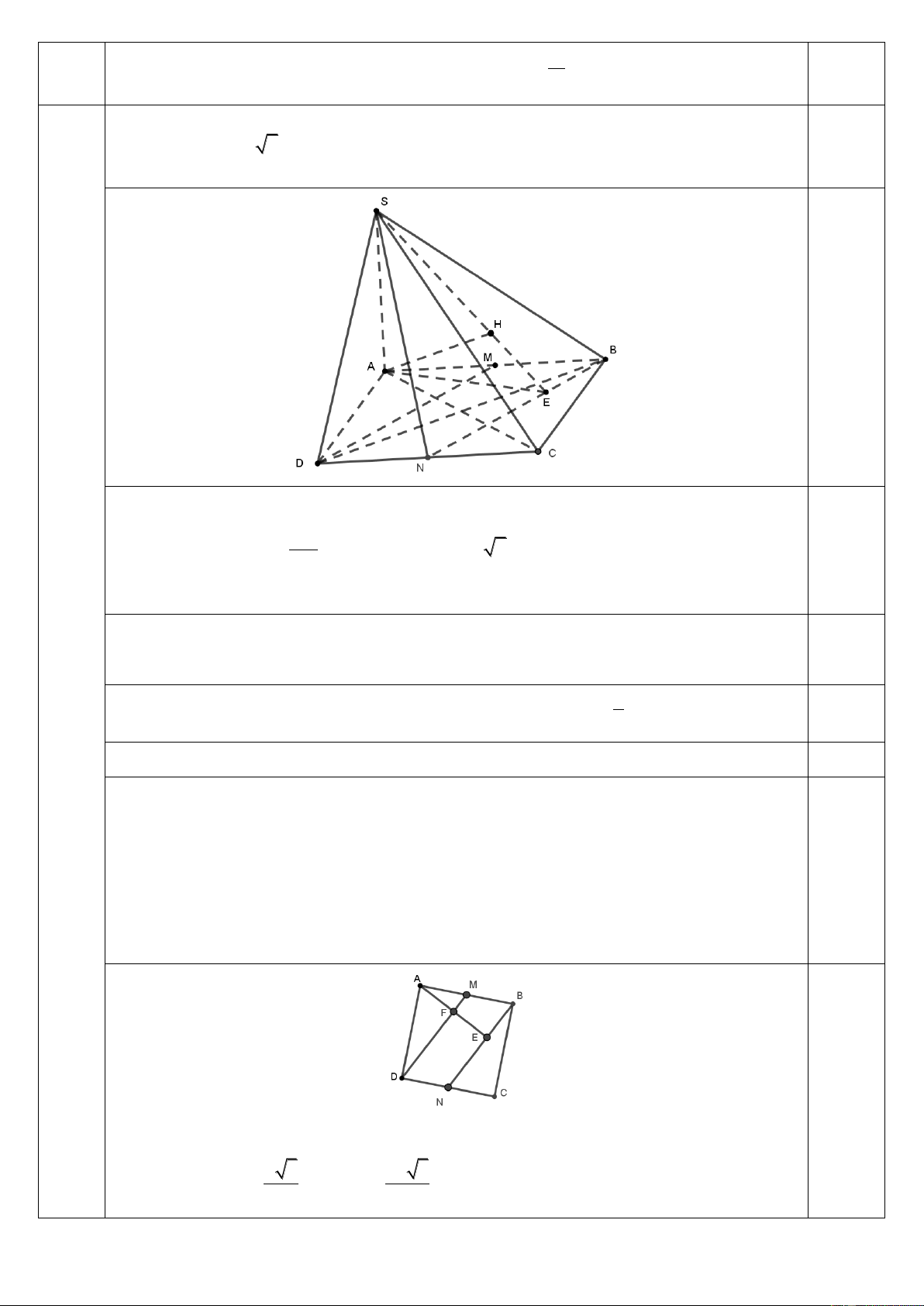
1) Cho hình chóp S.ABCD có đáy ABCD là hình vuông, SA vuông góc với mặt
phẳng đáy, SA  a 2, góc giữa đường thẳng SC và mặt phẳng đáy bằng 0 45 . Gọi M là 2,0 trung điểm của cạnh .
AB Tính theo a khoảng cách h giữa hai đường thẳng DM và . SB 0,25 Ta có 0 SCA  45 . SA Ta có 0 tan 45 
1 nên AC  SA  a 2. 0,25 AC Suy ra AB  . a Câu
Gọi N là trung điểm của cạnh .
CD Ta có DM // BN nên DM // (SBN). III Khi đ 0,25
ó h  d(DM , S )
B  d(DM , (SBN))  d(M , (SBN)). (5,0 điểm) 1
Vì M là trung điểm của cạnh AB nên h  d (M , (SBN ))  d ( , A (SBN )). 0,25 2
Kẻ AE  BN, E  BN và AH  SE, H S . E 0,25 Do SA  (ABC )
D nên BN  S . A BN  SA Ta có 
 BN  (SAE)  BN  AH. BN  AE 0,25 AH  BN Ta có 
 AH  (SBN). Do đó d( ,
A (SBN))  AH. AH  SE 0,25
Gọi F  AE  DM. Ta có FA  DM và F là trung điểm của AE . a 5 2a 5 Ta có AF  nên AE  . 5 5 1 1 1
Tam giác SAE vuông tại A nên ta có   2 2 2 AH SA AE 0,25 2a 7 a Suy ra AH  . Do đó 1 7
h  d (DM , SB)  AH  . 7 2 7
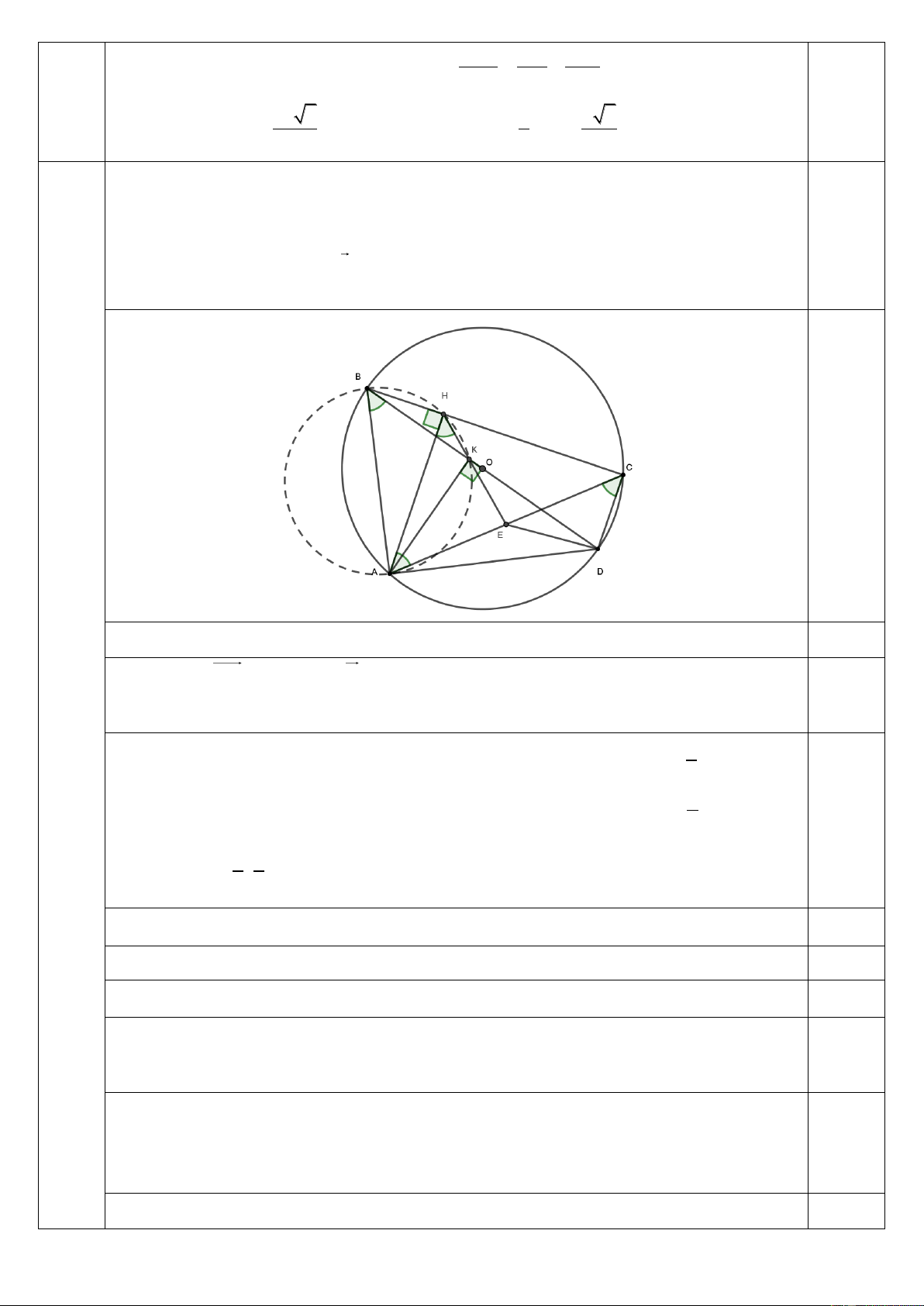
2) Trong mặt phẳng với hệ tọa độ Oxy, cho tứ giác ABCD nội tiếp trong đường tròn đường kính .
BD Gọi H , K lần lượt là hình chiếu vuông góc của điểm A trên các đường
thẳng BC, BD và E là giao điểm của hai đường thẳng HK và AC. Biết đường thẳng AC 3,0
đi qua điểm M (3;2) và nhận n  (1; 1
 ) làm vectơ pháp tuyến. Tìm tọa độ các điểm E và ,
A biết điểm H (1;3), K(2; 2) và hoành độ điểm A lớn hơn 2. 0,25
Phương trình đường thẳng AC là 1.(x  3) 1.( y  2)  0  x  y 1  0. 0,25 Ta có HK  (1; 1
 ) nên m  (1;1) là vec tơ pháp tuyến của đường thẳng HK. 0,25
Phương trình của đường thẳng HK là 1.(x  2) 1.( y  2)  0  x  y  4  0.  5   x
x  y 1  0  2
Do E  HK  AC nên ta có hệ  . Giải hệ, ta được  .
x  y  4  0 3  y   2 0,5  5 3  Vậy E ; .    2 2 
Ta có ABD  ACD (1) (góc nội tiếp cùng chắn cung AD ) 0,25
AH  BC và CD  BC nên AH // . CD 0,25
Suy ra HAE  ACD (2) (so le trong) 0,25 Ta có 0
AHB  AKB  90  Tứ giác ABHK nội tiếp đường tròn đường kính . AB 0,25
Suy ra ABK  AHK  AHE (3)
Từ (1), (2) và (3), ta suy ra AHE  HA . E
Do đó, tam giác EHA cân tại E. 0,25
Suy ra EA  EH.
Do A AC nên ( A ;
a a 1), với a  2. 0,5 2 2 2 2  5   5   3   3  Ta có 2 2
EA  EH  EA  EH  a   a       a  4.          2   2   2   2  Vậy ( A 4;3). 1 2u
Cho dãy số (u ) được xác định bởi: u  và n * u  , n   . n 1  3 n 1
2u (3n 1) 1 n
a) Tìm u và số hạng tổng quát u của dãy số. 4 n 3,0 1 1 1 b) Tính S    
(tổng gồm n số hạng) theo . n u u u 1 2 n 1 2 4 8 a) Ta có u  , u  , u  , u  . 1 0,75 3 2 7 3 27 4 91 Khi đó 2u 1 1 1 n u 3n 1 . n 1 2u (3n 1) 1 u 2 u n n 1 n 0,5 1 1  1  
 6(n 1) 14    6n 14 (1) u 2 u n 1   n  Đặt 1 v 
 6n 14. Ta có v 11. n u 1 0,25 n Câu IV Từ (1), 1 ta có v
 v . Do đó, (v ) là cấp số nhân với công bội 1 q  . (3,0 n 1  2 n n 2 điểm) 0,25 n 1   n  1 Suy ra 1
v  v .q  11. . n 1    2  1 1 Suy ra u   . n n 1 v  6n 14    n 1 11.  6n 14   0,25  2  b) Từ đó, ta có 1 1 1 S    
 v   v  6(1 2   n) 14n 0,25 1 n u u u 1 2 n n  1  1     2  n(n  1)  11.  6. 14n 0,5 1 2 1  2 n  1    2  22 1
      3n 11 . n 0,25   2    Cho hàm số 3 2
f (x)  ax  bx  cx  d (với , a , b , c d  ) thỏa mãn '
f (0)  4, f (0)  0, f (2)  0 và ' f (2)  0. Câu
a) Tìm hàm số f (x). V 3,0 (3,0 b) Giả sử 2 (
h x)  f (x  2x  )
m . Tìm tất cả các giá trị thực của tham số m để phương điểm) trình ' h (x)  0 có 5 nghiệm phân biệt
x , x , x , x , x thỏa mãn 1 2 3 4 5 4 4 4 4 4
x  x  x  x  x  229. 1 2 3 4 5 a) Ta có:
* f (0)  4  d  4.
* f (2)  0  8a  4b  2c  4  0  4a  2b  c  2  * ' 2
f (x)  3ax  2bx  . c '
* f (0)  0  c  0. 1,5 * '
f (2)  0  12a  4b  0. 3
 a  b  0 a 1 * Ta có hệ   
2a  b  1  b   3  Vậy 3 2
f (x)  x  3x  4. b) Ta có ' ' 2
h (x)  (2x  2) f (x  2x  ) m . 0,25 Ta có '
f (x)  0  x  0 hoặc x  2. x  1 2x  2  0  Khi đó ' 2
h (x)  0  
 x  2x  m  0 (1)  ' 2
 f (x  2x  m)  0 2  0,25
x  2x  m  2 (2) 
Dễ thấy (1) và (2) không có nghiệm chung. m  1
(1) có hai nghiệm phân biệt khác 1 khi và chỉ khi 
 m 1. Giả sử hai m 1
nghiệm đó là x , x . 1 2 m  3 0,25
(2) có hai nghiệm phân biệt khác 1 khi và chỉ khi 
 m  3. Giả sử hai m  3
nghiệm đó là x , x . 3 4 Với m  1 thì '
h (x)  0 có 5 nghiệm phân biệt. Ta có x  1. 5 x  x  2 0,25 Ta có 1 2 4 4 2 
 x  x  2m 16m 16. 1 2
x .x  m  1 2 x  x  2 Ta có 3 4 4 4 2 
 x  x  2m  24m  56. 3 4
x .x  m  2  0,25 3 4 4 4 4 4 4 2
x  x  x  x  x  229  4m  40m 156  0  m  3
 hoặc m 13 (loại). 1 2 3 4 5 0,25 Cho hàm số 4 2
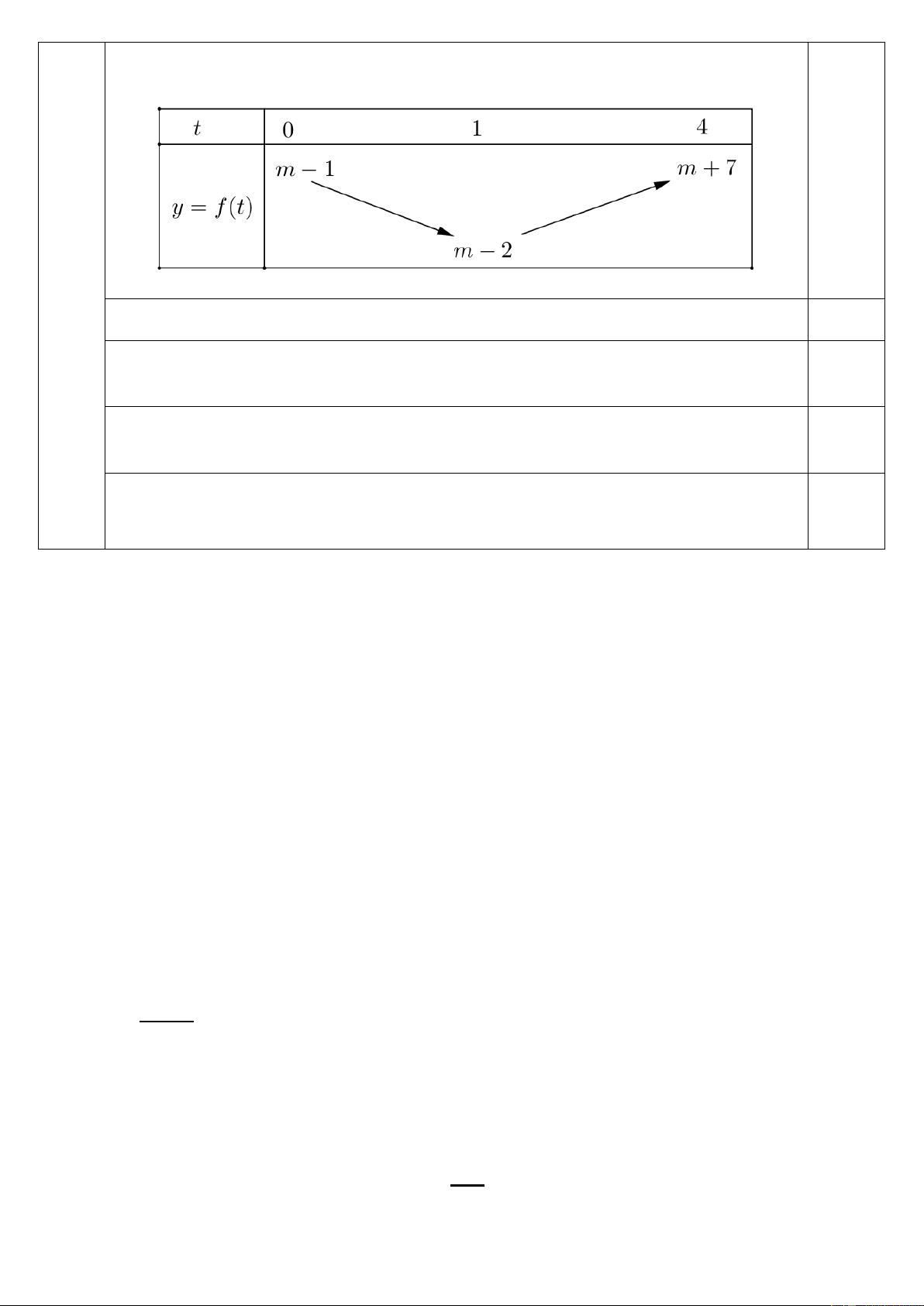
f (x)  x  2x  m 1 (với m là tham số thực). Tìm tất cả các giá trị 3,0
của tham số m để giá trị nhỏ nhất của hàm số g(x)  f (x) trên đoạn [0;2] bằng 2020. Câu Đặt 2
t  x . Ta có 2
y  f (t)  t  2t  m 1. VI 0,25 (3,0
Do x [0;2] nên t [0;4]. điểm) Ta có 2 2
y  f (t)  t  2t  m 1  (t 1)  m  2  m  2. 0,5
Ta có y  m  2  t  1[0;4].
Vẽ bảng biến thiên của hàm số y  f (t). 0,25
Dựa vào bảng biến thiên, ta có min f (x)  m  2 , max f (x)  m  7 . x   0; 2 0,5 x   0; 2
Trường hợp 1: Nếu m  2 thì min g(x)  m  2. x   0; 2 0,5
Khi đó, ta có m  2  2020  m  2022 ( nhận).
Trường hợp 2: Nếu m  7  0  m  7
 thì min g(x)  m  7. x   0; 2 0,5 Khi đó, ta có m
  7  2020  m  2  027 (nhận).
Trường hợp 3: Nếu (m  2)(m  7)  0  7
  m  2 thì min g(x)  0 (loại). x   0; 2 0,5
Suy ra m 2022; 202  7 .
Chú ý: Giải câu VI theo kiến thức lớp 12: Xét hàm số 4 2
y  f (x)  x  2x  m 1 liên tục trên đoạn 0; 2 . Ta có ' 3 y  4x  4 . x x  1  0;2  Cho '
y  0  x  0 0;2 . x 1  0;2
Ta có f (0)  m 1, f (1)  m  2 , f (2)  m  7.
* Trường hợp 1: Nếu m  2 thì min g(x)  m  2. x   0; 2
Khi đó, ta có m  2  2020  m  2022 ( nhận).
* Trường hợp 2: Nếu m  7  0  m  7
 thì min g(x)  m  7. x   0; 2 Khi đó, ta có m
  7  2020  m  2  027 (nhận).
* Trường hợp 3: Nếu (m  2)(m  7)  0  7
  m  2 thì min g(x)  0 (loại). x   0; 2
Suy ra m 2022; 202  7 . Chú ý:
1) Nếu học sinh làm bài không theo cách nêu trong đáp án nhưng đúng thì cho đủ số điểm
từng phần như hướng dẫn quy định.
2) Việc chi tiết hóa (nếu có) thang điểm trong hướng dẫn chấm phải bảo đảm không làm sai
lệch hướng dẫn chấm và phải được thống nhất thực hiện trong tổ chấm.
3) Điểm bài thi là tổng điểm không làm tròn. Hết