Đề thi học sinh giỏi Toán THPT cấp tỉnh năm 2020 – 2021 sở GD&ĐT Hưng Yên

SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI CHỌN HỌC SINH GIỎI THPT CẤP TỈNH HƯNG YÊN NĂM HỌC 2020 – 2021 TOANMATH.com Môn thi: TOÁN Đề thi gồm 01 trang
Thời gian làm bài: 180 phút (không kể thời gian phát đề) Câu I. (6,0 điểm)
1. Cho hàm số y  g  x 2  x  m  
1 x 1 (m là tham số thực). Tìm m để đồ thị C của hàm số y  f  x 3  x  m   2
1 x  1 m x 1 cắt trục hoành tại ba điểm phân biệt có hoành độ x , x , x thỏa 1 2 3 mãn 2 g  x  2  g x  2  g x  15 . 1 2  3
2. Cho hàm số y  f  x có đạo hàm f  x 2 '  9  x , x
   . Tìm tất cả các giá trị thực của tham số m để  1  hàm số y  f  2 x  2x   2 m   1 ln x  
 nghịch biến trên nửa khoảng 1; .  x  Câu II. (4,0 điểm)
1. Giải phương trình x   2 x  x   x 3 2 9 2
1 .3  2x  x  0  x   .
2. Cho các số thực a, b thỏa mãn log
6a  8b  4  1 và các số thực dương c, d thỏa mãn 2 2   a b 20
c  dlog 2c  d 2 2
 2c  3cd  d  4c  4d  0 . Tìm giá trị nhỏ nhất của biểu thức 3
T  a  c2  b  d 2 2 . Câu III. (5,0 điểm)
1. Cho hình chóp S.ABC có AB  AC  2a , BC  a , SA  3a a  0 . Tính thể tích khối chóp S.ABC theo a biết  SAB   SAC  60 .
2. Cho điểm A nằm trên mặt cầu S  tâm O, bán kính R  9 cm. Gọi I, K là hai điểm trên đoạn OA sao cho
OI  IK  KA . Các mặt phẳng lần lượt đi qua I, K cùng vuông góc với OA và cắt mặt cầu S  theo đường
tròn C , C . Gọi V , V lần lượt là thể tích khối nón đỉnh O, đáy là đường tròn C , C . Tính tỉ số 2  1  2  1  1 2 V1 . V2
3. Cho lăng trụ ABC.A' B 'C ' có đáy là tam giác vuông tại A, AB  AC  a a  0 , biết B ' A  B ' B  B 'C; 5
góc giữa hai mặt phẳng BCC ' B ' và  ABB ' A' bằng  với tan 
. Tính khoảng cách giữa hai 2 2
đường thẳng A'C ' và B 'C . Câu IV. (1,0 điểm) xdx Tìm nguyên hàm I   . 2 2x  3x 1 Câu V. (2,0 điểm) a  2
Cho dãy số a xác định như sau: 1 . n   2 2021a a 2023a 1, n 1      n 1  n n  a 1 a 1 a 1 a 1  Tính: 1 2 3 L  lim n      . n a 1 a 1 a 1 a 1  2 3 4 n 1   Câu VI. (2,0 điểm)
Gọi S là tập các số tự nhiên có 4 chữ số đôi một khác nhau lập từ các chữ số 1, 2, 3, 4, 5, 6, 7, 8, 9. Chọn
ngẫu nhiên một số từ tập S. Tính xác suất để số được chọn chia hết cho 3.
-------------------- HẾT -------------------- https://toanmath.com/
Thí sinh không được sử dụng tài liệu và máy tính cầm tay. Cán bộ coi thi không giải thích gì thêm.
Họ và tên thí sinh: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Số báo danh: . . . . . . . . . . . . . .
Chữ ký của cán bộ coi thi: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
NHÓM TOÁN VDC&HSG THPT
ĐỀ THI HỌC SINH GIỎI 2020 - 2021
ĐỀ THI HỌC SINH GIỎI - HƯNG YÊN
NĂM HỌC 2020 – 2021 Môn: Toán 12
HỌC HỎI - CHIA SẺ KIẾN THỨC
Thời gian: 90 phút (Không kể thời gian phát đề)
LINK NHÓM: ht ps://www.facebook.com/groups/1916660125164699 Câu 1. (6,0 điểm)
1. Cho hàm số y  gx 2
 x m  
1 x 1( m là tham số thực). Tìm m để đồ thị C của
hàm số y  f x 3
 x m  2
1 x 1mx1 cắt trục hoành tại ba điểm phân biệt có hoành
độ x , x , x thỏa mãn 2 g x  2  g x  2  g x 15 . 1 2  3 1 2 3
2. Cho hàm số y = f (x) có đạo hàm f ′(x) 2
= 9 − x ,∀x ∈  . Tìm tất cả các giá trị thực của tham số  1
m để hàm số y f ( 2 x 2x) ( 2 m )1 ln  = + + − x − 
 nghịch biến trên nửa khoảng  x  [1;+ ∞) . Câu 2. (4,0 điểm)
1. Giải phương trình x + ( 2
x − x − ) x 3 2 9
2 1 .3 − 2x − x = 0.
2. Cho các số thực a,b thỏa mãn log
6a + 8b − 4 =1 và các số thực dương c,d thỏa 2 2 ( ) a +b +20
mãn (c + d )log (2c + d ) 2 2
+ 2c + 3cd + d − 4c − 4d = 0 . Tìm giá trị nhỏ nhất của biểu thức 3
T = (a − c)2 + (b − d )2 2 . Câu 3. (5,0 điểm)
1. Cho hình chóp S.ABC có AB = AC = 2a, BC = a, SA = 3a . Thể tích khối chóp S.ABC theo a biết  = 
SAB SAC = 60 .°
2. Cho điểm A nằm trên mặt cầu (S ) tâm O bán kính R = 9(cm) . Gọi I, K là hai điểm trên
đoạn OA sao cho OI = IK = KA. Các mặt phẳng lần lượt đi qua I, K cùng vuông góc với OA
và cắt mặt cầu (S ) theo đường tròn (C , C . Gọi V ,V lần lượt là thể tích khối nón đỉnh O , 1 ) ( 2 ) 1 2 V
đáy là đường tròn (C , C . Tính tỉ số 1 . 1 ) ( 2 ) V2
3. Cho hình lăng trụ ABC.A′B C
′ ′ có đáy là tam giác vuông tại A , AB = AC = a ( a > 0 ), biết B A ′ = B B ′ = B C
′ ; góc giữa hai mặt phẳng (BCC B ′ ′) và ( ABB A ′ ′) bằng ϕ với 5 tanϕ = . 2 2
Tính khoảng cách giữa hai đường thẳng A′C′ và B C ′ . Câu 4. (4,0 điểm) Tìm nguyên hàm d x x I = ∫ . 2 2x − 3x +1
TÀI LIỆU ÔN THI HỌC SINH GIỎI Trang 1
NHÓM TOÁN VDC&HSG THPT
ĐỀ THI HỌC SINH GIỎI 2020 - 2021 Câu 5. (4,0 điểm) a = 2
Cho dãy số (a xác định như sau 1 . n )  2 2021a = + + ≥  + a a n n n 2023 n 1, 1 1  a +1 a +1 a +  n 1 Tính 1 2 lim  + +...+  .
n→+∞ a +1 a +1 a +  n+ 1 2 3 1  Câu 6. (2,0 điểm)
Gọi S là tập các số tự nhiên có 4 chữ số đôi một khác nhau lập từ các chữ số
1,2,3,4,5,6,7,8,9. Chọn ngẫu nhiên một số từ tập S. Tính xác suất để số được chọn chia hết cho 3.
------------------------HẾT------------------------ Trang 2
TÀI LIỆU ÔN THU THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT
ĐỀ THI HỌC SINH GIỎI 2020 - 2021 HƯỚNG DẪN GIẢI Câu 1. (6,0 điểm)
1. Cho hàm số y = g (x) 2 = x + (m + )
1 x +1( m là tham số thực). Tìm m để đồ thị (C) của hàm
số y = f (x) 3 = x + (m − ) 2
1 x + (1− m) x −1 cắt trục hoành tại ba điểm phân biệt có hoành độ x , 1
x , x thỏa mãn 2 g (x ) 2 + g (x ) 2 + g x =15 . 1 2 ( 3) 2 3
2. Cho hàm số y = f (x) có đạo hàm f ′(x) 2 = 9 − x , x
∀ ∈  . Tìm tất cả các giá trị thực của
tham số m để hàm số y f ( 2 x x) ( 2 m ) 1 2 1 ln x  = + + − − 
nghịch biến trên nửa khoảng x    [1;+ ∞) . Lời giải 1.
 Đồ thị hàm số y = f ( x) 3 = x + (m − ) 2
1 x + (1− m) x −1 cắt trục hoành tại ba điểm phân biệt
khi và chỉ khi phương trình 3 x + (m − ) 2
1 x + (1− m) x −1 = 0 ( )
1 có ba nghiệm phân biệt. x =1 Ta có ( ) 1 ⇔ (x − ) 1 ( 2 x + mx + ) 1 = 0⇔  . 2 x + mx +1 = 0
Do đó phương trình ( )
1 có ba nghiệm phân biệt khi và chỉ khi phương trình 2x +mx+1= 0 có m + 2 ≠ 0 m < 2 −
hai nghiệm phân biệt khác 1 ⇔  ⇔ (2). 2  m − 4 > 0 m > 2
 Khi đó, theo định lí Vi-et phương trình ( )
1 có ba nghiệm phân biệt là x , x và x =1 thỏa 1 2 3
x + x = −m mãn 1 2  (3). x x =  1 1 2  Ta có: 2 g (x) 4 = x + (m + ) 3 x + ( 2 m + m + ) 2 2 1 2 3 x + 2(m + ) 1 x +1.
 Chia biểu thức 2
g (x) cho f (x) ta được 2
g (x) = x +  (m + ) f
 ( x) + (m + ) 2 x + ( 2 3 . 5
m + 4m) x + m + 4.  Suy ra 2
g (x ) = (m + 5) 2 x + ( 2
m + 4m x + m + 4 1 1 ) 1 2
g (x ) = (m + 5) 2 x + ( 2
m + 4m x + m + 4 2 2 ) 2 2
g (x = g 1 = m + 5 .1+ m + 4m .1+ m + 4 = m + 6m + 9. 3 ) 2 ( ) ( ) ( 2 ) 2  Do đó: 2 g (x ) 2 + g (x ) 2
+ g x =15 ⇔ (m + 5)( 2 2
x + x + m + 4m x + x + m + 8m +17 =15 1 2 ) ( 2 )( 1 2) 2 1 2 ( 3)
⇔ (m + 5) (x + x )2 − 2x x  + ( 2
m + 4m)(x + x ) 2
+ m + 8m +17 =15 4 . 1 2 1 2 1 2   ( ) m =1
 Thay (3) vào (4) và rút gọn, ta được 2
m + 3m − 4 = 0 ⇔ 
. Kết hợp với điều kiện (2) m = 4 − ta được m = 4
− thỏa mãn yêu cầu bài toán. 2.  1 
 Xét hàm số g ( x) = f ( 2 x + 2x) + ( 2 m − ) 1 ln x −  có x   
TÀI LIỆU ÔN THI HỌC SINH GIỎI Trang 3
NHÓM TOÁN VDC&HSG THPT
ĐỀ THI HỌC SINH GIỎI 2020 - 2021 ′
g (x) = ( f ( 2x + x) ′ +( 2 m − ) 1 x  − = ( x + ) f ( 2 x + x) + ( 2 m − ) 1 1 2 1 ln 2 2 . 2 1  ′ ′ +    2 x x x      = ( + ) − ( + )2 2 + ( 2 − ) +   1 2 1 . 9 2 1 . x x x x m .   2  x
 Hàm số y = g ( x) nghịch biến trên nửa khoảng [1;+ ∞) khi và chỉ khi g′( x) ≤ 0, x ∀ ∈[1;+ ∞) . Khi đó: (x + ) − (x + x)2 2 + ( 2 m − ) x +   1 2 1 . 9 2 1 . ≤ 0, x ∀ ∈ 1;+ ∞    2 [ )  x m x (x x)2 2 2 2 1 2 2 9 ⇔ − ≤ + − , x ∀ ∈[1;+ ∞)  (*).  
Xét hàm số h(x) x (x x)2 2 2 2 2 9 = + − 
trên nửa khoảng [1;+ ∞) có:  
h′(x) = x (x + x)2 2  2 − + x ( x + ) ( 2 4 2 9 2 .2 2 2 . x + 2x)  
h′(x) = x(x − )(x + )( 2 x + x + ) 3 4 1 3 2 3 + 8x .(x + )
1 .(x + 2) > 0, x ∀ ∈[1;+ ∞) .
Bảng biến thiên của hàm số h(x) x (x x)2 2 2 2 2 9 = + − 
trên nửa khoảng [1;+ ∞) như sau:  
Dựa vào bảng biến thiên: điều kiện (*) xảy ra khi 2 m −1≤ 0 ⇔ 1 − ≤ m ≤1.
Vậy tất cả giá trị thực của tham số m thỏa mãn điều kiện đề bài là: −1≤ m ≤1. Câu 2. (4,0 điểm)
1. Giải phương trình x + ( 2
x − x − ) x 3 2 9
2 1 .3 − 2x − x = 0.
2. Cho các số thực a,b thỏa mãn log
6a + 8b − 4 =1 và các số thực dương c,d thỏa 2 2 ( ) a +b +20
mãn (c + d )log (2c + d ) 2 2
+ 2c + 3cd + d − 4c − 4d = 0 . Tìm giá trị nhỏ nhất của biểu thức 3
T = (a − c)2 + (b − d )2 2 . Lời giải 1.
 Đặt = 3x t
(t > 0) , phương trình đã cho trở thành: 2 t + ( 2 x − x − ) 3 2
2 1 .t − 2x − x = 0 (*)
∆ = (x − 2x − )2 2 1 − 4( 3 2 2 − x − x ) 4 2 3 2 3 2
= x + 4x +1− 4x − 2x + 4x + 8x + 4x 4 3 2
= x + 4x + 6x + 4x +1 = (x + )4 1 Trang 4
TÀI LIỆU ÔN THU THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT
ĐỀ THI HỌC SINH GIỎI 2020 - 2021  −( 2 x − 2x − ) 1 − (x + )2 1 t =  2 (*) ⇔  − 
( 2x −2x− )1+(x+ )2 1 t =  2 
− x − x − − x + x + x ( 2 2 )1 ( 2 2 )1 3 =  2 ⇔ 
− x − x − + x + x + x ( 2 2 )1 ( 2 2 )1 3 =  2 x 2 3 = −x ( ) 1 ⇔  3x = 2x +1  (2)  Phương trình ( )
1 vô nghiệm vì 3x > 0 và 2 −x ≤ 0 x ∀ ∈ . 
 Phương trình (2) ⇔ 3x − 2x −1 = 0. Xét hàm số = 3x y − 2x −1 x
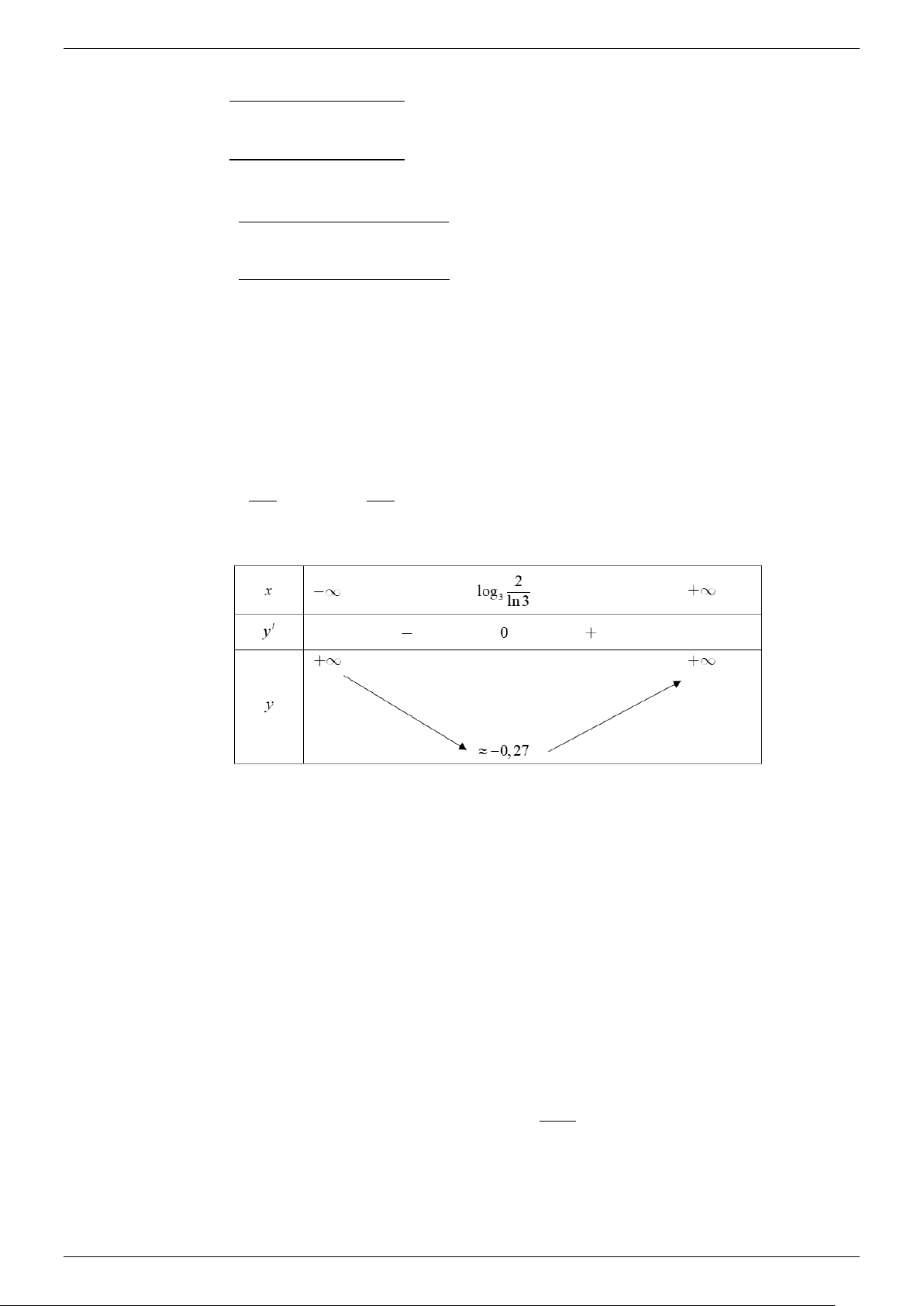
có tập xác định D =  , đạo hàm y′ = 3 ln 3− 2 . x 2 2 y′ = 0 ⇔3 = ⇔ x = log . 3 ln 3 ln 3
Ta có bảng biến thiên của hàm số như sau:
Dựa vào bảng biến thiên ta thấy phương trình (2) có 2 nghiệm.
Dễ nhận thấy 2 nghiệm của phương trình (2) là: x = 0 và x =1.
Vậy phương trình đã cho có đúng hai nghiệm là: x = 0 và x =1. 2.
 Với điều kiện: 6a + 8b − 4 > 0 (*) và 2 2
a + b + 20 >1 nên: log
6a + 8b − 4 =1 ⇔ a + b − = a + b + ⇔ (a − )2 + (b − )2 3 4 =1. 2 2 ( ) a +b +20 2 2 6 8 4 20
Do đó: M (a;b) bất kỳ thuộc đường tròn (C) (x − )2 + ( y − )2 : 3 4 =1
Đường tròn (C) có tâm I (3;4) , bán kính r =1.
 Vì: c + d > 0 nên:
(c + d)log (2c + d ) 2 2
+ 2c + 3cd + d − 4c − 4d = 0 ⇔ log 2c + d + 2c + d − 4 = 0 (1) 3 ( ) ( ) 3
Xét hàm số f (t) = log t + t − 4 với t > 0 có f ′(t) 1 =
+1 > 0 với t > 0 3 t ln 3
Suy ra f (t) đồng biến trên khoảng (0;+ ∞) ⇒ phương trình f (t) = 0 có tối đa một nghiệm t > 0.
Mặt khác ta có: f (3) = 0 . Vậy t = 3 là nghiệm duy nhất của phương trình f (t) = 0.
TÀI LIỆU ÔN THI HỌC SINH GIỎI Trang 5
NHÓM TOÁN VDC&HSG THPT
ĐỀ THI HỌC SINH GIỎI 2020 - 2021
Từ đó (1) ⇔ 2c + d = 3 ⇔ 2c + d − 3 = 0. Do đó: N (2 ;
c d ) là điểm bất kỳ thuộc đường thẳng ∆ : x + y −3 = 0.
 T = (a − c)2 + (b − d )2 2 2 = MN . Suy ra: 2 minT = min MN . 3+ 4 − 3 Xét: d(I;∆) =
= 2 2 >1 ⇒ ∆ nằm ngoài (C). Do đó: MN ≥ 2 2 − r = 2 2 −1. 2 2 1 +1
Khi đó min MN = 2 2 −1. Suy ra: T = ( − )2 min 2 2 1 = 9 − 4 2 .
Giá trị minT đạt được khi: N là hình chiếu của I lên ∆ và M = IN ∩(C)
+ Gọi ∆′ là đường thẳng đi qua I và vuông góc với ∆ thì: ∆′: 1
− (x − 3) + ( y − 4) = 0 ⇔ ∆′: x − y +1 = 0
Khi đó: ∆′∩ ∆ = N (1;2) ⇒ 1 c = , d = 2 2  
+ M = IN ∩(C) và MN = −(2 2 − ) 1 .MI  
 ON + (2 2 − ) 1 .OI  − −  Suy ra: 6 2 8 2 OM = =   1 (2 2 ) ; 1  2 2  + −   ⇒ 6 2 a − = , 8 2 b − =
thỏa mãn điều kiện (*) 2 2
Vậy: minT = 9 − 4 2 . Minh họa bằng hình vẽ: Câu 3. (5,0 điểm)
1. Cho hình chóp S.ABC có AB = AC = 2a, BC = a, SA = 3a . Thể tích khối chóp S.ABC theo a biết  = 
SAB SAC = 60 .°
2. Cho điểm A nằm trên mặt cầu (S ) tâm O bán kính R = 9(cm) . Gọi I, K là hai điểm trên
đoạn OA sao cho OI = IK = KA . Các mặt phẳng lần lượt đi qua I, K cùng vuông góc với OA
và cắt mặt cầu (S ) theo đường tròn (C , C . Gọi V ,V lần lượt là thể tích khối nón đỉnh O , 1 ) ( 2 ) 1 2
đáy là đường tròn (C , C . Tính tỉ số V1 . 1 ) ( 2 ) V2 Trang 6
TÀI LIỆU ÔN THU THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT
ĐỀ THI HỌC SINH GIỎI 2020 - 2021
3. Cho hình lăng trụ ABC.A′B C
′ ′ có đáy là tam giác vuông tại A , AB = AC = a ( a > 0 ), biết B A ′ = B B ′ = B C
′ ; góc giữa hai mặt phẳng (BCC B ′ ′) và ( ABB A ′ ′) bằng ϕ với 5 tanϕ = . 2 2
Tính khoảng cách giữa hai đường thẳng A′C′ và B C ′ . Lời giải 1.
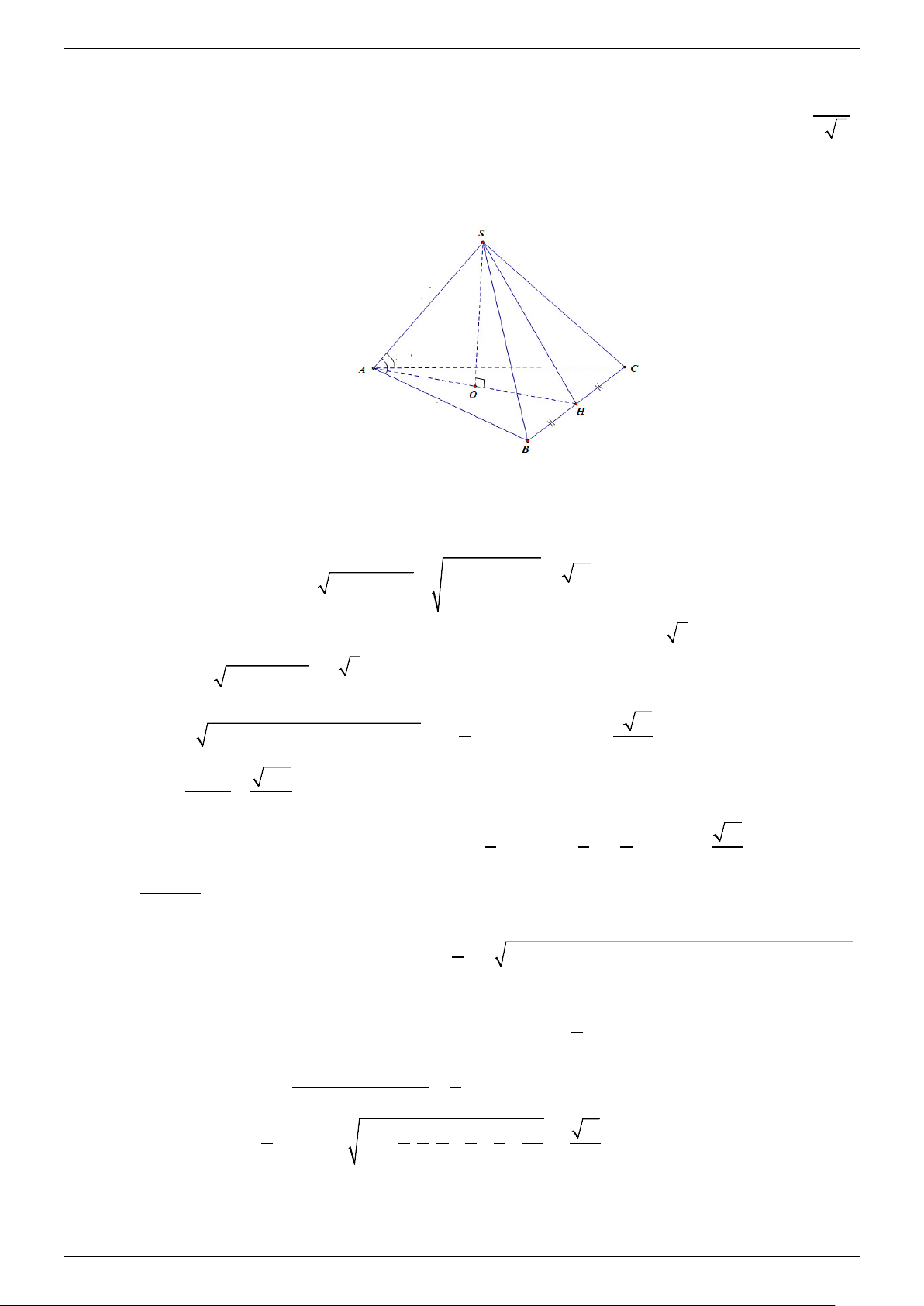
 Gọi H là trung điểm BC , ta có AB = AC nên AH ⊥ BC . Ta có SA ∆ B = SA
∆ C ( .cg.c) ⇒ SB = SC nên SH ⊥ BC , suy ra BC ⊥ (SAH) .
 Do đó (SAH ) ⊥ (ABC) . Trong mặt phẳng (SAH ) , kẻ SO ⊥ AH tại O ⇒ SO ⊥ (ABC). 2  a   Trong A ∆ BC , 2 2
AH = AB − HB = ( a)2 2 15 − =   a .  2  2  Xét S ∆ AB, ta có 2 2 2 o 2
SB = SA + AB − 2 . SA A .
B cos60 = 7a ⇒ SB = a 7 = SC . Có 2 2 3 3
SH = SB − BH = a . 2 1 3 11 2 S
= p p − SA p − SH p − AH p =
SA + AH + SH = a . SAH ( )( )( ), ( ) 2 4 2SSAH 165 SO = = a . AH 5 1 1 1 11
 Vậy Thể tích khối chóp S.ABC là: 3 V = SO S = SO AH BC = a . S ABC . ABC . . . 3 3 2 4 Cách 2:
Đặt AS = m , AB = n , AC = p ,  SAB = α ,  SAC = β ,  BAC = γ . 1
 Sử dụng công thức tính nhanh: 2 2 2 V = abc + α β γ − α − β − γ SABC 1 2cos cos cos cos cos cos 6 .
 Áp dụng : m = 3a, n = p = 2a , 1 cosα = cos β = cos60° = . 2
AB + AC − BC cosγ =  2 2 2 cos BAC = 7 = . 2A . B AC 8 1 11  Ta có 1 1 1 7 1 49 V = a a a + − − − 3 = a . SABC .3 .2 .2 . 1 2. . . 6 2 2 8 4 4 64 4 2.
TÀI LIỆU ÔN THI HỌC SINH GIỎI Trang 7
NHÓM TOÁN VDC&HSG THPT
ĐỀ THI HỌC SINH GIỎI 2020 - 2021
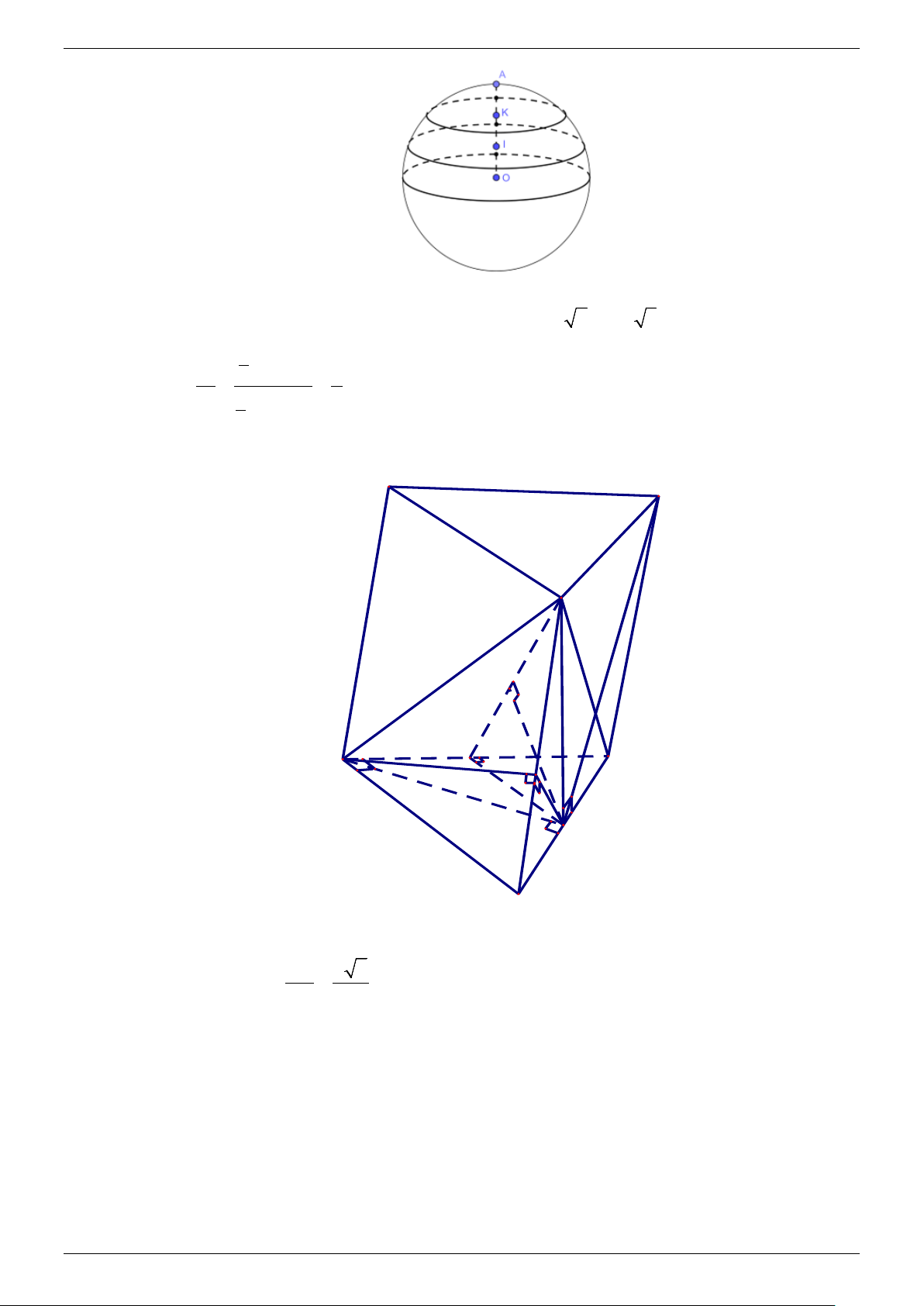
Từ giả thiết suy ra OI = IK = KA = 3.
Gọi r ,r lần lượt là bán kính của (C , C , ta có r = 6 2,r = 3 5 . 1 ) ( 2 ) 1 2 1 2 1 2 π.r .OI 1 Do đó V 3 4 1 = = . V 1 2 5 2 π.r .OK 2 3 3. A' C' B' Q M P A K C H B
 Gọi H là trung điểm của BC . Vì tam giác ABC vuông cân tại A nên: BC a 2
BH = CH = AH = =
, suy ra H là tâm của đường tròn ngoại tiếp tam giác ABC và 2 2 AH ⊥ BC .
Mặt khác, theo giả thiết ta có B A ′ = B B ′ = B C ′ nên B H
′ ⊥ ( ABC) ⇒ (B B
′ C) ⊥ ( ABC), ⇒ (B B
′ C)∩( ABC) = BC mà AH ⊥ BC ⇒ AH ⊥ (B B ′ C).
 Do đó AH ⊥ BB′ . Trong (BCC B
′ ′) kẻ HK ⊥ BB′ (K ∈ BB′) nên
( AHK ) ⊥ BB′ ⇒ AK ⊥ BB′ . Do đó góc giữa hai mặt phẳng (BCC B′′) và ( ABB A ′ ′) là 
AKH = ϕ , vì AH ⊥ (B B
′ C) ⇒ AH ⊥ HK nên A
∆ HK vuông tại H . Trang 8
TÀI LIỆU ÔN THU THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT
ĐỀ THI HỌC SINH GIỎI 2020 - 2021 a 2 AH 2 2a
 Xét tam giác AHK vuông tại H có: HK =  = = . AKH 5 tan 5 2 2
 Xét tam giác B HB ′
vuông tại H có HK là đường cao nên 1 1 1 1 1 1 2a 17 = + ⇒ = − ⇒ B H ′ = . 2 2 2 2 2 2 HK BH B H ′ B H ′ HK BH 17
 Trong ( ABC) kẻ HP ⊥ AC (P ∈ AC), mà AC ⊥ B H ′ , (B H
′ ⊥ ( ABC)) nên AC ⊥ (B HP ′ ).
⇒ ( ACB′) ⊥ (B HP ′
), ( ACB′)∩(B H ′ P) = B P ′ . Trong (B HP ′
) kẻ HQ ⊥ B P
′ , với Q ∈ B P
′ , do đó HQ ⊥ ( ACB′) tại Q .
Do đó HQ = d(H,( ACB′)). a
 Trong tam giác B HP ′
vuông tại H có HP = và HQ là đường cao nên 2 1 1 1 2a 33 = + ⇒ HQ = . 2 2 2 HQ PH B H ′ 33
 Ta có A′C′// AC ⇒ A′C′// ( ACB′) ⇒ d
( A′C ,′ B C
′ ) = d( A′C ,′( ACB′)) = d(C ,′( ACB′)). Gọi M = B C ′ ∩C H ′ ; Vì B C
′ ′ // HC nên ta có C M ′ B C ′ ′
d(C ,′( ACB′)) ′ = = 2 C M ⇒ =
= , vì CH ∩( AB C ′ ) = M . HM HC (H (ACB′)) 2 d , HM a a
 Nên (C′ ( ACB′)) = (H (ACB′)) 2 33 4 33 d , 2.d , = 2.HQ = 2. = . 33 33 a
 Vậy: ( A′C′ B C ′ ) 4 33 d , = . 33 Câu 4. (4,0 điểm) 1. Tìm nguyên hàm d x x I = ∫ . 2 2x − 3x +1 Lời giải Ta có d x x  1 1  1 I = ∫ ( ∫ . − )( = − = − − − + x − )  dx ln x 1 ln 2x 1 C x 1 2 1
 x −1 2x −1 2 Câu 5. (4,0 điểm) a = 2
Cho dãy số (a xác định như sau 1 . n )  2 2021a = + + ≥  + a a n n n 2023 n 1, 1 1  a +1 a +1 a +  n 1 Tính 1 2 lim  + +...+  .
n→+∞ a +1 a +1 a +  n+ 1 2 3 1  Lời giải  Ta có : 2 2021a = + + ⇔ − = + + + a a a + a a a n n 2023 n 1 2021( n n ) 2n 2 n 1 1 1 ⇔ 2021(a − = +
≥ ∀ suy ra dãy số (a tăng, suy ra a n ∗ ≥ ∀ ∈ n ) n 2, + a a n n n ) ( n )2 1 0, 1  .
 Mặt khác ta có:
TÀI LIỆU ÔN THI HỌC SINH GIỎI Trang 9
NHÓM TOÁN VDC&HSG THPT
ĐỀ THI HỌC SINH GIỎI 2020 - 2021 + 2 an 1 2021 2021a = + + ⇔ + = + + ⇔ = . + a a a + a a n n 2023 n 1 2021 n 1 n 1 n 2022 1 ( 1 ) ( )( ) a + + + a n 1 n 2022 1  a +1 a +1 a +    n 1 1 1 1  Vậy 1 2 lim  + +...+  = 2021 lim  + +...+  .
n→+∞ a +1 a +1 a +1 n→+∞ + + +  +   a a a n 2022 2022 n 2022 2 3 1 1 2  1 1 1
 Từ 2021(a + = + + ⇔ = − . + a a n 1 n 1 n 2022 1 ) ( )( ) a + a + a + n 2022 n 1 n+ 1 1  Suy ra tổng 1 1 1 S = + + + n ...
a + 2022 a + 2022 a + n 2022 1 2 1 1 1 1 1 1 ⇔ S = − + − + + − n ...
a +1 a +1 a +1 a +1 a + a + n 1 n+ 1 1 2 2 3 1 1 1 1 1 ⇔ S = − ⇔ S = − . n a +1 a + + + 1 n a n 3 n+ 1 1 1 1
Vì (a là dãy tăng, ta xét: n )
 TH1: Dãy số (a tăng và bị chặn trên. Giả sử lim a = b với điều kiện b ≥ 2. n ) n n→+∞ Khi đó 2 2
2021b = b + 2023b +1 ⇔ b + 2b +1 = 0 ⇔ b = 1
− (không thỏa mãn điều kiện). 1
 TH2: Dãy số (a tăng và không bị chặn trên. Khi đó lim a = +∞ suy ra = . n ) lim 0 n n→+∞ n→+∞ a + n+ 1 1 Vậy 1 lim S = . n n→+∞ 3  a +1 a +1 a +  n 1 Vậy 2021 1 2 lim  + +...+  = .
n→+∞ a +1 a +1 a +  n+ 1 3 2 3 1 Câu 6. (2,0 điểm)
Gọi S là tập các số tự nhiên có 4 chữ số đôi một khác nhau lập từ các chữ số
1,2,3,4,5,6,7,8,9. Chọn ngẫu nhiên một số từ tập S. Tính xác suất để số được chọn chia hết cho 3. Lời giải
 Từ 1, 2,3, 4,5,6,7,8,9 ta lập được 4
A = 3024 số tự nhiên có 4 chữ số đôi một khác nhau. 9
Suy ra số phần tử của không gian mẫu là n(Ω) 1 = C = 3024. 3024
 Gọi A là biến cố: “Số được chọn chia hết cho 3 ”.
 Các số tự nhiên từ 1 đến 9 chia thành 3 nhóm:
- Nhóm I gồm các số tự nhiên chia hết cho 3, gồm 3 số.
- Nhóm II gồm các số tự nhiên chia cho 3 dư 1, gồm 3 số.
- Nhóm III gồm các số tự nhiên chia cho 3 dư 2, gồm 3 số.
 Để chọn được số có 4 chữ số chia hết cho 3 khi và chỉ khi tổng 4 chữ số chia hết cho 3, ta có các trường hợp sau:
- 2 chữ số thuộc nhóm I, 1 chữ số thuộc nhóm II, 1 chữ số thuộc nhóm III có 2 1 1
4!.C .C .C 3 3 3 cách.
- 1 chữ số thuộc nhóm I, 3 chữ số thuộc nhóm II có 1 3 4!.C .C cách. 3 3
- 1 chữ số thuộc nhóm I, 3 chữ số thuộc nhóm III có 1 3 4!.C .C cách. 3 3 Trang 10
TÀI LIỆU ÔN THU THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT
ĐỀ THI HỌC SINH GIỎI 2020 - 2021
- 2 chữ số thuộc nhóm II, 2 chữ số thuộc nhóm III có 2 2 4!.C .C cách. 3 3
Suy ra n( A) = 4 ( 2 1 1 1 3 1 3 2 2
! C .C .C + C .C + C .C + C .C =1008. 3 3 3 3 3 3 3 3 3 ) n A 1008 1
 Vậy xác suất cần tìm là P ( A) ( ) = = = n(Ω) . 3024 3
------------------------HẾT------------------------
TÀI LIỆU ÔN THI HỌC SINH GIỎI Trang 11
Document Outline