Đề thi học sinh giỏi Toán THPT cấp tỉnh năm 2021 – 2022 sở GD&ĐT Lào Cai

SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THI CHỌN HỌC SINH GIỎI LỚP 12 LÀO CAI NĂM HỌC 2021 – 2022 MÔN THI: TOÁN
Thời gian: 90 phút (Không kể thời gian phát đề) x 1 Câu 1. a/ Cho hàm số y 
có đồ thị C  . Gọi I là giao điểm của của hai đường tiệm cận của C  . 3  x
Tìm tất cả các giá trị của tham số m để đường thẳng d : y  x  m cắt C  tại hai điểm phân biệt
M , N sao cho tam giác MNI có trọng tâm nằm trên C  . Lời giải Chọn C
Tập xác định D   \  3 . 1 1 x 1 lim  lim  lim x y
 1 y  1 là tiệm cận ngang của đồ thị C. x x 3 x  x  3 1 x
lim y    x  3 là tiệm cận đứng của đồ thị C  . x 3   I 3; 
1 là giao điểm của của hai đường tiệm cận của C  . x 1
Phương trình hoành độ giao điểm: 2
 x  m  x  2  m x  3m 1  0   * . 3  x
Đường thẳng d : y  x  m cắt C  tại hai điểm phân biệt  * có hai nghiệm phân biệt và khác 3  16   0    m ;  80; 2 m  8m  0
Đường thẳng d : y  x  m cắt C  tại hai điểm phân biệt M  x ; x  m , N x ; x  m với x , x là 1 1   2 2  1 2
nghiệm phương trình * .
M , N, I tạo thành tam giác khi m  4
 x  x  3 x  x  2m 1  m 1 
Tam giác MNI có trọng tâm 1 2 1 2 G ;  ; m 1      3 3   3     G  C  m 4 m 2 2  m 1 
 m  8m 12  0  . 8  m  m  6 Vậy m  2; m  6.
b/ Cho hàm số y  f  x liên tục trên  , biết f  x  x  x  3 6  2 2 2
x  8x  m  3m  4, x   .
Tìm tất cả các giá trị của tham số m để đồ thị hàm số y  f  x  có 5 điểm cực trị. x  0  f x  0  x  2  g   x 2 2
 x 8x  m  3m  4  0   *
Hàm số y  f  x  có 5 điểm cực trị  đồ thị hàm số y  f  x có hai điểm cực trị nằm bên phải
trục Oy  f  x  0 có hai nghiệm bội lẻ
 PT * có hai nghiệm trái dấu và khác 2 hoặc PT * có một nghiệm bằng 0 và nghiệm còn lại dương khác 2 . Trang 1/6 - WordToan  2 3  73 m 3m 16  0    m
PT * có hai nghiệm trái dấu và khác 2     2  m  1  ;4 . 2 m 3m  4  0 m  1;4 m  1 
 PT * có một nghiệm bằng 0 2
 m  3m  4  0  m  4 x  0 Với 2 m  1   x  8x  0   . Vậy m  1. x  8  0 x  0 Với 2
m  4  x  8x  0   . Vậy m  4 . x  8  0 Vậy m 1;4 . Câu 2 ( 4,0 điểm ) 2.9x  3.6x
a) Giải bất phương trình  2 . 6x  4x 2x 1
b) Tìm tất cả các giá trị của tham số m để phương trình 2 log
 3x  8x  m 1 có 2 3 2 27x  54x  9m  1  nghiệm phân biệt thuộc ;    .  2  Lời giải
a) Điều kiện: 6x  4x  x  0 .  3 x  2.  3 2.9x 3.6x     2  3 x  Ta có: 2   
 2 . Đặt t    , điều kiện t  0 và t  1. 6x  4x  2 x   2  1    3   1  1  2 x log 2t  3 2t  5t  2    3 0 t
Bất phương trình đã cho trở thành:  2   0  2 2    1 2 t 1  1 0  x  log 2 1   t  2 t 3  2  1   
Vậy tập nghiệm của bất phương trình là: S    ;  log  0;log 2 . 3 3  2  2   2   1 x  b) Điều kiện:  2 2 3  x 6x  m  0 2x 1 2 log  3x  8x  m 1 3 2 27x  54x  9m 2 2
 log (2x 1)  log (3x  6x  m)  3x 8x  m 1 (*) 3 3 Đặt 2 u  3x  6x  ,
m v  2x 1u  0,v  0.
Khi đó phương trình (*) tương đương: log u  u  log v  v . 3 3
Vì hàm số y  f (t)  log t  t đồng biến trên khoảng (0; ) nên 3
Trang 2/6 – Diễn đàn giáo viên Toán
log u  u  log v  v  u  v . 3 3 Suy ra 2 2
3x  6x  m  2x 1 3x  8x  m 1  0 .
Yêu cầu bài toán trở thành tìm m để phương trình : 2
3x  8x  m 1  0 có hai nghiệm phân biệt  1  thuộc khoảng ;    .  2  Ta có 2 2
3x  8x  m 1  0  m  3
 x  8x 1. Xét hàm số 2
g(x)  3x  8x 1 có bảng biến thiên sau  1  9 13
Vậy phương trình đã cho có 2 nghiệm phân biệt thuộc ;    khi  m  .  2  4 3
Câu 3. Cho hình chóp S.ABCD có đáy là hình thoi cạnh bằng a , đường chéo AC  a . Tam giác SAD là
tam giác cân tại S và SAD   ABCD . Biết SA tạo với đáy một góc bằng 45 .
a) Tính khoảng cách giữa hai đường thẳng chéo nhau AB và SC .
b) Gọi M là trung điểm SD , lấy điểm N thuộc cạnh SC sao cho SN  2NC , gọi P là giao điểm của
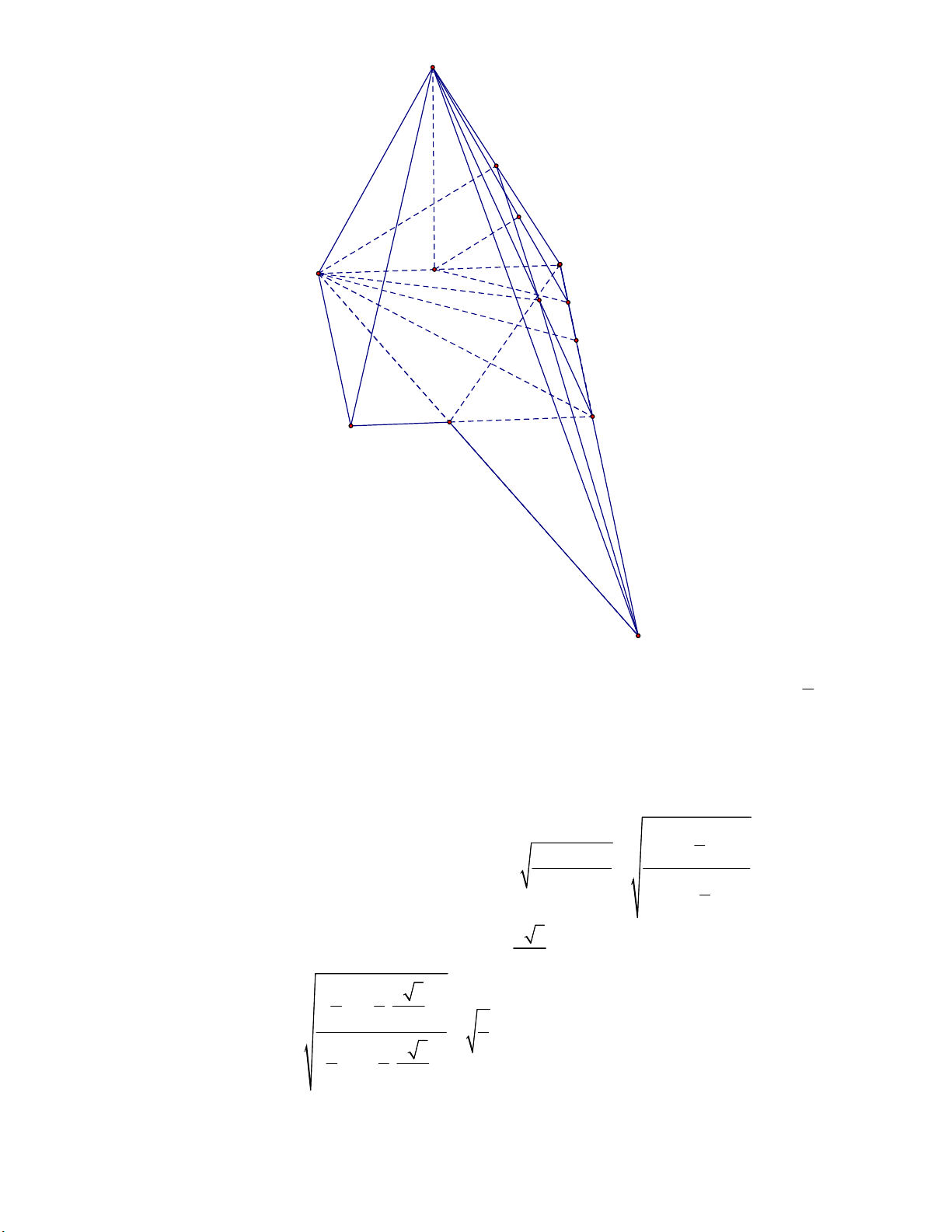
 AMN  với BC . Tính thể tích khối đa diện AMNPCD . Lời giải: Trang 3/6 - WordToan S M L A D H J N I B P C Q
a) Gọi H là trung điểm AD . a
Suy ra SH  AD  SH   ABCD   ; SA  ABCD    SAH  
SAH  45  SH  AH  . 2
Ta có AB//CD  AB// SCD  d  AB; SC   d  AB;SCD  d  ;
A SCD  2d H;SCD .
Đáy là hình thoi cạnh bằng a , đường chéo AC  a nên tam giác ACD đều.
Gọi I, J lần lượt là trung điểm CD, ID . Khi đó HJ  CD .
Gọi L là hình chiếu của H lên cạnh SJ .Khi đó ta chứng minh được HL  SCD. 2 2  1  HS . AI 2 2 HS .HJ    2 Do đó d H;SCD HL d  ; AB SC  2HL       . 2 2 2 HS  HJ 2  1  HS  AI    2  a 3
Ta có tam giác ACD đều cạnh bằng a nên AI  . 2 2 2  a   1 a 3  .    .   2  2 2   3 Vậy d  AB; SC  2  . 2 2     7 a 1 a 3     .   2  2 2  
b) Gọi Q  MN  CD  P  BC  . AQ
Trong tam giác SDQ có MS  MD, SN  2NC nên N là trọng tâm tam giác SDQ . Suy ra CD  CQ, PQ  . PA
Trang 4/6 – Diễn đàn giáo viên Toán VQPNC QP QN QC 1 5 Ta có  . .   V  V . V QA QM QD 6 AMNPDC 6 QAMD QAMD 2 3 1 1 1 1 1 a a 3 a 3 Lại có V  V  . .SH.S  .SH.S  . .  . MADQ 2 SADQ 2 3 AQD 6 ABCD 6 2 2 24 3 5 5a 3 Vậy V  V  . AMNPDC 6 QAMD 144
Câu 4. a) Có bao nhiêu số hạng là số nguyên trong khai triển   2002 3 2 5 .
b) Gọi S là tập hợp các số tự nhiên có 6 chữ số được lập từ tập A  0;1;2;3;4;5;6;7;8;  9 . Lấy
ngẫu nhiên 1 số từ tập S . Tính xác suất để lấy được số có dạng abcdef sao cho . a . b . c d. . e f  1400 . Lời giải
a) Có bao nhiêu số hạng là số nguyên trong khai triển   2002 3 2 5 . 2002k k
Số hạng tổng quát của khai triển   2002 3 2 5 là: k 2 3 T  C 2 5 . k 1  2002 k  2002k k    k  3n  2022 Để k 3 2 3 T  C 2
5 là số nguyên thì ta có:    ( , m n  ) . k 1  2002 2002  k  k  2m  2022     2 n  2 p Từ đó ta suy ra  , p   . 0  2 p  674 674 Vậy có
1  338 số p thoả mãn tức là có 338 số hạng là số nguyên trong khai triển 2   2002 3 2 5 .
b) Gọi S là tập hợp các số tự nhiên có 6 chữ số được lập từ tập A  0;1;2;3;4;5;6;7;8;  9 . Lấy
ngẫu nhiên 1 số từ tập S . Tính xác suất để lấy được số có dạng abcdef sao cho . a . b . c d. . e f  1400 . Lời giải
Số phần tử của không gian mẫu: n  5  9.10 .
Gọi X là biến cố lấy được số có dạng abcdef sao cho . a . b . c d. . e f  1400 . Ta có 3 2 2 2
1400  2 .5 .7  2.4.5 .7.1  8.5 .7.1.1 . 6! Trường hợp 1: a, , b c, d, ,
e f là 1 trong 6 số: 2, 2,2,5,5,7 có  120 số abcdef . 3!.2!.1! 6! Trường hợp 2: a, , b c, d, ,
e f là 1 trong 6 số: 2, 4,5,5,7,1 có  360 số abcdef . 1!.1!.1!2!.1! 6! Trường hợp 3: a, , b c, d, ,
e f là 1 trong 6 số: 8,5,5,7,1,1 có 180 số abcdef . 2!2!.1!.1!
Vậy số phần tử của tập X là n  X   120  360 180  660 . 660 22
Xác suất của biến cố X là P  X    . 5 4 9.10 3.10
Câu 5 (2,0 điểm) Cho a,b là những số thực thỏa mãn 2 2
a  ab  b  1. Tìm giá trị lớn nhất và giá trị nhỏ nhất 4 4 a  b  2 của biểu thức P  . 2 2 a  b 1 Trang 5/6 - WordToan Lời giải:
Theo giả thiết: a  ab  b   a  b2 2 2 1  3ab  1 (1). s  a  b Đặt  . Điều kiện: 2 s  4 p .  p  ab 1 Khi đó ( 1) trở thành: 2 2
s  3p  1  s  3 p 1  0  p   . 3 Mà 2
s  4 p nên 3 p 1  4 p  p  1. Ta có: 2 2 2 2
a  ab  b  1  a  b 1 ab . 2
a  b   a  b   a b     ab2  ab2 4 4 2 2 2 2 2 2 2 1 2  2 .
  ab2  ab2    p2  p   p  2 p 1  p  2 2 2 1 2 2 1 2 2 1 Suy ra P      . 1 ab 1 p  2 p  2 p  2 p  1 Xét hàm số f  p  2 1   với   p  1. p  2 3 2 2 p 1 p  2  p 1 2 2 p  p  2 2 2
 p  2 p 1  p  4p  5 ' f  p           .  p  22  p  22  p  22  p  1 ' f  p 2 0 p 4 p 5 0          1   p  5  ;1   3      1  16 Ta có: f      và f   1  0 .  3  15 ab  1 a  b  1
Suy ra: Giá trị lớn nhất của P là 0 khi   . a b 2     a  b  1   3  3  1 a  a   16 ab    
Giá trị nhỏ nhất của P là  khi 3 3  3   hoặc  . 15     3 a b 0  3 b    b   3  3
------------- Hết -------------
Trang 6/6 – Diễn đàn giáo viên Toán
Document Outline

• 20220302-095508_p0-đã chuyển đổi
• DDGVT08-HSG-TỈNH-LÀO-CAI-2021-2022