
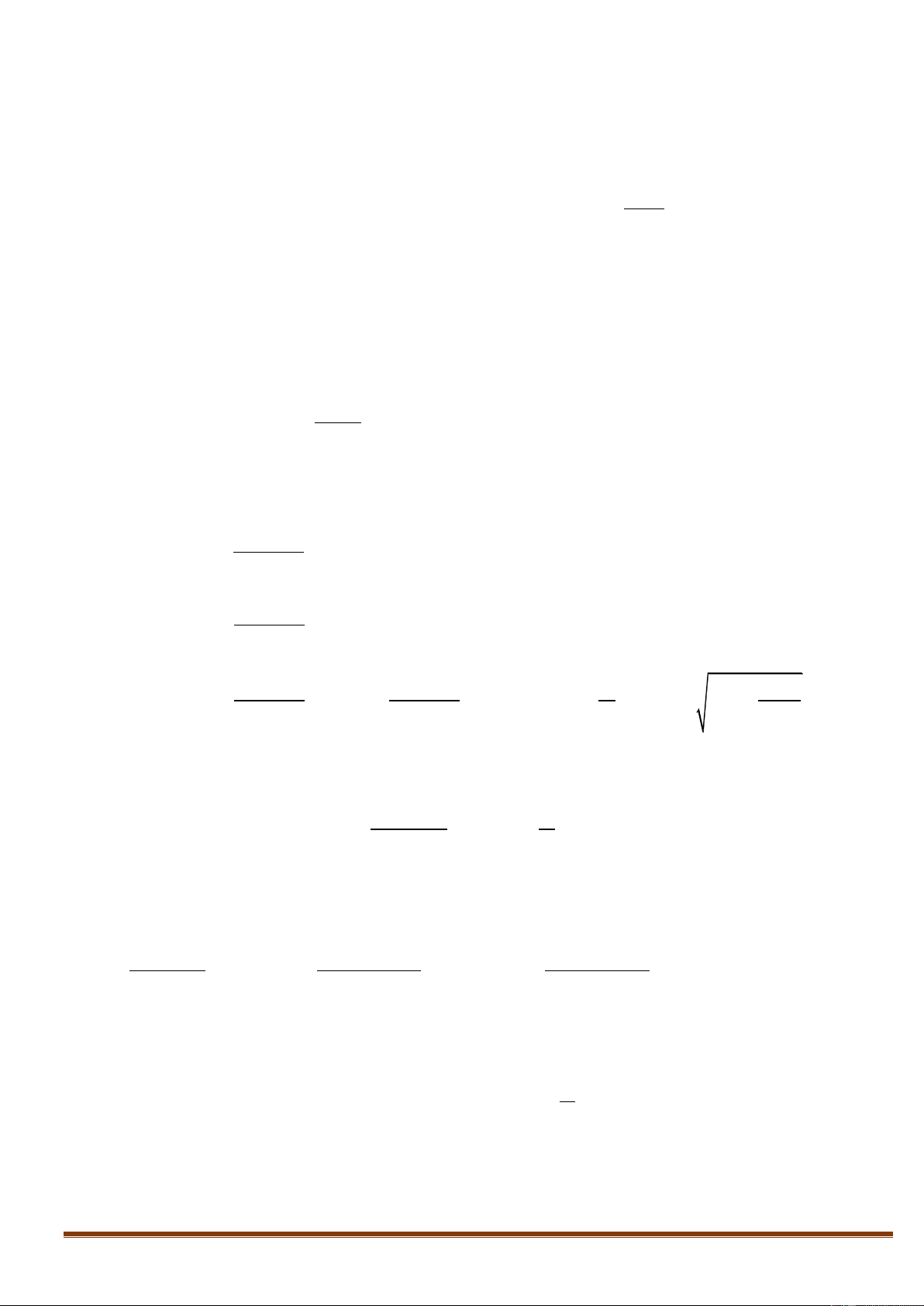



Preview text:
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI CHỌN HỌC SINH GIỎI CẤP TỈNH NĂM 2019 - 2020 Môn thi: TOÁN ĐỀ CHÍNH THỨC LỚP 12 THPT TỈNH QUẢNG BÌNH
Thời gian: 180 phút (không kể thời gian phát đề)
(Đề thi có 01 trang và 05 câu)
Câu 1 (2,0 điểm).
sin x + cos x + 1
a. Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số y = . 2 + sin 2x x b. Cho hàm số y =
có đồ thị (C )và điểm A (- 1; )
1 . Tìm các giá trị của m để đường thẳng 1 - x
(d): y = mx - m - 1 cắt đồ thị (C ) tại hai điểm phân biệt M ,N sao cho 2 2
A M + A N đạt giá trị nhỏ nhất.
Câu 2 (2,0 điểm). P
a. Cho hàm số f (x ) 1 = . Tính tỉ số
, với P = f '( ) 1 + 2f '( ) 2 + ... + 2019f '(201 ) 9 và 1 + 2019x Q Q = f '(- ) 1 + 2f '(- )
2 + ... + 2019f '(- 201 ) 9 .
b. Giải phương trình: log 3 é log 3x 1 1ù - - = x 2 ê 2 ( ) ë úû .
Câu 3 (2,0 điểm). A
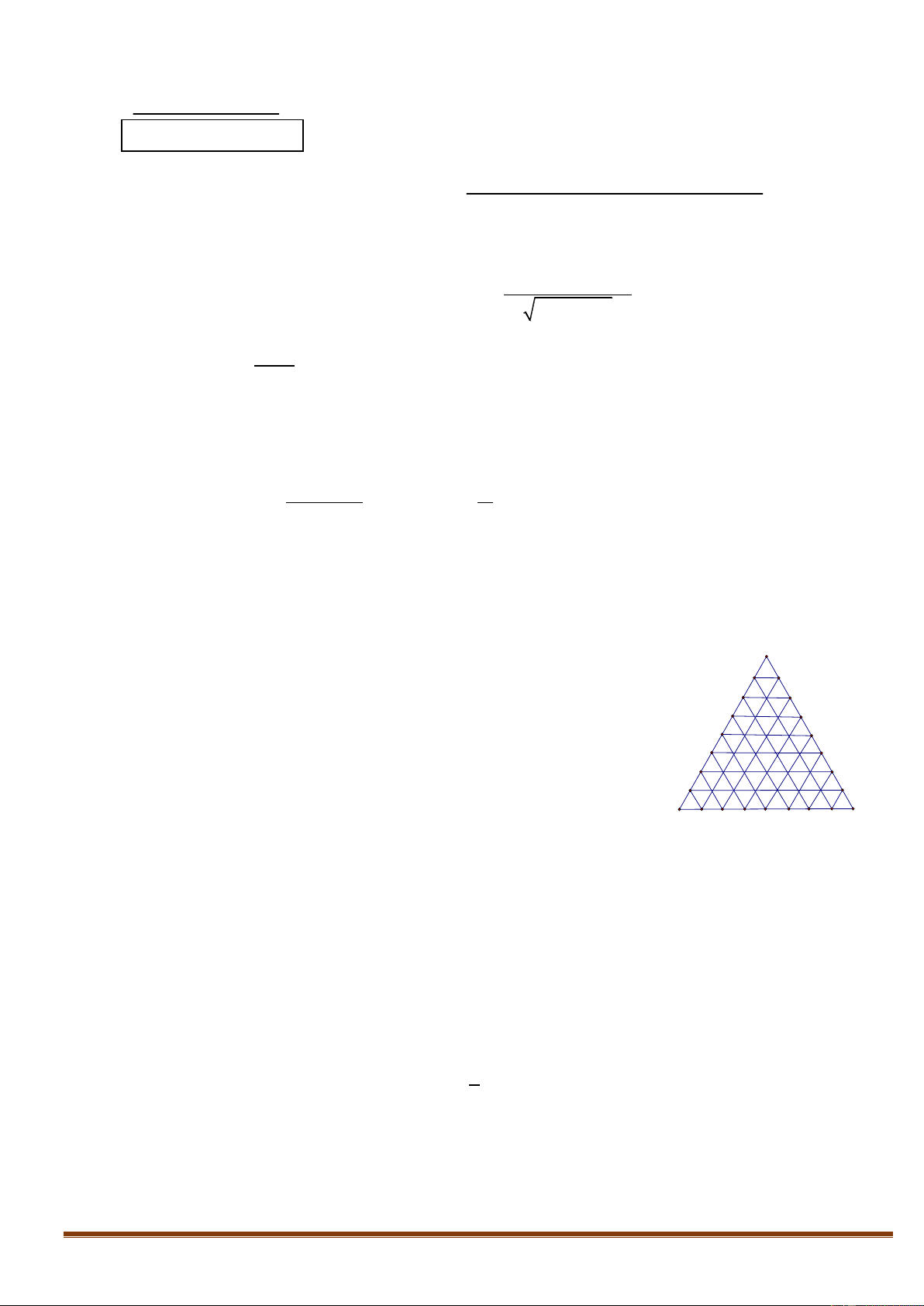
a. Cho tam giác đều ABC cạnh 8cm. Chia tam giác này thành 64 tam giác
đều cạnh 1cm bởi các đường thẳng song song với các cạnh tam giác ABC
(như hình vẽ). Gọi S là tập hợp các đỉnh của các tam giác cạnh 1cm. Chọn
ngẫu nhiên 4 đỉnh thuộc S. Tính xác suất sao cho 4 đỉnh được chọn là 4 đỉnh
của hình bình hành nằm trong miền trong của tam giác ABC và có cạnh chứa
các cạnh của các tam giác cạnh 1 cm ở trên. B C
b.Tìm công sai d của cấp số cộng (u có tất cả các số hạng đều dương và thỏa mãn: n )
íï u + u + ... + u
= 4 u + u + ... + u ï 1 2 2020 ( 1 2 1010 ) ì . 2 2 2
ï log u + log u + log u = 2 ï 3 2 3 5 3 14 ïî
Câu 4 (3,0 điểm). Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA (ABCD), SA = a. Một mặt phẳng
(a ) qua CD cắt SA, SB lần lượt tại M, N. Đặt AM = x, với 0 < x < a .
a. Tứ giác MNCD là hình gì? Tính diện tích tứ giác MNCD theo a và x. b. Xác đị 2
nh x để thể tích khối chóp S.MNCD bằng
lần thể tích khối chóp S.ABCD. 9
Câu 5 (1,0 điểm).
a. Cho các số thực phân biệt a,b > 1 . Chứng minh rằng: log (log b)> log (log b . a a b a ) Trang1
b. Cho các số thực a > a > ... > a > 1, n ³ 2 . Chứng minh rằng: 1 2 n ( ) log log a + log log a + ... + log log a + log log a > 0 . a a 2 a a 3 a a n a a 1 1 ( 1 ) 2 ( 2 ) n - 1 ( n - 1 ) n ( n )
............HẾT............
HƯỚNG DẪN GIẢI (THAM KHẢO)
sin x + cos x + 1
Câu 1a (1,0 điểm). Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số y = . 2 + sin 2x Hướng dẫn Đặ é ù t + 1 é ù t 2
sin x + cos x = t Î -
2; 2 Þ sin 2x = t - 1 ê ú , khi đó y =
= f (t ),t Î - 2; 2 . ë û ê ú 2 ë û t + 1 1 - t Ta có f '(t ) =
Þ f '(t )= 0 Þ t = 1 . ( 2t + ) 2 1 t + 1 1 - 2 1 + 2 Tính f (- 2)= ; f ( 2)= , f ( ) 1 = 2 . 3 3 1 - 2 3p p Suy ra: min y = Û x = -
+ k2p ; max y =
2 Û x = k2p, x = + k2p . 4 3 2 x
Câu 1b (1,0 điểm). Cho hàm số y =
có đồ thị (C )và điểm A (- 1; )
1 . Tìm các giá trị của m để đường 1 - x
thẳng (d): y = mx - m - 1 cắt đồ thị (C ) tại hai điểm phân biệt M , N sao cho 2 2
A M + A N đạt giá trị nhỏ nhất. Hướng dẫn Cách 1:
Dễ thấy đường thẳng (d): y = mx - m - 1 luôn đi qua điểm I (1;- )
1 là giao điểm của hai đường tiệm cận. 1 Ta có y ' =
> 0, " x ¹ 1 nên để đường thẳng (d) cắt (C ) tại hai điểm phân biệt M ,N thì m < 0 . (1 - x )2 Khi đó I (1;- )
1 luôn là trung điểm của đoạn MN. uuuur uuur 2 uuuur uuur uur 2 uuuur uuur uuuur uuur Ta có 2 2 A M + A N
= (AM + AN ) - 2AM AN = 4AI - 2AM AN = 32 - 2AM AN (*). uuuur uuur
Do A cố định nên: nếu ta xét được A M A N là số dương và trong tam giác AMN có cạnh MN nhỏ nhất thì tìm
được giá trị nhỏ nhất. Mà (C ) là Hypebol nên khi (d) là đường phân giác của góc tạo bởi hai tiệm cận thì
m = - 1 và (d): y = - x cắt (C )tại hai điểm phân biệt M (0; ) 0 , N (2;- )
2 và MN nhỏ nhất, ta có: Trang2 uuuur uuur A M A N = 1.3 + (- ) 1 (- 3) = 6 > 0, hơn nữa 2 2
A M + A N = 32 - 12 = 20 . Vậy ( 2 2
min A M + A N ) = 20 Û m = - 1. Cách 2:
Xét phương trình hoành độ x
giao điểm của (d) cắt và (C ): mx - m - 1 = , x ¹ 1 1 - x 2
Û mx - 2mx + m + 1 = 0 (vì x = 1 không là nghiệm). íï m ¹ 0 Để ï
phương trình có hai nghiệm phân biệt thì ì Þ m < 0 . 2 ï m - m ï (m + ) 1 > 0 ïî íï x + x = 2 ï 1 2 Theo đị ï nh lý Viet ta có: ì m + 1 . ïï x x = 1 2 ïî m 2 2 2 2 Mặt khác 2 2 A M + A N
= (x + 1 + x + 1 + m x - 1 - 2 + m x - 1 - 2 1 ) ( 2 ) ( ( 1 ) ) ( ( 2 ) ) 2(m + ) 1 é ù A M + A N = 10 - + m ( êx - )2 1 + (x - )2 2 2 2 1 -
ú 4 m x - 1 + m x - 1 + 8 1 2 ( ( 1 ) ( 2 )) m êë úû 2(m + ) 1 é ù A M + A N = 18 - + m ( êx + x )2 2 2 2
- 2x x - 2 x + x + 2ú 1 2 1 2 ( 1 2 ) m êë úû 2 m + 1 é 2 m + 1 ù æ ê ú 1 ö ç ÷ 1 2 2 ( ) 2 ( ) A M + A N = 18 - + m 2 - = 16 + 2 - ê ú ç m - ÷³ 16 + 4 ç ÷ (- m ). m ê m ç ú è m ÷ ø (- m ) ë û Þ ( 2 2
min A M + A N ) = 20 Û - m = 1 Û m = - 1. P
Câu 2a (1,0 điểm). Cho hàm số f (x ) 1 = . Tính tỉ số , với 1 + 2019x Q P = f '( ) 1 + 2f '( ) 2 + ... + 2019f '(201 )
9 và Q = f '(- ) 1 + 2f '(- )
2 + ... + 2019f '(- 201 ) 9 . Hướng dẫn x x f (x ) 1 = Þ f x = - Þ f - x = -
= f x " x Î ¡ . x ( ) 2019 ln 2019 2019 ln 2019 ' ' ' , 2 ( ) 2 ( ) 1 + 2019 (1 + 2019x ) (1 + 2019x )
Do đó f '(x) là hàm số chẵn, suy ra g(x)= - x.f '(x) là hàm số lẻ. 2019 2019 2019 P Vậy nếu P = - g å (k) thì Q = g å (- k)= - g å (k)= P Þ = 1 . = = Q k = 1 k 1 k 1
Câu 2b (1,0 điểm). Giải phương trình: log 3 é log 3x 1 1ù - - = x 2 ê 2 ( ) ë úû . Hướng dẫn Trang3 Đặt log 3 - 1 = Þ 3 = 1 + 2y x y x
, từ phương trình đã cho ta có: 2 ( ) 1 æ ö ç ÷ log 3 - 1 = Þ 3 = 1 + 2x y x y
. Như thế ta có điều kiện x,y Î ç ;+ ¥ ÷ ç
÷ và ta được hệ phương trình: 2 ( ) çè3 ÷ø íï 3x = 1 + 2y ï æ ö t 1 ì ç ÷
. Xét hàm ( ) = 1 + 2 - 3 , Î ç ;+ ¥ ÷Þ ' ç ÷ ( )= 2t f t t t f t ln 2 - 3 , ta có: ï 3y = 1 + 2x ï ç ÷ ïî è3 ø æ ö æ ö ç ÷ ç ÷ f (t ) t 3 3 1 ' = 0 Û 2 = Û t = log ç
÷= a Î ç ;+ ¥ ÷, và '( ) 2t f t =
ln 2 - 3 đồng biến nên ta có t = a 2 ç ÷ ç ÷ ç ÷ ln 2 èln 2ø çè3 ÷ ø
là điểm cực tiểu của f (t ), f ( )= 1 + 2a a
- 3a < 0 nên phương trình f (t ) = 0 có đúng hai nghiệm t = 1,t = 3 .
Mặt khác từ hệ phương trình, trừ theo vế ta có: 3( -
)= 2y - 2x Û 3 + 2x = 3 + 2y x y x y hay là 1 æ ö ç ÷
g (x ) = g (y ), với ( ) = 3 + 2t g t t
đồng biến trên ç ;+ ¥ ÷ ç ÷ ç
, suy ra x = y . è3 ÷ø
Cuối cùng phương trình đã cho Û f (x ) = 0 Û x = 1,x = 3 . Câu 3a (1,0 điểm). A
Cho tam giác đều ABC cạnh 8cm. Chia tam giác này thành 64 tam giác
đều cạnh 1cm bởi các đường thẳng song song với các cạnh tam giác
ABC (như hình vẽ). Gọi S là tập hợp các đỉnh của các tam giác cạnh
1cm. Chọn ngẫu nhiên 4 đỉnh thuộc S. Tính xác suất sao cho 4 đỉnh
được chọn là 4 đỉnh của hình bình hành nằm trong miền trong của tam
giác ABC và có cạnh chứa các cạnh của các tam giác cạnh 1 cm ở trên. B C Hướng dẫn
Trên cạnh BC ta có 9 đỉnh của các tam giác đều cạnh 1cm (kể cả B và C), trên đường thẳng tiếp theo song
song BC (phía trên BC) ta có 8 đỉnh của các tam giác đều cạnh 1cm, ... cuối cùng đến A có 1 đỉnh của tam
giác đều cạnh 1cm. Ta có n (S )= 9 + 8 + 7 + ... + 2 + 1 = 45.
Như thế số phần tử của không gian mẫu là:n ( ) 4 W = C . 45
Theo yêu cầu: nếu có hình bình hành tạo thành từ 4 đỉnh trong S thì 4 đỉnh đó chỉ có thể thuộc tam giác đều
cạnh 5cm (tức là bỏ đi tất cả các đỉnh của các tam giác cạnh 1cm nằm trên ba cạnh BC, CA, AB và cạnh có
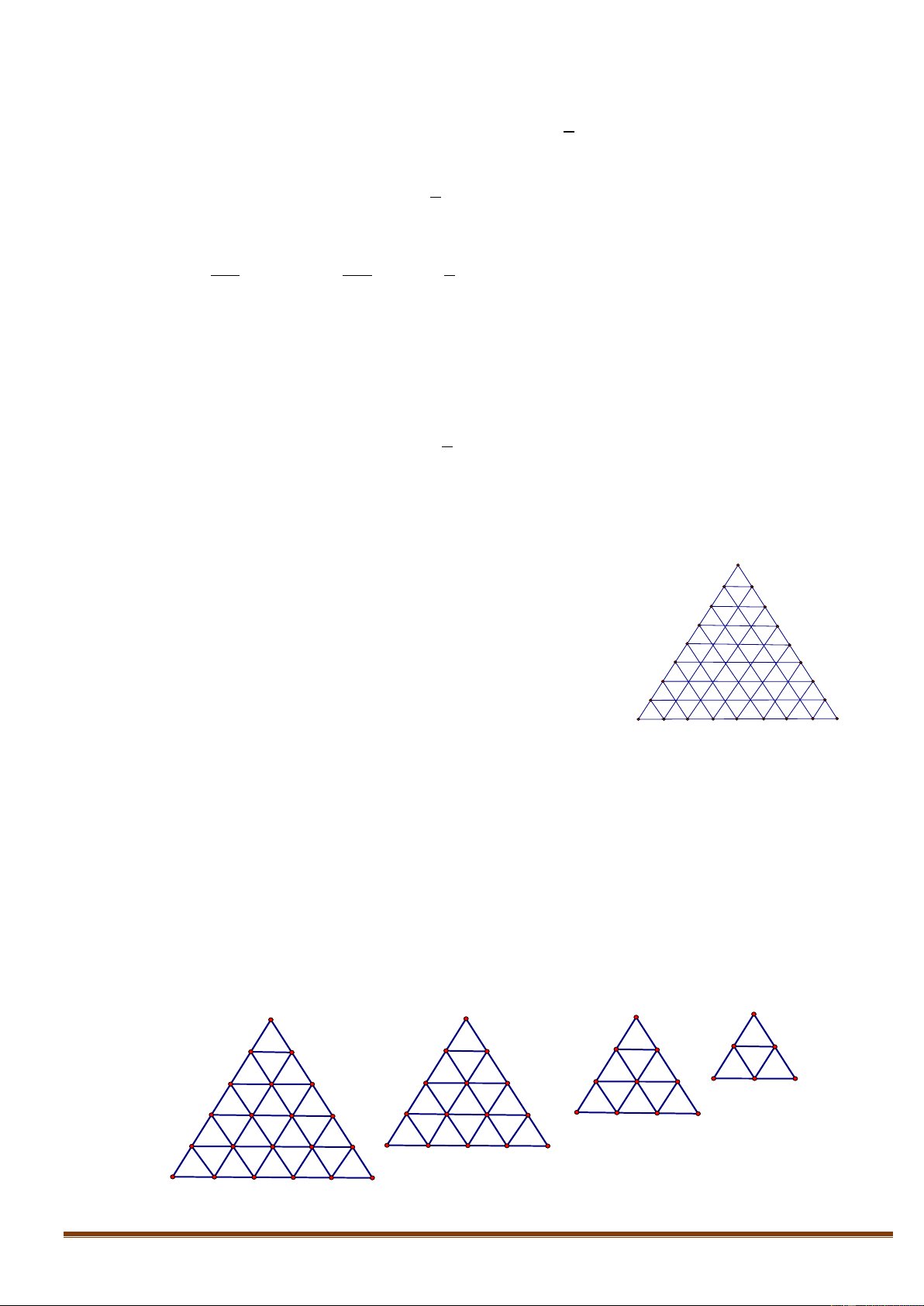
liên quan đến các đỉnh đó). P P P P K K T T K T K T H I H I H I H I G F G F G F D E D E M 1 2 N 3 4 Trang4
• Trường hợp 1: Các cạnh của hình bình hành nằm trên MN hoặc có đúng 1 đỉnh thuộc MN.
- Các hình bình hành có cạnh nằm trên MN và
+ Tạo bởi hai đoạn MN, DE: Ta cần chọn thêm 2 đường thẳng song song hoặc trùng với DM (hoặc song
song trùng EN) thì tạo ra hình bình hành và mỗi trường hợp này có 2
C cách. Như vậy có: 2 2 C + C = 20 5 5 5 hình bình hành.
+ Tạo bởi hai đoạn MN, GF: Lặp lại lập luận trên ta có có: 2 2
C + C = 12 hình. 4 4
+ Tạo bởi hai đoạn MN, HI: Lặp lại lập luận trên ta có có: 2 2
C + C = 6 hình. 3 3
+ Tạo bởi hai đoạn MN, KT: Lặp lại lập luận trên ta có có: 2 2
C + C = 2 hình. 2 2
Vậy các hình bình hành có cạnh nằm trên MN có 20 + 12 + 6 + 2 = 40 hình.
- Các hình bình hành có đúng 1 đỉnh thuộc MN
+ Đỉnh số 1 và số 4: đều có 4 hình bình hành
+ Đỉnh số 2 và số 3: đều có 3 hình bình hành.
Vậy các hình bình hành có đúng 1 đỉnh thuộc MN có 2.(4 + 3) = 14 hình.
Do đó trường hợp 1 ta có: 40 + 14 = 54 hình.
• Trường hợp 2: Các cạnh hình hành nằm trên DE nhưng không thuộc MN hoặc có đúng 1 đỉnh thuộc DE.
So với trường hợp 1 thì chỉ số tổ hợp giảm đi 1, ta làm tương tự và có: ( 2 2 C + C )+ ( 2 2 C + C )+ ( 2 2 C + C + 3 + 3 + 2 = 28 hình. 4 4 3 3 2 2 ) ( )
• Trường hợp 3: Các cạnh hình hành nằm trên GF nhưng không thuộc MN và DE hoặc có đúng 1 đỉnh thuộc GF. Tương tự ta có ( 2 2 C + C )+ ( 2 2 C + C + 2 + 2 = 12 hình. 3 3 2 2 ) ( )
• Trường hợp 4: Các cạnh hình hành nằm trên HI nhưng không thuộc MN, DE và GF hoặc có đúng 1 đỉnh thuộc HI. Ta có ( 2 2 C + C + 1 = 3 hình. 2 2 )
Số các hình bình hành trong bốn trường hợp là: 54 + 28 + 12 + 3 = 97 hình. 97 97
Vậy xác suất cần tìm là: p = = . 4 C 148995 45 Lưu ý:
Đề bài yêu cầu các đỉnh hình bình hành nằm trong miền trong của tam giác ABC nên số hình bình hành là
tương đối nhỏ. Nếu các đỉnh hình hành không ngoài tam giác ABC thì sẽ nhiều hình hơn.
Câu 3b (1,0 điểm). Tìm công sai d của cấp số cộng (u có tất cả các số hạng đều dương và thỏa mãn: n )
íï u + u + ... + u
= 4 u + u + ... + u ï 1 2 2020 ( 1 2 1010 ) ì . 2 2 2
ï log u + log u + log u = 2 ï 3 2 3 5 3 14 ïî Trang5 Hướng dẫn 2020(2u + 2019d 1010 2u + 1009d 1 ) ( 1 )
Từ phương trình đầu của hệ ta có: = 4. 2 2
Û 2u + 2019d = 4u + 2018d Û d = 2u Þ u = 3u ,u = 9u ,u = 27u thế vào phương trình thứ hai 1 1 1 2 1 5 1 14 1 của hệ, ta có:
(log 3 + log u )2 + (log 9 + log u )2 + (log 27 + log u )2 = 2 . Đặt log u = t , ta có phương trình: 3 3 1 3 3 1 3 3 1 3 1 ( + t - 1
t )2 + ( + t )2 + ( + t )2 2 1 2 3
= 2 Û 3t + 12t + 12 = 0 Û t = - 2 . Do đó 2 u = 3 = 3 = . 1 9 2 Vậy d = 2.u = . 1 9 Câu 4 (3,0 điểm).
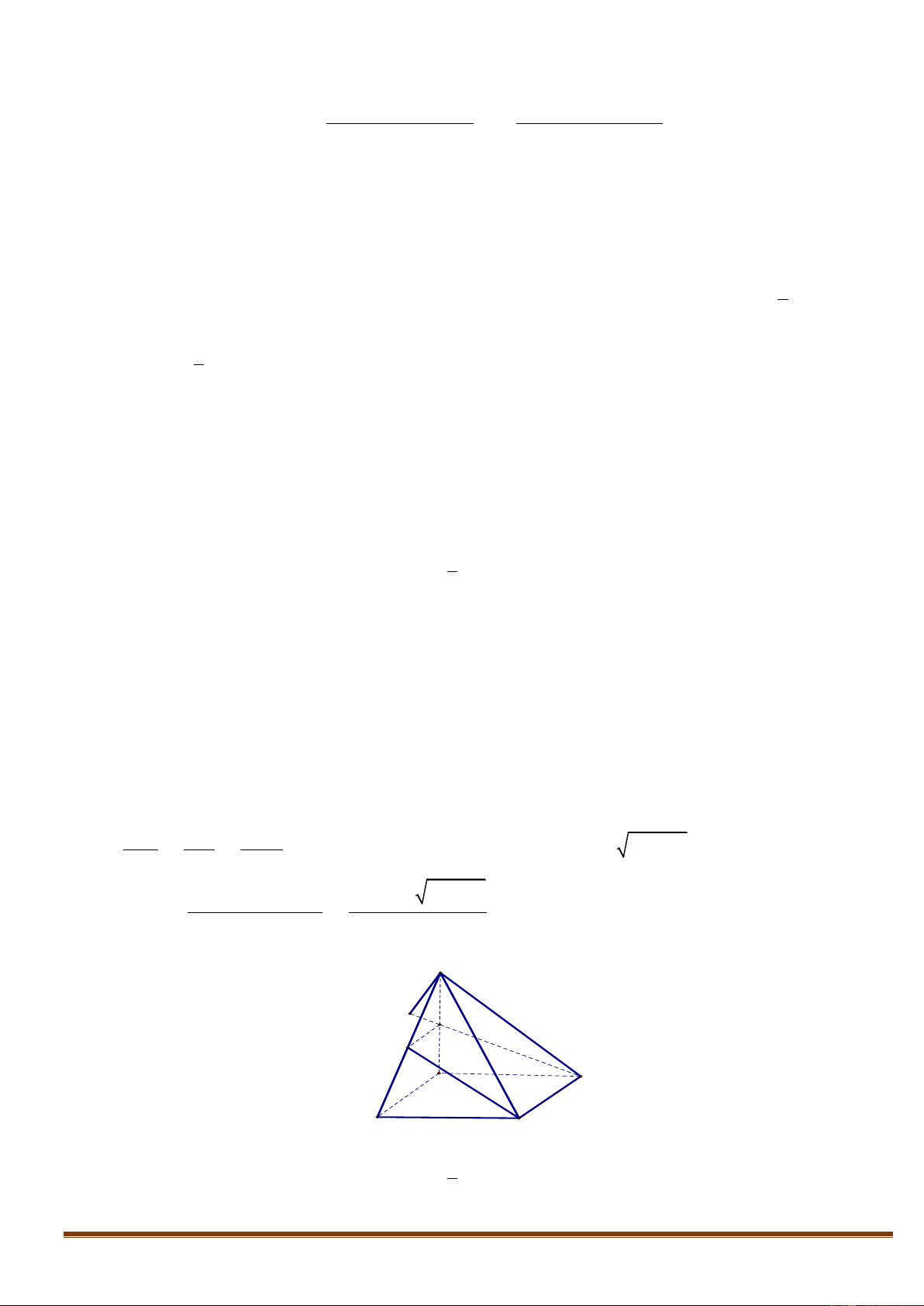
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc với mặt phẳng (ABCD), SA = a. Một mặt
phẳng (a ) qua CD cắt SA, SB lần lượt tại M, N. Đặt AM = x, với 0 < x < a .
a. Tứ giác MNCD là hình gì? Tính diện tích tứ giác MNCD theo a và x. b. Xác đị 2
nh x để thể tích khối chóp S.MNCD bằng
lần thể tích khối chóp S.ABCD. 9 Hướng dẫn
a. Tứ giác MNCD là hình gì? Tính diện tích tứ giác MNCD theo a và x.
Vì ABCD là hình vuông nên AB // CD, suy ra AB // (a ) do đó AB // MN hay ta có MNCD là hình thang. Mặt
khác: CD ^ AD, CD ^ SA nên CD ^ mp(SAD) suy ra MN ^ (SAD) suy ra MN ^ MD.
Vậy tứ giác MNCD là hình thang vuông tại D và M.
Từ đó ta có DM là đường cao của hình thang MNCD. MN SM a - x Ta có = =
Þ MN = a - x và MA = x nên 2 2 DM =
x + a . Do đó ta tính diện tích A B SA a
(CD + MN )DM ( a - x ) 2 2 . 2 x + a MNCD là: S = = . 2 2 S H M N A D B C b. Xác đị 2
nh x để thể tích khối chóp S.MNCD bằng
lần thể tích khối chóp S.ABCD. 9 Trang6 3 1 a Ta có V = SA.S =
(1). Kẻ SH vuông góc với DM, (H thuộc DM), ta có: S .A BCD 3 A BCD 3
MN ^ (SAD) (theo chứng minh câu a) nên MN ^ SH, suy ra SH ^ (MNCD), từ đó SH là đường cao của khối chóp S.MNCD.
Trong hai tam giác vuông đồng dạng SHM và DAM ta có: a - (a - x SH SM a x ) = = Þ SH =
do đó thể tích củakhối chóp S.MNCD là: 2 2 2 2 DA DM x + a x x + a
a (a - x ) (2a - x ) 2 2 x + a
a (a - x )(2 1 a - x ) V ' = . . = (2). 2 2 3 2 6 x + a
a (a - x )( a - x ) 3 2 2 a
Từ (1), (2) và yêu cầu bài toán ta có phương trình: = . 6 9 3 æ x öæ x ö ç ÷ç ÷ ç - ÷ç - ÷= Þ ç ÷ ç ç ÷ ( - t )( - t ) x = t = Î ( ) 2 Û t = Î ( ) 2a 9 1 2 4 9 1 2 4, 0;1 0;1 Û x = . è a ÷ç øè a ÷ ø a 3 3 2a 2 Vậy với x =
thì thể tích khối chóp S.MNCD bằng
lần thể tích khối chóp S.ABCD. 3 9
Câu 5a (0,5 điểm). Cho các số thực phân biệt a,b > 1 . Chứng minh rằng: log (log b)> log (log b . a a b a ) Hướng dẫn
Đặt log b = t > 0,t ¹ 1 t
Þ b = a . Khi đó bất đẳng thức cần chứng minh tương đương với: a log t > log t Û t - t > (*). t a ( ) ( ) 1 log 0 a a
Nếu t > 1 thì t - 1 > 0 & log t > 0 Þ ( ) * đúng. a
Nếu 0 < t < 1 thì t - 1 < 0 & log t < 0 Þ ( )
* đúng. Vậy ta có điều cần chứng minh. a
Câu 5b (0,5 điểm). Cho các số thực a > a > ... > a > 1, n ³ 2 . Chứng minh rằng: 1 2 n ( ) log log a + log log a + ... + log log a + log log a > 0 . a a 2 a a 3 a a n a a 1 1 ( 1 ) 2 ( 2 ) n - 1 ( n - 1 ) n ( n ) Hướng dẫn
Áp dụng bất đẳng thức trong câu 5a, ta có: log log a + log log a > log log a + log log a a a 2 a a 3 a a 2 a a 3 1 ( 1 ) 2 ( 2 ) 2 ( 1 ) 2 ( 2 ) Û log log a + log log a > log log a . log a = log log a . a a 2 a a 3 a a 2 a 3 a a 3 1 ( 1 ) 2 ( 2 ) 2 ( 1 2 ) 2 ( 1 ) Lặp lại lần nữa: log log a + log log a > log log a + log log a a a 3 a a 4 a a 3 a a 4 2 ( 1 ) 3 ( 3 ) 3 ( 1 ) 3 ( 3 ) Trang7 Û log log a + log log a > log log a . log a = log log a . a a 3 a a 4 a a 3 a 4 a a 4 2 ( 1 ) 3 ( 3 ) 3 ( 1 3 ) 3 ( 1 )
Cứ tiếp tục lặp lại như thế ta lần lượt thay được cơ số ngoài cùng của logarit và số lấy logarit trong cùng (chú
ý mỗi lần thay thì cơ số a không đổi), ký hiệu vế trái là P, cuối cùng ta có: 1 P > log a + a = a a = a = (đpcm). a a n a a a a n a a a n (log log log log log . log log log 0 1 1 1 1 ) n ( n ) n ( 1 n ) n ( 1 )
---------- HẾT ---------- Trang8




