SỞ GIÁO DỤC VÀ ĐÀO TẠO HÀ NỘI
Kỳ thi Olimpic cấp Cụm các môn văn hóa
CỤM THẠCH THẤT-QUỐC OAI
lớp 10 và 11 năm học 2023-2024 Môn: Toán 11 ĐỀ CHÍNH THỨC
Thời gian làm bài: 150 phút
(Đề thi gồm 01 trang)
Họ và tên thí sinh:…………………………………….Số báo danh:………………………… Câu 1 (5 điểm)
a) Giải phương trình 2
2 cos x  3sin x  0.
b) Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M , N , E lần lượt là trung
điểm của các đoạn thẳng AD, SD và SC . Chứng minh rằng (MNE) / /(SAB) . Câu 2 (5 điểm)
a) Cho các số 5x  y, 2x  3 y, x  2 y theo thứ tự lập thành cấp số cộng, các số 2 2
( y 1) , xy 1, (x 1) theo thứ tự lập thành cấp số nhân. Tìm x, y .
b) Gieo một con xúc sắc 4 lần. Tính xác suất để mặt 6 chấm xuất hiện ít nhất 1 lần. Câu 3 (4 điểm)
a) Tìm tất cả các giá trị của m để phương trình 2 log (2 )
x  log x  m 1  0 có đúng 2 2 2
nghiệm phân biệt thuộc khoảng 0;  1 . u   2 1 
b) Cho dãy số (u ) được xác định bởi 2  n u  2024u n n * u  , n  N  n 1  2025 Đặt u u u 1 2 n * S   ...
, n  N . Chứng minh rằng * S  2025, n   N . n u 1 u 1 u 1 n 2 3 n 1  Câu 4 (4 điểm)
Cho hình chóp S.ABC có đáy là tam giác đều cạnh a , SA  SB  SC , đường cao SO của
hình chóp S.ABC có độ dài bằng 2a.
a) Chứng minh rằng SA  BC .
b) M là điểm thuộc đường cao AH của tam giác ABC ( M khác A và H ). Mặt phẳng  P đi
qua M và vuông góc với AH cắt hình chóp theo thiết diện. Tìm vị trí của M để diện tích thiết diện lớn nhất.
Câu 5 (2 điểm). Cho các số thực a,b,c lớn hơn 1, thỏa mãn 2 log 5a  2 16b  2 27c  log
ab  bc  ca      2
 abbcca  144  
Tính giá trị của biểu thức T  a  2b  3c .
-----------------Hết-----------------
(Lưu ý: Học sinh không được sử dụng máy tính. Giám thị coi thi không giải thích gì thêm)
Chữ kí cán bộ coi thi số 1:................................Chữ kí cán bộ coi thi số 2:..........................
ĐÁP ÁN – MÔN TOÁN – LỚP 11-NĂM HỌC 2023-2024 CÂU NỘI DUNG ĐIỂM 1a Giải phương trình 2
2 cos x  3sin x  0. 3đ
PT đã cho tương đương với PT 2
2 sin x  3sin x  2  0 1.0  sin x  2    1  sin x   2 * sin x  2  vô nghiệm;   x   k2 1  * 6 sin x    , k  Z 1.0 2 5 x   k2  6
KL: Phương trình đã cho có 2 họ nghiệm là  5 x 
 k2 , x 
 k2 ,(k  Z) 1.0 6 6 1b
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N, E lần lượt là 2đ
trung điểm của các đoạn thẳng AD, SD và SC. Chứng minh rằng (MNE)//(SAB).
Hình vẽ. HS vẽ đúng hình
Ta có MN là đường trung bình của tam giác SAD
 MN / /SA  MN / /(SAB) (1) 0.5
Ta có NE là đường trung bình của tam giác SDC  NE / /CD 0.5
Do ABCD là h.b.h  CD / / AB  NE / / AB  NE / /(SAB) (2) 0.5
Từ (1) và (2) suy ra (MNE) / /(SAB) 0.5 2a
Cho các số 5x  y, 2x  3y, x  2 y theo thứ tự lập thành cấp số cộng, các số 3đ 2 2
( y 1) , xy 1, (x 1) theo thứ tự lập thành cấp số nhân. Tính x, y .
5x  y, 2x  3y, x  2 y theo thứ tự lập thành cấp số cộng
 2(2x 3y)  (x  2y)  (5x  y) 0.5
 2x  7y  0 (1) 2 2
( y 1) , xy 1, (x 1) theo thứ tự lập thành cấp số nhân 0.5 2 2 2
 (xy 1)  (y 1) (x 1)
xy 1  (y 1)(x 1) (2)
 xy1(y1)(1x) (3)  14 0.5 x 
2x  7y  0  Từ (1) và (2) ta có HPT 9   
x  y  2 4 y    9
x  0, y  0  1.0 2x  7 y  0 Từ (1) và (2) ta có HPT    9 9
2xy  x  y
x  , y    4 14  14  9 0.5 x     x  x  0 KL: 9  , 4  ,  4  9  y  0 y       y  9  14 2b
Gieo một con xúc sắc 4 lần. Tính xác suất để mặt 6 chấm xuất hiện ít nhất 1 lần. 2đ
Gọi Ai là biến cố “Lần thứ i xuất hiện mặt 6 chấm”, i 1;2;3;  4 suy ra các biến cố Ai độc lập.
A là biến cố “Mặt 6 chấm xuất hiện ít nhất 1 lần”  A :”Cả 4 lần đều
không xuất hiện mặt 6 chấm” 1.0 1 5
Ta có P( A )   P(A )  i 6 i 6 4  5  1,0 P( )
A  P( A A A A )  P( A ).P( A ).P( A ).P( A )  1 2 3 4 1 2 3 4    6  4  5   P( ) A  1    6  3a
Tìm tất cả các giá trị của m để phương trình 2
log 2x  log x  m 1  0 có đúng 2 2 2 2đ
nghiệm phân biệt thuộc khoảng 0;  1 . 2
log 2x  log x  m 1  0 0,5 2 2 2
 (1 log x)  log x  m 1  0 2 2 2
 log x  3log x  m  0 2 2
Đặt t  log x x
; (0;1)  t  0 ta được PT 2
t  3t  m  0 (1) 2 0.5
PT đã cho có đúng 2 nghiệm phân biệt thuộc khoảng (0; 1)
 PT (1) có 2 nghiệm âm phân biệt. 0,5  0.5
  9  4m  0   b 9  9 S    3
  0  0  m  . Vậy 0  m  a 4  4  c P   m  0  a 3b u   2 1  2đ
Cho dãy số (u ) được xác định bởi 2   n u 2024u n n * u  , n  N  n 1  2025 Đặ u u u t 1 2 n * S   ...
, n  N . Chứng minh rằng * S  2025, n   N n u 1 u 1 u 1 n 2 3 n 1 
* Chứng minh u  2, n  . (PP quy nạp) n u (u 1)
Ta có u  2 , Ta có k k u  u  1 k 1  k 2025 0,5
Giả sử u  2  u
 u  0  u  u  2 k k 1  k k 1  k
Suy ra u  2, n  . n Ta có 0,5 2 u  u u (u 1) n n n n u  u   n 1  n 2025 2025 2025(u
1)  (u 1)  u (u 1) n 1  n  n n u  1 1  n   2025   u 1 u 1 u 1 n 1   n n 1   Suy ra u u u 1 2 S   ... n  n u 1 u 1 u 1 0,5 2 3 n 1   1 1   1  2025  2025    20251   2025  u 1 u 1 u 1 u 1  1 n 1    n 1   n 1  Do u  2, n  nên S  2025 0.5 n n 4a
Cho hình chóp S.ABC có đáy là tam giác đều cạnh a , SA  SB  SC , đường cao SO 2đ
của hình chóp S.ABC có độ dài bằng 2a.
a) Chứng minh rằng SA  BC
Từ SA  SB  SC  OA  OB  OC  O là tâm đường tròn ngoại tiếp tam 1.0
giác ABC  O cũng là trực tâm của tam giác ABC  AO  BC
BC  SO( do SO  (ABC) 1.0 Ta có 
 BC  (SAO)  BC  SA BC  AO 4b
b) M là điểm thuộc đường cao AH của tam giác ABC ( M khác A và H ). Mặt phẳng 2đ
P đi qua M và vuông góc với AH cắt hình chóp theo thiết diện. Tìm vị trí của M
để diện tích thiết diện lớn nhất.
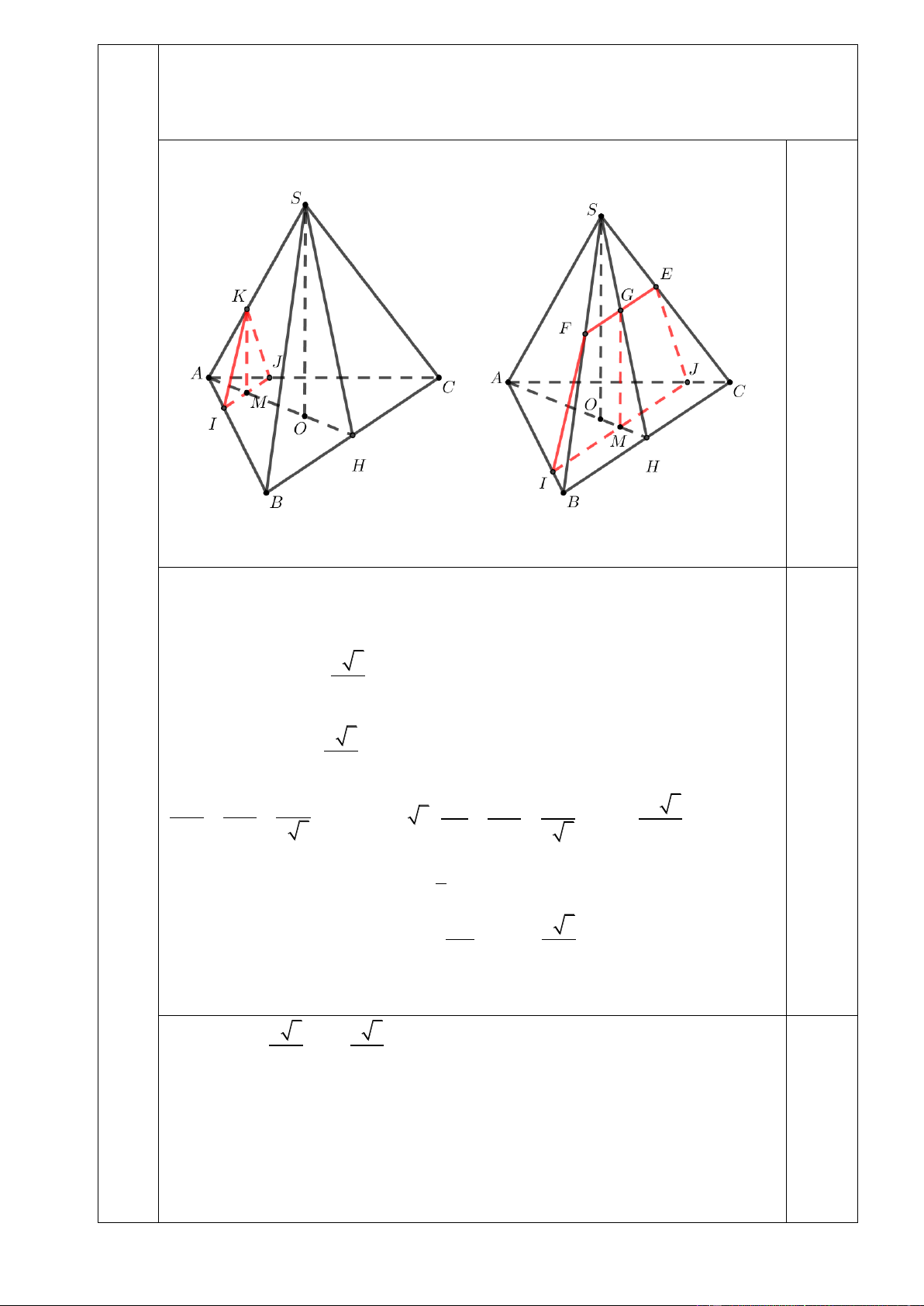
Vẽ đúng hình, dựng được thiết diện trong 2 trường hợp. 0.5 Hình 1 Hình 2
P qua M và vuông góc với AH nên P song song với đường thẳng BC ,
đồng thời P song song hoặc chứa SO .   Đặ a 3
t AM  x  0  x     2   0.5 a 3 +TH1: Khi 0  x 
thì thiết diện là một tam giác KIJ (hình 1). Ta có: 3 KM AM 3x    IJ AM x x KM  2 2 3 2x 3 ;    IJ  SO AO a 3 BC AH a 3 3 1
Diện tích thiết diện khi đó là 2 S 
KM .IJ  2x . Trong trường hợp này 2 2 2a a
diện tích thiết diện lớn nhất là S  3 khi x  . 3 3 a 3 a 3 + TH2: Khi  x 
thì thiết diện là hình thang IJEF (hình 2). 3 2 Ta có: IJ AM 2x 2x 3    IJ  ; BC AH a 3 3 0.5  a 3   x   EF SG OM 3     
 EF  2x 3  a BC SH OH a 3 6  a 3    x GM HM 2    
 GM  23a  2x 3 . SO HO a 3 6
Diện tích thiết diện khi đó là 1 S  IJ  EF  2 GM 
 x  a a x  1 . 4 3 3 3 2 3 
4x 33a6a4x 3. 2 3 3     
Khi đó   x  a a  x  2 2 1
1 4x 3 3a 6a 4x 3 3a S 4 3 3 6 4 3       3 3 2 4   2 Trong trườ 3a a
ng hợp này diện tích thiết diện lớn nhất là S  3 3 khi x  . 4 8 2 0.5 3a
Kết hợp 2 trường hợp ta có diện tích thiết diện lớn nhất là S  khi 4 3a 3 x  8 5
Cho a,b,c  1 thỏa mãn 2 log 5a  2 16b  2 27c  log
ab  bc  ca        2 . Giá trị ab bc ca 144 2đ
của biểu thức T  a  2b  3c . Ta có: a  b  c  ab  ac 
bc  a  b2   b  c2  a  c2 2 2 2 5 16 27 12 12 12 3 2 2 3 2 3  0. 0.5
Dấu đẳng thức xảy ra khi và chỉ khi a  2b  3c   1 . Suy ra 2 a  2 b  2 5 16
27c  12ab  bc  ca .  2 a  2 b  2 log 5 16 27c  log
12 ab  bc  ca   1          log   12 ab bc ca ab bc ca ab bc ca 0.5 .
(Do ab  bc  ca  1) Biểu thức đã cho: 2 log 5a  2 16b  2 27c  log
ab  bc  ca
abbcca   144    1 1 log 12 log
ab  bc  ca
abbcca 12   4  1 2. log 12. log
ab  bc  ca  1  1  1  0.5 abbc 2. ca 12   4
Dấu đẳng thức xảy ra khi và chỉ khi  1 log 12 .log
ab  bc  ca  ab  bc  ca  2 12 abbc 2 ca 12     4 Từ  
1 và 2 suy ra đẳng thức đã cho xảy ra khi a   12
a  2b  3c    b  6 .  0.5
ab  bc  ca   2 12 c   4
Suy ra a  2b  3c  12 .
Chú ý: Lời giải đúng theo cách khác vẫn chấm điểm tối đa.
Document Outline

• TOAN_11_DE HSG CUM 23-24
• TOAN_11_DAP AN HSG CUM 23-24