Đề thi Olympic Toán 11 năm 2023 – 2024 liên cụm trường THPT – Hà Nội

Xin giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 11 đề thi Olympic dành cho học sinh môn Toán 11 năm học 2023 – 2024 liên cụm trường THPT, thành phố Hà Nội; kỳ thi được diễn ra vào ngày 09 tháng 03 năm 2024; đề thi có đáp án và hướng dẫn chấm điểm. Mời bạn đọc đón xem!

43 22 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi Toán 11

Môn: Toán 11

Thông tin:

5 trang 6 tháng trước

Tác giả:

Profile M. Hậu
SỞ GIÁO DỤC VÀ ĐÀO TẠO HÀ NỘI
LIÊN CỤM TRƯỜNG THPT
KỲ THI OLYMPIC DÀNH CHO HỌC SINH
LỚP 10, LỚP 11
NĂM HỌC 2023 – 2024
Môn thi: TOÁN LỚP 11
Ngày thi: 09/3/2024
Thời gian làm bài: 150 phút
Câu I ( 5 điểm) Cho phương trình
cos2 3sin 4 0x x m
với
m
là tham số thực.
a) Giải phương trình khi
0.m
b) Tìm tất cả giá trị của
m
để phương trình đã cho có nghiệm thuộc khoảng
;.
2



Câu II ( 4 điểm) Cho hàm số
2
khi 1
44
.
13
khi 1
1
ax b
x
x
fx
xx
x
x
a) Tính
b) Biết
3
1,
4
f
tìm tất cả các cặp số thực
,ab
để hàm số
fx
liên tục tại
1.x
Câu III ( 3 điểm) Gọi
S
là tập hợp các số tự nhiên có
6
chữ số sao cho trong mỗi số đó, các chữ số
1,2,3
đều xuất hiện
2
lần.
a) Tính số phần tử của tập hợp
.S
b) Chọn ngẫu nhiên một số thuộc
.S
Tính xác suất để số đó là số chẵn.
c) Chọn ngẫu nhiên một số thuộc
.S
Tính xác suất để số đó có các chữ số giống nhau không
đứng cạnh nhau.
Câu IV ( 5 điểm) Cho hình chóp
.S ABC
có đáy
ABC
là tam giác vuông tại
, 60 ,AB
.AB a
Đường
thẳng
SB
vuông góc với mặt phẳng
()ABC
và
.SB a
Gọi
,OE
lần lượt là trung điểm của hai đoạn
thẳng
BC
và
.AB
a) Gọi
là góc giữa hai đường thẳng
SA
và
.CE
Tính
cos .
b) Một mặt phẳng song song với hai đường thẳng
,,OA SB
cắt các cạnh
, , ,AB SA SC BC
của
hình chóp
.S ABC
lần lượt tại các điểm
, , , .M N P Q
Chứng minh tứ giác
MNPQ
là hình
thang.
c) Tìm giá trị lớn nhất của diện tích tứ giác
.MNPQ
Câu V ( 3 điểm) Cho dãy số
n
u
được xác định bởi
1
2
1
3
.
3 4, 1,2,3,...
n n n
u
u u u n
a) Chứng minh
2, 1,2,3,...
n
un
b) Chứng minh
n
u
là dãy số tăng.
c) Chứng minh
1 2 2024
1 1 1
... 1.
1 1 1u u u
-----------------HẾT-----------------
Cán bộ coi thi không giải thích gì thêm.
Họ tên thí sinh:…………………………………… Số báo danh:………………..
Họ tên và chữ kí của cán bộ coi thi số 1: Họ tên và chữ kí của cán bộ coi thi số 2:
ĐỀ CHÍNH THỨC
SỞ GIÁO DỤC VÀ ĐÀO TẠO HÀ NỘI
LIÊN CỤM TRƯỜNG THPT
KỲ THI OLYMPIC DÀNH CHO HỌC SINH
LỚP 10, LỚP 11
NĂM HỌC 2023 – 2024
Môn thi: TOÁN LỚP 11
Ngày thi: 09/3/2024
HƯỚNG DẪN CHẤM
Bài
Câu
Nội dung
Điểm
I
a)
Với
0m
, phương trình đã cho trở thành
cos2 3sin 4 0xx
2
2sin 3sin 5 0xx
1,0
sin 1
5
sin
2
x
xl

2.
2
x k k
1,0
b)
Ta có
2
2sin 3sin 5m x x
Đặt
sintx
, khi
;
2
x




thì
1;1t 
.
Xét hàm số
2
2 3 5y t t
trên
1;1t 
.
1,0
Ta có Bảng biến thiên
t
3
11
4

y
49
8
60
1,0
Suy ra phương trình đã cho có nghiệm thuộc khoảng
;
2



khi và chỉ khi
49
0
8
m
.
1,0
II
a)
Ta có
11
13
lim lim
1
xx
xx
fx
x


1,0
2
11
2 2 3
lim lim
4
13
1 1 3
xx
x x x
xx
x x x


1,0
b)
Hàm số
fx
liên tục tại
1x
khi và chỉ khi
11
3
lim lim 1
4
xx
f x f x f


1
3
lim .
4
x
fx

1,0
Do
2
khi 1
44
ax b
f x x
x

nên để tồn tại
1
lim
x
fx
thì
2
.1 0a b b a
.
Khi đó
2
1 1 1
1
lim lim lim .
4 4 4 2
x x x
ax
ax b a
fx
x
Suy ra
fx
liên tục tại
3
3
2
1
24
3
2
a
a
x
ba
b





1,0
III
a)
Số các số tự nhiên có 6 chữ số trong đó các chữ số 1,2,3 đều xuất hiện 2 lần là:
222
6 4 2
90CCC
(số).
1,0
b)
Số các số tự nhiên chẵn có 6 chữ số trong đó các chữ số 1,2,3 đều xuất hiện 2 lần là:
22
53
30CC
(số).
0,5
Vậy xác suất cần tính là
30 1
.
90 3
P 
0,5
c)
Gọi
i
A
là tập hợp các số tự nhiên thuộc
S
sao cho 2 chữ số
i
đứng cạnh nhau
1;2;3 .i
Ta có
22
53
30
i
A C C
2
42
1 2 3 3
12
6
ij
A A C P
A A A P
Do đó số số tự nhiên thuộc
S
có 2 chữ số giống nhau đứng cạnh nhau là:
1 2 3 1 2 2 3 1 3 1 2 3
60A A A A A A A A A A A A
0,5
Suy ra số số tự nhiên thuộc
S
có 2 chữ số giống nhau không đứng cạnh nhau là:
90 60 30.
Vậy xác suất cần tính là
30 1
.
90 3
P 
0,5
IV
a)
Gọi
I
là trung điểm
SB
, , .EI SA SA CE EI CE
∥
0,5
Tính được
13
;
2
a
CE
2 17
;
22
aa
IE IC
.
0,5
Từ đó tính được
26
cos
26
IEC 
.
Suy ra
26
cos
26
1,0
I
E
B
C
A
S
b)
Ta có:
.
SAB MN
SB SAB MN SB
SB

∥
∥
ABC MQ
OA ABC
OA
∥
.MQ OA
∥
0,5
.
SBC PQ
SB SBC PQ SB
SB

∥
∥
0,5
Do
MN PQ MNPQ
∥
là hình thang.
0,5
c)
MN SB
MN MQ MNPQ
SB MQ
∥
là hình thang vuông.
.
.
2
MNPQ
MQ MN PQ
S
0,5
Đặt
0.BM x x a
Ta có
Cos 2 .
cos
AB AB
B BC a
BC B
Do
O
là trung điểm của
BC
1
.
2
AO OB BC a
đều, mà
MQ AO BMQ
∥
đều
.MQ BM x
Xét
SAB
ta có
MN AM
MN a x
SB AB
.
Xét
SBC
ta có
22
22
PQ CQ PQ a x a x
PQ
SB CB a a

0,5
Vậy
2
2
2
3 4 3
1 3 4 3
2
2 12 12 2 3
MNPQ
ax
x a x
x a x
x a x a
S








.
Vậy diện tích lớn nhất là
2
3
a
S
.
0,5
V
a)
Ta chứng minh
*
2, .
n
un
Với
1n
ta có
1
3 2.u 
Vậy khẳng định đúng với
1.n
Giả sử khẳng định đúng với
,nk
tức là
2.
k
u
0,5
Khi đó
2
11
2 3 2 1 2 0 2.
k k k k k k
u u u u u u

Theo nguyên lý quy nạp thì
*
2, .
n
un
0,5
P
N
Q
O
S
B
A
C
M
b)
Ta có
2
2*
1
4 4 2 0, .
n n n n n
u u u u u n
0,5
*
1
,.
nn
u u n
Suy ra
n
u
là dãy số tăng.
0,5
c)
Ta có
1
2 1 2 0
n n n
u u u
*
1
1
1 1 1 1
,
2 1 2 2 1
1 1 1
1 2 2
n n n n n
n n n
n
u u u u u
u u u
0,5
Suy ra
1 2 2024
1 1 1
...
1 1 1
S
u u u
1 2 2 3 2024 2025
1 2025
1 1 1 1 1 1
...
2 2 2 2 2 2
11
1
22
u u u u u u
uu




0,5
| 1/5
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

SỞ GIÁO DỤC VÀ ĐÀO TẠO HÀ NỘI
KỲ THI OLYMPIC DÀNH CHO HỌC SINH
LIÊN CỤM TRƯỜNG THPT LỚP 10, LỚP 11
NĂM HỌC 2023 – 2024
Môn thi: TOÁN LỚP 11 ĐỀ CHÍNH THỨC Ngày thi: 09/3/2024
Thời gian làm bài: 150 phút
Câu I ( 5 điểm) Cho phương trình cos 2x 3sin x m  4  0 với m là tham số thực.
a) Giải phương trình khi m  0.   
b) Tìm tất cả giá trị của m để phương trình đã cho có nghiệm thuộc khoảng  ; .    2  2 ax b khi x  1  4x4
Câu II ( 4 điểm) Cho hàm số f x   .
x 1 x  3 khi x 1  x 1
a) Tính lim f x  . x 1  b) Biết f   3 1 
, tìm tất cả các cặp số thực a,b để hàm số f x liên tục tại x 1. 4
Câu III ( 3 điểm) Gọi S là tập hợp các số tự nhiên có 6 chữ số sao cho trong mỗi số đó, các chữ số
1, 2,3 đều xuất hiện 2 lần.
a) Tính số phần tử của tập hợp S.
b) Chọn ngẫu nhiên một số thuộc S. Tính xác suất để số đó là số chẵn.
c) Chọn ngẫu nhiên một số thuộc S. Tính xác suất để số đó có các chữ số giống nhau không đứng cạnh nhau.
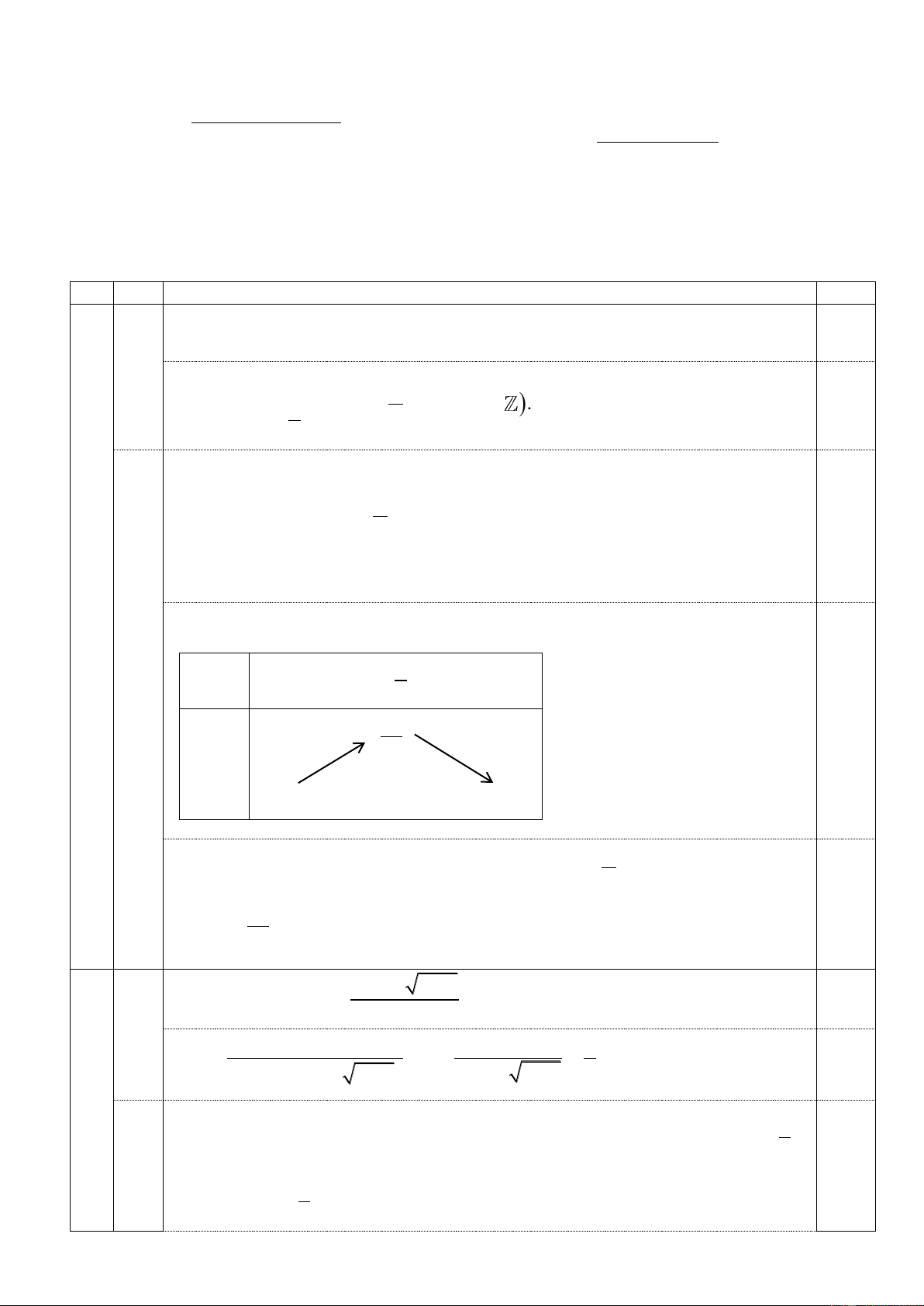
Câu IV ( 5 điểm) Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại , A B  60 ,  AB  . a Đường
thẳng SB vuông góc với mặt phẳng (ABC) và SB  .
a Gọi O, E lần lượt là trung điểm của hai đoạn thẳng BC và . AB
a) Gọi  là góc giữa hai đường thẳng SA và . CE Tính cos.
b) Một mặt phẳng song song với hai đường thẳng O , A S ,
B cắt các cạnh AB, S , A SC, BC của
hình chóp S.ABC lần lượt tại các điểm M , N, P, .
Q Chứng minh tứ giác MNPQ là hình thang.
c) Tìm giá trị lớn nhất của diện tích tứ giác MNP . Q u   3
Câu V ( 3 điểm) Cho dãy số u được xác định bởi 1 .  n  2 u
u 3u  4, n  1,2,3,...  n 1 n n
a) Chứng minh u  2, n  1,2,3,... n
b) Chứng minh u là dãy số tăng. n  1 1 1 c) Chứng minh  ... 1. u 1 u 1 u  1 1 2 2024
-----------------HẾT-----------------
Cán bộ coi thi không giải thích gì thêm.
Họ tên thí sinh:…………………………………… Số báo danh:………………..
Họ tên và chữ kí của cán bộ coi thi số 1:
Họ tên và chữ kí của cán bộ coi thi số 2:
SỞ GIÁO DỤC VÀ ĐÀO TẠO HÀ NỘI
KỲ THI OLYMPIC DÀNH CHO HỌC SINH
LIÊN CỤM TRƯỜNG THPT LỚP 10, LỚP 11
NĂM HỌC 2023 – 2024 Môn thi: TOÁN LỚP 11 Ngày thi: 09/3/2024 HƯỚNG DẪN CHẤM Bài Câu Nội dung Điểm I a)
Với m  0 , phương trình đã cho trở thành cos 2x  3sin x  4  0 1,0 2
 2sin x  3sin x  5  0 sin x 1 1,0    5
x   k2 k    .
sin x   l  2  2 b) Ta có 2 m  2
 sin x  3sin x  5 1,0   
Đặt t  sin x, khi x   ;   thì t  1  ;  1 .   2  Xét hàm số 2 y  2
t 3t  5 trên t  1  ;  1 . Ta có Bảng biến thiên t 3 1   1 1,0 4 y 49 8 6 0    1,0
Suy ra phương trình đã cho có nghiệm thuộc khoảng  ;   khi và chỉ khi  2  49 0  m  . 8 II a)
x 1 x  3 1,0 Ta có lim f   x lim x 1  x 1  x  1 2 x x  2 x  2 3 1,0  lim  lim    x 1  x  
1 x 1 x  3 x 1 
x 1 x  3 4 b) 1,0 3
Hàm số f x liên tục tại x 1 khi và chỉ khi lim f x  lim f x  f     1 x 1  x 1  4  f x    3 lim . x 1  4 1,0 ax b Do f x 2  khi x  1 lim f x thì 4x  nên để tồn tại    4 x 1  2 .
a 1  b  0  b  a . 2 ax b a x 1 a Khi đó lim f     x   lim lim .   x 1  x 1  x 1 4x  4  4 2  3 a 3 a     2
Suy ra f x liên tục tại x  1   2 4   3 b   a b     2 III a)
Số các số tự nhiên có 6 chữ số trong đó các chữ số 1,2,3 đều xuất hiện 2 lần là: 1,0 2 2 2 C C C  90 (số). 6 4 2 b)
Số các số tự nhiên chẵn có 6 chữ số trong đó các chữ số 1,2,3 đều xuất hiện 2 lần là: 0,5 2 2 C C  30(số). 5 3 30 1 0,5
Vậy xác suất cần tính là P   . 90 3 c)
Gọi A là tập hợp các số tự nhiên thuộc S sao cho 2 chữ số i đứng cạnh nhau 0,5 ii 1;2;  3 . Ta có 2 2
A C C  30 i 5 3 2
A A C P  12 i j 4 2
A A A P  6 1 2 3 3
Do đó số số tự nhiên thuộc S có 2 chữ số giống nhau đứng cạnh nhau là:
A A A A A A A A A A A A  60 1 2 3 1 2 2 3 1 3 1 2 3
Suy ra số số tự nhiên thuộc S có 2 chữ số giống nhau không đứng cạnh nhau là: 0,5 90  60  30. 30 1
Vậy xác suất cần tính là P   . 90 3 IV a) S
Gọi I là trung điểm SB 0,5
EI∥ SA  S ,
A CE  EI,CE. I Tính được 0,5 a 13 a a CE  2 17 ; IE  ; IC  . 2 2 2 B C E 26 1,0
Từ đó tính được cos IEC   . 26 A 26 Suy ra cos  26 b) S
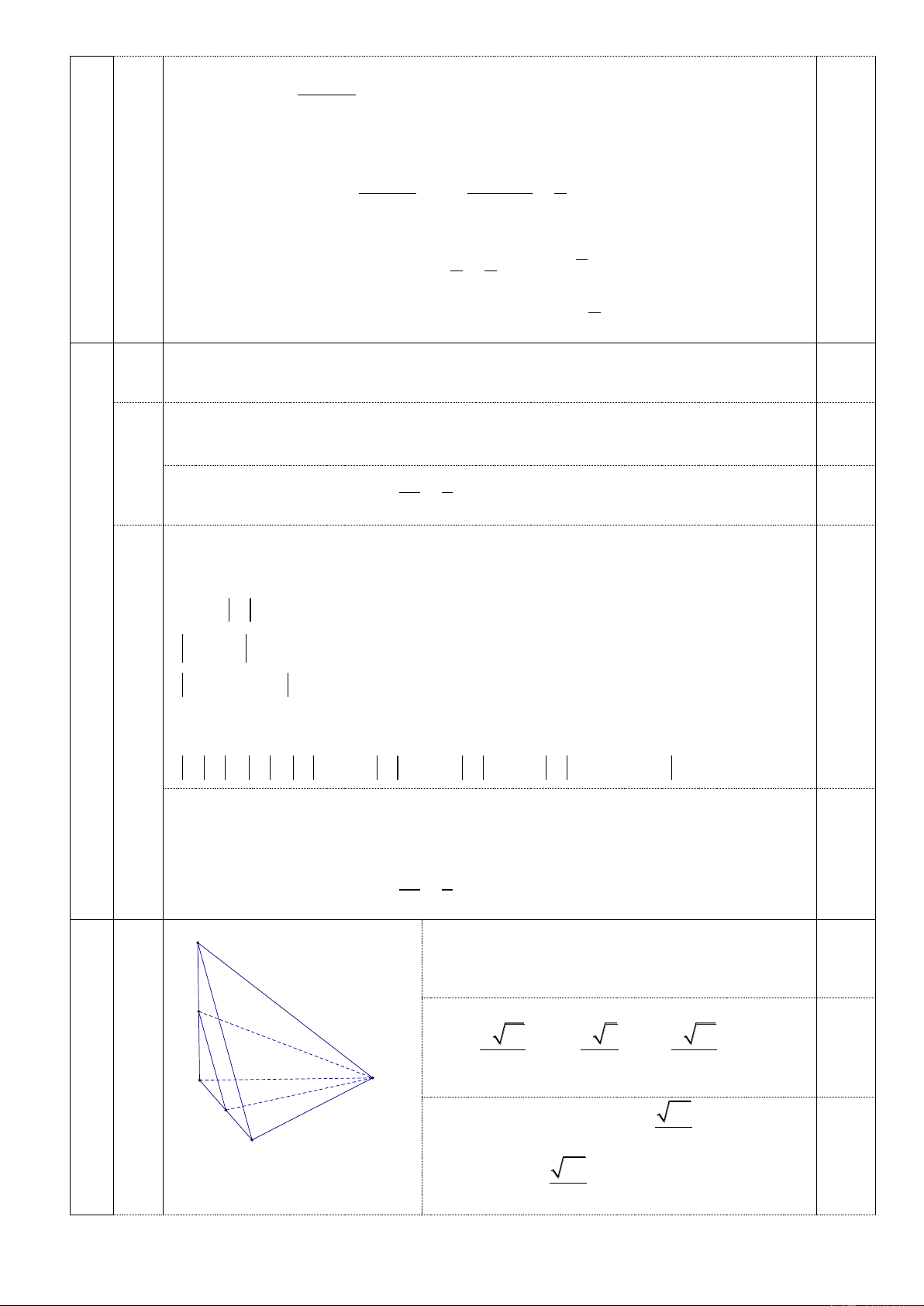
  SAB  MN 0,5 P
Ta có: SB  SAB  MN∥ S . B N SB  ∥   Q O
ABC  MQ B CO
A   ABC  MQ∥ O . A MOA  ∥  A
  SBC  PQ 0,5 
SB  SBC  PQ∥ S . BSB  ∥  
Do MN ∥ PQ MNPQ là hình thang. 0,5 c) MN ∥ SB  0,5
  MN MQ MNPQ là hình thang vuông. SB MQM .
Q MN PQS  . MNPQ 2
Đặt BM x0  x a. 0,5 AB AB Ta có Cos B   BC   2 . a BC cos B 1
Do O là trung điểm của BC AO OB BC  . a 2  BAO
đều, mà MQ∥ AO B
MQ đều  MQ BM  . x MN AM Xét SAB ta có 
MN a x. SB AB PQ CQ PQ 2a x 2a x Xét SBC ta có     PQ SB CB a 2a 2   2a x  0,5
xa x    2 3x  4a 3x 2 2
1  3x  4a  3x a Vậy S       . MNPQ 2 12 12  2  3 2 a
Vậy diện tích lớn nhất là S  . 3 V a) Ta chứng minh * u  2, n   . 0,5 n
Với n 1 ta có u  3  2. Vậy khẳng định đúng với n 1. 1
Giả sử khẳng định đúng với n k, tức là u  2. k Khi đó 2 u
 2  u 3u  2  u 1 u  2  0  u  2. 0,5 k 1  k k
k  k k 1 
Theo nguyên lý quy nạp thì * u  2, n   . n b) 0,5 Ta có u
u u  4u  4  u   n    n n n  2 n 2 2 * 0, . n 1 *
u u , n   . 0,5 n 1  n
Suy ra u là dãy số tăng. n  c) Ta có u
 2  u 1 u  2  0 0,5 n 1 
n  n  1 1 1 1 *     , n   u  2 u 1 u  2 u  2 u 1 n 1 
n  n n n 1 1 1    u 1 u  2 u  2 n n n 1  1 1 1 0,5 Suy ra S   ... u 1 u 1 u 1 1 2 2024  1 1   1 1   1 1          ...    u  2 u  2 u  2 u  2 u  2 u  2       1 2 2 3 2024 2025 1 1   1 u  2 u  2 1 2025