Đề thi Olympic Toán 8 năm 2023 – 2024 phòng GD&ĐT Thanh Oai – Hà Nội
Xin giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 8 đề thi Olympic môn Toán 8 năm học 2023 – 2024 phòng Giáo dục và Đào tạo huyện Thanh Oai, thành phố Hà Nội; kỳ thi được diễn ra vào ngày 02 tháng 04 năm 2024; đề thi có đáp án và hướng dẫn chấm điểm.
Preview text:
PHÒNG GDĐT THANH OAI
KỲ THI OLYMPIC LỚP 6, 7, 8 Năm học 2023 - 2024 ĐỀ CHÍNH THỨC
Môn: Toán – Lớp: 8
Ngày thi: 02 tháng 4 năm 2024
Thời gian làm bài: 120 phút
(Đề thi gồm 01 trang) Câu 1. (5 điểm) 2 2 x x x 1 1 2 x
1. Cho biểu thức A : 2 2 x 2x 1 x x 1 x x a) Rút gọn biểu thức A
b) Tìm x để A 0
c) Tìm giá trị nhỏ nhất của A khi x > 1 1 1 1 2 1
2. Cho các số x, y, z khác 0 thỏa mãn đồng thời 2 và 4 . Tính x y z 2 xy z
giá trị của biểu thức 2024
P (x 2 y z) Câu 2. (4 điểm)
1. Tìm đa thức f (x) , biết f (x) chia cho x 3 dư 5, f (x) chia cho x 5 dư 7, f (x)
chia cho x 3 x 5được thương là 2x và còn dư.
2. Tìm x, y nguyên thoả mãn 3xy – 1 = x2 + 2y Câu 3. (4 điểm)
1. Gieo hai con xúc xắc cân đối, đồng chất và giống hệt nhau. Tính xác suất để tổng
số chấm xuất hiện trên hai con xúc xắc này trong cùng một lần gieo là số lớn hơn 8
2. Tìm tất cả số nguyên tố p, q sao cho A= 2 2
p 3 pq q là bình phương của một số tự nhiên. Câu 4. (6 điểm)
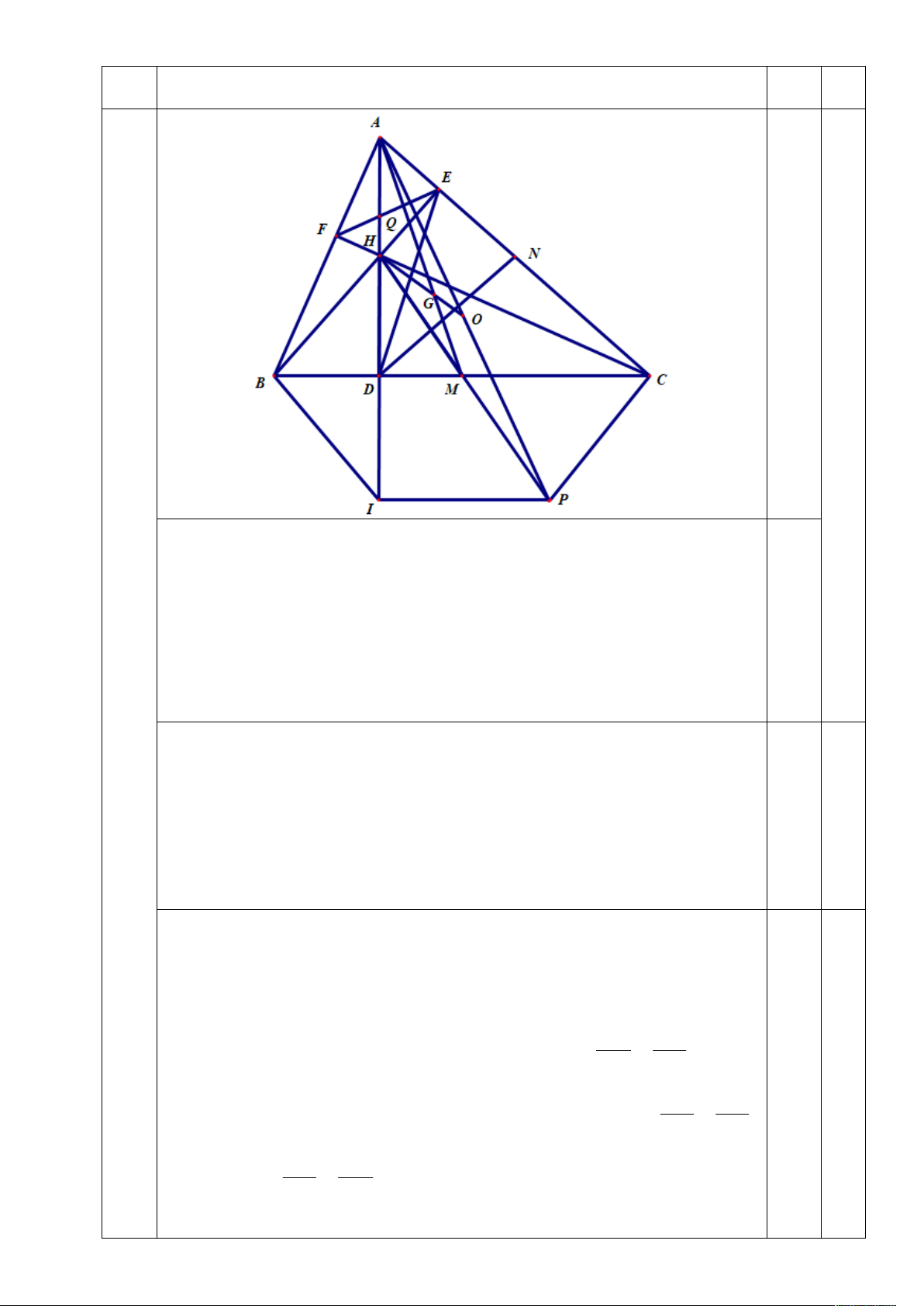
Cho tam giác ABC nhọn có các đường cao AD, BE , CF cắt nhau tại H. Gọi M,
N lần lượt là trung điểm của BC, AC; gọi I, P lần lượt là điểm đối xứng của H qua D và M.
a) Chứng minh rằng tứ giác BIPC là hình thang cân.
b) Trên đoạn thẳng AP lấy điểm O sao cho OP = OC. Gọi G là giao điểm của
OH và AM. Chứng minh ba điểm B, G, N thẳng hàng.
c) Gọi Q là giao điểm của AH và EF. Chứng minh rằng 2 A . Q D .
B DC AD .HQ Câu 5. (1 điểm)
Tìm các số tự nhiên x, y và số nguyên tố p sao cho x 4 p y 4 - Hết –
Cán bộ coi thi không giải thích gì thêm. Học sinh không sử dụng máy tính.
Họ và tên: ……………………………………………………. Số báo danh: …………
Học sinh Trường THCS: ………………………………………………………………
HƯỚNG DẪN CHẤM MÔN TOÁN 8 Câu Nội dung Điểm 1 a)
Với x 0; x 1. ta có: 3 2 2 2 2 x x x 1 1 2 x x x x 1 1 2 x A : : 2 2 x 2x 1 x x 1 x
x x 2 1 x x 1 x(x 1) 2 2 2 2 2 x x
(x 1)(x 1) x 2 x x x
x 1 x 2 x 1 : : x 2 1 x(x 1) x 2 1 x(x 1) 2 2 x x x 1
x(x 1) x(x 1) x : . x 2 1 x(x 1) x 2 1 x 1 x 1 b)
Lập luận được A 0 khi x 1, x 0; x 1 . 1 2 x c)
Với x 0; x 1.
A đạt giá trị nhỏ nhất khi đạt GTNN. x 1 2 2 2 x
(x 4x 4) (4x 4) (x 2) Mà 4. 0,5 x 1 x 1 x 1 Có 2
(x 2) 0 x và x > 1 suy ra x -1 > 0. 2 2 (x 2) (x 2) 0
4 4 A 4. . 0,5 x 1 x 1
Dấu “=” xảy ra x 2 0 x 2 (TMĐK). 0,5 2 0,5 0,5 Thay vào ta được 2024 1 1 1 0,5 P 2. 1 2 2 2 2 1.
f x x 3 A x 5
f (x) (x 5)B(x) 7 0,5
f (x) (x 3)(x 5).2x mx n Từ đó suy ra : f 3 5 3
m n 5 0,5 2 f 5 7 5
m n 7 0,5 Tìm ra m 1 ;n 2 Thay vào ta có đa thức 0,5 f x 3 2
2x 16x 29x 2
2. Theo đề ta có 3xy – 2y = x2 + 1 y(3x – 2) = x2 + 1 0,5
Do x, y nguyên nên suy ra x2 + 1 chia hết cho 3x – 2
Do đó 9.(x2 + 1) chia hết cho 3x – 2 do đó (3x+2).(3x - 2) + 13 0,5 chia hết cho 3x – 2
Suy ra 13 chia hết cho 3x – 2, mà x nguyên nên 2 3x – 2 1 3;1; 1; 1 3 3x 1 1;1; 3;1 5 x 1; 5 0,5
Thay x lần lượt vào (1) ta được y =2
Vậy các cặp số (x, y) là (1;2), (5;2) 0,5 3
1. Mỗi con xúc sắc có 6 mặt nên khi gieo 2 con xúc sắc thì có 6.6 = 0,5 36 khả năng xảy ra.
Gọi A là biến cố “Tổng số chấm trong 2 lần gieo là số lớn hơn 8”.
Các khả năng để biến cố A xảy ra là: (3,6); (4,5); (4,6);(5,4); (5,5); 1 2
(5,6); (6,3); (6,4); (6,5); (6,6): có 10 khả năng để biến cố A xảy ra.
Xác suất để tổng số chấm trong hai lần gieo là số lớn hơn 8 là: 10 5 0,5 P(A)= 36 18
2. Tìm tất cả số nguyên tố p, q sao cho A= 2 2
p 3 pq q là bình
phương của một số tự nhiên. Nếu .
p q không chia hết cho 3 thì 2 2
p , q chia 3 dư 1 nên A chia 3 0,25
dư 2, do đó A không là số chính phương 2 Suy ra .
p q chia hết cho 3, mà p,q nguyên tố, không mất tính TQ, 0,25 giả sử p = 3 2 2 0,25
A 9 9q q x (x N ) hay: 2 2
(2q 9) (2x) 45 0,25
(2q 9 2x)(2q 9 2x) 45 . Do x, q, p là các số tự nhiên nên: 0,25 2q+9-2x 1 3 5 2q+9+2x 45 15 9 0,5 q 7 loại loại p 3
Vậy p,q{(3;7);(7;3)} 0,25 4 0,25 2
a) Chứng minh BC//IP (đường trung bình trong tam giác HIK) 0,5
Chứng minh tứ giác BHCP là hình bình hành (2 đường chéo cắt 0,5
nhau tại trung điểm mỗi đường) nên CH = BP 0,5
Chứng minh tam giác HCI cân tại I nên CH= IC, do đó BP = CI.
Tứ giác BIPC là hình thang có 2 đường chéo vuông góc nên là hình 0,25 thang cân (đpcm)
b) Chứng minh PC vuông góc với AC, chứng minh O là trung điểm 0,5 2 của AP
Xét tam giác AHP có G là trọng tâm, nên AG = 2GM 0,5
Tam giác ABC có AM là đường trung tuyến mà AG = 2GM nên G 0,5
là trọng tâm tam giác ABC 0,5 Suy ra B,G,N thẳng hàng
c) Chứng minh được DH.DA=DB.DC (1) 0,5 2 Nên A . Q D . B DC A . Q DH.AD
Ta cần chứng minh: A . Q HD A . D HQ HQ QE
C/m được: EH là phân giác trong của ∆QED nên 0,5 HD DE AQ QE
Mà EH ⊥EA nên EA là phân giác ngoài của ∆QED nên AD DE 0,5 AQ HQ Từ đó ta có: do đó: A . Q HD A .
D HQ (2). Từ (1) và (2) 0,5 AD HD ta có đpcm 5 x 4 2 2
p y 4 ( y 2 y 2)( y 2 y 2) 1 2
y 2 y 2 a p
Vì p là số nguyên tố nên:
;(0 a b ;
x a,b N ) 0,25 2
y 2 y 2 b p
- Với a = 0 tìm được y =1; p = 5, x= 1 0,25 2
y 2 y 2 p
- Với b a 1 4 y p 2
y 2 y 2 p
+ Nếu 4 chia hết cho p thì p = 2 0,25
+ Nếu y chia hết cho p thì suy ra 2 chia hết cho p nên p =2
Thay p =2 vào giả thiết suy ra y chẵn Nếu x ≥ 3 thì x 4 2 8 , y 8
mà 4 không chia hết cho 8 nên vô lý suy ra
x ≤ 2 mà 2x 4 x 2 nên x = 2, tìm được y = 0 0,25
Vậy có 2 bộ số (x,y,p) là (1,1,5) và (2,0,2)
(Học sinh có cách giải khác, đúng vẫn cho điểm tối đa).