Đề thi Olympic Toán 9 năm 2023 – 2024 trường chuyên Lam Sơn – Thanh Hóa

SỞ GD & ĐT THANH HÓA
KỲ THI OLYMPIC CÁC TRƯỜNG THCS
TRƯỜNG THPT CHUYÊN LAM SƠN
HƯỚNG ĐẾN KỲ THI HSG LỚP 9 NĂM HỌC 2023 - 2024 Môn thi: TOÁN ĐỀ THI CHÍNH THỨC Ngày thi: 05/11/2023
(Đề thi có 01 trang)
Thời gian làm bài: 150 phút (không kể thời gian phát đề) Câu I. (4,0 điểm) 1. Rút gọn 3 3
A  5 2  7  5 2  7 .
2. Cho các số dương , a b thỏa mãn 2 2 a  b 
2024  a  2024  b .
Tính giá trị của biểu thức 2 2
P  a  b . Câu II. (4,0 điểm)
1. Giả sử đa thức P  x 5 3 2
 x  6x  x  9x  3 có 5 nghiệm phân biệt x , x , x , x , x . Xét đa thức 1 2 3 4 5 Q  x 2
 x  2 . Tính F  Q  x Q x Q x Q x Q x . 1 
 2   3   4   5  2 2 
 y  6x  xy  0
2. Giải hệ phương trình  . 2 2 2 1
  5x  x y  0 
Câu III. (4,0 điểm)
1. Cho A là số nguyên dương và phương trình nghiệm nguyên ax  by  c với các hệ số nguyên , a , b c thỏa mãn ,
a b nguyên tố cùng nhau, a  b  A . Chứng minh số nghiệm nguyên  x, y 3A
thỏa mãn điều kiện x  , A
y  A của phương trình đã cho không vượt quá . b
2. Tìm số nguyên dương n nhỏ nhất sao cho  n   2023 3 1 2 . Câu IV. (6,0 điểm)
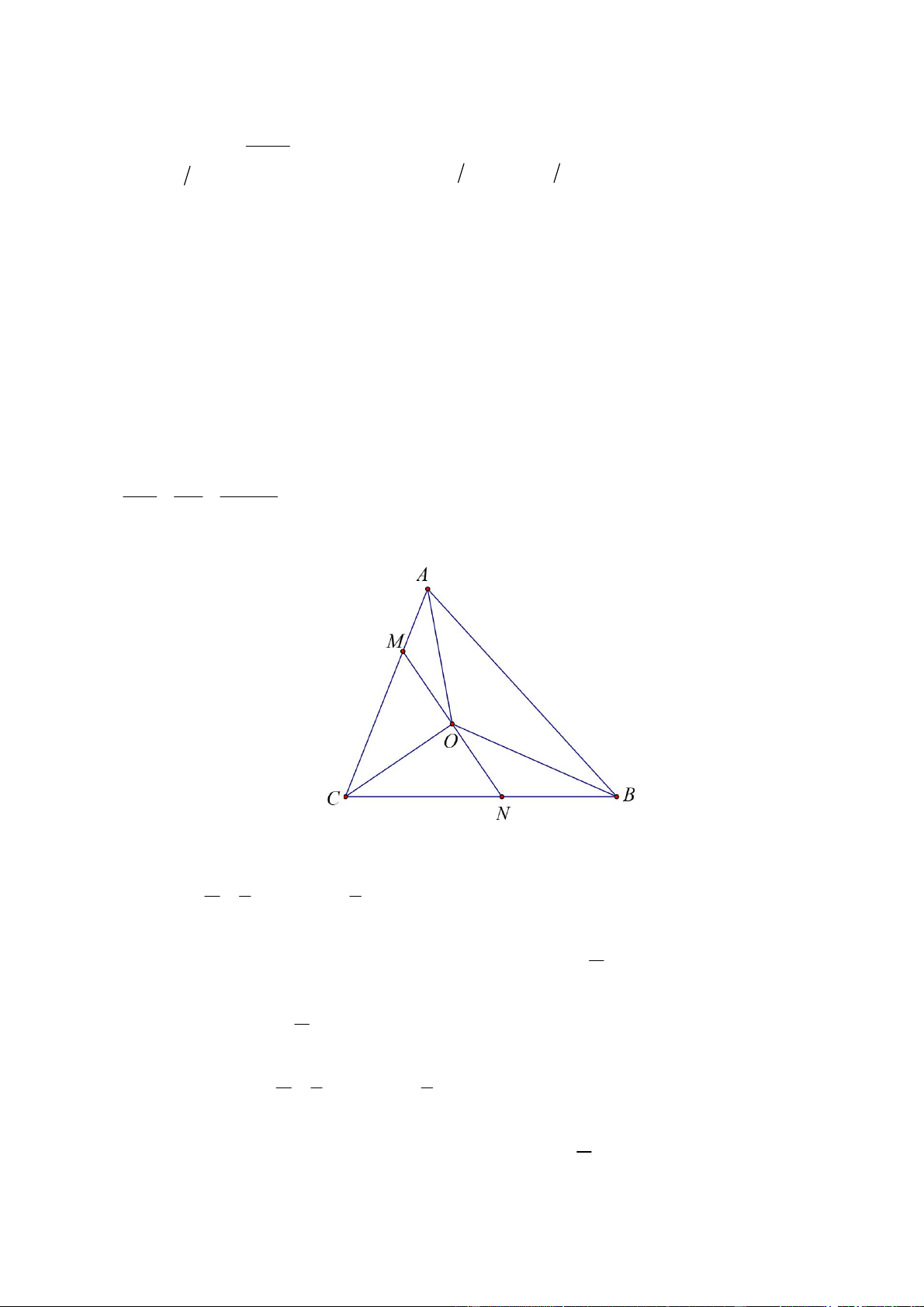
1. Gọi O là giao điểm ba đường phân giác trong của tam giác ABC . Đường thẳng qua O và
vuông góc với CO cắt CA tại M , cắt CB tại N . Chứng minh rằng:
a) Tam giác AOM đồng dạng với tam giác OBN . 2 AM BN OC b)    1. AC BC AC.BC
2. Cạnh BC của tam giác ABC tiếp xúc với đường tròn nội tiếp O của tam giác đó tại điểm D .
Chứng minh rằng tâm O của đường tròn này nằm trên đường thẳng đi qua trung điểm của các đoạn
thẳng BC và AD .
Câu V. (2,0 điểm) Tìm tất cả các tập hợp A   gồm hữu hạn các số thực sao cho x  A thì 2
x 1 x  A và 2
x 1 x  A .
--------------- Hết ---------------
Họ và tên thí sinh:................................................................Số báo danh:...........................................
Chữ ký của giám thị 1:.......................................... Chữ ký của giám thị 2:..........................................
SỞ GD & ĐT THANH HÓA
KỲ THI OLYMPIC CÁC TRƯỜNG THCS
TRƯỜNG THPT CHUYÊN LAM SƠN
HƯỚNG ĐẾN KỲ THI HSG LỚP 9 NĂM HỌC 2023 - 2024 Môn thi: TOÁN
ĐÁP ÁN ĐỀ THI CHÍNH THỨC Ngày thi: 05/11/2023
(Đáp án có 06 trang)
Thời gian làm bài: 150 phút (không kể thời gian phát đề) Câu I. (4,0 điểm)
1. (2,0 điểm) Rút gọn 3 3
A  5 2  7  5 2  7 . Giải. Ta có 3 3 3 3
A  5 2  7  5 2  7 
2 2  3.2  3 2 1  2 2  3.2  3 2 1 (1,0 điểm)    3    3 3 3 2 1 2 1  2  1 2 1  2 . (1,0 điểm)
2. (2,0 điểm) Cho các số dương , a b thỏa mãn 2 2 a  b 
2024  a  2024  b . Tính giá trị của biểu thức 2 2
P  a  b . Giải. Từ 2 2 2 2 a  b 
2024  a  2024  b  a  2024  b 
2024  a  b (0,5 điểm) 2 a   2 2024  b   2 2024  a  2 2 2 2 2  b a  b  2024 2024  a  b     (0,5 điểm) 2 2 2 2 a  2024  b 2024  a  b a  2024  b 2024  a  b 2 2 2 2 a  b  2024 a  b  2024      0   1 1 2 2
a  b  2024    0 2 2 2 2 a  2024  b 2024  a  b
 a  2024  b
2024  a  b  (0,5 điểm) 1 1 Vì   0 nên ta có 2 2 2 2
a  b  2024  0  a  b  2024 . 2 2 a  2024  b 2024  a  b Vậy P  2024 . (0,5 điểm) Câu II. (4,0 điểm)
1. (2,0 điểm) Giả sử đa thức P  x 5 3 2
 x  6x  x  9x  3 có 5 nghiệm phân biệt x , x , x , x , x . Xét 1 2 3 4 5
đa thức Q  x 2
 x  2 . Tính F  Q  x Q x Q x Q x Q x . 1 
 2   3   4   5 
Giải. Vì đa thức P  x 5 3 2
 x  6x  x  9x  3 có 5 nghiệm phân biệt x , x , x , x , x nên đa thức 1 2 3 4 5
P  x có thể viết dưới dạng P  x   x  x x  x x  x x  x x  x . (0,5 điểm) 1   2   3   4   5  Khi đó:
F  Q  x Q  x Q  x Q  x Q  x    2 x  2 2 x  2 2 x  2 2 x  2 2 x  2 (0,5 điểm) 1 2 3 4 5 1 2 3 4 5    2  x 2  x 2  x 2  x 2  x  2  x  2  x  2  x  2  x  2  x 1   2   3   4   5   1   2   3   4   5 
 P  2  P  2  (0,5 điểm) 1
 5  3  2     5  3  2 2 6 2 2 9 2 3 . 2 6 2 2 9  2  3                        1   2  1   2   1  . Vậy F  1  . (0,5 điểm) 2 2 
 y  6x  xy  0
2. (2,0 điểm) Giải hệ phương trình  . 2 2 2 1
  5x  x y  0  2 2 
 y  xy  6x
Giải. Viết lại hệ 
. Ta thấy x  0 không thỏa mãn. 2 2 2 1   x y  5  x  1 1 2 y  y  6  2  x x
Xét x  0 , hệ tương đương với  . (0,5 điểm) 1 2   y  5 2   x 2 2 1     
yz  y  z z y zy   6 6  Đặt  z ta có hệ    x 2 2 z  y  5  
 y  z 2  2 yz  5 
S  y  z SP  6 Đặt  ta có hệ  (0,5 điểm) P  2  yz S  2P  5  2  S  5 2 SP  6 S.  6
S  5S 12  0   S  3   2
S  3S  4  0   2   S  3 2 2    S      2 5 S     2 5 S  5 P  S  5 P     P  P  2   2 P   2  2   2 (0,5 điểm)  y  2  y  2   x  1 3    y  z z  1  Từ đó ta có  
dẫn đến  y 1 . 2    yz  y  1    1  z  2  x    2  1 
Vậy hệ đã cho có hai nghiệm  ;
x y  là 1; 2 và ;1   . (0,5 điểm)  2 
Câu III. (4,0 điểm)
1. (2,0 điểm) Cho A là số nguyên dương và phương trình nghiệm nguyên ax  by  c với các hệ số nguyên , a , b c thỏa mãn ,
a b nguyên tố cùng nhau, a  b  A . Chứng minh số nghiệm nguyên 3A
 x, y thỏa mãn điều kiện x  , A
y  A của phương trình đã cho không vượt quá . b Giải.
+) Trường hợp 1: a  0 2
Vì a,b  1 suy ra b  1 như vậy phương trình đã cho có dạng y  c hoặc y  c . Trong các
phương trình này số nghiệm nguyên  x, y của phương trình thỏa mãn điều kiện x  , A y  A
không vượt quá số điểm nguyên trên đoạn  ;
A A tức là số nghiệm nguyên đó nhỏ hơn hoặc bằng 3A
2A 1  3A  . b
+) Trường hợp 2: b  0 3A
Tương tự như Trường hợp 1 ta cũng có được số nghiệm nguyên đó nhỏ hơn hoặc bằng . b (0,5 điểm)
+) Trường hợp 3: a  0, b  0
Ta thấy rằng nếu  x, y và  x ', y ' là 2 nghiệm khác nhau của phương trình ax  by  c . Ta có
ax  by  c 
 a  x  x '  b y ' y . Vì a,b  1  x  x 'b  x  x '  b (0,5 điểm) ax ' by '   c
Giả sử  x , y , x , y , ..., x , y là tất cả các nghiệm nguyên khác nhau của phương trình thỏa 1 1   2 2   n n  mãn x  A
y  A i  n  * , , 1, n   i i 
Vì nếu x  x  y  y i j  n  * , 1,
n    nên không mất tính tổng quát, giả sử x  x  ... x . i j i j 1 2 n
x  x  b 2 1 
x  x  b Khi đó ta có 3 2 
 x  x  n 1 b (1) (0,5 điểm) n 1   ...  x  x   b n n 1  Mặt khác x   ;
A A , x   ;
A A  x  x  2 A (2) 1   n   n 1
Từ (1) và (2) suy ra 2A  n  
1 b  2 A  b  n b 3A
Vì b  A  3A  n b  n  (ĐPCM). (0,5 điểm) b
2. (2,0 điểm) Tìm số nguyên dương n nhỏ nhất sao cho  n   2023 3 1 2 Giải. Đặt  2k n
.l với k,l   và l là số lẻ, ta có l l l k k k k k n A           (0,5 điểm) 
 1   2   1 2 2 2 2 2   3 1 3 1 3 1 3 3 ... 3 1   l 1  l 2 1  k k k  k
Vì l là số lẻ nên  suy ra 2023 2 2023 A2  B  3 12  2    2     2 3 3 ... 3  1 2    3 2 k 1  k 1  k 1  k 1  k2 1 1
Ta có B   2     2   2     2   2    2   2 3 1 3 1 3 1 3 1 3 1 ... 3 1 3   1 (0,5 điểm) 2i 3  k 1  k 2   12 B B 1  2 .8  2 Do 2 
i  1, k 1 và 3 1  8 nên    . (0,5 điểm) 2i k k 3 3   1 4 B  B    2 .8   2 
Dẫn đến khi phân tích ra thừa số nguyên tố thì B có đúng k  2 thừa số 2. Suy ra 2023 B2
 k  2  2023  k  2021. Kiểm tra 2021 n  2 thấy thỏa mãn.
Như vậy số nguyên dương n nhỏ nhất là 2021 2 . (0,5 điểm) Câu IV. (6,0 điểm)
1. (4,0 điểm) Gọi O là giao điểm ba đường phân giác trong của tam giác ABC . Đường thẳng qua O
và vuông góc với CO cắt CA tại M , cắt CB tại N . Chứng minh rằng:
a) Tam giác AOM đồng dạng với tam giác OBN . 2 AM BN OC b)    1 AC BC AC.BC
Giải. a) (2,0 điểm) Ta có:   C 1 1 0 0  OMC  90   180 C   
A B (1) (0,5 điểm) 2 2 2      A 
mà OMC  MAO  MOA (góc ngoài tam giác OMA )  OMC   MOA 2 2   B
Từ (1); (2) suy ra MOA 
suy ra tam giác AOM đồng dạng với tam giác ABO (3). (0,5 điểm) 2  C 1 1 Tương tự  0 0  ONC  90   180 C   
A B (4) 2 2 2      B 
mà ONC  NBO  NOB (góc ngoài tam giác ONB )  ONC   NOB 5 (0,5 điểm) 2 4   A
Từ (4); (5) suy ra NOB 
suy ra tam giác OBN đồng dạng với tam giác ABO (6). 2
Từ (3) và (6) suy ra tam giác AOM đồng dạng với tam giác OBN . (0,5 điểm)
b) (2,0 điểm) Theo câu a) thì tam giác AOM đồng dạng với tam giác OBN suy ra AM OM 
 AM .BN  OM .ON (0,5 điểm) ON BN
Theo giả thiết ta có tam giác CMN cân tại C 2
 OM  ON  AM .BN  OM (0,5 điểm) mà 2 2 2
OM  CM  CO nên 2 2 2
AM .BN  CM  CO  CM .CN  CO .
Hay AM BN   AC  AM  CB  AM  2 . . BN  CO (0,5 điểm) 2 AM BN OC 2
 AC.BC  AM .CB  AC.BN  CO     1 (ĐPCM) (0,5 điểm) AC BC AC.BC
2. (2,0 điểm) Cạnh BC của tam giác ABC tiếp xúc với đường tròn nội tiếp O của tam giác đó
tại điểm D . Chứng minh rằng tâm O của đường tròn này nằm trên đường thẳng đi qua trung điểm
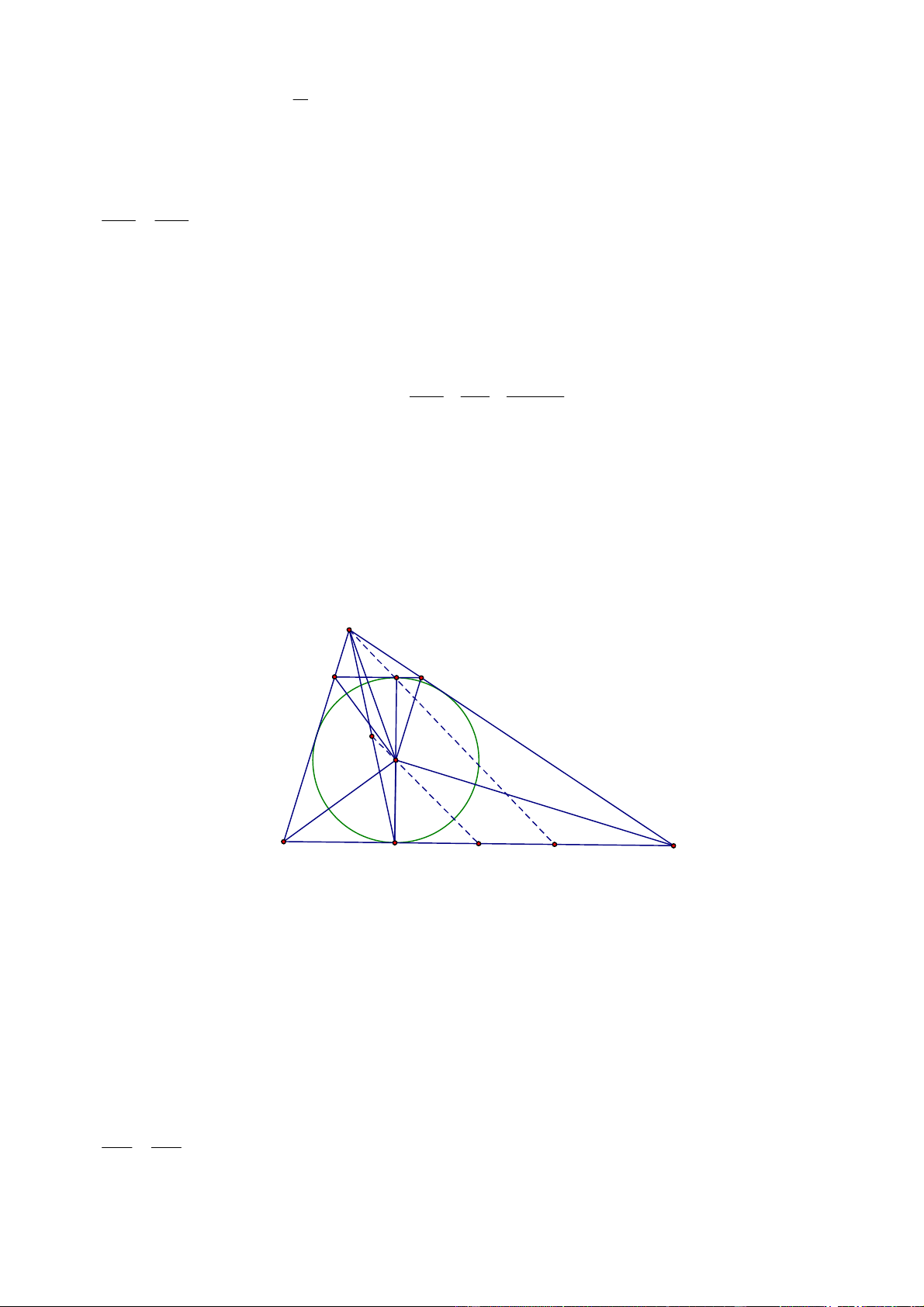
của các đoạn thẳng BC và AD . Giải. A E F I M O B D C N J
Gọi N là trung diểm BC , M là trung diểm AD , ta sẽ chứng minh M , , O N thẳng hàng.
Trên đoạn BC lấy điểm J sao cho BD  JC mà N là trung điểm của BC ⇒ ND  NJ
Kẻ đường kính DI của O , qua I vẽ tiếp tuyến cắt A ;
B AC lần lượt tại E và F .  
Ta có: EF  BC (vì cùng vuông góc DI ) suy ra IFC  FCD  180 (0,5 điểm)   
mà OF và OC là phân giác của góc IFC, FCD nên 0 FOC  90 .
Do đó tam giác IFO đồng dạng với tam giác DOC suy ra IF IO 2 
 IF.DC  R (1) ( R là bán kính đường tròn tâm O ) (0,5 điểm) DO DC 5
Chứng minh tương tự tam giác EOB vuông tại O suy ra tam giác EOI đồng dạng với tam giác OBD EI OI suy ra 2 
 IE.BD  R (2) OD BD IF IE IF IE
Từ (1) và (2) suy ra IF.DC  IE.BD     (0,5 điểm) BD DC JC BJ
Mà EF  BC suy ra E ;
B IJ ;CF đồng quy hay ,
A I , J thẳng hàng.
Trong tam giác DAJ có M ; ;
O N lần lượt là trung điểm của A ;
D DI; JD nên M , , O N thẳng hàng (ĐPCM). (0,5 điểm)
Câu V. (2,0 điểm) Tìm tất cả các tập hợp A   gồm hữu hạn các số thực sao cho x  A thì 2
x 1 x  A và 2
x 1 x  A .
Giải. Đặt f  x 2
 x  x  g  x 2 1;
 x  x 1
Do A   và hữu hạn nên gọi x , x lần lượt là phần tử lớn nhất và phần tử nhỏ nhất của A . 1 2   f  x  2  x 1    x  0 1 1
Vì f  x   ; A g  x  1  A      x  1  . 1 1 g  x  1 2   x x 1  0 1 1  1 Tương tự x  1  . (0,5 điểm) 2 Xét các trường hợp:
Nếu A có 1 phần tử thì A    1 ; A   
1 thử lại thấy thỏa mãn.
Nếu A có 2 phần tử thì A    1 ; A   
1 thử lại thấy thỏa mãn. (0,5 điểm)
Nếu A có hơn 2 phần tử thì 1   ; A 1 A (do 1
 , 1 lần lượt là phần tử nhỏ nhất và phần tử lớn nhất
của A ). Gọi x  ; A x  1   1   x  1 0 0 0 Nếu 2
0  x  1  1 x  x  1 vô lí; 0 0 0 Nếu 2 1   x  0  1   x  x  1  vô lí (0,5 điểm) 0 0 0
Suy ra x  0 và A  1;0; 
1 thử lại thấy thỏa mãn. 0
Vậy các tập hợp A thỏa mãn đề bài là A    1 ; A    1 ; A   1  ; 
1 ; A  1;0;  1 . (0,5 điểm)
--------------- Hết --------------- 6