Đề thi thử giữa kì 2 Toán 12 năm 2023 – 2024 trường THPT Tân Châu – An Giang

SỞ GD – ĐT AN GIANG
ĐỀ IỂ TRA T Ử GIỮA KÌ II
TRƯỜNG THPT TÂN CHÂU
MÔN TOÁN – KHỐI 12
Thời gian làm bài: 60 phút (không kể thời gian giao đề)
(Đề gồm có 5 trang) ã đề: 688
Họ và tên:………………………………. Lớp:…………….
Câu 1. Tìm nguyên hàm của hàm số   ln x f x  . x 1 A. f  x 2
dx  ln x  C . B. f  x 2 dx  ln x  C . 2 C. f
 xdx  ln xC D.   d x f x
x  e  C
Câu 2. Nguyên hàm của hàm số là A. . B. . C. . D. .
Câu 3. Nguyên hàm của hàm số là A. B. C. D. 3 3 Câu 4. Biết
f  x dx  2  
. Tính 5 f  x dx  . 1 1 2 A.  . B. 5 . C. 10 . D. 10  . 5 ln x e Câu 5. Để tính 
dx theo phương pháp đổi biến số, ta đặt: x 1
A. t  ln x B. ln  x t e
C. t  x D. t  x Câu 6. Tích phân bằng A. . B. . C. . D. .
Câu 7. Trong mặt phẳng Oxy , cho v  2; 
1 . Tìm ảnh A của điểm A 1
 ;2 qua phép tịnh tiến theo véctơ v  1 1 
A. A1;  1 . B. A ;   . C. A 3  ;3 . D. A3; 3   .  2 2  1 1
Câu 8. Cho hình phẳng  H  giới hạn bởi đồ thị hàm số y 
, trục Ox và hai đường thẳng x  1, x  2 . Khối x
tròn xoay tạo thành khi hình phẳng  H  quay quanh trục Ox có thể tích là 7  A. V  B. V  ln 2 C. V 
D. V   ln 2 3 2
Câu 9. Tính diện tích S của hình phẳng giới hạn bởi các đường 2
y  x  4x  3; x  0; x  3 và trục Ox. 1 12 10 8 A. S  . B. S  . C. S  . D. S  . 3 3 3 3
Câu 10. Cho hàm số y  f  x liên tục trên đoạn a;b . Gọi D là hình phẳng giới hạn bởi đồ thị của hàm số
y  f  x , trục hoành và hai đường thẳng x  a, x  b a  b . Thể tích của khối tròn xoay tạo thành khi D
quay quanh trục hoành được tính bởi công thức b b A. 2 2 V   f  xdx. B. 2 V   f  xdx. a a b b C. 2 V   f  xdx. D. 2 V  2 f  xdx. a a
Câu 11. Trong không gian tọa độ cho hai điểm A 1
 ;0;2 , B3;2; 2
  . Biết tập hợp các điểm M thỏa mãn 2 2
MA  MB  30 là một mặt cầu. Bán kính mặt cầu đó bằng A. 6 . B. 6 . C. 2 . D. 2 .
Câu 12. Trong không gian Oxyz , mặt cầu S   x  2   y  2   z  2 : 5 1 2  3 có bán kính bằng A. 3 B. 2 3 C. 3 D. 9
Câu 13. Trong không gian Tọa độ của là A. B. C. D.
Câu 14. Trong không gian toạ độ Oxyz , cho ba điểm A1;2;0 , B 3; 2  ;3 và C  2  ;1;  1 không thẳng hàng.
Nếu vectơ n   ;
a 1;b là pháp vectơ của mặt phẳng  ABC thì A. 2ab  1  .
B. a  b  1.
C. 2a  b 1.
D. a  b  3 .
Câu 15. Trong không gian với hệ tọa độ Oxyz , cho hai vectơ a  2;1; 2
  và vectơ b  1;0;2. Tìm tọa độ
vectơ c là tích có hướng của a và b .
A. c  2;6;  1 .
B. c  4;6;  1 .
C. c  4; 6  ;  1 .
D. c  2; 6  ;  1 .
Câu 16. Trong không gian Oxyz , cho hai mặt cầu S , S lần lượt có phương trình 2  1   2 2 2
S  :  x  32   y  22   z  20222  9, S : x 15  y  7  z  2022 144 . Gọi A , B là hai điểm 2        1 1
bất kì lần lượt thuộc S , S và P  M . A MB  AB . Tính giá 2  1 
M là một điểm tùy ý trong không gian. Đặt 2 8 trị min P . A. 88. B. 98. C. 90. D. 100. 2
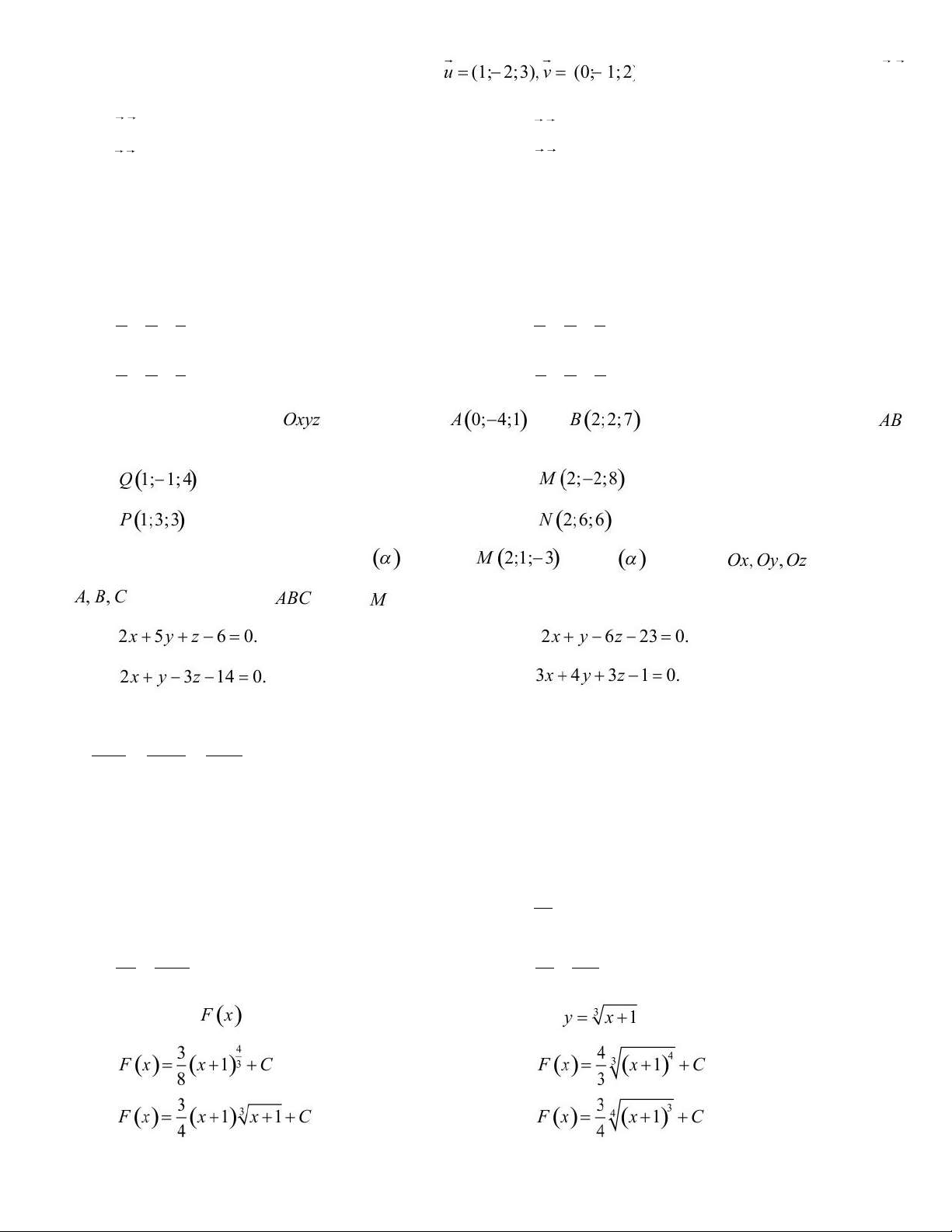
Câu 17. Trong không gian Oxyz , cho hai vectơ
. Tích vô hướng của hai véc tơ . u v là: A. . u v  (0; 2;6) . B. . u v  9 . C. . u v  8 . D. . u v  ( 1  ; 2  ; 1  ) .
Câu 18. Tìm m để bốn điểm (
A 1;1; 4), B(5; 1  ;3), C(2;2; ) m , (
D 3;1;5) đồng phẳng A. m  6. B. m  4. C. m  4.  D. m  6. 
Câu 19. Trong không gian với hệ toạ độ Oxyz , cho A ;
a 0;0 , B0; ;
b 0 , C 0;0;c , abc  0 . Khi đó phương
trình mặt phẳng  ABC là: x y z x y z A.    1. B.    1. a b c b a c x y z x y z C.    1. D.   1. a c b c b a
Câu 20. Trong không gian , cho hai điểm và
. Trung điểm của đoạn thẳng là điểm A. . B. . C. . D. .
Câu 21. Viết phương trình mặt phẳng đi qua , biết cắt trục lần lượt tại sao cho tam giác nhận làm trực tâm A. B. C. D. 2 2 2
Câu 22. Trong không gian Oxyz , cho mặt cầu S  :  x  
1   y  2   z  2  25 và đường thẳng x 1 y  2 z  5 d :  
. Có bao nhiêu điểm M thuộc tia Oy , với tung độ là số nguyên, mà từ M kẻ được đến 9 1 4
S hai tiếp tuyến cùng vuông góc với d ? A. 40 . B. 46 . C. 84 . D. 44 .
Câu 23. Họ nguyên hàm của hàm số   3   3x f x x là 4 x A. x 2 3  3x x ln x  C . B.  3 ln3 C . 4 4 x 1 x 3  4 3x x C.   C . D.   C . 4 x 1 4 ln 3 Câu 24. Hàm số
nào dưới đây là nguyên hàm của hàm số ? A. . B. . C. . D. . 3
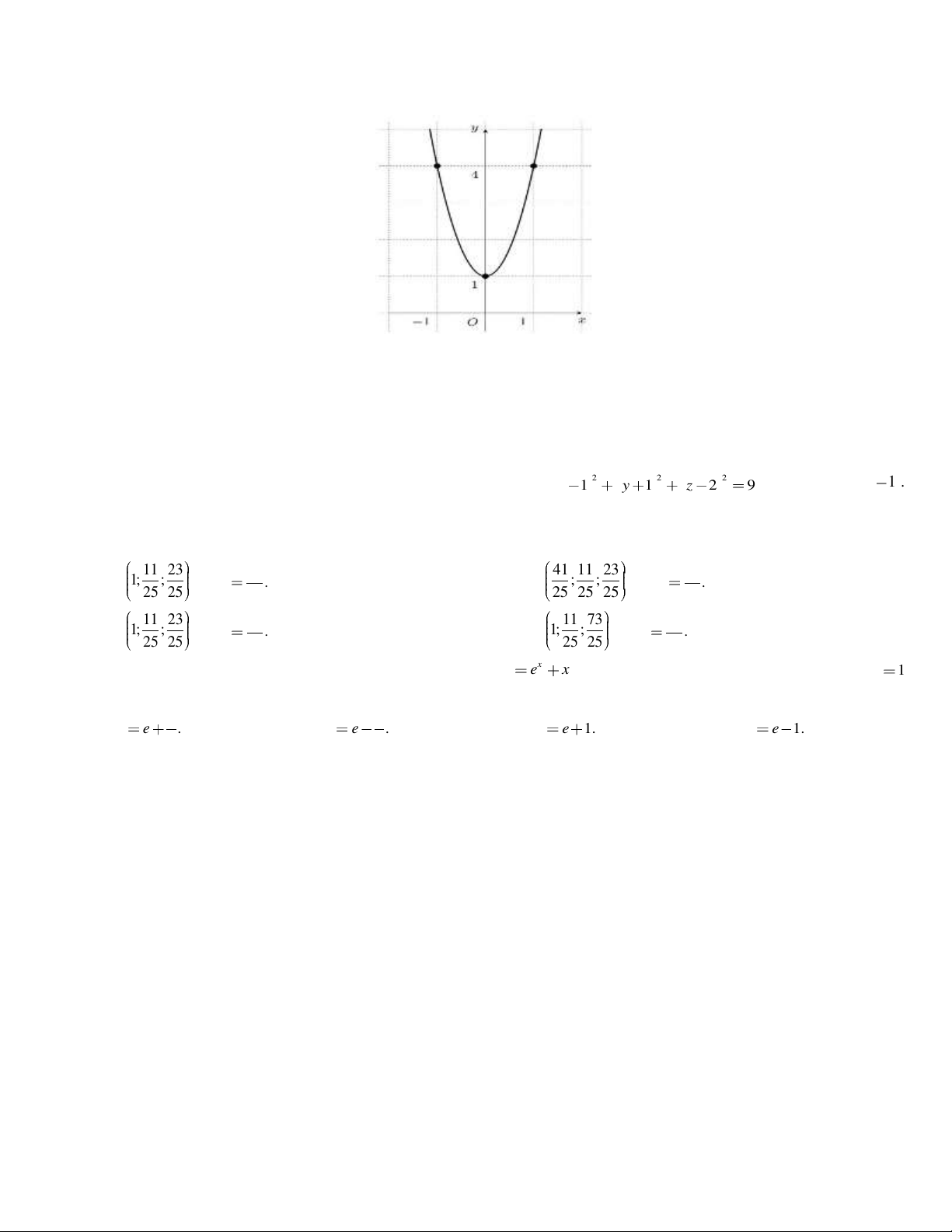
Câu 25. Cho hàm đa thức bậc ba y  f (x) có đồ thị hàm số y  f (
 x) được cho bởi hình vẽ sau. Giá trị biểu
thức f 3  f 2 bằng A. 20 . B. 51. C. 64 . D. 45 . Câu 26. Tính  3
4x  4dx bằng A. 3 4x  4x  . C B. 4 x  4x  . C C. 2 16x  . C D. 2 12x  . C
Câu 27. Trong không gian với hệ tọa độ Oxyz, cho mặt cầu 2 2 2 S : x 1 y 1 z 2
9 và điểm M 1;3; 1 .
Biết rằng các tiếp điểm của các tiếp tuyến kẻ từ M tới mặt cầu đã cho luôn thuộc vào đường tròn C . Tìm tâm
J và bán kính r của đường tròn C . 11 23 41 11 23 A. J 1; ; và 12 r . B. J ; ; và 12 r . 25 25 25 25 25 25 5 11 23 11 73 C. J 1; ; và 12 r . D. J 1; ; và 12 r . 25 25 5 25 25 25
Câu 28. Diện tích hình phẳng giới hạn bởi đồ thị hàm số x y e
x , trục hoành, trục tung và đường thẳng x 1 là: A. 1 S e . B. 1 S e . C. S e 1. D. S e 1. 2 2
Câu 29. Trong không gian Oxyz , cho các phương trình sau, phương trình nào không phải là phương trình của mặt cầu ? A. 2 2 2
2x  2y  2z  4x  2y  2z 16  0 . B. 2 2 2
x  y  z  2x  2y  2z  8  0 . C. 2 2 2
3x  3y  3z  6x 12y  24z 16  0 .
D.  x  2   y  2   z  2 1 2 1  9 .
Câu 30. Trong không gian Oxyz , cho mặt cầu S  có tâm I 1; 2;3 và tiếp xúc với trục hoành có dạng ? A.  2 2 2
x  2   y  2   z  2 1 2 3 13 .
B.  x  
1   y  2   z  3  5 . C.  2 2 2
x  2   y  2   z  2 1 2 3  9 .
D.  x  
1   y  2   z  3  25.
Câu 31. Trong không gian Oxyz , cho ba điểm A1;3;5, B2;0; 
1 và C 0;9;0 . Trọng tâm của tam giác ABC có toạ độ là A. 1;4;2 . B. 1;0;5 . C. 1;5;2 . D. 3;12;6 . 4
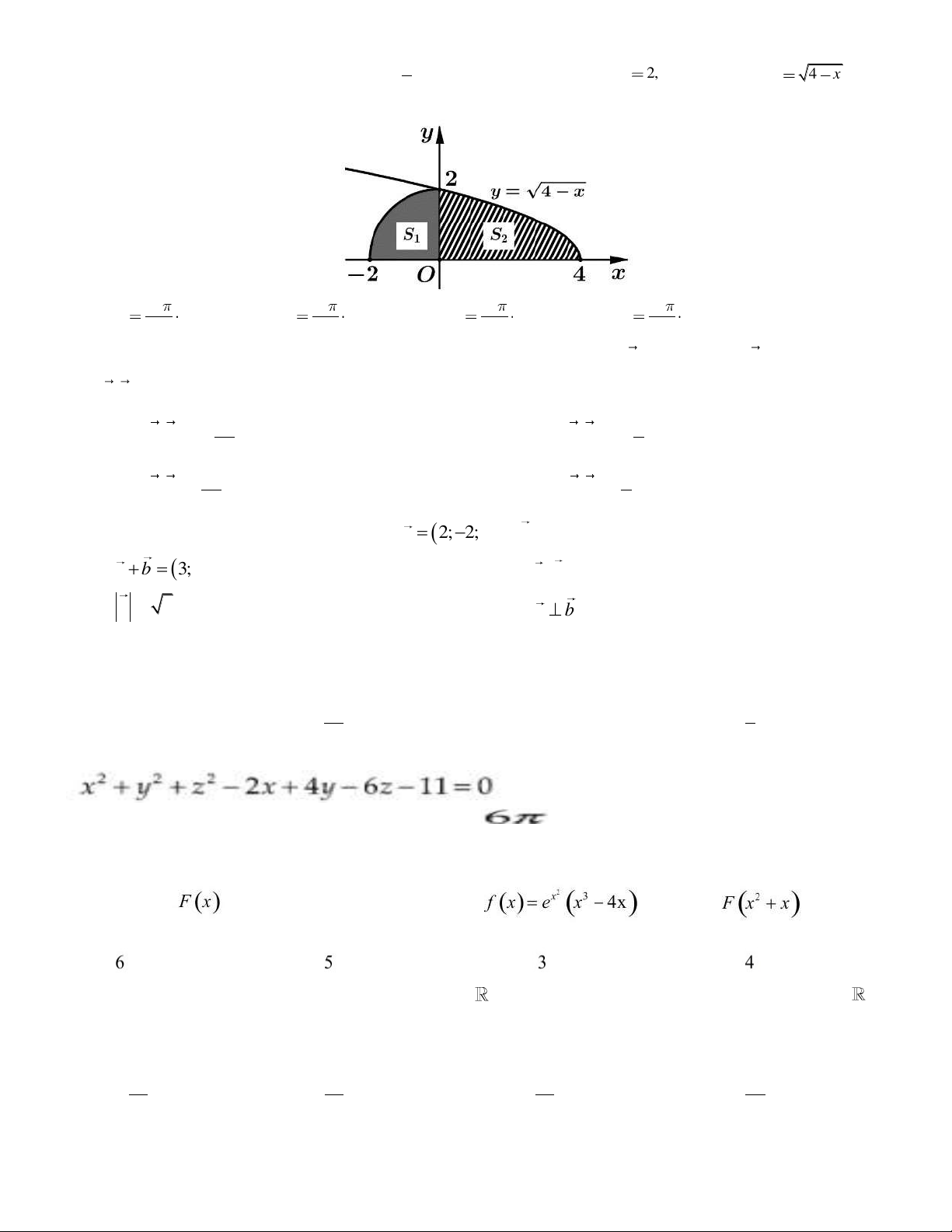
Câu 32. Cho hình phẳng H giới hạn bởi 1 đường tròn có bán kính R 2, đường cong y 4 x và trục 4
hoành mi n tô đậm như hình vẽ). Tính thể tích V của khối tạo thành khi cho hình H quay quanh trục Ox. 40 53 67 77 A. V B. V C. V D. V 3 6 6 6
Câu 33. Trong không gian với hệ trục tọa độ Oxyz , cho hai vectơ a  2;1;0 và b  1;0; 2 . Tính cosa,b . A. a b   2 cos , B. a b   2 cos , 25 5 C. a b  2 cos , D. a b  2 cos , 25 5
Câu 34. Trong không gian Oxyz, cho vectơ a  2; 2  ; 4  , b  1; 1  ; 
1 . Mệnh đ nào dưới đây sai?
A. a  b  3; 3  ; 3  
B. a , b cùng phương C. b  3
D. a  b
Câu 35. Trong không gian Oxyz , khoảng cách giữa hai mặt phẳng  P : x  2y  2z 16  0 và
Q: x 2y 2z 1 0 bằng 17 5 A. 5. B. . C. 6. D. . 3 3
Câu 36. Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): 2x+2y-z-7=0. Và mặt cầu (S):
.Viết phương trình mặt phẳng (Q) song song với (P)
và cắt (S) theo giáo tuyến là đường tròn có chu vi bằng A. (Q):2x+2y-z+17=0. B. (Q): 2x+2y-z-7=0. C. (Q): 2x+2y-z+7=0. D. (Q): 2x+2y-z-19=0. Câu 37. Cho
là một nguyên hàm của hàm số . Hàm số có bao nhiêu điểm cực trị? A. . B. . C. . D. .
Câu 38. Cho hàm số f  x có đạo hàm liên tục trên thỏa mãn f  3 x  3x  
1  3x  2 , với mọi x  .Tích 5 phân xf 
 xdx bằng 1 31 17 33 49 A.  . B. . C. . D. . 4 4 4 4 5
Câu 39. Một vật chuyển động theo quy luật ( ) với (giây) là khoảng thời gian từ khi vật
bắt đầu chuyển động và mét) là quãng đường vật di chuyển trong thời gian đó. Hỏi trong khoảng thời gian 6
giây, kể từ lúc bắt đầu chuyển động, vận tốc lớn nhất vật đạt được bằng A. 24 (m/s). B. 108 (m/s). C. 64 (m/s). D. 18 (m/s).
Câu 40. Trong không gian Oxyz, mặt cầu 2 2 2 ( ) S : x y z 2x 4y 1
0 có tâm I và bán kính R là: A. I(1; 2;0), R 2 B. I(1; 2;1), R 2
C. I(1; 2;1), R 6
D. I(1; 2;0), R 6
Câu 41. Trong không gian với hệ trục tọa độ Oxyz , cho a  i  2 j  3k; b  2i  k . Tọa độ của vectơ
u  2a  3b là A.  4  ;3; 4   . B. 8; 4  ; 9   . C. 4;4;3 . D.  4  ; 4  ; 3  .
Câu 42. Cho a  5; b  2, .
a b  1. Độ dài của vecto a  2b bằng mấy ? A. 30 B. 10 C. 9 D. 45
Câu 43. Trong không gian Oxyz cho ba vectơ a  1; 1
 ;2,b  3;0; 
1 , vectơ a  b có tọa độ là A. 6;0; 6   . B. 2;1; 3  . C.  2  ;1; 3   . D. 2; 1  ; 3  .
Câu 44. Cho hàm số f  x  4x1 ln x và F (x) là một nguyên hàm của f (x) thỏa mãn F(1)  2023 .
Tìm F (x) khi đó? A. 2 2
2x ln x  x  2022 . B. 2 2
2x ln x  x  2023. C. 2 2
2x ln x  2x . D. 2 2
2x ln x  2x  2022 .
Câu 45. Cho hàm số f  x thỏa mãn 3x
e 4 f  x  f ' x  2 f  x, f x  0 x
  0 và f 0 1. Tính ln 2
f  x dx  0 201 11 209 1 A. . B. . C. . D.  . 640 24 640 12 ----HẾT--- 6