Đề thi thử HSG Toán 12 THPT năm học 2017 – 2018 trường THPT Bình Xuyên – Vĩnh Phúc

TRƯỜNG THPT BÌNH XUYÊN
KÌ THI THỬ HSG LỚP 12 THPT NĂM HỌC 2017-2018
ĐỀ THI MÔN: TOÁN - THPT ĐỀ CHÍNH THỨC
Thời gian: 180 phút, không kể thời gian giao đề Câu 1 (2,5 điểm).
a) Tìm tất cả các giá trị thực của m để phương trình sau đây có đúng hai nghiệm thực phân biệt
m    x   x  2 2 2 2 2
 3x  4 4  x  m 12 x  b) Cho hàm số x 2 y  có đồ thị (C). x 1
Hãy lập phương trình đường thẳng (d) đi qua điểm M 3; 
1 và cắt đồ thị (C) tại hai điểm phân
biệt A, B sao cho MB  3MA Câu 2 (2,0 điểm).
a) Giải phương trình: 2 cos 4x  1 2 sin 2xcos x  3sin x  2  0 . 2 2 2 1 2 100 b) Tính tổng: 1 2 100 S  C  C  C 100 100 100 2 3 101 Câu 3 (1,5 điểm). 2 4 2 4
2  x y  2xy  y 1  2 
3 2 x 2y
Giải hệ phương trình: 
x, y 2
 x  y  x  3  Câu 4 (1,5 điểm).
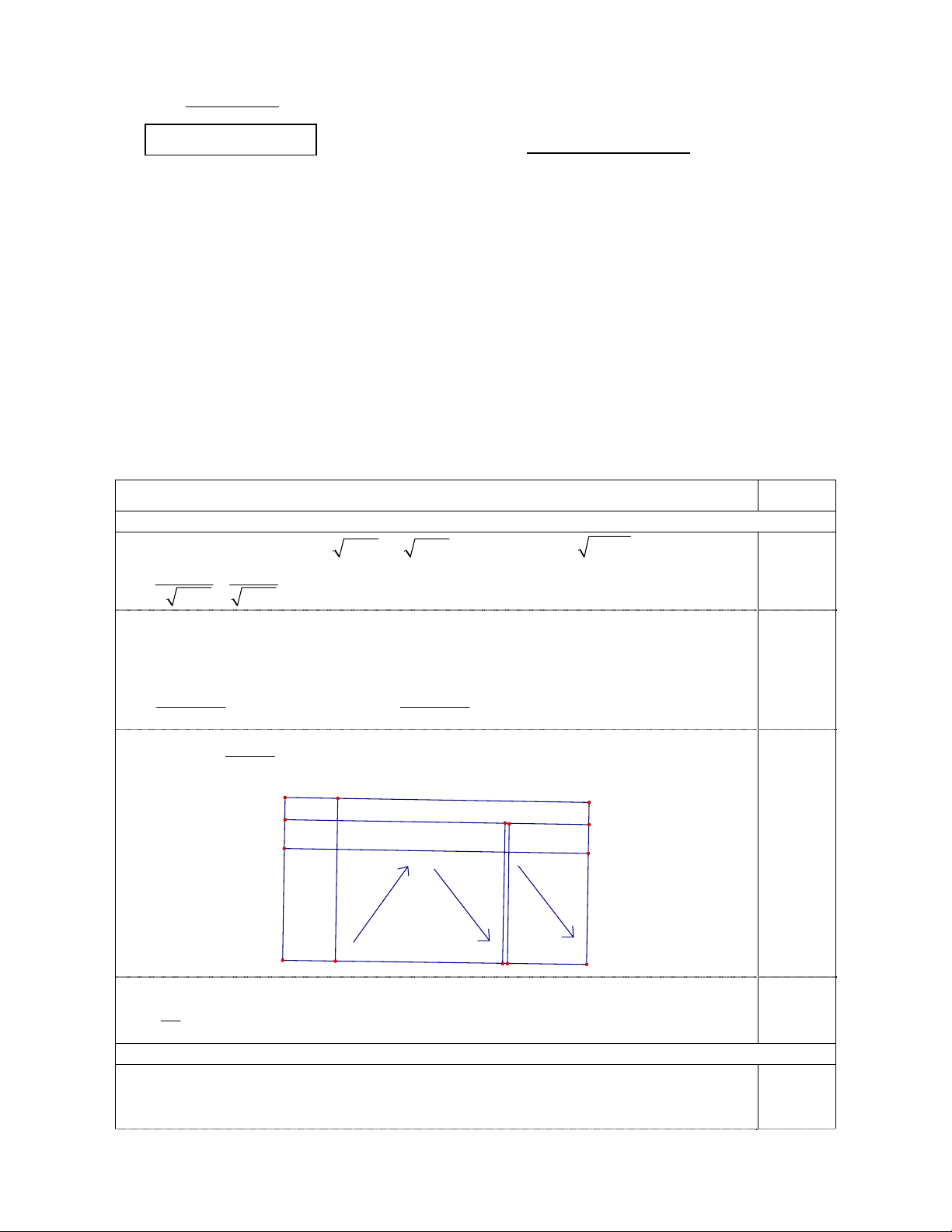
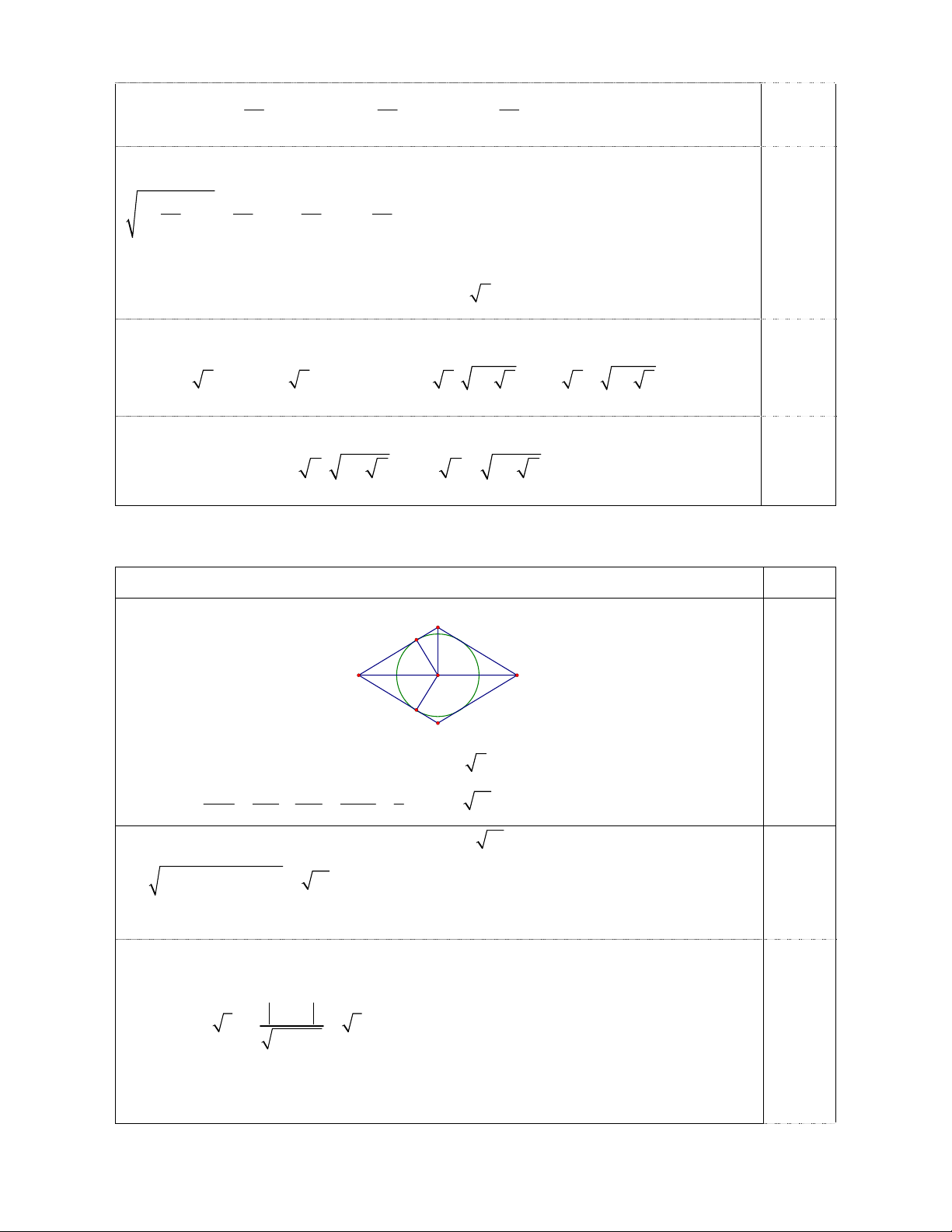
Trong mặt phẳng với hệ trục tọa độ vuông góc Oxy , cho đường tròn C và đường thẳng d  lần
lượt có phương trình  x  2   y  2 2
1  8 và x  2 y  3  0 . Cho hình thoi ABCD ngoại tiếp
đường tròn C và điểm A thuộc đường thẳng d  . Hãy tìm tọa độ các đỉnh ,
A B,C, D ; biết rằng
BD  2AC và tung độ của điểm A không nhỏ hơn 2 . Câu 5 (1,5 điểm).
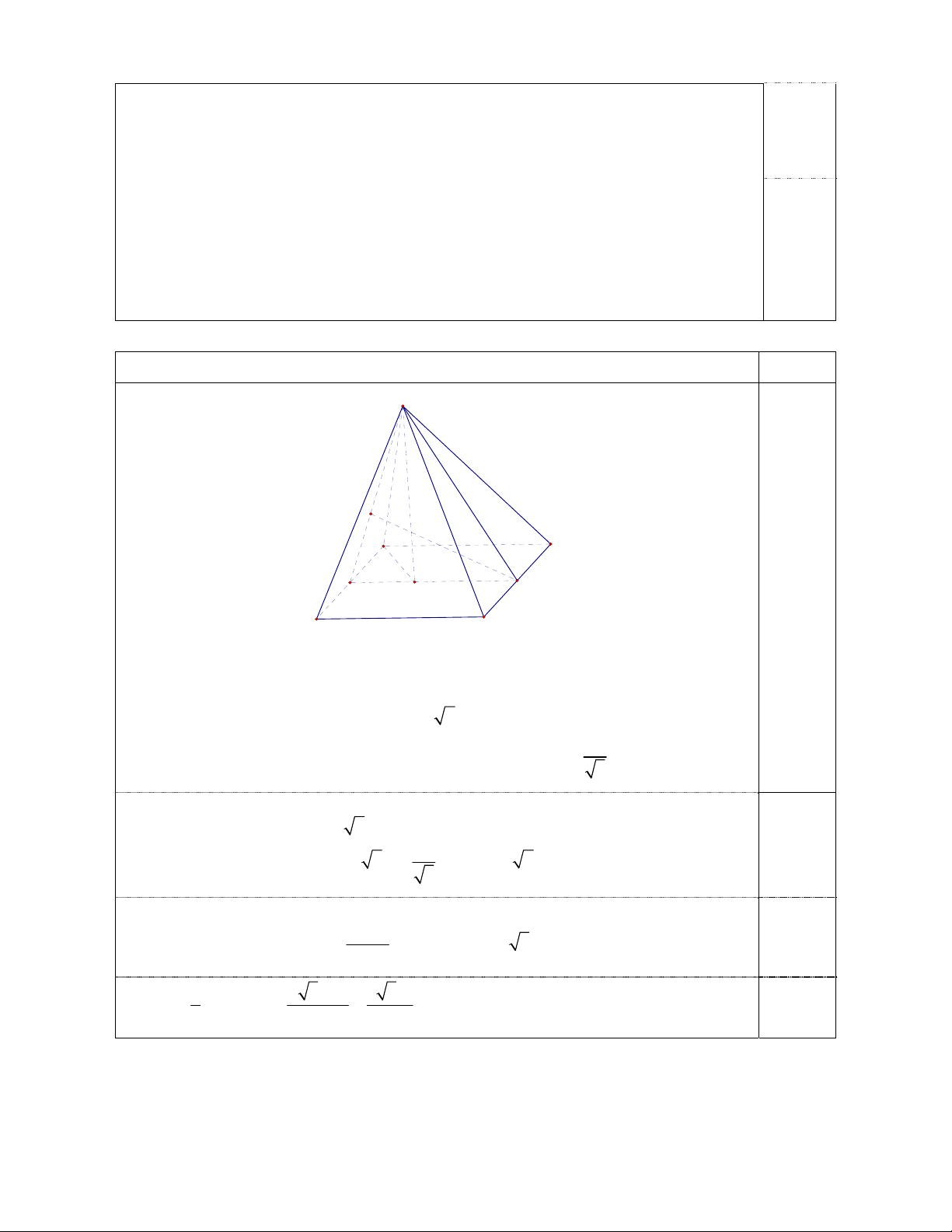
Cho hình chóp S.ABCD có đáy ABCD là hình vuông và tam giác SAB là tam giác cân tại đỉnh
S . Góc giữa đường thẳng SA và mặt phẳng đáy bằng 0
45 , góc giữa mặt phẳng SAB và mặt phẳng đáy bằng 0
60 . Tính thể tích khối chóp S.ABCD , biết rằng khoảng cách giữa hai đường
thẳng CD và SA bằng a 6 . Câu 6 (1,0 điểm).
Cho x, y, z là các số thực không âm thoả mãn điều kiện 2 2 2
x  y  z  1.
Tìm giá trị lớn nhất của biểu thức: P  6( y  z  x)  27xyz .
----------Hết---------
Thí sinh không được sử dụng máy tính cầm tay.
Cán bộ coi thi không giải thích gì thêm.
Họ và tên thí sinh ………………………………………….Số báo danh………………….
TRƯỜNG THPT BÌNH XUYÊN
KÌ THI THỬ HSG LỚP 12 THPT NĂM HỌC 2017-2018
HƯỚNG DẪN CHẤM MÔN: TOÁN – THPT
(Gồm 06 trang) ĐỀ CHÍNH THỨC
Lưu ý khi chấm bài:
- Đáp án chỉ trình bày một cách giải bao gồm các ý bắt buộc phải có trong bài làm của học
sinh. Khi chấm nếu học sinh bỏ qua bước nào thì không cho điểm bước đó.
- Nếu học sinh giải cách khác, giám khảo căn cứ các ý trong đáp án để cho điểm.
- Trong bài làm, nếu ở một bước nào đó bị sai thì các phần sau có sử dụng kết quả sai đó không được điểm.
- Học sinh được sử dụng kết quả phần trước để làm phần sau.
- Trong lời giải câu 5 nếu học sinh không vẽ hình thì không cho điểm.
- Điểm toàn bài tính đến 0,25 và không làm tròn.
Câu 1. (2,5 điểm) Nội dung Điểm a) 1,0 điểm Điều kiện 2
  x  2 , đặt 2 2
t  2  x  2 2  x  t  10  3x  4 4  x 1 1 0,25 ' t    0, x   
nên x 2;2  t 4;2 x  2;2 2 2  x 2  x
Khi đó pt đã cho có dạng: m   2 t   t  m 
 mt   2 2 10 12
1  t  2t  2
+) Nếu t  1 thay vào pt trên không thỏa mãn
+) Nếu t  1 pt trên có dạng 0,25 2 t  2t  2 2 t  2t  2 m 
(1). Xét hàm số f t  ,t  4  ;2 \  1 t 1 t 1 2 t  2t
Ta có f 't 
, f ' t  0  t  0,t  2. Ta có bảng biến thiên như sau: 2   t   1 t -4 0 1 2 f'(t) + 0 - - + 0,25 -2 f(t) 26 - 2 - 5 
Dựa vào bảng biến thiên ta được pt ban đầu có đúng hai nghiệm phân biệt 26    m  2  0,25 5 b) 1,5 điểm
Ta thấy nếu đường thẳng (d) không có hệ số góc thì nó chỉ cắt (C) tại đúng một điểm suy
ra (d) phải có hệ số góc. Giả sử (d) có hệ số góc là k thì phương trình của (d): 0,25
y  kx  3k 1. Phương trình hoành độ giao điểm là: 2 x  2 x  1 
 kx  3k 1   2 x 1 kx  2 
2k  1 x 3k 3  0 2
 kx  22k  
1 x  3k  3  0 (1) ( do x  1 không phải là nghiệm)
+) Để (d) cắt (C) tại hai điểm phân biệt thì (1) có hai nghiệm phân biệt k  0 0,50    k  0 2
 '  k  k 1  0
+) Giả sử A x ;kx  3k 1 , B x ;kx  3k 1 , trong đó x , x là hai nghiệm của (1) và 1 1   2 2  1 2 4k  2 3k  3
theo định lý Viet ta có: x  x  ; x x  (2) 0,25 1 2 1 2 k k
Ta xét hai trường hợp sau:  
TH1. MB  3.MA  x  3x  6
 , kết hợp với (2) ta được: 2 1 5k 1
3k  3 5k 1 3k  3 3k  3 1 x  , x  ; .   k  1  ;k   1 2 2k 2k 2k 2k k 5 0,25 1 1 2
+) k    (d) : y   x  5 5 5 +) k  1
  (d) : y  x  2   TH2. MB  3.
 MA  x  3
 x 12 , kết hợp với (2) ta được 2 1 4k 1 3 4k 1 3 3k  3 3  5 x  , x  ; .   k  1 2 k k k k k 2 0,25 3  5
Phương trình đường thẳng (d): y  x 3 1 2 Vậy ....
Câu 2. (2,0 điểm) Nội dung Điểm a) 1,0 điểm Pt   2
2 1 2sin 2x  1 2 sin 2xcos x  3sin x  2  0 0,25
 2 1 2 sin 2x1 2 sin 2x1 2 sin 2xcos x  3sin x  2  0
 1 2 sin 2x 2  2sin 2x  cos x  3sin x  2  0  2 0,25      x x  x  x sin 2x 1 2 sin 2 2sin 2 cos 3 sin  0  2 
 3sin x cos x  2sin 2x   x   k 2   +) 8 sin 2x   sin   k  2 4 3 x   k 0,25  8 3 1   
+) 3 sin x  cos x  2sin 2x 
sin x  cos x  sin 2x  sin 2x  sin x    2 2  6  3     2x  x   k
x    k  6  6     k   7 2  0,25 2x  x k      x   k  6  18 3
Vậy phương trình có các họ nghiệm là..... b) 1,0 điểm 2 2 k k   k 1 1 k  1  Ta có k   1,100 : C  C  k 1 k  C 100 100   100 k 1 k 1  k 1 0,25 k k 1 k  kC  C  C 100 100 100 k 1 100 99 k 100! k 1 k 1,100, kC k 100.C       k k 99
S  kC 100C 100.2 100 0,25 k  ! 100  k  99 ! 1 100 99 k 1  k 0 100 100 k   1,100, k k 0 100
S  C  C  C  2 1 2 100 100 100 k 1  k 0 1 k 1 100! 1 k 1 k 1,100, C C         100 k 1 k 1 k  ! 100  k  101 ! 101 0,25 100 100 101 1   k 1 k 1  1 k 1  0 1 1 S   C  C 
C C C     101 2 102 3 100 101 101 101 101   k 1  k 1 101 k 1 101 k0  101  
S  S  S  S       1     100 99 100 101 2 4947 1 100 2 2 1 2 102  0,25 1 2 3 101 101
Câu 3. (1,5 điểm) Nội dung Điểm 2   2 1 xy  2 4 2 4
 x y  2xy  y 1  23 2 2 y .  1 Hệ PT   2
 x  y  x  3  2 0,25 2 4 2 4
x y  2xy  y 1 0 Điều kiện  2 x  y  0  * Từ pt  
1 ta thấy y  0 chia hai vế phương trình   1 cho 2 y ta được : 2  1   1  1 1 2 x   x  1  2 3  2 , 3 
. Đặt t  x  * 2
t  y   2 2   2       y   y  2 y 2 y t 0,50
Xét hàm số f t 2
 2t  t 1, t
 2;, f t  2   0 t  2;. 2 t 1 ( Do 2 2 2
2 t 1  t  0  2 t 1  t  3t  4, t   2 ).
Vậy hàm số f t đồng biến trên 2;. 4  1  1 1
Từ 3  f x 
 f 3  x   3  x  3  4  2    2 2    y  y y
Thay 4 vào 2 ta được: 1 1 1 1 2 2 6 4 2 3   y   3   y 
 y  3y  y 1  0 5 2 2 2 4   y y y y 0,25  y 1
Từ 5   y  
1  y  2y   2 2 4 2 1  0   2 y 1 2 + 2
y  1 x  2   ; x y   2; 1,2; 1 0,25 + 2
y  1 2  x  3  2   ;
x y 3 2; 1 2 ,3 2; 1 2 
Vậy tập nghiệm của hệ phương trình là : 0,25 S  
 2; 1,2; 1,3 2; 1 2,3 2; 1 2
Câu 4 (1,5 điểm) Nội dung Điểm A H B D I 0,50 C
Đường tròn (C) có tâm I 2; 
1 , bán kính R  2 2 , IB  2IA . Trong tam giác vuông 1 1 1 5 1 IAB ta có:      IA  10 2 2 2 2 IH IA IB 4IA 8
Do A thuộc (d) nên A2t  3;t , kết hợp với IA  10   t 
2t  52  t  2 2 2
1  10  5t 18t 16  0   t  2  0,25 t  1,6
Suy ra A1;2 , do I là trung điểm AC nên C 3;4 . 
Giả sử đường thẳng AC có vtpt là n  a b 2 2
; , a  b  0 AB
Pt AB: a  x  
1  b y  2  0 . Ta có a  3b
d I; AB  8 
 8  a  3b2  8 2 2 a  b  2 2
 7a  6ab  b  0 0,25 2 2 a  b  a   ;7 b a  b
+) Nếu a  b , chọn a  1,b  1
  AB : x  y 1  0
+) Nếu 7a  b , chọn a  1,b  7  AB : x  7 y 15  0 5
Như vậy ta có nếu AB : x  y 1  0  AC : x  7 y 15  0 và ngược lại.
Giả sử AB : x  y 1  0  AC : x  7 y 15  0 0,25
Đường thẳng CD song song với AB nên CD : x  y  c  0 , do CD đi qua C nên
3  4  c  0  c  7  CD : x  y  7  0
x  y  7  0 x  8
Do đó tọa độ D là nghiệm của hệ     D8;  1 , kết hợp với I là
x  7y 15  0 y 1 trung điểm BD suy ra 0,25 B 4;3 .
Vậy tọa độ các đỉnh là: A1;2 , B4;3 ,C 3;4 và D 8;  1
Câu 4 (1,5 điểm) Nội dung Điểm S 0,25 P A D N M H B C
Gọi H là hình chiếu vuông góc của S lên mặt đáy, M là trung điểm AB và do tam giác
SAB cân tại S nên SM vuông góc với AB và kết hợp với SH vuông góc với đáy suy ra
AB vuông góc với mặt phẳng SMN nên theo giả thiết ta được: SA ABCD  0 ,( )  SAH 
 45  SA  SH 2
(SAB), ABCD  SM ,MH  2 0  S
 MH  60  SM  SH. 0,5 3
Từ điểm N kẻ NP vuông góc với SM thì dễ thấy NP là khoảng cách giữa hai đường
thẳng SA và CD suy ra NP  a 6 . Ta có 2 0,25 SH.MN  .
NP SM  SH.AB  a 6.SH
 AB  2 2a 3 Trong tam giác SAM ta có 2 4SH 0,25 2 2 2 2 2
SA  AM  SM  2SH 
 2a  SH  a 3 3 2 3 1 a 3.8a 8 3a V  SH.S   0,25 S.ABCD 3 ABCD 3 3 6
Câu 6. (1,0 điểm) Nội dung Điểm 1,0 điểm
Ta có P  6( y  z)  (27 yz  6)x 2  2 2 2 1 x
y  z  2( y  z )  2 1 x và 27 yz  6  27.  6 2 0,25 27  Do đó 2 2
P  6 2 1 x  x (1 x )  6  2    27  Xét hàm 2 2
f (x)  6 2 1 x  x (1 x )  6  trên 0;  1 , ta có: 2    0,25 6 2x 81 15 2 6 2 f '(x)    x  ; f ''(x)  8  1x   0 x  0;  1 . 2 1 x 2 2 2 2 (1 x ) 1 x  1 
Suy ra hàm f '(x) nghịch biến; ta lại có f '  0   .  3   1  1  1 
Do đó với mọi x  0; 
thì f '(x)  f '  0   ; với mọi x  ;1   thì 3    3  3  0,25  1   1 
f '(x)  f '  0  
Vì vậy, f (x)  f 10  
với mọi x 0;  1 .  3   3  1 2
Như vậy P  10 . Dấu đẳng thức xảy ra khi x  và y  z  . 3 3 0,25
Vậy giá trị lớn nhất của P là10 .
Chú ý: Có thể giải bài toán bằng cách không sử dung đạo hàm như sau: Đặt a  3 ;
x b  3y;c  3z , khi đó 2 2 2
a  b  c  9 và P  2(b  c  a)  abc
Ta chứng minh 2(b  c  a)  abc  10 (*) Thật vậy, ta có 2 2 2
(*)  4(b  c  a)  2abc  a  b  c 11 (1) Ta có 2 2 b  4  4 ;
b c  4  4c nên 2 2
4(b  c)  b  c  8 (2)
Đẳng thức xảy ra ở (2) khi b  c  2 . Ta chỉ cần chứng minh 2
4a  2abc  a  3 . Ta có 2 2 2 4
 a  2abc  4  a  .
a (b  c )  4
 a  a(9  a ) Mà 2 2 3 2 2 4
 a  a(9  a )  a  3  a  a  5a  3  0  (a 1) (a  3)  0 (luôn đúng) Vậy 2
4a  2abc  a  3 (3) . Từ (2) và (3) suy ra (1) được chứng minh, tức là (*) được chứng minh.
Đẳng thức xảy ra khi và chỉ khi a  1;b  c  2 . 1 2
Vậy giá trị nhỏ nhất của P là 10 khi x  và y  z  . 3 3
………. Hết………. 7