GIẢI ĐỀ THI THỬ TNTHPTQG LẦN 2
LƯƠNG THẾ VINH HÀ NỘI NĂM 2021 2022
Câu 1. Phương trình x 1 − x 1 − 0
2022 =1 ⇔ 2022 = 2022 ⇔ x −1 = 0 ⇔ x =1. Chọn B.
Câu 2. Hình nón có S = π = π rl , trong đó đường sinh l = 4, suy ra 4π r = 8π ⇔ r = 2 . xq 8 Chọn D
Câu 3. Xét hàm số 4 2
y  x 4x 3 có có 3
y   x  x   x 2 ' 4 8
4 x  2 và có nghiệm
duy nhất x = 0 , do đó đồ thị đã có một điểm cực trị. Chọn D x2  0
Câu 4. Bất phương trình log x 2 1     
 2  x  4  x  2;4 . 2     1 x2   2  Chọn C
Câu 5. Số hạng thứ tư của cấp số nhân 3 3
u = u .q =1.2 = 8. 4 1 Chọn D
Câu 6. Đồ thị hàm số hình vẽ là hàm số trùng phương, có hệ số a > 0 , đi qua gốc tọa độ. Chọn A
Câu 7. Trong không gian Oxyz . Điểm đối xứng với M (2;2; 1
− ) qua mặt phẳng Oyz là M '( 2; − 2; 1 − ) Chọn B b
Câu 8. Ý nghĩa hình học của tích phân, diện tích S = f ∫ (x)dx. a Chọn D
Câu 9. Đồ thị hàm số x y =
có tiệm cận ngang y =1, x − 2 Chọn D 
Câu 10. Mặt phẳng (P) qua M (1;0;1) và n =
− là (P) : 2x + y − 2z = 0 . P (2;1; 2) Chọn D    
Câu 11. Véc tơ a = (1;2; 2
− ) vuông góc với p = (2;1;2) , vì .
a p = 2 + 2 − 4 = 0 . Chọn B
Câu 12. Số phức liên hợp của z = 1− 3i là z = 1+ 3i . Chọn A Câu 13. Xét hàm 3
y = x + x +1 trên đoạn −1;2   , có max y = f (2) = 11. Chọn D
Câu 14. Tập xác định của hàm số ( 2
ln −x + 4) là D = ( 2; − 2) . Chọn D
Câu 15. Một nguyên hàm của f (x) 1 = là ln x − 3 . x − 3 Chọn C
Câu 16. Khối trụ có r = 2 và chiều cao h = 4 . Thể tích của khối trụ 2
V = π r h =16π . Chọn D 2
Câu 17. Khối trụ lăng trụ có diện tích đáy 2 3 S =
= 3 và chiều cao h = 2 . 4
Thể tích khối lăng trụ là V = 3.2 = 2 3 . Chọn D
Câu 18. Từ bảng biến thiên suy ra hàm số đồng biến trên (0;2) . Chọn C Câu 19. Hàm số có 2
y = x − mx + = (x − m)2 2 ' 3 6 3 3
+ 3− 3m . Để hàm số đồng biến trên  thì y ' ≥ 0, x ∀ . Suy ra 2
3− 3m ≥ 0 ⇔ m∈[ 1; − ]
1 . Số giá trị nguyên của m là 3. Chọn A
Câu 20. Tỉ số thể tích V SA' SB ' 1 V 2 1 = .
= ⇒ 4V = V +V ⇔ 3V = V ⇒ = 3. 2 2 1 2 1 V +V SA SB 4 V 2 1 2 Chọn B
Câu 21. Đồ thị hàm số x +1 y =
cắt Ox tại điểm ( 1; − 0) . Ta có k y − = − = , phương trình tt ( ) 1 ' 1 x − 2 3 tiếp tuyến là 1 y = − (x + )
1 ⇔ x + 3y +1 = 0 . Chọn D 3 Câu 22. Ta có log ( 3
ab = log a + 3log b . 2 ) 2 2 Chọn D
Câu 23. Xác suất để lấy được 2 bi đỏ là 5C2 2 p = = . 10C2 9 Chọn B
Câu 24. Phương trình 2x+x 1+ 2x 6x 2 2
= 8 = 2 ⇔ x − 5x +1 = 0 . Tổng các nghiệm bằng 5. Chọn A x −1 > 0
Câu 25. Bất phương trình ⇔ log 14 − 2x ≥ log x −1 ⇔  ⇔ 1< x < 5 . 4 ( ) 4 ( ) 14
 − 2x > x −1
Có 3 số nguyên thỏa mãn. Chọn B
Câu 26. Đường thẳng d ⊥ mp(P) : x + y − z +1= 0, d đi qua M (1;2;− )
1 nên có phương trình là:
x −1 y − 2 z +1 d : = = . Chọn D 1 1 1 −
Câu 27. Ta có: w = 1+ 3i . z = 10. 2 = 20 . Chọn D 2 2 4
Câu 28. Ta có I = f ∫ ( x) 1 x = f ∫ ( x) ( x) 1 = f ∫ (u) (u) 1 ' 2 d ' 2 d 2 ' d
= ( f (4) − f (2)) =1010. 2 2 2 1 1 2 Chọn D   Câu 29. Ta có α = (u n) 4 sin cos , = . 9 Chọn B
Câu 30. Giao điểm của đồ thị với Ox là x = 0, x = 2 . 2
Ý nghĩa hình học của tích phân, thể tích V = ( x− x )2 2 16 2 dx = ∫ π π . Chọn D 15 0
Câu 31. Đường kính khối cầu ngoại tiếp hình lập phương d = 2R = (2a) 3 ⇔ R = a 3 . 4 4 Thể tích khối cầu 3 3 3
V = π R = π.3a 3 = 4 3π a . Chọn B 3 3 2 a 3 Câu 32. Ta có = tan 60o SA AB
= a 3 . Diện tích đáy S = . ABC ∆ 4 2 3 1 a 3 a
Thể tích V = .a 3. = . Chọn D 3 4 4 a 3
Câu 33. Đường cao AH của tam giác đều ABC là AH = . 2 A' A 3a / 2 Góc cần tìm có tanϕ = =
= 3 ⇒ ϕ = 60o . Chọn C AH a 3 / 2
Câu 34. Từ hình vẽ ta có : 2
log = ⇔ = a ⇔ a = . a 2 2 2 2 Chọn A
Câu 35. Hình trụ có chiều cao h = AB = 2 , bán kính r = AD = 1 nên S = π rh = π . xq 2 4 Chọn D. x + 9
Câu 36. Đồ thị f (x) =
có tiệm cận ngang y = 0 và tiệm cận đứng x = 0 . Không có 2 x +10x
tiệm cận đứng x = 10 − vì x → 10
− căn bậc hai không có nghĩa.. Chọn D. 20 Câu 37. Xét  1 x  − 
khai triển có số hạng không chứa thỏa mãn 3 20 0 k × + = = 15 . Khi đó 3 x    3 +1
số hạng cần tìm là: C ×(− )5 15 5 1 = C − . Chọn B. 20 20
Câu 38. Ta có f '(x) cùng dấu với (x − 2)(x + 2) , do đó hoành độ điểm cực đại của đồ thị
f (x) là x = 2 − . Chọn C. Câu 39. Đặt 2 2 2
1+ x = u ⇒1+ x = u ⇒ xdx = udu . 3 2 f (u) 3
Đổi cận: x = 0 ⇒ u = 1; x = 2 2 ⇒ u = 3. Từ đó I = udu = ∫
2∫ f (u)du . 1 u 1 2 3 Suy ra I = f (x)dx + f (x) 47 2 2 dx = ∫ ∫ . Chọn A. 3 1 2
Câu 39. Gọi O là giao điểm AC ∩ BD . Tâm I mặt cầu ngoại tiếp hình chóp thuộc SO .
Gọi M là trung điểm CD , hạ IH ⊥ SM . Ta có SA = SC = AC = a 2 nên S ∆ AC đều. Từ đó 2 2 a 2. 3 a 6 SI = SO = . = ; 2 2 a 7
SM = SO + OM = . 3 3 2 3 2 Ta có IH SI a 6 / 3 a 42 SH ∆ I  SO ∆ M ⇒ = = ⇒ IH =
= d (I,(SCD)) . Chọn C. OM SM a 7 / 2 21
Câu 41. Dựa vào đồ thị f (x) trên đoạn [ 2;
− 2] , xét phương trình f (t) = m∈ . t = −  x = −  x = − x = π
+ Trường hợp 1: f (t) 2 2cos 2 cos 1 = 3 − ⇔ ⇒ ⇒ ⇒  . t 1  2cos x 1  cos x 1/ 2  = = = x = ±π / 3 Suy ra m = 3 − thỏa mãn. t = a ∈( 2; − − ) 1 2cos x = a x = ±α
+ Trường hợp 2: f (t) = 2 − ⇔  ⇒ ⇒ . Loại. t = b ∈  (0; ) 1  2cos x b  = x = ±β t = a ∈( 2; − ) 1 2cos x = a x = ±α 
+ Trường hợp 3: f (t) 1 t 0 2cosx 0  = − ⇔ = ⇒ = ⇒ x = ±  π / 2   . Loại. t = b∈  (1;2)
2cos x = b x = ±β
Tương tự, các trường hợp f (t) = 0, f (t) =1 dều loại.
Kết luận: có 1 giá trị nguyên m = 3
− thỏa mãn. Chọn C.
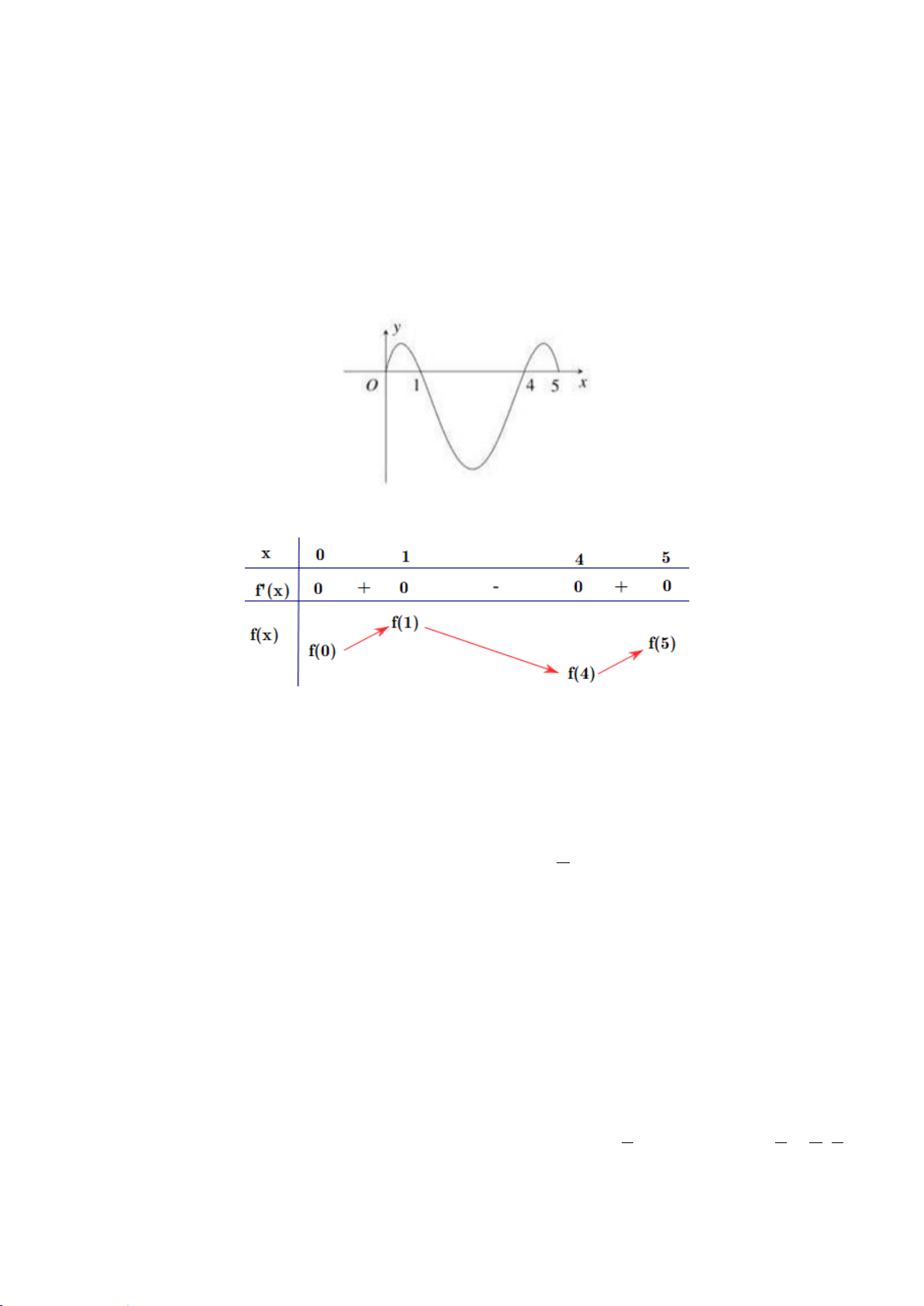
Câu 42. Cho đồ thị f '(x) .
Lập bảng xét dấu, ta có: max f (x) = max{ f ( ) 1 ; f (5)}. [0;5]
Dựa vào bảng xét dấu (hoặc đồ thị f '(x) ) ta có (Bài Vi phân):
 f (5) − f (3) ≈ (5 − 3) f '(3) = 2 f '(3) < 0 ⇒ f (5) < f (3) .  f ( )
1 − f (3) ≈ (1− 3) f '(3) = 2
− f '(3) > 0 ⇒ f ( ) 1 > f (3) .
Suy ra f (5) < f (3) < f ( )
1 ⇒ max f (x) = f ( ) 1 . Chọn D. [0;5]  1 x + x+m  > − x x (1) Câu 43. Ta có ( 2 ln 2 4 ) 2ln(2 ) 1 PT ⇔ 2022 > 2022 ⇔  2 .  2 2
2x + 4x + m > 4x − 4x +1 (2)
Vì có đúng 4 số nguyên x thỏa mãn nên, chọn x = 4 thì (2) đúng, suy ra:
48 + m > 64 −16 +1 ⇔ m >1.
Chọn x = 5 thì (2) phải sai, suy ra 70 + m ≤ 100 − 20 +1 ⇔ m ≤ 11.
Vậy các giá trị nguyên của m là: m ∈{2;3;4;...; } 11 . Chọn B.
Câu 44. Hạ AH, AK lần lượt vuông góc với mp(P) và đường thẳng d . Khi đó:
AH ≤ AK nên khoảng cách từ A đến mp(P) lớn nhất ⇔ AH ≡ AK . Ta có   
AK = (t − 3;t −1;2t + ) 1 ⊥ u = (1;1;2) nên 1
6t − 2 = 0 ⇔ t = . Do đó 8 2 5 AK  ; ;  = − − 3 3 3 3     . Chọn n = (8;2; 5
− ) ⇒ mp(P) :8x + 2y − 5z + 6 = 0 . Vậy a + b + d = 2 − 5 + 6 = 3. Chọn D.
Câu 45. Xét g (x) = f ( 2
x ) − 2x. Đặt 2
t = x ⇒ t ' = 2x . Khi đó g ' = t ' f '(t) − 2 = 2(xf '(t) − ) 1 .
+ Nếu x < 0 thì g ' = xf '(t) −1< 0 nên g ' = 0 vô nghiệm.
+ Xét x > 0 thì g = ⇔ f (t) 1 ' 0 ' =
phương trình có 4 nghiệm đơn phân biệt. t
Vậy g (x) có 4 cực trị. Chọn D.
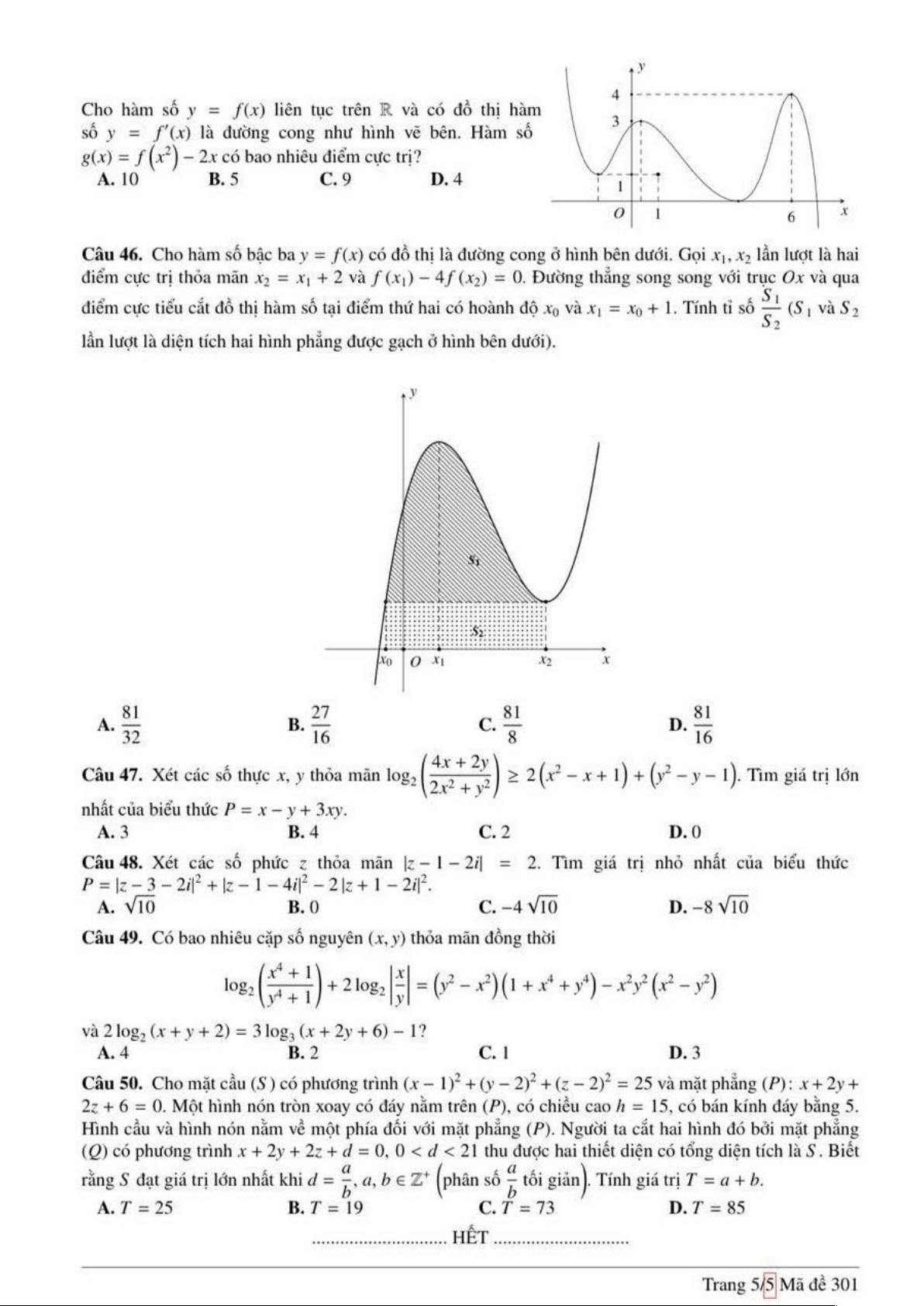
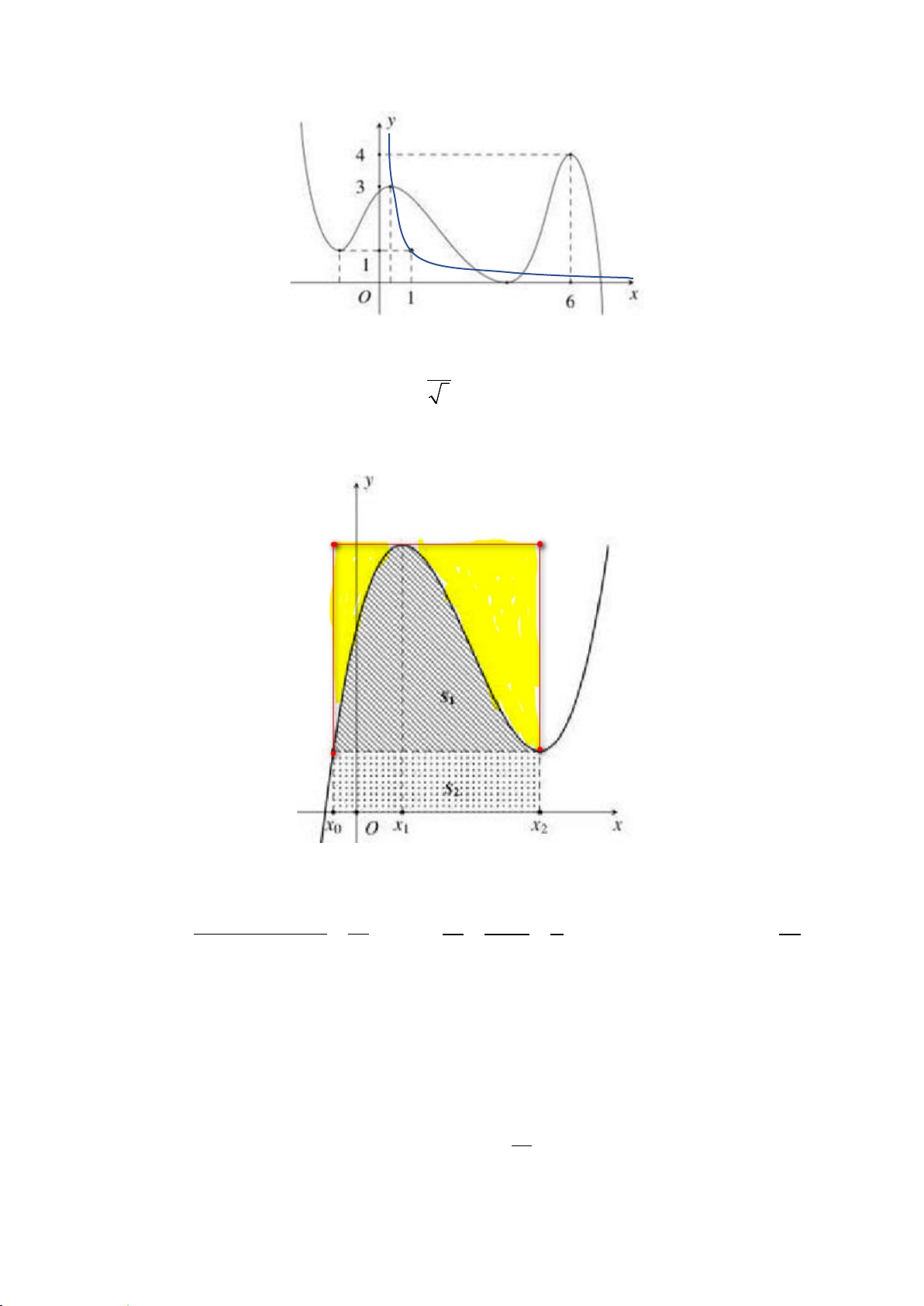
Câu 46. Cách 1. (Tính gần đúng – Dự đoán – Trắc nghiệm).
Vẽ thêm các đoạn thẳng (Hình minh họa), dựa vào ý nghĩa của tích phân trong hình
học, diện tích hình thang cong gần bằng một nửa diện tích hình chữ nhật. Ta có: (1+ 2)×(4.5− ) 1 21 S ≈ = , suy ra S 21/ 4 7 S 1 ≈
= = 1.75. Do đó chọn B có 1 ≈ 1.69 1 2 4 S 3×1 4 S 2 2
.Cách 2. (Tự luận).
Ta có f (x = 4 f x = 4 f x , trong đó x = x + 2 = x + 3 và x , x là nghiệm của 1 ) ( 2) ( 0) 2 1 0 1 2
đạo hàm, có phương trình dạng a(x − x x − x = 0 (*), với a > 0 . 1 ) ( 2 )
Đặt x + x = 2s thì x = 2 − + s; x = 1
− + s; x = 1+ s . Thay vào (*), ta có: 2 1 0 1 2 3   2
a x − sx + x 2 2  ( 2 2 s − ) 1  = 0 
, suy ra f (x) = a
− sx + (s − ) 1 x + 
 d , với 1 < s < 2 .  3 
+ Điều kiện f (x = f x ⇔ f s +1 = f s − 2 2 ) ( 0) ( ) ( ) (s + )3 3 1   −  ⇔  − ( + )2 s a s s 1 + (s − ) 1 (s + ) ( 2) 1  = a  − s(s − 2)2 2 + ( 2 s − ) 1 (s − 2) .  3    3   3   Giải ra ta có 5 3 − 1 9 s = ⇒ x =
; x = ; x = và f (x) x 5 2 9 = a − x + x +   d . 0 1 2 4 4 4 4  3 4 16  + Điều kiện f (  1   9 x 4 f x f     4 f  = ⇔ = 13 81 ⇔ a + d = 4 − a +  d 1 ) ( 2) 4  4      192  64  985 3   ⇒ d =
a , do đó f (x) x 5 2 9 985 = a −  x + x + . 576 3 4 16 576   Ta có 9 4a f   4a 4 = a  , S = x − x = và 2 ( 2 0) 4    9 9 3 9/4 3  x 5  2 9 985 4 9a S = a − ∫ S 9a / 4 27  x + x + − dx = . Vậy 1 = = . Chọn B. 1 S 4a / 3 16 −  3 4 16 576 9  4 3/4 2 Lời bình.
Bài toán tương đối khó và giải khá dài nên tốn nhiều thời gian.
Câu 47. Điều kiện 2 2
u = 2x + y > 0;v = 2x + y > 0. Từ giả thiết 2 log u ≥ 2( 2 x − x + ) 1 + ( 2
y − y −1 = v − u +1 ⇔ log u + u ≥ log v + v . 2 ) v 2 2
Dễ thấy hàm số f (t) = log t + t đồng biến nên suy ra 2 2
u = v ⇔ 2x + y = 2x + y (1). 2
Ta có P = x − y + 3xy , để tìm maxP ta xét xy > 0 , kết hợp 2x + y > 0 , nên x, y > 0 . Từ (1) ta có đánh giá 1
x + y = ( + )( x + y ) 1 2 2 1 2 ≥ (2x + y)2 2 2 2
⇔ 3u ≥ u ⇔ u ≤ 3 , suy 3 3 ra 3 2 3 y x y x − + ≤ ⇔ ≤
. Dấu bằng có khi 2x y = ⇔ x = y . 2 2 1 2 − −   + −  Do đó 3 y 3 y 3  ( ) 3 y 2 3 . 1 2 1 y P y y y y  ≤ − + =  + −  ≤   +    = 3. 2 2 2 2   2   
Vậy maxP = 3 tại x = y = 1. Chọn A.
Câu 48. Đặt z −1− 2i = a + bi ⇔ z = a +1+ (b + 2)i . Giả thiết là: 2 2
a + b = 4 . Khi đó : 2 2 2
P = z − 3 − 2i + z −1− 4i − 2 z +1− 2i .
= (a − 2)2 + b + a + (b − 2)2 − 2(a + 2)2 2 2 2 − 2b P = 4
− (3a + b) . Mặt khác 1 = ( + )(a + b ) 1 4 . 9 1 ≥ .(3a + b)2 2 2
⇒ 3a + b ≤ 2 10 . 10 10 3 10 10 Do đó P = 4
− (3a + b) ≥ 8
− 10 . Dấu bằng có khi a = ,b = . 5 5 Chọn D. Câu 49. Đặt 2 2
x = a > 0; y = b > 0. Từ giả thiết thứ nhất 2 + a 1 log
+ log a = b 1+ a + b − a 1+ b − a − a b + ba . 2 ( 2 ) 3 ( 2) 3 2 2 2 2 b +1 b ⇔ log ( 3 a + a) 3
+ a + a = log ( 3 b + b) 3
+ b + b . Dễ thấy hàm số f (t) = log t + t đồng 2 2 2 biến nên suy ra 3 3
a + a = b + b ⇔ (a − b)( 2 2
a + b + ab + )
1 = 0 ⇔ a = b . Suy ra x = y .
Thế vào giả thiết thứ hai, ta có 2log 2x + 2 = 3log 3x + 6 −1. 2 ( ) 3 ( ) Hay ta có 2 1
 + log x +1  = 3 1
 + log x + 2  −1 ⇔ 2log x +1 = 3log x + 2 = 6t  2 ( )  3 ( ) 2 ( ) 3 ( ) t t
⇒ +1 = 8t; + 2 = 9t x x . Do đó t t  8   1 8 1 9  + = ⇔ + = 1 ⇔ t =     1.  9   9  Vậy ( ;
x y) = (7;7) là cặp số nguyên duy nhất thỏa mãn bài toán. Chọn C.
Câu 50. Mặt cầu có tâm I (1;2;2), bán kính R = 5. Ta có d (I;(P)) = 5 = R nên mặt cầu tiếp xúc
với (P) tại H. Ta có bán kính đáy nón r = 5 = R , ngoài ra thì mp(Q) / /mp(P) .
Chọn (Q) cắt đoạn IH tại K, vì càng gần đáy nón thì diện tích thiết diện càng lớn. Đặt −
x = d ( Q P ) d 6 ( ),( ) = ,0 < x ≤ 5. 3
Khi đó bán kính thiết diện với mặt cầu (S ) là r = R − (5 − x)2 2 2 2 = 10x − x . 1 r 15 − x 15 − x 15 − x 2 2 ( )2
Bán kính thiết diện thứ hai thỏa mãn = ⇒ r = ⇒ r = . 2 2 r 15 3 9 15 − x 2 2 2 ( )2
Xét tổng r + r =10x − x +
là Parabol đạt GTLN tại 10 10 / 3 15 x − = − = 1 2 9  1  4 2 1 − +  9    d − 6 .Do đó 15 69 a = ⇔ d =
= . Suy ra T = a + b = 73 . 3 4 4 b Chọn C. Nhận xét.
Đề thi hay, phân loại tốt. Tuy nhiên đáp án D nhiều quá.
Document Outline

• de-thi-thu-thpt-quoc-gia-2022-mon-toan-lan-2-truong-luong-the-vinh-ha-noi
• GIẢI ĐỀ THI THỬ TNTHPTQG LẦN 2 LƯƠNG THẾ VINH HÀ NỘI 2021 2022
  • Câu 29. Ta có .