Đề thi thử Toán 2022 tốt nghiệp THPT chuẩn đề minh họa -Đề 10 (có lời giải chi tiết)
Đề thi thử Toán 2022 tốt nghiệp THPT chuẩn đề minh họa -Đề 10 có lời giải chi tiết. Tài liệu được biên soạn dưới dạng file PDF bao gồm 25 trang tổng hợp các kiến thức tổng hợp giúp các bạn tham khảo, ôn tập và đạt kết quả cao trong kỳ thi sắp tới. Mời các bạn đón xem!
Chủ đề: Đề thi THPTQG môn Toán năm 2022 75 tài liệu
Môn: Toán 2.2 K tài liệu
Tác giả:
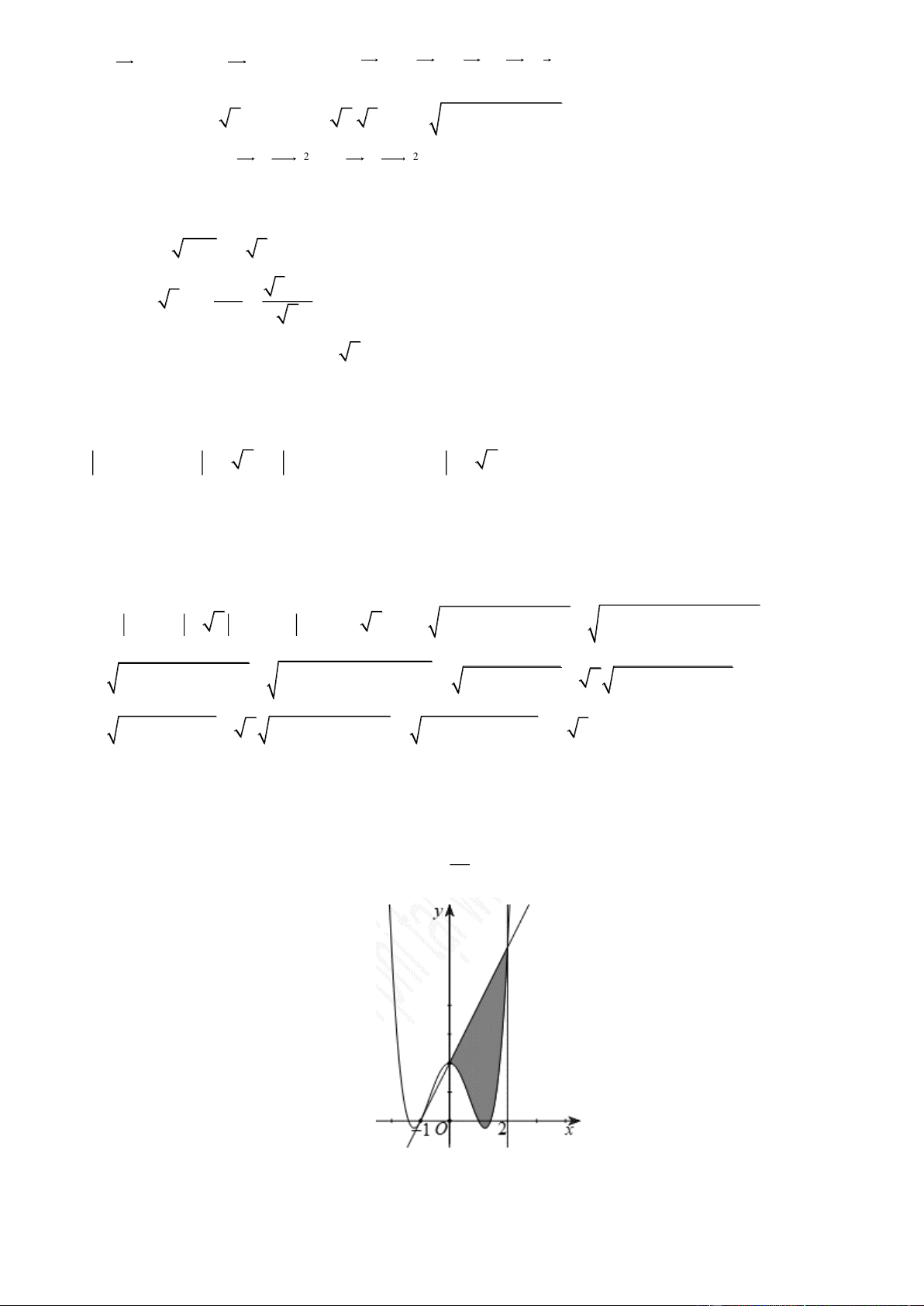
Preview text:
ĐỀ 10
ĐỀ ÔN THI TỐT NGHIỆP THPT NĂM 2022
BÁM SÁT ĐỀ MINH HỌA MÔN TOÁN Thời gian: 90 phút
Câu 1. Cho số phức z = 2 + i . Tính z .
A. z = 5
B. z = 5
C. z = 2 D. z = 3
Câu 2. Trong không gian với hệ tọa độ Oxyz , cho mặt cầu (S) có phương trình 2 2 2
x + y + z + 4x − 2 y − 4 = 0
.Tính bán kính R của (S). A. 1. B. 9 . C. 2 . D. 3 .
Câu 3. Điểm nào dưới đây thuộc đồ thị của hàm số 3
y = −x + 2x +1
A. Điểm M (0; − ) 1 . B. Điểm N ( 1 − ; 4 − ) .
C. Điểm P (1; 2) . D. Điểm Q ( 1 − ;4) .
Câu 4. Cho mặt cầu có diện tích bằng 2
16 a . Khi đó, bán kính mặt cầu bằng a 2 A. 2 2a B. 2a C. 2a D. 2
Câu 5. Trong các khẳng định sau, khẳng định nào sai? 2 x e x 2
A. 2x d = 2x x ln 2 + C . B. e dx = + C . 2 1 1 C. cos 2 d x x = sin 2x + C . D.
dx = ln x +1 + C ( x − ) 1 . 2 x +1
Câu 6. Cho hàm f ( x) có bảng biến thiên như sau:
Giá trị cực tiểu của hàm số đã cho bằng A. 3 . B. −5 . C. 0 . D. 2 .
Câu 7. Tập nghiệm của bất phương trình log x −1 1 là 0,5 ( ) 3 3 3 3 A. − ; − . B. 1; . C. ;+ . D. 1; . 2 2 2 2
Câu 8. Cho hình chóp S.ABC có đáy là tam giác đều cạnh a và chiều cao 4a . Tính thể tích của hình chóp đã cho. 3 2a 3 3 4a 3 3 a 3 3 a 3 A. V = . B. V = . C. V = . D. V = . 3 3 3 4 Trang 1 −
Câu 9. Tập xác định của hàm số y = ( x − ) 4 2 4 là A. . B. ( 2 − ;2) . C. \ 2 . D. \ 4 .
Câu 10. Giải phương trình log (x −1) = 3. 4
A. x = 65
B. x = 80
C. x = 82 D. x = 63 1 3 3 Câu 11. Cho f (x) dx = 1 − ; f (x) dx = 5 . Tính f (x) dx 0 0 1 A. 1. B. 4. C. 6. D. 5.
Câu 12. Cho số phức z = 3
− + 2i , số phức (1−i) z bằng A. 1 − −5i B. 5 − i . C. 1− 5i . D. 5 − + i .
Câu 13. Trong không gian Oxyz , cho mặt phẳng (P) : 4x + 3y + z −1 = 0 . Véctơ nào sau đây là một véctơ pháp
tuyến của (P) A. n = − − 4 (3;1; ) 1 . B. n = 3 (4;3 ) ;1 . C. n = − 2 (4; 1; ) 1 . D. 1 n = (4;3; ) 1 .
Câu 14. Trong không gian Oxyz cho a = (2;3;2) và b = (1;1;− )
1 . Vectơ a − b có tọa độ là A. (3;4; ) 1 . B. ( 1 − ;− 2;3). C. (3;5; ) 1 . D. (1;2;3) .
Câu 15. Tìm tọa độ điểm M là điểm biểu diễn số phức z biết z thỏa mãn phương trình (1+ i) z = 3 − 5i . A. M ( 1 − ;4) . B. M ( 1 − ;− 4). C. M (1; 4) .
D. M (1; − 4) .
Câu 16. Cho hàm số y = f ( x) có báng biến thiên như sau:
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là: A. 2. B. 3. C. 4. D. 1.
Câu 17. Với a là hai số thực dương tùy ý, log ( 3 a bằng 2 ) 3 1 A. log a . B. log a .
C. 3 + log a . D. 3log a . 2 2 2 3 2 2
Câu 18. Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên? Trang 2 A. 4 2
y = x + 2x . B. 3
y = −x − 3x . C. 3
y = x − 3x . D. 4 2
y = −x + 2x . x −1 y +1 z − 2
Câu 19. Trong không gian Oxyz , điểm nào dưới đây thuộc đường thẳng = = ? 2 1 − 3 A. Q( 2 − ;1;− ) 3 . B. P(2; 1 − ; ) 3 . C. M ( 1 − ;1; 2 − ) . D. N (1; 1 − ;2) .
Câu 20. Với k và n là hai số nguyên dương (k n) , công thức nào sao đây đúng? n k n n k ! k ! k ! k ! A. A = A = A = . D. A = n k !(n − . B. k )! n (k − . C. n)! n n k ! (n − . k )!
Câu 21. Diện tích đáy của khối lăng trụ có thể tích V và có chiều cao h là 3V 3h V h A. B = . B. B = . C. B = . D. B = . h V h V Câu 22. Cho ( ) lo 81 g 2.3 x f x = + 3 . Tính f ( ) 1 − A. f ( ) 1 1 = . B. f ( ) 1 1 = . C. f ( ) 1 = 1. D. f ( ) 1 = 1. 2 2
Câu 23. Cho hàm số y = f ( x) có bảng biến thiên như sau:
Hàm số y = f (x) nghịch biến trên khoảng nào dưới đây? (0;+) (− ; 2 − ) (0;2) ( 2 − ;0) A. B. C. D.
Câu 24. Cho hình trụ có diện tích xung quanh S
và độ dài đường sinh 3l . Bán kính đáy r của hình trụ đã cho xq
được tính theo công thức nào sau đây? 6S S S 2 l xq xq xq A. r = = = = . B. r . C. r . D. r . l 2 l 6 l Sxq Trang 3 Câu 25. Cho f ( ) x , g( ) x là các hàm số liên tục trên đoạn 2;6 và thỏa mãn 3 6 6
f (x)dx = 3; f (x)dx = 7; g(x)dx = 5
. Hãy tìm mệnh đề KHÔNG đúng. 2 3 3 6 3
A. [3g(x) − f (x)]dx = 8
B. [3 f (x) − 4]dx = 5 3 2 6 ln e 6 ln e C.
[2f (x) −1]dx = 16 D.
[4 f (x) − 2g(x)]dx = 16 2 3
Câu 26. Cho cấp số cộng (u có số hạng đầu u = 2 và u = 5 . Giá trị của u bằng n ) 2 3 5 A. 12 . B. 15 . C. 11. D. 25 . −x e
Câu 27. Họ nguyên hàm của hàm số x y = e 2 + là 2 cos x x 1 x 1 A. 2 x
e + tan x + C B. 2 x
e − tan x + C C. 2e − + C D. 2e + + C cos x cos x
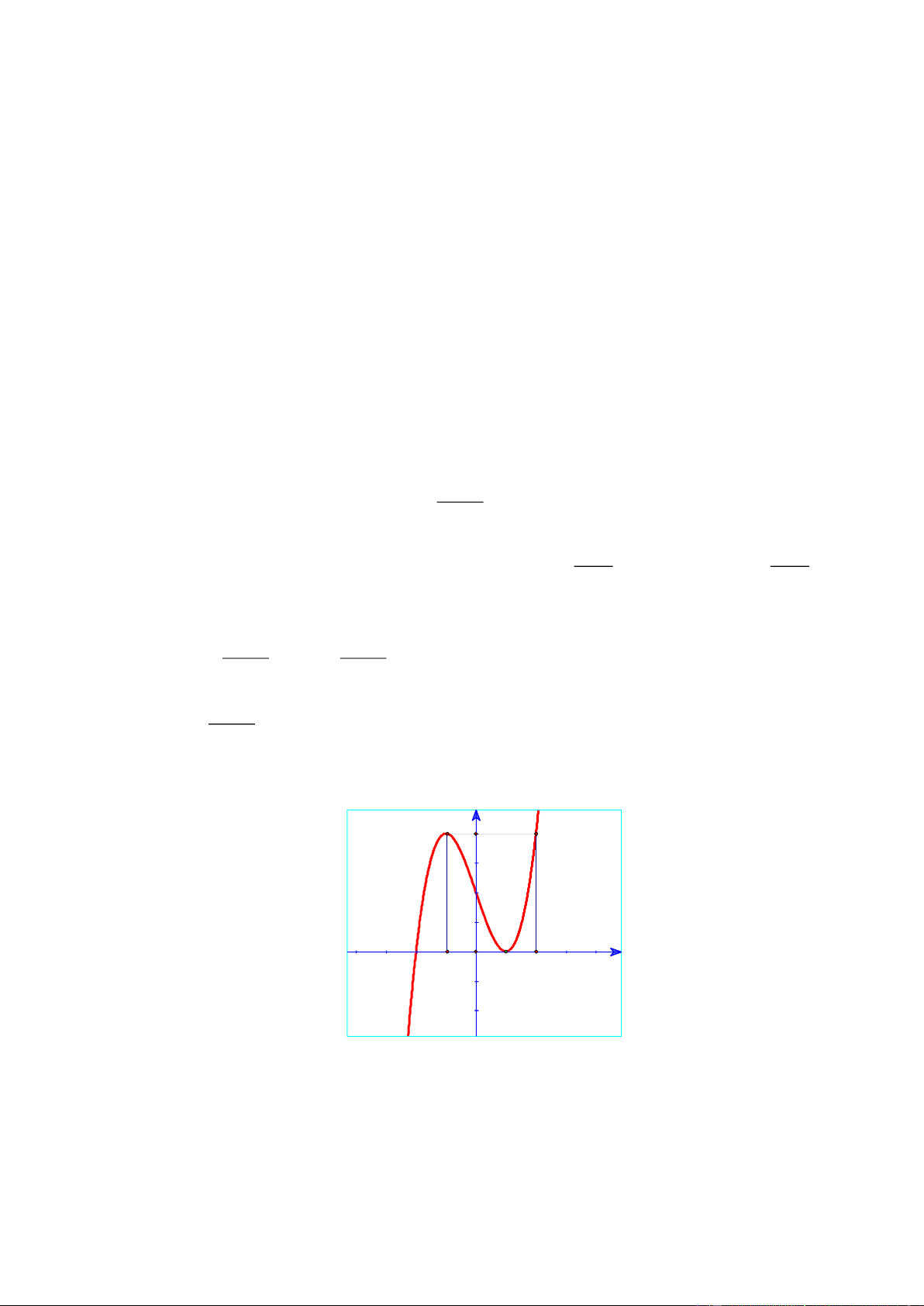
Câu 28. Cho hàm số y = f ( x) có đồ thị như hình vẽ. y 4 2 -2 O x -1 1 2
Hàm số đã cho đạt cực đại tại A. x = 4 . B. x = 0 . C. x = 1 − . D. x = 1 .
Câu 29. Cho hàm số y = f ( x) liên tục trên đoạn 1 − ;
1 và có đồ thị như hình vẽ.
Gọi M và m lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên đoạn 1 − ;
1 . Giá trị của M − m bằng A. 0 . B. 1. C. 2 . D. 3 .
Câu 30. Cho hàm số y = f ( x) 3
= x +3x . Hỏi khẳng định nào sau đây là khẳng định đúng ? Trang 4
A. Hàm số f ( x) đồng biến trên .
B. Hàm số f ( x) nghịch biến trên ( 1 − ;0) .
C. Hàm số f ( x) nghịch biến trên ( ;0 − ).
D. Hàm số f ( x) không đổi trên .
Câu 31. Cho log b = 2 và log c = 3 . Tính P = ( 2 3 log b c . a ) a a
A. P = 13
B. P = 31
C. P = 30
D. P = 108
Câu 32. Cho hình hộp chữ nhật AB D
C .A' B 'C ' D ' có AB = a , D
A = 2 2a , AA' = 3a . Góc giữa đường
thẳng A'C và mặt phẳng ( D ABC ) bằng A. 45 . B. 90 . C. 60 . D. 30 . 2 2 2 Câu 33. Cho
f (x)dx = 2 và
g(x)dx = 1 −
, khi đó x + 2 f (x) +3g(x)dx bằng 1 − 1 − 1 − 5 7 17 11 A. B. C. D. 2 2 2 2
Câu 34. Trong không gian Oxyz , mặt phẳng đi qua hai điểm A(0;1;0), B(2;0; )
1 và vuông góc với mặt phẳng
(P): x− y −5 = 0 có phương trình là
A. x + y − z +1 = 0.
B. x − 2y − 6z − 2 = 0 .
C. x − 2y − 6z + 2 = 0.
D. x + y − z −1 = 0 .
Câu 35. Số phức z thỏa mãn: z − (2 + 3i) z = 1− 9i là A. 2 + i . B. 2 − − i . C. 3 − − i . D. 2 − i
Câu 36. Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và ; D AB = AD = 2 ; a DC = a .
Điểm I là trung điểm đoạn ,
AD hai mặt phẳng (SIB) và (SIC) cùng vuông góc với mặt phẳng ( ABCD) . Mặt
phẳng (SBC) tạo với mặt phẳng ( ABCD) một góc 60. Tính khoảng cách từ D đến (SBC) theo a . a 15 9a 15 2a 15 9a 15 A. . B. . C. . D. . 5 10 5 20
Câu 37. Một hộp đựng 10 chiếc thẻ được đánh số từ 0 đến 9 . Lấy ngẫu nhiên ra 3 chiếc thẻ, tính xác suất để 3
chữ số trên 3 chiếc thẻ được lấy ra có thể ghép thành một số chia hết cho 5 . 8 7 2 3 A. . B. . C. . D. . 15 15 5 5
Câu 38. Trong không gian với hệ tọa độ Oxyz , cho (P): 2x − 5y + z −1 = 0 và A(1; 2; − ) 1 . Đường thẳng
qua A và vuông góc với ( P) có phương trình là x = 2 + t x = 3+ 2t x = 1+ 2t x = 3− 2t
A. y = −5 + 2t . B. y = 3 − − 5t .
C. y = 2 − 5t . D. y = 3 − + 5t . z = 1− t z = 1+ t z = 1+ t z = t − +
Câu 39. Có bao nhiêu số nguyên x ( 2
− 022;2022) thỏa mãn ( 2x 1 3
−7.3x + 2) log 2x −1 −2 0 ? 3 ( ) A. 2022 . B. 2021. C. 2018 . D. 2017 . Trang 5 Câu 40. Cho hàm số
f ( x) = x( x − )
1 ( x − 2)( x − )
3 ( x − 4)( x −5)( x − 6)( x − 7) . Hỏi đồ thị hàm số
y = f ( x) cắt trục hoành tại tất cả bao nhiêu điểm phân biệt? A. 1. B. 6 . C. 0 . D. 7 . 1
Câu 41. Cho hàm số y = f ( x) biết f ( ) 1 0 = và ( ) 2 = x f x
xe với mọi x
. Khi đó xf (x)dx bằng 2 0 e +1 e −1 e −1 e +1 A. . B. . C. . D. . 4 4 2 2
Câu 42. Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a . Hình chiếu vuông góc của S trên đáy là 2
điểm H trên cạnh AC sao cho AH =
AC ; mặt phẳng (SBC) tạo với đáy một góc 60o . Thể tích khối chóp 3 S.ABC là? 3 a 3 3 a 3 3 a 3 3 a 3 A. B. C. D. 12 48 36 24
Câu 43. Tìm số thực
m = a − b 20 (a, b là các số nguyên khác 0) để phương trình 2
2z + 2(m −1)z + (2m +1) = 0 có hai nghiệm phức phân biệt z1, z2 thỏa mãn z + z = 10 . Tìm a. 1 2 A.1 B. 2 C. 3 D.4
Câu 44. Cho số phức z thỏa mãn
(1+i) z +1−3i = 3 2 . Giá trị lớn nhất của biểu thức
P = z + 2 + i + 6 z − 2 − 3i bằng A. 5 6 . B. 15 (1+ 6 ) . C. 6 5 . D. 10 + 3 15 . Câu 45. Cho hàm số 4 2
y = ax + bx + c có đồ thị (C) , biết rằng (C) đi qua điểm A( 1
− ;0), tiếp tuyến d tại A
của (C ) cắt (C ) tại hai điểm có hoành độ lần lượt là 0 và 2 và diện tích hình phẳng giới hạn bởi d , đồ thị (C ) 28
và hai đường thẳng x = 0 ; x = 2 có diện tích bằng
(phần tô màu trong hình vẽ). 5
Diện tích hình phẳng giới hạn bởi (C ) và hai đường thẳng x = 1
− ; x = 0 có diện tích bằng 2 1 2 1 A. . B. . C. . D. . 5 4 9 5 Trang 6
Câu 46. Trong không gian Oxyz , cho các điểm A(1;2;0), B(2;0;2),C (2; 1
− ;3),D(1;1;3) . Đường
thẳng đi qua C và vuông góc với mặt phẳng ( ABD) có phương trình là x = 2 − + 4t x = 4 + 2t x = 2 − − 4t x = 2 + 4t A. y = 4 − + 3t .
B. y = 3 − t . C. y = 2 − − 3t . D. y = 1 − + 3t . z = 2 + t z = 1+ 3t z = 2 − t z = 3 − t
Câu 47. Cho hình nón tròn xoay có chiều cao bằng 2a , bán kính đáy bằng 3a . Một thiết diện đi qua đỉnh của 3a
hình nón có khoảng cách từ tâm của đáy đến mặt phẳng chứa thiết diện bằng
. Diện tích của thiết diện đó bằng 2 2 2a 3 2 2 2 12a 24a 3 A. . B. 12a 3 . C. . D. . 7 7 7 Câu 48. Có
bao nhiêu cặp số nguyên dương ( ;
x y) thỏa mãn điều kiện x 2020 và
3(9y + 2y) x + log (x + )3 1 − 2 ? 3 A. 4 . B. 2 . C. 3772 . D. 3774 .
Câu 49. Trong không gian với hệ tọa độ Oxyz , gọi điểm M ( ; a ;
b c) (với a , b , c là các phân số tối giản) thuộc mặt cầu (S) 2 2 2
: x + y + z − 2x − 4y − 4z − 7 = 0 sao cho biểu thức T = 2a + 3b + 6c đạt giá trị lớn nhất. Khi đó
giá trị biểu thức P = 2a − b + c bằng 12 51 A. . B. 8 . C. 6 . D. . 7 7
Câu 50. Cho hàm số y = f (x) có đạo hàm f ( ¢ x) 2 = x ( 2 x - x + )( 2 3
2 x - x), với mọi x Î ¡ . Có bao nhiêu
giá trị nguyên dương của tham số m để hàm số y = f ( 2
x −16x + 2m) có 5 điểm cực trị? A. 30 . B. 31. C. 32 . D. 33 .
LỜI GIẢI CHI TIẾT
Câu 1. Cho số phức z = 2 + i . Tính z .
A. z = 5
B. z = 5
C. z = 2 D. z = 3 Lời giải Chọn A Ta có 2 z = 2 +1 = 5 .
Câu 2. Trong không gian với hệ tọa độ Oxyz , cho mặt cầu (S) có phương trình 2 2 2
x + y + z + 4x − 2 y − 4 = 0
.Tính bán kính R của (S). A. 1. B. 9 . C. 2 . D. 3 . Lời giải ChọnD. Trang 7
Giả sử phương trình mặt cầu 2 2 2 2 2 2
(S) : x + y + z − 2ax − 2by − 2cz + d = 0 (a + b + c − d 0) Ta có: a = 2
− ,b =1,c = 0,d = 4 − Bán kính 2 2 2
R = a + b + c − d = 3.
Câu 3. Điểm nào dưới đây thuộc đồ thị của hàm số 3
y = −x + 2x +1
A. Điểm M (0; − ) 1 . B. Điểm N ( 1 − ; 4 − ) .
C. Điểm P (1; 2) . D. Điểm Q ( 1 − ;4) . Lời giải Chọn C
Câu 4. Cho mặt cầu có diện tích bằng 2
16 a . Khi đó, bán kính mặt cầu bằng a 2 A. 2 2a B. 2a C. 2a D. 2 Lời giải Chọn C Ta có: 2 2
S = 4 R =16 a R = 2a
Câu 5. Trong các khẳng định sau, khẳng định nào sai? 2 x e x 2
A. 2x d = 2x x ln 2 + C . B. e dx = + C . 2 1 1 C. cos 2 d x x = sin 2x + C . D.
dx = ln x +1 + C ( x − ) 1 . 2 x +1 Lời giải Chọn A 2x x Ta có: 2 dx = + C . ln 2
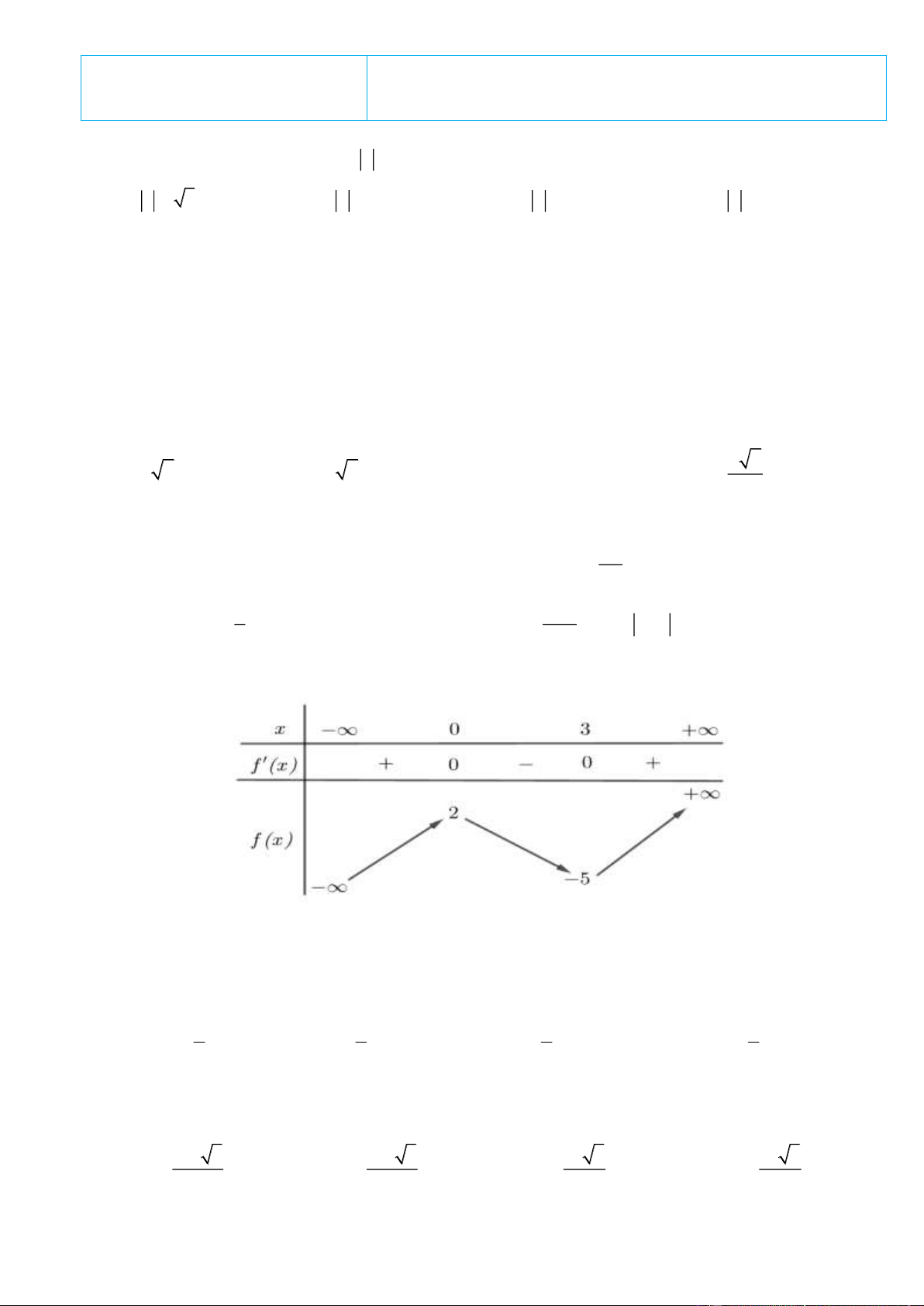
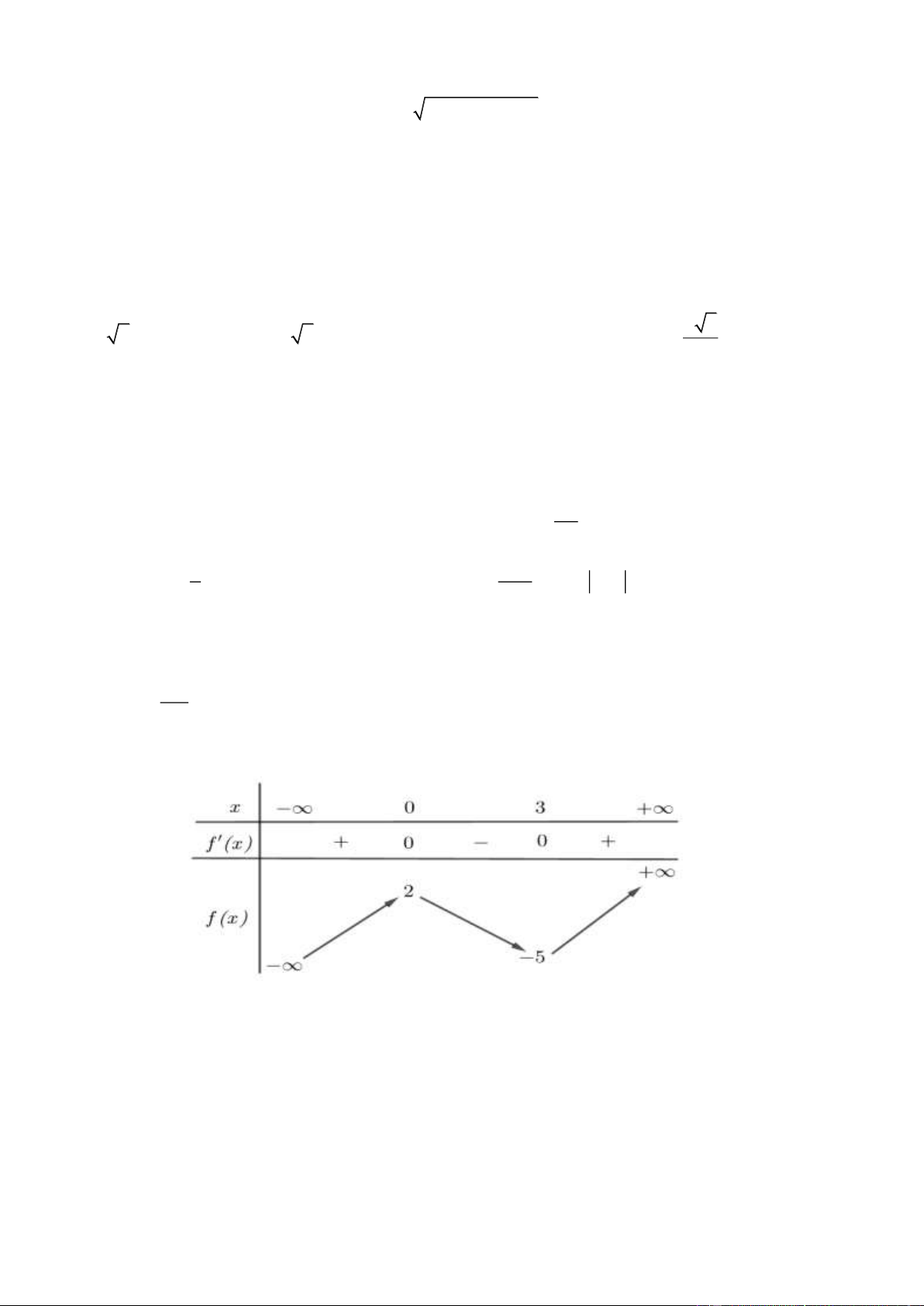
Câu 6. Cho hàm f ( x) có bảng biến thiên như sau:
Giá trị cực tiểu của hàm số đã cho bằng A. 3 . B. −5 . C. 0 . D. 2 . Lời giải Chọn B.
Từ BBT ta có hàm số đạt giá trị cực tiểu f (3) = 5 − tại x = 3
Câu 7. Tập nghiệm của bất phương trình log x −1 1 là 0,5 ( ) Trang 8 3 3 3 3 A. − ; − . B. 1; . C. ;+ . D. 1; . 2 2 2 2 Lời giải Bất phương trình 3
0 x −1 0,5 1 x . 2 3
Vậy tập nghiệm bất phương trình đã cho là: S= 1; . 2
Câu 8. Cho hình chóp S.ABC có đáy là tam giác đều cạnh a và chiều cao 4a . Tính thể tích của hình chóp đã cho. 3 2a 3 3 4a 3 3 a 3 3 a 3 A. V = . B. V = . C. V = . D. V = . 3 3 3 4 Lời giải Chọn C 2 a 3
Do đáy là tam giác đều nên S = . ABC 4 2 3 1 1 a 3 a 3 Mà V = S .h = . .4a = . 3 ABC 3 4 3 −
Câu 9. Tập xác định của hàm số y = ( x − ) 4 2 4 là A. . B. ( 2 − ;2) . C. \ 2 . D. \ 4 . Lời giải Chọn C
Câu 10. Giải phương trình log (x −1) = 3. 4
A. x = 65
B. x = 80
C. x = 82 D. x = 63 Lời giải Chọn A
ĐK: x −1 0 x 1
Phương trình log x −1 = 3 3
x −1 = 4 x = 65 . 4 ( ) 1 3 3 Câu 11. Cho f (x) dx = 1 − ; f (x) dx = 5 . Tính f (x) dx 0 0 1 A. 1. B. 4. C. 6. D. 5. Lời giải 3 1 3 3 3 1 Ta có f (x) dx = f (x) dx + f (x) dx f (x) dx = f (x) dx − f (x) dx = 5+ 1= 6 0 0 1 1 0 0 3 Vậy f (x) dx = 6 1
Câu 12. Cho số phức z = 3
− + 2i , số phức (1−i) z bằng Trang 9 A. 1 − −5i B. 5 − i . C. 1− 5i . D. 5 − + i . Lời giải Chọn D. Vì z = 3
− − 2i nên ta có (1−i) z = (1−i)( 3 − − 2i) = 5 − + i
Câu 13. Trong không gian Oxyz , cho mặt phẳng (P) : 4x + 3y + z −1 = 0 . Véctơ nào sau đây là một véctơ pháp
tuyến của (P) A. n = − − 4 (3;1; ) 1 . B. n = 3 (4;3 ) ;1 . C. n = − 2 (4; 1; ) 1 . D. 1 n = (4;3; ) 1 . Lời giải Chọn B
(P):4x +3y + z −1= 0. Véctơ n = 3 (4;3 )
;1 là một véctơ pháp tuyến của ( P) .
Câu 14. Trong không gian Oxyz cho a = (2;3;2) và b = (1;1;− )
1 . Vectơ a − b có tọa độ là A. (3;4; ) 1 . B. ( 1 − ;− 2;3). C. (3;5; ) 1 . D. (1;2;3) . Lời giải
Ta có: a − b = (2 −1;3 −1;2 + ) 1 = (1;2;3) .
Câu 15. Tìm tọa độ điểm M là điểm biểu diễn số phức z biết z thỏa mãn phương trình (1+ i) z = 3 − 5i . A. M ( 1 − ;4) . B. M ( 1 − ;− 4). C. M (1; 4) .
D. M (1; − 4) . Lời giải − i
Ta có (1+ i) z = 3 − 3 5 5i z =
z = − − i . 1+ 1 4 i Suy ra z = 1
− + 4i . Vậy M ( 1 − ;4) .
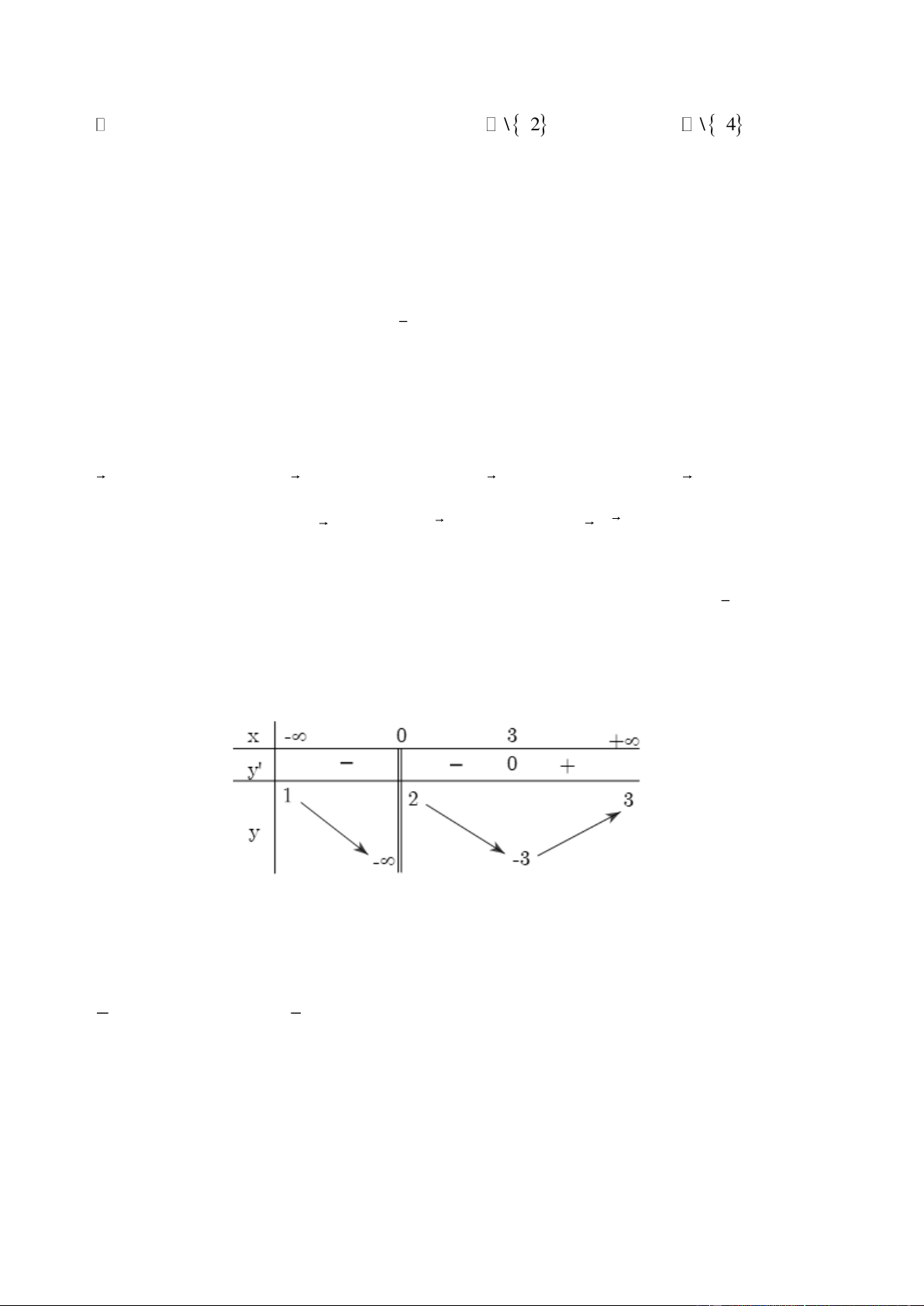
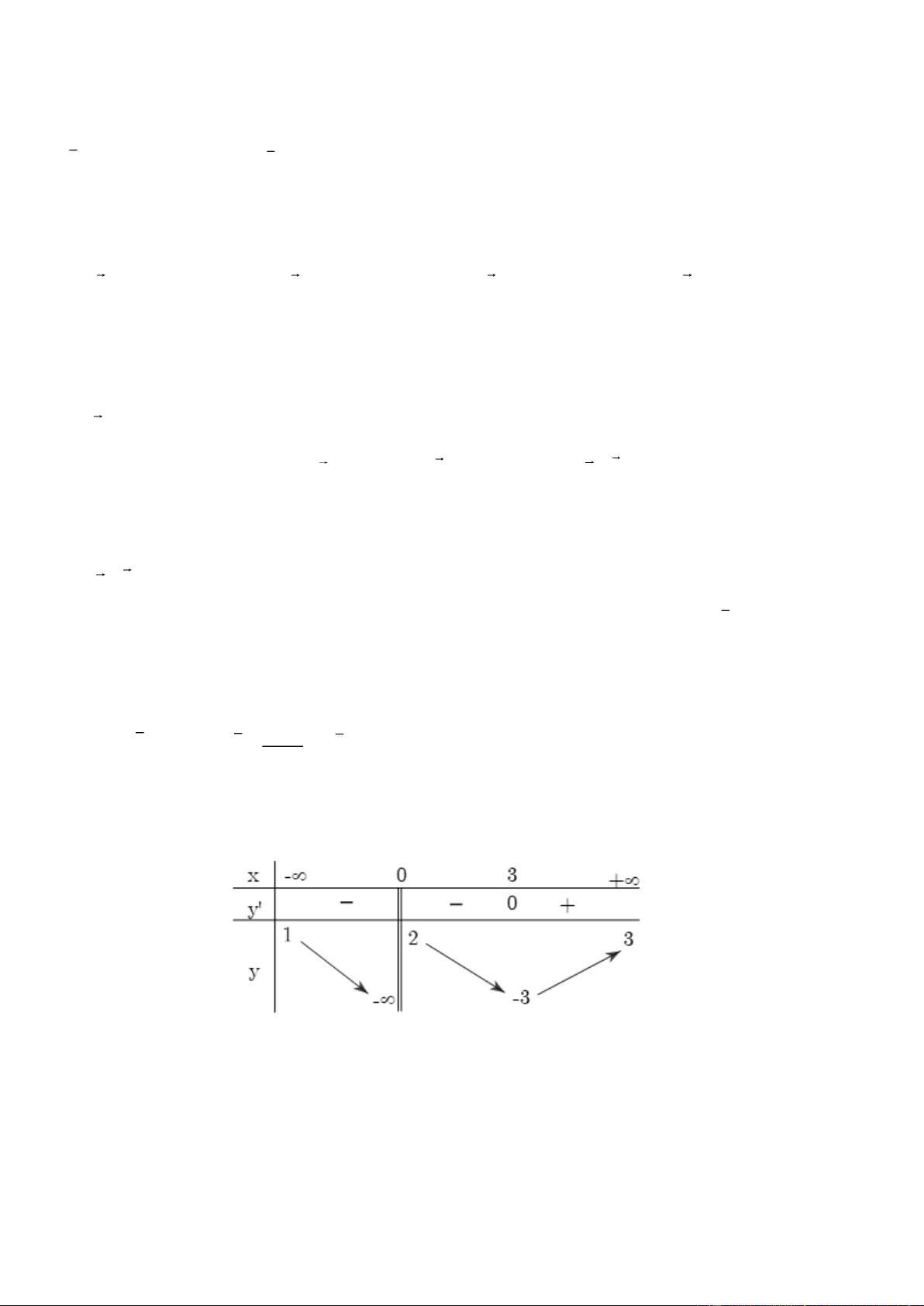
Câu 16. Cho hàm số y = f ( x) có báng biến thiên như sau:
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là: A. 2. B. 3. C. 4. D. 1. Lời giải Chọn B
Nhìn bảng biến thiên ta thấy x=0 hàm số không xác định nên x=0 là TCĐ của đồ thị hàm số
lim f ( x) = 3 y = 3 là TCN của đồ thị hàm số x→+ Trang 10
lim f ( x) =1 y =1là TCN của đồ thị hàm số x→−
Vậy hàm số có 3 tiệm cận
Câu 17. Với a là hai số thực dương tùy ý, log ( 3 a bằng 2 ) 3 1 A. log a . B. log a .
C. 3 + log a .
D. 3log a . 2 2 2 3 2 2 Lời giải Chọn D Ta có: log ( 3 a = 3log . a 2 ) 2
Câu 18. Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên? A. 4 2
y = x + 2x . B. 3
y = −x − 3x . C. 3
y = x − 3x . D. 4 2
y = −x + 2x . Lời giải Chọn C
Đây là đồ thị của hàm số bậc ba với hệ số a 0 nên chọn C. x −1 y +1 z − 2
Câu 19. Trong không gian Oxyz , điểm nào dưới đây thuộc đường thẳng = = ? 2 1 − 3 A. Q( 2 − ;1;− ) 3 . B. P(2; 1 − ; ) 3 . C. M ( 1 − ;1; 2 − ) . D. N (1; 1 − ;2) . Lời giải 1−1 1 − +1 2 − 2 Xét điểm N (1; 1 − ;2) ta có = = nên điểm N (1; 1 − ; 2
− ) thuộc đường thẳng đã cho. 2 1 − 3
Câu 20. Với k và n là hai số nguyên dương (k n) , công thức nào sao đây đúng? n k n n k ! k ! k ! k ! A. A = A = A = . D. A = n k !(n − . B. k )! n (k − . C. n)! n n k ! (n − . k )! Lời giải Chọn D n k ! A = n (n − k )!
Câu 21. Diện tích đáy của khối lăng trụ có thể tích V và có chiều cao h là Trang 11 3V 3h V h A. B = . B. B = . C. B = . D. B = . h V h V Lời giải Chọn C V
Diện tích đáy của khối lăng trụ có thể tích V =
và có chiều cao h là: B . h Câu 22. Cho ( ) lo 81 g 2.3 x f x = + 3 . Tính f ( ) 1 − A. f ( ) 1 1 = . B. f ( ) 1 1 = . C. f ( ) 1 = 1. D. f ( ) 1 = 1. 2 2 Lời giải Chọn A TXĐ: D = (0;+) . x 1 f ( x) log x log 81 = 2.3 .ln 3.(log x 81 = 2.3 .ln 3. 81 ) x ln 81 f ( ) 1 0 1 = 1 2.3 .ln 3. = 1 2.1.ln 3. = . ln 81 4 ln 3 2
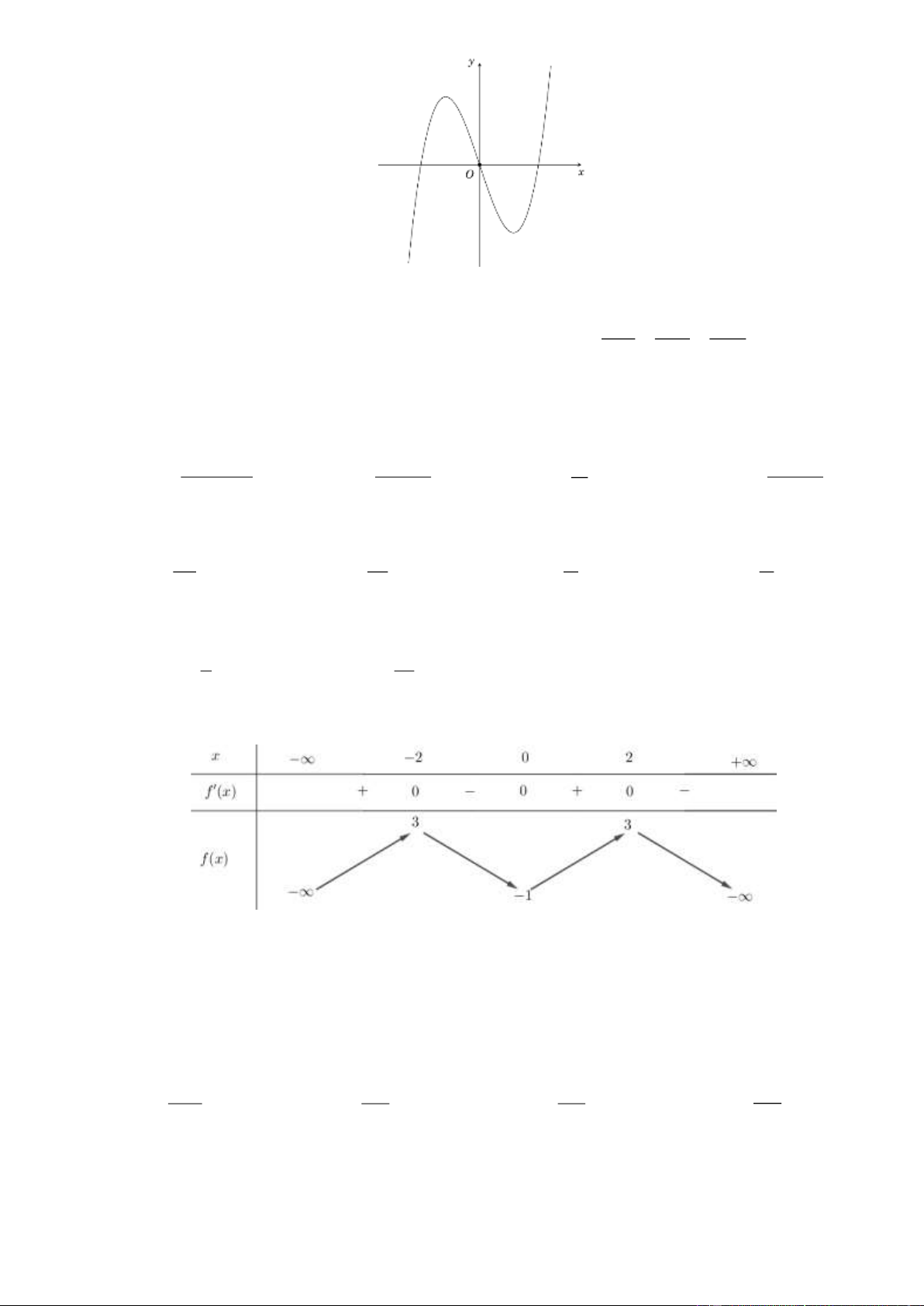
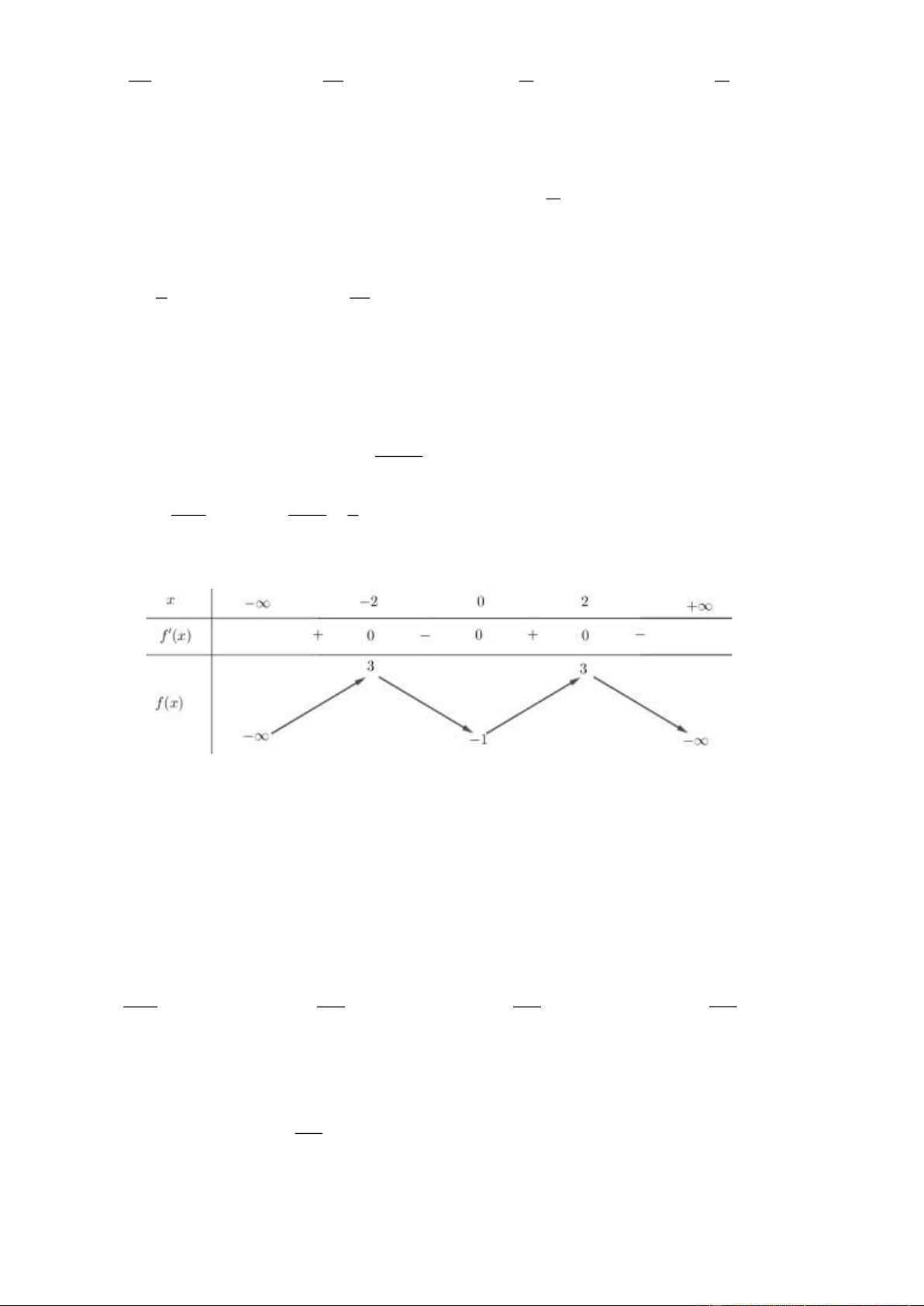
Câu 23. Cho hàm số y = f ( x) có bảng biến thiên như sau:
Hàm số y = f (x)nghịch biến trên khoảng nào dưới đây? (0;+) (− ; 2 − ) (0;2) ( 2 − ;0) A. B. C. D. Lời giải Chọn D
Câu 24. Cho hình trụ có diện tích xung quanh S
và độ dài đường sinh 3l . Bán kính đáy r của hình trụ đã cho xq
được tính theo công thức nào sau đây? 6S S S 2 l xq xq xq A. r = = = = . B. r . C. r . D. r . l 2 l 6 l Sxq Lời giải Chọn C S Bán kính đáy r xq
của hình trụ là: r = . 6 l Trang 12 Câu 25. Cho f ( ) x , g( ) x là các hàm số liên tục trên đoạn 2;6 và thỏa mãn 3 6 6
f (x)dx = 3; f (x)dx = 7; g(x)dx = 5
. Hãy tìm mệnh đề KHÔNG đúng. 2 3 3 6 3
A. [3g(x) − f (x)]dx = 8
B. [3 f (x) − 4]dx = 5 3 2 6 ln e 6 ln e C.
[2f (x) −1]dx = 16 D.
[4 f (x) − 2g(x)]dx = 16 2 3
Câu 26. Cho cấp số cộng (u có số hạng đầu u = 2 và u = 5 . Giá trị của u bằng n ) 2 3 5 A. 12 . B. 15 . C. 11. D. 25 . Lời giải Chọn C
Ta có: d = u − u = 5 − 2 = 3 u = u + d = 5 + 3 = 8 u = u + d = 11. 3 2 4 3 5 4 −x e
Câu 27. Họ nguyên hàm của hàm số x y = e 2 + là 2 cos x x 1 x 1 A. 2 x
e + tan x + C B. 2 x
e − tan x + C C. 2e − + C D. 2e + + C cos x cos x Lời giải −x e x x 1
Ta có: y = e 2 + = 2e + 2 2 cos x cos x x 1 = 2 + = 2 x ydx e dx
e + tan x + C . 2 cos x
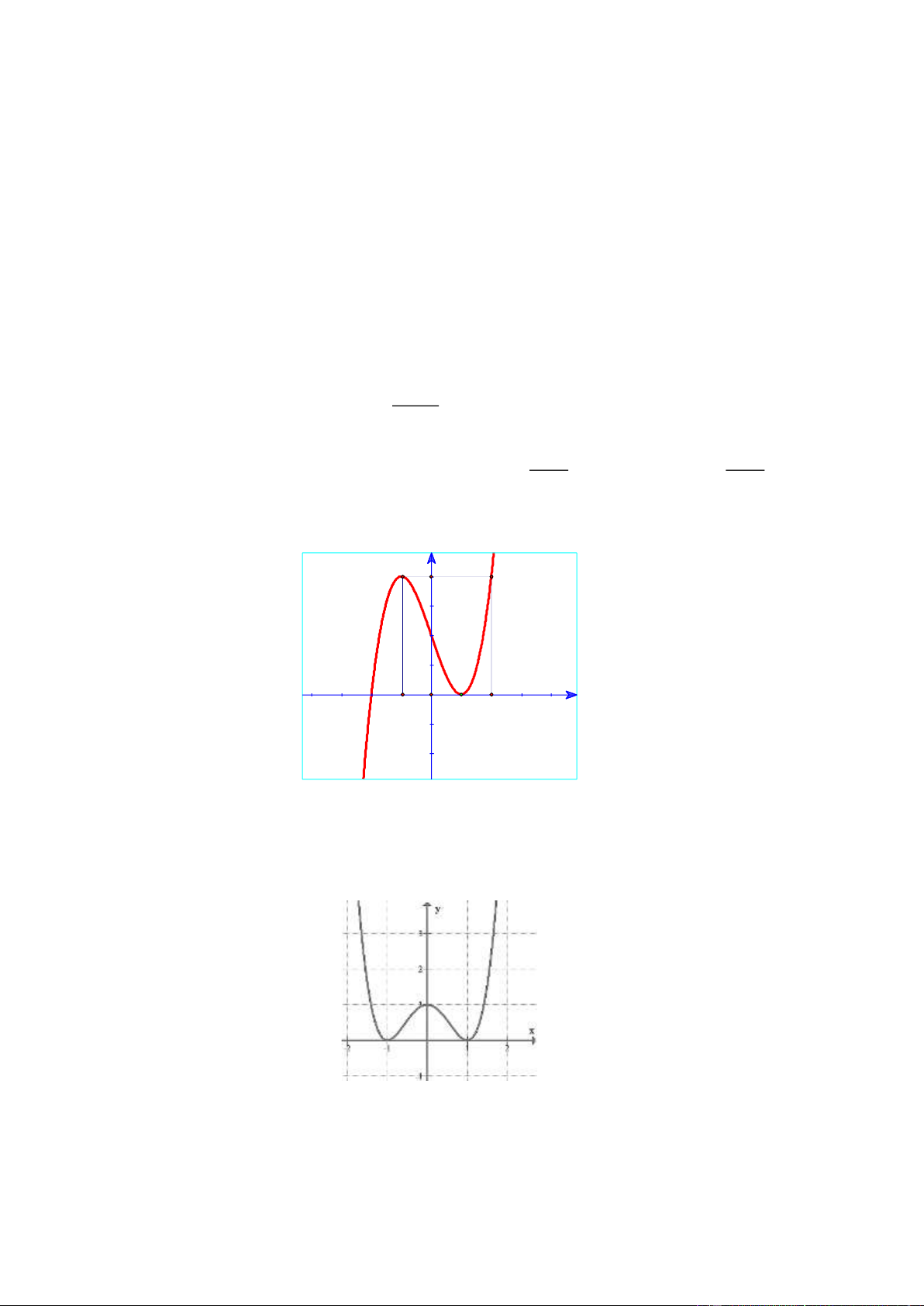
Câu 28. Cho hàm số y = f ( x) có đồ thị như hình vẽ. y 4 2 -2 O x -1 1 2
Hàm số đã cho đạt cực đại tại A. x = 4 . B. x = 0 . C. x = 1 − . D. x = 1 . Lời giải Chọn C
Câu 29. Cho hàm số y = f ( x) liên tục trên đoạn 1 − ;
1 và có đồ thị như hình vẽ. Trang 13
Gọi M và m lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên đoạn 1 − ;
1 . Giá trị của M − m bằng A. 0 . B. 1. C. 2 . D. 3 . Lời giải
Từ đồ thị ta thấy M =1, m = 0 nên M − m = 1.
Câu 30. Cho hàm số y = f ( x) 3
= x +3x . Hỏi khẳng định nào sau đây là khẳng định đúng ?
A. Hàm số f ( x) đồng biến trên .
B. Hàm số f ( x) nghịch biến trên ( 1 − ;0) .
C. Hàm số f ( x) nghịch biến trên ( ;0 − ).
D. Hàm số f ( x) không đổi trên . Lời giải Chọn đáp án A. Ta có: 3
y = f (x) = x + 3x . Tập xác định: D = . 2
f '(x) = 3x + 3 0 x .
Suy ra hàm số đồng biến trên .
Câu 31. Cho log b = 2 và log c = 3 . Tính P = ( 2 3 log b c . a ) a a
A. P = 13
B. P = 31
C. P = 30
D. P = 108 Lời giải Chọn A Ta có: ( 2 3 log
b c ) = 2log b + 3log c = 2.2 + 3.3 =13 . a a a
Câu 32. Cho hình hộp chữ nhật AB D
C .A' B 'C ' D ' có AB = a , D
A = 2 2a , AA' = 3a . Góc giữa đường
thẳng A'C và mặt phẳng ( D ABC ) bằng A. 45 . B. 90 . C. 60 . D. 30 . Lời giải Chọn D Trang 14
Ta thấy: hình chiếu của A'C xuống ( D
ABC ) là AC do đó ( A'C;( ABCD)) = ( A'C; AC ) = A'CA . Ta có: 2 2 AC = AB + AD = 3a .
Xét tam giác A'CA vuông tại C ta có:
(A CA) A'A 3a 3 tan ' = = = AC 3a 3 A'CA 30 = . 2 2 2 Câu 33. Cho
f (x)dx = 2 và
g(x)dx = 1 −
, khi đó x + 2 f (x) +3g(x)dx bằng 1 − 1 − 1 − 5 7 17 11 A. B. C. D. 2 2 2 2 Lời giải Chọn A 2 2 2 2 3 5
Ta có x + 2 f (x) + 3g(x)dx = xdx + 2
f (x)dx + 3 g(x)dx = + 4 − 3 = 2 2 1 − 1 − 1 − 1 −
Câu 34. Trong không gian Oxyz , mặt phẳng đi qua hai điểm A(0;1;0), B(2;0; )
1 và vuông góc với mặt phẳng
(P): x− y −5 = 0 có phương trình là
A. x + y − z +1 = 0 .
B. x − 2y − 6z − 2 = 0 .
C. x − 2y − 6z + 2 = 0.
D. x + y − z −1 = 0 .
Câu 35. Số phức z thỏa mãn: z − (2 + 3i) z = 1− 9i là A. 2 + i . B. 2 − − i . C. 3 − − i . D. 2 − i Lời giải Gọi
z = a + bi với 2
a,b ; i = 1 −
z = a −bi
z − (2 + 3i) z = 1− 9i a + bi − (2 + 3i)(a − bi) = 1− 9i
a +bi −(2a −2bi +3ai +3b) =1−9i − − = = a 3b 1 a 2 a − −3b +( 3
− a +3b)i =1−9i
z = 2 − i 3 − a + 3b = 9 − b = −1
Vậy chọn đáp án D. Trang 15
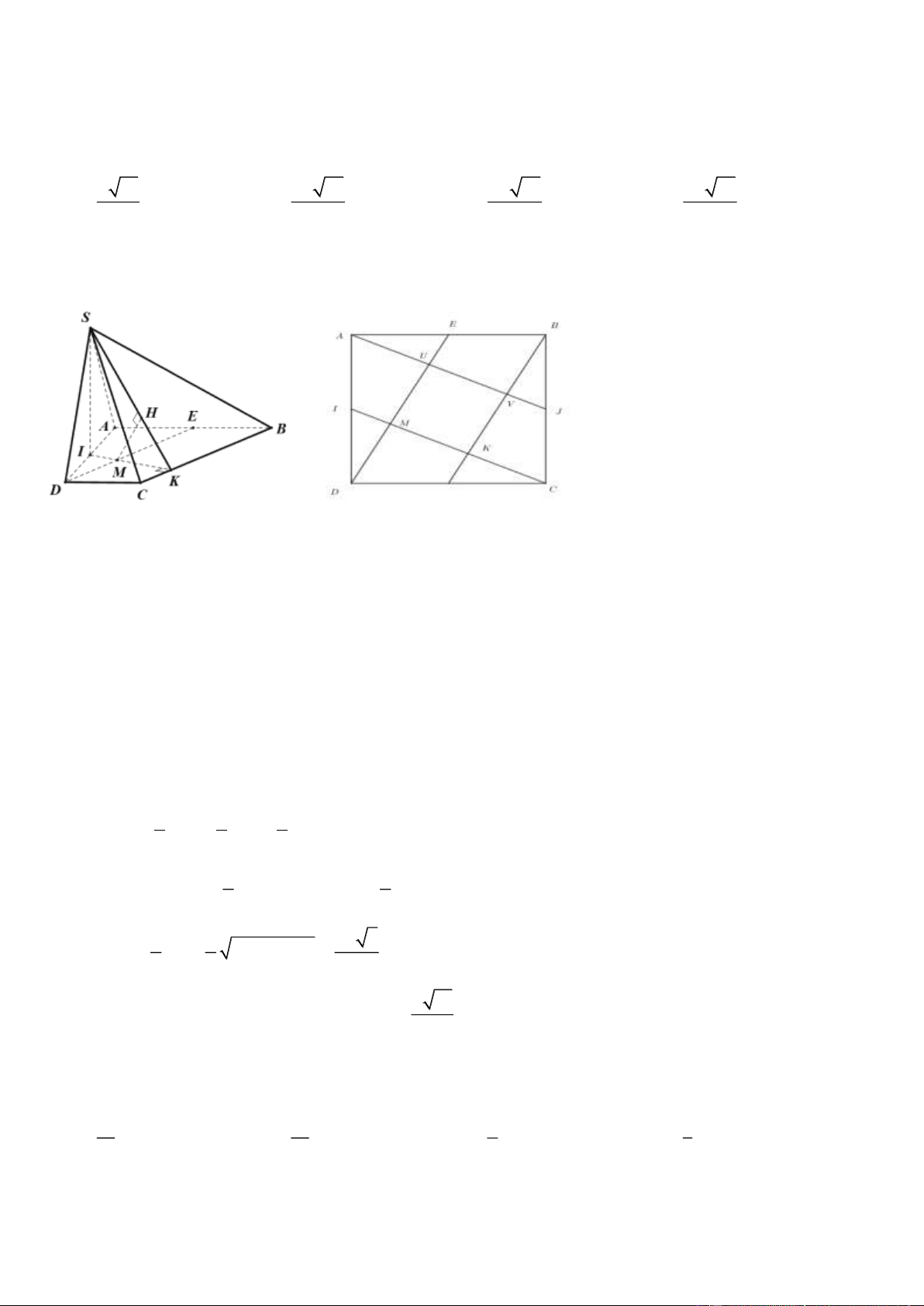
Câu 36. Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và ; D AB = AD = 2 ; a DC = a .
Điểm I là trung điểm đoạn ,
AD hai mặt phẳng (SIB) và (SIC) cùng vuông góc với mặt phẳng ( ABCD) . Mặt
phẳng (SBC) tạo với mặt phẳng ( ABCD) một góc 60. Tính khoảng cách từ D đến (SBC) theo a . a 15 9a 15 2a 15 9a 15 A. . B. . C. . D. . 5 10 5 20 Lời giải Chọn A
Theo đề ta có SI ⊥ ( ABCD).
Gọi K là hình chiếu vuông góc của I trên BC .
Suy ra: Góc giữa hai mặt phẳng ((SBC),( ABCD)) = SKI = 60
Gọi E là trung điểm của ,
AB M = IK D . E
Do BCDE là hình bình hành nên DE // (SBC) d ( ,
D (SBC)) = d (DE,(SBC)) = d (M,(SBC))
Gọi H là hình chiếu vuông góc của M trên SK . Suy ra d (M,(SCD)) = MH 1 1 1 Dễ thấy: IM = AU = KN = MK 2 2 2 1 5
IN = IM + MK + KN =
MK + MK + MK = MK 2 2 2 2 2a 5 Suy ra: 2 2 MK = IN = ID + DN = . 5 5 5 a 15
Trong tam giác MHK, ta có: MH = MK.sin 60 = 5
Câu 37. Một hộp đựng 10 chiếc thẻ được đánh số từ 0 đến 9 . Lấy ngẫu nhiên ra 3 chiếc thẻ, tính xác suất để 3
chữ số trên 3 chiếc thẻ được lấy ra có thể ghép thành một số chia hết cho 5 . 8 7 2 3 A. . B. . C. . D. . 15 15 5 5 Lời giải Chọn A Trang 16
Số phần tử của không gian mẫu là n() 3 = C =120 . 10
Gọi A là biến cố ‘‘ 3 chữ số trên 3 chiếc thẻ được lấy ra có thể ghép thành một số chia hết cho 5 ’’.
Để biến cố A xảy ra thì trong 3 thẻ lấy được phải có thẻ mang chữ số 0 hoặc chữ số 5 . Ta đi tìm số phần tử của
biến cố A , tức là 3 thẻ lấy ra không có thẻmang chữ số 0 và cũng không có thẻ mang chữ số 5 . Ta có n(A) 3
= C n( A) 3 3 = C −C = 64 . 8 10 8 n A 64 8
Vậy xác suất cần tìm là P( A) ( ) = = = . n() 120 15
Câu 38. Trong không gian với hệ tọa độ Oxyz , cho (P): 2x − 5y + z −1 = 0 và A(1; 2; − ) 1 . Đường thẳng
qua A và vuông góc với ( P) có phương trình là x = 2 + t x = 3+ 2t x = 1+ 2t x = 3− 2t
A. y = −5 + 2t . B. y = 3 − − 5t .
C. y = 2 − 5t . D. y = 3 − + 5t . z = 1− t z = 1+ t z = 1+ t z = t − Lời giải Chọn D
Mặt phẳng (P) có một vectơ pháp tuyến là n = (2; 5 − ; ) 1 .
Đường thẳng vuông góc với (P) nên có một vectơ chỉ phương là u = −n = ( 2 − ;5;− ) 1 . x = 1− 2t
đi qua A nên có phương trình y = 2 + 5t . z = −1−t Cho t = 1
− ta được điểm B(3; 3 − ;0). x = 3− 2t
Vì thế có phương trình y = 3 − + 5t . z = t − +
Câu 39. Có bao nhiêu số nguyên x ( 2
− 022;2022) thỏa mãn ( 2x 1 3
−7.3x + 2) log 2x −1 −2 0 ? 3 ( ) A. 2022 . B. 2021. C. 2018 . D. 2017 . Lời giải Chọn D 2x −1 0 9 Điều kiện x
log 2x −1 − 2 0 2 3 ( ) Ta có ( 2x 1
3 + − 7.3x + 2) log 2x −1 − 2 0 3 ( ) 2 x 1 3 + − 7.3x + 2 0 ( ) 1 log 2x −1 − 2 = 0 2 3 ( ) ( ) Trang 17 Giải ( ) + 1 : 2x 1 3 −7.3x + 2 0 ( x)2 3. 3 7.3x − + 2 0. 1 t 0 0 t Đặt
3x = t 0 ta được 3 . 2 3
t − 7t + 2 0 t 2 x 1 0 3 − x 1 0 3 3 x 1 − Suy ra 3 . x log 2 3 3 3 x log 2 3x 2 3
Vậy bất phương trình có tập nghiệm là (−;− 1 log 2;+ . 3 ) 9 9
Kết hợp điều kiện x ; + 2 2 9
Giải (2) : log 2x −1 − 2 = 0 x = (thỏa điều kiện) 3 ( ) 2
Do x là số nguyên , x ( 2
− 022;2022) x =5;6;...;202 1
Vậy có 2017 giá trị x cần tìm Câu 40. Cho hàm số
f ( x) = x( x − )
1 ( x − 2)( x − )
3 ( x − 4)( x −5)( x − 6)( x − 7) . Hỏi đồ thị hàm số
y = f ( x) cắt trục hoành tại tất cả bao nhiêu điểm phân biệt? A. 1. B. 6 . C. 0 . D. 7 . Lời giải Chọn D
Ta có f ( x) = 0 có các nghiệm: 0;1;2;3;4;5;6;7 .
Áp dụng định lý Lagrange lần lượt trên các đoạn: 0; 1 ;1; 2 ;2; 3 ;3; 4 ;4; 5 ;5; 6 ;6;7. f 1 − f 0
Chẳng hạn xét trên đoạn 0;
1 thì tồn tại x sao cho: f ( x =
f (x = f 1 − f 0 = 0. Suy 1 ) ( ) ( ) 1 ) ( ) ( ) 1 1− 0
ra x = x là một nghiệm của phương trình f ( x) = 0. 1
Làm tương tự vậy các khoảng còn lại ta suy ra f (x) = 0 có 7 nghiệm phân biệt hay đồ thị hàm số y = f ( x) cắt
trục hoành tại 7 điểm phân biệt. 1
Câu 41. Cho hàm số y = f ( x) biết f ( ) 1 0 = và ( ) 2 = x f x
xe với mọi x
. Khi đó xf (x)dx bằng 2 0 e +1 e −1 e −1 e +1 A. . B. . C. . D. . 4 4 2 2 Lời giải Chọn B 2 2 2 x 1 x 1 Ta có ( ) = ( ).d = . d = .d ( 2 ) = x f x f x x x e x e x e + C . 2 2 Trang 18 Mà ( ) = + = = ( ) 2 1 1 1 1 0 0 = x f C C f x e . 2 2 2 2 1 1 1 1 xf (x) e x x x − 2 2 1 1 dx = xe dx = e d ( 1 1 2 x ) 2 = e = . 2 4 4 4 0 0 0 0
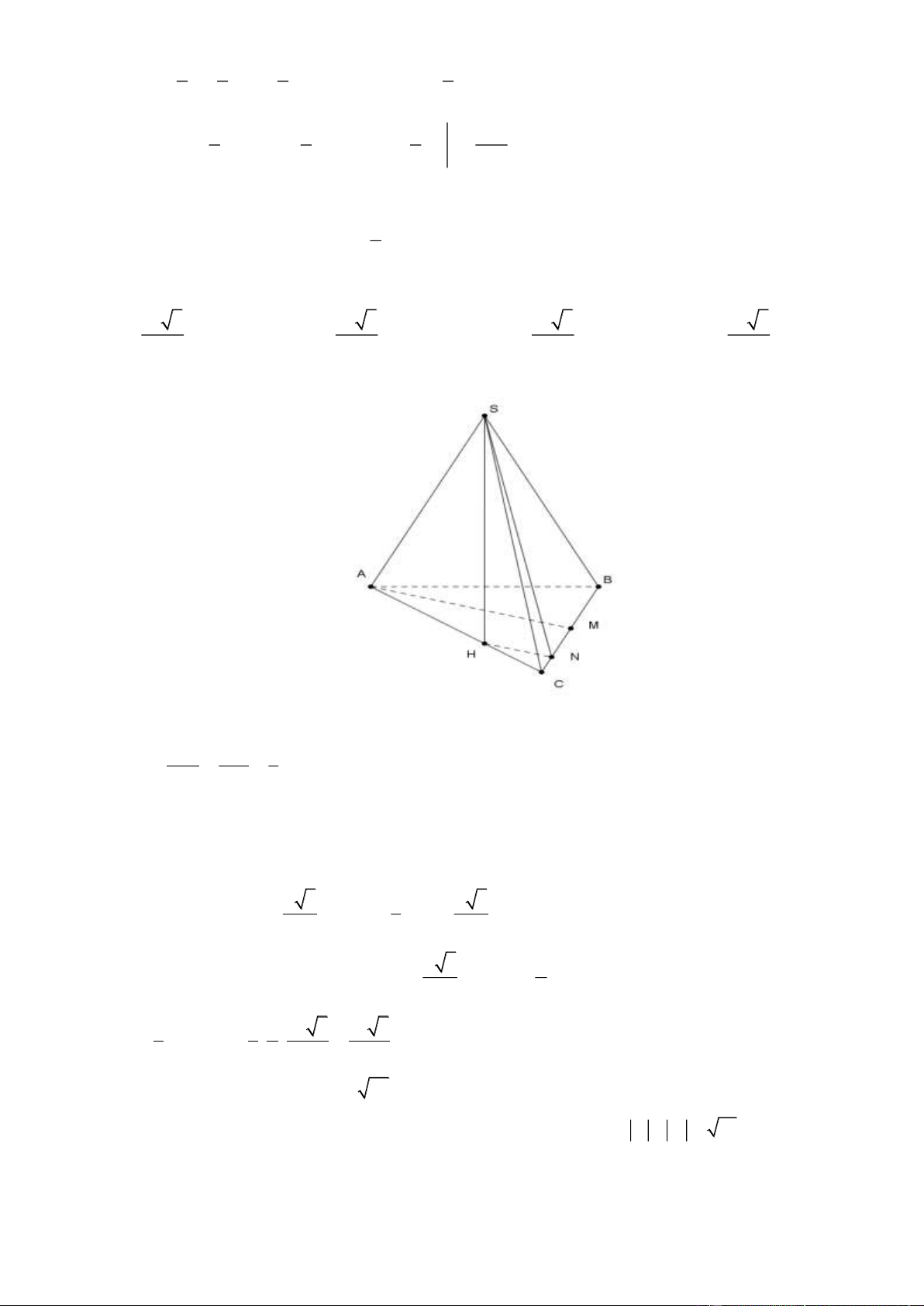
Câu 42. Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a . Hình chiếu vuông góc của S trên đáy là 2
điểm H trên cạnh AC sao cho AH =
AC ; mặt phẳng (SBC) tạo với đáy một góc 60o . Thể tích khối chóp 3 S.ABC là? 3 a 3 3 a 3 3 a 3 3 a 3 A. B. C. D. 12 48 36 24 Lời giải
Gọi M là trung điểm của BC . CN CH 1 N CM : =
= HN//AM . Mà CM CA 3 ABC
đều nên AM ⊥ BC HN ⊥ BC BC ⊥ (SHN ) . Nên ( );( ) = ; = = 60o SBC ABC SN HN SNH . a 3 1 a 3 Do ABC đều nên AM = HN = AM = . 2 3 6 a 3 a S
HN vuông tại H có SH = HN.sin SNH = .sin 60o = . 6 4 2 3 1 1 a a 3 a 3 V = SH.S = . . = . S.ABC 3 ABC 3 4 4 48
Câu 43. Tìm số thực
m = a − b 20 (a, b là các số nguyên khác 0) để phương trình 2
2z + 2(m −1)z + (2m +1) = 0 có hai nghiệm phức phân biệt z z + z = 1, z2 thỏa mãn 10 . Tìm a. 1 2 A.1 B. 2 C. 3 D.4 Lời giải Trang 19 2
' = m −6m−1R
TH1: ' 0 hay m ( ;
− 3 − 10) (3 + 10;+) Khi đó 2 2
z + z = 10 z + z + 2 z z = 10 1 2 1 2 1 2 2m +1 0 2 (1− m) =10 m =1+ 10 (loai) 2
(1− m) − (2m +1) + 2m +1 =10 2m +1 0 m = 3− 20 2
m −6m−11= 0
TH2: ' 0 hay m (3 − 10;3 + 10) 2 2 1− m + i (
− m − 6m −1)
1− m − i −(m − 6m −1)
Khi đó: z + z = 10 + = 10 1 2 2 2 Hay 2 2
(1− m) + (−m + 6m +1) = 10 m = 2
Vậy m = 2 hoặc m = 3 − 20
Câu 44. Cho số phức z thỏa mãn
(1+i) z +1−3i = 3 2 . Giá trị lớn nhất của biểu thức
P = z + 2 + i + 6 z − 2 − 3i bằng A. 5 6 . B. 15 (1+ 6 ) . C. 6 5 . D. 10 + 3 15 . Lời giải Chọn C Cách 1 ( − i
1+ i) z +1− 3i = 1 3 3 2 1+ i z +
= 3 2 z − (1+ 2i) = 3 ( ) 1 . 1+ i Gọi OM = ( ;
x y) , OI = (1; 2) là vec-tơ biểu diễn cho các số phức z = x + iy , w =1+ 2i . Từ ( )
1 có OM − OI = 3 MI = 3. 2 3
Suy ra M thuộc đường tròn (C ) tâm I (1; 2) bán kính R = 3 , (C ) : ( x − ) 1 + ( y − 2) = 9 Gọi OA = ( 2 − ;− )
1 , OB = (2;3) lần lượt là vec-tơ biểu diễn cho số phức a = 2
− −i , b = 2 +3i . Trang 20 Có IA = ( 3 − ;− 3) , IB = (1 ) ;1 . Suy ra IA = 3
− IB IA+3IB = 0 .
Lúc đó P = MA + 6MB = MA + 2. 3MB ( 2 2 3 MA + 3MB ) . 2 2 2 2
Có MA + 3MB = (IA − IM ) + 3(IB − IM ) 2 2 2
= 4IM + IA +3IB . Có 2 IM = 9 , 2 IA =18 , 2 IB = 2 , nên 2 2 MA + 3MB = 60 . Suy ra P 3.60 = 6 5 . MA 3MB Có P = 6 5 = . 1 2
Vậy giá trị lớn nhất của P là P = 6 5 . Cách 2. Giả sử M ( ;
x y) là điểm biểu diễn của số phức z khi đó
( +i) z + − i =
x − y + + (x + y − ) 2 2 1 1 3 3 2 1
3 i = 3 2 x + y − 2x − 4 y − 4 = 0
(x − )2 + ( y − )2 1 2
= 9 . Do đó M thuộc đường tròn tâm I (1;2), bán kính R = 3. a = x −1 Đặt Ta có 2 2
a + b = 9 . Gọi A = ( 2 − ;− ) 1 , B = (2; ) 3 b = y − 2
P = z + + i +
z − − i = MA +
MB = ( x + )2 + ( y + )2 +
(x− )2 +(y − )2 2 6 2 3 6 2 1 6 2 3
= (a + )2 +(b + )2 +
(a − )2 +(b− )2 3 3 6 1
1 = 6(a + b) + 27 + 6 ( 2 − )(a +b)+11
= 6(a +b)+ 27 + 2 ( 6
− )(a +b)+33 (1+ 2)(27 +3 ) 3 = 6 5 . Câu 45. Cho hàm số 4 2
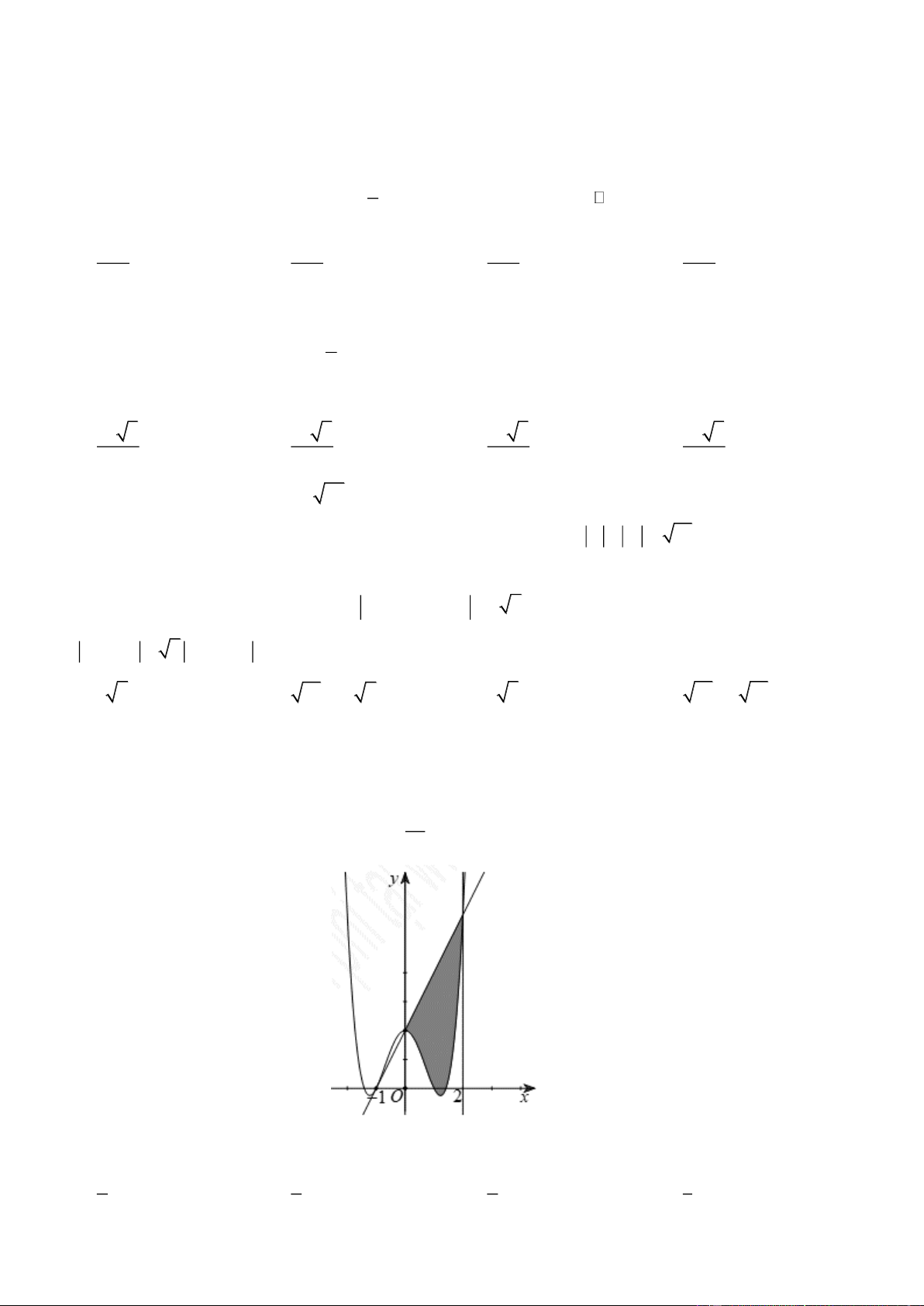
y = ax + bx + c có đồ thị (C) , biết rằng (C) đi qua điểm A( 1
− ;0), tiếp tuyến d tại A
của (C ) cắt (C ) tại hai điểm có hoành độ lần lượt là 0 và 2 và diện tích hình phẳng giới hạn bởi d , đồ thị (C ) 28
và hai đường thẳng x = 0 ; x = 2 có diện tích bằng
(phần tô màu trong hình vẽ). 5
Diện tích hình phẳng giới hạn bởi (C ) và hai đường thẳng x = 1
− ; x = 0 có diện tích bằng Trang 21 2 1 2 1 A. . B. . C. . D. . 5 4 9 5 Lời giải Ta có 3
y = 4ax + 2bx d : y = ( 4
− a − 2b)(x + ) 1 .
Phương trình hoành độ giao điểm của d và (C) là: (− a − b)(x + ) 4 2 4 2
1 = ax + bx + c ( ) 1 . Phương trình ( )
1 phải cho 2 nghiệm là x = 0 , x = 2 . − − = 4a 2b c 12
− a − 6b = 16a + 4b + c 4
− a − 2b − c = 0 (2) .
28a +10b + c = 0 (3) 2 28
Mặt khác, diện tích phần tô màu là = ( 4
− a − 2b)(x + ) 4 2
1 − ax − bx − c dx 5 0 28 = (− 112 32 28 a − b) 32 8 4 4 2 −
a − b − 2c a + b + 2c = − (4). 5 5 3 5 3 5
Giải hệ 3 phương trình (2) , (3) và (4) ta được a =1, b = 3 − , c = 2 . Khi đó, (C) 4 2
: y = x − 3x + 2 , d : y = 2( x + ) 1 . 0 0 1 Diện tích cần tìm là 4 2 S =
x − 3x + 2 − 2 (x + ) 1 dx = ( 4 2
x − 3x − 2x) dx = . 5 1 − 1 −
Câu 46. Trong không gian Oxyz , cho các điểm A(1;2;0), B(2;0;2),C (2; 1
− ;3),D(1;1;3) . Đường
thẳng đi qua C và vuông góc với mặt phẳng ( ABD) có phương trình là x = 2 − + 4t x = 4 + 2t x = 2 − − 4t x = 2 + 4t A. y = 4 − + 3t .
B. y = 3 − t . C. y = 2 − − 3t . D. y = 1 − + 3t . z = 2 + t z = 1+ 3t z = 2 − t z = 3 − t Lời giải Chọn A AB = (1; 2 − ;2) AD = (0; 1 − ;3) AB AD = ( 4 − ; 3 − ;− ) 1
Đường thẳng qua C (2; 1
− ;3) và vuông góc với mặt phẳng ( ABD) có phương trình x = 2 − 4t y = 1 − − 3t z = 3− t Trang 22 Điểm E ( 2 − ; 4
− ;2) thuộc đường thẳng trên, suy ra đường thẳng cần tìm trùng với đường thẳng có phương trình x = 2 − + 4t y = 4 − + 3t z = 2+t
Chọn đáp án đúng là đáp án C
Câu 47. Cho hình nón tròn xoay có chiều cao bằng 2a , bán kính đáy bằng 3a . Một thiết diện đi qua đỉnh của
hình nón có khoảng cách từ tâm của đáy đến mặt phẳng chứa thiết diện bằng 3a . Diện tích của thiết diện đó bằng 2 2 2a 3 2 2 2 12a 24a 3 A. . B. 12a 3 . C. . D. . 7 7 7 Lời giải Chọn D
Xét hình nón đỉnh S có chiều cao SO = 2a , bán kính đáy OA = 3a .
Thiết diện đi qua đỉnh của hình nón là tam giác SAB cân tại S .
+ Gọi I là trung điểm của đoạn thẳng AB . Trong tam giác SOI , kẻ OH ⊥ SI , H SI . AB ⊥ OI +
AB ⊥ (SOI ) AB ⊥ OH . AB ⊥ SO OH ⊥ SI +
OH ⊥ (SAB) ( ( )) 3 , = = a d O SAB OH . OH ⊥ AB 2 1 1 1 4 1 7 6
Xét tam giác SOI vuông tại O , ta có = − = − = = a OI . 2 2 2 OI OH SO 2 2 2 9a 4a 36a 7 2 36a 8a 2 2 2
SI = SO + OI = 4a + = . 7 7 2 36a 3 3a
Xét tam giác AOI vuông tại I , 2 2 2 AI =
AO − OI = 9a − = 7 7 Trang 23 6 3a AB = 2AI = . 7 2 1 1 8a 6 3a 24a 3
Vậy diện tích của thiết diện là: S = .SI.AB = . . = . S AB 2 2 7 7 7 Câu 48. Có
bao nhiêu cặp số nguyên dương ( ;
x y) thỏa mãn điều kiện x 2020 và
3(9y + 2y) x + log (x + )3 1 − 2 ? 3 A. 4 .
B. 2 . C. 3772 . D. 3774 . Lời giải: Chọn D 3
Ta có 3(9y + 2 ) + log +1 − 2 3.9y y x x
+ 6y x +3log x +1 − 2 3 ( ) 3 ( ) 2 y 1 3 + +3(2y + ) 1 ( x + ) 1 + 3log x +1 . (*) 3 ( ) Xét hàm số ( ) = 3t f t
+3t có ( ) = 3t f t .ln 3 + 3 0, t .
Suy ra hàm số ( ) = 3t f t
+3t đồng biến trên . Do đó ( ) * f (2y ) 1 f (log (x ) 1 ) 2y 1 log ( x ) 2 y 1 1 3 + + + + + −1 x . 3 3 − y+ log 2021 1 Vì x 2020 nên 2 1 3 3 −1 2020 y 2,9 . 2
Với giả thiết y nguyên dương suy ra y 1; 2 .
Với y =1 có 26 x 2020 suy ra có 1995 cặp số ( ; x y) thỏa mãn .
Với y = 2 có 242 x 2020 suy ra có 1779 cặp số ( ; x y) thỏa mãn .
Vậy có tất cả 3774 cặp số ( ;
x y) thỏa mãn đề bài.
Câu 49. Trong không gian với hệ tọa độ Oxyz , gọi điểm M ( ; a ;
b c) (với a , b , c là các phân số tối giản) thuộc mặt cầu (S) 2 2 2
: x + y + z − 2x − 4y − 4z − 7 = 0 sao cho biểu thức T = 2a + 3b + 6c đạt giá trị lớn nhất. Khi đó
giá trị biểu thức P = 2a − b + c bằng 12 51 A. . B. 8 . C. 6 . D. . 7 7 Lời giải Chọn C
x + y + z − x − y − z − =
(x − )2 + ( y − )2 + (z − )2 2 2 2 2 4 4 7 0 1 2 2 = 16 .
M (a b c) (S ) (a − )2 + (b − )2 + (c − )2 ; ; 1 2 2 =16 . 2 2 2 Ta có:
(a − )+ (b− )+ (c − ) ( 2 2 2 2 1 3 2 6 2 2 + 3 + 6 ). ( a − )
1 + (b − 2) + (c − 2) .
2a + 3b + 6c − 20 28 2a + 3b + 6c − 20 28 2a + 3b + 6c 48. Trang 24 15 a =
2a + 3b + 6c = 48 7
2a + 3b + 6c = 48
a −1 b − 2 26 Dấu " = " xảy ra khi: =
3a − 2b = 1 − b = 2 3 7 3a − c = 1
a −1 c − 2 38 = c = 2 6 7 15 26 38
Vậy P = 2a − b + c = 2. − + = 6 . 7 7 7
Câu 50. Cho hàm số y = f (x) có đạo hàm f ( ¢ x) 2 = x ( 2 x - x + )( 2 3
2 x - x), với mọi x Î ¡ . Có bao nhiêu
giá trị nguyên dương của tham số m để hàm số y = f ( 2
x −16x + 2m) có 5 điểm cực trị? A. 30 . B. 31. C. 32 . D. 33 . Lời giải Chọn B
Ta có: y¢= f ( 2 ¢ x - 16x + 2 )
m (2x - 16). x é = 8 ê 2 x é = 8 x
ê - 16x + 2m = 1 (1) ê ê Cho y¢= 0 Û Û ê ê . f ê ( 2
¢ x - 16x + 2m) 2 = 0 x
ê - 16x + 2m = 0 (2) ë ê 2 x
ê - 16x + 2m = 2 (3) ë
Do các nghiệm của (1) đều là nghiệm bội bậc chẵn còn (2) và (3) không thể có nghiệm trùng nhau nên hàm số đã
cho có 5 điểm cực trị khi (2) và (3) có 2 nghiệm phân biệt khác 8 . ' ìï D > 0 ï ì 2 ï ï 64- 2m > 0 ï ï ï ' ï D > 0 ï ï 64- 2m + 2 > 0 3 í ï Û í
Û m < 32 mà m nguyên dương nên m có 31 giá trị. 2
ïï 8 - 16.8+ m ¹ 0 ï - 64+ m ¹ 0 ï ï ï ïï 2 ï 8 - 16.8+ m ¹ 2 ï ï - + ¹ î 64 m 2 î Trang 25