Đề thi thử Toán THPT Quốc gia 2019 trường chuyên Hạ Long – Quảng Ninh lần 1

Đề thi thử Toán THPT Quốc gia 2019 trường chuyên Hạ Long – Quảng Ninh lần 1; đề gồm 6 trang với 50 câu hỏi và bài toán trắc nghiệm khách quan

Chủ đề:

Đề thi THPTQG môn Toán năm 2019 79 tài liệu

Môn:

Toán 1.8 K tài liệu

Thông tin:
30 trang 9 tháng trước
Tác giả:
T
Thanh Hoa
docx.com.vn

Bình luận

Vui lòng đăng nhập hoặc đăng ký để gửi bình luận.

Đề thi thử Toán THPT Quốc gia 2019 trường chuyên Hạ Long – Quảng Ninh lần 1

Đề thi thử Toán THPT Quốc gia 2019 trường chuyên Hạ Long – Quảng Ninh lần 1; đề gồm 6 trang với 50 câu hỏi và bài toán trắc nghiệm khách quan

34 17 lượt tải Tải xuống

Chủ đề: Đề thi THPTQG môn Toán năm 2019 79 tài liệu

Môn: Toán 1.8 K tài liệu

Thông tin:

30 trang 9 tháng trước

Tác giả:

Profile Thanh Hoa
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC. Đề thi thử Lần 1 - Lớp 12 – Chuyên Hạ Long 18-19
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán! Trang 1 Mã đề: 743
Câu 1. Tính thể tích
V
của khối nón có chiều cao
=ha
và bán kính đáy
3=ra
.
A.
3
3
=
a
V
. B.
3
3=Va
. C.
3
3
3
=
a
V
. D.
3
=Va
.
Câu 2. Tìm tập nghiệm
S
của phương trình
.
A.
1=S
. B.
0;1=S
. C.
1; 2=−S
. D.
1;2=S
.
Câu 3. Trong không gian với hệ tọa độ
Ox ,yz
cho tam giác
ABC
với
( )
1;1;2A
,
( )
3;0;1−B
,
( )
8;2; 6−C
. Tìm tọa độ trọng tâm
G
của tam giác
ABC
.
A.
( )
2; 1;1−G
. B.
( )
2;1;1G
. C.
( )
2;1; 1−G
. D.
( )
6;3; 3−G
.
Câu 4. Tính diện tích xung quanh của khối trụ
S
có bán kính đáy
4=r
và chiều cao
3=h
.
A.
48=S
. B.
24=S
. C.
96=S
. D.
12=S
.
Câu 5. Cho hàm số
2
logyx=
. Khẳng định nào sau đây sai ?
A. Đồ thị hàm số nhận trục tung làm tiệm cận đứng.
B. Đồ thị hàm số cắt trục hoành tại điểm
( )
1;0A
.
C. Đồ thị hàm số luôn nằm phía trên trục hoành.
D. Hàm số đồng biến trên khoảng
( )
0;+
.
Câu 6. Cho hình lăng trụ đều
.ABC A B C
có cạnh đáy và cạnh bên cùng bằng
a
. Tính thể tích của
khối lăng trụ đó.
A.
3
6
12
a
. B.
3
6
4
a
. C.
3
3
12
a
. D.
3
3
4
a
.
Câu 7. Cho hàm số
32
1
35
3
y x x x= − − +
nghịch biến trên khoảng nào?
A.
( )
3; +
. B.
( )
;− +
. C.
( )
;1− −
. D.
( )
1;3−
.
Câu 8. Đồ thị hàm số
2
6
1
x
y
x
−
=
−
có mấy đường tiệm cân?
A.
1
. B.
3
. C.
2
. D.
0
.
Câu 9. Đường cong bên là đồ thị của một trong bốn hàm số được
liệt kê dưới đây. Hỏi đó là hàm số nào?
A.
3
1y x x= − + −
.
B.
3
1y x x= + +
.
C.
3
1y x x= − − +
. D.
3
1y x x= − + +
.
TRƯỜNG THPT CHUYÊN HẠ LONG
(Đề thi có 06 trang)
ĐỀ THI THỬ THPT QUỐC GIA LẦN 1
NĂM HỌC 2018 - 2019
Môn: Toán
Thời gian làm bài: 90 phút (không kể thời gian phát đề)
Họ và tên: ....................................................................... Lớp: .............
MÃ ĐỀ THI
121
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC. Đề thi thử Lần 1 - Lớp 12 – Chuyên Hạ Long 18-19
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán! Trang 2 Mã đề: 743
Câu 10. Tìm họ nguyên hàm của hàm số
( )
3x
f x e=
A.
( )
31
31
x
e
f x dx C
x
+
=+
+
.
B.
( )
3
3
x
f x dx e C=+
.
C.
( )
3
f x dx e C=+
. D.
( )
3
3
x
e
f x dx C=+
.
Câu 11. Cho khối chóp
.S ABC
có
SA
,
SB
,
SC
đôi một vuông góc và
=SA a
,
=SB b
,
=SC c
. Tính
thể tích
V
của khối chóp đó theo
a
,
b
,
c
.
A.
6
=
abc
V
. B.
3
=
abc
V
. C.
2
=
abc
V
. D.
=V abc
.
Câu 12. Tìm tập xác định
D
của hàm số
( )
2
3
log 2= − −y x x
.
A.
( )
1;2=−D
. B.
( ) ( )
; 1 2;= − − + D
.
C.
( )
2;= + D
. D.
( )
;1= − −D
.
Câu 13. Trong không gian với hệ tọa độ
Oxyz
, cho mặt cầu
2 2 2
: 2 4 4 25 0S x y z x y z
.
Tìm tọa độ tâm
I
và bán kính mặt cầu
S
.
A.
1; 2;2 ; 34IR
.
B.
1;2; 2 ; 5IR
.
C.
2;4; 4 ; 29IR
.
D.
1; 2;2 ; 6IR
.
Câu 14. Tìm họ nguyên hàm của hàm số
cos 2f x x x
.
A.
2
sinf x dx x x C
.
B.
2
sinf x dx x x C
.
C.
2
sinf x dx x x
.
D.
2
sinf x dx x x
.
Câu 15. Cho hàm số
( )
y f x=
liên tục trên và có bảng biến thiên
Khẳng định nào sau đây sai?
A.
0
1x =
là điểm cực tiểu của hàm số.
B. Hàm số đồng biến trên khoảng
( )
1;0−
và
( )
1; +
.
C.
( )
0;2M
là điểm cực tiểu của đồ thị hàm số.
D.
( )
1f −
là một giá trị cực tiểu của hàm số.
Câu 16. Tìm số hạng không chứa
x
trong khai triển
12
2
1
x
x

−


?
A.
459−
. B.
495−
. C.
495
. D.
459
.
Câu 17. Cho hàm số
( )
y f x=
có đạo hàm
( )
( )( )
( )( )
2
' 1 12 1 1
xx
f x e e x x= + − + −
trên . Hỏi hàm số
có bao nhiêu điểm cực trị?
x
-∞
1−
0
1
+∞
y
- 0 + 0 - 0 +
y
+
+
2
1
1
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC. Đề thi thử Lần 1 - Lớp 12 – Chuyên Hạ Long 18-19
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán! Trang 3 Mã đề: 743
A.
1
. B.
2
. C.
3
. D.
4
.
Câu 18. Cho khối lăng trụ tam giác
.ABC A B C
có thể tích
V
. Gọi
M
là trung điểm của
'CC
. Mặt
phẳng
( )
MAB
chia khối lăng trụ thành hai phần. Tính tỷ số thể tích hai phần đó (số bé chia số
lớn).
A.
2
5
. B.
3
5
. C.
1
5
. D.
1
6
.
Câu 19: Tính thể tích
V
của khối cầu nội tiếp hình lập phương cạnh
a
A.
3
6
a
V
=
. B.
3
4
3
a
V
=
. C.
3
3
a
V
=
. D.
3
2
a
V
=
.
Câu 20: Cho khối chóp tứ giác đều
.S ABCD
có cạnh đáy bằng
a
, các mặt bên tạo với mặt đáy bằng
60
. Tính thể tích khối chóp đó.
A.
3
3
2
a
. B.
3
3
12
a
. C.
3
3
6
a
. D.
3
3
3
a
.
Câu 21. Cho hàm số
( )
fx
thỏa mãn
( ) ( )
'1
x
f x x e=+
và
( )
01f =
. Tính
( )
2.f
A.
( )
2
2 4 1.fe=+
B.
( )
2
2 2 1.fe=+
C.
( )
2
2 3 1.fe=+
D.
( )
2
2 1.fe=+
Câu 22. Viết phương trình tiếp tuyến của đồ thị hàm số
32
31y x x= − +
biết nó song song với đường
thẳng
9 6.yx=+
A.
9 26, 9 6.y x y x= + = −
B.
9 26.yx=−
C.
9 26.yx=+
D.
9 26, 9 6.y x y x= − = +
Câu23.Tính độ dài đường cao tứ diện đều cạnh
a
.
A.
2
3
a
. B.
6
9
a
. C.
6
3
a
. D.
6
6
a
.
Câu24. Tìm tất cả các giá trị thực của tham số
m
để hàm số
32
32y x x mx= − + +
đồng biến trên ?
A.
3m
. B.
3m
. C.
3m
. D.
3m
.
Câu 25. Cho khối chóp
.S ABC
có
( )
SA ABC⊥
,
, , 2SA a AB a AC a= = =
và
0
120BAC =
. Tính thể tích
khối chóp
.S ABC
.
A.
3
3
3
a
. B.
3
3a
. C.
3
3
6
a
. D.
3
3
2
a
.
Câu 26. Cho tam giác
ABC
vuông cân tại
A
, đường cao
4AH =
. Tính diện tích xung quanh
xq
S
của
hình nón nhận được khi quay tam giác
ABC
xung quanh trục
AH
.
A.
42
xq
S
=
. B.
16 2
xq
S
=
. C.
82
xq
S
=
. D.
32 2
xq
S
=
.
Câu 27. Tính đạo hàm của hàm số
( )
1
, 0; 1
ln
x
y x x
x
+
=
A.
( )
2
ln 1
ln
xx
y
xx
−−
=
. B.
( )
2
ln 1
ln
x x x
y
xx
−−
=
.
C.
( )
2
ln 1
ln
xx
y
x
−−
=
. D.
ln 1
ln
xx
y
xx
−−
=
.
Câu 28. Phương trình
2
sin 3 sinxcos 1xx+=
có bao nhiêu nghiệm thuộc
0; 3


.
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC. Đề thi thử Lần 1 - Lớp 12 – Chuyên Hạ Long 18-19
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán! Trang 4 Mã đề: 743
A. 7. B. 6. C. 4. D. 5.
Câu 29. Việt nam là quốc gia nằm ở phía Đông bán đảo Đông Dương thuộc khu vực Đông Nam Á. Với
dân số ước tính 93,7 triệu dân vào đầu năm 2018, Việt Nam là quốc gia đông dân thứ 15 trên
thế giới và là quốc gia đông dân thứ 8 của châu Á, tỉ lệ tăng dân số hàng năm 1,2%. Giả sử rằng
tỉ lệ tăng dân số từ năm 2018 đến năm 2030 không thay đổi thì dân số nước ta đầu năm 2030
khoảng bao nhiêu?
A.118,12 triệu dân. B.106,12 triệu dân. C.118,12 triệu dân. D.108,12 triệu dân.
Câu 30. Dãy số nào là cấp số cộng?
A.
( )
*
2 , .
n
n
u n n= +
B.
( )
*
3 1, .
n
u n n= +
C.
( )
*
3 , .
n
n
un=
D.
( )
*
31
,.
2
n
n
un
n
+
=
+
Câu 31. Tìm nguyên hàm
1
.
ln 1
dx
xx+
A.
3
2
(ln 1)
3
xC++
. B.
ln 1xC++
. C.
2
1
(ln 1)
2
xC++
. D.
2 ln 1xC++
.
Câu 32. Trong không gian với hệ tọa độ
Oxyz
, cho hai vec tơ
( 2; 3;1)a = − −
,
(1;0;1)b =
. Tính
( , )cos a b
.
A.
1
( , )
27
cos a b
−
=
. B.
1
( , )
27
cos a b =
. C.
3
( , )
27
cos a b
−
=
. D.
3
( , )
27
cos a b =
.
Câu 33. Trong không gian với hệ trục tọa độ
Oxyz
cho tam giác
,ABC
với
( )
1;2;1 ,A
( )
3;0;3 ,B −
( )
2;4; 1C −
. Tìm tọa độ điểm
D
sao cho tứ giác
ABCD
là hình bình hành.
A.
( )
6; 6;3D −
. B.
( )
6;6;3D
. C.
( )
6; 6; 3D −−
. D.
( )
6;6; 3D −
.
Câu 34. Gọi
,Mm
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
2
3
2
++
=
−
xx
y
x
trên
2;1−
.
Tính
2=+T M m
.
A.
25
2
=T
. B.
11=−T
. C.
7=−T
. D.
10=−T
.
Câu 35. Biết
1
ln 1 ln 2 ,( , ).
( 1)( 2)
x
dx a x b x C a b
xx
+
= − + − +
−−
Tính giá trị của biểu thức
.ab+
A.
1ab+=
. B.
5ab+=
. C.
5ab+=
. D.
1ab+ = −
.
Câu 36. Tính tổng tất cả các giá trị của
m
biết đồ thị hàm số
32
2 ( 3)x 4y x mx m= + + + +
và đường
thẳng
4yx=+
cắt nhau tại 3 điểm phân biệt
(0;4), , A B C
sao cho
82
IBC
S =
với
(1;3).I
A.
3
. B.
8
. C.
1
. D.
5
.
Câu 37. Gọi S là tập hợp tất cả các giá trị của m để hàm số
4 2 4
22y x mx m m= − + +
có ba điểm cực trị
đồng thời các điểm cực trị của đồ thị lập thành tam giác có bán kính đường tròn ngoại tiếp bằng
1. Tính tổng tất cả các phần tử của S.
A.
15
2
+
. B.
25
2
+
. C. 0. D.
35
2
+
.
Câu 38. Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A, D và AB=AD=a, DC=2a, tam
giác đều và nằm trên mặt phẳng vuông góc với đáy. Gọi H là hình chiếu vuông góc của D trên
AC và M là trung điểm của HC. Tính diện tích mặt cầu ngoại tiếp hình chóp S.BDM theo a.
A.
2
7
9
a
. B.
2
13
9
a
. C.
2
13
3
a
. D.
2
7
3
a
.
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC. Đề thi thử Lần 1 - Lớp 12 – Chuyên Hạ Long 18-19
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán! Trang 5 Mã đề: 743
Câu 39. Trong không gian
Oxyz
, cho tam giác
ABC
với
(1;2;0), (3;2; 1), ( 1; 4;4)A B C− − −
. Tìm tập hợp
tất cả các điểm
M
sao cho
2 2 2
52MA MB MC+ + =
A. Mặt cầu tâm
( 1;0; 1)I −−
, bán kính
2r =
. B. Mặt cầu tâm
( 1;0; 1)I −−
, bán kính
2r =
C. Mặt cầu tâm
(1;0;1)I
, bán kính
2r =
. D. Mặt cầu tâm
(1;0;1)I
, bán kính
2r =
.
Câu 40. Cho hàm số
()y f x=
có đạo hàm trên và có đồ thị hàm số
'( )y f x=
hình bên. Hàm số
(3 )y f x=−
đồng biến trên
khoảng nào dưới đây?
A.
( )
2; 1−−
. B.
( )
1;2−
C.
( )
2; +
. D.
( ; 1)− −
Câu 41. Trong mặt phẳng
( )
P
cho hình vuông
ABCD
cạnh
a
. Trên đường thẳng qua
A
và vuông góc
với mặt phẳng
( )
P
lấy điểm
S
sao cho
SA a=
. Mặt cầu đường kính
AC
cắt các đường thẳng
,,SB SC SD
lần lượt tại
,,M B N C P D
. Tính diện tích tứ giác
AMNP
.
A.
2
6
2
a
. B.
2
2
12
a
C.
2
2
4
a
. D.
2
3
6
a
.
Câu 42. Gọi
K
là tập nghiệm của bất phương trình
2 1 2 1
7 7 2018 2018.
x x x
x
+ + + +
− +
Biết rằng tập hợp
tất cả các giá trị của tham số
m
sao cho hàm số
( ) ( )
32
2 3 2 6 2 3 3 5y x m x m x m= − + + + − +
đồng
biến trên
K
là
)
;ab
− +
, với
,ab
là các số thực. Tính
.S a b=+
A.
14S
. B.
8S
. C.
10S
. D.
11S
.
Câu 43. Cho tứ diện
SABC
có
ABC
là tam giác nhọn. Gọi hình chiếu vuông góc của
S
lên mặt phẳng
( )
ABC
trùng với trực tâm tam giác
ABC
. Khẳng định nào sau đây là sai khi nói về tứ diện đã
cho?
A. Các đoạn thẳng nối các trung điểm các cặp cạnh đối của tứ diện bằng nhau.
B. Tổng các bình phương của mỗi cặp cạnh đối của tứ diện bằng nhau.
C. Tồn tại một đỉnh của tứ diện có ba cạnh xuất phát từ đỉnh đó đôi một vuông góc với nhau.
D. Tứ diện có các cặp cạnh đối vuông góc với nhau.
Câu 44. Cho hàm số
( )
y f x=
liên tục trên thỏa mãn
( ) ( )
2
2 . ,
x
f x x f x e x
−
+ =
và
( )
00f =
.
Tính
( )
1f
.
A.
( )
2
1fe=
. B.
( )
1
1f
e
=−
. C.
( )
2
1
1f
e
=
. D.
( )
1
1f
e
=
.
Câu 45. Cho hình chóp
.S ABCD
có đáy là hình vuông cạnh
2a
. Biết rằng
0
90ASB ASD
, mặt
phẳng chứa
AB
vuông góc với
ABCD
cắt
SD
tại
N
. Tìm giá trị lớn nhất của thể tích tứ diện
DABN
.
A.
3
2
3
a
. B.
3
23
3
a
. C.
3
4
3
a
. D.
3
43
3
a
.
Câu 46. Cho hàm số
32
3 3 3y x m x
có đồ thị
C
. Tìm tất cả các giá trị của
m
sao cho qua
điểm
1; 1A
kẻ được đúng hai tiếp tuyến đến
C
, một tiếp tuyến là
1
:1y
và tiếp
tuyến thứ hai là
2
thỏa mãn :
2
tiếp xúc
C
với tại
N
đồng thời cắt
C
tại điểm
P
(khác
N
) có hoành độ bằng 3.
A. Không tồn tại m thỏa mãn. B.
2m
.
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC. Đề thi thử Lần 1 - Lớp 12 – Chuyên Hạ Long 18-19
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán! Trang 6 Mã đề: 743
C.
0; 2mm
. D.
2m
.
Câu 47. Cho bất phương trình
( )
2 2 2
2 2 2
.9 2 1 .6 .4 0
x x x x x x
m m m
− − −
− + +
. Tìm
m
để bất phương trình
nghiệm đúng
1
2
x
.
A.
3
2
m
. B.
3
2
m
. C.
0m
. D.
0m
.
Câu 48. Cho hình vuông
ABCD
cạnh bằng
1
, điểm
M
là trung điểm của
CD
. Cho hình vuông
ABCD
(
Tính cả các điểm trong của nó ) quay quanh trục là đường thẳng
AM
ta được một khối tròn
xoay. Tính thể tích khối tròn xoay đó.
A.
7 10
15
. B.
75
30
. C.
72
30
. D.
72
15
Câu 49. Trong chuyện cổ tích Cây tre trăm đốt (các đốt được đánh thứ tự từ 1 đến 100), khi không vác
được cây tre dài tận 100 đốt như vậy về nhà, anh Khoai ngồi khoc, Bụt liền hiện lên, bày cho
anh ta: “Con hãy hô câu thần chú Xác suất, xác suất thì cây tre sẽ rời ra, con sẽ mang được về
nhà”. Biết rằng cây tre 100 đốt được tách ra một cách ngẫu nhiên thành các đoạn ngắn có chiều
dài 2 đốt và 5 đốt (có thể chỉ có một loại). Xác suất để số đoạn 2 đốt nhiều hơn số đoạn 5 đốt
đúng 1 đoạn gần với giá trị nào trong các giá trị dưới đây?
A.
0,142
. B.
0,152
. C.
0,132
. D.
0,122
.
Câu 50. Cho hàm số
( )
y f x=
liên tục trên
R
và có đồ thị như hình vẽ. Hỏi hàm số
( )
( )
y f f x=
có
bao nhiêu điểm cực trị.
A. 6. B. 7. C. 8. D. 9.
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC. Đề thi thử Lần 1 - Lớp 12 – Chuyên Hạ Long 18-19
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán! Trang 7 Mã đề: 743
1.D
2.D
3.C
4.B
5.C
6.D
7.D
8.B
9.D
10.D
11.A
12.B
13.A
14.A
15.C
16.C
17.B
18.C
19.A
20.C
21.B
22.B
23.C
24.A
25.C
26.B
27.B
28.B
29.D
30.B
31.D
32.A
33.D
34.B
35.A
36.C
37.A
38.D
39.C
40.B
41.D
42.A
43.C
44.D
45.A
46.A
47.C
48.B
49.A
50.D
Câu 1. Tính thể tích
V
của khối nón có chiều cao
=ha
và bán kính đáy
3=ra
.
A.
3
3
=
a
V
. B.
3
3=Va
. C.
3
3
3
=
a
V
. D.
3
=Va
.
Lời giải
Tác giả: Trần Lê Hương Ly; Fb: Trần Lê Hương Ly
Chọn D
Ta có
2
1
3
V r h
=
( )
2
1
3.
3
= aa
3
= a
.
Câu 2. Tìm tập nghiệm
S
của phương trình
2
32
91
−+
=
xx
.
A.
1=S
. B.
0;1=S
. C.
1; 2=−S
. D.
1;2=S
.
Lời giải
Tác giả: Trần Lê Hương Ly; Fb: Trần Lê Hương Ly
Chọn D
2
3 2 2
1
9 1 3 2 0
2
−+
=
= − + =
=
xx
x
xx
x
.
Câu 3. Trong không gian với hệ tọa độ
Ox ,yz
cho tam giác
ABC
với
( )
1;1;2A
,
( )
3;0;1−B
,
( )
8;2; 6−C
. Tìm tọa độ trọng tâm
G
của tam giác
ABC
.
A.
( )
2; 1;1−G
. B.
( )
2;1;1G
. C.
( )
2;1; 1−G
. D.
( )
6;3; 3−G
.
Lời giải
Tác giả: Lưu Huệ Phương; Fb: Lưu Huệ Phương
Chọn C
Gọi
( )
;;G x y z
là trọng tâm của
ABC
. Khi đó:
TRƯỜNG THPT CHUYÊN HẠ LONG
(Đề thi có 06 trang)
ĐỀ THI THỬ THPT QUỐC GIA LẦN 1
NĂM HỌC 2018 - 2019
Môn: Toán
Thời gian làm bài: 90 phút (không kể thời gian phát đề)
Họ và tên: ....................................................................... Lớp: .............
MÃ ĐỀ THI
121
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC. Đề thi thử Lần 1 - Lớp 12 – Chuyên Hạ Long 18-19
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán! Trang 8 Mã đề: 743
3
3
3
++
=
++
=
++
=
A B C
A B C
A B C
xxx
x
yyy
y
zzz
z
1 3 8
3
1 0 2
3
216
3
−+
=
++
=
+−
=
x
y
z
2
1
1
=
=
=−
x
y
z
( )
2;1; 1−G
.
Câu 4. Tính diện tích xung quanh của khối trụ
S
có bán kính đáy
4=r
và chiều cao
3=h
.
A.
48=S
. B.
24=S
. C.
96=S
. D.
12=S
.
Lời giải
Tác giả: Lưu Huệ Phương; Fb: Lưu Huệ Phương
Chọn B
Diện tích xung quanh của hình trụ là:
2=
xq
S rh
2 .4.3=
24=
.
Câu 5. Cho hàm số
2
logyx=
. Khẳng định nào sau đây sai ?
A. Đồ thị hàm số nhận trục tung làm tiệm cận đứng.
B. Đồ thị hàm số cắt trục hoành tại điểm
( )
1;0A
.
C. Đồ thị hàm số luôn nằm phía trên trục hoành.
D. Hàm số đồng biến trên khoảng
( )
0;+
.
Lời giải
Tác giả: Hà Lê; Fb: Ha Le
Chọn C
Hàm số
2
logyx=
có đồ thị như sau:
Từ đồ thị hàm số ta thấy các khẳng định
,,A B D
là đúng, khẳng định
C
sai.
Câu 6. Cho hình lăng trụ đều
.ABC A B C
có cạnh đáy và cạnh bên cùng bằng
a
. Tính thể tích của
khối lăng trụ đó.
A.
3
6
12
a
. B.
3
6
4
a
. C.
3
3
12
a
. D.
3
3
4
a
.
Lời giải
Tác giả: Hà Lê; Fb: Ha Le
Chọn D
Vì
.ABC A B C
là hình lăng trụ đều nên ta có:
23
.
33
..
44
ABC A B C ABC
aa
V S AA a
= = =
.
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC. Đề thi thử Lần 1 - Lớp 12 – Chuyên Hạ Long 18-19
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán! Trang 9 Mã đề: 743
Câu 7. Cho hàm số
32
1
35
3
y x x x= − − +
nghịch biến trên khoảng nào?
A.
( )
3; +
. B.
( )
;− +
. C.
( )
;1− −
. D.
( )
1;3−
.
Lời giải
Tác giả:Nguyễn Trí Chính; Fb: Nguyễn Trí Chính.
Chọn D
( )
32
1
35
3
y f x x x x= = − − +
, TXĐ
D =
.
2
23y x x
= − −
,
2
0 2 3 0y x x
= − − =
1
3
x
x
=−
=
.
Có
10a =
nên hàm số
( )
y f x=
nghịch biến trong
( )
1;3−
.
Câu 8. Đồ thị hàm số
2
6
1
x
y
x
−
=
−
có mấy đường tiệm cân?
A.
1
. B.
3
. C.
2
. D.
0
.
Lời giải
Tác giả: Nguyễn Trí Chính; Fb: Nguyễn Trí Chính.
Chọn B
( ) ( )
2
6
1
x
C y f x
x
−
==
−
, TXĐ
\ 1;D =−
.
Có
22
11
66
lim ; lim
11
xx
xx
xx
−+
→→
−−
= − = +
−−
1x=
là tiệm cân đứng của
( )
C
.
Có
22
11
66
lim ; lim
11
xx
xx
xx
−+
→− →−
−−
= − = +
−−
1x = −
là tiệm cân đứng của
( )
C
.
Có
22
66
lim lim 0
11
xx
xx
xx
→+ →−
−−
==
−−
0y=
là tiệm cận ngang của
( )
C
.
Vậy
( )
C
có
3
tiệm cận.
Câu 9. Đường cong bên là đồ thị của một trong bốn hàm số được liệt kê dưới đây. Hỏi đó là hàm số
nào?
A.
3
1y x x= − + −
.
B.
3
1y x x= + +
. C.
3
1y x x= − − +
. D.
3
1y x x= − + +
.
Lời giải
Tác giả : Trần Thị Kim Oanh, FB: Oanh Trần
Chọn D
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC. Đề thi thử Lần 1 - Lớp 12 – Chuyên Hạ Long 18-19
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán! Trang 10 Mã đề: 743
Quan sát đồ thị ta có nhận xét sau:
Đường cong là đồ thị là hàm số dạng
32
y ax bx cx d= + + +
có
0, 0ad
, hàm số có hai điểm
cực trị trái dấu hay
0ac
, suy ra đáp án D
Câu 10. Tìm họ nguyên hàm của hàm số
( )
3x
f x e=
A.
( )
31
31
x
e
f x dx C
x
+
=+
+
.
B.
( )
3
3
x
f x dx e C=+
.
C.
( )
3
f x dx e C=+
. D.
( )
3
3
x
e
f x dx C=+
.
Lời giải
Tác giả : Trần Thị Kim Oanh, FB: Oanh Trần
Chọn D
Ta có
3
3
3
x
x
e
e dx C=+
Câu 11. Cho khối chóp
.S ABC
có
SA
,
SB
,
SC
đôi một vuông góc và
=SA a
,
=SB b
,
=SC c
. Tính
thể tích
V
của khối chóp đó theo
a
,
b
,
c
.
A.
6
=
abc
V
. B.
3
=
abc
V
. C.
2
=
abc
V
. D.
=V abc
.
Lời giải
Tác giả: Bùi Thị Kim Oanh ; Fb: Bùi Thị Kim Oanh
Chọn A
Ta có
( )
⊥
⊥
⊥
SA SB
SA SBC
SA SC
.
Do đó
1 1 1
. . . .
3 3 2 6
= = =
SBC
abc
V SA S a bc
.
Câu 12. Tìm tập xác định
D
của hàm số
( )
2
3
log 2= − −y x x
.
A.
( )
1;2=−D
. B.
( ) ( )
; 1 2;= − − + D
.
C.
( )
2;= + D
. D.
( )
;1= − −D
.
Lời giải
Tác giả: Bùi Thị Kim Oanh ; Fb: Bùi Thị Kim Oanh
Chọn B
Điều kiện:
2
1
20
2
−
− −
x
xx
x
.
Tập xác định của hàm số là
( ) ( )
; 1 2;= − − + D
.
Câu 13. Trong không gian với hệ tọa độ
Oxyz
, cho mặt cầu
2 2 2
: 2 4 4 25 0S x y z x y z
.
Tìm tọa độ tâm
I
và bán kính mặt cầu
S
.
A.
1; 2;2 ; 34IR
.
B.
1;2; 2 ; 5IR
.
C.
2;4; 4 ; 29IR
.
D.
1; 2;2 ; 6IR
.
Lời giải
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC. Đề thi thử Lần 1 - Lớp 12 – Chuyên Hạ Long 18-19
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán! Trang 11 Mã đề: 743
Tác giả: Nguyễn Văn Mộng; Fb: Nguyễn Văn Mộng.
Chọn A
Mặt cầu
S
có tâm
2
22
1; 2;2 ; 1 2 2 25 34IR
.
Vậy, ta chọn A.
Câu 14. Tìm họ nguyên hàm của hàm số
cos 2f x x x
.
A.
2
sinf x dx x x C
.
B.
2
sinf x dx x x C
.
C.
2
sinf x dx x x
.
D.
2
sinf x dx x x
.
Lời giải
Tác giả: Nguyễn Văn Mộng; Fb: Nguyễn Văn Mộng
Chọn A
2
cos 2 sinf x dx x x dx x x C
.
Vậy, ta chọn A.
Câu 15. Cho hàm số
( )
y f x=
liên tục trên và có bảng biến thiên
Khẳng định nào sau đây sai?
A.
0
1x =
là điểm cực tiểu của hàm số.
B. Hàm số đồng biến trên khoảng
( )
1;0−
và
( )
1; +
.
C.
( )
0;2M
là điểm cực tiểu của đồ thị hàm số.
D.
( )
1f −
là một giá trị cực tiểu của hàm số.
Lời giải
Tác giả: Bùi Văn Khánh; Fb: Khánh Bùi Văn
Chọn C
+) Dựa vào BBT thì
( )
0;2M
là điểm cực đại của đồ thị hàm số. Do đó đáp án C sai.
Câu 16. Tìm số hạng không chứa
x
trong khai triển
12
2
1
x
x

−


?
A.
459−
. B.
495−
. C.
495
. D.
459
.
Lời giải
Tác giả: Bùi Văn Khánh; Fb: Khánh Bùi Văn
Chọn C
+) Ta có:
( )
( )
( )
12
12 12
12
2 2 24 3
00
11
1 1 .
k
k
kk
k k k
nn
kk
x C x C x
xx
−
−
==
− = − = −

+) Số hạng tổng quát của khai triển là
( )
24 3
1.
k
kk
n
Cx
−
−
+) Số hạng trong khai triển không chứa
x
ứng với
24 3 0 8.kk− = =
Vậy số hạng không chứa
x
trong khai triển là:
8
12
495.C =
x
-∞
1−
0
1
+∞
y
- 0 + 0 - 0 +
y
+
+
2
1
1
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC. Đề thi thử Lần 1 - Lớp 12 – Chuyên Hạ Long 18-19
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán! Trang 12 Mã đề: 743
Câu 17. Cho hàm số
( )
y f x=
có đạo hàm
( )
( )( )
( )( )
2
' 1 12 1 1
xx
f x e e x x= + − + −
trên . Hỏi hàm số
có bao nhiêu điểm cực trị?
A.
1
. B.
2
. C.
3
. D.
4
.
Lời giải
Tác giả: Vũ Danh Được; Fb: Danh Được Vũ
Chọn B
Ta có
( )
ln12
' 0 1
1
x
f x x
x
=
= = −
=
Bảng xét dấu của
( )
'fx
như sau:
Từ đó ta thấy hàm số có hai điểm cực trị tại
1x =−
và
ln2x =
.
Câu 18. Cho khối lăng trụ tam giác
.ABC A B C
có thể tích
V
. Gọi
M
là trung điểm của
'CC
. Mặt
phẳng
( )
MAB
chia khối lăng trụ thành hai phần. Tính tỷ số thể tích hai phần đó (số bé chia số
lớn).
A.
2
5
. B.
3
5
. C.
1
5
. D.
1
6
.
Lời giải
Tác giả: Vũ Danh Được; Fb: Danh Được Vũ
Chọn C
Gọi chiều cao của hình lăng trụ
.ABC A B C
là
h
thì
.
ABC
V h S
=
.
Gọi chiều cao của hình chóp
.M ABC
là
'h
thì
'
2
h
h =
.
-
+
-
+
f '
x
( )
x
0
0
0
1
-1
ln2
+
∞
-
∞
h'
h
M
B
C
C'
A'
B'
A
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC. Đề thi thử Lần 1 - Lớp 12 – Chuyên Hạ Long 18-19
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán! Trang 13 Mã đề: 743
Do đó
.
1 1 1
'. . .
3 6 6
M ABC ABC ABC
V h S h S V

= = =
.
Suy ra thể tích của khối đa diện
.ABM A B C
bằng
15
..
66
V V V−=
.
Vậy tỉ số thể tích của hai phần (số bé chia số lớn) là
1
5
.
Câu 19: Tính thể tích
V
của khối cầu nội tiếp hình lập phương cạnh
a
A.
3
6
a
V
=
. B.
3
4
3
a
V
=
. C.
3
3
a
V
=
. D.
3
2
a
V
=
.
Lời giải
Tác giả: Đào Văn Tiến;face : Đào Văn Tiến
Chọn A
Hình lập phương có cạnh bằng
a
suy ra mặt cầu nội tiếp hình lập phương có bán kính là
2
a
r =
.
Từ đó suy ra thể tích của khối cầu nội tiếp hình lập phương là
33
3
44
.
3 3 8 6
aa
Vr

= = =
.
Câu 20: Cho khối chóp tứ giác đều
.S ABCD
có cạnh đáy bằng
a
, các mặt bên tạo với mặt đáy bằng
60
. Tính thể tích khối chóp đó.
A.
3
3
2
a
. B.
3
3
12
a
. C.
3
3
6
a
. D.
3
3
3
a
.
Lời giải
Chọn C
Gọi
H
là trung điểm
CD
,
O
là giao điểm hai đường chéo, suy ra
( )
SO ABCD⊥
Từ giả thiết ta có góc giữa mặt bên và mặt đáy là
60SHO =
Ta có
3
;
22
aa
OH SO==
suy ra thể tích khối chóp là
3
2
1 3 3
..
3 2 6
aa
Va==
.
Câu 21. Cho hàm số
( )
fx
thỏa mãn
( ) ( )
'1
x
f x x e=+
và
( )
01f =
. Tính
( )
2.f
A.
( )
2
2 4 1.fe=+
B.
( )
2
2 2 1.fe=+
C.
( )
2
2 3 1.fe=+
D.
( )
2
2 1.fe=+
Lời giải
Tác giả: Lê Cảnh Dương FB: Cảnh Dương Lê
S
A
B
C
D
O
H
0
60
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC. Đề thi thử Lần 1 - Lớp 12 – Chuyên Hạ Long 18-19
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán! Trang 14 Mã đề: 743
Chọn B
Ta có
( ) ( ) ( ) ( )
22
2
00
2 0 ' 1 2
x
f f f x dx x e dx e− = = + =

(phương pháp từng phần)
( ) ( )
22
2 2 0 2 1.f e f e = + = +
Câu 22. Viết phương trình tiếp tuyến của đồ thị hàm số
32
31y x x= − +
biết nó song song với đường
thẳng
9 6.yx=+
A.
9 26, 9 6.y x y x= + = −
B.
9 26.yx=−
C.
9 26.yx=+
D.
9 26, 9 6.y x y x= − = +
Lời giải
Tác giả: Lê Cảnh Dương FB: Cảnh Dương Lê
Chọn B
Gọi
0
x
là hoành độ tiếp điểm của tiếp tuyến. Do tiếp tuyến song song đường thẳng
96yx=+
nên
( )
0
2
0 0 0
0
1
' 9 3 6 9 .
3
x
y x x x
x
=−
= − =
=
Với
( )
0
1 1 3:xy= − − = −
PTTT
( )
9 1 3 9 6y x y x= + − = +
(loại).
Với
( )
0
3 3 1:xy= =
PTTT
( )
9 3 1 9 26.y x y x= − + = −
Câu23.Tính độ dài đường cao tứ diện đều cạnh
a
.
A.
2
3
a
. B.
6
9
a
. C.
6
3
a
. D.
6
6
a
.
Lời giải
Tác giả: Minh Anh Phuc; Fb: Minh Anh Phuc
Chọn C
Xét tứ diện
.S ABC
là tứ diện đều cạnh
a
, gọi
O
làm tâm của đáy. Ta có đường cao của tứ
diện là
2
2
2 2 2 2
2 3 6
.
3 2 3 3
a a a
SO SA AO a a

= − = − = − =



.
Câu24. Tìm tất cả các giá trị thực của tham số
m
để hàm số
32
32y x x mx= − + +
đồng biến trên ?
A.
3m
. B.
3m
. C.
3m
. D.
3m
.
Lời giải
M
O
C
B
A
S
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC. Đề thi thử Lần 1 - Lớp 12 – Chuyên Hạ Long 18-19
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán! Trang 15 Mã đề: 743
Tác giả: Minh Anh Phuc; Fb: Minh Anh Phuc
Chọn A
2
36y x x m
= − +
.
y
là hàm số bậc hai và
30a =
nên hàm số đã cho đồng biến trên
0yx
0
9 3 0m −
3m
.
Câu 25. Cho khối chóp
.S ABC
có
( )
SA ABC⊥
,
, , 2SA a AB a AC a= = =
và
0
120BAC =
. Tính thể tích
khối chóp
.S ABC
.
A.
3
3
3
a
. B.
3
3a
. C.
3
3
6
a
. D.
3
3
2
a
.
Lời giải
Tác giả: Phạm Thị Phương Thúy; Fb: thuypham
Chọn C
Diện tích tam giác
ABC
là:
02
1 1 3
. .sin . .2 .sin120
2 2 2
ABC
S AB AC A a a a= = =
.
Thể tích khối chóp
.S ABC
là:
23
.
1 1 3 3
..
3 3 2 6
S ABC ABC
V SA S a a a= = =
.
Câu 26. Cho tam giác
ABC
vuông cân tại
A
, đường cao
4AH =
. Tính diện tích xung quanh
xq
S
của
hình nón nhận được khi quay tam giác
ABC
xung quanh trục
AH
.
A.
42
xq
S
=
. B.
16 2
xq
S
=
. C.
82
xq
S
=
. D.
32 2
xq
S
=
.
Lời giải
Tác giả: Phạm Thị Phương Thúy; Fb:thuypham
Chọn B
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC. Đề thi thử Lần 1 - Lớp 12 – Chuyên Hạ Long 18-19
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán! Trang 16 Mã đề: 743
Tam giác
ABC
vuông cân tại
A
có đường cao
4AH =
AH
là đường trung tuyến và
1
4.
2
AH BC HB= = =
Hình nón nhận được có đường cao
4AH =
, bán kính đáy
4HB =
42AB=
là đường sinh.
Vậy diện tích xung quanh của hình nón tạo thành là:
. . .4.4 2 16 2
xq
S BH AB
= = =
.
Câu 27. Tính đạo hàm của hàm số
( )
1
, 0; 1
ln
x
y x x
x
+
=
A.
( )
2
ln 1
ln
xx
y
xx
−−
=
. B.
( )
2
ln 1
ln
x x x
y
xx
−−
=
.
C.
( )
2
ln 1
ln
xx
y
x
−−
=
. D.
ln 1
ln
xx
y
xx
−−
=
.
Lời giải
Tác giả: Lương Thị Hương Liễu; Fb: Lương Hương Liễu.
Chọn B
Ta có:
( ) ( ) ( )
( )
( )
( )
( )
2 2 2
1
ln 1
1 ln ln 1
ln 1
ln ln ln
xx
x x x x
x x x
x
y
x x x x

−+
+ − +
−−
= = =
Câu 28. Phương trình
2
sin 3 sinxcos 1xx+=
có bao nhiêu nghiệm thuộc
0; 3


.
A. 7. B. 6. C. 4. D. 5.
Lời giải
Tác giả: Lương Thị Hương Liễu; Fb: Lương Hương Liễu.
Chọn B
( )
2
1 cos 2 3
sin 3 sin xcos 1 sin 2 1 cos 2 3 sin 2 1
22
22
1
66
6
2 sin 2 1 sin 2 '
5
6 6 2
22
66
2
x
x x x x x
xk
xk
x x k
xk
xk



−
+ = + = − + =
−
+ = +
=+
− −
+ = + =
−
+ = +
=+
Với
,
0;1;2.
6
0; 3
x k k
k
x
= +
=

Với
,
0;1;2.
2
0; 3
x k k
k
x
= +
=

Vậy phương trình đã cho có 6 nghiệm thuộc đoạn
0; 3


.
Câu 29. Việt nam là quốc gia nằm ở phía Đông bán đảo Đông Dương thuộc khu vực Đông Nam Á. Với
dân số ước tính 93,7 triệu dân vào đầu năm 2018, Việt Nam là quốc gia đông dân thứ 15 trên
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC. Đề thi thử Lần 1 - Lớp 12 – Chuyên Hạ Long 18-19
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán! Trang 17 Mã đề: 743
thế giới và là quốc gia đông dân thứ 8 của châu Á, tỉ lệ tăng dân số hàng năm 1,2%. Giả sử rằng
tỉ lệ tăng dân số từ năm 2018 đến năm 2030 không thay đổi thì dân số nước ta đầu năm 2030
khoảng bao nhiêu?
A.118,12 triệu dân. B.106,12 triệu dân. C.118,12 triệu dân. D.108,12 triệu dân.
Lời giải
Tác giả:Phạm Thị Thu Trang; Fb: Trang Phạm
Chọn D
Dân số việt nam năm 2019 là:
( )
1
93,7 93,7.0,012 93,7. 1 0,012D = + = +
triệu dân
Dân số việt nam năm 2020 là:
( ) ( ) ( )
2
2
93,7. 1 0,012 93,7. 1 0,012 .0,012 93,7. 1 0,012D = + + + = +
triệu dân
…
Như vậy dân số Việt nam tăng theo cấp số nhân và được tính theo công thức:
( )
93,7. 1 0,012
n
n
D =+
với
n
là số năm tính từ 2018.
Vậy dân số Việt nam năm 2030 là:
( )
12
12
93,7. 1 0,012 108,12D = +
triệu dân. Chọn D.
Nhận xét: Đề bài có 2 đáp án giống nhau là A và C.
Câu 30. Dãy số nào là cấp số cộng?
A.
( )
*
2 , .
n
n
u n n= +
B.
( )
*
3 1, .
n
u n n= +
C.
( )
*
3 , .
n
n
un=
D.
( )
*
31
,.
2
n
n
un
n
+
=
+
Lời giải
Tác giả:Phạm Thị Thu Trang; Fb: Trang Phạm
Chọn B
Với dãy số
( )
*
2,
n
n
u n n= +
, xét hiệu:
( )
1*
1
1 2 n 2 2 1,
n n n
nn
u u n n
+
+
− = + + − − = +
thay
đổi theo
n
nên
( )
*
2,
n
n
u n n= +
không là cấp số cộng. (A loại)
Với dãy số
( )
*
3 1,
n
u n n= +
, xét hiệu:
( )
( )
*
1
3 1 1 3 1 3,
nn
u u n n n
+
− = + + − − =
là hằng số
nên
( )
*
3 1,
n
u n n= +
là cấp số cộng. (B đúng)
Với dãy số
( )
*
3,
n
n
un=
, xét hiệu:
( )
1*
1
3 3 2.3 ,
n n n
nn
u u n
+
+
− = − =
thay đổi theo
n
nên
( )
*
3,
n
n
un=
không là cấp số cộng. (C loại)
Với dãy số
( )
*
31
,
2
n
n
un
n
+
=
+
, xét hiệu:
( )
( )( )
( )
*
1
3 1 1
3 1 5
,
1 2 2 2 3
nn
n
n
u u n
n n n n
+
++
+
− = − =
+ + + + +
thay đổi theo
n
nên
( )
*
31
,
2
n
n
un
n
+
=
+
không là cấp số cộng. (D loại)
Câu 31. Tìm nguyên hàm
1
.
ln 1
dx
xx+
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC. Đề thi thử Lần 1 - Lớp 12 – Chuyên Hạ Long 18-19
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán! Trang 18 Mã đề: 743
A.
3
2
(ln 1)
3
xC++
. B.
ln 1xC++
. C.
2
1
(ln 1)
2
xC++
. D.
2 ln 1xC++
.
Lời giải
Tác giả: Nguyễn Mạnh Dũng; Fb: dungmanhnguyen
Chọn D
1
2
1
(ln 1) (ln 1) 2 ln 1 .
ln 1
dx x d x x C
xx
−
= + + = + +
+

Câu 32. Trong không gian với hệ tọa độ
Oxyz
, cho hai vec tơ
( 2; 3;1)a = − −
,
(1;0;1)b =
. Tính
( , )cos a b
.
A.
1
( , )
27
cos a b
−
=
. B.
1
( , )
27
cos a b =
. C.
3
( , )
27
cos a b
−
=
. D.
3
( , )
27
cos a b =
.
Lời giải
Tác giả: Nguyễn Mạnh Dũng; Fb: dungmanhnguyen
Chọn A
Ta có:
2 2 2 2 2 2
2.1 3.0 1.1 1
.
( , ) .
27
.
( 2) ( 3) 1 . 1 0 1
ab
cos a b
ab
− + − + −
= = =
− + − + + +
Câu 33. Trong không gian với hệ trục tọa độ
Oxyz
cho tam giác
,ABC
với
( )
1;2;1 ,A
( )
3;0;3 ,B −
( )
2;4; 1C −
. Tìm tọa độ điểm
D
sao cho tứ giác
ABCD
là hình bình hành.
A.
( )
6; 6;3D −
. B.
( )
6;6;3D
. C.
( )
6; 6; 3D −−
. D.
( )
6;6; 3D −
.
Lời giải
Tác giả : Nguyễn Hoàng Hưng, FB: Nguyễn Hưng
Chọn D
Gọi
( )
;;D x y z
Ta có:
( ) ( )
4; 2;2 , 2 ;4 ; 1AB DC x y z= − − = − − − −
Tứ giác
ABCD
là hình bình hành
( )
2 4 6
4 2 6 6;6; 3
1 2 3
xx
AB DC y y D
zz
− = − =

= − = − = −


− − = = −

.
Câu 34. Gọi
,Mm
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
2
3
2
++
=
−
xx
y
x
trên
2;1−
.
Tính
2=+T M m
.
A.
25
2
=T
. B.
11=−T
. C.
7=−T
. D.
10=−T
.
Lời giải
Tác giả : Nguyễn Hoàng Hưng, FB: Nguyễn Hưng
Chọn B
Hàm số
2
3
2
++
=
−
xx
y
x
xác định và liên tục trên đoạn
2;1−
.
( )
2
2
45
2
xx
y
x
−−
=
−
,
2
1 2;1
0 4 5 0
5 2;1
x
y x x
x
= − −
= − − =
= −
.
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC. Đề thi thử Lần 1 - Lớp 12 – Chuyên Hạ Long 18-19
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán! Trang 19 Mã đề: 743
( ) ( ) ( )
5
2 , 1 5, 1 1
4
y y y
−
− = = − − = −
.
Vậy
1, 5 2 11M m T M m= − = − = + = −
.
Câu 35. Biết
1
ln 1 ln 2 ,( , ).
( 1)( 2)
x
dx a x b x C a b
xx
+
= − + − +
−−
Tính giá trị của biểu thức
.ab+
A.
1ab+=
. B.
5ab+=
. C.
5ab+=
. D.
1ab+ = −
.
Lời giải
Tác giả: Nguyễn Hoa; Fb:Hoa Nguyễn
Chọn A
1 2( 2) 3( 1)
( 1)( 2) ( 1)( 2)
x x x
dx dx
x x x x
+ − − + −
=
− − − −

23
12
dx
xx
−

=+

−−

2ln 1 3ln 2 .x x C= − − + − +
2, 3 1.a b a b = − = + =
Câu 36. Tính tổng tất cả các giá trị của
m
biết đồ thị hàm số
32
2 ( 3)x 4y x mx m= + + + +
và đường
thẳng
4yx=+
cắt nhau tại 3 điểm phân biệt
(0;4), , A B C
sao cho
82
IBC
S =
với
(1;3).I
A.
3
. B.
8
. C.
1
. D.
5
.
Lời giải
Tác giả: Nguyễn Hoa; Fb:Hoa Nguyễn
Chọn C
Phương trình hoành độ giao điểm
32
2 ( 3) x 4 4x mx m x+ + + + = +
2
0
( ) 2 2 0 (1)
x
f x x mx m
=
= + + + =
'
2
(1)
0
20
( ; 1) (2; ) \ 2
20
(0) 0
mm
YCBT m
m
f

− −
− − + −

+
Khi đó 3 giao điểm phân biệt là
1 1 2 2
(0;4), ( ,x 4), ( ,x 4)A B x C x++
với
12
12
x2
.x 2
xm
xm
+ = −
=+
.
Ta có:
22
2 1 2 1
( ) ( 4 4)BC x x x x= − + + − −
22
2 1 2 1 2 1
2( ) 2 ( ) 4 .x x x x x x

= − = + −

2
2 2 2.BC m m = − −
Ta có
: 4 4 0d y x x y= + − + =
( , ) 2.d I d=
2
1
( , ). 2 4 2
2
ABC
S d I d BC m m= − − =
2
34 0mm − − =
1 137
( / )
2
.
1 137
( / )
2
m t m
m t m
+
=
−
=
Do đó tổng tất cả các giá trị của
m
là
1.
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC. Đề thi thử Lần 1 - Lớp 12 – Chuyên Hạ Long 18-19
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán! Trang 20 Mã đề: 743
Câu 37. Gọi S là tập hợp tất cả các giá trị của m để hàm số
4 2 4
22y x mx m m= − + +
có ba điểm cực trị
đồng thời các điểm cực trị của đồ thị lập thành tam giác có bán kính đường tròn ngoại tiếp bằng
1. Tính tổng tất cả các phần tử của S.
A.
15
2
+
. B.
25
2
+
. C. 0. D.
35
2
+
.
Lời giải
Tác giả: Hoàng Dũng; Fb: Hoang Dung
Chọn A
Ta có
32
4 4 4 ( ).y x mx x x m
= − = −
2
0
'0
x
y
xm
=
=
=
Hàm số có ba điểm cực trị
Phương trình
2
4 ( ) 0x x m−=
có 3 nghiệm phân
Phương trình
2
xm=
có 2 nghiệm phân biệt khác 0.
0.m
Khi
0m
đồ thị hàm số có ba điểm cực trị là
( )
4
0; 2A m m+
,
( )
42
;2B m m m m−+
,
( )
42
;2C m m m m− − +
và
( ) ( )
22
; , ;AB m m AC m m= − = − −
không cùng phương nên ba
điểm
, , A B C
luôn tạo thành ba đỉnh của một tam giác.
*)CÁCH 1: Gọi
( )
0;Ia
là tâm đường tròn ngoại tiếp tam giác ABC. Ta có IA=IB=IC=1.
Ta được
( )
( )
( )
( )
4
2
2
42
4
2
4
42
2
42
1
21
15
21
21
2
21
15
21
2
21
0.45
m
m m a
m
m m m m a
m m a
m m a
m m m m a
m
m m m m a
m
=
+ − =
−−
=
+ − + − =
+ − =


+ − = −
−+
+ − + − =
=
+ − + − =
−
.
Kết hợp với điều kiện
0m
ta được
15
1;
2
S

−+

=



.
Suy ra: Tổng tất cả các phần tử của S bằng
15
2
+
*)CÁCH 2:
( ) ( )
2 2 4
; , ;AB m m AC m m AB m m AC ABC= − = − − = + =
cân tại A.
Gọi
H
là trung điểm của
BC
thì
( )
42
0; 2H m m m−+
và
AH
là đường cao của
.ABC
Gọi
R
là bán kính đường tròn ngoại tiếp
ABC
thì
..
1
.
42
ABC
AB AC BC
S AH BC
R
==
4
2
2
..
2 . 2
2
AB AC BC m m
AB
R
AH BC AH
m
+
= = =
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC. Đề thi thử Lần 1 - Lớp 12 – Chuyên Hạ Long 18-19
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán! Trang 21 Mã đề: 743
Theo đề
4
2
4 2 2
00
11
2
2 ( 1)( 1) 0
mm
mm
R
m
m m m m m m



+
= =

+ = − + − =


1
15
2
m
m
=
−+
=
.
Câu 38. Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A, D và AB=AD=a, DC=2a, tam
giác đều và nằm trên mặt phẳng vuông góc với đáy. Gọi H là hình chiếu vuông góc của D trên
AC và M là trung điểm của HC. Tính diện tích mặt cầu ngoại tiếp hình chóp S.BDM theo a.
A.
2
7
9
a
. B.
2
13
9
a
. C.
2
13
3
a
. D.
2
7
3
a
.
Lời giải
Tác giả: Hoàng Dũng; Fb: Hoang Dung
Chọn D
Dựng hình ( hình vẽ).
Ta có
2 2 2 2 2 2
1 1 1 1 1 5 2
44
5
a
DH
DH DA DC a a a
= + = + = =
.
Mặt khác
22
4 4 2
5 5 5
CD a a a
HC HM DH
AC
a
= = = = =
.
O
O
M
H
A
B
D
C
A
D
C
B
S
H
M
N
E
E
G
I
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC. Đề thi thử Lần 1 - Lớp 12 – Chuyên Hạ Long 18-19
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán! Trang 22 Mã đề: 743
Do đó tam giác DHM vuông cân tại H. Suy ra
45DMA DEA= =
.
Do vậy năm điểm A, D, E, M, B cùng nằm trên đường tròn ngoại tiếp hình vuông
.ABED
Suy ra mặt cầu ngoại tiếp hình chóp S.BDM là mặt cầu ngoại tiếp hình chóp S.ABED.
Gọi R=ID là bán kính mặt cầu ngoại tiếp hình chóp S.ABED.
Ta có
22
2
2 2 2 2
3 2 7
6 2 12
a a a
R ID OI OD
= = + = + =
.
Suy ra diện tích mặt cầu ngoại tiếp hình chóp S.BDM bằng
22
2
77
44
12 3
aa
R

==
.
Câu 39. Trong không gian
Oxyz
, cho tam giác
ABC
với
(1;2;0), (3;2; 1), ( 1; 4;4)A B C− − −
. Tìm tập hợp
tất cả các điểm
M
sao cho
2 2 2
52MA MB MC+ + =
A.Mặt cầu tâm
( 1;0; 1)I −−
, bán kính
2r =
. B. Mặt cầu tâm
( 1;0; 1)I −−
, bán kính
2r =
C. Mặt cầu tâm
(1;0;1)I
, bán kính
2r =
. D. Mặt cầu tâm
(1;0;1)I
, bán kính
2r =
.
Lời giải
Tác giả:Nguyễn Lệ Hoài; Fb: Hoài lệ
ChọnC
Gọi
( ; ; )M x y z
. Khi đó
( ) ( ) ( ) ( ) ( ) ( )
2 2 2 2 2 2
2 2 2 2 2 2
1 2 3 2 ( 1) 1 4 ( 4)MA MB MC x y z x y z x y z+ + = − + − + + − + − + + + + + + + −
2 2 2
3 3 3 6 6 52.x y z x z= + + − − +
Theo đề
2 2 2
52MA MB MC+ + =
2 2 2
3 3 3 6 6 52 52x y z x z + + − − + =
2 2 2
( 1) ( 1) 2x y z − + + − =
M
thuộc mặt cầu có tâm mặt cầu tâm
(1;0;1)I
, bán kính
2r =
Câu 40. Cho hàm số
()y f x=
có đạo hàm trên và có đồ thị hàm số
'( )y f x=
hình bên. Hàm số
(3 )y f x=−
đồng biến trên khoảng nào dưới đây?
A.
( )
2; 1−−
. B.
( )
1;2−
C.
( )
2; +
. D.
( ; 1)− −
Lời giải
Tác giả:Nguyễn Lệ Hoài; Fb: Hoài lệ
Chọn B
+ Theo đề ta có hàm số
(x) (3 )y g f x= = −
có đạo hàm trên
.
'( ) (3 )'. '(3 ) '(3 )g x x f x f x= − − = − −
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC. Đề thi thử Lần 1 - Lớp 12 – Chuyên Hạ Long 18-19
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán! Trang 23 Mã đề: 743
+ Tìm
x
sao cho
'( ) 0.gx
'( ) 0gx
3 1 4
'(3 ) 0 '(3 ) 0 .
1 3 4 1 2
xx
f x f x
xx
− −

− − −

− −

3 1 4
'( ) 0 '(3 ) 0 '(3 ) 0 3 1 2
3 4 1
xx
g x f x f x x x
xx
− = − =


= − − = − = − = =


− = = −

: hữu hạn nghiệm.
Vậy hàm số
(3 )y f x=−
đồng biến trên mỗi tập
)
1;2 , 4;− +
.
Soi các phương án của đề bài ta chọn phương án
.B
Câu 41. Trong mặt phẳng
( )
P
cho hình vuông
ABCD
cạnh
a
. Trên đường thẳng qua
A
và vuông góc
với mặt phẳng
( )
P
lấy điểm
S
sao cho
SA a=
. Mặt cầu đường kính
AC
cắt các đường thẳng
,,SB SC SD
lần lượt tại
,,M B N C P D
. Tính diện tích tứ giác
AMNP
.
A.
2
6
2
a
. B.
2
2
12
a
C.
2
2
4
a
. D.
2
3
6
a
.
Lời giải
Tác giả : Phạm Ngọc Hưng, FB: Phạm Ngọc Hưng
Chọn D
Ta có
( )
SB MD
SB MAD SB AM
SB AD
⊥
⊥ ⊥
⊥
Tương tự
;AN SC AP SD⊥⊥
.
Ta có
2 6 6
;;
2 3 6
a a a
AM AP AN MN= = = =
Suy ra
2
1 2 6 3
2 2. . . .
2 2 6 6
AMNP AMN
a a a
S S AM MN
= = = =
Câu 42. Gọi
K
là tập nghiệm của bất phương trình
2 1 2 1
7 7 2018 2018.
x x x
x
+ + + +
− +
Biết rằng tập hợp
tất cả các giá trị của tham số
m
sao cho hàm số
( ) ( )
32
2 3 2 6 2 3 3 5y x m x m x m= − + + + − +
đồng
biến trên
K
là
)
;ab
− +
, với
,ab
là các số thực. Tính
.S a b=+
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC. Đề thi thử Lần 1 - Lớp 12 – Chuyên Hạ Long 18-19
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán! Trang 24 Mã đề: 743
A.
14S
. B.
8S
. C.
10S
. D.
11S
.
Lời giải
Tác giả : Phạm Ngọc Hưng, FB: Phạm Ngọc Hưng
Chọn A
ĐK:
1.x −
Ta có
( ) ( )
2 1 2 1 2 1 2 1
7 7 2018 2018 7 1009 2 1 7 1009 2 1
x x x x x x
x x x x
+ + + + + + + +
− + + + + + + +
( ) ( )
2 1 2 1f x x f x + + + +
với
( )
7 1009 , 2
t
f t t t= + −
.
Do
( )
7 ln 7 1009 0, 2
t
f t t
= + −
nên ta có
2 1 2 1 1.x x x x+ + + +
Do điều kiện
1x −
nên
1;1K =−
.
( ) ( )
32
2 3 2 6 2 3 3 5y x m x m x m= − + + + − +
đồng biến trên
0,K y x K
( )
2
6 6 2 6(2 3) 0,x m x m x K − + + +
2
23
,
2
xx
m x K
x
− + −
−
Đặt
( )
2
23
, 1;1
2
xx
g x x
x
− + −
= −
−
. Ta tính được
( )
;11
2
max 2 2 3 2 2 3
12
a
g x m
b
−
=
= − −
=
Vậy
14.S a b= + =
Câu 43. Cho tứ diện
SABC
có
ABC
là tam giác nhọn. Gọi hình chiếu vuông góc của
S
lên mặt phẳng
( )
ABC
trùng với trực tâm tam giác
ABC
. Khẳng định nào sau đây là sai khi nói về tứ diện đã
cho?
A. Các đoạn thẳng nối các trung điểm các cặp cạnh đối của tứ diện bằng nhau.
B. Tổng các bình phương của mỗi cặp cạnh đối của tứ diện bằng nhau.
C. Tồn tại một đỉnh của tứ diện có ba cạnh xuất phát từ đỉnh đó đôi một vuông góc với nhau.
D. Tứ diện có các cặp cạnh đối vuông góc với nhau.
Lời giải
Tác giả: Đặng Phước Thiên; Fb: Đặng Phước Thiên
Chọn C
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC. Đề thi thử Lần 1 - Lớp 12 – Chuyên Hạ Long 18-19
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán! Trang 25 Mã đề: 743
+) Ta có:
( )
AB SH
AB SHC AB SC
AB CH
⊥
⊥ ⊥
⊥
Tương tự ta có:
BC SA⊥
và
CA SB⊥
. Do đó, phương án D đúng.
+) Gọi
, , ,M N P Q
theo thứ tự là trung điểm các cạnh
, , ,SA SB BC AC
.
Suy ra:
MNPQ
là hình bình hành.
Lại có:
PQ AB
NP SC PQ NP
SC AB
⊥
⊥
Suy ra:
MNPQ
là hình chữ nhật
MP NQ=
.
Chứng minh tương tự, ta được phương án B đúng.
+) Do
MNPQ
là hình chữ nhật nên phương án A đúng.
+) Giả sử tồn tại một đỉnh của tứ diện mà xuất phát từ đỉnh đó các cạnh của tứ diện đội một
vuông góc nhau.
Suy ra đỉnh đó chỉ có thể là
S
.
Khi đó,
H
là tâm đường tròn ngoại tiếp
ABC
ABC
đều.
Câu 44. Cho hàm số
( )
y f x=
liên tục trên thỏa mãn
( ) ( )
2
2 . ,
x
f x x f x e x
−
+ =
và
( )
00f =
.
Tính
( )
1f
.
A.
( )
2
1fe=
. B.
( )
1
1f
e
=−
. C.
( )
2
1
1f
e
=
. D.
( )
1
1f
e
=
.
Lời giải
Tác giả: Đặng Phước Thiên; Fb: Đặng Phước Thiên
Chọn D
Ta có:
( ) ( ) ( ) ( )
2 2 2
2 . 2 1
x x x
f x x f x e f x e xe f x
−

+ = + =
( ) ( )
22
. 1 .
xx
f x e f x e x C

= = +

( )
2
x
xC
fx
e
+
=
.
Lại có:
( )
0 0 0fC= =
.
( ) ( )
2
1
1
x
x
f x f
e
e
= =
.
M
N
H
Q
P
A
B
C
E
F
S
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC. Đề thi thử Lần 1 - Lớp 12 – Chuyên Hạ Long 18-19
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán! Trang 26 Mã đề: 743
Câu 45. Cho hình chóp
.S ABCD
có đáy là hình vuông cạnh
2a
. Biết rằng
0
90ASB ASD
, mặt
phẳng chứa
AB
vuông góc với
ABCD
cắt
SD
tại
N
. Tìm giá trị lớn nhất của thể tích tứ diện
DABN
.
A.
3
2
3
a
. B.
3
23
3
a
. C.
3
4
3
a
. D.
3
43
3
a
.
Lời giải
Nguyễn Xuân Giao; giaonguyen
Chọn A
Gọi
O AC BD
, là mặt phẳng chứa
AB
và vuông góc với
ABCD
Ta có
SA SB
SA SBD BD SA
SA SD
.
Lại có
BD AC
BD SAC
BD SA
.
Trong
SAC
dựng đường thẳng qua
O
vuông góc với
SA
cắt
SC
tại
I
.
Ta có
OI AC
OI ABCD OI
OI BD
suy ra giao tuyến của và
SAC
là đường thẳng qua
A
, song song với
OI
, cắt
SC
tại
M
.
Có
AB CD
nên giao tuyến của và
SCD
là đường thẳng qua
M
, song song với
CD
, cắt
SD
tại
N
.
Có
1 2 2
. , . , .
3 3 3
DANB ABD ABD ABD
V S d N ABD S d I ABD S IO
.
Để
DANB
V
lớn nhất thì
OI
lớn nhất.
Ta có
SA SBD SA SO
.
Đặt
SA x
(
02xa
). Ta có
22
2SO a x
;
22
2
2
x a x
SH
a
;
22
2
2
ax
OH
a
;
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC. Đề thi thử Lần 1 - Lớp 12 – Chuyên Hạ Long 18-19
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán! Trang 27 Mã đề: 743
22
4
2
ax
CH CO OH
a
;
2 2 2
22
2 2 2 2
42
. 4 2
2
.
4 4 2
x a x
CO SH x a x a
OI a a
CH a x a x
.
Dấu bẳng xảy ra khi
22
2
42
3
a
x a x x
. Khi đó
3
2
22
.2 .
3 2 3
DANB
aa
Max V a
.
Câu 46. Cho hàm số
32
3 3 3y x m x
có đồ thị
C
. Tìm tất cả các giá trị của
m
sao cho qua
điểm
1; 1A
kẻ được đúng hai tiếp tuyến đến
C
, một tiếp tuyến là
1
:1y
và tiếp
tuyến thứ hai là
2
thỏa mãn :
2
tiếp xúc
C
với tại
N
đồng thời cắt
C
tại điểm
P
(khác
N
) có hoành độ bằng 3.
A. Không tồn tại m thỏa mãn. B.
2m
.
C.
0; 2mm
. D.
2m
.
Lời giải
Chọn A
Ta thấy
1
là một tiếp tuyến của
C
nên
32
2
3 3 3 1
3 6 3 0
x m x
x m x
có nghiệm.
Có
32
3
2
23
3 3 3 1
2
2
3 6 3 0
31
xm
x m x
m
x
x m x
m
.
Khi
2m
ta có
C
có phương trình
32
33y x x
.
Tiếp tuyến qua điểm
1; 1A
có dạng
: 1 1y k x
.
là một tiếp tuyến của
C
32
2
3 3 1 1
36
x x k x
x x k
có nghiệm.
Có
3 2 2
3
2
2
1
9
3 3 3 6 1 1
2 6 4 0
2
36
36
0
x
k
x x x x x
xx
x
x x k
x x k
k
Vậy có hai tiếp tuyến qua A có phương trình là
1
:1y
và
2
: 9 8yx
Phương trình hoành độ giao điểm của
2
và
C
:
32
1
3 3 9 8
5
x
x x x
x
Khi đó
2
và
C
không cắt nhau tại điểm có hoành độ là 3. Vậy không có giá trị của m.
Câu 47. Cho bất phương trình
( )
2 2 2
2 2 2
.9 2 1 .6 .4 0
x x x x x x
m m m
− − −
− + +
. Tìm
m
để bất phương trình
nghiệm đúng
1
2
x
.
A.
3
2
m
. B.
3
2
m
. C.
0m
. D.
0m
.
Lời giải
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC. Đề thi thử Lần 1 - Lớp 12 – Chuyên Hạ Long 18-19
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán! Trang 28 Mã đề: 743
Tác giả: Phạm Nguyên Bằng; Fb: Phạm Nguyên Bằng
Chọn C
Chia cả hai vế của bất phương trình cho
2
2
4
xx−
ta được:
( )
22
22
93
. 2 1 0
42
x x x x
m m m
−−
− + +
. Với
2
2
2
13
2 0 1
22
xx
x x x
−

−


.
Đặt
2
2
3
,1
2
xx
tt
−

=


. Khi đó bài toán trở thành tìm
m
để bất phương trình
( )
2
. 2 1 . 0 1m t m t m t− + +
.
-Với
1 0 1t =
( Luôn đúng).
-Với
2
11
21
t
t m t
tt
−+
. Xét
( )
2
1
21
t
f t t
tt
=
−+
;
( )
( )
2
2
2
1
01
21
t
f t t
tt
−+
=
−+
.
Khi đó
( )
lim 0
t
m f t
→+
=
.
Vậy
0m
thỏa mãn yêu cầu bài toán.
Câu 48. Cho hình vuông
ABCD
cạnh bằng
1
, điểm
M
là trung điểm của
CD
. Cho hình vuông
ABCD
(
Tính cả các điểm trong của nó ) quay quanh trục là đường thẳng
AM
ta được một khối tròn
xoay. Tính thể tích khối tròn xoay đó.
A.
7 10
15
. B.
75
30
.
C.
72
30
. D.
72
15
.
Lời giải
Tác giả: Phạm Nguyên Bằng ; Fb: Phạm Nguyên Bằng
Chọn B
Khi quay hình vuông quanh
AM
thì phần thể tích khi quay mặt
( )
ADM
bị trùng vào phần thể
tích của
( )
ABCM
.
Khi đó
nonABB noncutBCC B nonCMC
V V V V
= + −
.
Ta dễ dàng tính được các cạnh
1 2 1 1
; ; ;
5 5 5 2 5
AH BH CK MK= = = =
.
Khi đó
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC. Đề thi thử Lần 1 - Lớp 12 – Chuyên Hạ Long 18-19
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán! Trang 29 Mã đề: 743
2
1 4 5
. . .
3 75
nonABB
V AH HB

==
.
( )
22
1 14 5
..
3 75
noncutBCC B
V BH CK BH CK HK


= + + =
.
2
15
..
3 150
nonCMC
V MK CK
==
.
Vậy
75
30
V
=
.
Câu 49. Trong chuyện cổ tích Cây tre trăm đốt (các đốt được đánh thứ tự từ 1 đến 100), khi không vác
được cây tre dài tận 100 đốt như vậy về nhà, anh Khoai ngồi khoc, Bụt liền hiện lên, bày cho
anh ta: “Con hãy hô câu thần chú Xác suất, xác suất thì cây tre sẽ rời ra, con sẽ mang được về
nhà”. Biết rằng cây tre 100 đốt được tách ra một cách ngẫu nhiên thành các đoạn ngắn có chiều
dài 2 đốt và 5 đốt (có thể chỉ có một loại). Xác suất để số đoạn 2 đốt nhiều hơn số đoạn 5 đốt
đúng 1 đoạn gần với giá trị nào trong các giá trị dưới đây?
A.
0,142
. B.
0,152
. C.
0,132
. D.
0,122
.
Lời giải
Tác giả:Trịnh Thanh; Fb: Deffer Song
Chọn A
Giả sử có
x
đoạn 2 đốt và
y
đoạn 5 đốt được tách ra từ cây tre 100 đốt đã cho (
,x y Z
và
0, 0xy
).
* Ta có:
2 5 100xy+=
5x
5xm=
2 20my+=
2y
và
0 20y
.
Mà
yZ
nên
2;4;6;...;18;20y
.
Với mỗi bộ các số
( )
;xy
tìm được cho ta số các đoạn 2 đốt và 5 đốt được tách ra từ đó có số
các cách để tách cây tre 100 đốt thành
x
đoạn 2 đốt và
y
đoạn 5 đốt là
y
xy
C
+
.
Do vậy, số cách để tách cây tre 100 đốt thành các đoạn 2 đốt và đoạn 5 đốt là:
0 2 4 6 8 10 12 14 16 18 20
50 47 44 41 38 35 32 29 26 23 20
545813093C C C C C C C C C C C+ + + + + + + + + + =
* Để tách cây tre 100 đốt thành các đoạn ngắn có chiều dài 2 đốt và 5 đốt sao cho số đoạn 2 đốt
nhiều hơn số đoạn 5 đốt đúng 1 đoạn thì ta còn phải có
1xy−=
.
Khi đó:
15, 14xy==
.
Số cách để tách cây tre 100 đốt thành 15 đoạn 2 đốt và 14 đoạn 5 đốt là:
15
29
C
.
Vậy xác suất để số đoạn 2 đốt nhiều hơn số đoạn 5 đốt đúng 1 đoạn là
15
29
0,1421
545813093
C
.
Câu 50. Cho hàm số
( )
y f x=
liên tục trên
R
và có đồ thị như hình vẽ. Hỏi hàm số
( )
( )
y f f x=
có
bao nhiêu điểm cực trị.
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC. Đề thi thử Lần 1 - Lớp 12 – Chuyên Hạ Long 18-19
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán! Trang 30 Mã đề: 743
A.6. B.7. C.8. D.9.
Lời giải
Tác giả:Trịnh Thanh; Fb: Deffer Song
Chọn D
* Từ đồ thị hàm số
( )
y f x=
nhận thấy
+)
( )
02
xa
f x x
xb
=
= =
=
với
0
0 2 3x a b
.
+)
( )
02f x a x
hoặc
xb
.
+)
( )
0f x x a
hoặc
2 xb
.
* Ta có:
( )
( )
( )
( )
( )
.y f f x y f f x f x
= =
.
( )
( )
( )
0
0
0
f f x
y
fx
=
=
=
* Phương trình
( )
( )
( )
( )
( )
02
f x a
f f x f x
f x b
=
= =
=
với
0
0 2 3x a b
.
Mỗi đường thẳng
yb=
,
2y =
,
ya=
đều cắt đồ thị hàm số đã cho tại 2 điểm phân biệt lần lượt
tính từ trái qua phải có hoành độ là
1
x
và
6
x
;
2
x
và
5
x
;
3
x
và
4
x
nên:
( ) ( )
( ) ( )
( ) ( )
1 2 3 0 4 5 6
16
25
34
3
2
x x x x x x x
f x f x b
f x f x
f x f x a
==
==
==
* Cũng từ đồ thị hàm số đã cho suy ra:.
Do đó:
( )
( )
( )
02f f x a f x
hoặc
( )
f x b
.
Ta có BBT:
x
−
1
x
2
x
3
x
a
2 b
4
x
5
x
6
x
+
( )
fx
– – – – 0 + 0 – 0 + + + +
( )
( )
f f x
+ 0 – 0 + 0 – – – – 0 + 0 – 0 +
( )
( )
f f x


– 0 + 0 – 0 + 0 – 0 + 0 – 0 + 0 – 0 +
Vậy hàm số có 9 điểm cực trị.
| 1/30

Tài liệu khác của Toán

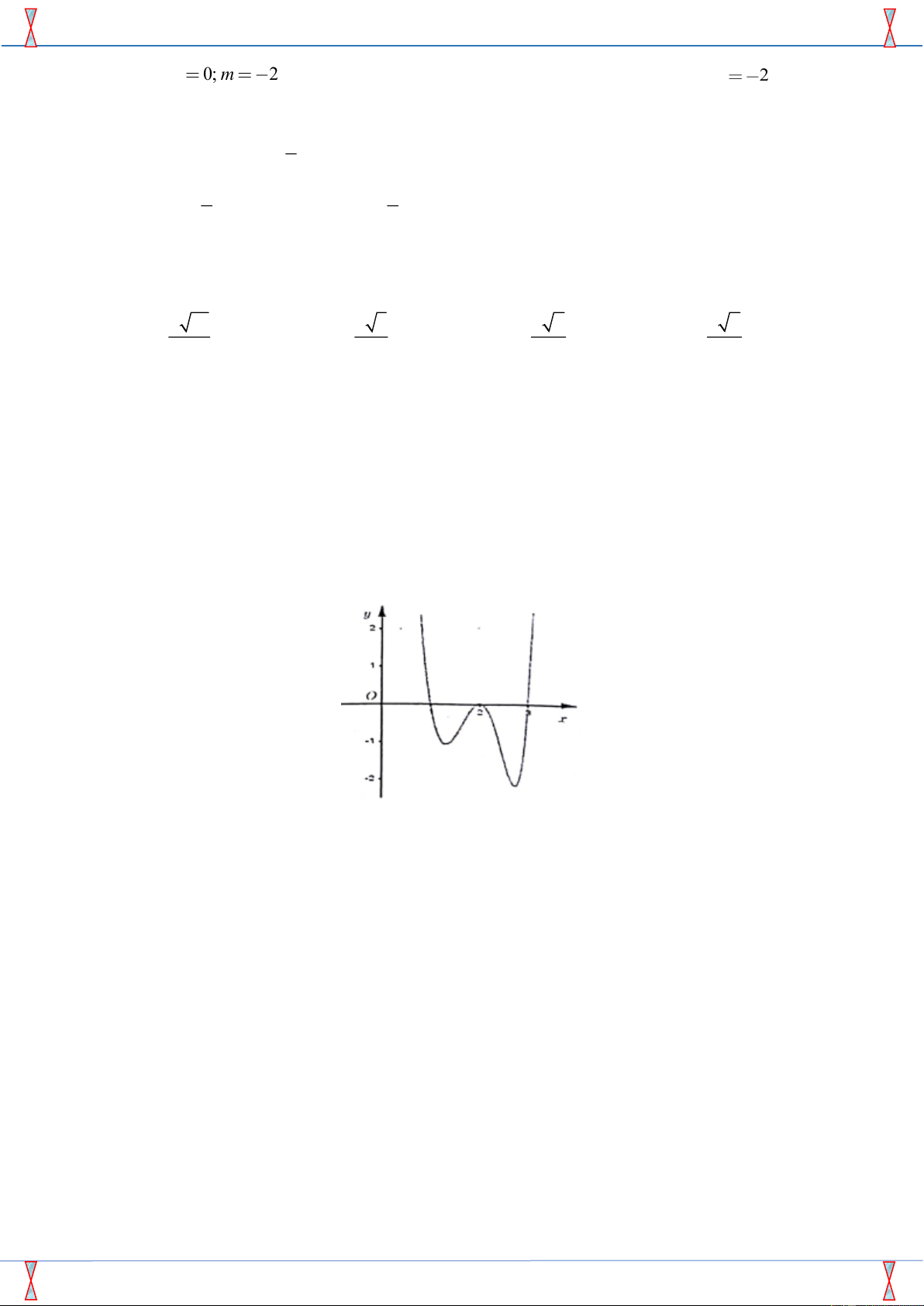
Preview text:

Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC.
Đề thi thử Lần 1 - Lớp 12 – Chuyên Hạ Long 18-19
TRƯỜNG THPT CHUYÊN HẠ LONG
ĐỀ THI THỬ THPT QUỐC GIA LẦN 1 (Đề thi có 06 trang) NĂM HỌC 2018 - 2019 Môn: Toán
Thời gian làm bài: 90 phút (không kể thời gian phát đề) MÃ ĐỀ THI 121
Họ và tên: ....................................................................... Lớp: .............
Câu 1. Tính thể tích V của khối nón có chiều cao h = a và bán kính đáy r = a 3 . 3 3 A.   = a 3 V . B. 3 V = 3 a . C. = a V . D. 3 V =  a . 3 3
Câu 2. Tìm tập nghiệm x − x+
S của phương trình 2 3 2 9 =1. A. S =   1 . B. S = 0;  1 .
C. S = 1;−  2 . D. S = 1;  2 .
Câu 3. Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC với A(1;1;2) , B(−3;0; ) 1 ,
C (8; 2; −6) . Tìm tọa độ trọng tâm G của tam giác ABC . A. G (2;−1; ) 1 . B. G (2;1; ) 1 . C. G (2;1;− ) 1 .
D. G (6;3;−3) .
Câu 4. Tính diện tích xung quanh của khối trụ S có bán kính đáy r = 4 và chiều cao h = 3. A. S = 48 . B. S = 24 . C. S = 96 . D. S =12 .
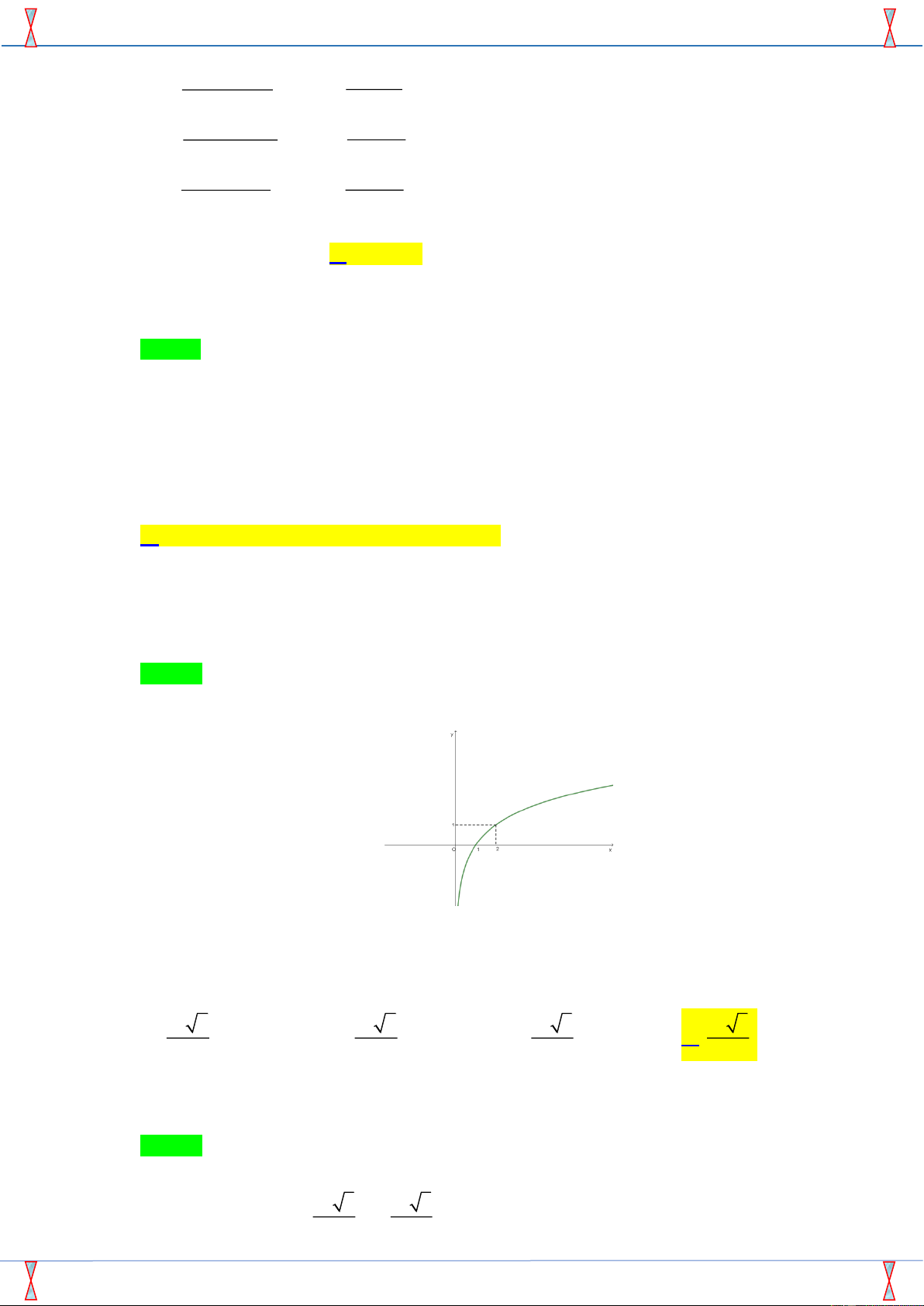
Câu 5. Cho hàm số y = log . Khẳng định nào sau đây sai ? 2 x
A. Đồ thị hàm số nhận trục tung làm tiệm cận đứng.
B. Đồ thị hàm số cắt trục hoành tại điểm A(1;0) .
C. Đồ thị hàm số luôn nằm phía trên trục hoành.
D. Hàm số đồng biến trên khoảng (0;+ ) .
Câu 6. Cho hình lăng trụ đều AB . C A BC
  có cạnh đáy và cạnh bên cùng bằng a . Tính thể tích của khối lăng trụ đó. 3 3 3 3 A. a 6 . B. a 6 . C. a 3 . D. a 3 . 12 4 12 4 Câu 7. Cho hàm số 1 3 2 y =
x − x − 3x + 5 nghịch biến trên khoảng nào? 3 A.(3;+) . B.( ; − +) . C.( ; − − ) 1 . D.( 1 − ;3) .
Câu 8. Đồ thị hàm số x − 6 y =
có mấy đường tiệm cân? 2 x −1 A.1. B. 3. C. 2 . D. 0 .
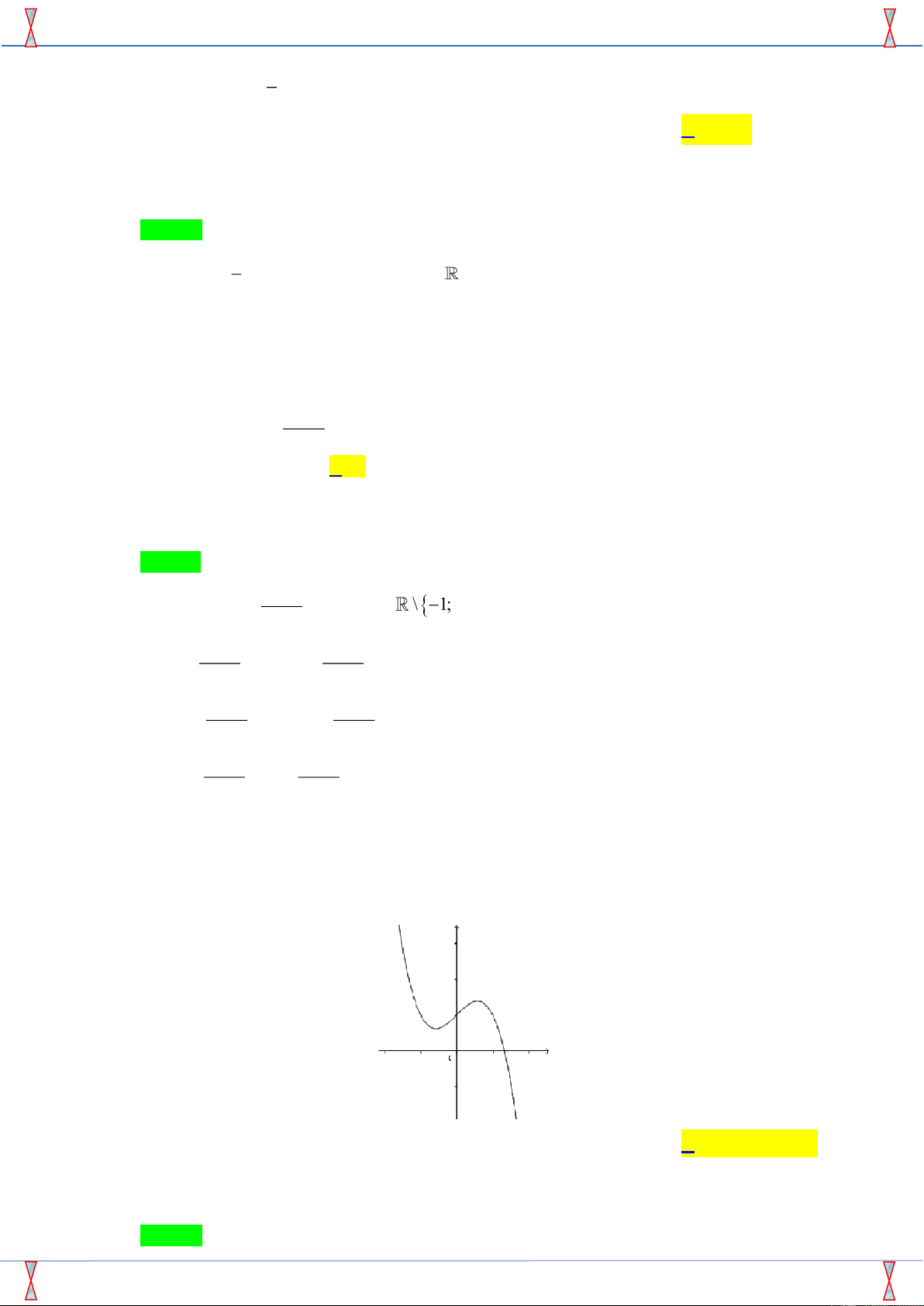
Câu 9. Đường cong bên là đồ thị của một trong bốn hàm số được
liệt kê dưới đây. Hỏi đó là hàm số nào? A. 3
y = −x + x −1. B. 3
y = x + x +1. C. 3
y = −x − x +1. D. 3
y = −x + x +1.
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán!
Trang 1 Mã đề: 743
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC.
Đề thi thử Lần 1 - Lớp 12 – Chuyên Hạ Long 18-19
Câu 10. Tìm họ nguyên hàm của hàm số ( ) 3x f x = e x+ A.  ( ) 3 1 e f x dx = + C . B.  ( ) 3 = 3 x f x dx e + C . 3x +1 x C.  ( ) e 3
f x dx = e + C . D. f  (x) 3 dx = + C . 3
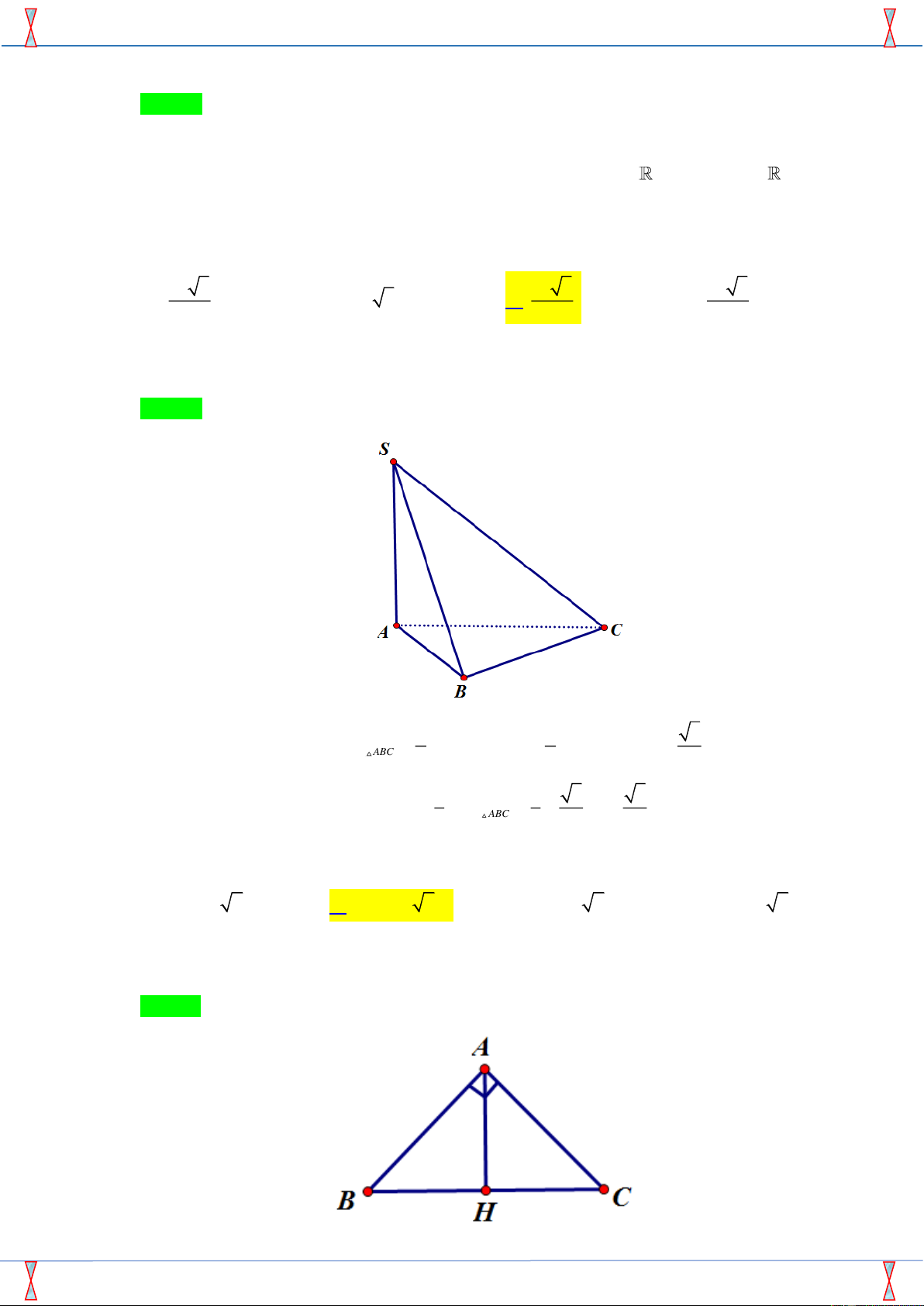
Câu 11. Cho khối chóp S.ABC có SA, SB , SC đôi một vuông góc và SA = a , SB = b , SC = c . Tính
thể tích V của khối chóp đó theo a , b , c . A. = abc V . B. = abc V . C. = abc V .
D. V = abc . 6 3 2
Câu 12. Tìm tập xác định D của hàm số y = log ( 2 x − x − 2 . 3 )
A. D = (−1;2).
B. D = (−;− ) 1  (2; + ) .
C. D = (2;+ ).
D. D = (−;− ) 1 .
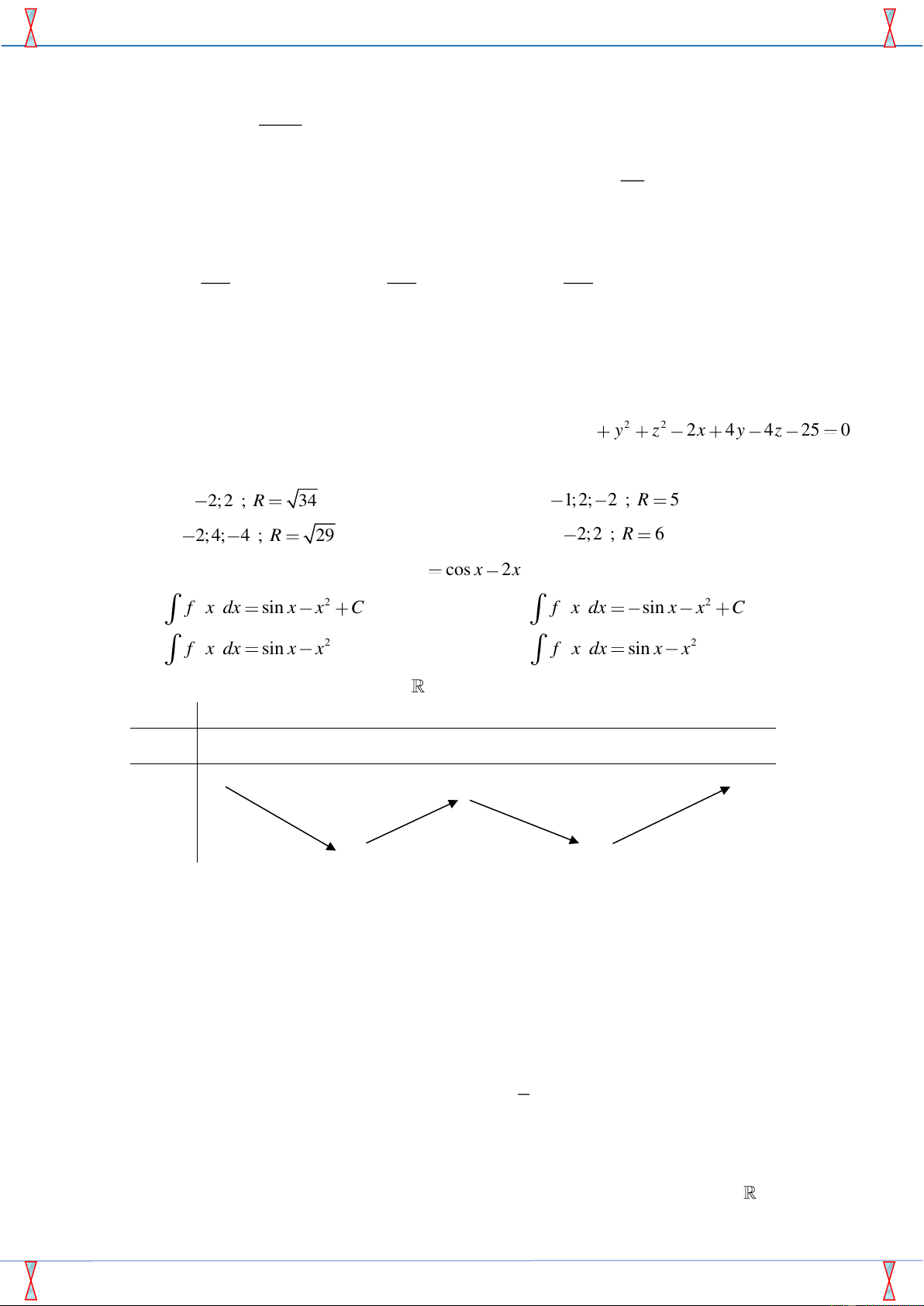
Câu 13. Trong không gian với hệ tọa độ Oxyz , cho mặt cầu 2 2 2 S : x y z 2x 4 y 4z 25 0 .
Tìm tọa độ tâm I và bán kính mặt cầu S .
A. I 1; 2;2 ; R 34 .
B. I 1;2; 2 ; R 5 .
C. I 2;4; 4 ; R 29 .
D. I 1; 2;2 ; R 6 .
Câu 14. Tìm họ nguyên hàm của hàm số f x cos x 2x . A. 2 f x dx sin x x C . B. 2 f x dx sin x x C . C. 2 f x dx sin x x . D. 2 f x dx sin x x .
Câu 15. Cho hàm số y = f (x) liên tục trên và có bảng biến thiên x -∞ −1 0 1 +∞ y - 0 + 0 - 0 + +  +  y 2 1 1
Khẳng định nào sau đây sai?
A. x =1 là điểm cực tiểu của hàm số. 0
B. Hàm số đồng biến trên khoảng (−1;0) và (1;+) .
C. M (0;2) là điểm cực tiểu của đồ thị hàm số. D. f (− )
1 là một giá trị cực tiểu của hàm số. 12
Câu 16. Tìm số hạng không chứa  1  x trong khai triển 2 x −   ?  x A. 459 − . B. 495 − . C. 495 . D. 459 .
Câu 17. Cho hàm số y = f (x) có đạo hàm ( ) = ( x + )( x f x e e − )(x+ )(x− )2 ' 1 12 1 1 trên . Hỏi hàm số
có bao nhiêu điểm cực trị?
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán!
Trang 2 Mã đề: 743
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC.
Đề thi thử Lần 1 - Lớp 12 – Chuyên Hạ Long 18-19 A. 1. B. 2 . C. 3. D. 4 .
Câu 18. Cho khối lăng trụ tam giác AB . C A BC
  có thể tích V . Gọi M là trung điểm của CC '. Mặt
phẳng (MAB) chia khối lăng trụ thành hai phần. Tính tỷ số thể tích hai phần đó (số bé chia số lớn). A. 2 . B. 3 . C. 1 . D. 1 . 5 5 5 6
Câu 19: Tính thể tích V của khối cầu nội tiếp hình lập phương cạnh a 3 3 3 3 A. a 4 aaa V = . B. V = . C. V = . D. V = . 6 3 3 2
Câu 20: Cho khối chóp tứ giác đều S.ABCD có cạnh đáy bằng a , các mặt bên tạo với mặt đáy bằng
60 . Tính thể tích khối chóp đó. 3 3 3 3 A. a 3 . B. a 3 . C. a 3 . D. a 3 . 2 12 6 3
Câu 21. Cho hàm số f (x) thỏa mãn '( ) = ( + ) 1 x f x x
e và f (0) = 1. Tính f (2). A. f ( ) 2 2 = 4e +1. B. f ( ) 2 2 = 2e +1. C. f ( ) 2 2 = 3e +1. D. f ( ) 2 2 = e +1.
Câu 22. Viết phương trình tiếp tuyến của đồ thị hàm số 3 2
y = x − 3x +1 biết nó song song với đường
thẳng y = 9x + 6.
A. y = 9x + 26, y = 9x − 6.
B. y = 9x − 26.
C. y = 9x + 26.
D. y = 9x − 26, y = 9x + 6.
Câu23.Tính độ dài đường cao tứ diện đều cạnh a . A. a 2 . B. a 6 . C. a 6 . D. a 6 . 3 9 3 6
Câu24. Tìm tất cả các giá trị thực của tham số m để hàm số 3 2
y = x − 3x + mx + 2 đồng biến trên ? A. m  3 . B. m  3. C. m  3 . D. m  3 .
Câu 25. Cho khối chóp S.ABC có SA ⊥ ( ABC) , SA = a, AB = a, AC = 2a và 0
BAC = 120 . Tính thể tích
khối chóp S.ABC . 3 3 3 A. a 3 . B. a 3 a 3 3 a 3 . C. . D. . 3 6 2
Câu 26. Cho tam giác ABC vuông cân tại A , đường cao AH = 4. Tính diện tích xung quanh S của xq
hình nón nhận được khi quay tam giác ABC xung quanh trục AH . A. S = 4 2 . B. S =16 2 . C. S = 8 2 . D. S = 32 2 . xq xq xq xq Câu 27. +
Tính đạo hàm của hàm số x 1 y =
,(x  0; x  ) 1 ln x A. ln x − x − 1
x ln x − x − 1 y = . B. y = . x (ln x)2 x (ln x)2 C. ln x − x − 1 x − x − y = . D. ln 1  = . ( y ln x)2 x ln x
Câu 28. Phương trình 2
sin x + 3 sin x cos x = 1 có bao nhiêu nghiệm thuộc 0 ; 3    .
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán!
Trang 3 Mã đề: 743
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC.
Đề thi thử Lần 1 - Lớp 12 – Chuyên Hạ Long 18-19 A. 7. B. 6. C. 4. D. 5.
Câu 29. Việt nam là quốc gia nằm ở phía Đông bán đảo Đông Dương thuộc khu vực Đông Nam Á. Với
dân số ước tính 93,7 triệu dân vào đầu năm 2018, Việt Nam là quốc gia đông dân thứ 15 trên
thế giới và là quốc gia đông dân thứ 8 của châu Á, tỉ lệ tăng dân số hàng năm 1,2%. Giả sử rằng
tỉ lệ tăng dân số từ năm 2018 đến năm 2030 không thay đổi thì dân số nước ta đầu năm 2030 khoảng bao nhiêu? A.118,12 triệu dân. B.106,12 triệu dân. C.118,12 triệu dân. D.108,12 triệu dân.
Câu 30. Dãy số nào là cấp số cộng? A. n u = n + n
B.u = n + nn ( * 3 1, ). n ( * 2 , ). + C. 3n 1 n u = n D.u = , n n ( * ). n ( * 3 , ). n + 2
Câu 31. Tìm nguyên hàm 1 . dxx ln x+1 A. 2 1 3 (ln x +1) + C .
B. ln x +1 + C . C. 2
(ln x +1) + C . D. 2 ln x +1 + C . 3 2
Câu 32. Trong không gian với hệ tọa độ Oxyz , cho hai vec tơ a = ( 2 − ; 3
− ;1) , b = (1;0;1) . Tính cos(a,b) . A. 1 − −
cos(a, b) = . B. 1
cos(a, b) = . C. 3
cos(a, b) = . D. 3
cos(a, b) = . 2 7 2 7 2 7 2 7
Câu 33. Trong không gian với hệ trục tọa độ Oxyz cho tam giác ABC, với A(1;2; ) 1 , B ( 3 − ;0;3), C (2; 4; − )
1 . Tìm tọa độ điểm D sao cho tứ giác ABCD là hình bình hành. A. D(6; 6 − ;3) . B. D(6;6;3).
C. D(6;−6;−3) . D. D(6;6; 3 − ) . 2 Câu 34. Gọi x + x + 3
M , m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = trên −2;  1 . x − 2
Tính T = M + 2m . A. 25 T = . B. T = 11 − . C. T = 7 − . D. T = 10 − . 2 Câu 35. Biết x +1
dx = a ln x −1 + b ln x − 2 + C, ( , a b  ). 
Tính giá trị của biểu thức a + . b
(x −1)(x − 2)
A. a +b =1.
B. a +b = 5.
C. a +b = 5.
D. a +b = 1 − .
Câu 36. Tính tổng tất cả các giá trị của m biết đồ thị hàm số 3 2
y = x + 2mx + (m + 3) x+ 4 và đường
thẳng y = x + 4 cắt nhau tại 3 điểm phân biệt (
A 0; 4), B, C sao cho S = 8 2 với I(1;3). IBC A. 3 . B. 8 . C. 1. D. 5.
Câu 37. Gọi S là tập hợp tất cả các giá trị của m để hàm số 4 2 4
y = x − 2mx + 2m + m có ba điểm cực trị
đồng thời các điểm cực trị của đồ thị lập thành tam giác có bán kính đường tròn ngoại tiếp bằng
1. Tính tổng tất cả các phần tử của S. A. 1+ 5 . B. 2 + 5 . C. 0. D. 3+ 5 . 2 2 2
Câu 38. Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A, D và AB=AD=a, DC=2a, tam
giác đều và nằm trên mặt phẳng vuông góc với đáy. Gọi H là hình chiếu vuông góc của D trên
AC và M là trung điểm của HC. Tính diện tích mặt cầu ngoại tiếp hình chóp S.BDM theo a. 2  2  2  2  A. 7 a . B. 13 a . C. 13 a . D. 7 a . 9 9 3 3
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán!
Trang 4 Mã đề: 743
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC.
Đề thi thử Lần 1 - Lớp 12 – Chuyên Hạ Long 18-19
Câu 39. Trong không gian Oxyz , cho tam giác ABC với (
A 1; 2;0), B(3; 2; 1 − ),C( 1 − ; 4 − ;4) . Tìm tập hợp
tất cả các điểm M sao cho 2 2 2
MA + MB + MC = 52
A. Mặt cầu tâm I( 1 − ;0; 1
− ) , bán kính r = 2 .
B. Mặt cầu tâm I( 1 − ;0; 1
− ) , bán kính r = 2
C. Mặt cầu tâm I(1;0;1) , bán kính r = 2 .
D. Mặt cầu tâm I(1;0;1) , bán kính r = 2 .
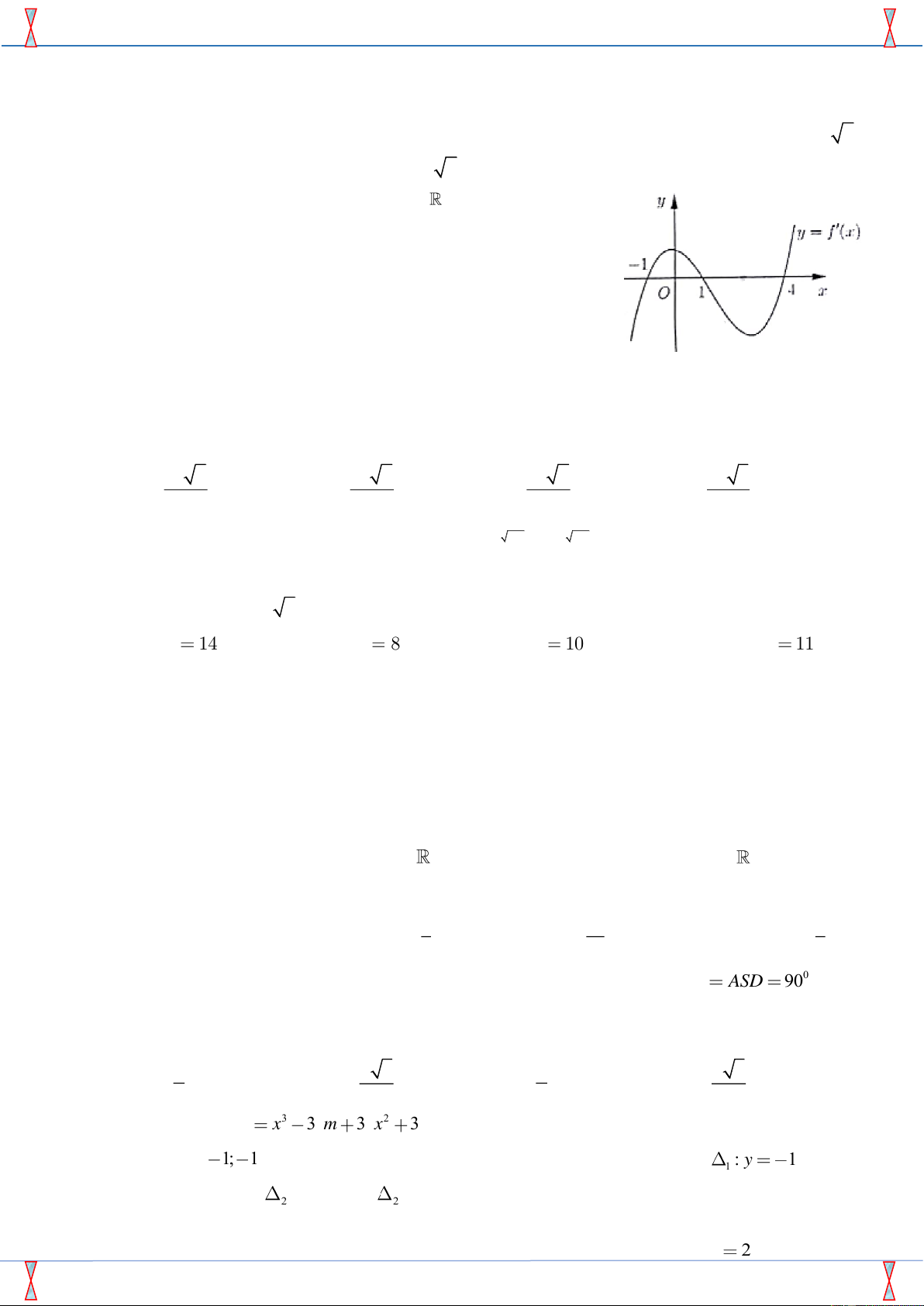
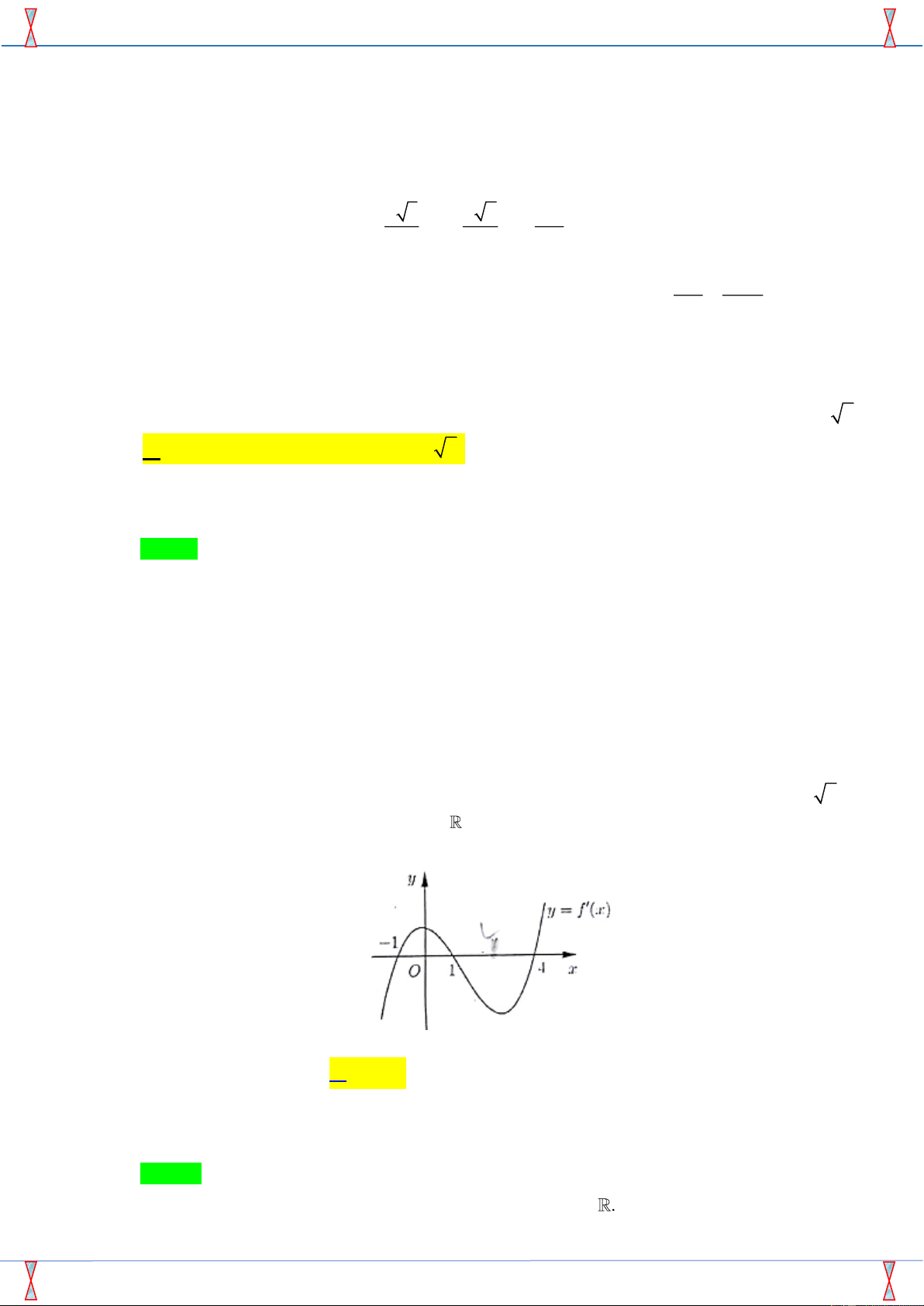
Câu 40. Cho hàm số y = f (x) có đạo hàm trên và có đồ thị hàm số
y = f '(x) hình bên. Hàm số y = f (3 − x) đồng biến trên khoảng nào dưới đây? A. (−2;− ) 1 . B. (−1;2) C. (2;+) . D.(− ;  1 − )
Câu 41. Trong mặt phẳng (P) cho hình vuông ABCD cạnh a . Trên đường thẳng qua A và vuông góc
với mặt phẳng (P) lấy điểm S sao cho SA = a . Mặt cầu đường kính AC cắt các đường thẳng
SB, SC, SD lần lượt tại M B, N C, P D . Tính diện tích tứ giác AMNP . 2 2 2 2 A. a 6 . B. a 2 C. a 2 . D. a 3 . 2 12 4 6
Câu 42. Gọi K là tập nghiệm của bất phương trình 2x+ x 1+ 2+ x 1 7 7 + −
+ 2018x  2018. Biết rằng tập hợp
tất cả các giá trị của tham số 3 2
m sao cho hàm số y = 2x − 3(m + 2) x + 6 (2m + 3) x − 3m + 5 đồng
biến trên K là a − b;+ 
), với a, b là các số thực. Tính S =a+ .b A.S 14 . B. S 8 . C. S 10. D. S 11.
Câu 43. Cho tứ diện SABC có ABC là tam giác nhọn. Gọi hình chiếu vuông góc của S lên mặt phẳng
( ABC) trùng với trực tâm tam giác ABC . Khẳng định nào sau đây là sai khi nói về tứ diện đã cho?
A. Các đoạn thẳng nối các trung điểm các cặp cạnh đối của tứ diện bằng nhau.
B. Tổng các bình phương của mỗi cặp cạnh đối của tứ diện bằng nhau.
C. Tồn tại một đỉnh của tứ diện có ba cạnh xuất phát từ đỉnh đó đôi một vuông góc với nhau.
D. Tứ diện có các cặp cạnh đối vuông góc với nhau.
Câu 44. Cho hàm số y = f (x) liên tục trên thỏa mãn ( ) + ( ) 2 2 . −x f x x f x = e , x   và f (0) = 0. Tính f ( ) 1 . A. 1 f ( ) 2 1 = e . B. f ( ) 1 1 = − . C. f ( ) 1 = . D. f ( ) 1 1 = . e 2 e e
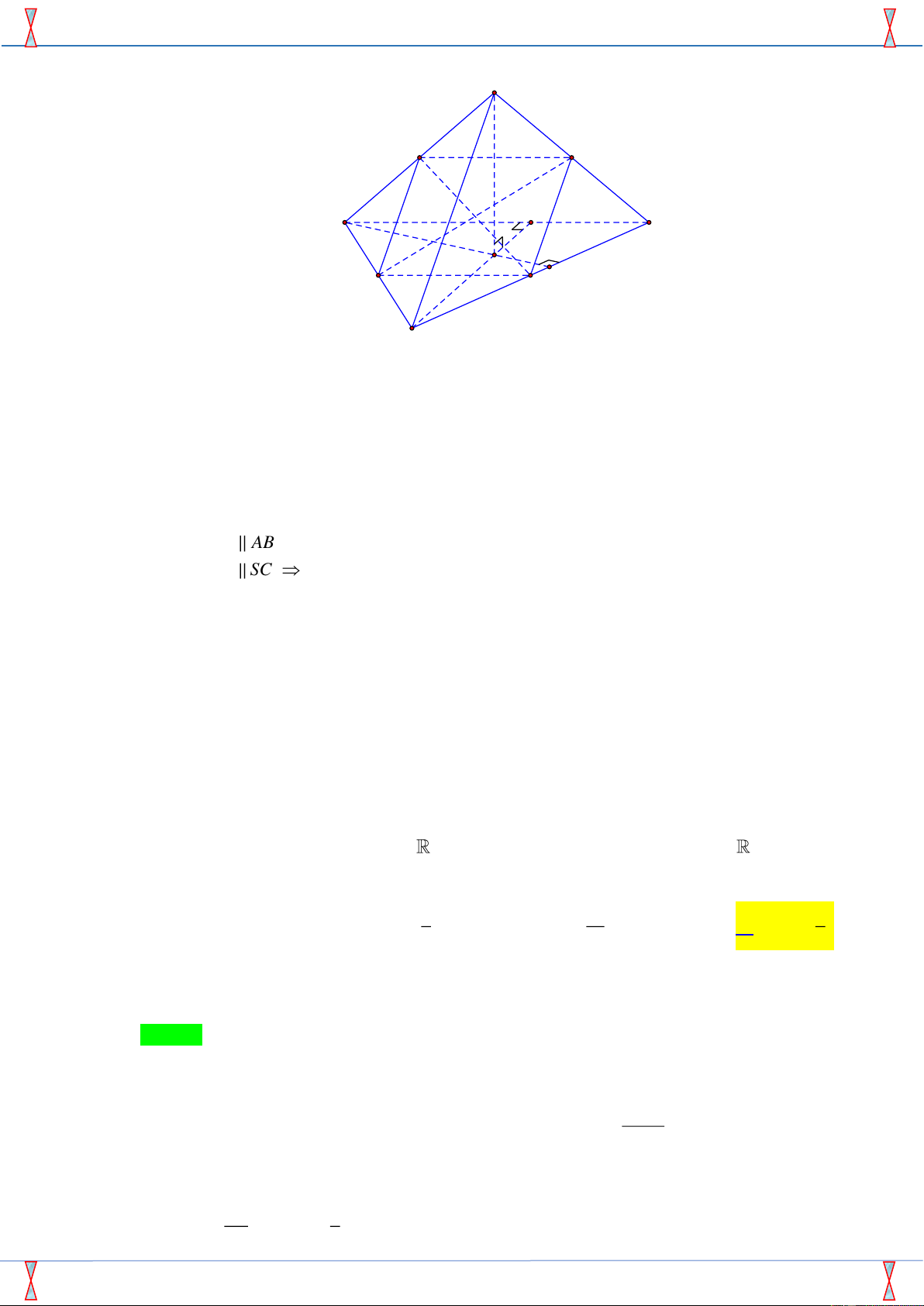
Câu 45. Cho hình chóp S.ABCD có đáy là hình vuông cạnh 2a . Biết rằng 0 ASB ASD 90 , mặt
phẳng chứa AB vuông góc với ABCD cắt SD tại N . Tìm giá trị lớn nhất của thể tích tứ diện DABN . A. 2 3 2 3 4 4 3 3 a . B. 3 3 a . C. 3 3 a . D. 3 3 a . Câu 46. Cho hàm số 3 2 y x 3 m 3 x
3 có đồ thị C . Tìm tất cả các giá trị của m sao cho qua
điểm A 1; 1 kẻ được đúng hai tiếp tuyến đến C , một tiếp tuyến là : y 1 và tiếp 1 tuyến thứ hai là thỏa mãn : tiếp xúc 2 2
C với tại N đồng thời cắt C tại điểm P (khác N ) có hoành độ bằng 3.
A. Không tồn tại m thỏa mãn. B. m 2.
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán!
Trang 5 Mã đề: 743
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC.
Đề thi thử Lần 1 - Lớp 12 – Chuyên Hạ Long 18-19 C. m 0; m 2 . D. m 2.
Câu 47. Cho bất phương trình 2 x −x − ( + ) 2 2 2 2x −x 2 .9 2 1 .6 + .4 x −x m m m
 0. Tìm m để bất phương trình nghiệm đúng 1 x   . 2 A. 3 m  . B. 3 . D. m  0 . 2 m  . C. m  0 2
Câu 48. Cho hình vuông ABCD cạnh bằng 1, điểm M là trung điểm của CD. Cho hình vuông ABCD(
Tính cả các điểm trong của nó ) quay quanh trục là đường thẳng AM ta được một khối tròn
xoay. Tính thể tích khối tròn xoay đó. A. 7 10  . B. 7 5  . C. 7 2  . D. 7 2  15 30 30 15
Câu 49. Trong chuyện cổ tích Cây tre trăm đốt (các đốt được đánh thứ tự từ 1 đến 100), khi không vác
được cây tre dài tận 100 đốt như vậy về nhà, anh Khoai ngồi khoc, Bụt liền hiện lên, bày cho
anh ta: “Con hãy hô câu thần chú Xác suất, xác suất thì cây tre sẽ rời ra, con sẽ mang được về
nhà”. Biết rằng cây tre 100 đốt được tách ra một cách ngẫu nhiên thành các đoạn ngắn có chiều
dài 2 đốt và 5 đốt (có thể chỉ có một loại). Xác suất để số đoạn 2 đốt nhiều hơn số đoạn 5 đốt
đúng 1 đoạn gần với giá trị nào trong các giá trị dưới đây? A. 0,142 . B. 0,152 . C. 0,132 . D. 0,122 .
Câu 50. Cho hàm số y = f (x) liên tục trên R và có đồ thị như hình vẽ. Hỏi hàm số y = f ( f (x)) có
bao nhiêu điểm cực trị. A. 6. B. 7. C. 8. D. 9.
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán!
Trang 6 Mã đề: 743
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC.
Đề thi thử Lần 1 - Lớp 12 – Chuyên Hạ Long 18-19
TRƯỜNG THPT CHUYÊN HẠ LONG
ĐỀ THI THỬ THPT QUỐC GIA LẦN 1 (Đề thi có 06 trang) NĂM HỌC 2018 - 2019 Môn: Toán
Thời gian làm bài: 90 phút (không kể thời gian phát đề) MÃ ĐỀ THI 121
Họ và tên: ....................................................................... Lớp: ............. 1.D 2.D 3.C 4.B 5.C 6.D 7.D 8.B 9.D 10.D 11.A 12.B 13.A 14.A 15.C 16.C 17.B 18.C 19.A 20.C 21.B 22.B 23.C 24.A 25.C 26.B 27.B 28.B 29.D 30.B 31.D 32.A 33.D 34.B 35.A 36.C 37.A 38.D 39.C 40.B 41.D 42.A 43.C 44.D 45.A 46.A 47.C 48.B 49.A 50.D
Câu 1. Tính thể tích V của khối nón có chiều cao h = a và bán kính đáy r = a 3 . 3 3 A.   = a 3 V . B. 3 V = 3 a . C. = a V . D. 3 V =  a . 3 3 Lời giải
Tác giả: Trần Lê Hương Ly; Fb: Trần Lê Hương Ly Chọn D Ta có 1 2
V =  r h =  (a )2 1 3 .a 3 =  a . 3 3
Câu 2. Tìm tập nghiệm x − x+
S của phương trình 2 3 2 9 =1. A. S =   1 . B. S = 0;  1 .
C. S = 1;−  2 . D. S = 1;  2 . Lời giải
Tác giả: Trần Lê Hương Ly; Fb: Trần Lê Hương Ly Chọn D x = 2 1 x −3x+2 2 9
=1  x − 3x + 2 = 0   . x = 2
Câu 3. Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC với A(1;1;2) , B(−3;0; ) 1 ,
C (8; 2; −6) . Tìm tọa độ trọng tâm G của tam giác ABC . A. G (2;−1; ) 1 . B. G (2;1; ) 1 . C. G (2;1;− ) 1 .
D. G (6;3;−3) . Lời giải
Tác giả: Lưu Huệ Phương; Fb: Lưu Huệ Phương Chọn C
Gọi G ( x; y; z) là trọng tâm của ABC . Khi đó:
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán!
Trang 7 Mã đề: 743
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC.
Đề thi thử Lần 1 - Lớp 12 – Chuyên Hạ Long 18-19 x + x +  1− 3+8 x = xA B C x = 3   3  x = 2  y + y + y  1+ 0 + 2   y = A B C  y =
 y =1  G (2;1;− ) 1 . 3  3    z = −  1 z + z +  2 +1− 6 z = zA B C z =  3  3
Câu 4. Tính diện tích xung quanh của khối trụ S có bán kính đáy r = 4 và chiều cao h = 3. A. S = 48 . B. S = 24 . C. S = 96 . D. S =12 . Lời giải
Tác giả: Lưu Huệ Phương; Fb: Lưu Huệ Phương Chọn B
Diện tích xung quanh của hình trụ là: S = rh = 2.4.3 = 24 . xq 2
Câu 5. Cho hàm số y = log . Khẳng định nào sau đây sai ? 2 x
A. Đồ thị hàm số nhận trục tung làm tiệm cận đứng.
B. Đồ thị hàm số cắt trục hoành tại điểm A(1;0) .
C. Đồ thị hàm số luôn nằm phía trên trục hoành.
D. Hàm số đồng biến trên khoảng (0;+ ) . Lời giải
Tác giả: Hà Lê; Fb: Ha Le Chọn C Hàm số y = log có đồ thị như sau: 2 x
Từ đồ thị hàm số ta thấy các khẳng định ,
A B, D là đúng, khẳng định C sai.
Câu 6. Cho hình lăng trụ đều AB . C A BC
  có cạnh đáy và cạnh bên cùng bằng a . Tính thể tích của khối lăng trụ đó. 3 3 3 3 A. a 6 . B. a 6 . C. a 3 . D. a 3 . 12 4 12 4 Lời giải
Tác giả: Hà Lê; Fb: Ha Le Chọn D Vì AB . C A BC
 là hình lăng trụ đều nên ta có: 2 3 a 3 a 3 V =  = = .    S AA a ABC A B C ABC . . . 4 4
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán!
Trang 8 Mã đề: 743
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC.
Đề thi thử Lần 1 - Lớp 12 – Chuyên Hạ Long 18-19 Câu 7. Cho hàm số 1 3 2 y =
x − x − 3x + 5 nghịch biến trên khoảng nào? 3 A.(3;+) . B.( ; − +) . C.( ; − − ) 1 . D.( 1 − ;3) . Lời giải
Tác giả:Nguyễn Trí Chính; Fb: Nguyễn Trí Chính. Chọn D
y = f ( x) 1 3 2
= x − x − 3x + 5, TXĐ 3 D = . x = 1 − 2
y = x − 2x − 3 , 2
y = 0  x − 2x − 3 = 0   . x = 3
Có a =1 0 nên hàm số y = f (x) nghịch biến trong ( 1 − ;3) .
Câu 8. Đồ thị hàm số x − 6 y =
có mấy đường tiệm cân? 2 x −1 A.1. B. 3. C. 2 . D. 0 . Lời giải
Tác giả: Nguyễn Trí Chính; Fb: Nguyễn Trí Chính. Chọn B ( −
C ) y = f ( x) x 6 = , TXĐ D = \−1; . 2 x −1 Có x − 6 x − 6 lim = − ;  lim
= +  x =1 là tiệm cân đứng của (C) . − 2 + 2 x 1 → − x x 1 1 → x −1 Có x − 6 x − 6 lim = − ;  lim = +  x = 1
− là tiệm cân đứng của (C) . − 2 + 2 x→ 1 − − x x → 1 1 − x −1 Có x − 6 x − 6 lim = lim
= 0  y = 0 là tiệm cận ngang của (C) . 2 2 x→+ x −1
x→− x −1
Vậy (C) có 3 tiệm cận.
Câu 9. Đường cong bên là đồ thị của một trong bốn hàm số được liệt kê dưới đây. Hỏi đó là hàm số nào? A. 3
y = −x + x −1. B. 3
y = x + x +1. C. 3
y = −x − x +1 . D. 3
y = −x + x +1. Lời giải
Tác giả : Trần Thị Kim Oanh, FB: Oanh Trần Chọn D
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán!
Trang 9 Mã đề: 743
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC.
Đề thi thử Lần 1 - Lớp 12 – Chuyên Hạ Long 18-19
Quan sát đồ thị ta có nhận xét sau:
Đường cong là đồ thị là hàm số dạng 3 2
y = ax + bx + cx + d có a  0, d  0 , hàm số có hai điểm
cực trị trái dấu hay ac  0, suy ra đáp án D
Câu 10. Tìm họ nguyên hàm của hàm số ( ) 3x f x = e x+ A.  ( ) 3 1 e f x dx = + C . B.  ( ) 3 = 3 x f x dx e + C . 3x +1 x C.  ( ) e 3
f x dx = e + C . D. f  (x) 3 dx = + C . 3 Lời giải
Tác giả : Trần Thị Kim Oanh, FB: Oanh Trần Chọn D 3x Ta có 3 e x e dx = +  3 C
Câu 11. Cho khối chóp S.ABC có SA, SB , SC đôi một vuông góc và SA = a , SB = b , SC = c . Tính
thể tích V của khối chóp đó theo a , b , c . A. = abc V . B. = abc V . C. = abc V .
D. V = abc . 6 3 2 Lời giải
Tác giả: Bùi Thị Kim Oanh ; Fb: Bùi Thị Kim Oanh Chọn ASA ⊥ Ta có SB
SA ⊥ (SBC) . SA ⊥ SC Do đó 1 1 1 = . . = abc V SA S a bc . SBC . . = 3 3 2 6
Câu 12. Tìm tập xác định D của hàm số y = log ( 2 x − x − 2 . 3 )
A. D = (−1;2).
B. D = (−;− ) 1  (2; + ) .
C. D = (2;+ ).
D. D = (−;− ) 1 . Lời giải
Tác giả: Bùi Thị Kim Oanh ; Fb: Bùi Thị Kim Oanh Chọn Bx  1 − Điều kiện: 2
x − x − 2  0   . x  2
Tập xác định của hàm số là D = (−;− ) 1  (2;+ ) .
Câu 13. Trong không gian với hệ tọa độ Oxyz , cho mặt cầu 2 2 2 S : x y z 2x 4 y 4z 25 0 .
Tìm tọa độ tâm I và bán kính mặt cầu S .
A. I 1; 2;2 ; R 34 .
B. I 1;2; 2 ; R 5 .
C. I 2;4; 4 ; R 29 .
D. I 1; 2;2 ; R 6 . Lời giải
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán!
Trang 10 Mã đề: 743
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC.
Đề thi thử Lần 1 - Lớp 12 – Chuyên Hạ Long 18-19
Tác giả: Nguyễn Văn Mộng; Fb: Nguyễn Văn Mộng. Chọn A
Mặt cầu S có tâm 2 2 2 I 1; 2; 2 ; R 1 2 2 25 34 . Vậy, ta chọn A.
Câu 14. Tìm họ nguyên hàm của hàm số f x cos x 2x . A. 2 f x dx sin x x C . B. 2 f x dx sin x x C . C. 2 f x dx sin x x . D. 2 f x dx sin x x . Lời giải
Tác giả: Nguyễn Văn Mộng; Fb: Nguyễn Văn Mộng Chọn A 2 f x dx
cos x 2x dx sin x x C . Vậy, ta chọn A.
Câu 15. Cho hàm số y = f (x) liên tục trên và có bảng biến thiên x -∞ −1 0 1 +∞ y - 0 + 0 - 0 + +  +  y 2 1 1
Khẳng định nào sau đây sai?
A. x =1 là điểm cực tiểu của hàm số. 0
B. Hàm số đồng biến trên khoảng (−1;0) và (1;+) .
C. M (0;2) là điểm cực tiểu của đồ thị hàm số. D. f (− )
1 là một giá trị cực tiểu của hàm số. Lời giải
Tác giả: Bùi Văn Khánh; Fb: Khánh Bùi Văn Chọn C
+) Dựa vào BBT thì M (0;2) là điểm cực đại của đồ thị hàm số. Do đó đáp án C sai. 12
Câu 16. Tìm số hạng không chứa  1  x trong khai triển 2 x −   ?  x A. 459 − . B. 495 − . C. 495 . D. 459 . Lời giải
Tác giả: Bùi Văn Khánh; Fb: Khánh Bùi Văn Chọn C 12 12 k 12 +) Ta có:  1 −    x −
= (− ) C (x )12 2 2 k k 1 1 = (−     )k k k 24−3 1 C . k x n nx  =  x k 0 k =0
+) Số hạng tổng quát của khai triển là ( )k k 24 3 1 C . k x − − n
+) Số hạng trong khai triển không chứa x ứng với 24−3k = 0  k = 8.
Vậy số hạng không chứa x trong khai triển là: 8 C = 495. 12
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán!
Trang 11 Mã đề: 743
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC.
Đề thi thử Lần 1 - Lớp 12 – Chuyên Hạ Long 18-19
Câu 17. Cho hàm số y = f (x) có đạo hàm ( ) = ( x + )( x f x e e − )(x+ )(x− )2 ' 1 12 1 1 trên . Hỏi hàm số
có bao nhiêu điểm cực trị? A. 1. B. 2 . C. 3. D. 4 . Lời giải
Tác giả: Vũ Danh Được; Fb: Danh Được Vũ Chọn Bx = ln12 Ta có 
f '( x) = 0  x = −1  x =  1
Bảng xét dấu của f '( x) như sau: x -∞ -1 1 ln2 +∞ + 0 - 0 - 0 + f ' x ( )
Từ đó ta thấy hàm số có hai điểm cực trị tại x = 1 − và x = ln 2 .
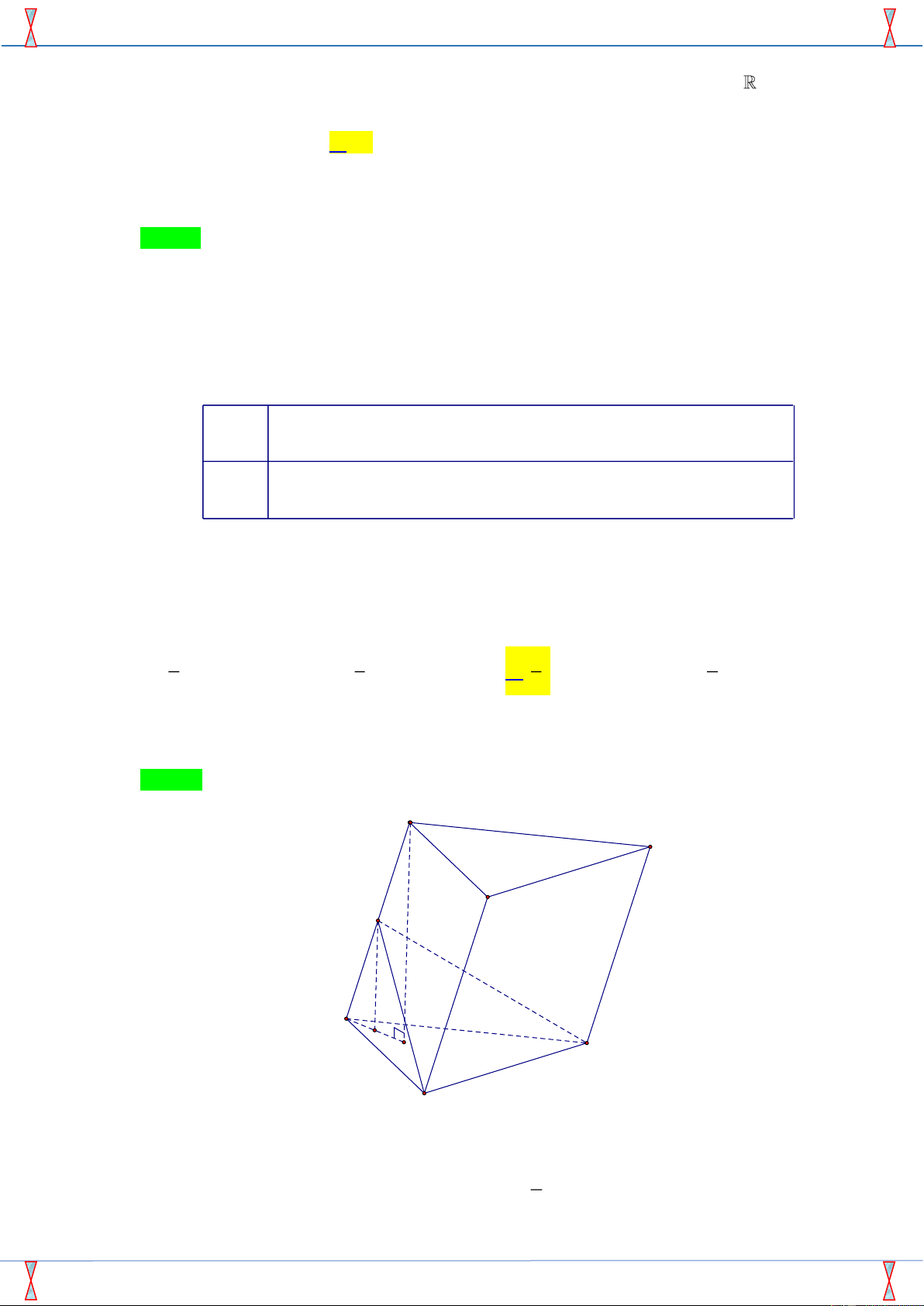
Câu 18. Cho khối lăng trụ tam giác AB . C A BC
  có thể tích V . Gọi M là trung điểm của CC '. Mặt
phẳng (MAB) chia khối lăng trụ thành hai phần. Tính tỷ số thể tích hai phần đó (số bé chia số lớn). A. 2 . B. 3 . C. 1 . D. 1 . 5 5 5 6 Lời giải
Tác giả: Vũ Danh Được; Fb: Danh Được Vũ Chọn C C' B' A' M h h' C B A
Gọi chiều cao của hình lăng trụ AB . C A BC
  là h thì V = . h S . ABC
Gọi chiều cao của hình chóp h
M .ABC là h ' thì h ' = . 2
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán!
Trang 12 Mã đề: 743
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC.
Đề thi thử Lần 1 - Lớp 12 – Chuyên Hạ Long 18-19 S Do đó A D 0 60 O H B C 1 1 1 = = = . M V .ABC h '.S ABC . h S ABC . 3 6 6 V  
Suy ra thể tích của khối đa diện ABM.A BC   bằng 1 5 V − .V = . . 6 6 V
Vậy tỉ số thể tích của hai phần (số bé chia số lớn) là 1 . 5
Câu 19: Tính thể tích V của khối cầu nội tiếp hình lập phương cạnh a 3 3  3 3 A. a 4 aaa V = . B. V = . C. V = . D. V = . 6 3 3 2 Lời giải
Tác giả: Đào Văn Tiến;face : Đào Văn Tiến Chọn A
Hình lập phương có cạnh bằng a
a suy ra mặt cầu nội tiếp hình lập phương có bán kính là r = . 2 3 3  
Từ đó suy ra thể tích của khối cầu nội tiếp hình lập phương là 4 3 4 = r = . a a V = . 3 3 8 6
Câu 20: Cho khối chóp tứ giác đều S.ABCD có cạnh đáy bằng a , các mặt bên tạo với mặt đáy bằng
60 . Tính thể tích khối chóp đó. 3 3 3 3 A. a 3 . B. a 3 . C. a 3 . D. a 3 . 2 12 6 3 Lời giải Chọn C
Gọi H là trung điểm CD,O là giao điểm hai đường chéo, suy ra SO ⊥ ( ABCD)
Từ giả thiết ta có góc giữa mặt bên và mặt đáy là SHO = 60 3 Ta có a a 3 1 a 3 a 3 OH = ; =
suy ra thể tích khối chóp là 2 V = .a . = . 2 SO 2 3 2 6
Câu 21. Cho hàm số f (x) thỏa mãn '( ) = ( + ) 1 x f x x
e và f (0) = 1. Tính f (2). A. f ( ) 2 2 = 4e +1. B. f ( ) 2 2 = 2e +1. C. f ( ) 2 2 = 3e +1. D. f ( ) 2 2 = e +1. Lời giải
Tác giả: Lê Cảnh Dương FB: Cảnh Dương Lê
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán!
Trang 13 Mã đề: 743
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC.
Đề thi thử Lần 1 - Lớp 12 – Chuyên Hạ Long 18-19 Chọn B 2 2
Ta có f (2) − f (0) = f '
 (x)dx = (x+ ) x 2
1 e dx = 2e (phương pháp từng phần) 0 0  f ( ) 2 = e + f ( ) 2 2 2 0 = 2e +1.
Câu 22. Viết phương trình tiếp tuyến của đồ thị hàm số 3 2
y = x − 3x +1 biết nó song song với đường
thẳng y = 9x + 6.
A. y = 9x + 26, y = 9x − 6.
B. y = 9x − 26.
C. y = 9x + 26.
D. y = 9x − 26, y = 9x + 6. Lời giải
Tác giả: Lê Cảnh Dương FB: Cảnh Dương Lê Chọn B Gọi = + 0
x là hoành độ tiếp điểm của tiếp tuyến. Do tiếp tuyến song song đường thẳng y 9x 6 x = 1 −
nên y '(x = 9  3x − 6x = 9   . 0 ) 2 0 0 0 x =  3 0
Với x = −1 y −1 = −3:
y = 9 x +1 − 3  y = 9x + 6 0 ( ) PTTT ( ) (loại).
Với x = 3  y 3 =1:
y = 9 x − 3 +1  y = 9x − 26. 0 ( ) PTTT ( )
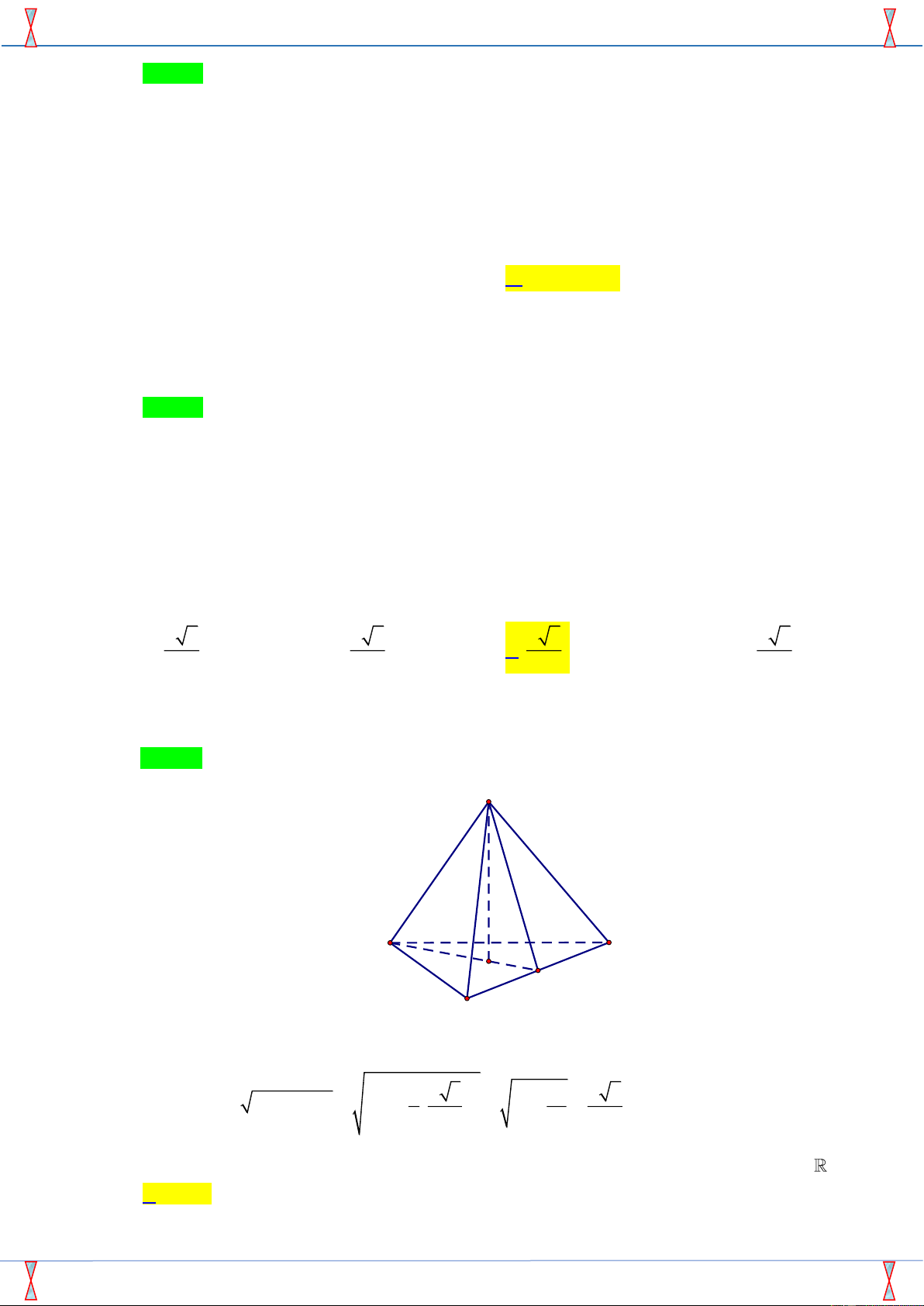
Câu23.Tính độ dài đường cao tứ diện đều cạnh a . A. a 2 . B. a 6 . C. a 6 . D. a 6 . 3 9 3 6 Lời giải
Tác giả: Minh Anh Phuc; Fb: Minh Anh Phuc Chọn C S A C O M B
Xét tứ diện S.ABC là tứ diện đều cạnh a , gọi O làm tâm của đáy. Ta có đường cao của tứ 2 2   diện là 2 2 2 2 a 3 2 a a 6 SO = SA − AO = a −  .  = − =  . 3 2 a    3 3
Câu24. Tìm tất cả các giá trị thực của tham số m để hàm số 3 2
y = x − 3x + mx + 2 đồng biến trên ? A. m  3 . B. m  3. C. m  3 . D. m  3 . Lời giải
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán!
Trang 14 Mã đề: 743
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC.
Đề thi thử Lần 1 - Lớp 12 – Chuyên Hạ Long 18-19
Tác giả: Minh Anh Phuc; Fb: Minh Anh Phuc Chọn A 2
y = 3x − 6x + m .
y là hàm số bậc hai và a = 3  0 nên hàm số đã cho đồng biến trên  y  0 x    
  0  9 −3m  0  m  3.
Câu 25. Cho khối chóp S.ABC có SA ⊥ ( ABC) , SA = a, AB = a, AC = 2a và 0
BAC = 120 . Tính thể tích
khối chóp S.ABC . 3 3 3 A. a 3 . B. a 3 a 3 3 a 3 . C. . D. . 3 6 2 Lời giải
Tác giả: Phạm Thị Phương Thúy; Fb: thuypham Chọn C Diện tích tam giác 1 1 3 ABC là: 0 2 S = AB AC A = a a = a . ABC . .sin . .2 .sin120 2 2 2 Thể tích khối chóp 1 1 3 3 S.ABC là: 2 3 V = SA S = a a = a . S ABC . ABC . . 3 3 2 6
Câu 26. Cho tam giác ABC vuông cân tại A , đường cao AH = 4. Tính diện tích xung quanh S của xq
hình nón nhận được khi quay tam giác ABC xung quanh trục AH . A. S = 4 2 . B. S =16 2 . C. S = 8 2 . D. S = 32 2 . xq xq xq xq Lời giải
Tác giả: Phạm Thị Phương Thúy; Fb:thuypham Chọn B
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán!
Trang 15 Mã đề: 743
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC.
Đề thi thử Lần 1 - Lớp 12 – Chuyên Hạ Long 18-19
Tam giác ABC vuông cân tại A có đường cao AH = 4  AH là đường trung tuyến và 1 AH = BC = HB = 4. 2
Hình nón nhận được có đường cao AH = 4, bán kính đáy HB = 4  AB = 4 2 là đường sinh.
Vậy diện tích xung quanh của hình nón tạo thành là: S =  BH AB =  =  . xq . . .4.4 2 16 2
Câu 27. Tính đạo hàm của hàm số x + 1 y =
,(x  0; x  ) 1 ln x A. ln x − x − 1
x ln x − x − 1 y = . B. y = . x (ln x)2 x (ln x)2 C. ln x − x − 1 x − x − y = . D. ln 1  = . ( y ln x)2 x ln x Lời giải
Tác giả: Lương Thị Hương Liễu; Fb: Lương Hương Liễu. Chọn B Ta có: (   − +
x + 1) ln x − (ln x) (x + 1) 1 ln x
(x 1) xlnx−x−1 x y = = = (lnx)2 (lnx)2 x (ln x)2
Câu 28. Phương trình 2
sin x + 3 sin x cos x = 1 có bao nhiêu nghiệm thuộc 0 ; 3    . A. 7. B. 6. C. 4. D. 5. Lời giải
Tác giả: Lương Thị Hương Liễu; Fb: Lương Hương Liễu. Chọn B − 2 1 cos 2x 3
sin x + 3 sin x cos x = 1  +
sin 2x = 1  − cos 2x + 3 sin 2x = 1 2 2  −    + 2x = + k2 x = + k   1    −   −  6 6 6  2sin +  2x =  1  sin +  2x =      '(k  )  6   6  2   − 5   + 2x = + k2 x = + k  6 6  2    = +   Với x k , k  6  k = 0;1; 2. x  0;3        = +   Với x k , k  2  k = 0;1; 2. x  0;3    
Vậy phương trình đã cho có 6 nghiệm thuộc đoạn 0; 3    .
Câu 29. Việt nam là quốc gia nằm ở phía Đông bán đảo Đông Dương thuộc khu vực Đông Nam Á. Với
dân số ước tính 93,7 triệu dân vào đầu năm 2018, Việt Nam là quốc gia đông dân thứ 15 trên
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán!
Trang 16 Mã đề: 743
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC.
Đề thi thử Lần 1 - Lớp 12 – Chuyên Hạ Long 18-19
thế giới và là quốc gia đông dân thứ 8 của châu Á, tỉ lệ tăng dân số hàng năm 1,2%. Giả sử rằng
tỉ lệ tăng dân số từ năm 2018 đến năm 2030 không thay đổi thì dân số nước ta đầu năm 2030 khoảng bao nhiêu? A.118,12 triệu dân. B.106,12 triệu dân. C.118,12 triệu dân. D.108,12 triệu dân. Lời giải
Tác giả:Phạm Thị Thu Trang; Fb: Trang Phạm Chọn D
Dân số việt nam năm 2019 là: D = 93,7 + 93,7.0,012 = 93,7. 1+ 0,012 1 ( ) triệu dân
Dân số việt nam năm 2020 là:
D = 93, 7.(1+ 0, 012) + 93, 7.(1+ 0, 012).0, 012 = 93, 7.(1+ 0, 012)2 triệu dân 2 …
Như vậy dân số Việt nam tăng theo cấp số nhân và được tính theo công thức:
D = 93, 7.(1+ 0,012)n với n là số năm tính từ 2018. n
Vậy dân số Việt nam năm 2030 là: D = 93,7.(1+ 0,012)12 108,12 triệu dân. Chọn D. 12
Nhận xét: Đề bài có 2 đáp án giống nhau là A và C.
Câu 30. Dãy số nào là cấp số cộng? A. n u = n + n
B.u = n + nn ( * 3 1, ). n ( * 2 , ). + C. 3n 1 n u = n D.u = , n n ( * ). n ( * 3 , ). n + 2 Lời giải
Tác giả:Phạm Thị Thu Trang; Fb: Trang Phạm Chọn B Với dãy số n u = n + n  , xét hiệu: n 1 u
− u = n +1+ 2 + − − = +  thay + n 2n 2n n n n 1,( * 1 ) n ( * 2 , ) đổi theo n nên n u = n + n
không là cấp số cộng. (A loại) n ( * 2 , )
Với dãy số u = n + n
, xét hiệu: u −u = n + + − n − = n  là hằng số n+ n 3( ) 1 1 3 1 3,( * 1 ) n ( * 3 1, )
nên u = n + n
là cấp số cộng. (B đúng) n ( * 3 1, ) Với dãy số n u = n  , xét hiệu: n 1 u − u = 3 + − =  thay đổi theo + 3n 2.3n n n n ,( * 1 ) n ( * 3 , ) n nên n u = n
không là cấp số cộng. (C loại) n ( * 3 , ) + Với dãy số 3n 1 u = n  , xét hiệu: n ,( * ) n + 2 3(n + ) 1 +1 3n +1 5 u −u = − = n  thay đổi theo n+ n ,( * 1 ) n nên n +1+ 2 n + 2 (n+ 2)(n+3) 3n +1 u = n
không là cấp số cộng. (D loại) n ,( * ) n + 2
Câu 31. Tìm nguyên hàm 1 . dxx ln x+1
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán!
Trang 17 Mã đề: 743
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC.
Đề thi thử Lần 1 - Lớp 12 – Chuyên Hạ Long 18-19 A. 2 1 3 (ln x +1) + C .
B. ln x +1 + C . C. 2
(ln x +1) + C . D. 2 ln x +1 + C . 3 2 Lời giải
Tác giả: Nguyễn Mạnh Dũng; Fb: dungmanhnguyen Chọn D 1 1 − 2
dx = (ln x +1) d (ln x +1) = 2 ln x +1 + C.   x ln x +1
Câu 32. Trong không gian với hệ tọa độ Oxyz , cho hai vec tơ a = ( 2 − ; 3
− ;1) , b = (1;0;1) . Tính cos(a,b) . A. 1 − −
cos(a, b) = . B. 1
cos(a, b) = . C. 3
cos(a, b) = . D. 3
cos(a, b) = . 2 7 2 7 2 7 2 7 Lời giải
Tác giả: Nguyễn Mạnh Dũng; Fb: dungmanhnguyen Chọn A Ta có: . a b 2. − 1+ 3. − 0 +1.1 1 −
cos(a,b) = = = . 2 2 2 2 2 2 a . b ( 2) − + ( 3 − ) +1 . 1 + 0 +1 2 7
Câu 33. Trong không gian với hệ trục tọa độ Oxyz cho tam giác ABC, với A(1;2; ) 1 , B ( 3 − ;0;3), C (2; 4; − )
1 . Tìm tọa độ điểm D sao cho tứ giác ABCD là hình bình hành. A. D(6; 6 − ;3) . B. D(6;6;3).
C. D(6;−6;−3) . D. D(6;6; 3 − ) . Lời giải
Tác giả : Nguyễn Hoàng Hưng, FB: Nguyễn Hưng Chọn D
Gọi D (x; y; z) Ta có: AB = ( 4 − ; 2 − ;2), DC = (2 − ; x 4 − ; y 1 − − z) 2 − x = 4 − x = 6 Tứ giác  
ABCD là hình bình hành  AB = DC  4 − y = −2   y = 6  D (6;6; −3) .  1  − − z = 2 z = 3 −   2 Câu 34. Gọi x + x + 3
M , m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = trên −2;  1 . x − 2
Tính T = M + 2m . A. 25 T = . B. T = 11 − . C. T = 7 − . D. T = 10 − . 2 Lời giải
Tác giả : Nguyễn Hoàng Hưng, FB: Nguyễn Hưng Chọn B 2 Hàm số x + x + 3 y =
xác định và liên tục trên đoạn −2;  1 . x − 2 2 x − 4x − 5
x = −1−2;  1 y = , 2
y = 0  x − 4x − 5 = 0  . (  x − 2)2 x = 5  −2; 1
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán!
Trang 18 Mã đề: 743
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC.
Đề thi thử Lần 1 - Lớp 12 – Chuyên Hạ Long 18-19 − y (− ) 5 2 = , y( ) 1 = 5 − , y(− ) 1 = 1 − . 4 Vậy M = 1 − , m = 5
−  T = M + 2m = −11. Câu 35. Biết x +1
dx = a ln x −1 + b ln x − 2 + C, ( , a b  ). 
Tính giá trị của biểu thức a + . b
(x −1)(x − 2)
A. a +b =1.
B. a +b = 5.
C. a +b = 5.
D. a +b = 1 − . Lời giải
Tác giả: Nguyễn Hoa; Fb:Hoa Nguyễn Chọn A x +1 2
− (x − 2) + 3(x −1) =  (  −1)( − 2) dx ( −1)( − 2) dx x x x x  −2 3  = +  −1 −2 dxx x
= −2ln x −1 + 3ln x − 2 + C.  a = 2
− ,b = 3  a + b = 1.
Câu 36. Tính tổng tất cả các giá trị của m biết đồ thị hàm số 3 2
y = x + 2mx + (m + 3) x+ 4 và đường
thẳng y = x + 4 cắt nhau tại 3 điểm phân biệt (
A 0; 4), B, C sao cho S = 8 2 với I(1;3). IBC A. 3 . B. 8 . C. 1. D. 5. Lời giải
Tác giả: Nguyễn Hoa; Fb:Hoa Nguyễn Chọn C
Phương trình hoành độ giao điểm 3 2
x + 2mx + (m + 3) x+ 4 = x + 4 x = 0   2
f (x) = x + 2mx + m + 2 = 0 (1) ' 2   0  (1)
m − m − 2  0 YCBT      m(− ;  1 − ) (2;+) \−  2  f (0)  0 m + 2  0 x + x = −2
Khi đó 3 giao điểm phân biệt là (0 m
A ; 4), B(x , x + 4), C(x , x + 4) với 1 2 . 1 1 2 2 x .x = m+  2 1 2 Ta có: 2 2
BC = (x − x ) + (x + 4 − x − 4) 2 2 = − =  + −  2 1 2 1 2(x x ) 2 (x x ) 4x . 2 1  2 1 2 1 x  2
BC = 2 2 m − m − 2.
Ta có d : y = x + 4  x − y + 4 = 0  d(I,d) = 2.  1+ 137 1 m = (t/m) 2 2 S
= d I d BC m − m − = 2
m − m − 34 = 0   . ABC ( , ). 2 4 2 2  1− 137 m = (t/m)  2
Do đó tổng tất cả các giá trị của m là 1.
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán!
Trang 19 Mã đề: 743
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC.
Đề thi thử Lần 1 - Lớp 12 – Chuyên Hạ Long 18-19
Câu 37. Gọi S là tập hợp tất cả các giá trị của m để hàm số 4 2 4
y = x − 2mx + 2m + m có ba điểm cực trị
đồng thời các điểm cực trị của đồ thị lập thành tam giác có bán kính đường tròn ngoại tiếp bằng
1. Tính tổng tất cả các phần tử của S. A. 1+ 5 . B. 2 + 5 . C. 0. D. 3+ 5 . 2 2 2 Lời giải
Tác giả: Hoàng Dũng; Fb: Hoang Dung Chọn A Ta có 3 2
y = 4x − 4mx = 4x(x − ) m .  = 0 ' = 0 x y   2 x = m
Hàm số có ba điểm cực trị  Phương trình 2 4x(x − )
m = 0 có 3 nghiệm phân  Phương trình 2
x = m có 2 nghiệm phân biệt khác 0.  m  0. Khi 4 4 2
m  0 đồ thị hàm số có ba điểm cực trị là A(0;m + 2m) , B( m;m − m + 2m) , 2 2 C ( 4 2
− m;m − m + 2m) và AB = ( m;−m ), AC = (− m;−m ) không cùng phương nên ba điểm ,
A B, C luôn tạo thành ba đỉnh của một tam giác.
*)CÁCH 1: Gọi I (0;a) là tâm đường tròn ngoại tiếp tam giác ABC. Ta có IA=IB=IC=1.  = 4 m 1
m + 2m − a =1    (   1 − − 5  4 + − =  + − + − = = m 2m a  )2 1  ( 4 2 2 )2 1 m m m m m a     2 Ta được   + .  (  − + 2 − )2 4 4 2 = 1
m + 2m − a m m m m a = −1   1 − + 5  m =   m + 
(m −m + m−a)2 4 2 2 2 = 1  m  0.45 −  − + 
Kết hợp với điều kiện  m  0 ta được 1 5 S = 1;  .  2   
Suy ra: Tổng tất cả các phần tử của + S bằng 1 5 2 *)CÁCH 2: AB = ( 2
m −m ) AC = ( 2 − m −m ) 4 ; , ;
AB = m + m = AC ABC cân tại A. Gọi 4 2
H là trung điểm của BC thì H (0;m − m + 2m) và AH là đường cao của . ABC
Gọi R là bán kính đường tròn ngoại tiếp ABC  thì A . B AC.BC 1 S = = AH BC ABC . 4R 2 2 4 A . B AC.BC AB m + mR = = = 2 2AH.BC 2AH 2m
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán!
Trang 20 Mã đề: 743
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC.
Đề thi thử Lần 1 - Lớp 12 – Chuyên Hạ Long 18-19 m =1 4 m  +  0 m   0 Theo đề =1 m m R  =1      2 4 2  2 2 1 − +  5 m
m + m = 2m
(m −1)(m + m −1) = 0 m =  2 .
Câu 38. Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A, D và AB=AD=a, DC=2a, tam
giác đều và nằm trên mặt phẳng vuông góc với đáy. Gọi H là hình chiếu vuông góc của D trên
AC và M là trung điểm của HC. Tính diện tích mặt cầu ngoại tiếp hình chóp S.BDM theo a. 2  2  2  2  A. 7 a . B. 13 a . C. 13 a . D. 7 a . 9 9 3 3 Lời giải
Tác giả: Hoàng Dũng; Fb: Hoang Dung Chọn D S A B H G I O A B M H N D C E O M D C E Dựng hình ( hình vẽ). Ta có 1 1 1 1 1 5 2a = + = + =  = . 2 2 2 2 2 2 4 4 DH DH DA DC a a a 5 2 2 Mặt khác CD 4a 4a 2a HC = = =  HM = = DH . AC 5a 5 5
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán!
Trang 21 Mã đề: 743
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC.
Đề thi thử Lần 1 - Lớp 12 – Chuyên Hạ Long 18-19
Do đó tam giác DHM vuông cân tại H. Suy ra DMA = 45 = DEA.
Do vậy năm điểm A, D, E, M, B cùng nằm trên đường tròn ngoại tiếp hình vuông . ABED
Suy ra mặt cầu ngoại tiếp hình chóp S.BDM là mặt cầu ngoại tiếp hình chóp S.ABED.
Gọi R=ID là bán kính mặt cầu ngoại tiếp hình chóp S.ABED. 2 2 2     Ta có 2 2 2 2 a 3 a 2 7a
R = ID = OI + OD =   +   =  . 6   2      12 2 2
Suy ra diện tích mặt cầu ngoại tiếp hình chóp aa S.BDM bằng 2 7 7 4 R = 4 = . 12 3
Câu 39. Trong không gian Oxyz , cho tam giác ABC với (
A 1; 2;0), B(3; 2; 1 − ),C( 1 − ; 4 − ;4) . Tìm tập hợp
tất cả các điểm M sao cho 2 2 2
MA + MB + MC = 52
A.Mặt cầu tâm I( 1 − ;0; 1
− ) , bán kính r = 2 .
B. Mặt cầu tâm I( 1 − ;0; 1
− ) , bán kính r = 2
C. Mặt cầu tâm I(1;0;1) , bán kính r = 2 .
D. Mặt cầu tâm I(1;0;1) , bán kính r = 2 . Lời giải
Tác giả:Nguyễn Lệ Hoài; Fb: Hoài lệ ChọnC Gọi M ( ;
x y; z) . Khi đó
MA + MB + MC = ( x − )2 + ( y − )2 + z + ( x − )2 + ( y − )2 + z +
+ (x + )2 + ( y + )2 2 2 2 2 2 2 1 2 3 2 ( 1) 1 4 + (z − 4) 2 2 2
= 3x + 3y + 3z − 6x − 6z + 52. Theo đề 2 2 2
MA + MB + MC = 52 2 2 2
 3x + 3y + 3z − 6x − 6z + 52 = 52 2 2 2
 (x −1) + y + (z −1) = 2
M thuộc mặt cầu có tâm mặt cầu tâm I(1;0;1) , bán kính r = 2
Câu 40. Cho hàm số y = f (x) có đạo hàm trên và có đồ thị hàm số y = f '(x) hình bên. Hàm số
y = f (3 − x) đồng biến trên khoảng nào dưới đây? A. (−2;− ) 1 . B. (−1;2) C. (2;+) . D.(− ;  1 − ) Lời giải
Tác giả:Nguyễn Lệ Hoài; Fb: Hoài lệ Chọn B
+ Theo đề ta có hàm số y = g(x) = f (3− x) có đạo hàm trên .
g '(x) = (3 − x) '. f '(3 − x) = − f '(3 − x)
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán!
Trang 22 Mã đề: 743
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC.
Đề thi thử Lần 1 - Lớp 12 – Chuyên Hạ Long 18-19
+ Tìm x sao cho g '(x)  0. 3− x  1 − x  4
g '(x)  0  − f '(3 − x)  0  f '(3 − x)  0     . 1   3− x  4  1 −  x  2 3 − x = 1 − x = 4  
g '(x) = 0  − f '(3 − x) = 0  f '(3 − x) = 0  3 − x = 1  x = 2   : hữu hạn nghiệm. 3− x = 4 x = 1 −  
Vậy hàm số y = f (3− x) đồng biến trên mỗi tập  1 − ;2, 4;+) .
Soi các phương án của đề bài ta chọn phương án . B
Câu 41. Trong mặt phẳng (P) cho hình vuông ABCD cạnh a . Trên đường thẳng qua A và vuông góc
với mặt phẳng (P) lấy điểm S sao cho SA = a . Mặt cầu đường kính AC cắt các đường thẳng
SB, SC, SD lần lượt tại M B, N C, P D . Tính diện tích tứ giác AMNP . 2 2 2 2 A. a 6 . B. a 2 C. a 2 . D. a 3 . 2 12 4 6 Lời giải
Tác giả : Phạm Ngọc Hưng, FB: Phạm Ngọc Hưng Chọn D  ⊥ Ta có SB MD
SB ⊥ (MAD)  SB ⊥ AMSB ⊥ AD
Tương tự AN ⊥ SC; AP ⊥ SD . Ta có a 2 a 6 a 6 AM = AP = ; AN = ; = 2 3 MN 6 2 Suy ra 1 a 2 a 6 a 3 S = S = AM MN = = AMNP 2 AMN 2. . . . 2 2 6 6
Câu 42. Gọi K là tập nghiệm của bất phương trình 2x+ x 1+ 2+ x 1 7 7 + −
+ 2018x  2018. Biết rằng tập hợp
tất cả các giá trị của tham số 3 2
m sao cho hàm số y = 2x − 3(m + 2) x + 6 (2m + 3) x − 3m + 5 đồng
biến trên K là a − b;+ 
), với a, b là các số thực. Tính S =a+ .b
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán!
Trang 23 Mã đề: 743
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC.
Đề thi thử Lần 1 - Lớp 12 – Chuyên Hạ Long 18-19 A.S 14 . B. S 8 . C. S 10. D. S 11. Lời giải
Tác giả : Phạm Ngọc Hưng, FB: Phạm Ngọc Hưng Chọn A ĐK: x  1. − Ta có 2x+ x 1 + 2+ x 1 + 2x+ x 1 x + ( x x ) 2+ x 1 7 7 2018 2018 7 1009 2 1 7 + − +   + + +  +1009(2+ x+1)
f (2x + x +1)  f (2+ x +1) với ( ) = 7t f t +1009t, t  2 − . Do ( ) = 7t f t ln 7 +1009  0, t   2
− nên ta có 2x + x +1  2 + x +1  x 1.
Do điều kiện x  1
− nên K = −1;  1 . 3
y = x − (m + ) 2 2 3
2 x + 6(2m + 3) x −3m + 5 đồng biến trên K y  0, x   K 2
 6x − 6(m + 2) x + 6(2m + 3)  0, x   K 2 −x + 2x −3  m  ,   2 x K − x 2 Đặt − + − g ( x) x 2x 3 = , x 1 − ;  1 . Ta tính được 2 − x  = g ( x) a 2 max
= 2 − 2 3  m  2 − 2 3   −;1 1 b  =12
Vậy S = a +b =14.
Câu 43. Cho tứ diện SABC có ABC là tam giác nhọn. Gọi hình chiếu vuông góc của S lên mặt phẳng
( ABC) trùng với trực tâm tam giác ABC . Khẳng định nào sau đây là sai khi nói về tứ diện đã cho?
A. Các đoạn thẳng nối các trung điểm các cặp cạnh đối của tứ diện bằng nhau.
B. Tổng các bình phương của mỗi cặp cạnh đối của tứ diện bằng nhau.
C. Tồn tại một đỉnh của tứ diện có ba cạnh xuất phát từ đỉnh đó đôi một vuông góc với nhau.
D. Tứ diện có các cặp cạnh đối vuông góc với nhau. Lời giải
Tác giả: Đặng Phước Thiên; Fb: Đặng Phước Thiên Chọn C
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán!
Trang 24 Mã đề: 743
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC.
Đề thi thử Lần 1 - Lớp 12 – Chuyên Hạ Long 18-19 S M N F A B H E Q P C  ⊥ +) Ta có: AB SH
AB ⊥ (SHC)  AB ⊥ SCAB ⊥ CH
Tương tự ta có: BC ⊥ SA và CA ⊥ SB . Do đó, phương án D đúng.
+) Gọi M , N, P, Q theo thứ tự là trung điểm các cạnh ,
SA SB, BC, AC .
Suy ra: MNPQ là hình bình hành. PQ AB
Lại có: NP SC PQ ⊥ NPSC ⊥ AB
Suy ra: MNPQ là hình chữ nhật  MP = NQ .
Chứng minh tương tự, ta được phương án B đúng.
+) Do MNPQ là hình chữ nhật nên phương án A đúng.
+) Giả sử tồn tại một đỉnh của tứ diện mà xuất phát từ đỉnh đó các cạnh của tứ diện đội một vuông góc nhau.
Suy ra đỉnh đó chỉ có thể là S .
Khi đó, H là tâm đường tròn ngoại tiếp ABC   ABC  đều.
Câu 44. Cho hàm số y = f (x) liên tục trên thỏa mãn ( ) + ( ) 2 2 . −x f x x f x = e , x   và f (0) = 0. Tính f ( ) 1 . A. 1 f ( ) 2 1 = e . B. f ( ) 1 1 = − . C. f ( ) 1 = . D. f ( ) 1 1 = . e 2 e e Lời giải
Tác giả: Đặng Phước Thiên; Fb: Đặng Phước Thiên Chọn D Ta có: ( ) + ( ) 2 −x =  ( ) 2 2 2 . x + 2 x f x x f x e f x e xe f ( x) = 1 +   ( ) 2  x C x  =  ( ) 2 . 1 . x f x e f x e = x + C    f (x) = . 2 x e
Lại có: f (0) = 0  C = 0.  f (x) x 1 =  f 1 = . 2 ( ) x e e
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán!
Trang 25 Mã đề: 743
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC.
Đề thi thử Lần 1 - Lớp 12 – Chuyên Hạ Long 18-19
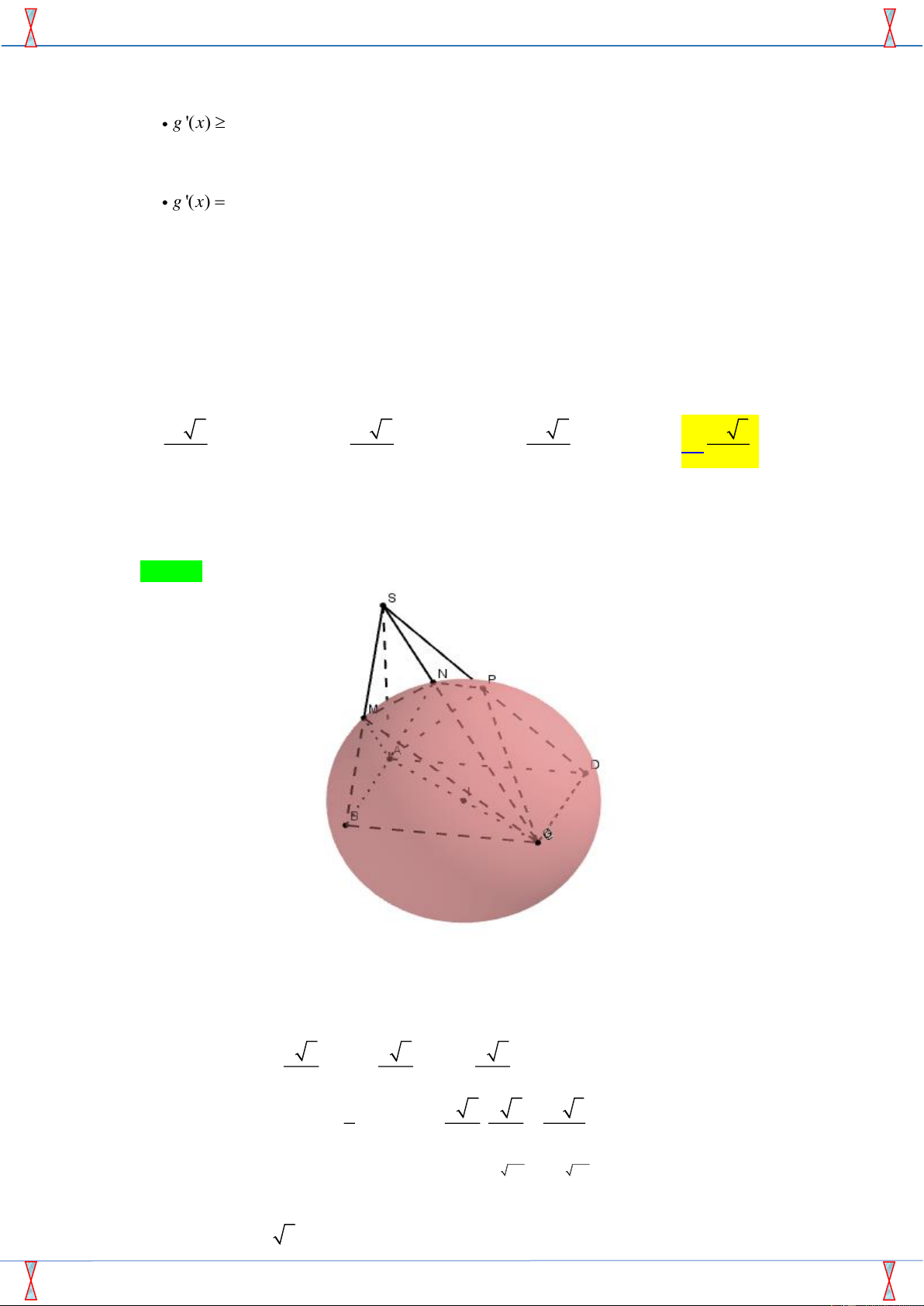
Câu 45. Cho hình chóp S.ABCD có đáy là hình vuông cạnh 2a . Biết rằng 0 ASB ASD 90 , mặt
phẳng chứa AB vuông góc với ABCD cắt SD tại N . Tìm giá trị lớn nhất của thể tích tứ diện DABN . A. 2 3 2 3 4 4 3 3 a . B. 3 3 a . C. 3 3 a . D. 3 3 a . Lời giải
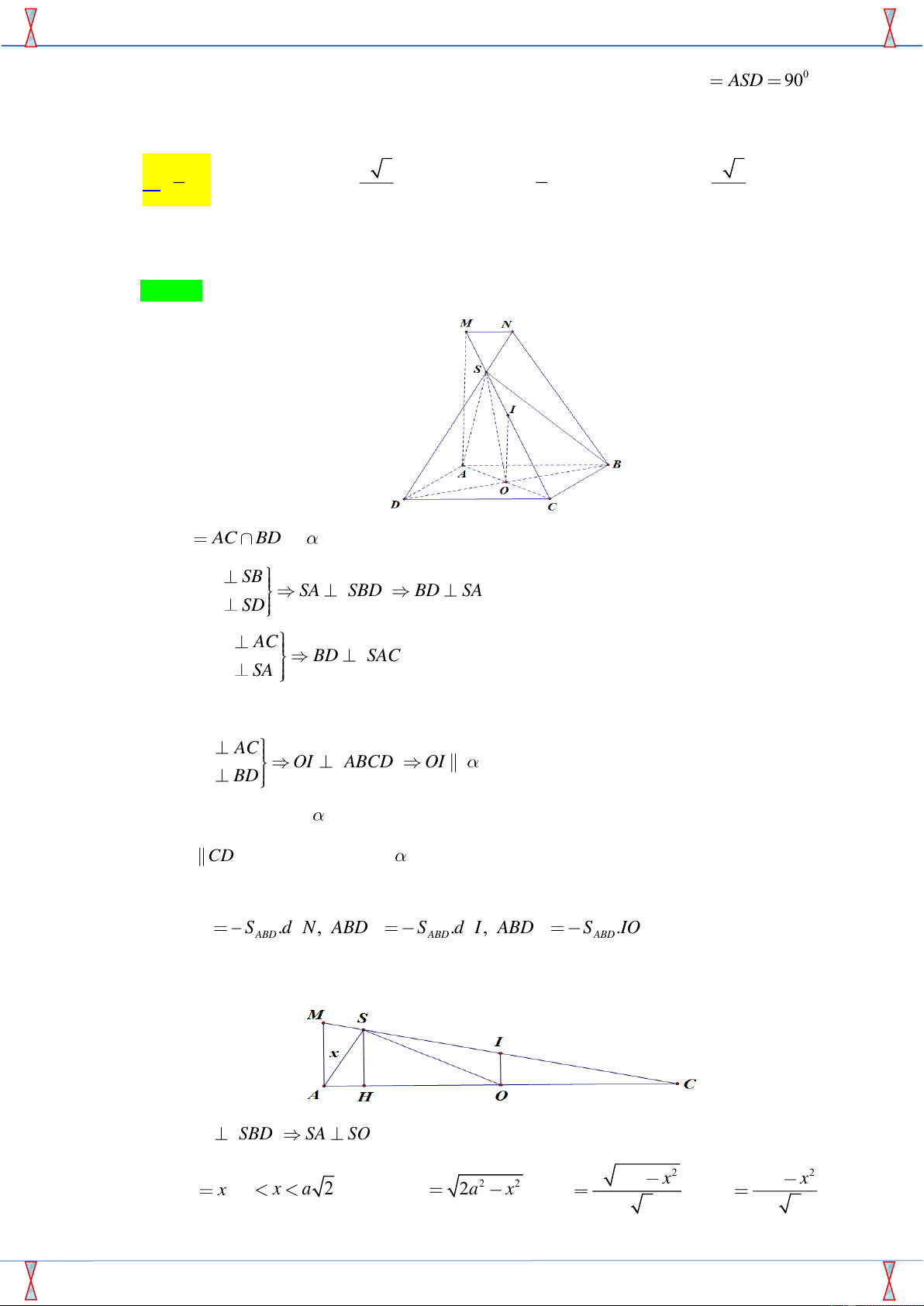
Nguyễn Xuân Giao; giaonguyen Chọn A Gọi O AC BD ,
là mặt phẳng chứa AB và vuông góc với ABCD Ta có SA SB SA SBD BD SA . SA SD Lại có BD AC BD SAC . BD SA
Trong SAC dựng đường thẳng qua O vuông góc với SA cắt SC tại I . Ta có OI AC OI ABCD OI OI BD suy ra giao tuyến của
và SAC là đường thẳng qua A , song song với OI , cắt SC tại M .
Có AB CD nên giao tuyến của
và SCD là đường thẳng qua M , song song với CD , cắt SD tại N . Có 1 2 2 V S d N ABD S d I ABD S IO . DANB ABD . , ABD . , ABD . 3 3 3 Để V
lớn nhất thì OI lớn nhất. DANB Ta có SA SBD SA SO . 2 2 2 2 Đặt x 2a x 2a x SA x ( 0 x a 2 ). Ta có 2 2 SO 2a x ; SH ; OH ; a 2 a 2
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán!
Trang 26 Mã đề: 743
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC.
Đề thi thử Lần 1 - Lớp 12 – Chuyên Hạ Long 18-19 2 2 2 x 4a 2x 2 2 4 2 2 a x C . O SH x 4a 2x 2 a CH CO OH ; OI . a . 2 2 a 2 2 a 2 CH 4a x 4a x 2 3 Dấu bẳng xảy ra khi 2 2 2 4 2 a 2 a 2a x a x x . Khi đó 2 Max V a . DANB .2 . 3 3 2 3 Câu 46. Cho hàm số 3 2 y x 3 m 3 x
3 có đồ thị C . Tìm tất cả các giá trị của m sao cho qua
điểm A 1; 1 kẻ được đúng hai tiếp tuyến đến C , một tiếp tuyến là : y 1 và tiếp 1 tuyến thứ hai là thỏa mãn : tiếp xúc 2 2
C với tại N đồng thời cắt C tại điểm P (khác N ) có hoành độ bằng 3.
A. Không tồn tại m thỏa mãn. B. m 2. C. m 0; m 2 . D. m 2. Lời giải Chọn A 3 2 x 3 m 3 x 3 1 Ta thấy
là một tiếp tuyến của có nghiệm. 1 C nên 2 3x 6 m 3 x 0 3 2 x 3 m 3 x 3 1 x 2 m 3 m 2 Có . 2 3 3x 6 m 3 x 0 m 3 1 x 2 Khi m
2 ta có C có phương trình 3 2 y x 3x 3.
Tiếp tuyến qua điểm A 1; 1 có dạng : y k x 1 1. 3 2 x 3x 3 k x 1 1
là một tiếp tuyến của C có nghiệm. 2 3x 6x k x 1 3 2 2 3 x 3x 3 3x 6x x 1 1 2x 6x 4 0 k 9 Có 2 2 3x 6x k 3x 6x k x 2 k 0
Vậy có hai tiếp tuyến qua A có phương trình là : y 1và : y 9x 8 1 2 x 1
Phương trình hoành độ giao điểm của và x 3x 3 9x 8 2 C : 3 2 x 5 Khi đó và 2
C không cắt nhau tại điểm có hoành độ là 3. Vậy không có giá trị của m.
Câu 47. Cho bất phương trình 2 x −x − ( + ) 2 2 2 2x −x 2 .9 2 1 .6 + .4 x −x m m m
 0. Tìm m để bất phương trình nghiệm đúng 1 x   . 2 A. 3 m  . B. 3 . D. m  0 . 2 m  . C. m  0 2 Lời giải
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán!
Trang 27 Mã đề: 743
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC.
Đề thi thử Lần 1 - Lớp 12 – Chuyên Hạ Long 18-19
Tác giả: Phạm Nguyên Bằng; Fb: Phạm Nguyên Bằng Chọn C
Chia cả hai vế của bất phương trình cho 2 2
4 x −x ta được: 2 2 2 2 x − x 2  9 x − x    2 1  3 x −xm − ( m + ) 3 . 2 1 + m      0. Với 2 x
 2x − x  0     1.  4   2  2  2  2 2  3 x −x Đặt  t = ,t   
1. Khi đó bài toán trở thành tìm m để bất phương trình  2  2 . m t − (2m + )
1 .t + m  0 t   1.
-Với t =1 0 1 ( Luôn đúng). 2 -Với 1 t t t − +1 tm t
 1. Xét f (t) = t
 1; f (t) =  0 t   1. 2 t − 2t +1 2 t − 2t +1 (t −2t + )2 2 1
Khi đó m  lim f (t) = 0. t→+
Vậy m  0 thỏa mãn yêu cầu bài toán.
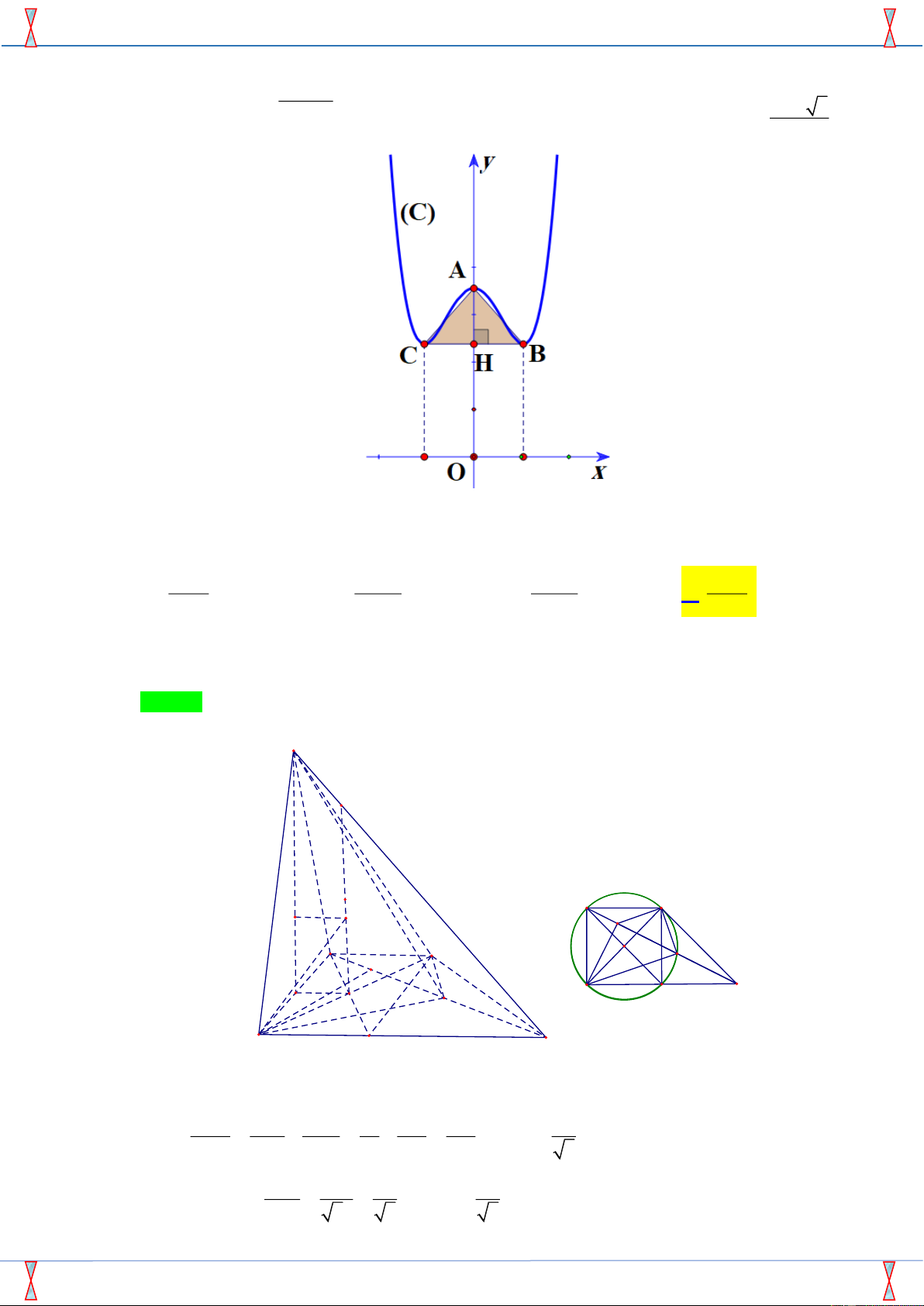
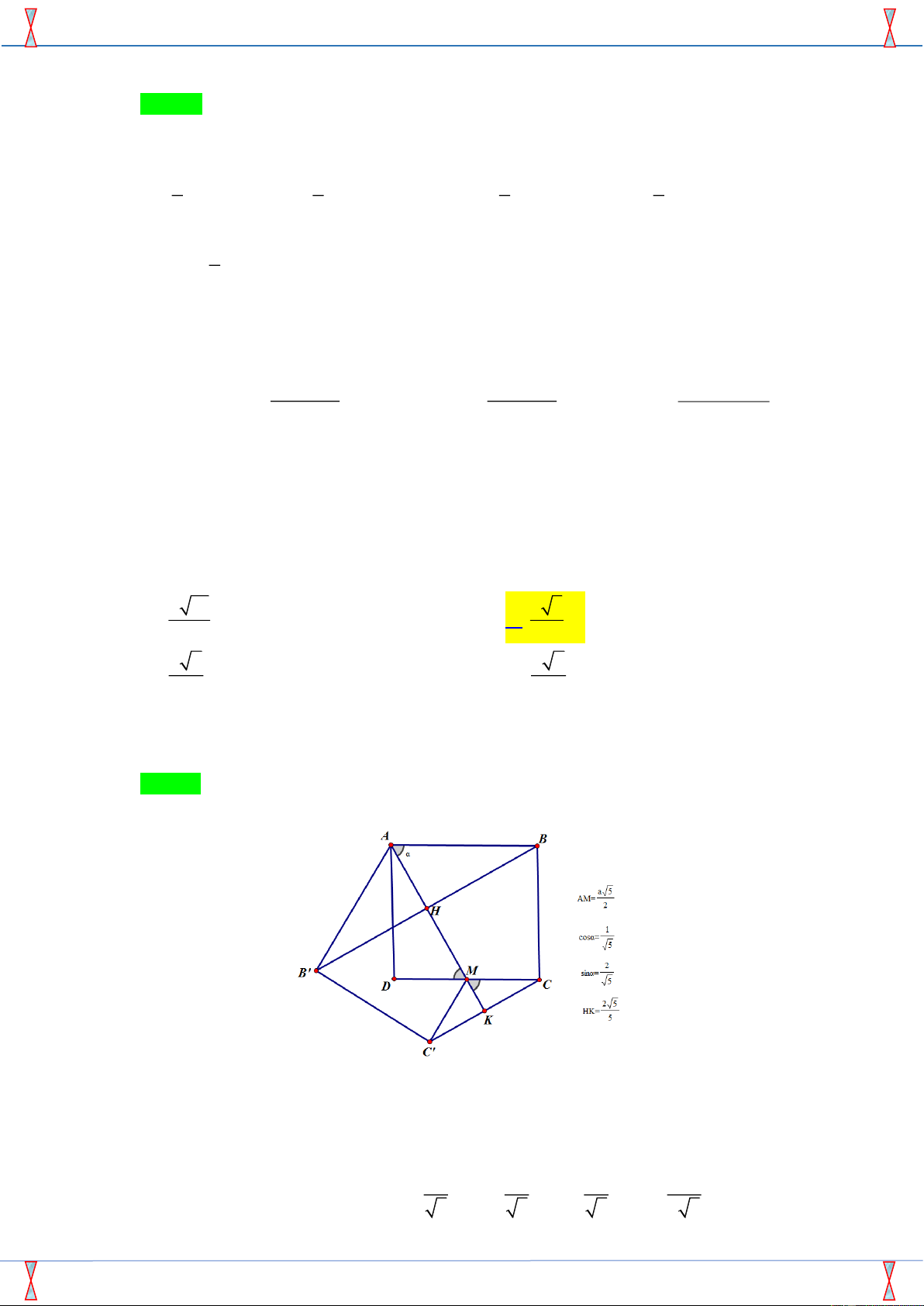
Câu 48. Cho hình vuông ABCD cạnh bằng 1, điểm M là trung điểm của CD. Cho hình vuông ABCD(
Tính cả các điểm trong của nó ) quay quanh trục là đường thẳng AM ta được một khối tròn
xoay. Tính thể tích khối tròn xoay đó. A. 7 10  . B. 7 5  . 15 30 C. 7 2  . D. 7 2  . 30 15 Lời giải
Tác giả: Phạm Nguyên Bằng ; Fb: Phạm Nguyên Bằng Chọn B
Khi quay hình vuông quanh AM thì phần thể tích khi quay mặt ( ADM ) bị trùng vào phần thể tích của ( ABCM ) . Khi đó V =V + − .  V   V nonABB noncutBCC B nonCMC
Ta dễ dàng tính được các cạnh 1 2 1 1 AH = ;BH = ;CK = ;MK = . 5 5 5 2 5 Khi đó
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán!
Trang 28 Mã đề: 743
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC.
Đề thi thử Lần 1 - Lớp 12 – Chuyên Hạ Long 18-19 1 2 4 5 V = = .  AH HBnonABB . . . 3 75 1 V = + + = .    BH CK BH CK HKnoncutBCC B ( 2 2 ) 14 5 . . 3 75 1 2 5 V = = .  MK CKnonCMC . . 3 150 Vậy 7 5 V =  . 30
Câu 49. Trong chuyện cổ tích Cây tre trăm đốt (các đốt được đánh thứ tự từ 1 đến 100), khi không vác
được cây tre dài tận 100 đốt như vậy về nhà, anh Khoai ngồi khoc, Bụt liền hiện lên, bày cho
anh ta: “Con hãy hô câu thần chú Xác suất, xác suất thì cây tre sẽ rời ra, con sẽ mang được về
nhà”. Biết rằng cây tre 100 đốt được tách ra một cách ngẫu nhiên thành các đoạn ngắn có chiều
dài 2 đốt và 5 đốt (có thể chỉ có một loại). Xác suất để số đoạn 2 đốt nhiều hơn số đoạn 5 đốt
đúng 1 đoạn gần với giá trị nào trong các giá trị dưới đây? A. 0,142 . B. 0,152 . C. 0,132 . D. 0,122 . Lời giải
Tác giả:Trịnh Thanh; Fb: Deffer Song Chọn A
Giả sử có x đoạn 2 đốt và y đoạn 5 đốt được tách ra từ cây tre 100 đốt đã cho ( x, y Z và
x  0, y  0 ).
* Ta có: 2x + 5y =100  x 5  x = 5m  2m + y = 20  y 2 và 0  y  20 .
Mà y Z nên y 2;4;6;...;18;  20 . Với mỗi bộ các số ( ;
x y ) tìm được cho ta số các đoạn 2 đốt và 5 đốt được tách ra từ đó có số
các cách để tách cây tre 100 đốt thành x đoạn 2 đốt và y đoạn 5 đốt là y C . x+ y
Do vậy, số cách để tách cây tre 100 đốt thành các đoạn 2 đốt và đoạn 5 đốt là: 0 2 4 6 8 10 12 14 16 18 20
C + C + C + C + C + C + C + C + C + C + C = 545813093 50 47 44 41 38 35 32 29 26 23 20
* Để tách cây tre 100 đốt thành các đoạn ngắn có chiều dài 2 đốt và 5 đốt sao cho số đoạn 2 đốt
nhiều hơn số đoạn 5 đốt đúng 1 đoạn thì ta còn phải có x − y =1.
Khi đó: x =15, y =14 .
Số cách để tách cây tre 100 đốt thành 15 đoạn 2 đốt và 14 đoạn 5 đốt là: 15 C . 29 15
Vậy xác suất để số đoạn 2 đốt nhiều hơn số đoạn 5 đốt đúng 1 đoạn là 29 C  0,1421. 545813093
Câu 50. Cho hàm số y = f (x) liên tục trên R và có đồ thị như hình vẽ. Hỏi hàm số y = f ( f (x)) có
bao nhiêu điểm cực trị.
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán!
Trang 29 Mã đề: 743
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC.
Đề thi thử Lần 1 - Lớp 12 – Chuyên Hạ Long 18-19 A.6. B.7. C.8. D.9. Lời giải
Tác giả:Trịnh Thanh; Fb: Deffer Song Chọn D
* Từ đồ thị hàm số y = f (x) nhận thấy x = a +) 
f ( x) = 0  x = 2 với 0  x a  2  b  3 . 0 x = b
+) f (x)  0  a x  2 hoặc x b .
+) f (x)  0  x a hoặc 2  x b. * Ta có:
y = f ( f ( x))  y = f ( f ( x)). f ( x) .
f ( f (x)) = 0
y = 0   f   ( x) = 0
f (x) = a
* Phương trình f ( f (x)) = 0   f (x) = 2 với 0  x a  2  b  3 . 0  f  ( x) = b
Mỗi đường thẳng y = b, y = 2 , y = a đều cắt đồ thị hàm số đã cho tại 2 điểm phân biệt lần lượt
tính từ trái qua phải có hoành độ là 1x và 6x ; 2x và 5x ; 3x và 4x nên:
x x x x  3    1 2 3 0 4 x 5 x 6 xf ( = =  1 x ) f ( 6 x ) bf
 ( x = f x = 2 2 ) ( 5)  f ( = =  3 x ) f ( 4 x ) a
* Cũng từ đồ thị hàm số đã cho suy ra:.
Do đó: f ( f (x))  0  a f (x)  2 hoặc f (x)  b . Ta có BBT: x − 1 x 2 x 3 x a 2 b 4 x 5 x 6 x + f ( x) – – – – 0 + 0 – 0 + + + +
f ( f ( x)) + 0 – 0 + 0 – – – – 0 + 0 – 0 + 
f ( f (x))  
– 0 + 0 – 0 + 0 – 0 + 0 – 0 + 0 – 0 +
Vậy hàm số có 9 điểm cực trị.
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán!
Trang 30 Mã đề: 743