TRƯỜNG THPT QUẢNG XƯƠNG I
ĐỀ THI THỬ THPT QUỐC GIA LẦN 1 NĂM HỌC 2018 - 2019 ĐỀ CHÍNH THỨC MÔN: TOÁN
( Đ ề thi gồm 6 trang)
Thời gian làm bài: 90 phút (không kể thời gian phát đề) MÃ ĐỀ 468
Họ tên thí sinh: ……………………………….SBD: ………… Phòng thi: ……………… Câu 1.
Với a là số thực dương bất kì, mệnh đề nào dưới đây đúng? 1
A. log 2018a  2018.log a . B. 2018 log a  log a . 2018 1
C. log 2018a  log a . D. 2018 log a  2018.log a . 2018 Câu 2.
Trong các hàm số dưới đây, hàm số nào nghịch biến trên tập số thực  ? x x     2  A. y  2   .
B. y  log x .
C. y  log  x  . D. y  .   1 1    3   e  3 4 x  2 Câu 3.
Đồ thị hàm số y 
có bao nhiêu đường tiệm cận đứng. 2 x  4x  3 A. 0 . B. 2 . C. 1. D. 3. Câu 4.
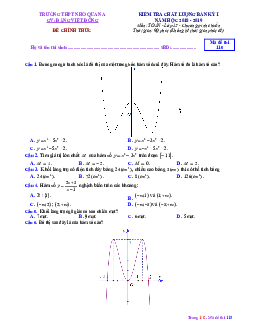
Đồ thị sau đây là của hàm số 4 2
y  x  3x  3 . Với giá trị nào của m thì phương trình 4 2
x  3x  3  m có đúng ba nghiệm phân biệt. y 1 1 O x 3 5 A. m  4  . B. m  3  . C. m  0 . D. m  5  . Câu 5. Đồ thị của hàm số 3 2
y  x  3x  2x 1 và đồ thị hàm số 2
y  3x  2x 1 có tất cả bao nhiêu điểm chung? A. 0 . B. 2 . C. 3 . D. 1. Câu 6.
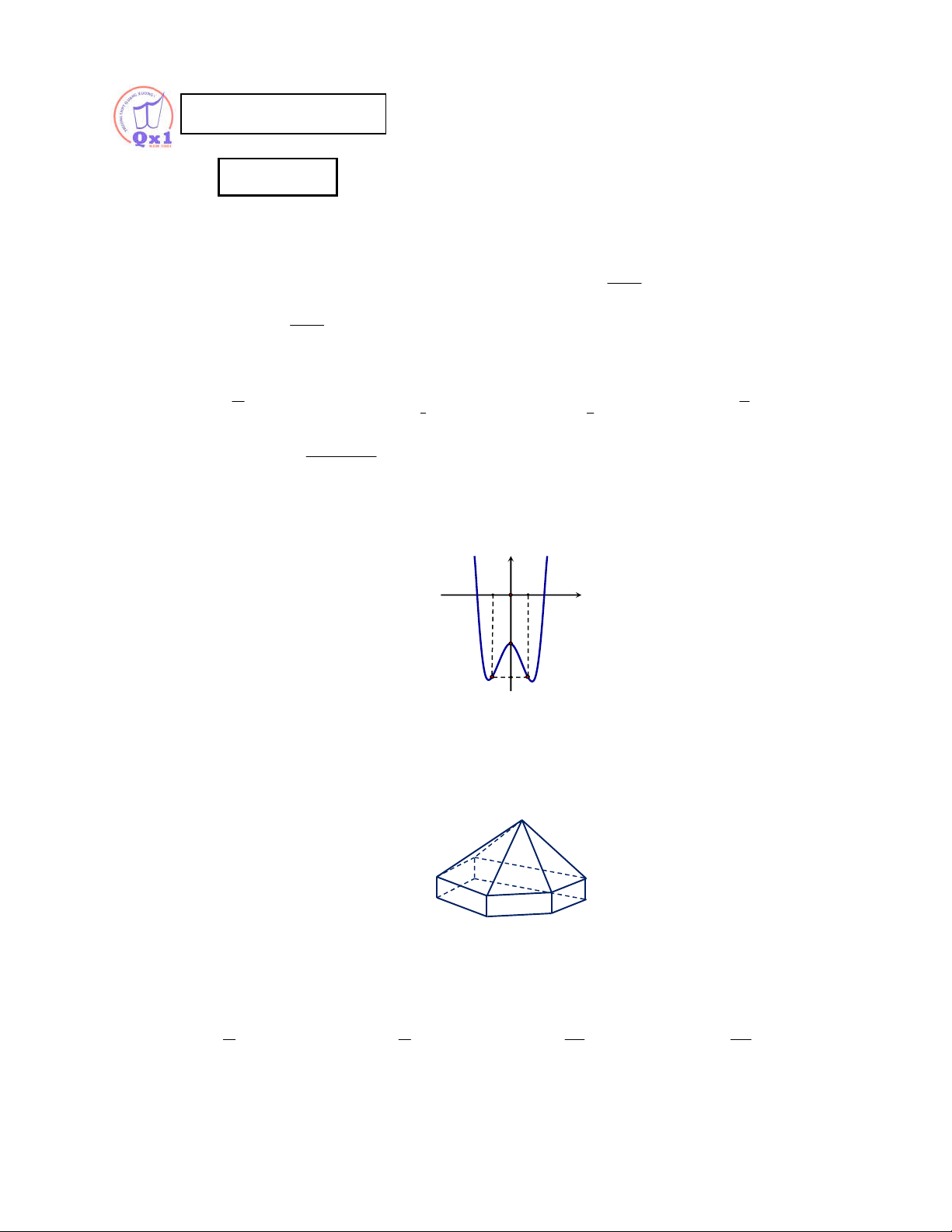
Hình đa diện sau có bao nhiêu mặt? A. 11 . B. 20 . C. 12 . D. 10 . Câu 7.
Số đỉnh của một hình bát diện đều là. A. 12 . B. 14 . C. 8 . D. 6 . Câu 8.
Tìm nghiệm của phương trình sin 2x  1 .   3 k A. x   k 2 . B. x   k . C. x   k 2 . D. x  . 2 4 4 2 Câu 9.
Từ các chữ số 1; 2 ; 3 có thể lập được bao nhiêu số tự nhiên có 3 chữ số khác nhau đôi một? A. 8 . B. 6 . C. 9 . D. 3 .
Câu 10. Cho hàm số y  f  x xác định, liên tục và có đạo hàm trên khoảng  ;
 , có bảng biến thiên như hình sau:
Trang 1/6 - Mã đề thi 468 x  1 1  y  0  0  2  y  1
Mệnh đề nào sau đây đúng?
A. Hàm số nghịch biến trên khoảng 1; .
B. Hàm số đồng biến trên khoảng  ;    1 .
C. Hàm số nghịch biến trên khoảng  ;   1 .
D. Hàm số đồng biến trên khoảng  1  ;  .
Câu 11. Đồ thị hàm số nào sau đây có đúng 1 điểm cực trị A. 4 2
y  x  3x  4 . B. 3 2
y  x  6x  9x  5 . C. 3 2
y  x  3x  3x  5 . D. 4 2
y  2x  4x  1 .
Câu 12. Hệ số của số hạng chứa 5
x trong khai triển   12 1 x là: A. 972 . B. 495 . C. 792 . D. 924 . 2018
Câu 13. Tiệm cận ngang của đồ thị hàm số y 
là đường thẳng có phương trình? x 1 A. y  2018 . B. x  0 . C. y  0 . D. x  1 . 2x 1
Câu 14. Phương trình tiếp tuyến của đồ thị hàm số y 
tại điểm có hoành độ bằng 2  là x 1
A. y  3x  5 . B. y  3  x  1 .
C. y  3x 11 . D. y  3  x 1. a b
Câu 15. Cho  2019  2018   2019  2018 . Kết luận nào sau đây đúng?
A. a  b .
B. a  b .
C. a  b .
D. a  b . 2n 1
Câu 16. Tính giới hạn lim . 3n  2 2 3 1 A. . B. . C. . D. 0 . 3 2 2
Câu 17. Cho S.ABCD có đáy ABCD là hình vuông cạnh a . Biết SA   ABCD và SA  a . Tính thể tích
của khối chóp S.ABCD . 3 a 3 3a 3 a A. V  . B. V  . C. V  . D. 3 V  a . 3 2 6
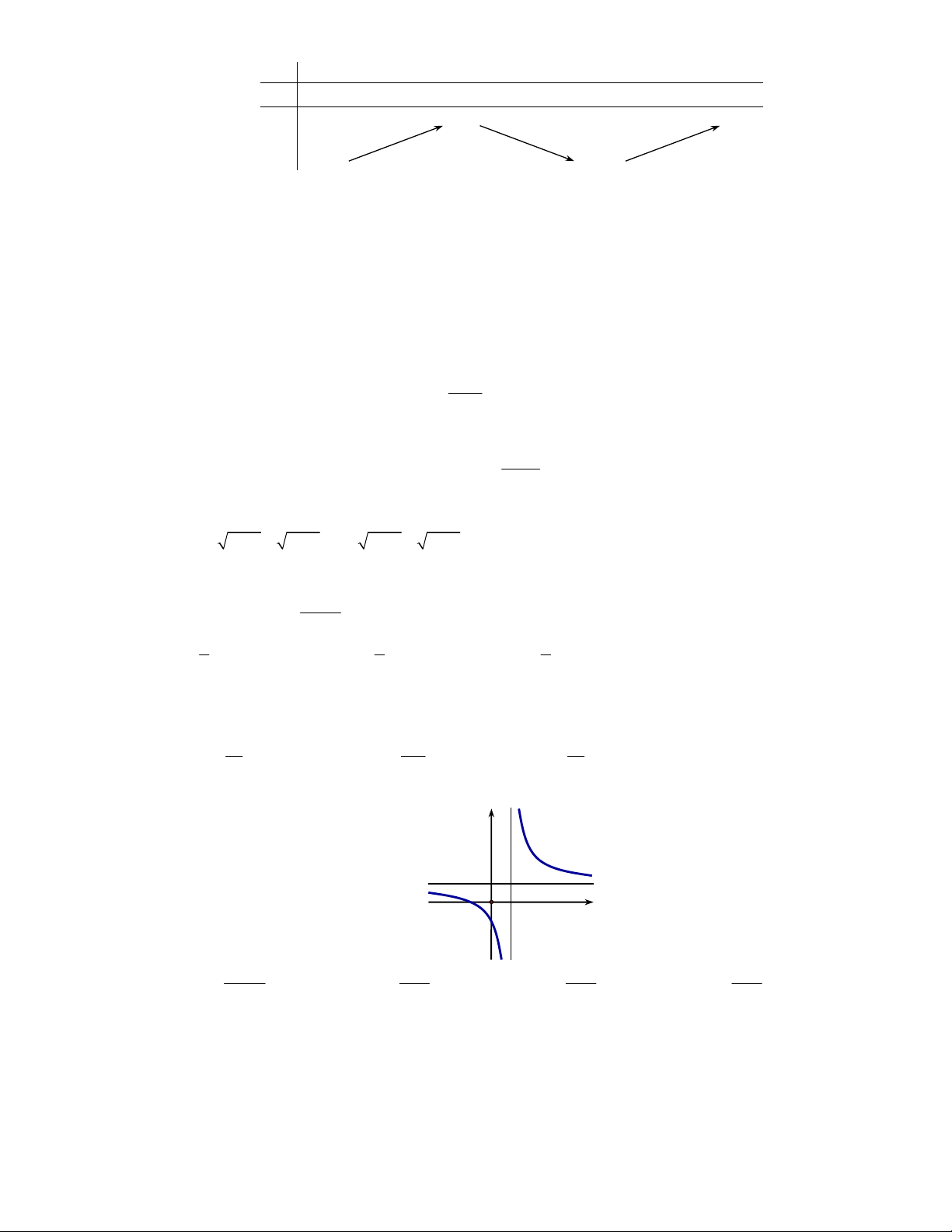
Câu 18. Đồ thị hình dưới là đồ thị hàm số nào trong các hàm số sau? y 1 1 O x 1 1 2x  3 x x 1 x  1 A. y  . B. y  . C. y  . D. y  . 2x  2 x 1 x  1 x 1
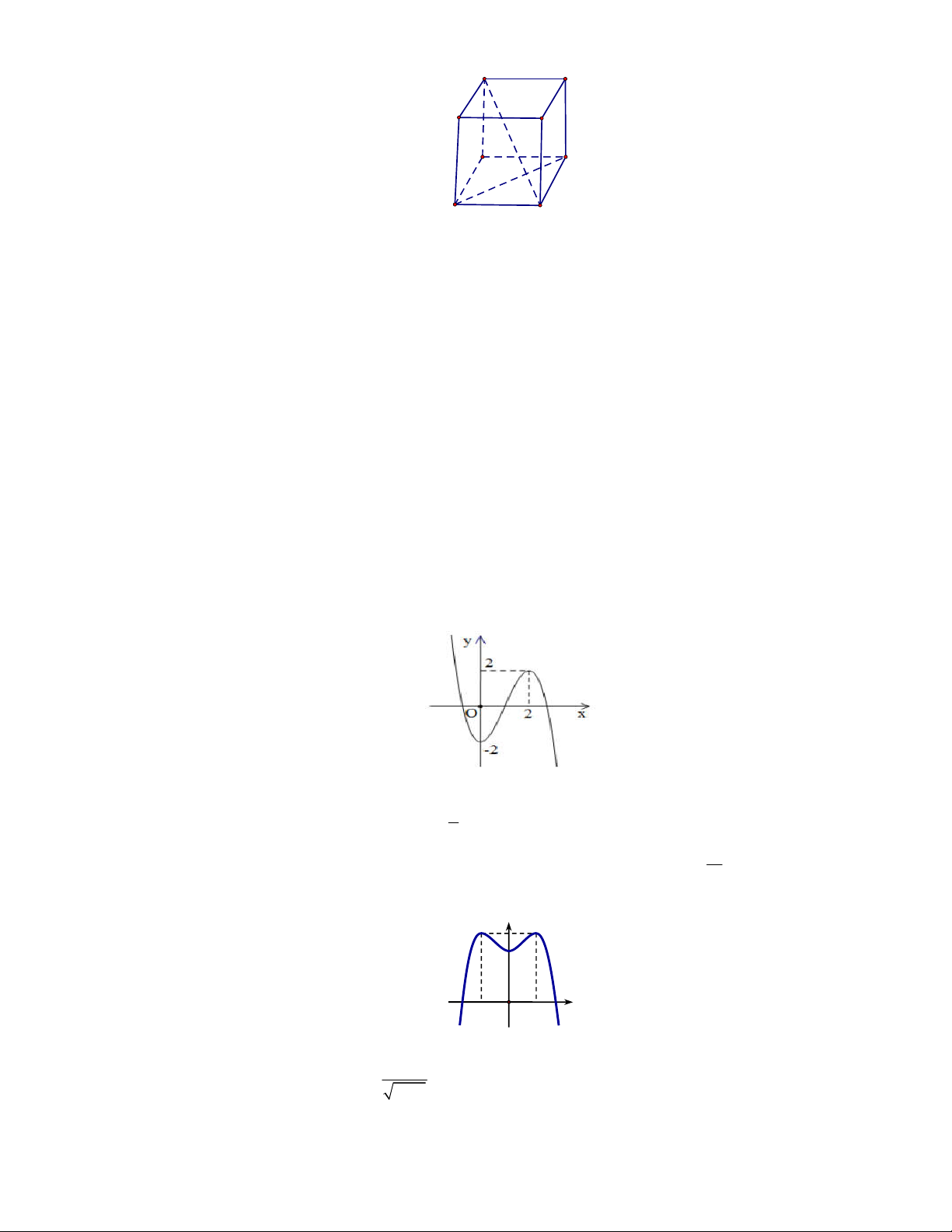
Câu 19. Cho hình lập phương ABCD. A′B′C′D′ (tham khảo hình vẽ dưới). Góc giữa hai đường thẳng AC và BD′ bằng.
Trang 2/6 - Mã đề thi 468 D' C' A' B' D C A B A. 300. B. 900. C. 600. D. 450.
Câu 20. Tính thể tích V của khối trụ có bán kính đáy và chiều cao đều bằng 3 . A. V  9 .
B. V  12 . C. V  3 .
D. V  27 .
  
Câu 21. Cho hình bình hành ABCD . Tổng các vectơ AB  AC  AD là     A. AC . B. 2 AC . C. 3AC . D. 5AC .
Câu 22. Trong mặt phẳng Oxy , cho các điểm A1;3, B4;0,C 2; 5
  . Tọa độ điểm M thỏa    
mãn MA  MB  3MC  0 là A. M 1;18 . B. M  1  ;18 . C. M 1; 18   . D. M  18  ;  1 .
Câu 23. Cho tam giác ABC có A1; 2
  , đường cao CH : x  y 1  0 , đường thẳng chứa cạnh BC có
phương trình 2x  y  5  0 . Tọa độ điểm B là A. 4;3 . B. 4;3 . C.  4  ;3 . D.  4  ; 3  
Câu 24. Cho cấp số nhân u ;u  1,q  2 . Hỏi số 2048 là số hạng thứ mấy? n 1 A. 12 . B. 9 . C. 11 . D. 10 .
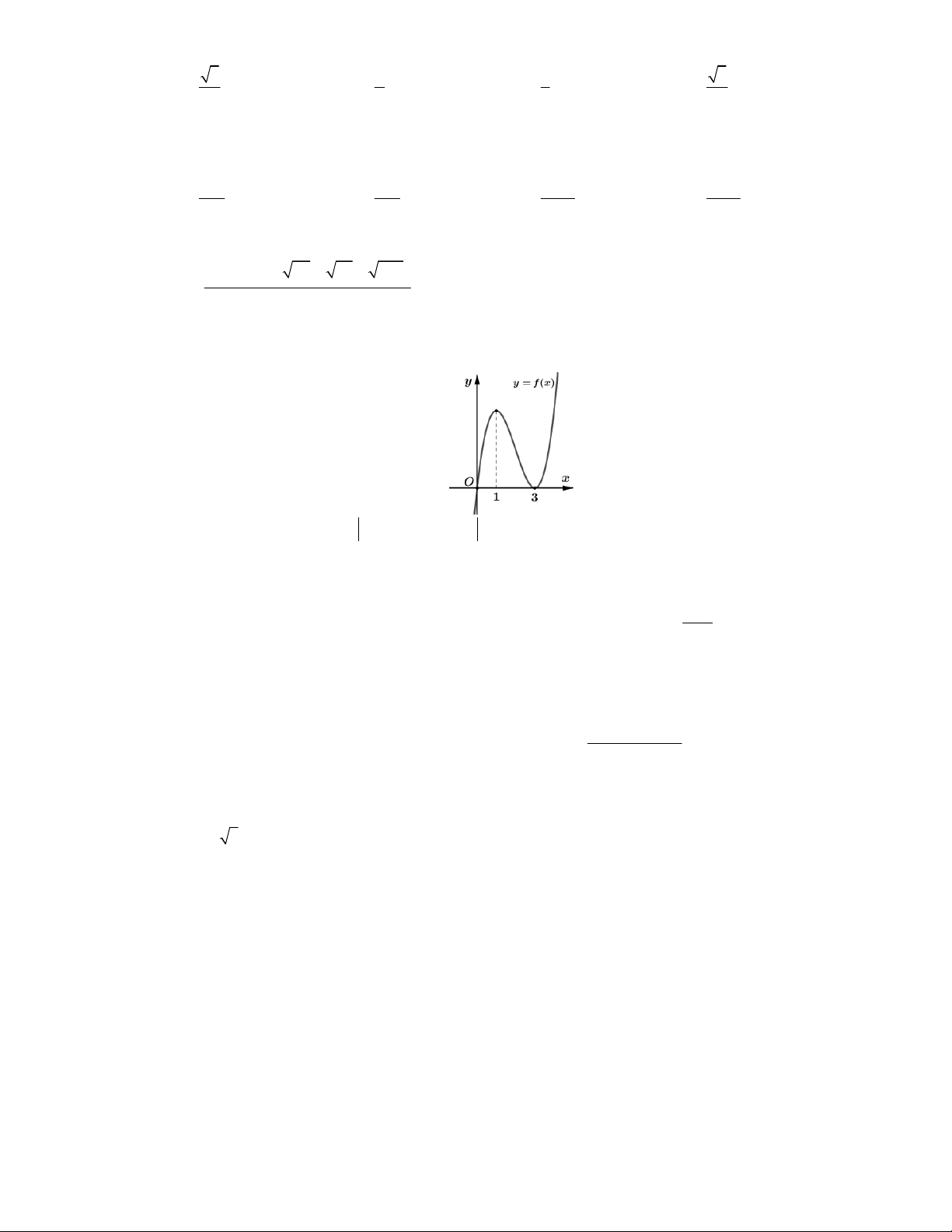
Câu 25. Cho hàm số y  f  x có đồ thị trong hình bên. Phương trình f  x  1 có bao nhiêu nghiệm
thực phân biệt nhỏ hơn 2 . A. 0 . B. 1 . C. 2 . D. 3 . 4
Câu 26. Giá trị nhỏ nhất của hàm số f  x  x  trên đoạn 1;  3 bằng. x 13 A. 5 . B. 4 . C. 3 . D. . 3 Câu 27. Hàm số 4 2
y  ax  bx  c có đồ thị có dạng như hình vẽ dưới đây. Mệnh đề nào sau đây đúng? y O x
A. a  0 ; b  0 ; c  0 .
B. a  0 ; b  0 ; c  0 . C. a  0 ; b  0 ; c  0 . D. a  0 ; b  0 ; c  0 . 1
Câu 28. Tập xác định của hàm số y   ln  x   1 là: 2  x
A. D  1; 2 .
B. D  1;  .
C. D  1; 2 .
D. D  ;2  .
Trang 3/6 - Mã đề thi 468 2 x 2 x 3  1 
Câu 29. Phương trình x 1  7   
có bao nhiêu nghiệm?  7  A. 0 . B. 1. C. 3 . D. 2 . 2 2
x  y  x 12  y 
Câu 30. Giải hệ phương trình 
ta được hai nghiệm (x ; y ) và (x ; y ) . Tính giá trị 1 1 2 2 2 2
x y  x  12  biểu thức 2 2 2
T  x  x  y . 1 2 1 A. T  25  . B. T  0 . C. T  25 . D. T  50 .
Câu 31. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , cạnh bên SA vuông góc với đáy
và SA  a 3 . Khoảng cách từ A đến mặt phẳng SBC  bằng 2a 5 a a 3 A. . B. a 3 . C. . D. . 5 2 2
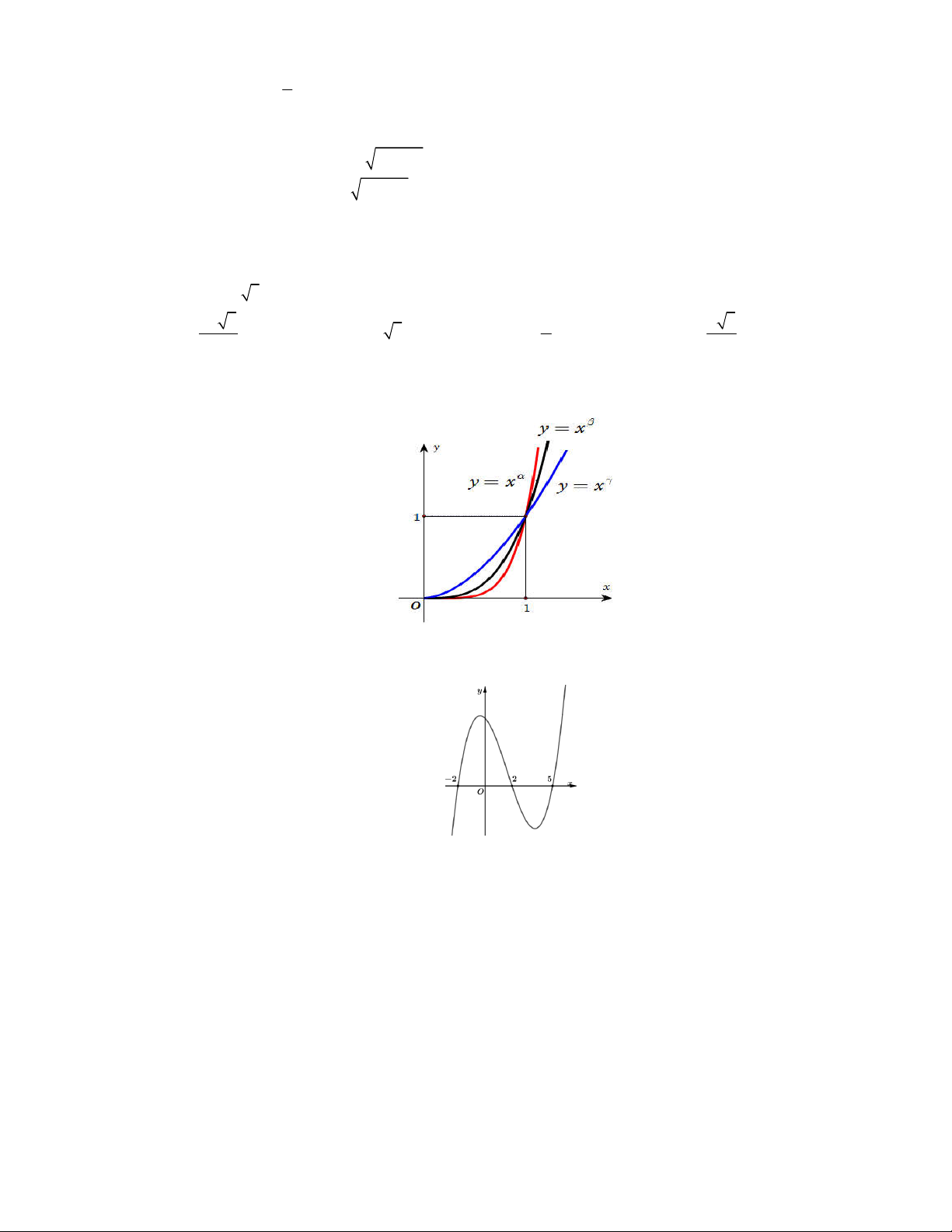
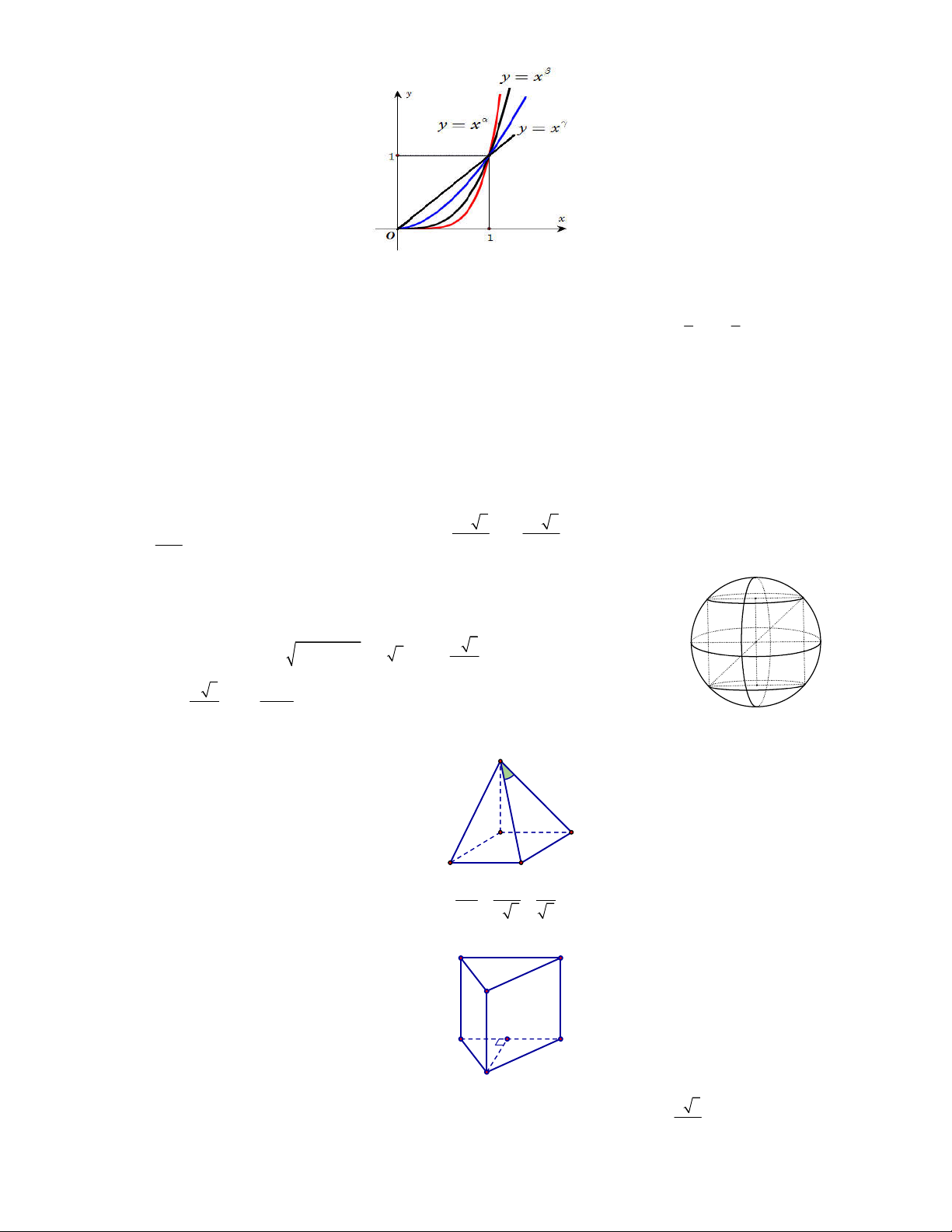
Câu 32. Cho đồ thị của ba hàm số y x , y x , y x   
trên khoảng 0;  trên cùng một hệ trục tọa
độ như hình vẽ bên. Mệnh đề nào sau đây đúng?
A.       0 .
B. 0        1.
C. 0        1.
D. 1       .
Câu 33. Cho hàm số y  f  x. Đồ thị hàm số y  f  x như hình bên dưới
Hàm số g  x  f 3  2x nghịch biến trên khoảng nào trong các khoảng sau? A. 0;2 . B. 1;3 . C.  ;    1 . D.  1  ; 
Câu 34. Trong mặt phẳng 2 2
Oxy cho đường tròn C  :  x   1   y   1
 4 . Phép vị tự tâm O (với O là
gốc tọa độ) tỉ số k  2 biến C  thành đường tròn nào trong các đường tròn có phương trình sau? A.  2 2
x  2   y  2 1 1
 8 . B.  x  2   y  2  8 . C.  2 2
x  2   y  2 2 2  16 .
D.  x  2   y  2 16 .
Câu 35. Cho hai đường thẳng phân biệt a , b và mặt phẳng  P , trong đó a  P .Trong các mệnh đề
sau đây có bao nhiêu mệnh đề đúng?
(I).Nếu b // a thì b   P . (II). Nếu b   P thì b // a .
(III). Nếu b  a thì b //  P . (IV). Nếu b //  P thì b  a . A. 1. B. 2 . C. 4 . D. 3 .
Trang 4/6 - Mã đề thi 468
Câu 36. Tập nghiệm của bất phương trình log x 1  log
2  x là S  a;b   ;
c d  với a,b,c, d là 1   3   3
các số thực. Khi đó tổng a  b  c  d bằng. A. 4 . B. 1. C. 3 . D. 2.
Câu 37. Một hình trụ có trục OO chứa tâm của một mặt cầu bán kính R , các đường tròn đáy của hình
trụ đều thuộc mặt cầu trên, đường cao của hình trụ đúng bằng R . Tính thể tích V của khối trụ? 3 3 R 3  R 3  R A. V  . B. 3 V   R . C. V  . D. V  . 4 4 3
Câu 38. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , cạnh bên SA vuông góc với mặt
đáy và SA  a 2 . Tìm số đo của góc giữa đường thẳng SC và mặt phẳng SAD . A. o 45 . B. o 30 . C. o 90 . D. o 60 .
Câu 39. Cho hình lăng trụ đứng ABC.AB C
  có đáy là tam giác ABC vuông tại A có BC  2a ,
AB  a 3 . Khoảng cách giữa hai đường thẳng AA và BC là. a 21 a 3 a 5 a 7 A. . B. . C. . D. . 7 2 2 3
Câu 40. Có bao nhiêu giá trị nguyên của tham số m để phương trình  2
x  5x  4 x  m  0 có đúng hai nghiệm phân biệt. A. 4 . B. 2 . C. 3 . D. 1.
Câu 41. Cho hàm số y  f  x có đồ thị như hình vẽ dưới. Gọi M ,m lần lượt là giá trị lớn nhất và giá trị  3 7 
nhỏ nhất của hàm số y  f  2
x  2x trên đoạn  ; 
. Tìm khẳng định sai trong các khẳng 2 2    định sau. M
A. M  m  7 .
B. M .m  10 .
C. M  m  3 . D.  2 . m
Câu 42. Cho lăng trụ ABC.A B C có diện tích mặt bên ABB A bằng 6 , khoảng cách giữa cạnh CC và 1 1 1 1 1 1
mặt phẳng  ABB A bằng 8. Thể tích khối lăng trụ ABC.A B C bằng. 1 1  1 1 1 A. 24 . B. 8 . C. 16 . D. 32 . x  1
Câu 43. Cho hàm số y 
có đồ thị (C) , biết cả hai đường thẳng d : y  a x  b ;d : y  a x  b đi x 1 1 1 1 2 2 2 5
qua điểm I (1;1) và cắt đồ thị (C) tại 4 điểm tạo thành một hình chữ nhật. Khi a  a  , giá trị 1 2 2
biểu thức P  b .b bằng. 1 2 5 1 1 5 A. . B. . C.  . D.  . 2 2 2 2
Câu 44. Cho hình chóp S.ABCD có SC  x 0  x  3 , các cạnh còn lại đều bằng 1.Thể tích lớn nhất
của khối chóp S.ABCD bằng.
Trang 5/6 - Mã đề thi 468 3 1 1 3 A. . B. . C. . D. . 4 4 3 6
Câu 45. Thầy Tuấn có 15 cuốn sách gồm 4 cuốn sách Toán, 5 cuốn sách Lý và 6 cuốn sách Hoá. Các
cuốn sách đôi một khác nhau. Thầy chọn ngẫu nhiên 8 cuốn sách để làm phần thưởng cho một
học sinh. Tính xác suất để số cuốn sách còn lại của thầy Tuấn có đủ 3 môn. 54 661 2072 73 A. B. C. D. 715 . 715 . 2145 . 2145 .
Câu 46. Cho a,b, c là các số thực dương khi đó giá trị lớn nhất của biểu thức
8a  3b  4 3
ab  bc  abc  P 
gần với giá trị nào nhất trong các đáp án sau.
1  a  b  c2 A. 4, 65 . B. 4, 66 . C. 4, 67 . D. 4, 64 .
Câu 47. Cho hàm số y  f  x có đồ thị như hình vẽ bên dưới
Để đồ thị hàm số   2
h x  f  x  f  x  m có số điểm cực trị ít nhất thì giá trị nhỏ nhất của
tham số m  m .Tìm mệnh đề đúng trong các mệnh đề sau: 0
A. m  (0;1) . B. m  ( 1  ;0) . C. m  ( ;  1  ) .
D. m  (1;) 0 0 0 0 2x
Câu 48. Biết hai điểm B(a;b),C( ;
c d ) thuộc hai nhánh của đồ thị hàm số y  sao cho tam giác x 1
ABC vuông cân tại đỉnh (
A 2;0) , khi đó giá trị biểu thức T  ab  cd bằng. A. 6 . B. 0 . C. 9  . D. 8 .
Câu 49. Biết đồ thị hàm số 2 y  . a log x  .
b log x  c cắt trục hoành tại hai điểm phân biệt có hoành độ 2 2
(a  b)(2a  b)
thuộc đoạn [1;2] . Khi đó giá trị lớn nhất của biểu thức P  bằng.
a(a  b  c) A. 2 . B. 5 . C. 3 . D. 4 .
Câu 50. Cho khối chóp S.ABCD có đáy là hình bình hành,  0
AB  3, AD  4, BAD  120 . Cạnh bên
SA  2 3 vuông góc với đáy. Gọi M,N,P lần lượt là trung điểm các cạnh SA, AD và BC và  là
góc giữa hai mặt phẳng (SAC) và (MNP). Chọn khẳng định đúng trong các khẳng định sau đây. A.   0 60 ;  90  . B.   0 0 ;  30  . C.   0 30 ;  45  . D.   0 45 ;  60 
---------------HẾT-------------
Lưu ý - Kết quả thi được đăng tải trên Website : quangxuong1.edu.vn vào ngày 10/12/2018
- Lịch thi thử lần 2 vào ngày 13/1/2019.
Chúc các em thành công!
Trang 6/6 - Mã đề thi 468
TRƯỜNG THPT QUẢNG XƯƠNG I
ĐÁP ÁN ĐỀ THI THỬ THPT QUỐC GIA LẦN 1 NĂM HỌC 2018 - 2019 ĐỀ CHÍNH THỨC MÔN: TOÁN
( Đ áp án có 4 trang)
Thời gian làm bài: 90 phút (không kể thời gian phát đề) MÃ ĐỀ 468 Câu 1. Chọn D Câu 2. Chọn D Câu 3. Chọn B Câu 4. Chọn B Câu 5. Chọn C Câu 6. Chọn A Câu 7. Chọn D Câu 8. Chọn B Câu 9. Chọn B Câu 10. Chọn B Câu 11. Chọn A Câu 12. Chọn C Câu 13. Chọn C Câu 14. Chọn C Câu 15. Chọn B Câu 16. Chọn A Câu 17. Chọn A Câu 18. Chọn D Câu 19. Chọn B Câu 20. Chọn D Câu 21. Chọn.B Câu 22. Chọn C Câu 23.
Chọn.C Ta có AB  CH   AB : x  y 1  0 Có B  AB  BC  B  4  ;3 . Câu 24.
Chọn A Ta có n 1  n 1  n 1  11
u  u .q  1.2  2048  2
 2  n 1  11  n  12 . n 1 Câu 25. Chọn C Câu 26. Chọn B Câu 27. Chọn A
Ta có a  0 ,giao điểm với trục tung có tung độ dương nên c  0 .Có 3 cực trị nên b trái dấu a, hay b  0 . Câu 28. Chọn C Câu 29. Chọn D Câu 30. Chọn B ĐK 2 2 y  x .Từ 2 2 2 2 2 2 2 2 x 
y  x  12  y  x  2x y  x  y  x  144  24 y  y . 2 2
 x y  x  144  24 y (1) Thay 2 2
x y  x  12 vào (1) ta được: y  5 .  x  3 hoặc x  4 .  {(3;5), (4;5)} .Ta có 2 2 2
T  3  4  5  0 . Câu 31. Chọn D . SA AB a 3.a a 3
Ta vẽ AH  SB tại H  AH   SBC . d  ,
A  SBC   AH    . 2 2 SA  AB 2 2 3a  a 2 Câu 32. Chọn D
●Với 0  x  1 thì    1
x  x  x  x 
      1 .● Với x  1 thì 1
x  x  x  x 
1       . Trang 1/4 - Câu 33. Chọn C  1 5  2   x  2  2   3  2x  2  x 
f  x  0  .  
, g x  2
 f 3  2x. g x  0  f 3  2x  0   2 2 .  x  5  3  2x  5   x  1   Câu 34. Chọn C   x  2 2 2 V
I  I   OI   2OI 
 I 2;2 .Và R  2R  4 .  C :  x  2   y  2  16 . O;2      y  2  Câu 35. Chọn D
(III) sai do b có thể nằm trong  P . Câu 36. Chọn D
x 1  0, 2  x  0  1  x  2  1 5   1 5  Ta có  1    S   1;   
; 2 .  a  b  c  d  2 . log  log 2  x 2     
 x  x 1  0 2 2 3 3         x 1 Câu 37. Lời giải O' Chọn A R 3
Đường kính đáy của khối trụ r   R2 2 2 2
 R  R 3  r  . 2 2 3  R 3  3 R O 2
 V   r h     R  .  2  4   Câu 38. Chọn B S A a D a B C   CD a 1 
Dễ thấy CD   SAD  SC  SAD  ( ,
)  CSD .  tan CSD    .Vậy CSD  30 . SD a 3 3 Câu 39. Chọn B B C  A H B C A a 3
Ta có AA//  BCC B
  d (AA , BC)  d ( ,
A (BCC ' B ')) . Hạ AH  BC  AH   BCC B   .  AH  . 2 Câu 40.
Chọn C 1  m  4  m {1, 2, 3} Trang 2/4 - Câu 41. Chọn A  3 7   21  21 Đặt 2
t  x  2x , x   ;  t  1  ; 
từ đồ thị xét hàm y  f t , t  1  ;
ta có m  2, M  5 . 2 2   4         4  A Câu 42. Chọn A 1 C1 B1
Chia khối lăng trụ ABC.A B C theo mặt phẳng  ABC thành khối chóp C .ABC và khối chóp tứ giác 1  1 1 1 1 1 2 1 1 C .ABB A V  V  V  V , V  .S .d ; A ABB A  .6.8  16 . C . ABB A ABB A   1 1   1 1 1 , C .ABC C . ABB A 1 3 1 1 1 3 1 1 1 1 1 3 3 3 A  V  16.  24 . 2 B C Câu 43. Chọn C
Gọi  ,  lần lượt góc của tia Ox và phần đồ thị phia trên Ox của d , d khi đó ta có: 1 2
a  tan , a  tan  theo tính chất đối xứng của hình ta có 1 2 1 1 1 0
    90  a 
 a  2; a   b  1  ;b  1 1 2 a 2 1 2 2 2 Câu 44. Chọn B 1 1 2 3  x Do SBD   AB 
D suy ra AO  SO  OC do đó SAC 
vuông tại S . Ta có 2 AO  AC 
1 x  BO  2 2 2  2  x  2 1 3  x  2 2 . SA SC x x 3  x  1  S  , SH   Vậy V   ABCD 2 S .ABCD 2 2 SA  SC 2 1 x 6 4 Câu 45. Chọn B
Số phần tử không gian mẫu: n  8
 C Gọi A là biến cố: “Số cuốn sách còn lại của thầy Tuấn có đủ ba môn” 15
Khi đó A là biến cố: “Số cuốn sách còn lại của thầy Tuấn không đủ ba môn “. Xét các khả năng xẩy ra:
KN 1: 7 cuốn sách còn lại chỉ có Toán và Lý. Số cách chọn là: 7 C 9
KN 2: 7 cuốn sách còn lại chỉ có Toán và Hóa. Số cách chọn là: 7 C 10
KN 3: 7 cuốn sách còn lại chỉ có Hóa và Lý. Số cách chọn là: 7 C 11 7 7 7
C  C  C 661
Vậy: P  A  1 P  A 9 10 11  1  8 C 715 15 Câu 46. Chọn.B  a  4b b  4c
a  4b 16c  a  b   3
ab  bc  abc  8a  3b  4 8 3 4      4 4 12  28
a  b  c P    
1 a  b  c2
1 a  b  c2
3 1 a  b  c2 t 14 16 4 1
Đặt a  b  c  t, ta có t  0. f (t) 
với t  0. Lập BBT GTLN của P bằng khi a  ;b  ; c  . 2 1 t 3 21 21 21 Câu 47. Chọn A Xét g  x 2
 f  x  f  x  m 
 g x  f  x 2 f  x 1.   Trang 3/4 -  2 x  1 g   1  f   1  f   1  m  m
 f  x  0    g x
theo do thi f  x  0  
 x  3 . 
Ta tính được g 3  m .
2 f  x  1  
x  a a  0   1
g a  m    4 2  1  1
Đồ thị hàm số g  x có 3 điểm cực trị.Để ĐTHS h  x 2
 f  x  f  x  m  f  x   m  
có số điểm cực trị ít nhất là 3 2    4 1 1
đồ thị hàm số g  x nằm phía trên trục Ox (kể cả tiếp xúc).  m   m  . 0 4 4 Câu 48. Chọn D 2 2 Gọi B(a; 2  ), C( ; c 2 
) ( giả sử a  1  c ). Gọi H,K lần lượt là hình chiếu của B,C lên trục Ox: a 1 c 1  0       0
AB  AC; BAC  90  CAK  ACK  BAH  ACK; BHA  CKA  90  A  BH  C
 AK  AH  CK , HB  AK 2 2 a  1  2  a  2  và 2   c  2    B( 1
 ;1), C(3; 3)  T  8 c 1 a 1 c  3  Câu 49. Chọn C
Đặt t  log x , theo bài ra phương trình 2 . a log x  .
b log x  c  0 có hai nghiệm phân biệt thuộc đoạn [1; 2] hay phương trình 2 2 2 2
at  bt  c  0 có hai nghiệm phân biệt t ,t [0;1] ta có: 1 2 b b 2 ( )  3  2 2
(a  b)(2a  b)
(t  t )  3(t  t )  2 a a 1 2 1 2 P    .
a(a  b  c) b c
1 t  t  t .t 1 2 1 2 1  a a Vì 2 2 2
0  t t  t .t ; t  1  (t +t )  3t .t 1  P  3  P  3 . 1 2 1 1 2 2 1 2 1 2 max Câu 50. Chọn A S MN / /SD Ta có   
 (MNP) / /(SCD)  ((SAC), (MNP))  ((SAC), (SCD))  . NP / /CD 
Gọi H là hình chiếu vuông góc của A xuống (SCD), K là hình chiếu của H xuống SC     AKH M K 1 1 1 3 H V  V  . .3.4. .2 3  6. 2 2
AC  13  SC  25. S .ACD S . 2 ABCD 3 2 2 N A D SD  12 16  28  S  3 6. SCD 3V . SA AC 2 39 AH 5 26 Ta có S . ACD AH   6 ; AK    sin        0 60 ;  90  . S 2 2 5 AK 26 B C P SCD SA  AC Trang 4/4 -
Document Outline