Đề thi thử Toán tốt nghiệp THPT 2022 lần 2 trường chuyên Biên Hòa – Hà Nam

Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 12 đề thi thử môn Toán ôn thi tốt nghiệp THPT năm học 2021 – 2022 lần 2 trường THPT chuyên Biên Hòa, tỉnh Hà Nam 

51 26 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi THPTQG môn Toán năm 2022

Môn: Toán

Thông tin:

33 trang 7 tháng trước

Tác giả:

Profile Thanh Hoa
ĐỀ THI THỬ TN THPT LẦN 2 NĂM 2022
TRƯỜNG THPT CHUYÊN BIÊN HÒA - HÀ NAM
Câu 1. Trên mặt phẳng tọa độ , số phức được biểu diễn bởi điểm
Oxy
2 3 z i
A. . B. . C. . D. .
2;3P
3;2N
2;3Q
3; 2M
Câu 2. Tìm công thức sai?
A. . B. .
C. . D. .
d
x x
e x e C
0 1
ln
d
x
x
a
a x C a
a
Câu 3. Trong không gian , viết phương trình mặt phẳng đi qua điểm và có
Oxyz
P
1;0;3M
véctơ pháp tuyến .
1;3; 4
n
A. . B. . C. . D. .
3 4 13 0 x y z
3 4 13 0 x y z
3 4 3 0 x y z
3 4 13 0 x y z
Câu 4. Có bao nhiêu số có ba chữ số khác nhau được tạo thành từ các chữ số 1, 2, 3, 4, 5?
A. . B. . C. . D. .
3
5
A
5
P
3
5
C
3
P
Câu 5. Tìm công bội của một cấp số nhân có và .
q
n
u
1
1
2
u
6
16u
A. . B. . C. . D. .
1
2
q
2 q
2q
1
2
q
Câu 6. Đồ thị hàm số nào sau đây cắt trục tung tại điểm có tung độ âm
A. . B. . C. . D. .
2 3
1
x
y
x
- +
=
+
3 4
1
x
y
x
+
=
-
4 1
2
x
y
x
+
=
+
2 3
3 1
x
y
x
-
=
-
Câu 7. Trong không gian , cho mặt cầu có phương trình .
Oxyz
2 2 2
2 4 6 5 0x y z x y z+ + - + + + =
Hãy xác định tâm I, bán kính R của mặt cầu
A. . B. .
( )
1;2;3 , 3I R- =
( )
1; 2; 3 , 3I R- - =
C. D.
( )
1;2;3 , 9I R- =
( )
1;2;3 , 14I R- =
Câu 8. Đường thẳng nào sau đây là tiệm cận ngang của đồ thị hàm số ?
2
2
x
y
x
+
=
-
A. B. . C. . D.
2x =
2x =-
1y =
1y = -
Câu 9. Cho . Tính
1 3
0 1
1; 5.f x dx f x dx
3
0
f x dx
A. . B. C. . D. .
1
4.
6
5
Câu 10. Đồ thị hàm số nào dưới đây có dạng như hình vẽ
A. . B. . C. . D. .
1
1
x
y
x
1
1
x
y
x
2
1
x
y
x
2 1
1
x
y
x
Câu 11. Diện tích toàn phần của khối trụ có chiều cao và bán kính đáy ?
3 6h
6R
A. . B. . C. . D. .
24
tp
S
48
tp
S
36
tp
S
24 6
tp
S
Câu 12. Cho khối lăng trụ có diện tích đáy bằng , chiều cao bằng . Tính thể tích khối lăng trụ ?
2 3
4
A. . B. . C. . D. .
48
8 3
8 3
3
12 3
Câu 13. Cho khối chóp có đáy là tam giác vuông cân tại , , ,
.S ABC
ABC
A
2AB
12SA
. Tính thể tích khối chóp
SA ABC
.S ABC
A. . B. . C. . D. .
8
16
24
6
Câu 14. Tính thể tích của khối cầu có bán kính ?
V
2R b
A.
3
16
3
V b
. B. . C. . D. .
3
8
3
V b
3
32
3
V b
3
16V b
Câu 15. Trong không gian , đường thẳng có một véctơ chỉ phương là
Oxyz
1 2
: 3
2 3
x t
y
z t
A. . B. . C. . D. .
2;0; 3
1; 3;2
2;0; 3
2; 3;3
Câu 16. Biết và , khi đó bằng;
2
1
2f x dx
2
1
6g x dx
A. . B. . C. . D. .
8
4
4
8
Câu 17. Trong không gian , viết phương trình mặt phẳng đi qua 2 điểm
Oxyz
P
đồng thời vuông góc với mặt phẳng ?
1;0;3 , 1; 1; 2M N
: 2 2022 0Q x y z
A. . B. .C. . D. .
3 4 0x y z
3 2 0x y z
3 2 0x y z
3 2 0x y z
Câu 18. Cho hàm số có đồ thị như hình vẽ.
y f x
Hàm số đồng biến trên khoảng nào dưới đây?
A. . B. . C. . D. .
2;2
0;2
; 0
2;
Câu 19. Trong không gian , cho . Tính độ dài của ?
Oxyz
2 3 , 4a j k b i j k
2v a b
A. . B. . C. . D. .
74
3 6
5 2
42
Câu 20. Trong không gian , viết phương trình đường thẳng đi qua và vuông góc
Oxyz
1;1;0M
với mặt phẳng ?
: 4 2 0Q x y z
A. . B. . C. . D. .
1
4
1
x t
y t
z
1
1 4
x t
y t
z t
1
1 4
x t
y t
z t
1
1 4
x t
y t
z t
Câu 21. Chọn ngẫu nhiên hai số khác nhau từ 15 số nguyên dương đầu tiên. Xác suất để chọn được hai
số có tổng là một số lẻ là:
A. . B. . C. . D. .
1
7
8
15
4
15
1
14
Câu 22. Gọi lần lượt có điểm biểu diễn là và trên mặt phẳng phức ở hình bên. Tìm số phức
1 2
,z z
M
N
1 2
w 3 ? z z
A. . B. . C. . D. .
12 10w i
12 2w i
10 6w i
9 2w i
Câu 23. Cho số phức thỏa mãn . Môđun của bằng
z
2 8i z i
5 2z i
A. . B. . C. . D. .
2 5
4 5
3 2
10
Câu 24. Họ nguyên hàm của hàm số là:
F x
2
cos
1 cos
x
f x
x
A. . B. . C. . D. .
cos
sin
x
F x C
x
1
sin
F x C
x
1
sin
F x C
x
2
1
sin
F x C
x
Câu 25. Trong các hàm số sau, hàm số nào đồng biến trên khoảng ?
1;
A. . B. . C. . D. .
3
1y x x
3
1
x
y
x
4 2
3y x x
2
2 3
x
y
x
Câu 26. Tập xác định của hàm số là:
1
3
1y x
A. . B. . C. . D. .
0;
1;
1;
Câu 27. Cho hàm số liên tục trên và có bảng xét dấu đạo hàm như sau:
( )f x
( )f x
Hàm số có bao nhiêu điểm cực trị?
( )f x
A. . B. . C. . D. .
2
4
1
3
Câu 28. Tính đạo hàm của hàm số ?
2
log (2 1)y x
A. . B. . C. . D. .
1
'
(2 1)ln 2
y
x
2
'
(2 1)ln 2
y
x
2
'
2 1
y
x
1
'
2 1
y
x
Câu 29. Cho hai số phức , . Ta có khi:
( 3) (2 1)z x y y i
' 2 (2 5)z x x y i
'z z
A. . B. . C. . D. .
5 4
;
3 3
x y
1; 3x y
1; 2x y
5
; 0
3
x y
Câu 30. Tìm tập nghiệm của bất phương trình
2
4
1
2
2
x x
x
A. . B. . C. . D. .
2; 
; 2 2; 
2;
2;2
Câu 31. Gọi là hai nghiệm của phương trình khi đó bằng:
1 2
,x x
2
2
log 1 3 x x
1 2
x x
A. . B. . C. . D. .
1
3
2
2
Câu 32. Cho hình chóp tứ giác có đáy là hình chữ nhật. Biết , các cạnh bên
.S ABCD
, 2 AB a AD a
bằng nhau và bằng . Tính góc giữa hai đường thẳng
2a
, ?BC SA
A. . B. . C. . D. .
90
120
60
45
Câu 33. Cho hàm số có bảng biến thiên như sau:
y f x
Giá trị cực đại của hàm số đã cho bằng
A. . B. . C. . D. .
0
5
3
2
Câu 34. Cho . Tính
2
0
d 5f x x
2
0
3 2sin d ?I f x x x
A. . B. . C. . D. .
13I
17I
7I
3I
Câu 35. Với là số thực dương tùy ý, bằng
a
3
a a
A. . B. . C. . D. .
3
2
a
2
3
a
-
2
3
a
4
3
a
Câu 36. Tìm giá trị lớn nhất của hàm số trên là
2
3
1
x
y
x
+
=
-
[ ]
2;4
A. . B. . C. . D. .
[ ]
2;4
19
max
3
y =
[ ]
2;4
max 6y =
[ ]
2;4
11
max
3
y =
[ ]
2;4
max 7y =
Câu 37. Cho , với , là các số thực lớn hơn 1. Tính .
log 2
a
x =
log 3
b
x =
a
b
2
log
a
b
P x=
A. . B. . C. . D. .
6P =
6P =-
1
6
P =
1
6
P =-
Câu 38. Cho hình chóp có đáy là hình vuông cạnh , . Tính khoảng
.S ABCD
ABCD
a
( )
SA ABCD^
cách từ điểm đến mặt phẳng .
B
( )
SAC
A. . B. . C. . D. .
2
a
2
2
a
2
3
a
2
4
a
Câu 39. Gọi là tổng các giá trị thực của để phương trình có nghiệm phức
T
m
2
4 6 1 2 0z z m
thoả mãn . Tính ?
2z
T
A. . B. . C. . D. .
15
2
17
2
19
2
29
2
Câu 40. Có bao nhiêu giá trị nguyên dương của tham số để tập nghiệm của bất phương trình
m
chứa không quá số nguyên.
2
3 3 3 2 0
x x
m
9
A. . B. . C. . D. .
3281
3283
3280
3279
Câu 41. Một khối đồ chơi có dạng khối nón có chiều cao trong đó chứa một lượng nước. Nếu
40 cmh
đặt khối đồ chơi theo hình thì chiều cao của nước bằng chiều cao khối nón. Hỏi nếu
1
H
3
4
đặt khối đồ chơi theo hình thì chiều cao của nước gần với giá trị nào sau đây?
2
H
h
A. cm. B. cm. C. cm. D. cm.
8.98
7.23
6.68
6.86
Câu 42. Trong không gian , cho đường thẳng và . Gọi là
Oxyz
1 2
: 1
2
x t
y
z t
( ) : 2 2 0Q x y z
đường thẳng đối xứng với qua . Hỏi đi qua điểm nào sau đây?
( )Q
A. . B. . C. . D. .
(2;0; 3)
( 2; 1; 3)
(2; 5;3)
( 1; 1;3)
Câu 43. Biết rằng là một nguyên hàm của hàm số trên khoảng . Gọi là
sinx x
f x
; 
F x
một nguyên hàm của thỏa mãn , giá trị của bằng:
2 cosf x x
3
2 4
F
( )F
A. . B. . C. . D. .
5
2
3
2
3
2
5
2
Câu 44. Cho hình chóp , có , đáy là hình thoi cạnh , , góc giữa
.S ABCD
SA ABCD
a
60BAD
SA
và bằng . Gọi là trọng tâm tam giác . Tính thể tích khối tứ diện
SBD
60
G
SCD
?SAGB
A. . B. . C. . D. .
3
3
13
a
3
6
a
3
3
72
a
3
3
36
a
Câu 45. Cho hàm số có đạo hàm liên tục trên và bảng xét dấu đạo hàm như sau
y f x
Số điểm cực tiểu của hàm số là
4 2 6 4 2
3 4 6 2 3 12g x f x x x x x
A. . B. . C. . D. .
4
3
0
2
Câu 46. Cho số phức thỏa mãn . Gọi , lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của
z
2z
M
m
biểu thức . Tính giá trị của
2
1 4T z z z
2 2
M m
A. . B. . C. . D. .
45
384
85
115
Câu 47. Cho hàm số có đồ thị . Biết rằng đồ thị cắt trục tung tại điểm có tung độ
( )y f x
C
C
bằng và đồ thị hàm số cho bởi hình vẽ bên.
1
2
y f x
Tính diện tích hình phẳng giới hạn bởi đồ thị và đồ thị hàm số ?
C
3
2
2 2
3
y x x
A. . B. . C. . D. .
17 3
5
32 3
5
16 3
5
14 3
5
Câu 48. Cho hàm số liên tục trên và có đạo hàm có bao
y f x
2022
2
12 2f x x x x
nhiêu giá trị nguyên của để hàm số có ba điểm
2021;2021m
2
2022 2021y f x x m
cực trị dương.
A. . B. . C. . D.
4038
2021
2020
2019
Câu 49. Trong không gian , cho mặt phẳng và 2 mặt cầu
Oxyz
: 2 2 5 0P x y z
; . Gọi
2 2
2
1
: 2 1 1S x y z
2 2 2
2
: 4 2 3 4S x y z
, ; ; ,M A a b c B
lần lượt thuộc sao cho nhỏ nhất? Tính ?
1 2
, ,P S S
MA MB
a b c
A. . B. . C. . D. .
3
3
1
1
Câu 50. Cho hàm số . Tìm số nguyên lớn nhất để ?
2022 2022
x x
f x
m
3 2021 0f m f m
A. . B. . C. . D. .
505
505
506
506
-------------------------- HẾT --------------------------
ĐÁP ÁN
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
C
B
B
A
C
B
B
C
B
B
B
B
A
C
A
A
D
B
A
C
B
B
A
C
C
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
B
A
B
C
D
A
D
D
A
C
D
B
B
C
C
C
C
D
D
D
D
C
B
C
C
LỜI GIẢI CHI TIẾT
Câu 1. Trên mặt phẳng tọa độ , số phức được biểu diễn bởi điểm
Oxy
2 3 z i
A. . B. . C. . D. .
2;3P
3;2N
2;3Q
3; 2M
Lời giải
Chọn C
Số phúc được biểu diễn bởi điểm .
2 3 z i
2;3Q
Câu 2. Tìm công thức sai?
A. . B. .
C. . D. .
d
x x
e x e C
0 1
ln
d
x
x
a
a x C a
a
Lời giải
Chọn B
Vì nên phương án B sai.
sin d cos
x x x C
Câu 3. Trong không gian , viết phương trình mặt phẳng đi qua điểm và có véctơ
Oxyz
P
1;0;3M
pháp tuyến .
1;3; 4
n
A. . B. . C. . D. .
3 4 13 0 x y z
3 4 13 0 x y z
3 4 3 0 x y z
3 4 13 0 x y z
Lời giải
Chọn B
Phương trình mặt phẳng cần lập là .
P
01 1 3 0 4 3 z 14 30 3 x y z x y
Câu 4. Có bao nhiêu số có ba chữ số khác nhau được tạo thành từ các chữ số 1, 2, 3, 4, 5?
A. . B. . C. . D. .
3
5
A
5
P
3
5
C
3
P
Lời giải
Chọn A
Số các số có ba chữ số khác nhau được tạo thành từ các chữ số 1, 2, 3, 4, 5 là .
3
5
A
Câu 5. Tìm công bội của một cấp số nhân có và .
q
n
u
1
1
2
u
6
16u
A. . B. . C. . D. .
1
2
q
2 q
2q
1
2
q
Lời giải
Chọn C
Ta có .
5 5
6
6 1
1
. 32 2
u
u u q q q
u
Câu 6. Đồ thị hàm số nào sau đây cắt trục tung tại điểm có tung độ âm
A. . B. . C. . D. .
2 3
1
x
y
x
- +
=
+
3 4
1
x
y
x
+
=
-
4 1
2
x
y
x
+
=
+
2 3
3 1
x
y
x
-
=
-
Lời giải
Chọn B
Đồ thị hàm số cắt trục tung tại điểm có tung độ âm khi .
ax b
y
cx d
+
=
+
0
b
d
<
Do đó đồ thị hàm số cắt trục tung tại điểm có tung độ âm.
3 4
1
x
y
x
+
=
-
Câu 7. Trong không gian , cho mặt cầu có phương trình . Hãy
Oxyz
2 2 2
2 4 6 5 0x y z x y z+ + - + + + =
xác định tâm I, bán kính R của mặt cầu
A. . B. .
( )
1;2;3 , 3I R- =
( )
1; 2; 3 , 3I R- - =
C. D.
( )
1;2;3 , 9I R- =
( )
1;2;3 , 14I R- =
Lời giải
Chọn B
Mặt cầu có tâm và bán kính
2 2 2
2 4 6 5 0x y z x y z+ + - + + + =
( )
1; 2; 3I - -
( ) ( ) ( )
2 2 2
1 2 3 5 3.R = + - + - - =
Câu 8. Đường thẳng nào sau đây là tiệm cận ngang của đồ thị hàm số ?
2
2
x
y
x
+
=
-
A. B. . C. . D.
2x =
2x =-
1y =
1y = -
Lời giải
Chọn C
Ta có nên đồ thị hàm số có tiệm cận ngang
lim 1
x
y
®±¥
=
1.y =
Câu 9. Cho . Tính
1 3
0 1
1; 5.f x dx f x dx
3
0
f x dx
A. . B. C. . D. .
1
4.
6
5
Lời giải
Chọn B
Ta có
( ) ( ) ( )
3 1 3
0 0 1
d d d 1 5 4.f x x f x x f x x= + = - + =
ò ò ò
Câu 10. Đồ thị hàm số nào dưới đây có dạng như hình vẽ
A. . B. . C. . D. .
1
1
x
y
x
1
1
x
y
x
2
1
x
y
x
2 1
1
x
y
x
Lời giải
Chọn B
Đồ thị hàm số có tiệm cận ngang nên loại đáp án D
1y =
Đồ thị hàm số có tiệm cận đứng nên loại đáp án A và C
1x =
Vậy chọn đáp án B
Câu 11. Diện tích toàn phần của khối trụ có chiều cao và bán kính đáy ?
3 6h
6R
A. . B. . C. . D. .
24
tp
S
48
tp
S
36
tp
S
24 6
tp
S
Lời giải
Chọn B
Diện tích toàn phần của hình trụ là .
2
2
2 2 2 . 6.3 6 2 . 6 48
tp
S Rh R
Câu 12. Cho khối lăng trụ có diện tích đáy bằng , chiều cao bằng . Tính thể tích khối lăng trụ ?
2 3
4
A. . B. . C. . D. .
4 8
8 3
8 3
3
12 3
Lời giải
Chọn B
Thể tích của khối lăng trụ .
2 3.4 8 3V Bh
Câu 13. Cho khối chóp có đáy là tam giác vuông cân tại , , ,
.S ABC
A B C
A
2AB
12SA
. Tính thể tích khối chóp
SA ABC
.S ABC
A. . B. . C. . D. .
8
16
24
6
Lời giải
Chọn A
Diện tích vuông cân tại là
A B C
A
2 2
1 1
.2 2
2 2
S AB
Thể tích khối chóp là .
1 1
. .2.12 8
3 3
V S h
Câu 14. Tính thể tích của khối cầu có bán kính ?
V
2R b
A.
3
16
3
V b
. B. . C. . D. .
3
8
3
V b
3
32
3
V b
3
16V b
Lời giải
Chọn C
Thể tích khối cầu là .
3
3 3
4 4 32
. 2
3 3 3
V R b b
Câu 15. Trong không gian , đường thẳng có một véctơ chỉ phương là
Oxyz
1 2
: 3
2 3
x t
y
z t
A. . B. . C. . D. .
2; 0; 3
1; 3;2
2; 0; 3
2; 3; 3
Lời giải
Chọn A
Từ phương trình ta có đường thẳng có một véctơ chỉ phương là .
2;0;3u
Do đó cũng là một véctơ chỉ phương của đường thẳng .
2;0; 3u u
Câu 16. Biết và , khi đó bằng;
2
1
2f x dx
2
1
6g x dx
2
1
f x g x dx
A. . B. . C. . D. .
8
4
4
8
Lời giải
Chọn A
Ta có .
2 2 2
1 1 1
2 6 8f x g x dx f x dx g x dx
Câu 17. Trong không gian , viết phương trình mặt phẳng đi qua 2 điểm
Oxyz
P
đồng thời vuông góc với mặt phẳng ?
1; 0;3 , 1; 1; 2M N
: 2 2022 0Q x y z
A. . B.
.C. . D.
.
3 4 0x y z
3 2 0x y z
3 2 0x y z
3 2 0x y z
Lời giải
Chọn D
Gọi là vecto pháp tuyến của mặt phẳng .
n
P
Do mặt phẳng đi qua 2 điểm đồng thời vuông góc với mặt phẳng
P
1; 0;3 , 1; 1; 2M N
nên ta có: .
: 2 2022 0Q x y z
2; 1; 5
; 4; 12;4
2;1;1
Q
Q
n MN
n MN n
n n
Chọn là VTPT của .
1
1; 3;1n
P
Khi đó đi qua và có VTPT nên có phương trình:
P
M
1
n
3 2 0x y z
Câu 18. Cho hàm số có đồ thị như hình vẽ.
y f x
Hàm số đồng biến trên khoảng nào dưới đây?
A. . B. . C. . D. .
2;2
0;2
; 0
2;
Lời giải
Chọn B
Nhìn đồ thị ta thấy hàm số đồng biến trên khoảng .
0;2
Câu 19. Trong không gian , cho . Tính độ dài của ?
Oxyz
2 3 , 4a j k b i j k
2v a b
A. . B. . C. . D. .
74
3 6
5 2
42
Lời giải
Chọn A
Ta có
0; 2; 3 , 4;1;1 2 4; 3; 7 74
a b v a b v
Câu 20. Trong không gian , viết phương trình đường thẳng đi qua và vuông góc
Oxyz
1;1; 0M
với mặt phẳng ?
: 4 2 0Q x y z
A. . B.
. C. . D.
.
1
4
1
x t
y t
z
1
1 4
x t
y t
z t
1
1 4
x t
y t
z t
1
1 4
x t
y t
z t
Lời giải
Chọn C
Do vuông góc với mặt phẳng nên ta có vecto chỉ phương của đương
: 4 2 0Q x y z
thẳng là:
1; 4; 1
u
Khi đó phương trình :
1
1 4
x t
y t
z t
Câu 21. Chọn ngẫu nhiên hai số khác nhau từ 15 số nguyên dương đầu tiên. Xác suất để chọn được hai
số có tổng là một số lẻ là:
A. . B. . C. . D. .
1
7
8
15
4
15
1
14
Lời giải
Chọn B
Chọn ngẫu nhiên hai số khác nhau từ 15 số nguyên dương đầu tiên, ta có số phần tử của không
gian mẫu là .
2
15
105n C
Trong 15 số nguyên dương đầu tiên có 8 số lẻ và 7 số chẵn
Gọi là biến cố: “chọn được hai số có tổng là một số lẻ”.
A
Khi đó hai số được chọn có một số là số chẵn và 1 số là số lẻ.
Số phần tử của biến cố là .
A
7.8 56n A
Khi đó .
56 8
105 15
n A
P A
n
Câu 22. Gọi lần lượt có điểm biểu diễn là và trên mặt phẳng phức ở hình bên. Tìm số phức
1 2
,z z
M
N
1 2
w 3 ? z z
A. . B. . C. . D. .
12 10w i
12 2w i
10 6w i
9 2w i
Lời giải
Chọn B
Ta có ; .
1
3 4z i
2
3 2z i
Khi đó .
1 2
3 4 3 3 23 12 2w i i iz z
Câu 23. Cho số phức thỏa mãn . Môđun của bằng
z
2 8i z i
5 2z i
A. . B. . C. . D. .
2 5
4 5
3 2
10
Lời giải
Chọn A
Ta có .
8
2 8 3 2
2
i
i z i z i
i
Khi đó .
5 2 3 2 5 2 2 4z i i i i
Vậy .
2
2
5 2 2 4 2 5z i
Câu 24. Họ nguyên hàm của hàm số là:
F x
2
cos
1 cos
x
f x
x
A. . B. . C. . D. .
cos
sin
x
F x C
x
1
sin
F x C
x
1
sin
F x C
x
2
1
sin
F x C
x
Lời giải
Chọn C
Ta có .
2 2 2
cos cos 1 1
d d d d sin
1 cos sin sin sin
x x
f x x x x x C
x x x x
Vậy .
1
sin
F x C
x
Câu 25. Trong các hàm số sau, hàm số nào đồng biến trên khoảng ?
1;
A. . B. . C. . D. .
3
1y x x
3
1
x
y
x
4 2
3y x x
2
2 3
x
y
x
Lời giải
Chọn C
+ Xét phương án : Ta có .
A
2
3
3
3 1 0
3
3
x
y x
x
Bảng xét dấu
Hàm số đồng biến trên . Phương án không thỏa mãn.
3 3
;
3 3
A
+ Xét phương án : Ta có .
B
2
0, 1
4
1
y x
x
Hàm số nghịch biến trên và . Phương án không thỏa mãn.
; 1
1;
B
+ Xét phương án : Ta có .
C
3
2
2
2
4 2 0
2
0
x
y x x x
x
Bảng xét dấu
Hàm số đồng biến trên và .
2
;0
2
2
;
2

Khi đó hàm số đồng biến trên . Phương án thỏa mãn.
1;
C
+ Xét phương án : Ta có .
D
2
3
0,
2
1
2 3
y x
x
Hàm số đồng biến trên và . Phương án không thỏa mãn.
3
;
2
3
;
2
D
Câu 26. Tập xác định của hàm số là:
1
3
1y x
A. . B. . C. . D. .
0;
1;
1;
Lời giải
Chọn B
Điều kiện .
1 0 1x x
Vậy tập xác định của hàm số đã cho là .
1;
Câu 27. Cho hàm số liên tục trên và có bảng xét dấu đạo hàm như sau:
( )f x
( )f x
Hàm số có bao nhiêu điểm cực trị?
( )f x
A. . B. . C. . D. .
2
4
1
3
Lời giải
Chọn A
Hàm số liên tục trên và có đổi dấu khi đi qua các điểm và
( )f x
( )f x
1x
0x
hàm số có 2 điểm cực trị.
Câu 28. Tính đạo hàm của hàm số ?
2
log (2 1)y x
A. . B. . C. . D. .
1
'
(2 1) ln 2
y
x
2
'
(2 1) ln 2
y
x
2
'
2 1
y
x
1
'
2 1
y
x
Lời giải
Chọn B
Ta có .
2
2 1 '
2
' log (2 1) '
(2 1).ln 2 (2 1).ln 2
x
y x
x x
Câu 29. Cho hai số phức , . Ta có khi:
( 3) (2 1)z x y y i
' 2 (2 5)z x x y i
'z z
A. . B. . C. . D. .
5 4
;
3 3
x y
1; 3x y
1; 2x y
5
; 0
3
x y
Lời giải
Chọn C
Ta có .
3 2 3 1
'
2 1 2 5 2 3 4 2
x y x x y x
z z
y x y x y y
Câu 30. Tìm tập nghiệm của bất phương trình
2
4
1
2
2
x x
x
A. . B. .C. . D. .
2;
; 2 2;
2;
2; 2
Lời giải
Chọn D
Ta có .
2
2
4 4 2 2
1
2 2 2 4 4 0 2 2
2
x x
x x x x
x x x x x
Vậy tập nghiệm của bất phương trình là: .
2; 2S
Câu 31. Gọi là hai nghiệm của phương trình khi đó bằng:
1 2
,x x
2
2
log 1 3 x x
1 2
x x
A. . B. . C. . D. .
1
3
2
2
Lời giải
Chọn A
Ta có:
1
2 2 3 2
2
2
1 29
2
log 1 3 1 2 7 0
1 29
2
x
x x x x x x
x
.
1 2
1 x x
Cách 2:
2 2 3 2
2
log 1 3 1 2 7 0 x x x x x x
Theo định lí Vi-et, ta có: .
1 2
1 x x
Câu 32. Cho hình chóp tứ giác có đáy là hình chữ nhật. Biết , các cạnh bên
.S A B C D
, 2 AB a AD a
bằng nhau và bằng . Tính góc giữa hai đường thẳng
2a
, ?BC SA
A. . B. . C. . D. .
90
120
60
45
Lời giải
Chọn D
2
a
a
2
C
B
D
A
a
S
Ta có: Vì nên góc
// BC AD
, , SA BC SA AD SAD
Mặt khác, ta có: nên tam giác vuông cân tại .
2 2 2
SD SA AD
SAD
S
45 SAD
Câu 33. Cho hàm số có bảng biến thiên như sau:
y f x
Giá trị cực đại của hàm số đã cho bằng
A. . B. . C. . D. .
0
5
3
2
Lời giải
Chọn D
Từ BBT, suy ra: giá trị cực đại của hàm số đã cho bằng tại .
2
0x
Câu 34. Cho . Tính
2
0
d 5f x x
2
0
3 2sin d ?I f x x x
A. . B. . C. . D. .
13I
17I
7I
3I
Lời giải
Chọn A
Ta có:
2 2 2 2
2
0 0 0 0
0
3 2sin d 3 d 2 sin d 3. d 2cos 3.5 2 0 1 13
I f x x x f x x x x f x x x
Câu 35. Với là số thực dương tùy ý, bằng
a
3
a a
A. . B. . C. . D. .
3
2
a
2
3
a
-
2
3
a
4
3
a
Lời giải
Chọn C
Ta có .
1 4 2
3
3 3 3
.a a a a a a= = =
Câu 36. Tìm giá trị lớn nhất của hàm số trên là
2
3
1
x
y
x
+
=
-
[ ]
2; 4
A. . B. . C. . D. .
[ ]
2;4
19
max
3
y =
[ ]
2;4
max 6y =
[ ]
2;4
11
max
3
y =
[ ]
2;4
max 7y =
Lời giải
Chọn D
TXĐ: . Hàm số xác định trên .
{ }
\ 1D =
[ ]
2; 4
Ta có .
( )
( )
( )
( )
( )
( )
( ) ( )
2 2
2
2
2 2 2
3 . 1 3 . 1
2 . 1 3
2 3
1 1 1
x x x x
x x x
x x
y
x x x
¢
¢
+ - - + -
- - -
- -
¢
= = =
- - -
.
0y
¢
=
( )
2
2
2 3
0
1
x x
x
- -
Û =
-
2
2 3 0x xÛ - - =
[ ]
[ ]
1 2;4
3 2;4
x
x
é
=- Ï
ê
Û
ê
= Î
ê
ë
Ta có , , .
( )
2 7y =
( )
3 6y =
( )
19
4
3
y =
Vậy .
[ ]
2;4
max 7y =
Câu 37. Cho , với , là các số thực lớn hơn 1. Tính .
log 2
a
x =
log 3
b
x =
a
b
2
log
a
b
P x=
A. . B. . C. . D. .
6P =
6P = -
1
6
P =
1
6
P = -
Lời giải
Chọn B
Theo bài , , .
log 2
a
x =
log 3
b
x =
1
log
2
x
aÞ =
1
log
3
x
b =
Suy ra .
2
2
2
1 1 1 1
log 6
1 2
log log log 2log
log
2 3
a
x x x x
b
x
P x
a
a b a b
b
= = = = = = -
- -
-
Câu 38. Cho hình chóp có đáy là hình vuông cạnh , . Tính khoảng
.S A B C D
AB C D
a
( )
SA ABCD^
cách từ điểm đến mặt phẳng .
B
( )
SA C
A. . B. . C. . D. .
2
a
2
2
a
2
3
a
2
4
a
Lời giải
Chọn B
Theo bài mà nên .
( )
SA ABCD^
( )
BO ABCDÌ
SA BO^
Vì là hình vuông nên và
AB C D
B O A C^
2BD a=
Ta có .
( )
{ }
,
BO AC
SA BO
SA AC SAC
SA AC A
ì
^
ï
ï
ï
ï
^
ï
ï
í
Ì
ï
ï
ï
ï
Ç =
ï
ï
î
( )
BO SACÞ ^
( )
( )
2
,
2 2
BD a
d B SAC BOÞ = = =
Câu 39. Gọi là tổng các giá trị thực của để phương trình có nghiệm phức
T
m
2
4 6 1 2 0z z m
thoả mãn . Tính ?
2z
T
A. . B. . C. . D. .
15
2
17
2
19
2
29
2
Lời giải
Chọn C
.
2
3 4 1 2 5 8m m
+) Nếu , phương trình có 2 nghiệm thực. Khi đó
5
0 5 8 0
8
m m
.
2 2z z
Thế vào phương trình ta được: (nhận).
2z
29
16 12 1 2 0
2
m m
Thế vào phương trình ta được: (nhận).
2z
5
16 12 1 2 0
2
m m
+) Nếu , phương trình có 2 nghiệm phức thỏa mãn
5
0 5 8 0
8
m m
1 2
,z z
. Khi đó (nhận).
2 1 1 2
, 2z z z z
2
2
1 2 1
1 2 15
. 2
4 2
m
z z z m
Ta có .
29 5 15 19
2 2 2 2
T
Câu 40. Có bao nhiêu giá trị nguyên dương của tham số để tập nghiệm của bất phương trình
m
chứa không quá số nguyên.
2
3 3 3 2 0
x x
m
9
A. . B. . C. . D. .
3281
3 2 83
3 2 80
3 2 79
Lời giải
Chọn C
Ta có .
2
2
2
3 3 0
1
3 2 0
3 3 3 2 0
3 3 0
2
3 2 0
x
x
x x
x
x
m
m
m
Do là số nguyên dương nên
m
3
log 2 0m
Xét hệ : hệ vô nghiệm
1
2
3
1
3
2
3 3 0
2
2
3 2 0
log 2 0
0
x
x
x
x
m
x m
x
Xét hệ : .
2
2
3
3 3
1 3
2
3 3 0
3
2 2
log 2
2
3 2 0
log 2 log 2
x
x
x x
x m
m
x m x m
Để có không quá số nguyên thỏa mãn đề bài thì
9
x
.
8
3
1 1 6561
1 log 2 8 2 3
3 6 2
m m m
Do là số nguyên dương nên có giá trị của .
m
1; 2; 3;...;3280m
3 2 80
m
Câu 41. Một khối đồ chơi có dạng khối nón có chiều cao trong đó chứa một lượng nước. Nếu
40 cmh
đặt khối đồ chơi theo hình thì chiều cao của nước bằng chiều cao khối nón. Hỏi nếu
1
H
3
4
đặt khối đồ chơi theo hình thì chiều cao của nước gần với giá trị nào sau đây?
2
H
h
A. cm. B. cm. C. cm. D. cm.
8.98
7.23
6.68
6.86
Lời giải
Chọn C
Gọi lần lượt là tâm của đường tròn đáy phần chứa nước , tâm của đường tròn đáy
,H H
¢
1
( )H
phần không chứa nước
2
( )H
Ta có (g-g)
SA O SD H ∽
.
3
4
HD SH
OA SO
Þ = =
Ở hình , gọi là thể tích phần chứa nước, là thể tích khối nón có chiều cao
1
( )H
n
V
V
h
, .
2
1
. .
3
V HO SO= p
2
1
. .
3
n
V HD SH= p
.
2
2 2
2
1
. .
3 3 27 27
3
. .
1
4 4 64 64
. .
3
n
n
HD SH
V
HD SH
V V
V HO SO
HO SO
æ ö æ ö
÷ ÷
ç ç
= = = = Þ =
÷ ÷
ç ç
÷ ÷
ç ç
è ø è ø
p
p
Ở hình , phần thể tích chứa nước, là phần thể tích không chứa nước.
2
( )H
n
V
1
V
Ta có (g-g) .
SAO SD H
¢ ¢
∽
HD SH
k
OA SO
¢ ¢
Þ = =
.
3
3
1
1 1
27 37 37 37 37
64 64 64 64 4
n n
V
V V V V V V V V V k k
V
- = Û = - = - = Þ = Þ = Þ =
cm.
3 3 3
37 37 37
1 1 .40 6,68
4 4 4
SH SO h OH SO SH SO
æ ö æ ö
÷ ÷
ç ç
÷ ÷
¢ ¢ ¢ ¢
Þ = Þ = = - = - = - »
ç ç
÷ ÷
ç ç
÷ ÷
÷ ÷
ç ç
è ø è ø
Câu 42. Trong không gian , cho đường thẳng và . Gọi là
Oxyz
1 2
: 1
2
x t
y
z t
( ): 2 2 0Q x y z
đường thẳng đối xứng với qua . Hỏi đi qua điểm nào sau đây?
( )Q
A. . B. . C. . D. .
(2;0; 3)
( 2; 1; 3)
(2; 5;3)
( 1; 1;3)
Lời giải
Chọn C
Véc tơ chỉ phương , véc tơ pháp tuyến .
(2;0;1)u
(1; 2;1)
Q
n
Gọi
( ) (1 2 ;1;2 )M Q M t t=DÇ Þ - + ÎD
.
( ) 1 2 2.1 2 2 0 1 ( 1;1;3)M Q t t t MÎ Þ - + - - + = Û = Þ -
Lấy , là đường thẳng qua và vuông góc với
(1;1;2)A ÎD
d
A
1
( ) : 1 2
2
x m
Q y m
z m
ì
= +
ï
ï
ï
ï
= +
í
ï
ï
= -
ï
ï
î
Gọi là hình chiếu của lên , .
H
A
( )Q
( ) (1 ;1 2 ;2 )H d Q H m m m d= Ç Þ + + - Î
.
1 1 5
( ) 1 2(1 2 ) 2 2 0 ;0;
2 2 2
H Q m m m m H
æ ö
÷
ç
Î Þ + + + - + + = Û =- Þ
÷
ç
÷
ç
è ø
Ta có là điểm đối xứng của qua là trung điểm của
A
¢
A
( )Q HÞ
A A
¢
.
2
2 1 1 0
2 0 1 1 (0; 1;3)
2
2 5 2 3
2
H
H
H H
H
H
A
A
A
A
A
A
A
A
A
A
A
A
x x
x
x x x
y y
y y y y A
z z z
z z
z
¢
¢
¢
¢
¢
¢
ì
+
ï
ï
=
ï
ï
ì
ï
= - = - =
ï
ï
ï
ï
ï
+
ï
ï
¢
= Û = - = - =- Þ -
í í
ï ï
ï ï
ï ï
= - = - =
ï ï
+
î
ï
=
ï
ï
ï
î
.
( 1; 2; 0)A M
¢
Þ = -
có véc tơ chỉ phương , qua là .
¢
D
( 1;2;0)u
(0; 1;3)A
¢
-
: 1 2
3
x t
y t
z
ì
=-
ï
ï
ï
ï
¢
D =- +
í
ï
ï
=
ï
ï
î
Ta thấy điểm .
(2; 5;3)
Câu 43. Biết rằng là một nguyên hàm của hàm số trên khoảng . Gọi là
sinx x
f x
;
F x
một nguyên hàm của thỏa mãn , giá trị của bằng:
2 cosf x x
3
2 4
F
( )F
A. . B.
. C. . D.
.
5
2
3
2
3
2
5
2
Lời giải
Chọn D
Ta có: là một nguyên hàm của hàm số
sinx x
f x
Nên
sin sin .cos sin .cosf x x x x x x x x x
Suy ra .
sin .cosf x x x x
cos cos sin 2 cos sinf x x x x x x x x
Suy ra .
2
2 cos 2. 2 cos sin cos 4 cos sin 2f x x x x x x x x x
Ta có:
2
2
d2 cosf x x x F x
2
2
2
4cos si dn 2 xx x xx F
.
7
4 2
F F
7 3
4 4
F
5
2
F
Câu 44. Cho hình chóp , có , đáy là hình thoi cạnh , , góc giữa
.S A B C D
SA ABCD
a
60BAD
và bằng . Gọi là trọng tâm tam giác . Tính thể tích khối tứ diện
S A
SBD
60
G
S C D
?SA G B
A. . B. . C. . D. .
3
3
13
a
3
6
a
3
3
72
a
3
3
36
a
Lời giải
Chọn D
a
60
0
K
O
A
B
C
D
S
H
G
Gọi là trung điểm của , là trọng tâm tam giác .
K
CD
G
SCD
2 2
.
3 3
SABG
SABG SABK
SABK
V
SG
V V
V SK
Gọi là hình chiếu lên , khi đó
H
A
SO
0
, 60 .SA SBD ASH ASO
Các tam giác đều cạnh ,
,ABD BCD
a
3
.
2
a
AO
Trong tam giác vuông ta có
SAO
.
2
tan
AO a
SA
ASO
Vì ,
BK C D BK AB
2
1 1 3 3
. . . .
2 2 2 4
ABK
a a
S AB BK a
2 3
1 1 3 3
. . . .
3 3 4 2 24
SABK ABK
a a a
V S SA
3 3
2 2 3 3
. . .
3 3 24 36
SABG SABK
a a
V V
Câu 45. Cho hàm số có đạo hàm liên tục trên và bảng xét dấu đạo hàm như sau
y f x
Số điểm cực tiểu của hàm số là
4 2 6 4 2
3 4 6 2 3 12g x f x x x x x
A. . B. . C. . D. .
4
3
0
2
Lời giải
Chọn D
Đạo hàm
3 4 2 5 3
2 4 2 2
12 2 4 6 12 12 24
12 2 4 6 1 .
g x x x f x x x x x
x x f x x x
4 2 2
0
0 2
4 6 1 0. 1
x
g x x
f x x x
Ta có .
2
4 2 2 4 2
4 6 2 2 2, 4 6 2 0x x x x f x x f
Suy ra nên phương trình vô nghiệm.
4 2 2
4 6 1 0,f x x x x
1
Bảng biến thiên
Dựa vào bảng biến thiên thì hàm số có hai điểm cực tiểu.
g x
Câu 46. Cho số phức thỏa mãn . Gọi , lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của
z
2z
M
m
biểu thức . Tính giá trị của
2
1 4T z z z
2 2
M m
A. . B. . C. . D. .
4 5
384
8 5
115
Lời giải
Chọn D
Đặt suy ra .
, ,z x yi x y
2 2 2
4 4 2 2x y x x
Ta có
2 2
2
2
1 4 1 .
1 1 1 2 2 1
2 5 2 2 1 .
T z z z z z z z z
z z z z x y x
x x
Xét hàm số , với .
1
2 5 4 2,khi
2
2 5 2 1
1
2 5 2 4 ,khi
2
x x x
f x x x
x x x
2; 2x
Có .
1 1
4,
2
2 5
1 1
4,
2
2 5
x
x
f x
x
x
Hàm số không có đạo hàm tại điểm .
f x
1
2
x
.
1 79
0 4 0 2; 2
32
2 5
f x x
x
Bảng biến thiên
Câu 31:
Dựa theo bảng biến thiên thì , .
6m
11M
Vậy .
2 2
115M m
Câu 47. Cho hàm số có đồ thị . Biết rằng đồ thị cắt trục tung tại điểm có tung độ
( )y f x
C
C
bằng và đồ thị hàm số cho bởi hình vẽ bên.
1
2
y f x
Tính diện tích hình phẳng giới hạn bởi đồ thị và đồ thị hàm số ?
C
3
2
2 2
3
y x x
A. . B. . C. . D. .
17 3
5
32 3
5
16 3
5
14 3
5
Lời giải
Chọn C
Từ hình vẽ ta thấy được
2
3 2
1 1 1f x a x x a x x x
Mà
4 3
3 2 2
2
0 2 2 1 2
2 3
x x
f f x x x x f x x x C
Do đồ thị cắt trục tung tại điểm có tung độ bằng nên
C
1
2
1
0
2
f
4 3
2
2 1
2
2 3 2
x x
f x x x
Đặt
3
2
2 2
3
y g x x x
Xét phương trình hoành độ giao điểm
f x g x
.
4 3 4
2 3 2 2
2 1 2 3
2 2 2 0 3 3
2 3 2 3 2 2
x x x
x x x x x x x
Khi đó diện tích hình phẳng giới hạn bởi hai đồ thị của hai hàm số và là:
f x
g x
.
3 3
4
2
0
3
3 16 3
d 2 d
2 2 5
x
S f x g x x x x
Câu 48. Cho hàm số liên tục trên và có đạo hàm có bao
y f x
2022
2
12 2f x x x x
nhiêu giá trị nguyên của để hàm số có ba điểm
2021; 2021m
2
2022 2021y f x x m
cực trị dương.
A. . B. . C. . D.
40 38
2021
20 20
20 19
Lời giải
Chọn B
.
2022
2
0
12 2 2
12
x
f x x x x x
x
Xét hàm số
2
2022 2021g x f x x m
2
2 2022 2022 2021g x x f x x m
Ta có
2 2
2 2
2 2
11 11
2022 2021 0 2022 2021
0
2022 2021 2 2022 2 2021
2022 2021 12 2022 12 2021
x x
x x m x x m
g x
x x m x x m
x x m x x m
Xét hàm số
2
2022h x x x
Ta có bảng biến thiên của hàm số trên
2
2022h x x x
0;
Để hàm số có 3 điểm cực trị dương
g x
.
2021 0
0
2020; 2019;...;0
2021 2 0
22121 2
2021 22121
2021 2021
m
m
m
m
m l
m
Câu 49. Trong không gian , cho mặt phẳng và 2 mặt cầu
Oxyz
: 2 2 5 0P x y z
; . Gọi lần
2 2
2
1
: 2 1 1S x y z
2 2 2
2
: 4 2 3 4S x y z
, ; ; ,M A a b c B
lượt thuộc sao cho nhỏ nhất? Tính ?
1 2
, ,P S S
MA MB
a b c
A. . B. . C. . D. .
3
3
1
1
Lời giải
Chọn C
Mặt cầu có tâm , bán kính .
1
S
2; 0; 1I
1
1R
Mặt cầu có tâm , bán kính .
2
S
4; 2;3J
2
2R
Ta có: và nên và
1 2
2 14IJ R R
2 2 5 2 2 5 0
I I I J J J
x y z x y z
1
S
2
S
nằm phác phía so với mặt phẳng .
P
Gọi lần lượt là giao điểm của đoạn với và
,C D
I J
1
S
2
S
Ta có có phương trình tham số:
I J
2 3
1 2
x t
y t
z t
Tọa độ là nghiệm của hệ phương trình: .
C
2 2
2
14
14
2 3
3 14
2
14
1 2
14
2 1 1
14
; ;
2 14
1
14
t
x t
y t
x
z t
y
x y z
d C P d I P
z
Suy ra
3 14 14 2 14
2 ; ; 1
14 14 14
C
Khi đó :
P M A M B A I BJ IJ
.
M A M B C I D J C I D J C D M A M B C D
Suy ra .
min 1 2
2 14 3P C D IJ R R
Dấu bằng xảy ra khi và thẳng hàng.
;A C B D
, ,M C D
Vậy .
3 14 14 2 14
2 ; ; 1
14 14 14
A
1a b c
Câu 50. Cho hàm số . Tìm số nguyên lớn nhất để ?
2022 2022
x x
f x
m
3 2021 0f m f m
A. . B. . C. . D. .
50 5
505
50 6
506
Lời giải
Chọn C
Hàm số xác định .
2022 2022
x x
f x
x
Khi đó với , ta có .
x
( ) 2022 2022
x x
f x f x
Suy ra là hàm số lẻ.
( )f x
1
Mặt khác
2022 2022 2022 ln 2022 2022 ln 2022 0,
x x x x
f x f x x
Do đó hàm số đồng biến trên .
( )f x
2
Ta có .
3 2021 0f m f m
3 2021f m f m
Theo suy ra .
1
3 2021f m f m
Theo ta được . Vậy số nguyên lớn nhất là .
2
2021
3 2021
4
m m m
m
50 6
-----------------------HẾT-----------------------
| 1/33
| | Tải xuống

Có thể bạn quan tâm:

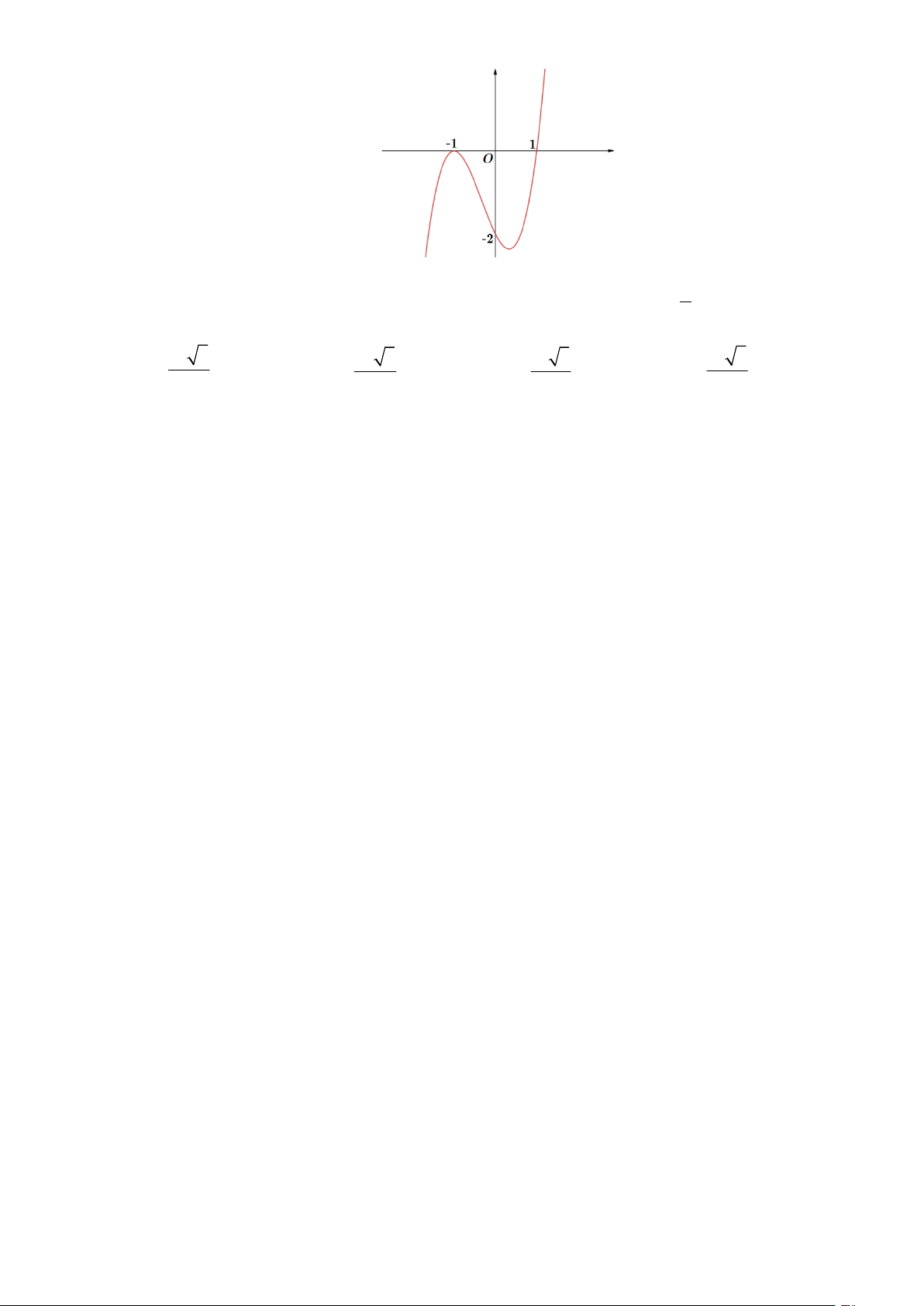
Preview text:


ĐỀ THI THỬ TN THPT LẦN 2 NĂM 2022
TRƯỜNG THPT CHUYÊN BIÊN HÒA - HÀ NAM Câu 1.
Trên mặt phẳng tọa độ Oxy , số phức z  2
  3i được biểu diễn bởi điểm A. P 2;3 . B. N  3  ;2 . C. Q  2  ;3 . D. M 3; 2   . Câu 2. Tìm công thức sai? A. cos d  sin  . B.   .  x x x C sin d cos  x x x C x a C. d   . D. x a dx
C 0  a  1 .  x x e x e C    ln a Câu 3.
Trong không gian Oxyz , viết phương trình mặt phẳng P đi qua điểm M  1  ;0;3 và có 
véctơ pháp tuyến n  1;3; 4   .
A. x  3y  4z 13  0 . B. x  3y  4z 13  0 . C. x  3y  4z  3  0 . D. x  3y  4z 13  0 . Câu 4.
Có bao nhiêu số có ba chữ số khác nhau được tạo thành từ các chữ số 1, 2, 3, 4, 5? A. 3 A . B. P . C. 3 C . D. P . 5 5 5 3 1 Câu 5.
Tìm công bội q của một cấp số nhân u u u  16 n  có và . 1 2 6 1 1 A. q  . B. q  2  . C. q  2 . D. q   . 2 2 Câu 6.
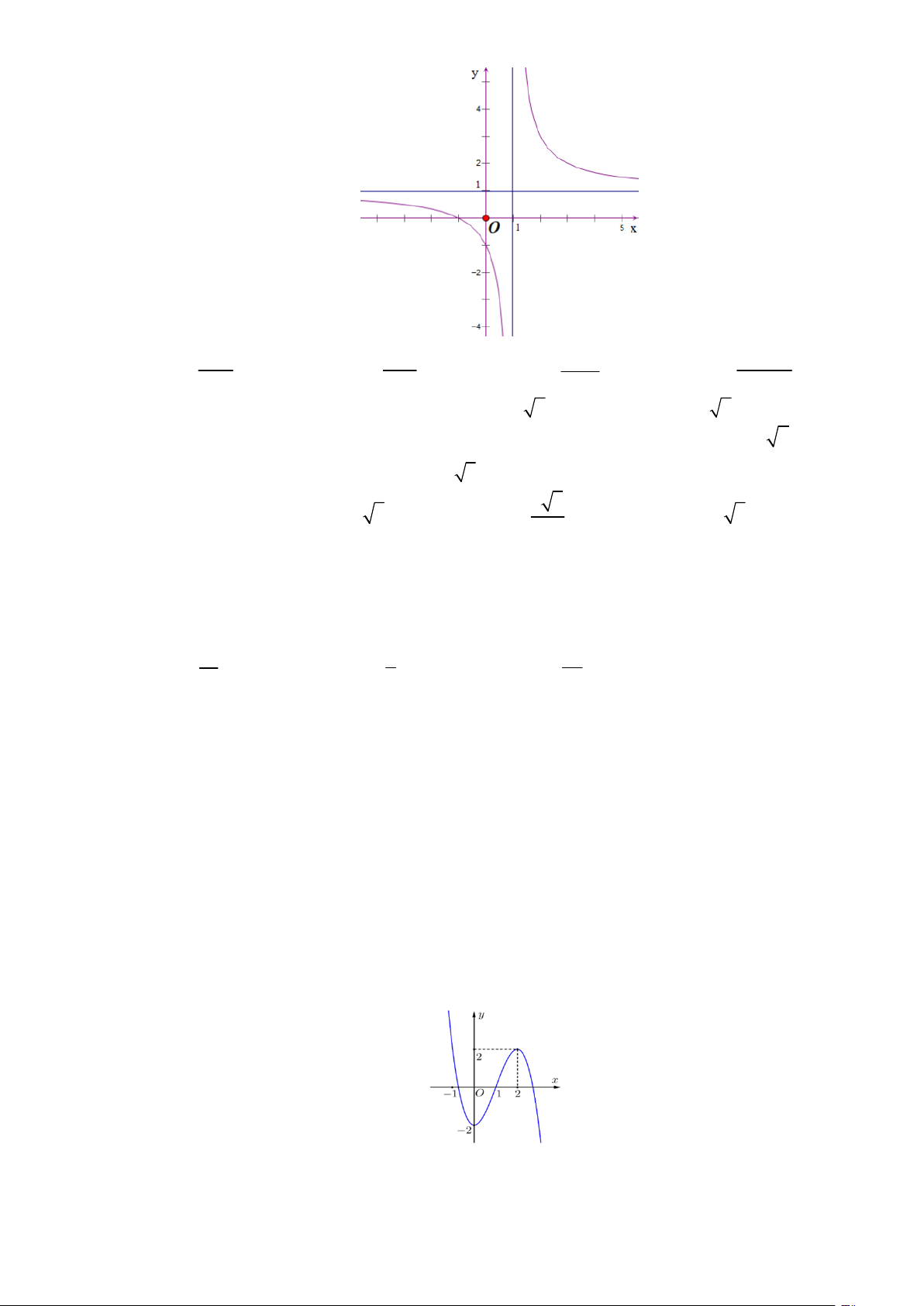
Đồ thị hàm số nào sau đây cắt trục tung tại điểm có tung độ âm -2x +3 3x + 4 4x +1 2x -3 A. y = . B. y = . C. y = . D. y = . x +1 x -1 x + 2 3x -1 Câu 7.
Trong không gian Oxyz , cho mặt cầu có phương trình 2 2 2
x + y + z -2x + 4y +6z +5 = 0 .
Hãy xác định tâm I, bán kính R của mặt cầu A. I (-1;2; ) 3 , R = 3. B. I (1;-2;- ) 3 , R = 3. C. I (-1;2; ) 3 , R = 9 D. I (-1;2; ) 3 , R = 14 x + 2 Câu 8.
Đường thẳng nào sau đây là tiệm cận ngang của đồ thị hàm số y = ? x -2 A. x = 2 B. x = -2. C. y =1. D. y = -1 1 3 3 Câu 9. Cho f
 xdx  1  ; f
 xdx  5.. Tính f xdx  0 1 0 A. 1. B. 4. C. 6 . D. 5.
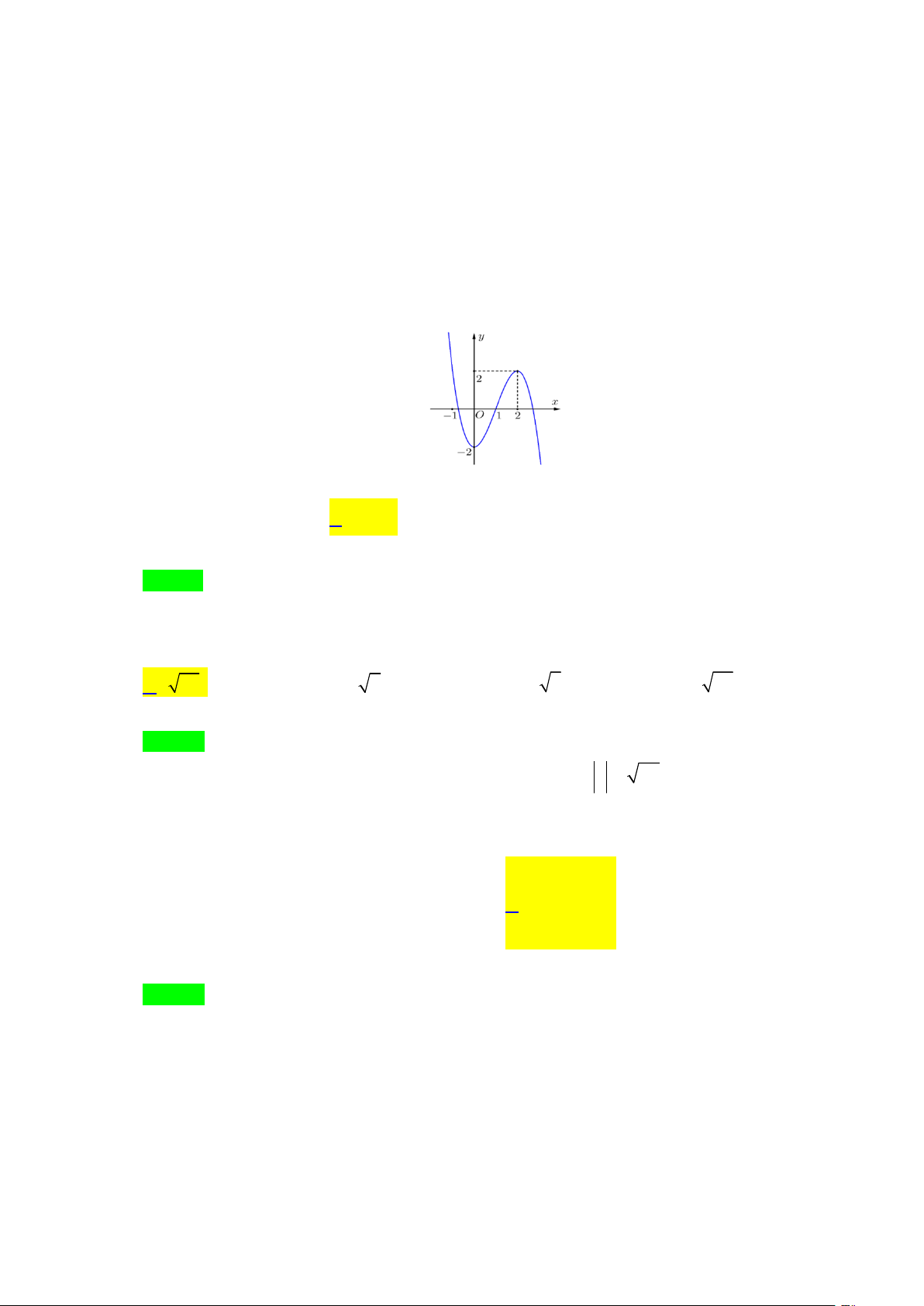
Câu 10. Đồ thị hàm số nào dưới đây có dạng như hình vẽ x 1 x 1 x  2 2  x 1 A. y  . B. y  . C. y  . D. y  . x 1 x 1 x 1 x 1
Câu 11. Diện tích toàn phần của khối trụ có chiều cao h  3 6 và bán kính đáy R  6 ?
A. S  24.
B. S  48.
C. S  36.
D. S  24 6. tp tp tp tp
Câu 12. Cho khối lăng trụ có diện tích đáy bằng 2 3 , chiều cao bằng 4 . Tính thể tích khối lăng trụ ? 8 3 A. 48 . B. 8 3 . C. . D. 12 3 . 3
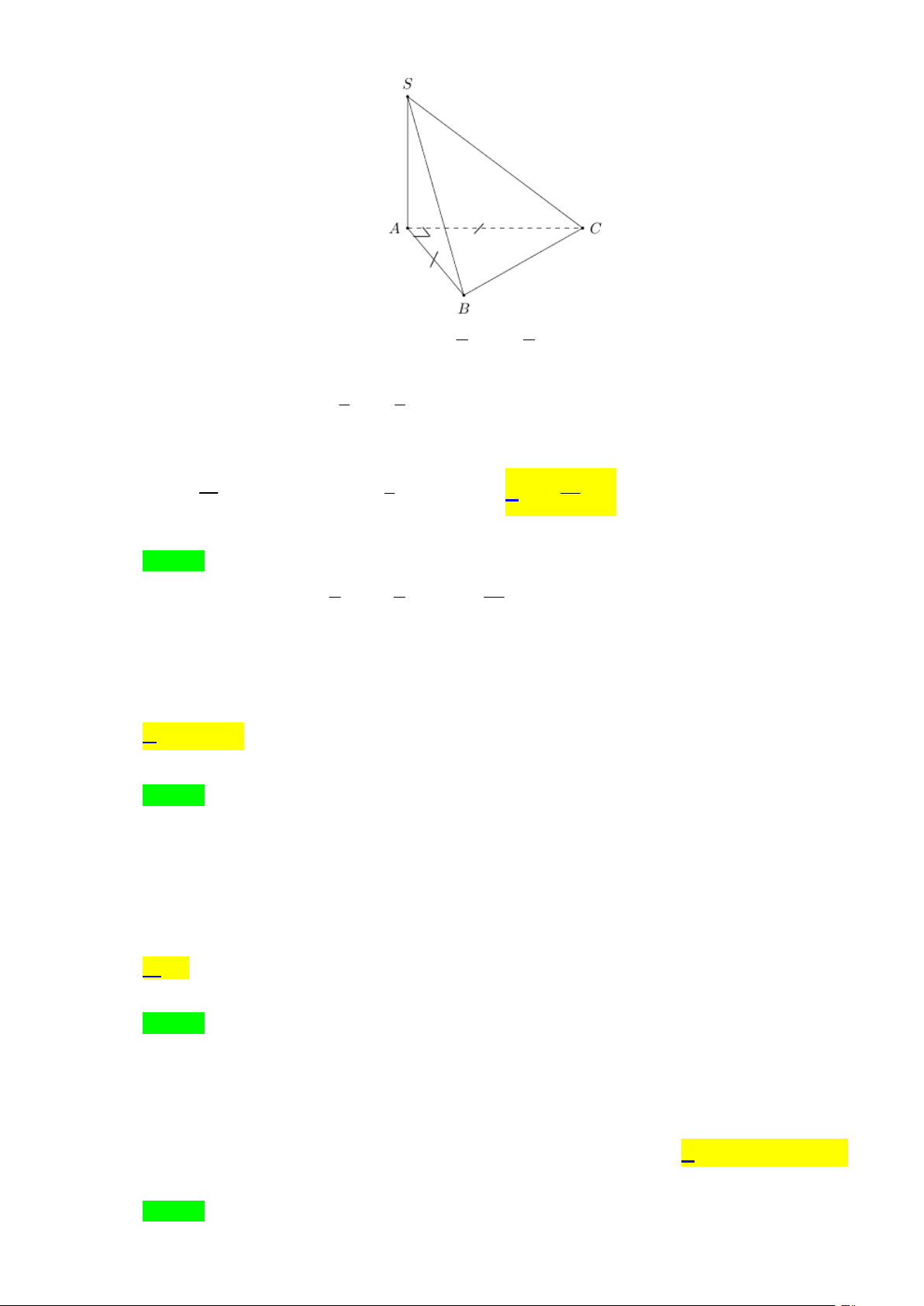
Câu 13. Cho khối chóp S.ABC có đáy ABC là tam giác vuông cân tại A , AB  2 , SA  12 ,
SA   ABC . Tính thể tích khối chóp S.ABC A. 8 . B. 16 . C. 24 . D. 6 .
Câu 14. Tính thể tích V của khối cầu có bán kính R  2b ? 16 8 32 A. 3 V b . B. 3 V b . C. 3 V b . D. 3 V  16b . 3 3 3 x 1 2t
Câu 15. Trong không gian Oxyz , đường thẳng  : y  3 
có một véctơ chỉ phương là z  23tA. 2;0; 3   . B. 1; 3  ;2. C.  2  ;0; 3   . D.  2  ; 3  ;3 . 2 2 2 Câu 16. Biết f
 xdx  2 và g
 xdx  6  , khi đó  f
  x gxdx bằng;  1 1 1 A. 8 . B. 4  . C. 4 . D. 8  .
Câu 17. Trong không gian Oxyz , viết phương trình mặt phẳng P đi qua 2 điểm M  1  ;0;3, N 1; 1  ; 2
  đồng thời vuông góc với mặt phẳng Q : 2x y z  2022  0 ?
A. x  3y z  4  0 . B. x  3y z  2  0 .C. x  3y z  2  0 . D. x  3y z  2  0 .
Câu 18. Cho hàm số y f x có đồ thị như hình vẽ.
Hàm số đồng biến trên khoảng nào dưới đây? A. 2;2 . B. 0;2 . C. ;0 . D. 2;.          
Câu 19. Trong không gian Oxyz , cho a  2 j  3k,b  4i j k . Tính độ dài của v  2a b ? A. 74 . B. 3 6 . C. 5 2 . D. 42 .
Câu 20. Trong không gian Oxyz, viết phương trình đường thẳng  đi qua M  1  ;1;0 và vuông góc
với mặt phẳng Q : x  4y z  2  0 ? x  1 tx  1 t
x  1 t
x  1 t    
A. y  4 t .
B. y  1 4t .
C. y  1 4t .
D. y  1 4t . z      1 z    t z    t z   t
Câu 21. Chọn ngẫu nhiên hai số khác nhau từ 15 số nguyên dương đầu tiên. Xác suất để chọn được hai
số có tổng là một số lẻ là: 1 8 4 1 A. . B. . C. . D. . 7 15 15 14
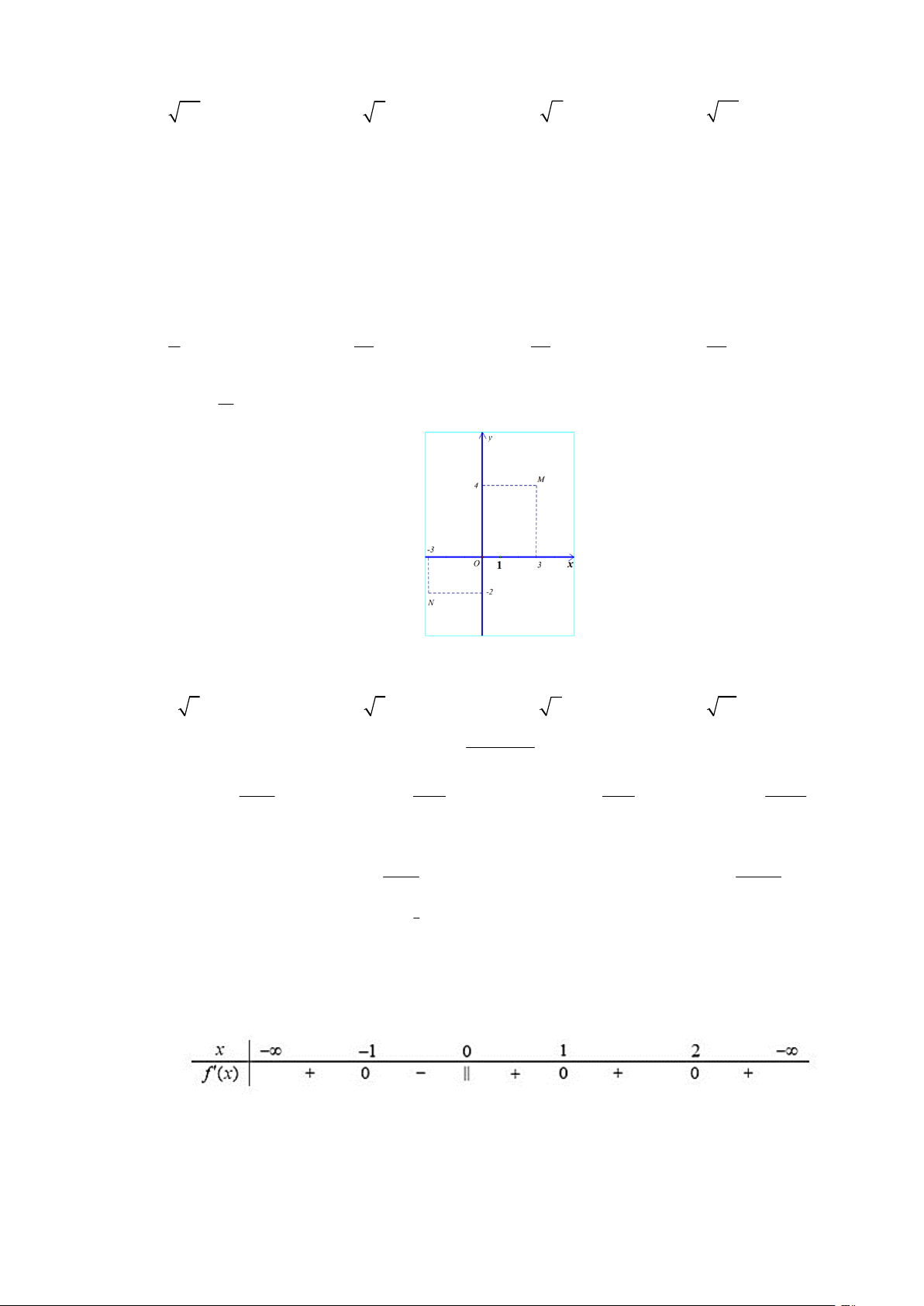
Câu 22. Gọi z , z lần lượt có điểm biểu diễn là M và N trên mặt phẳng phức ở hình bên. Tìm số phức 1 2
w  z  3z ? 1 2
A. w  12 10i .
B. w  12  2i .
C. w  10  6i .
D. w  9  2i .
Câu 23. Cho số phức z thỏa mãn 2  iz  8  i . Môđun của z  5  2i bằng A. 2 5 . B. 4 5 . C. 3 2 . D. 10 . cos x
Câu 24. Họ nguyên hàm F x của hàm số f x  là: 2 1 cos x x 1
A. F x cos  
C . B. F x 1 
C . C. F x 1  
C . D. F x   C . sinx sinx sinx 2 sin x
Câu 25. Trong các hàm số sau, hàm số nào đồng biến trên khoảng 1; ?  x x A. 3
y  x x  3 1 . B. y  . C. 4 2
y x x  2 3 . D. y  . x 1 2x  3
Câu 26. Tập xác định của hàm số y   x  13 1 là: A. 0;   . B. 1;  . C.  . D. 1; .
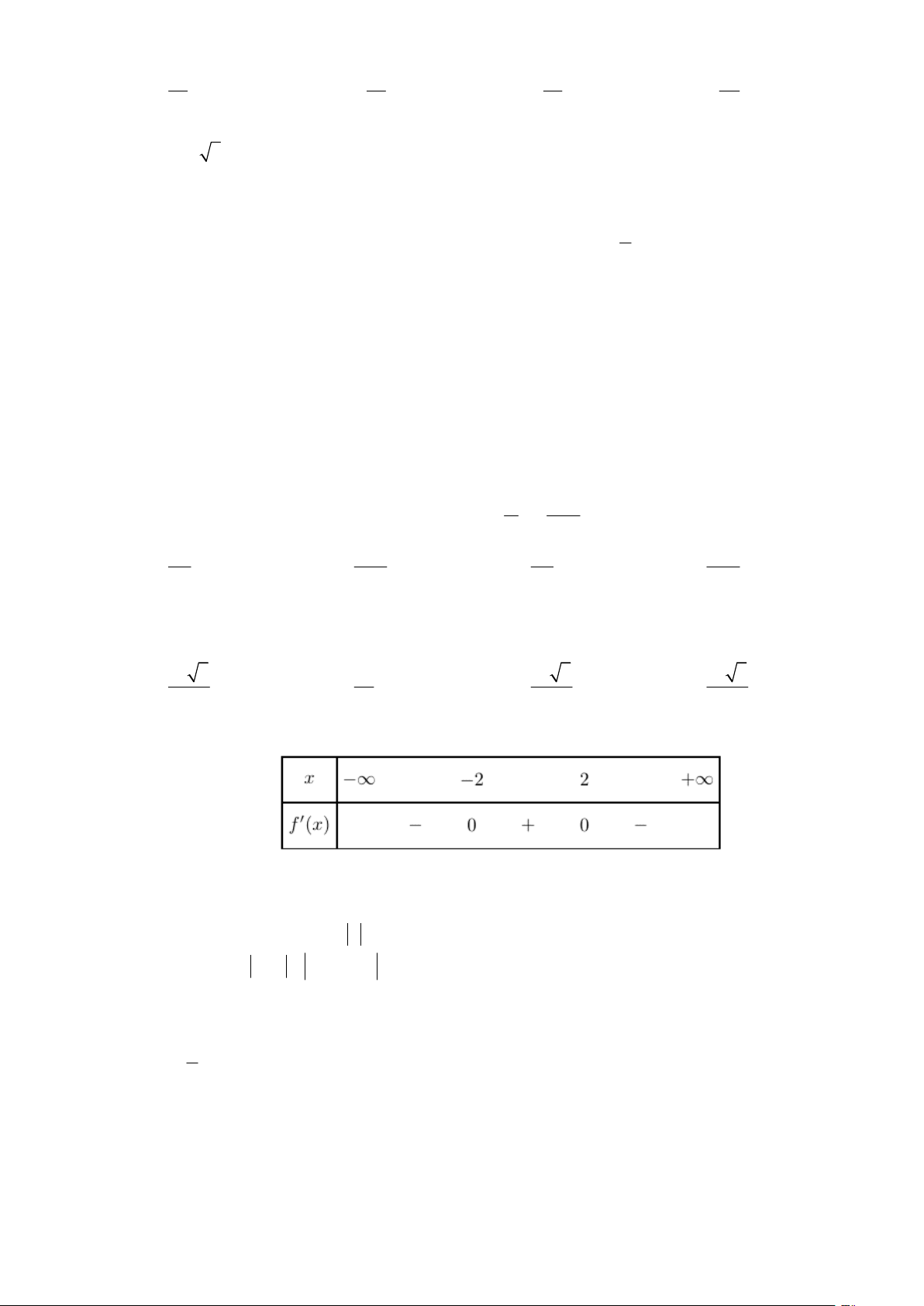
Câu 27. Cho hàm số f (x) liên tục trên  và có bảng xét dấu đạo hàm f (x) như sau:
Hàm số f (x) có bao nhiêu điểm cực trị? A. 2 . B. 4 . C. 1. D. 3 .
Câu 28. Tính đạo hàm của hàm số y  log (2x 1) ? 2 1 2 2 1 A. y '  . B. y '  . C. y '  . D. y '  . (2x 1) ln 2 (2x 1) ln 2 2x 1 2x 1
Câu 29. Cho hai số phức z  (x y  3)  (2y 1)i , z '  2x  (2x y  5)i . Ta có z z ' khi: 5 4
A. x   ; y  .
B. x  1; y  3 .
C. x  1; y  5 2 .
D. x  ; y  0 . 3 3 3 2  1 x x
Câu 30. Tìm tập nghiệm của bất phương trình x4  2    2  A.  2  ; . B.  ;  2
  2; . C. 2; . D.  2  ;2 .
Câu 31. Gọi x , x là hai nghiệm của phương trình log  2
x x 1  3 x x 2  khi đó bằng: 1 2 1 2 A. 1  . B. 3 . C. 2  . D. 2 .
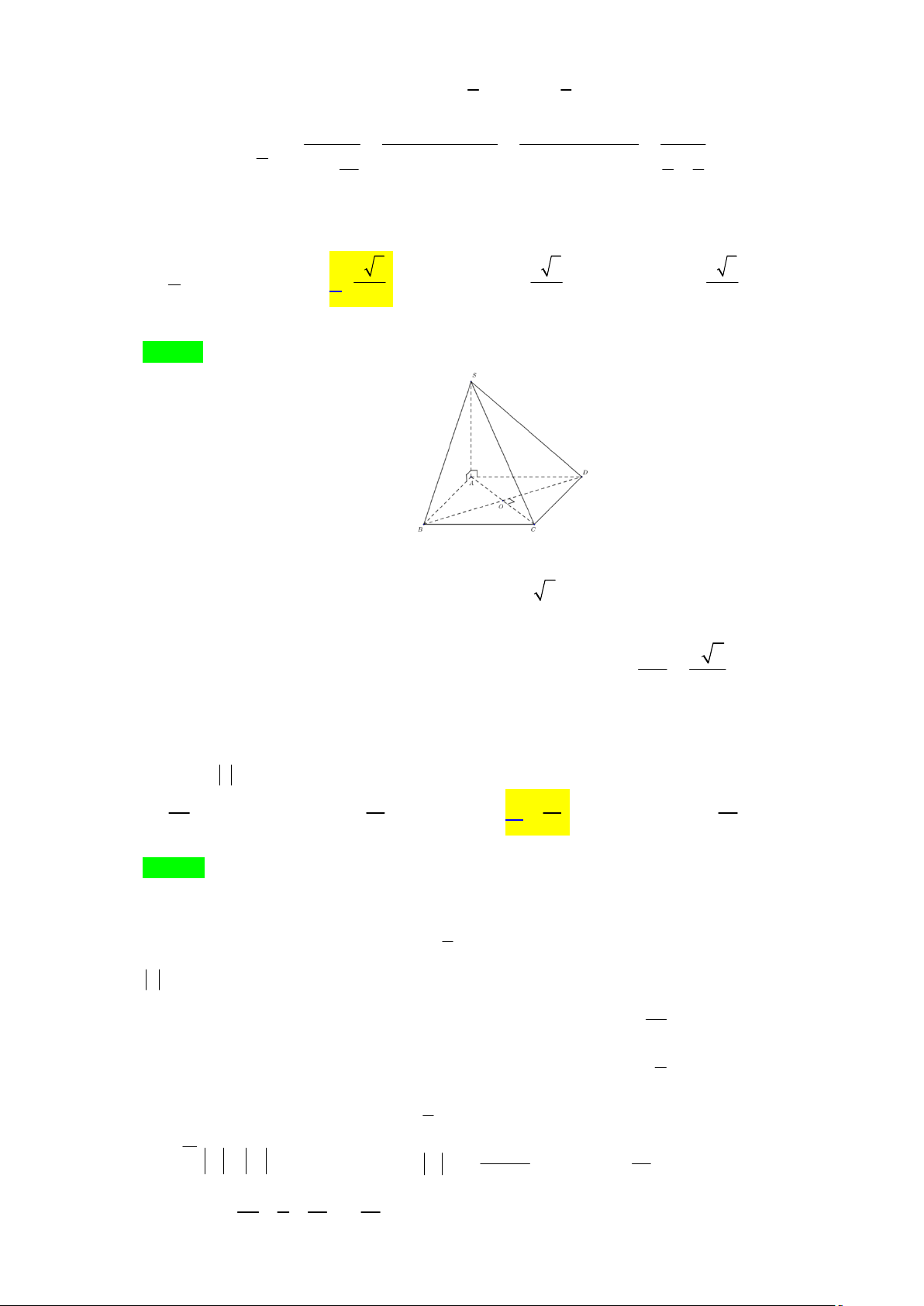
Câu 32. Cho hình chóp tứ giác S.ABCD có đáy là hình chữ nhật. Biết AB a, AD  2a , các cạnh bên
bằng nhau và bằng a 2 . Tính góc giữa hai đường thẳng BC, SA? A. 90 . B. 120 . C. 60 . D. 45 .
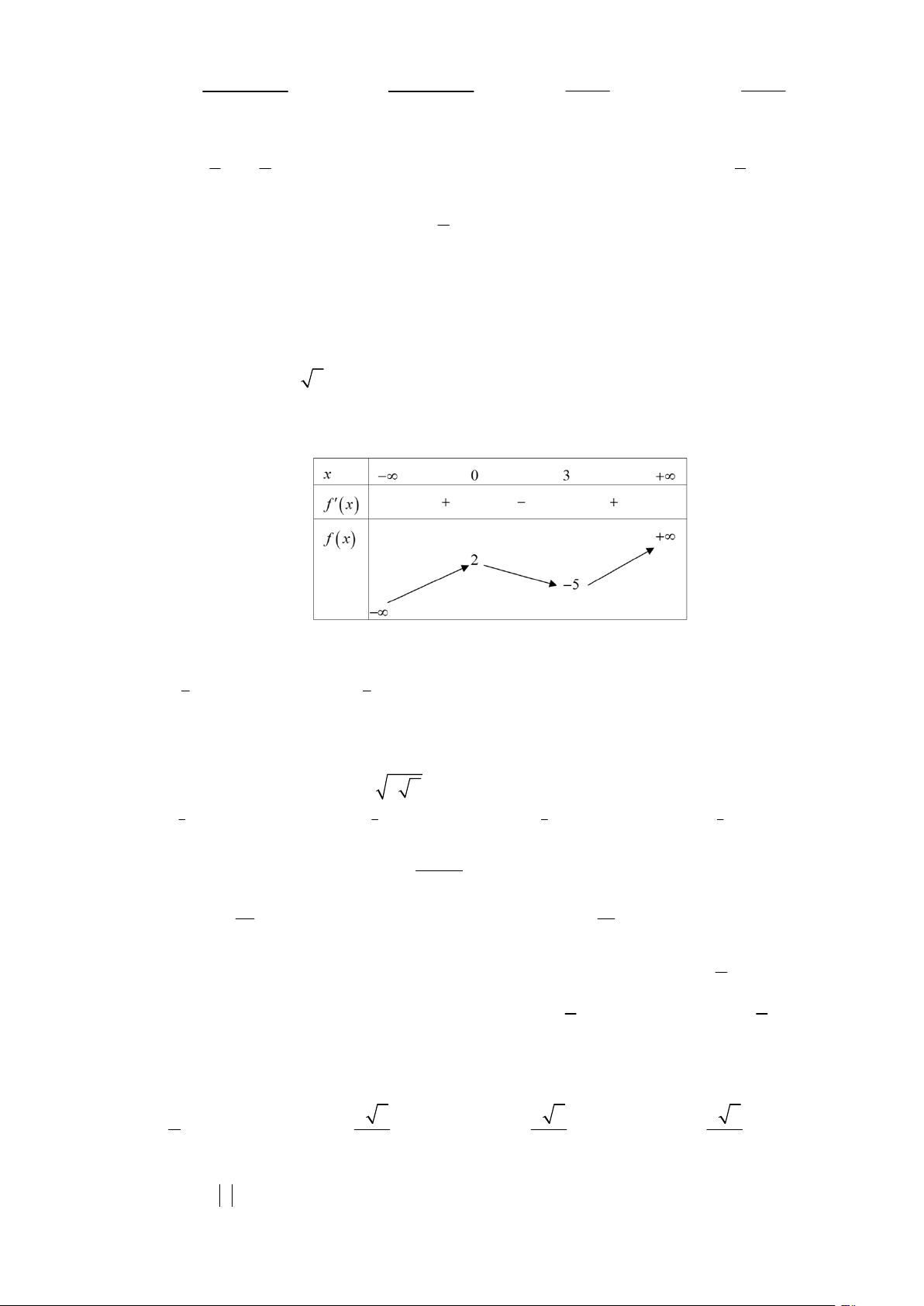
Câu 33. Cho hàm số y f x có bảng biến thiên như sau:
Giá trị cực đại của hàm số đã cho bằng A. 0 . B. 5 . C. 3 . D. 2 . 2 2 Câu 34. Cho f
 xdx  5. Tính I  3f
  x2sin xdx?  0 0 A. I  13 . B. I  17 . C. I  7 . D. I  3 .
Câu 35. Với a là số thực dương tùy ý, 3 a a bằng 3 2 - 2 4 A. 2 a . B. 3 a . C. 3 a . D. 3 a . 2 x +3
Câu 36. Tìm giá trị lớn nhất của hàm số y = trên [2;4] là x -1 19 11 A. max y = . B. max y = 6 . C. max y = . D. max y = 7 . [2;4] 3 [2;4] [2;4] 3 [2;4]
Câu 37. Cho log x = 2 , log x = 3 với a , b là các số thực lớn hơn 1. Tính P = log x . a b a 2 b A. P = 6 . B. P = - 1 6 . C. P = 1 . D. P = - . 6 6
Câu 38. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , SA ^(ABCD). Tính khoảng
cách từ điểm B đến mặt phẳng (SAC). a a 2 a 2 a 2 A. . B. . C. . D. . 2 2 3 4
Câu 39. Gọi T là tổng các giá trị thực của m để phương trình 2
4z  6z 1 2m  0 có nghiệm phức
thoả mãn z  2 . Tính T ? 15 17 A. . B.  19 . C.  29 . D.  . 2 2 2 2
Câu 40. Có bao nhiêu giá trị nguyên dương của tham số m để tập nghiệm của bất phương trình  x2 3
 33x  2m  0 chứa không quá 9 số nguyên. A. 3281. B. 3283 . C. 3280 . D. 3279 .
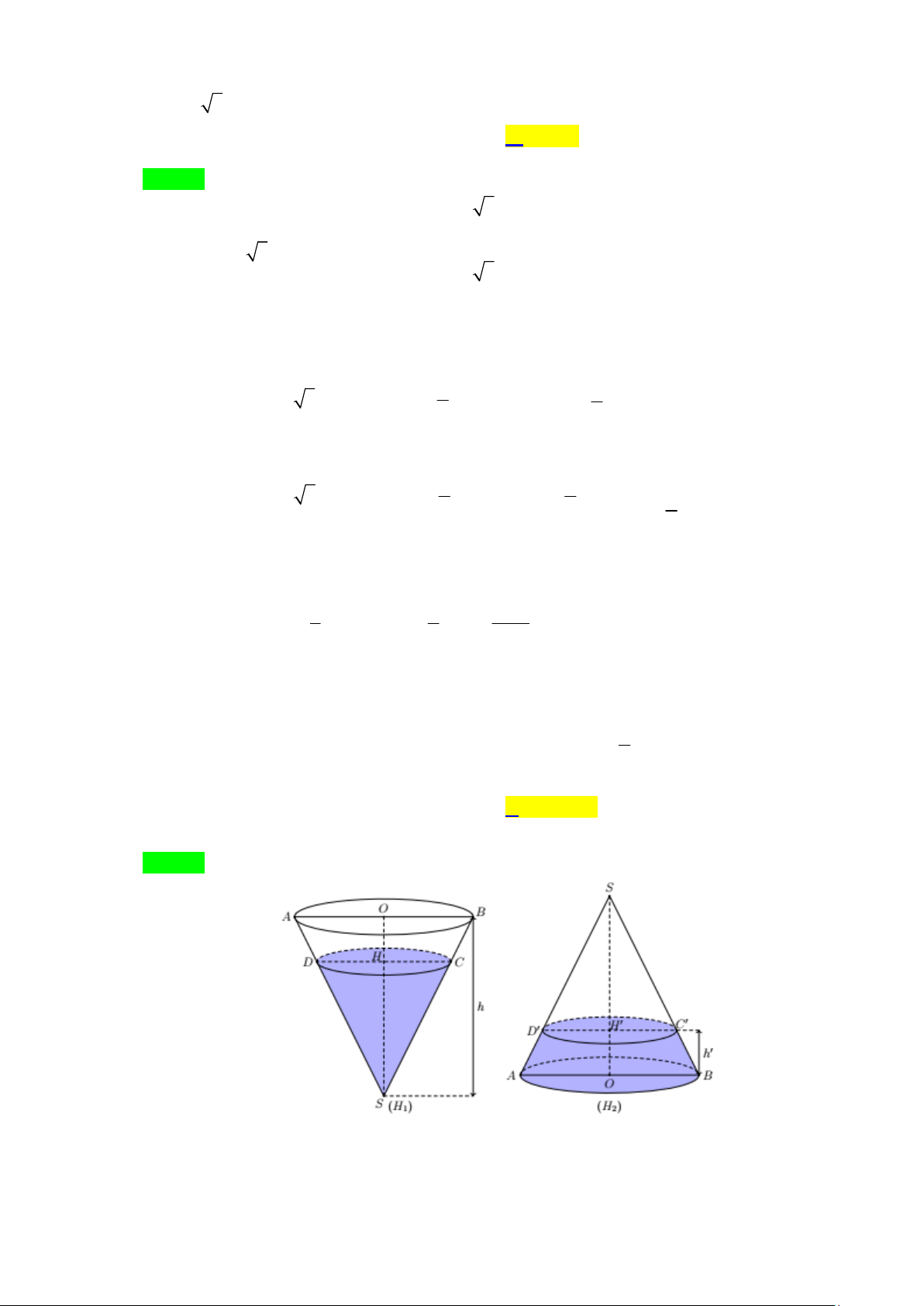
Câu 41. Một khối đồ chơi có dạng khối nón có chiều cao h  40 cm trong đó chứa một lượng nước. Nếu 3
đặt khối đồ chơi theo hình H1 thì chiều cao của nước bằng chiều cao khối nón. Hỏi nếu 4
đặt khối đồ chơi theo hình H h 2  thì chiều cao
của nước gần với giá trị nào sau đây? A. 8.98 cm. B. 7.23 cm. C. 6.68 cm. D. 6.86 cm. x  1 2t
Câu 42. Trong không gian Oxyz , cho đường thẳng  : y 1
và (Q) : x  2y z  2  0 . Gọi   là z  2t
đường thẳng đối xứng với  qua (Q) . Hỏi 
 đi qua điểm nào sau đây? A. (2;0; 3  ) . B. ( 2  ; 1  ; 3  ) . C. (2; 5  ;3) . D. ( 1  ; 1  ;3) .
Câu 43. Biết rằng xsin x là một nguyên hàm của hàm số f x trên khoảng  ;
  . Gọi F x là   3 
một nguyên hàm của 2 f  xcos x thỏa mãn F
, giá trị của F() bằng:    2  4 5 3  3 5  A. . B. . C. . D. . 2 2 2 2
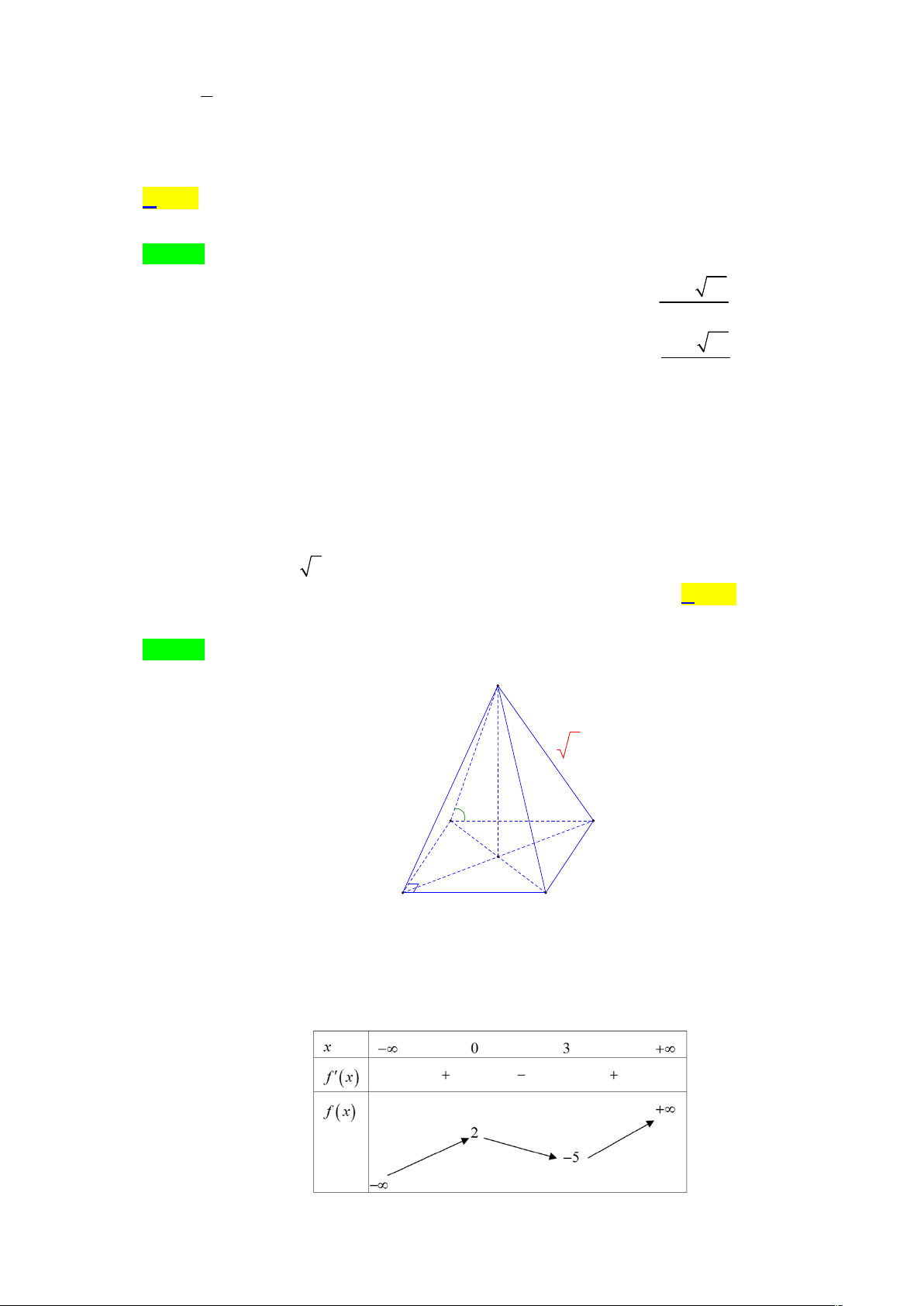
Câu 44. Cho hình chóp S.ABCD , có SA   ABCD , đáy là hình thoi cạnh a , 
BAD  60 , góc giữa SA
và SBD bằng 60 . Gọi G là trọng tâm tam giác SCD . Tính thể tích khối tứ diện SAGB? 3 a 3 3 a 3 a 3 3 a 3 A. . B. . C. . D. . 13 6 72 36
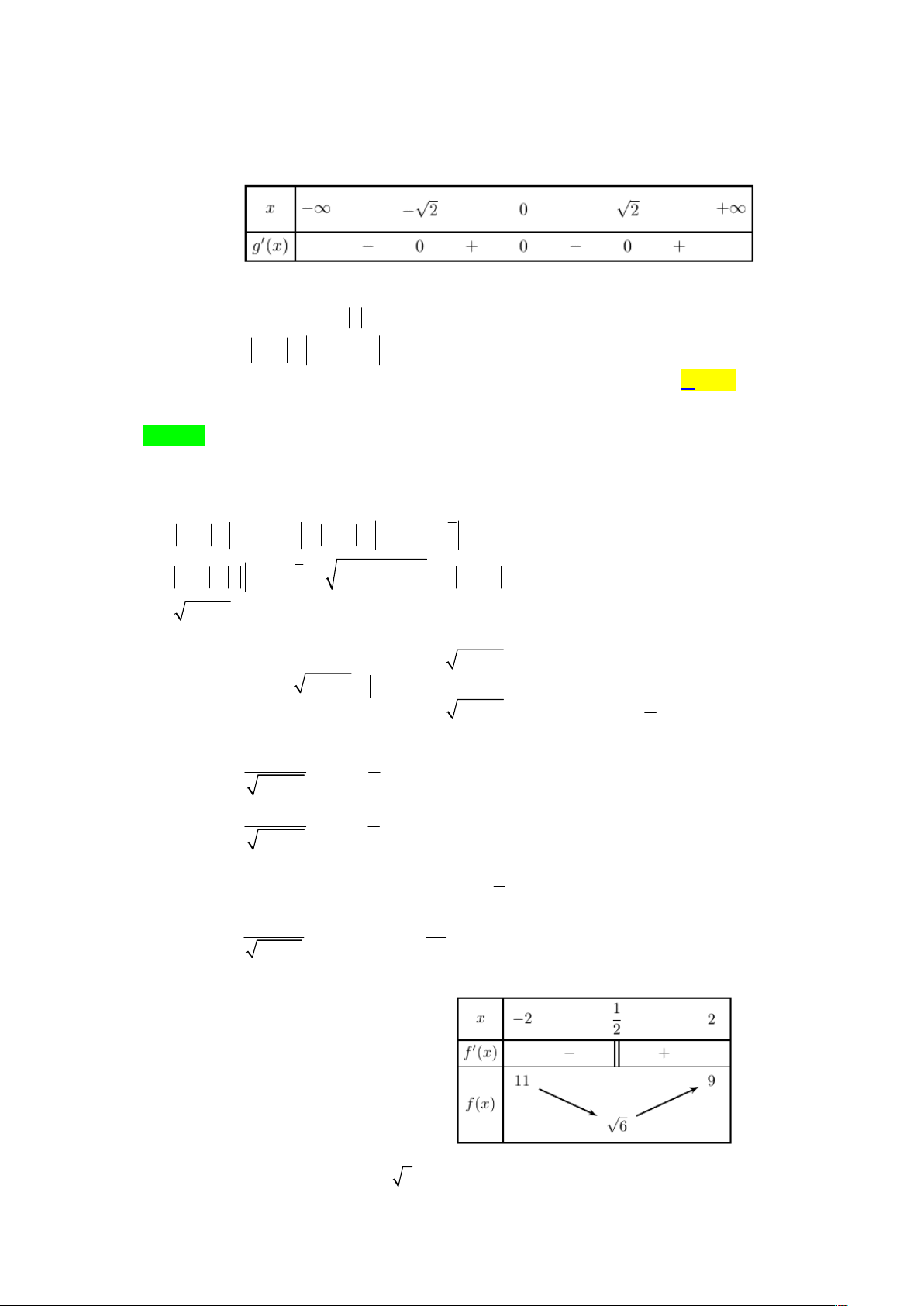
Câu 45. Cho hàm số y f x có đạo hàm liên tục trên  và bảng xét dấu đạo hàm như sau
Số điểm cực tiểu của hàm số g x  f  4 2
x x   6 4 2 3 4
6  2x  3x 12x là A. 4 . B. 3 . C. 0 . D. 2 .
Câu 46. Cho số phức z thỏa mãn z  2 . Gọi M , m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của biểu thức 2
T z 1  z z  4 . Tính giá trị của 2 2 M m A. 45 . B. 384 . C. 85 . D. 115 .
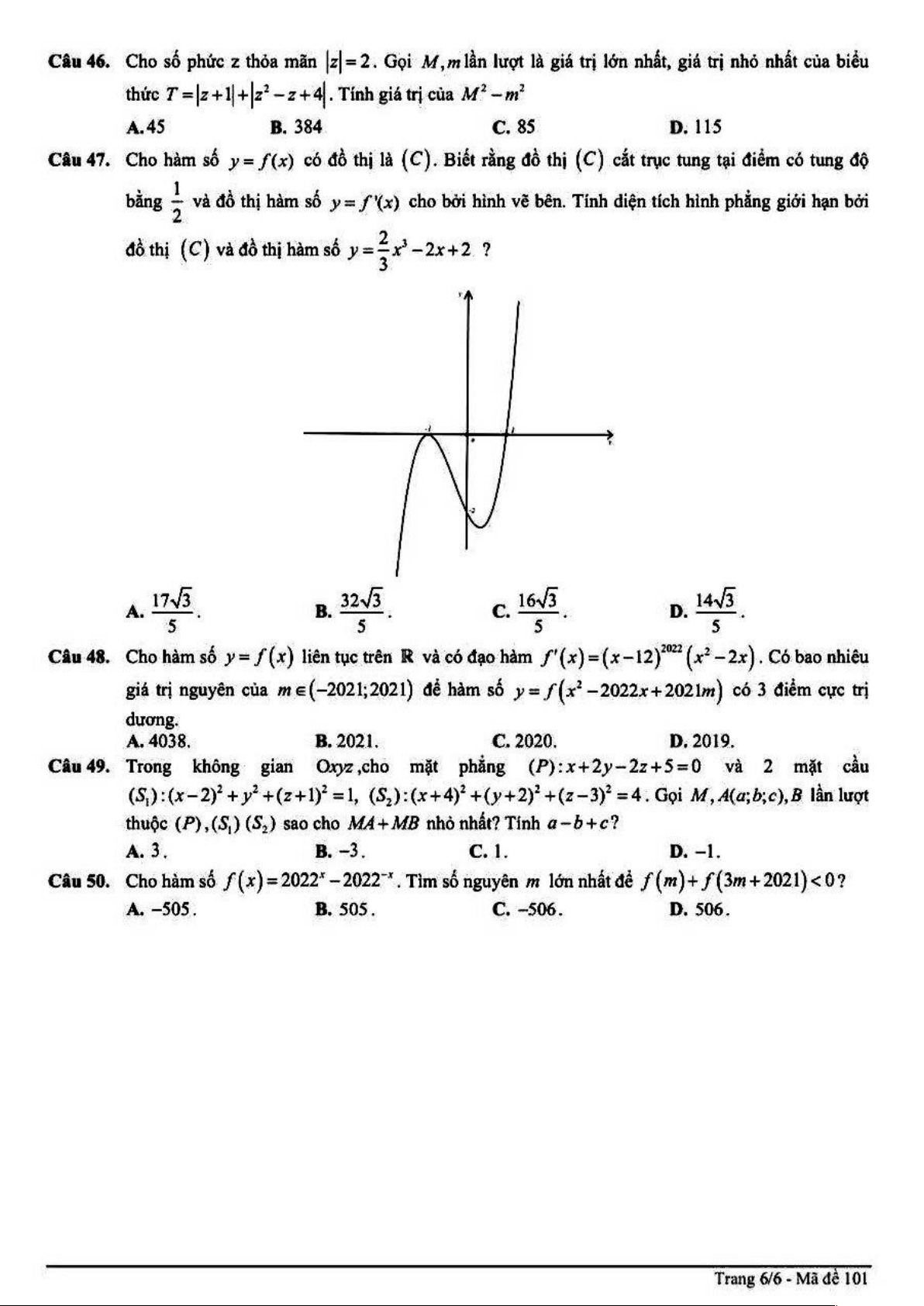
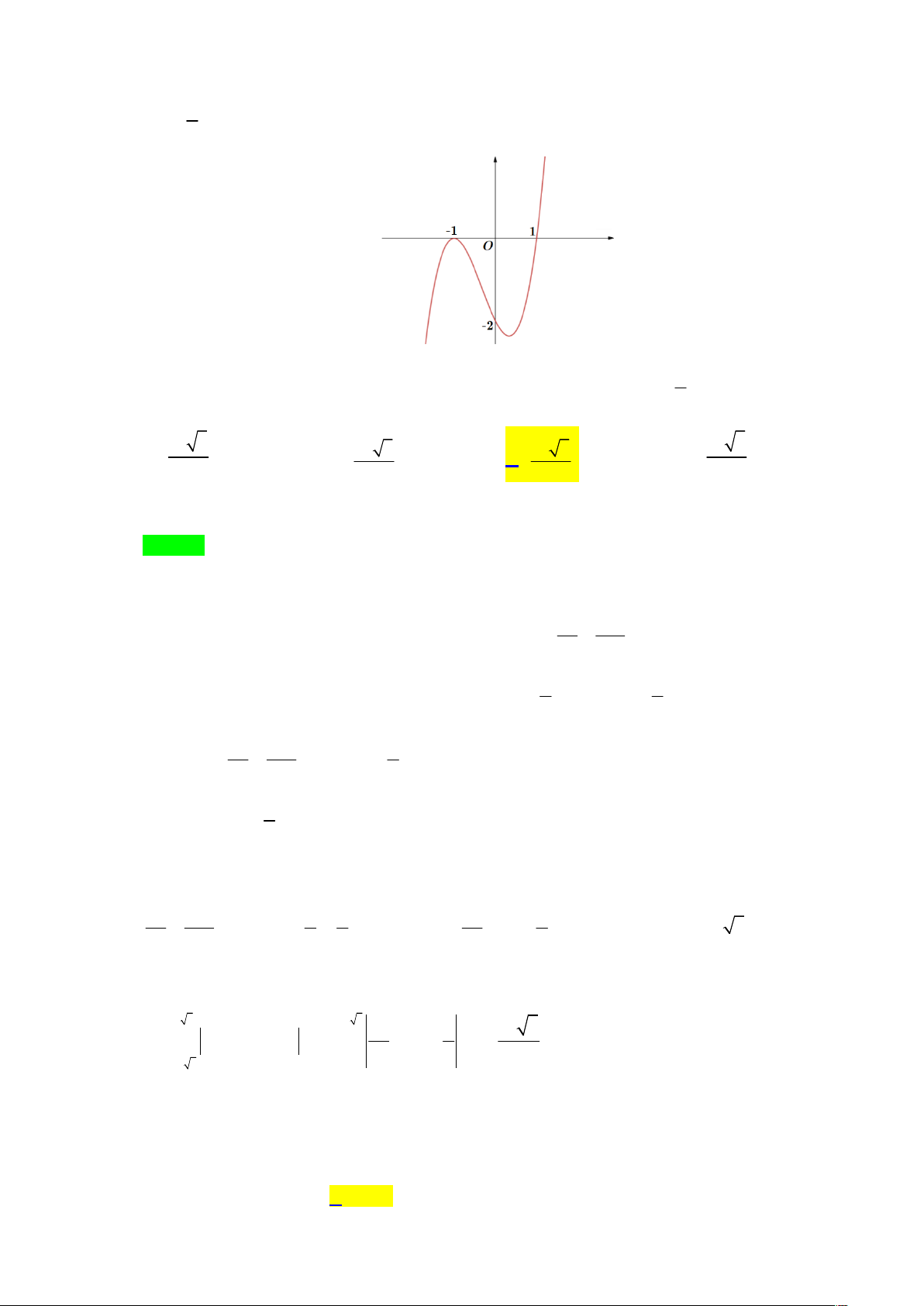
Câu 47. Cho hàm số y f (x) có đồ thị C . Biết rằng đồ thị C cắt trục tung tại điểm có tung độ 1
bằng và đồ thị hàm số y f  x cho bởi hình vẽ bên. 2 2
Tính diện tích hình phẳng giới hạn bởi đồ thị C và đồ thị hàm số 3
y x  2x  2 ? 3 17 3 32 3 16 3 14 3 A. . B. . C. . D. . 5 5 5 5
Câu 48. Cho hàm số y f x liên tục trên  và có đạo hàm f  x   x  2022  2 12
x  2x có bao
nhiêu giá trị nguyên của m   2  021;202 
1 để hàm số y f  2
x  2022x  2021m có ba điểm cực trị dương. A. 4038 . B. 2021. C. 2020 . D. 2019
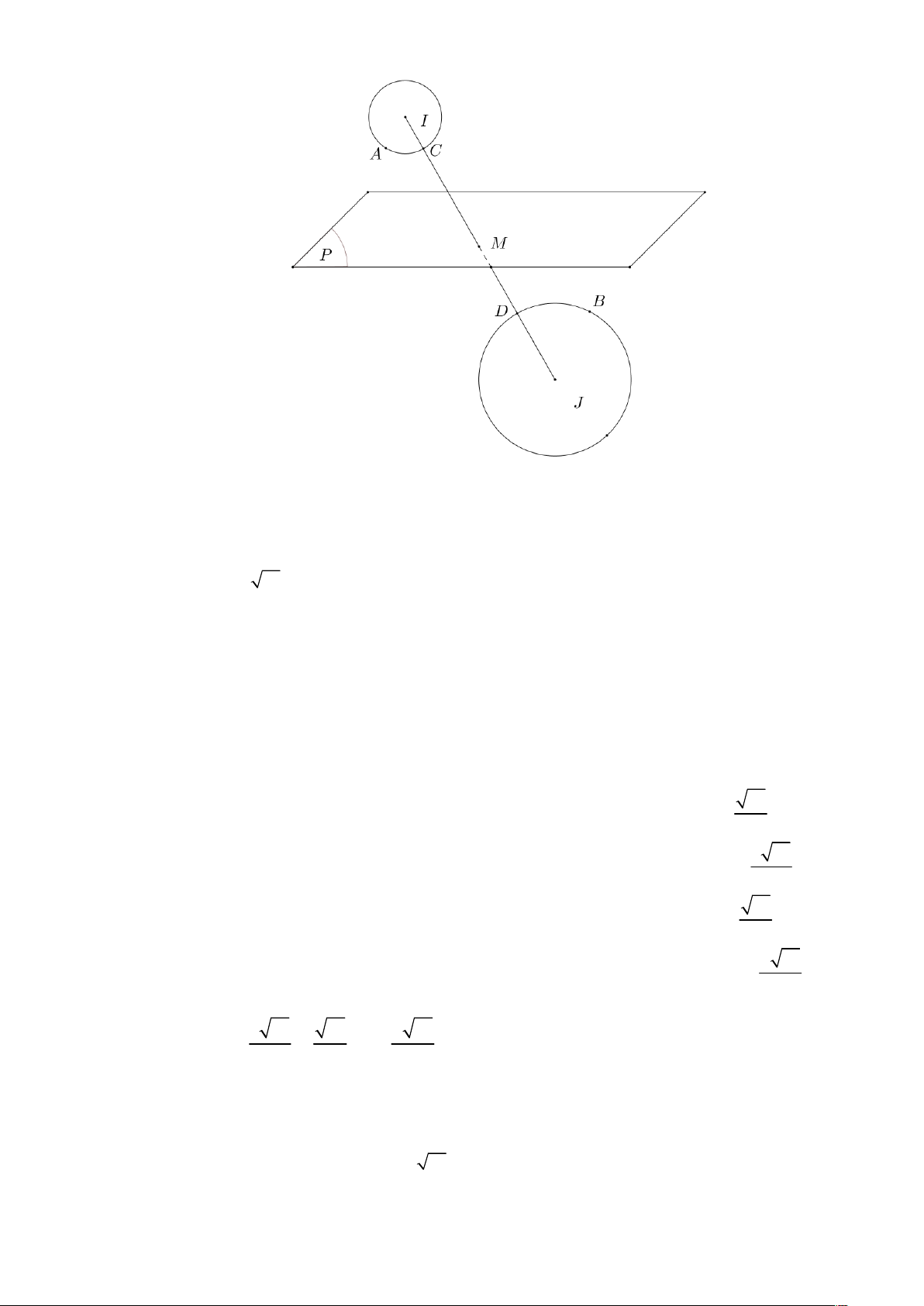
Câu 49. Trong không gian Oxyz , cho mặt phẳng P : x  2y  2z  5  0 và 2 mặt cầu
S : x  2  y z 1 1 S : x  4  y  2  z 3  4 M , A ; a ; b c, B 2   2  2  2 1   2  2 2 ; . Gọi
lần lượt thuộc P,S , S MA MB
a b c 1   2  sao cho nhỏ nhất? Tính ? A. 3 . B. 3 . C. 1. D. 1  .
Câu 50. Cho hàm số   2022x 2022 x f x   
. Tìm số nguyên m lớn nhất để f m  f 3m  202  1  0 ? A. 505 . B. 505 . C. 506 . D. 506 .
-------------------------- HẾT -------------------------- ĐÁP ÁN 1 2 3 4 5 6 7 8
9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
C B B A C B B C B B B B A C A A D B A C B B A C C
26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50
B A B C D A D D A C D B B C C C C D D D D C B C C LỜI GIẢI CHI TIẾT
Câu 1. Trên mặt phẳng tọa độ Oxy , số phức z  2
  3i được biểu diễn bởi điểm A. P 2;3 . B. N  3  ;2 . C. Q  2  ;3 . D. M 3; 2   . Lời giải Chọn C Số phúc z  2
  3i được biểu diễn bởi điểm Q  2  ;3 .
Câu 2. Tìm công thức sai? A. cos d  sin  . B.   .  x x x C sin d cos  x x x C x a C. d   . D. x a dx
C 0  a  1 .  x x e x e C    ln a Lời giải Chọn B
Vì sin d   cos  nên phương án B sai.  x x x C
Câu 3. Trong không gian Oxyz , viết phương trình mặt phẳng P đi qua điểm M  1  ;0;3 và có véctơ 
pháp tuyến n  1;3; 4   .
A. x  3y  4z 13  0 . B. x  3y  4z 13  0 . C. x  3y  4z  3  0 . D. x  3y  4z 13  0 . Lời giải Chọn B
Phương trình mặt phẳng P cần lập là 1 x  
1  3 y  0  4 z  3  0  x  3y  4z 13  0 .
Câu 4. Có bao nhiêu số có ba chữ số khác nhau được tạo thành từ các chữ số 1, 2, 3, 4, 5? A. 3 A . B. P . C. 3 C . D. P . 5 5 5 3 Lời giải Chọn A
Số các số có ba chữ số khác nhau được tạo thành từ các chữ số 1, 2, 3, 4, 5 là 3 A . 5 1
Câu 5. Tìm công bội q của một cấp số nhân u u u  16 n  có và . 1 2 6 1 1 A. q  . B. q  2  . C. q  2 . D. q   . 2 2 Lời giải Chọn C u Ta có 5 5 6
u u .q q   32  q  2 . 6 1 u1
Câu 6. Đồ thị hàm số nào sau đây cắt trục tung tại điểm có tung độ âm -2x +3 3x + 4 4x +1 2x -3 A. y = . B. y = . C. y = . D. y = . x +1 x -1 x + 2 3x -1 Lời giải Chọn B ax +b b
Đồ thị hàm số y =
cắt trục tung tại điểm có tung độ âm khi < 0 . cx + d d 3x + 4
Do đó đồ thị hàm số y =
cắt trục tung tại điểm có tung độ âm. x -1
Câu 7. Trong không gian Oxyz , cho mặt cầu có phương trình 2 2 2
x + y + z -2x + 4y +6z +5 = 0 . Hãy
xác định tâm I, bán kính R của mặt cầu A. I (-1;2; ) 3 , R = 3. B. I (1;-2;- ) 3 , R = 3. C. I (-1;2; ) 3 , R = 9 D. I (-1;2; ) 3 , R = 14 Lời giải Chọn B Mặt cầu 2 2 2
x + y + z -2x + 4y +6z +5 = 0 có tâm I (1;-2;- ) 3 và bán kính R = ( )2 +(- )2 +(- )2 1 2 3 -5 = 3. x + 2
Câu 8. Đường thẳng nào sau đây là tiệm cận ngang của đồ thị hàm số y = ? x -2 A. x = 2 B. x = -2. C. y =1. D. y = -1 Lời giải Chọn C
Ta có lim y =1 nên đồ thị hàm số có tiệm cận ngang y =1. x®±¥ 1 3 3 Câu 9. Cho f
 xdx  1  ; f
 xdx  5.. Tính f  xdx 0 1 0 A.1. B. 4. C. 6 . D. 5 . Lời giải Chọn B 3 1 3 Ta có f
ò (x)dx = f
ò (x)dx+ f
ò (x)dx =-1+5= 4. 0 0 1
Câu 10. Đồ thị hàm số nào dưới đây có dạng như hình vẽ x  1 x 1 x  2 2x 1 A. y  . B. y  . C. y  . D. y  . x  1 x 1 x 1 x 1 Lời giải Chọn B
Đồ thị hàm số có tiệm cận ngang y =1 nên loại đáp án D
Đồ thị hàm số có tiệm cận đứng x = 1 nên loại đáp án A và C
Vậy chọn đáp án B
Câu 11. Diện tích toàn phần của khối trụ có chiều cao h  3 6 và bán kính đáy R  6 ?
A. S  24.
B. S  48.
C. S  36.
D. S  24 6 tp . tp tp tp Lời giải Chọn B
Diện tích toàn phần của hình trụ là S  Rh  R  2 2 2 2
2 . 6.3 6 2 . 6  48 tp .
Câu 12. Cho khối lăng trụ có diện tích đáy bằng 2 3 , chiều cao bằng 4 . Tính thể tích khối lăng trụ ? 8 3 A. 4 8 . B. 8 3 . C. . D. 12 3 . 3 Lời giải Chọn B
Thể tích của khối lăng trụ V Bh  2 3.4  8 3 .
Câu 13. Cho khối chóp S.ABC có đáy A B C là tam giác vuông cân tại A , AB  2 , SA  12 ,
SA   ABC  . Tính thể tích khối chóp S.ABC A. 8 . B. 16. C. 24 . D. 6 . Lời giải Chọn A 1 1
Diện tích  A B C vuông cân tại A là 2 2 S AB  .2  2 2 2 1 1
Thể tích khối chóp là V S.h  .2.12  8 . 3 3
Câu 14. Tính thể tích V của khối cầu có bán kính R  2b ? 16 8 32 A. 3 V b . B. 3 V b . C. 3 V b . D. 3 V 16b . 3 3 3 Lời giải Chọn C 4 4 32
Thể tích khối cầu là V  R .2b3 3 3  b . 3 3 3 x  1 2t
Câu 15. Trong không gian Oxyz , đường thẳng   : y  3 
có một véctơ chỉ phương là z  23tA. 2; 0; 3 . B. 1; 3; 2.
C. 2; 0; 3 . D. 2; 3;3 . Lời giải Chọn A 
Từ phương trình ta có đường thẳng  có một véctơ chỉ phương là u     2;0; 3 .   Do đó u u    
2;0; 3 cũng là một véctơ chỉ phương của đường thẳng  . Câu 16. Biết 2 2 2 f
 xdx  2 và g
 xdx  6 , khi đó  f
  x g x dx bằng;  1 1 1 A. 8 . B. 4 . C. 4 . D.  8 . Lời giải Chọn A Ta có 2  f
  x g x 2  dx f   x 2 dx g
 xdx  2  6  8 . 1 1 1
Câu 17. Trong không gian Oxyz , viết phương trình mặt phẳng P đi qua 2 điểm
M 1; 0;3, N 1; 1; 2 đồng thời vuông góc với mặt phẳng Q  : 2x y z  2022  0 ?
A. x 3y z  4  0 . B. x 3y z  2  0 .C. x  3y z  2  0 . D. x  3y z  2  0 . Lời giải Chọn D
Gọi n là vecto pháp tuyến của mặt phẳng P .
Do mặt phẳng P đi qua 2 điểm M 1;0;3, N 1; 1; 2 đồng thời vuông góc với mặt phẳng  
n MN 2; 1  ; 5  
   
Q : 2x y z  2022  0 nên ta có:  
n  MN;n   4; 1  2;4 . n n 2;1;          1 Q Q  Chọn n  1; 3;1 P  1   là VTPT của . 
Khi đó  P  đi qua M và có VTPT n nên có phương trình: x  3y z  2  0 1
Câu 18. Cho hàm số y f x có đồ thị như hình vẽ.
Hàm số đồng biến trên khoảng nào dưới đây? A. 2;  2 . B. 0;  2 . C. ;0 . D. 2;   . Lời giải Chọn B
Nhìn đồ thị ta thấy hàm số đồng biến trên khoảng 0;  2 .          
Câu 19. Trong không gian Oxyz , cho a  2 j  3k,b  4i j k . Tính độ dài của v  2a b? A. 74 . B. 3 6 . C. 5 2 . D. 42 . Lời giải Chọn A      
Ta có a  0;2;3,b  4;1; 
1  v  2a b  4;3; 7  v  74
Câu 20. Trong không gian Oxyz, viết phương trình đường thẳng  đi qua M 1;1;0 và vuông góc
với mặt phẳng Q  : x  4 y z  2  0 ? x 1tx  1 t
x  1 t
x  1t    
A.y  4 t .
B.y  1 4t .
C.y 1 4t .
D.y 1 4t . z      1 z    t z   t z  t Lời giải Chọn C
Do  vuông góc với mặt phẳng Q  : x  4 y z  2  0 nên ta có vecto chỉ phương của đương 
thẳng  là: u  1;4;1   
x  1 t
Khi đó phương trình  : y 1 4tz   t
Câu 21. Chọn ngẫu nhiên hai số khác nhau từ 15 số nguyên dương đầu tiên. Xác suất để chọn được hai
số có tổng là một số lẻ là: 1 8 4 1 A. . B. . C. . D. . 7 15 15 14 Lời giải Chọn B
Chọn ngẫu nhiên hai số khác nhau từ 15 số nguyên dương đầu tiên, ta có số phần tử của không
gian mẫu là n   2  C  105 . 15
Trong 15 số nguyên dương đầu tiên có 8 số lẻ và 7 số chẵn
Gọi A là biến cố: “chọn được hai số có tổng là một số lẻ”.
Khi đó hai số được chọn có một số là số chẵn và 1 số là số lẻ.
Số phần tử của biến cố A là n A  7.8  56 . n A 56 8
Khi đó P A      . n  105 15
Câu 22. Gọi z , z lần lượt có điểm biểu diễn là M và N trên mặt phẳng phức ở hình bên. Tìm số phức 1 2
w  z  3z ? 1 2
A. w  12  10i .
B. w  12  2i .
C. w  10  6i .
D. w  9  2i . Lời giải Chọn B
Ta có z  3  4i ; z  3   2i . 1 2
Khi đó w  z 3z  3 4i 3 3
 2i 122i 1 2   .
Câu 23. Cho số phức z thỏa mãn 2  iz  8  i . Môđun của z  5  2i bằng A. 2 5 . B. 4 5 . C. 3 2 . D. 10 . Lời giải Chọn Ai Ta có   i 8 2
z  8  i z   3  2i . 2  i
Khi đó z  5  2i  3  2i  5  2i  2  4i .
Vậy z    i   2 2 5 2 2  4  2 5 . cos x
Câu 24. Họ nguyên hàm F x của hàm số f x  là: 2 1 cos x x 1
A. F x cos  
C . B. F x 1 
C . C. F x 1  
C . D. F x   C . sinx sinx sinx 2 sin x Lời giải Chọn C cos x cos x 1 1 Ta có f
 xdx  dx  dx  d sin x    C    2 2 2   . 1 cos x sin x sin x sin x Vậy F x 1    C . sinx
Câu 25. Trong các hàm số sau, hàm số nào đồng biến trên khoảng 1;   ?  x x A. 3
y  x x  3 1 . B. y  . C. 4 2
y x x  2 3 . D. y  . x 1 2x  3 Lời giải Chọn C  3 x  3
+ Xét phương án A : Ta có 2 y  3
x 1  0   .  3 x    3 Bảng xét dấu  3 3 
Hàm số đồng biến trên  ;
 . Phương án A không thỏa mãn.  3 3    4 
+ Xét phương án B : Ta có y   0, x   1  . x  2 1
Hàm số nghịch biến trên ;1 và 1; . Phương án B không thỏa mãn.  2 x  2   + Xét phương án 2 C : Ta có 3
y  4x  2x  0  x   . 2  x  0   Bảng xét dấu  2   2 
Hàm số đồng biến trên   ;0 và  ;  .  2      2  
Khi đó hàm số đồng biến trên 1;   . Phương án C thỏa mãn. 1 3
+ Xét phương án D : Ta có y   0, x   . 2x 32 2  3   3 
Hàm số đồng biến trên  ;    và ; 
. Phương án D không thỏa mãn.  2   2 
Câu 26. Tập xác định của hàm số y   x  13 1 là: A. 0;   . B. 1;   . C.  . D. 1;   . Lời giải Chọn B
Điều kiện x  1  0  x  1 .
Vậy tập xác định của hàm số đã cho là 1;   .
Câu 27. Cho hàm số f (x) liên tục trên  và có bảng xét dấu đạo hàm f ( ) x như sau:
Hàm số f (x) có bao nhiêu điểm cực trị? A. 2 . B. 4 . C. 1. D. 3 . Lời giải Chọn A
Hàm số f (x) liên tục trên  và có f ( )
x đổi dấu khi đi qua các điểm x  1 và x  0 
hàm số có 2 điểm cực trị.
Câu 28. Tính đạo hàm của hàm số y  log (2x 1) ? 2 2 1 A. 1 2 y '  . B. y '  . C. y '  . D. y '  . (2 x  1) ln 2 (2 x  1) ln 2 2x 1 2x 1 Lời giải Chọn B 2x 1 ' 2
Ta có y '  log (2x 1) '   2    . (2x 1).ln 2 (2x 1).ln 2
Câu 29. Cho hai số phức z  (x y 3) (2y 1)i , z '  2x  (2x y 5)i . Ta có z z ' khi: 5 4 5
A. x   ; y  .
B. x 1; y  3.
C. x 1; y  2.
D. x  ; y  0 . 3 3 3 Lời giải Chọn C
x y  3  2xx y  3 x  1
Ta có z z '       .
2y 1  2x y  5
2x  3y  4  y  2 2 x x
Câu 30. Tìm tập nghiệm của bất phương trình  1  x  4  2    2 
A. 2;   .
B. ; 2  2;   .C. 2; . D. 2; 2 . Lời giải Chọn D 2 x x Ta có  1 2  x4 xx x4 2 2  2  2  2
 x x x  4  x  4  0  2   x  2 .    2 
Vậy tập nghiệm của bất phương trình là: S  2; 2 .
Câu 31. Gọi x , x là hai nghiệm của phương trình log  2
x x 1  3 x  2  khi đó x bằng: 1 2 1 2 A.  1 . B.  3 . C. 2 . D. 2 . Lời giải Chọn A  1   29 x  2
Ta có: log x x   1 2 2 3 2
1  3  x x 1  2  x x  7  0   2  1   29 x  2  2
x x  1  . 1 2 Cách 2: log  2 x x   2 3 2
1  3  x x 1 2  x x 7  0 2
Theo định lí Vi-et, ta có: x x  1  . 1 2
Câu 32. Cho hình chóp tứ giác S .A B C D có đáy là hình chữ nhật. Biết AB  ,
a AD  2a, các cạnh bên
bằng nhau và bằng a 2 . Tính góc giữa hai đường thẳng B , C S ? A A. 90 . B. 120 . C. 60 . D. 45. Lời giải Chọn D S a 2 2a D A a B C
Ta có: Vì BC // AD nên góc S ,
A BC  S , A AD   SAD Mặt khác, ta có: 2 2 2
SD SA AD nên tam giác SAD vuông cân tại S   SAD  45 .
Câu 33. Cho hàm số y f x có bảng biến thiên như sau:
Giá trị cực đại của hàm số đã cho bằng A. 0 . B.  5 . C. . 3 D. 2 . Lời giải Chọn D
Từ BBT, suy ra: giá trị cực đại của hàm số đã cho bằng 2 tại x  0 . 2 2 Câu 34. Cho f
 xdx 5. Tính I  3f
 x2sin xdx?  0 0 A. I  13 . B. I  17 . C. I  7 . D. I  3 . Lời giải Chọn A Ta có: 2 2 2 2 I  3
  f x2sin xdx  3 
f xdx 2 sin d x x  3.   f x 2 dx  2 cos x  3.5  20   1  13 0 0 0 0 0
Câu 35. Với a là số thực dương tùy ý, 3 a a bằng 3 2 - 2 4 A. 2 a . B. 3 a . C. 3 a . D. 3 a . Lời giải Chọn C 1 4 2 Ta có 3 3 3 3 a a = .
a a = a = a . 2 x +3
Câu 36. Tìm giá trị lớn nhất của hàm số y = trên 2; 4 là x 1 - [ ] 19 11 A. max y = . B. max y = 6 . C. max y = . D. max y = 7 . [2;4] 3 [2;4] [2;4] 3 [2;4] Lời giải Chọn D
TXĐ: D =  \ 1 . Hàm số xác định trên 2;4 . { } [ ]
( 2x )3¢ (.x )1 ( 2x )3 (.x )1¢ + - - + - 2x (.x- ) 2 2 1 - x -3 x -2x-3 Ta có y¢ = = = . (x- )2 1 (x- )2 1 (x- )2 1 2 éx =-1Ï 2;4 y¢ = 0 x - 2x - 3 Û = 2 0 Û x -2x 3 - = [ ] 0 ê Û . ( ê x - )2 1 x ê = 3Î[2;4] ë
Ta có y 2 = 7 , y 3 = 6 , y( ) 19 4 = . ( ) ( ) 3 Vậy max y = 7 . [2;4]
Câu 37. Cho log x = 2 , log x =3 với a , b là các số thực lớn hơn 1. Tính P = log x a . a b 2 b 1 A. P = 6 . B. P = - 6 . C. P = 1 . D. P = - . 6 6 Lời giải Chọn B
Theo bài log x = 2 , log x = 1 3 Þ log a = 1 , log b = . a b x 2 x 3 1 1 1 1
Suy ra P = log x = = = = =-6 a . 2 a log a -log b log a -2log b 1 2 2 b log x x x x - x 2 b 2 3
Câu 38. Cho hình chóp S .A B C D có đáy ABCD là hình vuông cạnh a , SA ^ ABCD . Tính khoảng ( )
cách từ điểm B đến mặt phẳng SAC . ( ) a a 2 a 2 a 2 A. . B. . C. . D. . 2 2 3 4 Lời giải Chọn B
Theo bài SA ^ ABCD mà BO Ì ABCD nên SA ^ BO . ( ) ( )
Vì ABCD là hình vuông nên BO ^ AC và BD=a 2 ìïBO ^ AC ïïïSA^ BO ï BD a Ta có ï
Þ BO ^ SAC Þ d (B (SAC) 2 , = BO = = . íï ( ) S , A AC Ì(SAC) ï 2 2 ïïïSAÇ AC = ï { } A î
Câu 39. Gọi T là tổng các giá trị thực của m để phương trình 2
4z  6z 1 2m  0 có nghiệm phức
thoả mãn z  2 . Tính T ? 15 17 A. . B.  19 . C.  29 . D.  . 2 2 2 2 Lời giải Chọn C     2 3  41 2  m  5 8m . 5
+) Nếu   0  5  8m  0  m  , phương trình có 2 nghiệm thực. Khi đó 8
z  2  z  2 . Thế z  29
2 vào phương trình ta được: 16  12  1  2m  0  m   (nhận). 2 Thế z   5
2 vào phương trình ta được: 16 12  1  2m  0  m   (nhận). 2 5
+) Nếu   0  5  8m  0  m  , phương trình có 2 nghiệm phức z , z   thỏa mãn 8 1 2
z z , z z  2 2 1  2m 15 2 2 1 1 2
. Khi đó z .z z   2  m  (nhận). 1 2 1 4 2 29 5 15 19 Ta có T       . 2 2 2 2
Câu 40. Có bao nhiêu giá trị nguyên dương của tham số m để tập nghiệm của bất phương trình  x2 3
 33x  2m  0 chứa không quá 9 số nguyên. A. 3281. B. 3 2 8 3 . C. 3 2 8 0 . D. 3 2 7 9 . Lời giải Chọn C x2  3   3  0    1  3x   2m  0 Ta có  x2 3
 33x  2m  0   . x2  3   3  0  2 3x   2m  0
Do m là số nguyên dương nên log 2m  0 3  1 x  3 2 3   3  0 x  2  x   Xét hệ 1 :    2   2 hệ vô nghiệm 3x   2m  0
x  log 2m  0   x  0 3    1  3 x2 3   3  0 x  2  x   3 Xét hệ 2 :    2   2
   x  log 2m 3   . 3x   2m  0 2 x  log 2mx  log 2m  3    3  
Để có không quá 9 số nguyên x thỏa mãn đề bài thì 1 1 6561 1
  log 2m  8   2m  3   m  3   8 . 3 6 2
Do m là số nguyên dương nên m  1; 2;3;...;328 
0  có 3 2 8 0 giá trị của m.
Câu 41. Một khối đồ chơi có dạng khối nón có chiều cao h  40 cm trong đó chứa một lượng nước. Nếu 3
đặt khối đồ chơi theo hình H1 thì chiều cao của nước bằng chiều cao khối nón. Hỏi nếu 4
đặt khối đồ chơi theo hình H h 2  thì chiều cao
của nước gần với giá trị nào sau đây? A. 8.98 cm. B. 7.23 cm. C. 6.68 cm. D. 6.86 cm. Lời giải Chọn C
Gọi H,H¢ lần lượt là tâm của đường tròn đáy phần chứa nước (H ) , tâm của đường tròn đáy 1
phần không chứa nước (H ) 2 Ta có SAO  ∽ SD H (g-g) HD SH 3 Þ = = . OA SO 4
Ở hình (H ) , gọi V là thể tích phần chứa nước, V là thể tích khối nón có chiều cao 1 n h 1 1 2 V = . p HO .SO , 2
V = p.HD .SH . 3 n 3 1 2 . p HD .SH 2 2 V
æHDö SH æ3ö 3 27 27 n 3 = =ç ÷ ç ÷ . =ç ÷ çè ÷ ç ÷ . = ÞV = V . V 1 n ø çè ÷ 2 HO SO 4ø 4 64 64 . p HO .SO 3
Ở hình (H ) , V phần thể tích chứa nước, V là phần thể tích không chứa nước. 2 n 1 ¢ ¢ Ta có SAO S  ∽ D H ¢ ¢ (g-g) HD SH Þ = = k . OA SO 3 27 37 V 37 37 37 1 3 V V
- =V ÛV =V V
- =V - V = V Þ = Þk = Þk = 1 n 1 n . 64 64 V 64 64 4 3 3 3 37 æ 37 ö æ 37 ö Þ SH ¢ =
SO Þ h¢ = OH ¢ = SO-SH ¢ = 1 ç ÷ ç - ÷SO ç ÷ = 1 ç ÷ ç - ÷.40 ç ÷ è ç ÷ » 6,68 cm. 4 4 ø ç 4 ÷ è ø x  1 2t
Câu 42. Trong không gian Oxyz , cho đường thẳng   : y 1 và ( )
Q : x 2y z 2  0. Gọi   là z  2 t
đường thẳng đối xứng với  qua ( ) Q . Hỏi 
 đi qua điểm nào sau đây? A. (2;0; 3  ). B. ( 2  ; 1  ; 3  ) . C. (2; 5  ;3). D. ( 1  ; 1  ;3). Lời giải Chọn C
Véc tơ chỉ phương u  (2;0;1) , véc tơ pháp tuyến n  (1; 2;1) .  Q Gọi M =DÇ( )
Q ÞM(1-2 ;t1;2+t)ÎD M Î( ) Q 1 Þ -2t+2.1-2 t
- +2=0Ût =1ÞM( 1 - ;1;3). ìïx =1+m ï Lấy ( A 1;1;2) ÎD, ï
d là đường thẳng qua A và vuông góc với (Q) : y í =1+ 2m ïïïz=2-m ïî
Gọi H là hình chiếu của A lên ( )
Q , H =d Ç( ) Q ÞH(1+ ; m 1+2 ; m 2- ) m Îd . 1 æ1 5ö H Î( ) Q Þ1+m+2(1+2 )
m -2+m+2 = 0 Û m =- Þ H ç ;0; ÷ ç ÷. 2 çè2 2÷ø
Ta có A ¢ là điểm đối xứng của A qua ( )
Q ÞH là trung điểm của AA¢ ìï x + x A A ïx ¢ ï = H ï 2 ì ï
ïx = 2x - x = - = H 1 1 0 A¢ A ï ï ï y + y ï A ï A y ¢ ï í = Û y
í = y - y = - =- Þ A¢ - H 2 H 0 1 1 (0; 1;3) A¢ A . ï 2 ï ï ï ï ïz ï +
ï = 2z - z = - = H 5 2 3 z z A¢ A A ï î A ïz ¢ = H ï 2 ïî 
Þ A¢M = (-1; 2; 0) .  ìïx = t - ï
D ¢ có véc tơ chỉ phương u ( 1
 ;2;0), qua A¢(0;-1;3) là D¢:ïy í = -1+ 2t . ïïïz=3 ïî Ta thấy điểm (2; 5  ;3)   .
Câu 43. Biết rằng x sin x là một nguyên hàm của hàm số f  x trên khoảng ;  . Gọi F x  là   3 
một nguyên hàm của 2 f xcos x thỏa mãn F   
, giá trị của F() bằng:  2  4 5 3  3 5  A. . B. . C. . D. . 2 2 2 2 Lời giải Chọn D
Ta có: x sin x là một nguyên hàm của hàm số f  x
Nên f x  xsin x    sin x  .
x cos x  sin x  x.cosx
Suy ra f x   sin x x.cos x .
f  x    cos x  cos x x sin x   2 cos x x sin x
Suy ra f  xx   x x x  2 2 cos 2. 2 cos sin
cos x  4 cos x x sin 2 x . Ta có: 2 f
  xcos x dx F  x 2
4 cos x x sin 2x d  x F  x    2 2 2 2 7  
F   F 7 3    
F    F  5  . 4  2  4 4 2
Câu 44. Cho hình chóp S .A B C D , có SA   ABCD  , đáy là hình thoi cạnh a , 
BAD  60 , góc giữa
S A và SBD  bằng 60 . Gọi G là trọng tâm tam giác S C D . Tính thể tích khối tứ diện S A G B ? 3 a 3 3 a 3 a 3 3 a 3 A. . B. . C. . D. . 13 6 72 36 Lời giải Chọn D S H A G D a 600 O K B C
Gọi K là trung điểm của CD , G là trọng tâm tam giác SCD . V SG 2 2 SABG   V  .V V SK 3 SABG 3 SABK SABK
Gọi H là hình chiếu A lên SO , khi đó SA SBD    ASH   0 , ASO  60 . a 3 Các tam giác AB ,
D BCD đều cạnh a , AO  . 2 Trong tam giác vuông AO a
SAO ta có SA   tan  . ASO 2 2 1 1 a 3 a 3
Vì BK CD BK AB , SA . B BK  . . a  . ABK 2 2 2 4 2 3 1 1 a 3 a a 3 3 3 2 2 a 3 a 3 V  .S .SA  . .   V  .V  .  . SABK ABK 3 3 4 2 24 SABG 3 SABK 3 24 36
Câu 45. Cho hàm số y f x có đạo hàm liên tục trên  và bảng xét dấu đạo hàm như sau
Số điểm cực tiểu của hàm số g x  f  4 2
x x   6 4 2 3 4
6  2x 3x 12x là A. 4 . B. 3 . C. 0 . D. 2 . Lời giải Chọn D Đạo hàm
g x  1  2 3
x  2xf  4 2
x  4x  6 5 3
12x 12x  24x  1  2x 2
x  2  f    4 2
x  4x  6 2  x 1.  x  0 
g x  0  x   2  f    4 2
x  4x  6 2
x 1  0.   1 2 Ta có 4 2
x x    2 x      x
    f  4 2 4 6 2 2 2,
x  4x  6  f  2    0 . Suy ra f  4 2
x x   2 4
6  x 1 0, x
  nên phương trình 1 vô nghiệm. Bảng biến thiên
Dựa vào bảng biến thiên thì hàm số g x  có hai điểm cực tiểu.
Câu 46. Cho số phức z thỏa mãn z  2 . Gọi M , m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của biểu thức 2
T z 1  z z  4 . Tính giá trị của 2 2 M m A. 4 5 . B. 384. C. 8 5 . D. 115 . Lời giải Chọn D
Đặt z x yi,  x, y    suy ra 2 2 2
x y  4  x  4  2   x  2 . Ta có 2 2
T z 1  z z  4  z 1  z z z.z
z 1  z z 1 z  x  2 2
1  y  2 2x 1
 2x  5  2 2x 1 .  1
2x  5  4x  2, khi x  
Xét hàm số f x 2
 2x  5  2x 1  
, với x  2; 2 . 1
 2x  5  2  4x,khi x   2  1 1  4, x   2x 5 2
Có f  x   . 1 1   4, x   2x  5 2 1
Hàm số f x  không có đạo hàm tại điểm x  . 2 f   x 1 79  0 
 4  0  x    2; 2 . 2 x  5 32 Bảng biến thiên Câu 31:
Dựa theo bảng biến thiên thì m  6 , M  11. Vậy 2 2 M m 115.
Câu 47. Cho hàm số y f ( )
x có đồ thị C. Biết rằng đồ thị C cắt trục tung tại điểm có tung độ 1
bằng và đồ thị hàm số y f   x  cho bởi hình vẽ bên. 2 2
Tính diện tích hình phẳng giới hạn bởi đồ thị C và đồ thị hàm số 3 y x  2x  2 ? 3 17 3 14 3 A. . B. 32 3 . C. 16 3 . D. . 5 5 5 5 Lời giải Chọn C
Từ hình vẽ ta thấy được f  x  a x  2  x    a  3 2 1 1
x x x   1 4 3 Mà  x x
f 0  2  f x   2  2 3 2
x x x  1  f x 2  
x  2x C 2 3 1
Do đồ thị C cắt trục tung tại điểm có tung độ bằng nên f   1 0  2 2 4 3
f xx 2 x 1 2    x  2x  2 3 2 2
Đặt y g x 3
x  2x  2 3
Xét phương trình hoành độ giao điểm f x  g x 4 3 4 x 2 x 1 2 x 3 2 3 2 2   x  2x  
x  2 x  2   x
 0  x  3  x   3 . 2 3 2 3 2 2
Khi đó diện tích hình phẳng giới hạn bởi hai đồ thị của hai hàm số f x  và g x  là: 3 3 4 S f
 x gxx 3 16 3 2 dx  2  x  dx  .  2 2 5  3 0 Câu 48. Cho hàm số 2022
y f x liên tục trên  và có đạo hàm f  x   x    2 12
x  2x có bao
nhiêu giá trị nguyên của 2
m  2021; 2021 để hàm số y f x  2022x  2021  m có ba điểm cực trị dương. A. 4038 . B. 2021. C. 2020 . D. 2019 Lời giải Chọn Bx  0
f x  x 122022  2 x 2x       x  2 .  x  12 
Xét hàm số g x  f  2
x  2022x  2021 
m gx   x   f  2 2 2022
x  2022x  2021  mx  11  x  11  2  2
x  2022x  2021m  0
x  2022x  2  021m
Ta có g x  0     2 2
x  2022x  2021m  2
x  2022x  2  2021m   2 2
x  2022x  2021m  12
x  2022x  12  2021m
Xét hàm số h x 2  x  2022x
Ta có bảng biến thiên của hàm số h x 2
x  2022x trên 0; Để hàm số g x  có 3 điểm cực trị dương  2  021m  0  m  0  2  021m  2  0    22121 2  m  2  020; 2  019;...;0 .     m  l    2  021m  2  2121  2021 2021
Câu 49. Trong không gian Oxyz , cho mặt phẳng P  : x  2 y  2z  5  0 và 2 mặt cầu
S : x2  y z1 1 S : x4  y2  z3 4
M , A a;b; c  2   2  2  2 1   2  2 2 ; . Gọi , B lần
lượt thuộc P ,S , S MA MB
a b c 1   2  sao cho nhỏ nhất? Tính ? A. 3 . B.  3 . C. 1. D.  1 . Lời giải Chọn C Mặt cầu S I 2; 0; 1 R  1 1  có tâm , bán kính . 1 Mặt cầu S J 4; 2;3 R  2 2  có tâm , bán kính . 2
Ta có: IJ  2 14  R R và  x  2 y  2z  5 x y z   SS2  1  I I I  2 2 5 J J J  0 nên và 1 2
nằm phác phía so với mặt phẳng P . Gọi ,
C D lần lượt là giao điểm của đoạn IJ với SS2  1  và
x  2  3t Ta có 
I J có phương trình tham số:  y tz  1   2t   14 t     14 x  2  3t     3 14 y tx  2   Tọa độ  14
C là nghiệm của hệ phương trình: z  1   2t  .     x  2   14
2  y  z  2 2 1  1 y    14
d C;P d I;P     2 14 z  1    14  3 14 14 2 14  Suy ra C  2  ; ; 1     14 14 14    Khi đó :
P M A M B AI BJ IJ
M A M B CI DJ CI DJ CD M A M B CD . Suy ra P
CD IJ R R  2 14  3 min  1 2  .
Dấu bằng xảy ra khi A  ;
C B D và M, , C D thẳng hàng.  3 14 14 2 14  Vậy A 2  ; ; 1  
  a b c  1 .  14 14 14   
Câu 50. Cho hàm số   2022x 2022 x f x   
. Tìm số nguyên m lớn nhất để f m   f 3m  2021  0 ? A.  505 . B. 505 . C.  506 . D. 506 . Lời giải Chọn C
Hàm số   2022x 2022 x f x   
xác định x   .
Khi đó với  x   , ta có ( )  2022x  2022x f x
  f x .
Suy ra f (x) là hàm số lẻ. 1
Mặt khác    2022x  2022x     2022x ln 2022  2022x f x f x
ln 2022  0, x  
Do đó hàm số f (x) đồng biến trên  . 2
Ta có f m   f 3m  2021  0  f m    f 3m  2021 .
Theo 1 suy ra  f m   f 3m  2021 . 2021
Theo 2 ta được m  3
m  2021  m  
. Vậy số nguyên m lớn nhất là  506 . 4
-----------------------HẾT-----------------------
Document Outline

  • de-thi-thu-toan-tot-nghiep-thpt-2022-lan-2-truong-chuyen-bien-hoa-ha-nam
  • 109. Đề thi thử tốt nghiệp THPT năm 2021-2022 môn Toán - CHUYÊN BIÊN HÒA - HÀ NAM (LẦN 2) (File word có lời giải chi tiết).Image.Marked