














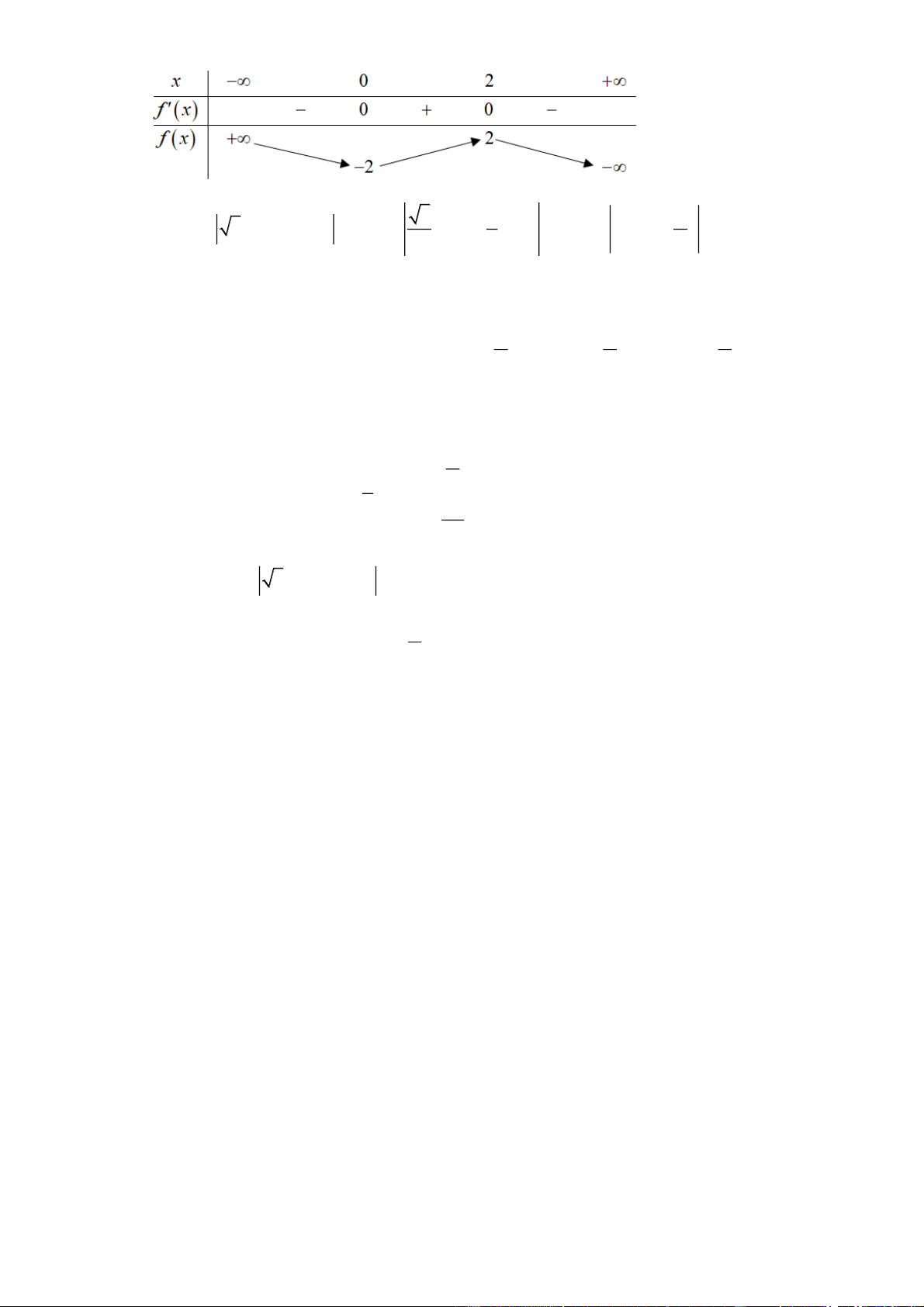
Preview text:
TRƯỜNG THPT CHUYÊN HÀ TĨNH
ĐỀ THI THỬ TỐT NGHIỆP THPT NĂM 2022 Bài thi: TOÁN Thời gian: 90 phút Câu 1:
Phần ảo của số phức z = 7
− + 6i bằng
A. −6i . B. −6 . C. 6 . D. 6i . Câu 2:
Cho hai số phức z = 3− 7i và z = 2 + 3i . Tìm số phức z = z + z . 1 2 1 2
A. z = 3 −10i .
B. z = 1−10i .
C. z = 3 + 3i .
D. z = 5 − 4i . Câu 3:
Cho mặt cầu bán kính R = 2 . Diện tích mặt cầu đã cho bằng 32 16 A. 8 . B. . C. . D. 16 . 3 3 Câu 4:
Trong không gian Oxyz , vectơ u (1; 1
− ;2) là một vectơ chỉ phương của đường thẳng nào sau đây? x = 2 + t x = 1− t x −1 1− y z − 2 x y +1 z − 2 A. = = . B. = =
. C. y = t − .
D. y = −1+ t . 1 1 − 2 1 1 − 2 z = 1 − − 2t z = 2 + 2t Câu 5:
Biết log 5 = a . Khi đó log5 bằng: 2 1 a a +1 A. .
B. a +1 . C. . D. . a a +1 a Câu 6:
Số nghiệm của phương trình log x + 3 =1+ log x +1 là 2 ( ) 2 ( ) A. 2 . B. 3 . C. 0 . D. 1. 2 5 5 f (x)dx = −1 f (x)dx = 3 −2 f (x)dx Câu 7: Nếu 1 và 2 thì 1 bằng A. 2 − . B. 4 − . C. 4 . D. 2 . Câu 8:
Có bao nhiêu cách xếp chỗ ngồi cho 4 bạn học sinh vào dãy có 4 ghế? A. 24 cách. B. 4 cách. C. 8 cách. D. 12 cách. Câu 9:
Diện tích xung quanh của hình trụ có bán kính đáy a 3 và đường cao 2a là? A. 2 6 a . B. 2 4 3 a . C. 2 3 a . D. 2 2 3 a .
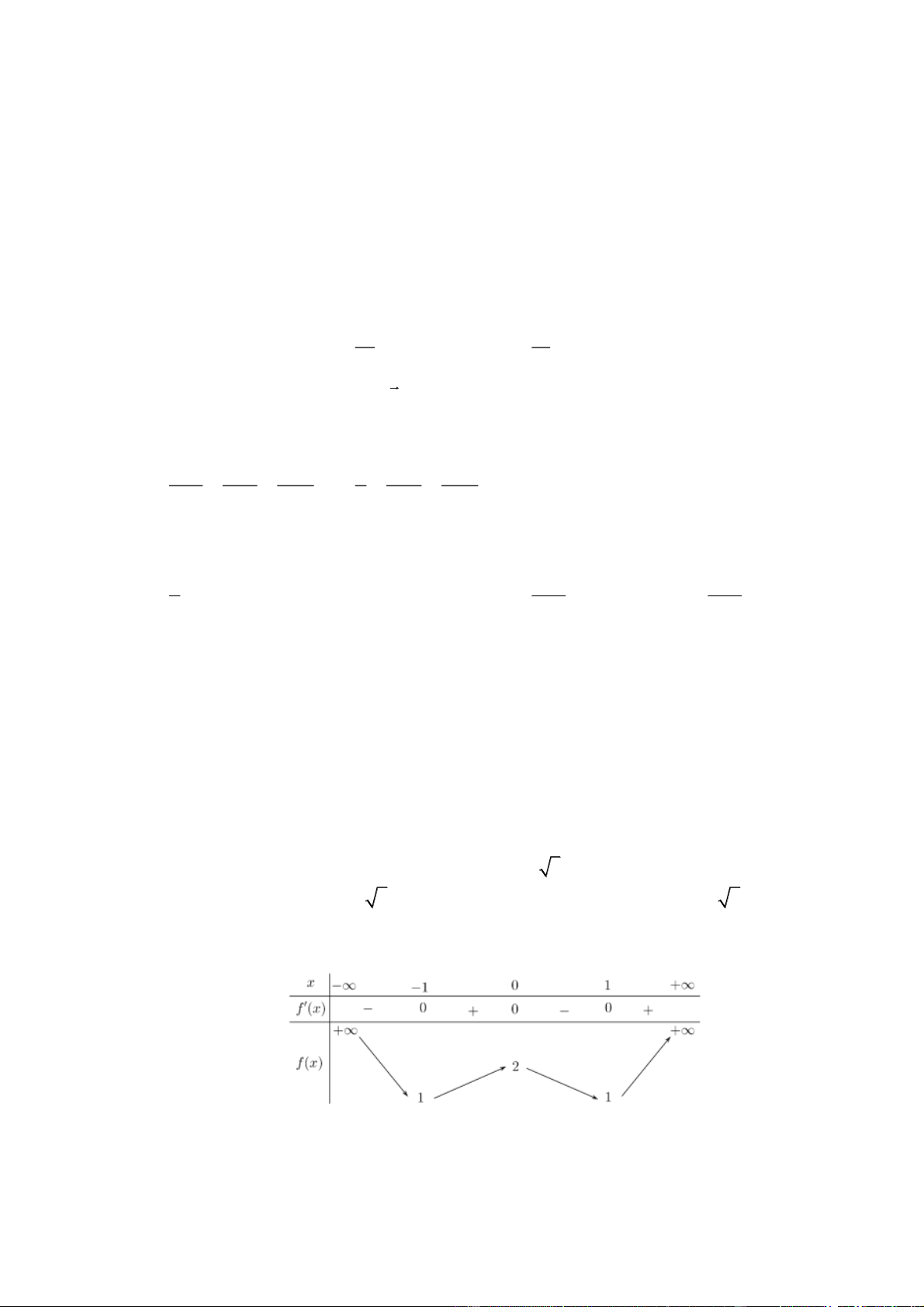
Câu 10: Cho hàm số y = f ( x) có bảng biến thiên như sau:
Số nghiệm thực của phương trình 2 f (x) −11= 0 là A. 2 . B. 3 . C. 4 . D. 0 .
Câu 11: Cho một cấp số cộng (u có u = 5
− ;u = 30 . Công sai của cấp số cộng bằng n ) 1 8 Trang 1 A. 5 . B. 6 . C. 3 . D. 4 .
Câu 12: Số điểm cực trị của hàm số y = x ( 2 x − )( 2
4 −x + 3x − 2) là A. 4 . B. 3 . C. 1. D. 2 .
Câu 13: Trong không gian Oxyz , tọa độ tâm của mặt cầu (S ) 2 2 2
: x + y + z + 8y − 2z + 8 = 0 là: A. ( 4 − ;0; ) 1 . B. (0; 4 − ; ) 1 . C. (0;4; ) 1 − . D. (1;0; 4 − ) .
Câu 14: Cho khối chóp S.ABC có diện tích đáy bằng 2
2a , đường cao SH = 3a . Thể tích khối chóp bằng: 3 3a A. 3 a . B. 3 2a . C. 3 3a . D. . 2
Câu 15: Tập nghiệm của bất phương trình log x 3 là: 2 A. (0;9 . B. (0; 8 . C. (0;8) . D. ( ;8 − . x + y − z
Câu 16: Trong không gian Oxyz , đường thẳng 1 3 : =
= đi qua điểm nào dưới đây? 3 1 − 2
A. P(1;−3; 0) .
B. M (3;−1; 0) .
C. Q (3;−1; 2) . D. N ( 1 − ; 3; 0) . 2 2 f (x)dx = 2 3 − f
(x)+ 2xdx Câu 17: Nếu 0 thì 0 bằng A. 2 . B. 1. C. 1 − . D. 2 − .
Câu 18: Trên khoảng (0;+ ) , họ nguyên hàm của hàm số f ( x) 3 = 2 x là 2 3 A. f (x) 3 dx =
x x + C . B. f (x) 3 2 dx =
x x + C . 3 2 3 2 C. f (x) 3 dx =
x x + C . D. f (x) 3 2 dx = x x + C . 2 3
Câu 19: Tập xác định của hàm số y = (x − )2 ln 1 là
A. D = 1;+ ) . B. D = \ 1 .
C. D = (1;+ ) . D. D = .
Câu 20: Trong các hàm số sau, hàm số nào nghịch biến trên ? x −1 A. 3 2
y = −x − x . B. y = . x + 2 C. 2
y = 2x + 5 . D. 3 2
y = −x + 3x − 9x + 2 .
Câu 21: Cho hàm số y = f ( x) có đồ thị như hình vẽ bên. Hàm số đã cho đồng biến trên khoảng nào dưới đây? Trang 2 A. ( 1 − ; ) 1 . B. (0;2) . C. (0;+). D. (0;4) . x
Câu 22: Tiệm cận ngang của đồ thị hàm số y =
là đường thẳng có phương trình 2 2x − 5 1 1
A. y = − . B. y = .
C. y = 0. D. y = 2 . 5 2
Câu 23: Mô-đun của số phức z = 5 − 2i bằng A. 29 . B. 3 . C. 21 . D. 29 .
Câu 24: Trong không gian tọa độ Oxyz , cho hai véc-tơ u = ( 1 − ;1;3) và v = ( 2 − ;1; 3 − ) . Tính độ dài
2u − 3v . A. 152 . B. 322 . C. 242 . D. 216 .
Câu 25: Cho hàm số y = f ( x) có đồ thị hình vẽ bên. Giá trị cực đại của hàm số đã cho là A. 1. B. 1 − . C. 0 . D. 2 .
Câu 26: Cho hàm số f ( x) =1− sin x . Khẳng định nào dưới đây đúng? A. f
(x) dx = x−sin x+C . B. f
(x) dx = x+cosx+C . C. f
(x) dx = x−cosx+C . D. f
(x) dx = x+sin x+C . 2
Câu 27: Trên tập số thực , đạo hàm của hàm số 3x x y − = là: 2 A. 1 3x x y − − = . B. ( ) 2 2 1 3x x y x − = − . C. ( ) 2 2 1 3x x y x − = − ln 3 . D. ( ) 2 2 1 3x x y x x − − = − . Trang 3
Câu 28: Có tất cả bao nhiêu giá trị nguyên của tham số m thuộc đoạn 1 − 0;1 0 để hàm số 1 3 2 y =
x − 2x + mx − 3 đồng biến trên (2;6) ? 3 A. 4 . B. 5 . C. 7 . D. 6 . 2x +1
Câu 29: Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = trên đoạn x −1
2;4. Khi đó M −m bằng: A. 3 . B. 2 . C. 2 − . D. 4 .
Câu 30: Cho lăng trụ đều AB . C A B C
có cạnh đáy bằng 2a , độ dài cạnh bên bằng a 3 . Thể tích V
của khối lăng trụ bằng: 3 1 A. 3 V = a . B. 3 V = a . C. 3 V = 3a . D. 3 V = a . 4 4
Câu 31: Cho hình chóp S.ABC có SA vuông góc với mặt phẳng ( ABC ), SA = a 3 , tam giác ABC
đều cạnh có độ dài bằng a . Gọi = ( A ,
B (SBC)) , khi đó sin bằng: 3 15 5 15 A. B. . C. . D. . 5 3 3 5 log . a log 3
Câu 32: Với mọi a,b thoả mãn 3 2
+ logb =1. Khẳng định nào dưới đây đúng? 1+ log 5 2
A. a log 5 + b = 1
B. a + b = 1.
C. a = 1− b log 5 . D. ab = 10 . 2 2
Câu 33: Đề kiểm tra chất lượng sản phẩm từ công ty sữa, người ta gửi đến bộ phận kiểm nghiệm 5 hộp
sữa cam, 4 hộp sữa dâu và 3 hộp sữa nho. Bộ phận kiểm nghiệm chọn ngẫu nhiên 3 hộp để
phân tích mẫu. Xác suất để 3 hộp sữa được chọn có cả 3 loại là: 3 1 3 1 A. . B. . C. . D. . 55 22 11 110
Câu 34: Trong không gian với hệ trục toạ độ Oxyz , cho ba điểm A( 1 − ;2; ) 1 , B(2;−1; ) 3 và C ( 2
− ;1;2). Đường thẳng đi qua A đồng thời vuông góc với BC và trục Oy có phương trình là: x = 1 − + t x = −1− t x = −1− t x = 1 − + t A. y = 2 . B. y = 2 . C. y = 2 . D. y = 2 . z = 1+ 4t z = 1 + 4t z = 1 − 4t z = 1+ 4t
Câu 35: Trong không gian với hệ trục tọa độ Oxyz , mặt phẳng ( ) vuông góc với mặt phẳng (Oxy) , + − − đồ x 2 y 2 z 3
ng thời ( ) song song và cách đường thẳng : = = một khoảng bằng 5 1 − 2 3 − có phương trình là
A. 2x + y + 7 = 0 hoặc 2x + y − 3 = 0 .
B. 2x − y + 7 = 0 hoặc 2x − y + 5 = 0 .
C. 2x + y + 7 = 0 hoặc 2x + y − 5 = 0.
D. 2x + y + 7 = 0 hoặc 2x − y − 3 = 0 .
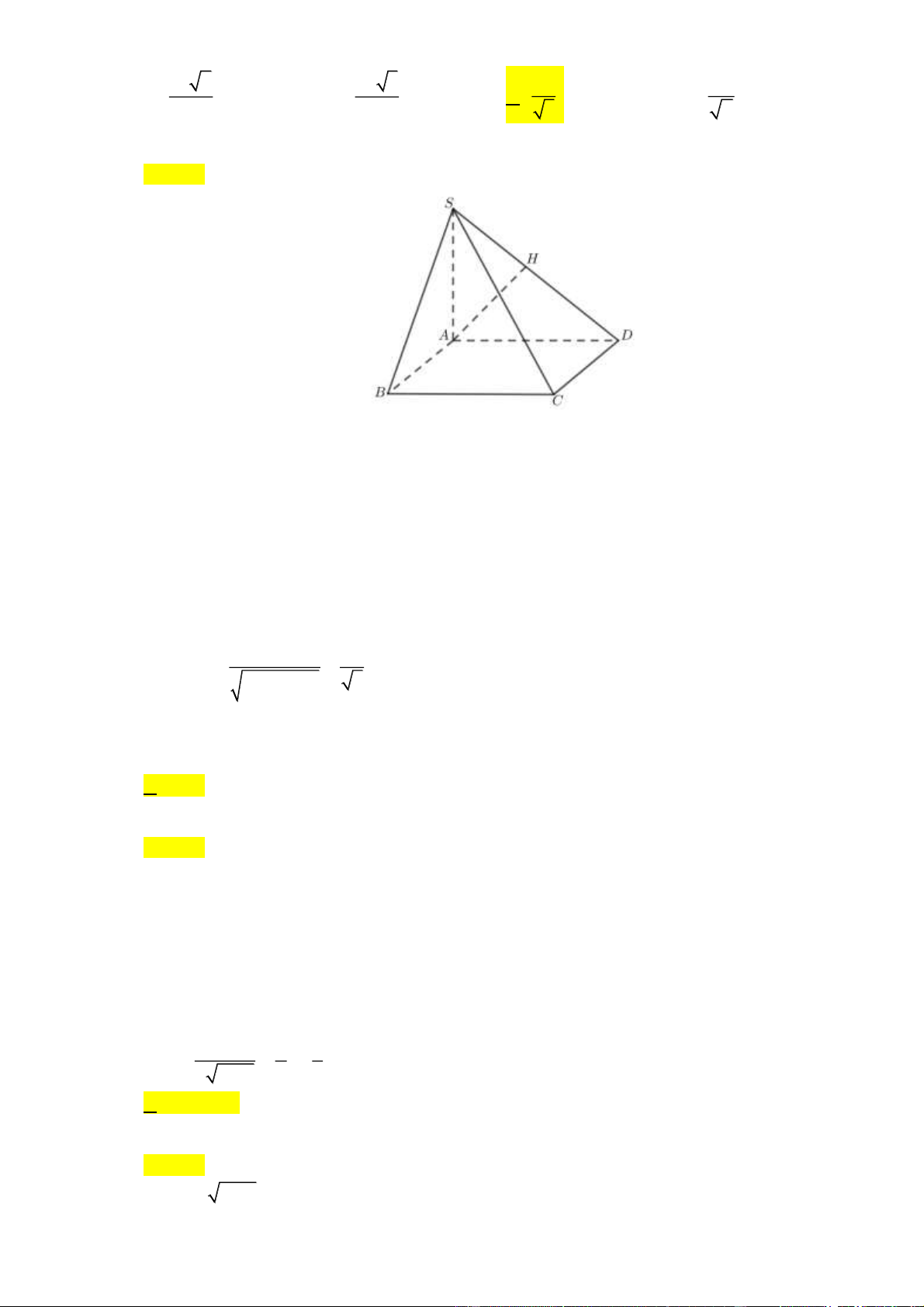
Câu 36: Cho hình chóp S.ABCD có SA ⊥ ( ABCD) , đáy ABCD là hình chữ nhật. Biết AD = 2 , a
SA = a . Khoảng cách từ A đến (SCD) bằng: Trang 4 3a 2 2a 3 2a 3a A. . B. . C. . D. . 2 3 5 7
Câu 37: Biết số phức z = 3
− + 4i là một nghiệm của phương trình 2
z + az + b = 0 , trong đó a,b là các
số thực. Giá trị của a − b bằng: A. 19 − . B. 31 − . C. 11 − . D. 1. 12 dx 1 b Câu 38: Cho = .ln với , a ,
b c là các số nguyên dương. Khẳng định nào dưới đây đúng? x x + 4 a c 5
A. a = b − c .
B. b = c − a .
C. c = a − b .
D. b = 2c .
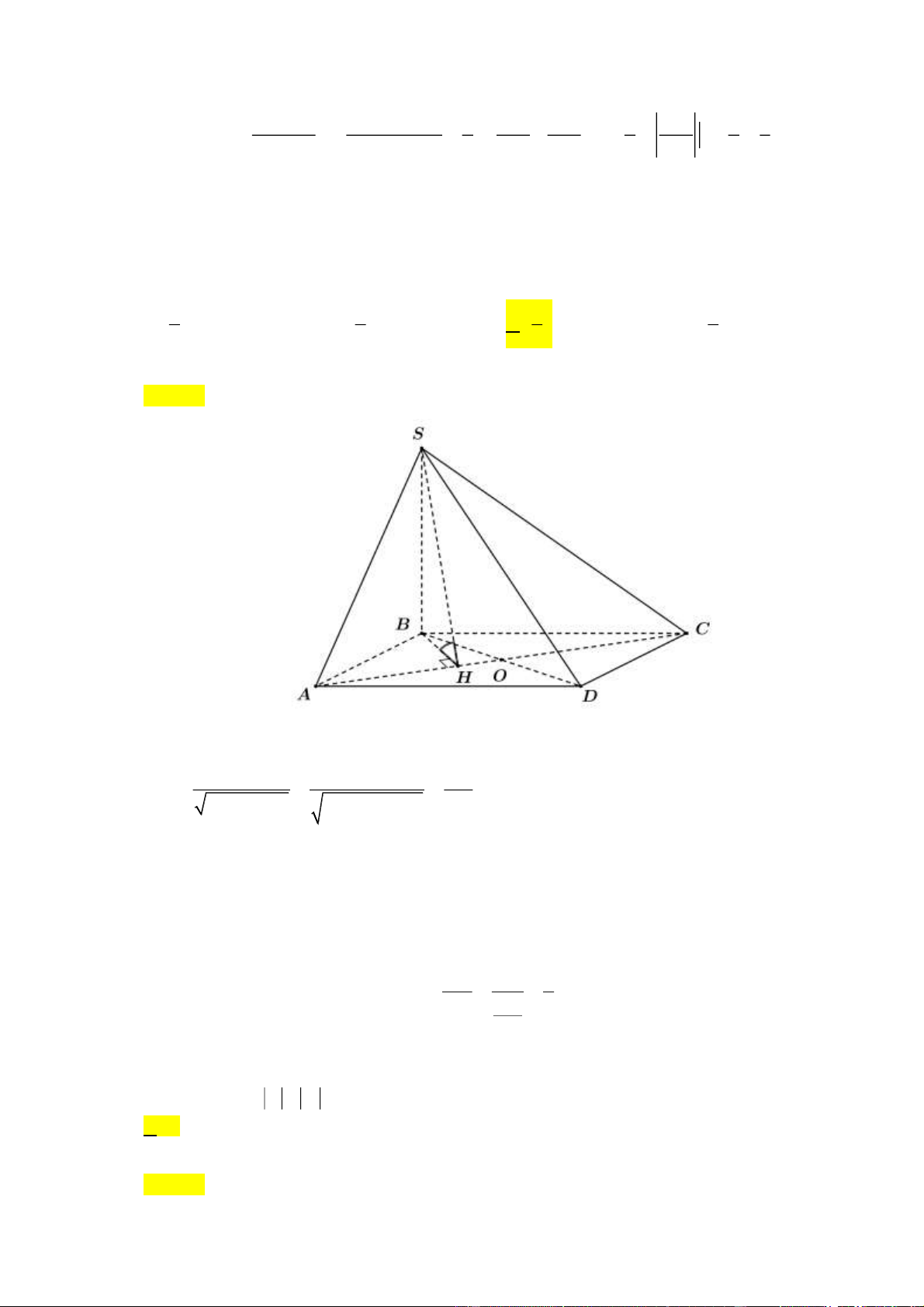
Câu 39: Cho hình chóp S.ABCD có cạnh bên SB vuông góc với mặt đáy và ABCD là hình chữ nhật. Biết SB = 2 , a AB = 3 ,
a BC = 4a và gọi là góc giữa mặt phẳng (SAC) và mặt đáy. Giá trị tan bằng 3 4 5 6 A. . B. . C. . D. . 4 3 6 5
Câu 40: Có bao nhiêu giá trị thực của m để phương trình 2 z + (m − ) 2 4 4
1 z + m − 3m = 0 có hai nghiệm
z , z thỏa mãn z + z = 2? 1 2 1 2 A. 2. B. 3. C. 4. D. 1.
Câu 41: Cho z , z thỏa mãn z = 2 , z = 3 và z z là số thuần ảo. Giá trị lớn nhất của 1 2 1 2 1 2
P = 4z − 3z +1− 2i bằng: 1 2 A. 65 + 5 . B. 145 + 5 . C. 15 + 5 . D. 5 + 5 .
y = f ( x) (0;+)
2x f ( x) + f ( x) = 4x x f ( ) 1 = 2 Câu 42: Cho hàm số liên tục trên thỏa mãn . Biết . f (4) Giá trị của bằng: 15 17 15 17 A. . B. . C. . D. . 4 4 2 2
Câu 43: Cho phương trình 2 log x − ( 2
m − 2m log x + m + 3 = 0 ( m là tham số thực). Gọi S là tập hợp 2 ) 2
tất cả các giá trị của m để phương trình có hai nghiệm phân biệt x , x thỏa mãn x .x = 8 . 1 2 1 2
Tổng các phần tử của S là: A. 5 . B. 2 − . C. 1 − . D. 2 .
Câu 44: Cho hai hàm số f ( x) 3 2
= ax −3x +bx +1− 2d và g (x) 2
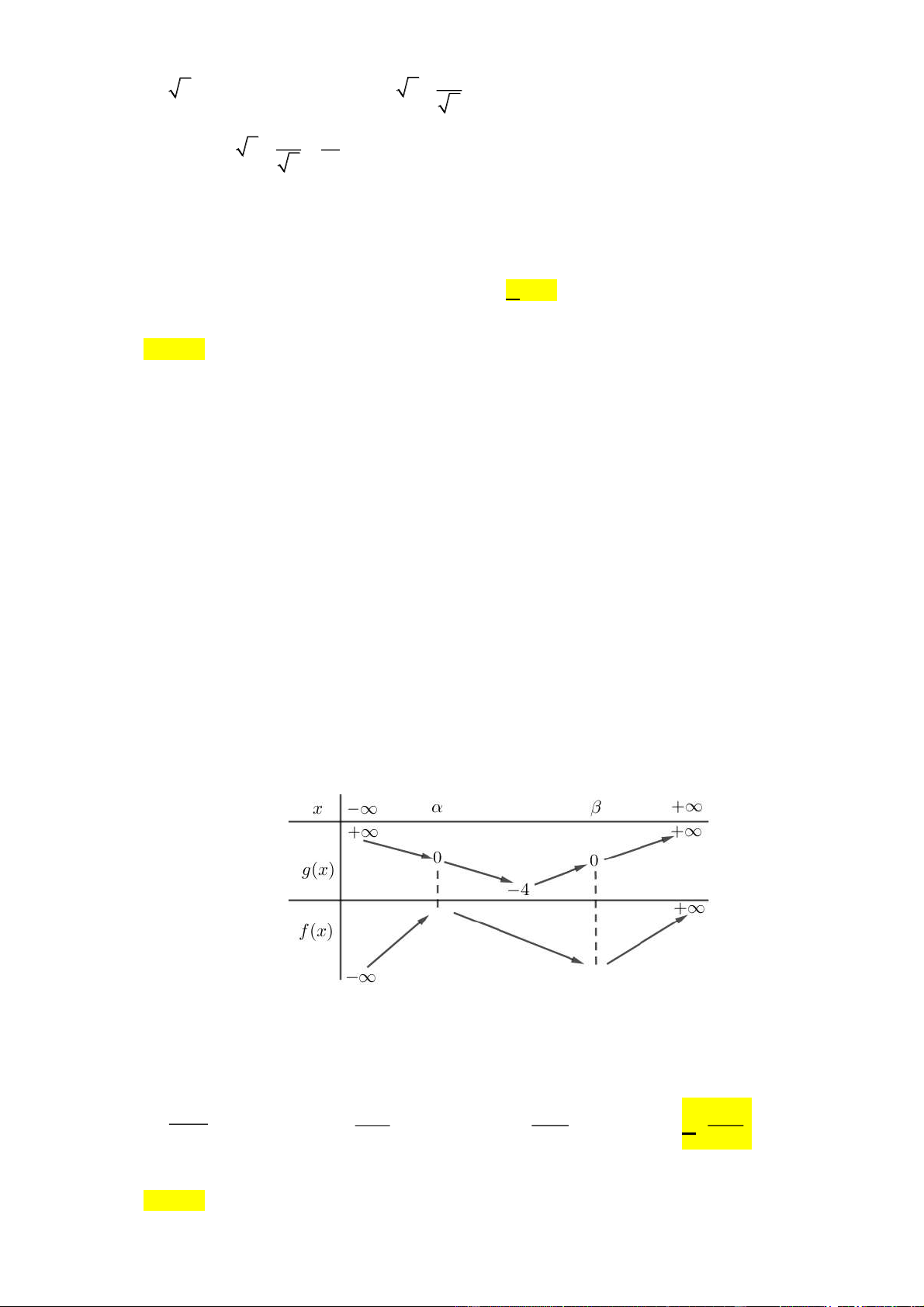
= cx − 2x + d có bảng biến thiên như sau: Trang 5
Biết rằng đồ thị hai hàm số đã cho cắt nhau tại ba điểm phân biệt có hoành độ x , x , x thỏa 1 2 3 mãn 2 2 2 x + x + x
= 30 . Diện tích hình phẳng giới hạn bởi các đường cong 1 2 3
y = f ( x), y = g ( x), x = 3
− , x = 6 bằng: 2113 1123 1231 1321 A. . B. . C. . D. . 12 12 12 12
Câu 45: Cho hàm số f ( x) 3 2
= x −3x +1, gọi S là tập tất cả các giá trị nguyên của tham số để phương trình f (x) 2 −
(2m+ 4) f (x)+ m(m+ 4) = 0 có đúng 4 nghiệm phân biệt. Tổng các
phần tử của S bằng A. −5 . B. 17 − . C. 18 − . D. 21 − . Câu 46: Có bao nhiêu cặp số nguyên dương (x, y) thỏa mãn 3 2
2x − 3x +1 log
=14x + 3y − 7( 2
x +1 đồng thời 1 x 2022 7 )
6xy +1+ 2x + 3y A. 1347. B. 1348 . C. 674 . D. 673 . x +1 y z − 2
Câu 47: Trong không gian với hệ trục tọa độ Oxyz, cho đường thẳng d : = = và mặt 1 2 1 phẳng ( )
P : x − 2y − 2z − 7 = 0 và điểm (
A 1;1;3). Đường thẳng đi qua A cắt d và mặt
phẳng (P) lần lượt tại M và N sao cho M là trung điểm của AN , biết rằng có một vectơ chỉ phương u = ( ; a ;
b 6) . Khi đó giá trị của T =14a − 5b bằng:
A. T = 63. B. T = 81.
C. T = 72. D. T = 81. −
Câu 48: Trong không gian Oxyz , cho mặt cầu 2 2 2
(S) : (x +1) + ( y − 9) + z = 18. và các điểm ( A 8;0;0), (4
B ; 4;0), Điểm M (x ; y ; z ) bất kì thuộc mặt cầu (S) . Biết MA + 3MB đạt giá trị nhỏ nhất M M M
tại điểm M có tọa độ (x ; y ; z ) . Giá trị của biểu thức T = 4x − 9 y bằng 0 0 0 0 0 A. T = 46. − B. T = 124. −
C. T = 46.
D. T = 124.
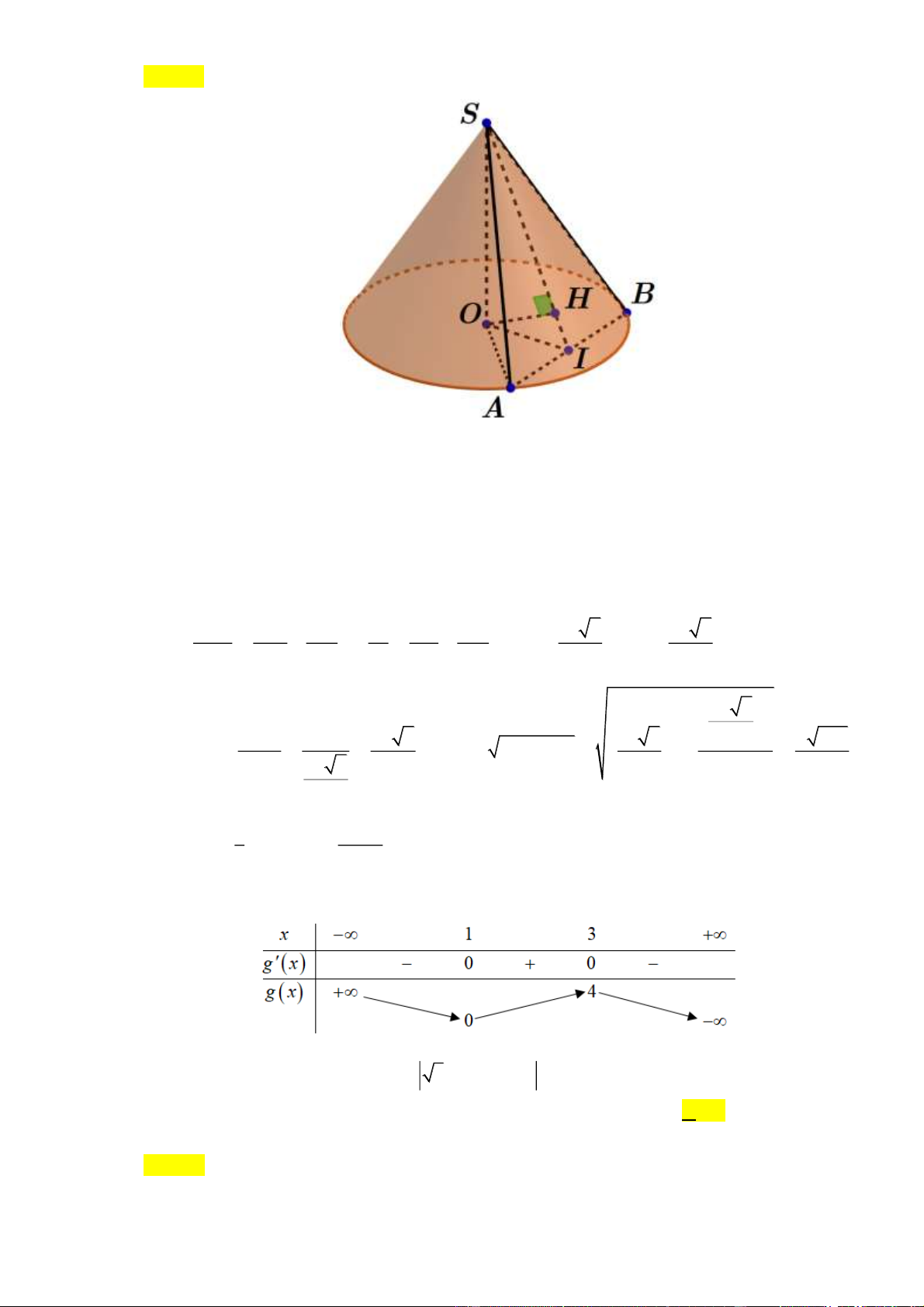
Câu 49: Cho khối nón đỉnh S có đường cao bằng 3a . S ,
A SB là hai đường sinh của khối nón. Khoảng
cách từ tâm đường tròn đáy đến mặt phẳng (SAB) bằng a và diện tích tam giác SAB bằng 2
3a . Tính thể tích khối nón. 3 145 a 3 145 a 3 145 a 3 145 a A. . B. . C. . D. . 48 72 54 36
Câu 50: Cho hàm số y = f ( x) có bảng biến thiên của hàm số g ( x) = f ( x − ) 1 + 2 như sau:
Giá trị lớn nhất của hàm số y = f (− 3 sin x − cos x + 2) + 2cos 2x + 4sin x −1 là: A. −9 . B. 2 − . C. 2 . D. 4 .
---------- HẾT ---------- Trang 6 BẢNG ĐÁP ÁN 1 2 3 4 5 6 7 8
9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
C D D B C D B A B A A A B B B D D C B D A C A C A
26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50
B C C B C D D C B D C A A C A B D C D D A B A B D
HƯỚNG DẤN GIẢI CHI TIẾT Câu 1:
Phần ảo của số phức z = 7
− + 6i bằng
A. −6i . B. −6 . C. 6 . D. 6i . Lời giải Chọn C
Ta có Phần ảo của số phức z = 7 − + 6i bằng 6 . z = 3 − 7i z = 2 + 3i z = z + z Câu 2: Cho hai số phức 1 và 2 . Tìm số phức 1 2 .
A. z = 3 −10i .
B. z = 1−10i .
C. z = 3 + 3i .
D. z = 5 − 4i . Lời giải Chọn A
T a có: z = z + z = 3 − 7i + 2 + 3i = 5 − 4i . 1 2 Câu 3:
Cho mặt cầu bán kính R = 2 . Diện tích mặt cầu đã cho bằng 32 16 A. 8 . B. . C. . D. 16 . 3 3 Lời giải Chọn C Ta có: 2 2
S = 4 R = 4.2 =16 . Câu 4:
Trong không gian Oxyz , vectơ u (1; 1
− ;2) là một vectơ chỉ phương của đường thẳng nào sau đây? x = 2 + t x = 1− t x −1 1− y z − 2 x y +1 z − 2 A. = = . B. = =
. C. y = t − .
D. y = −1+ t . 1 1 − 2 1 1 − 2 z = 1 − − 2t z = 2 + 2t Lời giải Chọn B + − Ta có: vectơ x y z u (1; 1
− ;2) là một vectơ chỉ phương của đường thẳng 1 2 = = . 1 1 − 2 Câu 5:
Biết log 5 = a . Khi đó log5 bằng: 2 1 a a +1 A. .
B. a +1 . C. . D. . a a +1 a Lời giải Chọn C log 5 log 5 log 5 a Ta có 2 2 2 log 5 = = = = log 10 log 2.5 1+ log 5 1+ . a 2 2 ( ) 2 Trang 7 Câu 6:
Số nghiệm của phương trình log x + 3 =1+ log x +1 là 2 ( ) 2 ( ) A. 2 . B. 3 . C. 0 . D. 1. Lời giải Chọn D x + 3 0 x 3 − Điều kiện: x −1 x +1 0 x 1 −
Phương trình đã cho tương đương log x + 3 = log 2 + log x +1 2 ( ) 2 2 ( )
log x + 3 = log 2 x +1 2 ( ) 2 ( )
x + 3 = 2(x + ) 1
x − 2x = 2 −3 x =1 (nhận)
Vậy tập nghiệm của phương trình S = 1 . 2 5 5 Câu 7: Nếu f
(x)dx = −1 và f
(x)dx = 3 thì −2 f
(x)dx bằng 1 2 1 A. 2 − . B. 4 − . C. 4 . D. 2 . Lời giải Chọn B 5 5 2 5 Ta có: 2 − f (x)dx = 2 − f (x)dx = 2 − f
(x)dx+ f
(x)dx = −2(−1+3) = −4. 1 1 1 2 Câu 8:
Có bao nhiêu cách xếp chỗ ngồi cho 4 bạn học sinh vào dãy có 4 ghế? A. 24 cách. B. 4 cách. C. 8 cách. D. 12 cách. Lời giải Chọn A
Số cách xếp chỗ ngồi cho 4 bạn học sinh vào dãy có 4 ghế là 4! = 24 cách. Câu 9:
Diện tích xung quanh của hình trụ có bán kính đáy a 3 và đường cao 2a là? A. 2 6 a . B. 2 4 3 a . C. 2 3 a . D. 2 2 3 a . Lời giải Chọn B
Diện tích xung quanh của hình trụ là 2 S
= 2rh = 2 a 3 2a = 4 3 a . xq
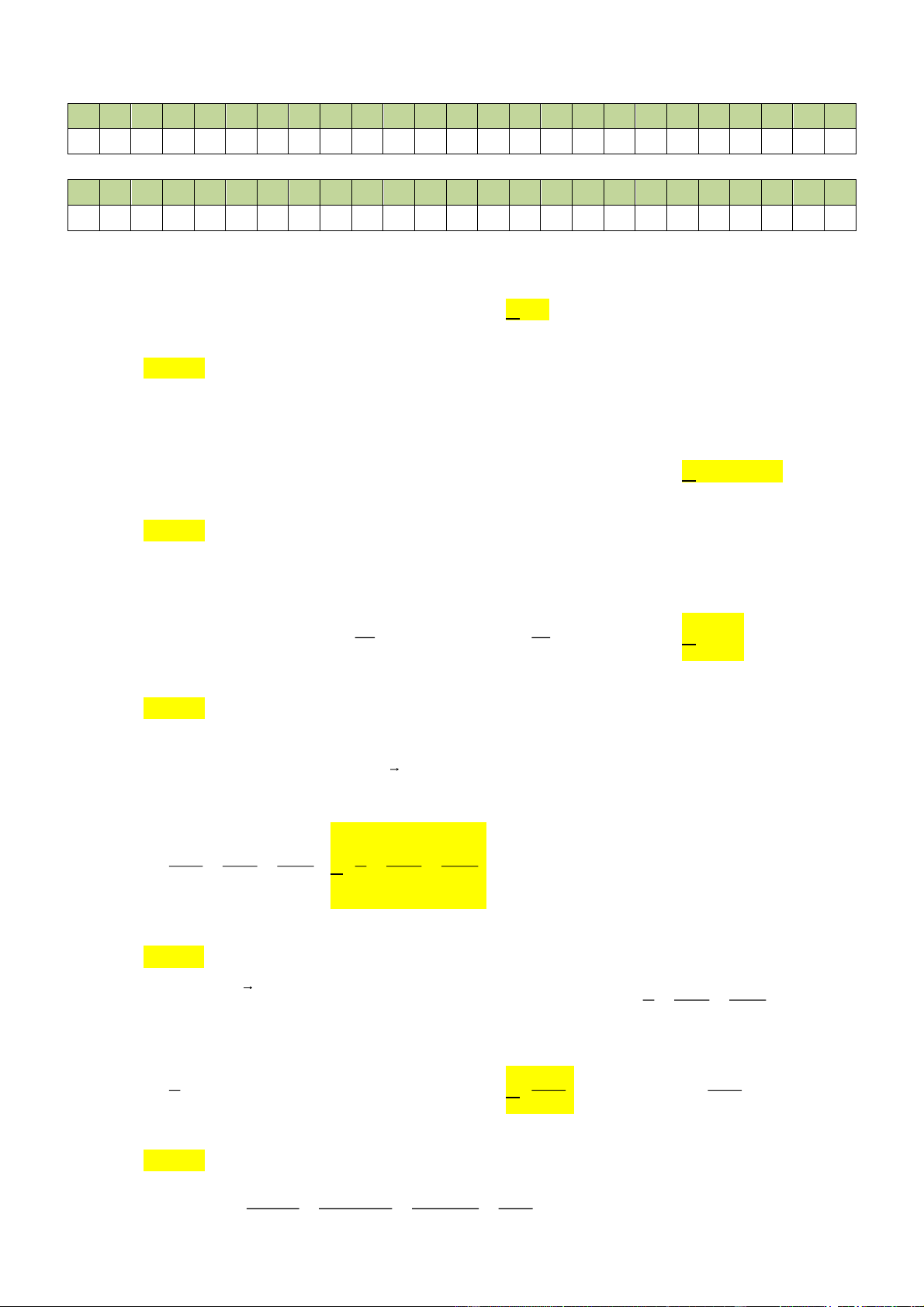
Câu 10: Cho hàm số y = f ( x) có bảng biến thiên như sau: Trang 8
Số nghiệm thực của phương trình 2 f (x) −11= 0 là A. 2 . B. 3 . C. 4 . D. 0 . Lời giải Chọn A
Ta có: f ( x) − = f (x) 11 2 11 0 = 2
Số nghiệm của phương trình là số giao điểm của đồ thị hàm số y = f (x) và đường thẳng 11 y = . 2
Dựa vào bảng biến thiên, ta thấy đồ thị hàm số y = f (x) cắt đường thẳng 11 y = tại 2 điểm 2 phân biệt.
Vậy phương trình 2 f (x) −11= 0 có 2 nghiệm phân biệt.
Câu 11: Cho một cấp số cộng (u có u = 5
− ;u = 30 . Công sai của cấp số cộng bằng n ) 1 8 A. 5 . B. 6 . C. 3 . D. 4 . Lời giải Chọn A
Ta có u = u + 7d 30 = 5
− + 7d d = 5 . 8 1
Câu 12: Số điểm cực trị của hàm số y = x ( 2 x − )( 2
4 −x + 3x − 2) là A. 4 . B. 3 . C. 1. D. 2 . Lời giải Chọn A
Ta có y = x (x − )(−x + x − ) = −x(x − )(x + )(x − )2 2 2 4 3 2 1 2 2 . 2 2 2
Ta có y = − ( x − )
1 ( x + 2)( x − 2) − x ( x + 2)( x − 2) − x ( x − )
1 ( x − 2) − 2x ( x − )
1 ( x + 2)( x − 2) Trang 9 x = 2 = ( x − = y x − 2)( 2 0 3 2
5x − 2x −10x + 4) = 0 x = 2 . 3 2
5x − 2x −10x + 4 = 0 2 x = 5
Số điểm cực trị của hàm số là 4 .
Câu 13: Trong không gian Oxyz , tọa độ tâm của mặt cầu (S ) 2 2 2
: x + y + z + 8y − 2z + 8 = 0 là: A. ( 4 − ;0; ) 1 . B. (0; 4 − ; ) 1 . C. (0;4; )1 − . D. (1;0; 4 − ) . Lời giải Chọn B 2 2 Ta có (S ) 2 2 2 2
: x + y + z + 8y − 2z + 8 = 0 x + ( y + 4) + ( z − ) 1 = 9 .
Toạ độ tâm của (S ) là (0; 4 − ; ) 1 .
Câu 14: Cho khối chóp S.ABC có diện tích đáy bằng 2
2a , đường cao SH = 3a . Thể tích khối chóp bằng: 3 3a A. 3 a . B. 3 2a . C. 3 3a . D. . 2 Lời giải Chọn B 1 1 Ta có 2 3 V = . B h =
.2a .3a = 2a . 3 3
Câu 15: Tập nghiệm của bất phương trình log x 3 là: 2 A. (0;9 . B. (0; 8 . C. (0;8) . D. ( ;8 − . Lời giải Chọn B x 0 x 0
Ta có log x 3 x (0; 8 . 3 x 2 x 8
Tập nghiệm của bất phương trình log x 3 là (0; 8 . 2 x + y − z
Câu 16: Trong không gian Oxyz , đường thẳng 1 3 : =
= đi qua điểm nào dưới đây? 3 1 − 2
A. P(1;− 3; 0) .
B. M (3;−1; 0) .
C. Q (3;−1; 2) . D. N ( 1 − ; 3; 0) . Lời giải Chọn D
Thay tọa độ điểm N ( 1
− ; 3; 0) vào phương trình đường thẳng ta được 1 − +1 3−3 0 = = (đúng). 3 1 − 2
Vậy đường thẳng đi qua điểm N ( 1 − ; 3; 0). 2 2 f (x)dx = 2 3 − f
(x)+ 2xdx Câu 17: Nếu 0 thì 0 bằng A. 2 . B. 1. C. 1 − . D. 2 − . Trang 10 Lời giải Chọn D 2 2 2 2 Ta có 3 − f
(x)+ 2xdx = 3 − f (x) 2 dx + 2x dx = 3 − .2 + x = 6 − + 4 = 2 − . 0 0 0 0
Câu 18: Trên khoảng (0;+ ) , họ nguyên hàm của hàm số f ( x) 3 = 2 x là 2 3 A. f (x) 3 dx =
x x + C . B. f (x) 3 2 dx =
x x + C . 3 2 3 2 C. f (x) 3 dx =
x x + C . D. f (x) 3 2 dx = x x + C . 2 3 Lời giải Chọn C 1 4 3 3 Ta có f (x) 3 3 3 3
dx = 2 x dx = 2x dx = x + C = x x + C . 2 2
Câu 19: Tập xác định của hàm số y = (x − )2 ln 1 là
A. D = 1;+ ) . B. D = \ 1 .
C. D = (1;+ ) . D. D = . Lời giải Chọn B
Hàm số đã cho xác định khi và chỉ khi ( x − )2 1 0 x 1. Vậy D = \ 1 .
Câu 20: Trong các hàm số sau, hàm số nào nghịch biến trên ? x −1 A. 3 2
y = −x − x . B. y = . x + 2 C. 2
y = 2x + 5 . D. 3 2
y = −x + 3x − 9x + 2 . Lời giải Chọn D Xét hàm số 3 2
y = −x + 3x − 9x + 2 . Ta có D =
và y = − x + x − = − ( x − )2 2 3 6 9 3 1 − 6 0, x . Vậy hàm số 3 2
y = −x + 3x − 9x + 2 nghịch biến trên .
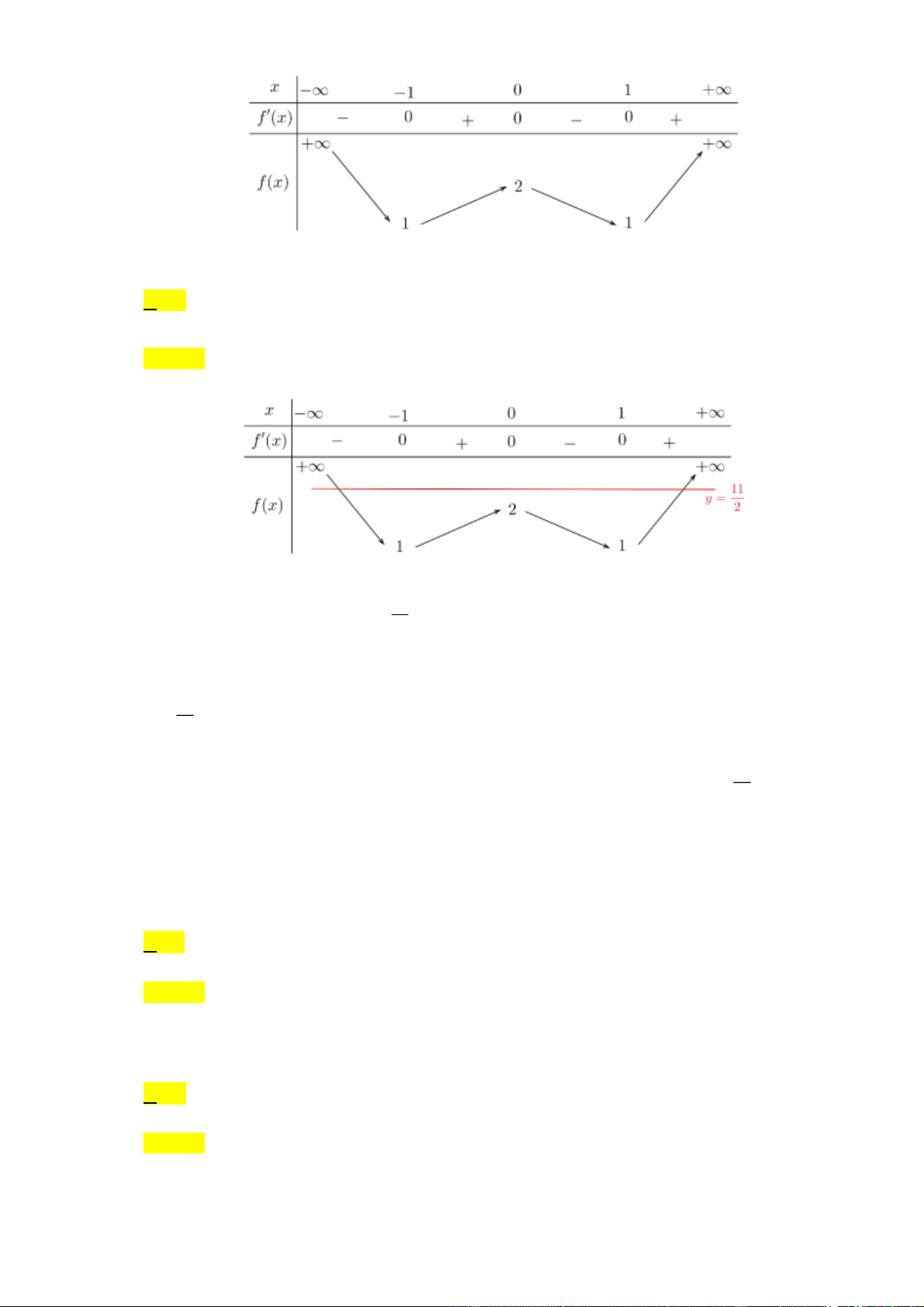
Câu 21: Cho hàm số y = f ( x) có đồ thị như hình vẽ bên. Hàm số đã cho đồng biến trên khoảng nào dưới đây? Trang 11 A. ( 1 − ; ) 1 . B. (0;2) . C. (0;+). D. (0;4) . Lời giải Chọn A
Dựa vào đồ thị, ta thấy hàm số đồng biến trên khoảng ( 1 − ; ) 1 . x
Câu 22: Tiệm cận ngang của đồ thị hàm số y =
là đường thẳng có phương trình 2 2x − 5 1 1
A. y = − . B. y = .
C. y = 0. D. y = 2 . 5 2 Lời giải Chọn C x x Ta có lim
= 0 nên tiệm cận ngang của đồ thị hàm số y = là đường thẳng có 2
x→+ 2x − 5 2 2x − 5
phương trình y = 0.
Câu 23: Mô-đun của số phức z = 5 − 2i bằng A. 29 . B. 3 . C. 21 . D. 29 . Lời giải Chọn A
Mô-đun của số phức z = 5 − 2i bằng 2 2 z = 5 + 2 = 29 .
Câu 24: Trong không gian tọa độ Oxyz , cho hai véc-tơ u = ( 1 − ;1;3) và v = ( 2 − ;1; 3 − ) . Tính độ dài
2u − 3v . A. 152 . B. 322 . C. 242 . D. 216 . Lời giải Chọn C
Ta có 2u − 3v = (4; 1
− ;15) nên u − v = + (− )2 2 2 2 3 4 1 +15 = 242 .
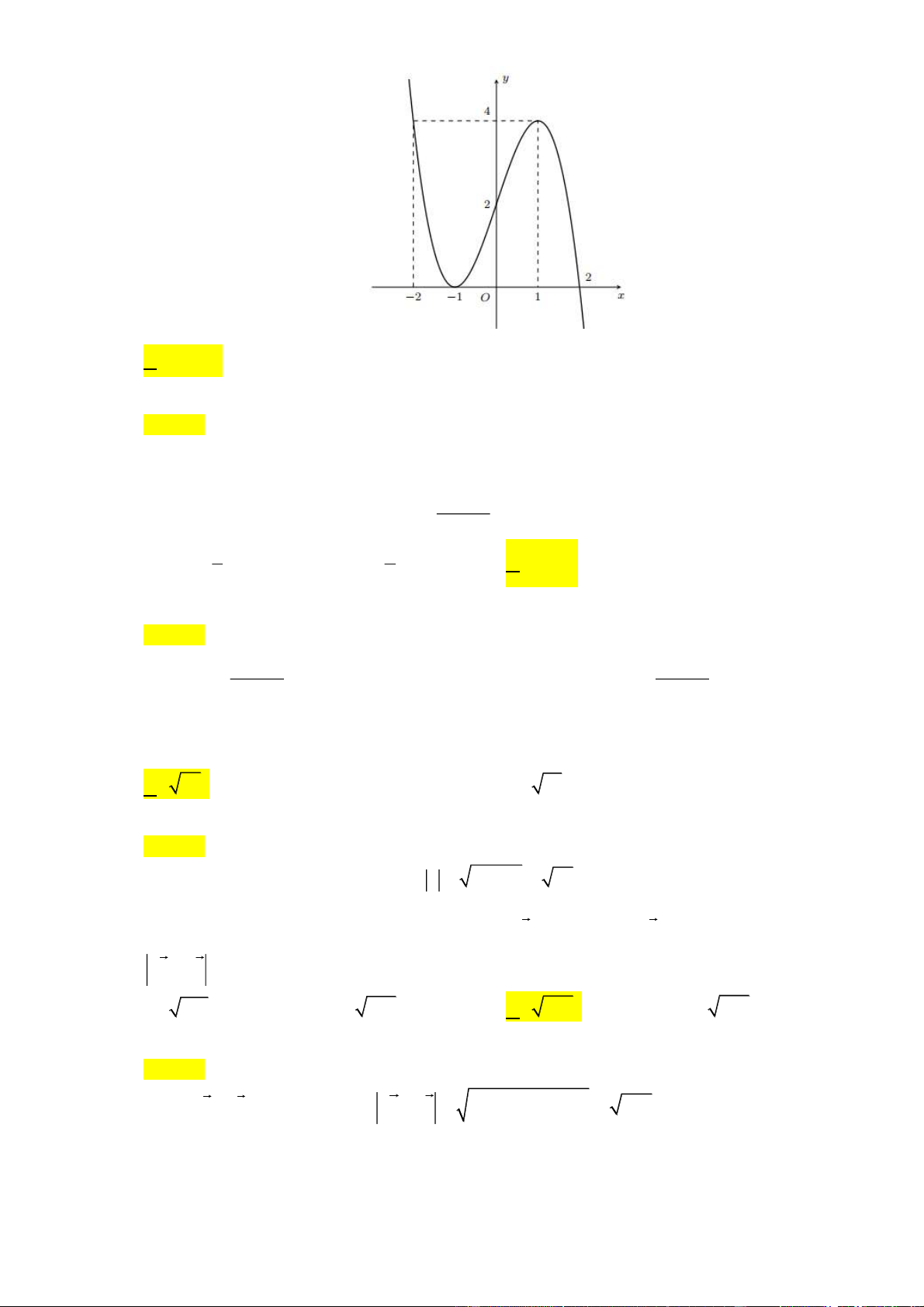
Câu 25: Cho hàm số y = f ( x) có đồ thị hình vẽ bên. Giá trị cực đại của hàm số đã cho là Trang 12 A. 1. B. 1 − . C. 0 . D. 2 . Lời giải Chọn A
Giá trị cực đại của hàm số đã cho là y =1 tại điểm x = 0 .
Câu 26: Cho hàm số f ( x) =1− sin x . Khẳng định nào dưới đây đúng? A. f
(x) dx = x−sin x+C . B. f
(x) dx = x+cosx+C . C. f
(x) dx = x−cosx+C . D. f
(x) dx = x+sin x+C . Lời giải Chọn B Ta có f
(x) dx = (1−sin x) dx = x+cosx+C . 2
Câu 27: Trên tập số thực , đạo hàm của hàm số 3x x y − = là: 2 A. 1 3x x y − − = . B. ( ) 2 2 1 3x x y x − = − . C. ( ) 2 2 1 3x x y x − = − ln 3 . D. ( ) 2 2 1 3x x y x x − − = − . Lời giải Chọn C Ta có ( ) 2 2 1 3x x y x − = − ln 3 .
Câu 28: Có tất cả bao nhiêu giá trị nguyên của tham số m thuộc đoạn 1 − 0;1 0 để hàm số 1 3 2 y =
x − 2x + mx − 3 đồng biến trên (2;6) ? 3 A. 4 . B. 5 . C. 7 . D. 6 . Lời giải Chọn C Ta có 2
y = x − 4x + m .
Để hàm số đống biến trên khoảng (2;6) y x ( ) 2 ' 0
2;6 m −x + 4x x (2;6) .
Xét hàm số f ( x) 2
= −x + 4x trên (2;6) .
Có f ( x) = 2
− x + 4; f (x) = 0 x = 2 . Bảng biến thiên: Trang 13
Theo bảng biến thiên ta có: m f (x) x
(2;6) m 4 mà m 1 − 0;1 0 , m
m4;5;6;7;8;9;1 0 .
Vậy có 7 số nguyên m thỏa mãn. 2x +1
Câu 29: Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = trên đoạn x −1
2;4. Khi đó M −m bằng: A. 3 . B. 2 . C. 2 − . D. 4 . Lời giải Chọn B + Xét hàm số 2x 1 y = . x −1 Tập xác định: D = \
1 , có 2;4 D . 4 − Ta có: y = (
hàm số nghịch biến trên đoạn 2;4 . x − ) 0 x D 2 1
Do đó: M = y(2) = 5, m = y(4) = 3 M − m = 5−3 = 2 .
Câu 30: Cho lăng trụ đều AB . C A B C
có cạnh đáy bằng 2a , độ dài cạnh bên bằng a 3 . Thể tích V
của khối lăng trụ bằng: 3 1 A. 3 V = a . B. 3 V = a . C. 3 V = 3a . D. 3 V = a . 4 4 Lời giải Chọn C
Ta có lăng trụ đều AB . C A B C
có đáy là tam giác đều cạnh 2a và chiều cao là độ dài cạnh bên (2a)2 3 bằng a 3 3 V = a 3. = 3a . 4
Câu 31: Cho hình chóp S.ABC có SA vuông góc với mặt phẳng ( ABC ) , SA = a 3 , tam giác ABC
đều cạnh có độ dài bằng a . Gọi = ( A ,
B (SBC)) , khi đó sin bằng: 3 15 5 15 A. B. . C. . D. . 5 3 3 5 Lời giải Chọn D Trang 14 S H C A I B
Gọi I là trung điểm của BC . Kẻ AH ⊥ SI, H SI .
Vì tam giác ABC đều nên AI ⊥ BC . Lại có SA ⊥ BC nên BC ⊥ (SAI ) .
Suy ra BC ⊥ AH . Vì AH ⊥ SI nên AH ⊥ (SBC) = (A ,
B (SBC)) = ( A , B HB) = ABH . a
Ta có AI là đường cao trong tam giác đều nên 3 AI =
; AH là đường cao trong tam giác 2 a 3 a 3. S . A AI a 15 vuông nên 2 AH = = = . 2 2 SA + AI ( a ) 2 5 2 a 3 3 + 2
Tam giác AHB vuông tại H nên AH a 15 15 sin = = : a = AB 5 5 log . a log 3
Câu 32: Với mọi a,b thoả mãn 3 2
+ logb =1. Khẳng định nào dưới đây đúng? 1+ log 5 2
A. a log 5 + b = 1
B. a + b = 1.
C. a = 1− b log 5 . D. ab = 10 . 2 2 Lời giải Chọn D log . a log 3 log 3.log a log a Ta có 3 2 2 3 2 + logb =1 + logb =1 + logb =1 1+ log 5 log 2 + log 5 log 10 2 2 2 2
loga +logb =1 logab =1 ab =10
Câu 33: Đề kiểm tra chất lượng sản phẩm từ công ty sữa, người ta gửi đến bộ phận kiểm nghiệm 5 hộp
sữa cam, 4 hộp sữa dâu và 3 hộp sữa nho. Bộ phận kiểm nghiệm chọn ngẫu nhiên 3 hộp để
phân tích mẫu. Xác suất để 3 hộp sữa được chọn có cả 3 loại là: 3 1 3 1 A. . B. . C. . D. . 55 22 11 110 Lời giải Chọn C
Gọi A là biến cố 3 hộp sữa được chọn có cả 3 loại. Ta có n() 3
= C = 220; n( A) 1 1 1
= C .C .C = 60 . 12 5 4 3 Trang 15 n A
Xác suất để 3 hộp sữa được chọn có cả 3 loại là: P( A) ( ) 60 3 = = = n () 220 11
Câu 34: Trong không gian với hệ trục toạ độ Oxyz , cho ba điểm A( 1 − ;2; ) 1 , B(2;−1; ) 3 và C ( 2
− ;1;2). Đường thẳng đi qua A đồng thời vuông góc với BC và trục Oy có phương trình là: x = 1 − + t x = −1− t x = −1− t x = 1 − + t A. y = 2 . B. y = 2 . C. y = 2 . D. y = 2 . z = 1+ 4t z = 1 + 4t z = 1 − 4t z = 1+ 4t Lời giải Chọn B BC = ( 4 − ;2;− )
1 ; Vectơ chỉ phương của Oy là j = (0;1;0) .
Vì đường thẳng đồng thời vuông góc với BC và trục Oy nên đường thẳng có vectơ chỉ
phương là n = j; BC = ( 1 − ;0;4) x = −1− t
Đường thẳng đi qua A , có vectơ chỉ phương là n = ( 1
− ;0;4) có phương trình là y = 2 z =1+ 4t
Câu 35: Trong không gian với hệ trục tọa độ Oxyz , mặt phẳng ( ) vuông góc với mặt phẳng (Oxy) , + − − đồ x 2 y 2 z 3
ng thời ( ) song song và cách đường thẳng : = =
một khoảng bằng 5 có phương 1 − 2 3 − trình là
A. 2x + y + 7 = 0 hoặc 2x + y − 3 = 0 .
B. 2x − y + 7 = 0 hoặc 2x − y + 5 = 0 .
C. 2x + y + 7 = 0 hoặc 2x + y − 5 = 0.
D. 2x + y + 7 = 0 hoặc 2x − y − 3 = 0 . Lời giải Chọn D
Mặt phẳng (Oxy) có VTPT k = (0;0 )
;1 ; Đường thẳng có VTCP u = ( 1 − ;2;−3 d )
n = k ,u = (2;1;0)
Phương trình mặt phẳng ( ) có dạng: 2x + y + d = 0 Lấy M ( 2 − ;2; ) 3 − + + =
d ( ( )) = d (M ( )) 2.( 2) 2 d d 7 , , = = 5 5 d = 3 −
Vậy phương trình mặt phẳng ( ) là 2x + y + 7 = 0 hoặc 2x − y −3 = 0 .
Câu 36: Cho hình chóp S.ABCD có SA ⊥ ( ABCD) , đáy ABCD là hình chữ nhật. Biết AD = 2 , a
SA = a . Khoảng cách từ A đến (SCD) bằng: Trang 16 3a 2 2a 3 2a 3a A. . B. . C. . D. . 2 3 5 7 Lời giải Chọn C
Vẽ AH ⊥ SD tại H ( ) 1 C D ⊥ AD Ta có: ⊥ ⊥ CD ⊥ SA (SA ⊥
(ABCD)) CD (SAD) AH CD(2) Từ ( )
1 ,(2) AH ⊥ (SCD)
Do đó: AH là khoảng cách từ A đến (SCD) 2 . a a 2a Vậy AH = = . ( a)2 2 5 2 + a
Câu 37: Biết số phức z = 3
− + 4i là một nghiệm của phương trình 2
z + az + b = 0 , trong đó a,b là các
số thực. Giá trị của a − b bằng: A. 19 − . B. 31 − . C. 11 − . D. 1. Lời giải Chọn D
Ta có nghiệm còn lại của phương trình là: z = 3 − − 4i 1 z + z = 6 − −a = 6 − a = 6 1 .
z z = 25 b = 25 1
Vậy a − b = 19 − . 12 dx 1 b Câu 38: Cho = .ln với , a ,
b c là các số nguyên dương. Khẳng định nào dưới đây đúng? x x + 4 a c 5
A. a = b − c .
B. b = c − a .
C. c = a − b .
D. b = 2c . Lời giải Chọn D Đặt: 2 t =
x + 4 t = x + 4 2tdt = dx Trang 17
Đổi cận: x = 5 t = 3, x =12 t = 4 4 4 4 2tdt 2dt 1 1 1 1 t − 2 1 5 Từ đó ta có: ( = = − dt = = ln t − 4) 4 t (t − 2)(t + 2) ln 3 2
2 t − 2 t + 2 2 t + 2 2 3 3 3 3
Vậy a = b − c .
Câu 39: Cho hình chóp S.ABCD có cạnh bên SB vuông góc với mặt đáy và ABCD là hình chữ nhật. Biết SB = 2 , a AB = 3 ,
a BC = 4a và gọi là góc giữa mặt phẳng (SAC) và mặt đáy. Giá trị tan bằng 3 4 5 6 A. . B. . C. . D. . 4 3 6 5 Lời giải Chọn C
Trong tam giác vuông BAC , gọi H là chân đường cao hạ từ B lên AC , khi đó B . A BC 3 . a 4a 12 = = = a BH . 2 2 BA + BC ( a)2 +( a)2 5 3 4 AC ⊥ SB Ta có
AC ⊥ (SBH ) . AC ⊥ BH
Mà (SAC) ( ABCD) = AC nên = ((SAC),( AB D C )) = SHB . SB 2a 5
Tam giác SHB vuông tại B có tan = = = . BH 12a 6 5
Câu 40: Có bao nhiêu giá trị thực của m để phương trình 2 z + (m − ) 2 4 4
1 z + m − 3m = 0 có hai nghiệm
z , z thỏa mãn z + z = 2? 1 2 1 2 A. 2. B. 3. C. 4. D. 1. Lời giải Chọn A 2 Ta có: = (m− ) − ( 2 2 1
2 m − 3m) = 2m + 2 . Trang 18 TH1: 0 m 1 − .
Khi đó phương trình có hai nghiệm thực z , z . 1 2
Ta có z + z = 2 ( z + z = 4 ( z + z
− 2z z + 2 z z = 4 1 2 )2 1 2 )2 1 2 1 2 1 2 2
m − 3m 0 ( m − )2 1 = 4 m = 3(n) ( − ) 2 2 m − m m − 2 3 3m m 1 − 2. + 2 = 4 . 4 4 2
m − 3m 0 m = 1 − (n) ( m − ) vn 2 1 − ( 2 m − 3m) ( ) = 4 TH2: 0 m 1 − .
Khi đó phương trình có hai nghiệm phức phân biệt z , z . 1 2 Ta có
z + z = 2 2 z = 2 z = 1 1 2 1 1 m = l 2 − (m − )
1 + i − (2m + 2) 0( ) =1 4(m − )2 2
1 − 2m − 2 = 2 4m −10m = 0 5 . 2 m = (l) 2
Vậy có 2 giá trị m thỏa yêu cầu bài toán.
Câu 41: Cho z , z thỏa mãn z = 2 , z = 3 và z z là số thuần ảo. Giá trị lớn nhất của 1 2 1 2 1 2
P = 4z − 3z +1− 2i bằng: 1 2 A. 65 + 5 . B. 145 + 5 . C. 15 + 5 . D. 5 + 5 . Lời giải Chọn B 2 2 2
Ta có: 4z − 3z = 4z −3z 4z − 3z
=16 z + 9 z −12 z z + z z 1 2 ( 1 2 1 2) 1 2 ( 1 2 ) ( 1 2 )
=164 +99−120 =145 4z −3z = 145 1 2
Ta có: 4z − 3z +1− 2i 4z − 3z + 1− 2i = 145 + 5 1 2 1 2 k 0 “ =”
4z −3z = 29 1− 2i 1 2 ( )
4z − 3z = k 1− 2i 1 2 ( )
y = f ( x) (0;+)
2x f ( x) + f ( x) = 4x x f ( ) 1 = 2 Câu 42: Cho hàm số liên tục trên thỏa mãn . Biết . f (4) Giá trị của bằng: 15 17 15 17 A. . B. . C. . D. . 4 4 2 2 Lời giải Chọn D 1
Ta có: 2x f ( x) + f ( x) = 4x x x f ( x) +
f (x) = 2x ( x f (x)) = 2x 2 x ( ) 2
x f x = x + C Mà f ( ) 1 = 2 nên 2
1 2 =1 + C C = 1 Trang 19
x f (x) 2 = x +1 ( ) 1 f x = x x + x f ( ) 1 17 4 = 4 4 + = 4 2
Câu 43: Cho phương trình 2 log x − ( 2
m − 2m log x + m + 3 = 0 ( m là tham số thực). Gọi S là tập hợp 2 ) 2
tất cả các giá trị của m để phương trình có hai nghiệm phân biệt x , x thỏa mãn x .x = 8 . 1 2 1 2
Tổng các phần tử của S là: A. 5 . B. 2 − . C. 1 − . D. 2 . Lời giải Chọn C
Điều kiện xác định: x 0 .
Đặt t = log x . 2
Giả sử phương trình đã cho có hai nghiệm phân biệt x , x thỏa mãn 1 2
x .x = 8 log x + log x = 3 t + t = 3 . 1 2 2 1 2 2 1 2
Yêu cầu bài toán trở thành: “ Tìm m để phương trình 2 t − ( 2
m − 2m)t + m + 3 = 0 có hai
nghiệm phân biệt t , t thỏa mãn t + t = 3”. 1 2 1 2 2 = ( m − m − m + m − 2m) ( 2 2 2 4 3 0 2 ) − 4(m + 3) ( ) 0 m = −1 m = 1 − . 2 t
+ t = m − 2m = 3 1 2 m = 3 Vậy S = −
1 suy ra tổng các phần tử của tập S bằng 1 − .
Câu 44: Cho hai hàm số f ( x) 3 2
= ax −3x +bx +1− 2d và g (x) 2
= cx − 2x + d có bảng biến thiên như sau:
Biết rằng đồ thị hai hàm số đã cho cắt nhau tại ba điểm phân biệt có hoành độ x , x , x thỏa 1 2 3 mãn 2 2 2 x + x + x
= 30 . Diện tích hình phẳng giới hạn bởi các đường cong 1 2 3
y = f ( x), y = g ( x), x = 3
− , x = 6 bằng: 2113 1123 1231 1321 A. . B. . C. . D. . 12 12 12 12 Lời giải Chọn D Trang 20 Ta có: f ( x) 2 '
= 3ax −6x +b .
Dựa vào bảng biến thiên ta thấy hàm y = g ( x) giao với trục hoành tại hai điểm có hoành độ
chính là hai hoành độ cực trị của đồ thị hàm y = f (x) nên ta suy ra g (x) = k. f (x) 1 k = c = 3ka 3
Do đó: g ( x) = k. f ( x) 2
cx − 2x + d = k ( 2
3ax − 6x + b) 2 = 6k c = a . d = kb b d = 3 b Suy ra: f ( x) 3 2
= ax − x + bx + g (x) 2 3 2; = ax − 2x + . 3 1 1 3 3
Từ bảng biến thiên ta có: g = 4 − − + = 4 − b = −12 . a a b a Phương trình hoành độ giao điểm: b b 3 2 2 3
ax − x + bx + = ax − x +
ax + (− − a) 2 3 2 2 3
x + (b + 2) x + 2 − = 0 3 3 2 Viet: 2 2 2
x + x + x = x + x + x
− 2 x x + x x + x x 1 2 3 ( 1 2 3) ( 1 2 2 3 1 3) 3 2 2 −10 a =1 a + 3 b + 2 a + 3 30 = − 2. 30 = − 2. a 3 a = 1 ( vì a 0 ) a a a a a = − 29 x = 2 −
Suy ra: f ( x) − g ( x) 3 2
= x − 4x − 7x +10 = 0 x =1 . x = 5
Vậy diện tích hình phẳng giới hạn bởi các đường cong y = f ( x), y = g ( x), x = 3 − , x = 6 bằng: 6 1321 3 2 S =
x − 4x − 7x +10 dx = . 12 3 −
Câu 45: Cho hàm số f ( x) 3 2
= x −3x +1, gọi S là tập tất cả các giá trị nguyên của tham số m để phương trình f (x) 2 −
(2m+ 4) f (x)+ m(m+ 4) = 0 có đúng 4 nghiệm phân biệt. Tổng các
phần tử của S bằng A. −5 . B. 17 − . C. 18 − . D. 21 − . Lời giải Chọn D
Ta có bảng biến thiên của hàm số f (x) 3 2
= x −3x +1 là: Trang 21
Xét phương trình f (x) 2 −
(2m+ 4) f (x)+ m(m+ 4) = 0
f (x) = m + 4 f ( x) = m
Phương trình đã cho có 4 nghiệm phân biệt khi 1 trong 3 TH sau xảy ra m + = TH1: 4 1 m = 3 − m = 3 − . − m + TH2: 3 4 1 7 − m 3 − m 3 − . − m TH3: 3 1 3 − m 1 m + 4 . 1 Kết hợp cả 3 TH ta có 7
− m 1 S = 6 − ; 5 − ; 4 − ; 3 − ; 2 − ; 1 − ; 0
Vậy tổng các phần tử của S bằng 21 − Câu 46: Có bao nhiêu cặp số nguyên dương (x, y) thỏa mãn 3 2
2x − 3x +1 log
=14x + 3y − 7( 2
x +1 đồng thời 1 x 2022 7 )
6xy +1+ 2x + 3y A. 1347. B. 1348 . C. 674 . D. 673 . Lời giải Chọn A Ta có 3 2
2x − 3x +1 log
=14x + 3y − 7( 2 x +1 7 )
6xy +1+ 2x + 3y (2x + ) 1 ( x − )2 1 2 log = 7 − x −1 + 3y 7 (2x + ) 1 (3y + ) ( ) 1 log 7(x − )2 1 + 7 ( x − )2 1
= log 3y +1 + 3y +1 7 7 ( ) Xét hàm số
f (t ) = log t + t (t 0) 7 f (t ) 1 ' = +1 0 t 0 t.ln 7
Suy ra hàm số f (t) đồng biến trên (0;+)
Khi đó f ( (x − )2 ) = f ( y + ) y + = (x − )2 7 1 3 1 3 1 7 1 .
Với mỗi giá trị của x cho một giá trị của y . Để y nguyên thì ( x − )2 7 1 chia 3 dư 1
x 3 hoặc x chia 3 dư 2.
1 x 2022 . Trong các số từ 2 đến 2021 có 674 số nguyên chia 3 dư 1.
Vậy có 2021− 674 =1347 giá trị nguyên của x hay có 1347 cặp số nguyên ( x, y)thỏa mãn. Trang 22 x +1 y z − 2
Câu 47: Trong không gian với hệ trục tọa độ Oxyz, cho đường thẳng d : = = và mặt 1 2 1 phẳng ( )
P : x − 2y − 2z − 7 = 0 và điểm (
A 1;1;3). Đường thẳng đi qua A cắt d và mặt
phẳng (P) lần lượt tại M và N sao cho M là trung điểm của AN , biết rằng có một vectơ chỉ phương u = ( ; a ;
b 6) . Khi đó giá trị của T =14a − 5b bằng:
A. T = 63. B. T = 81.
C. T = 72. D. T = 81. − Lời giải Chọn B
M d M (t −1;2t;2 + t)
M là trung điểm của AN N (2t − 3;4t −1;2t + ) 1
Do N (P) 2t − 3− 2(4t − ) 1 − 2(2t + ) 1 − 7 = 0 t = 1 − M ( 2 − ; 2 − ; ) 1 ; N ( 5 − ; 5 − ;− ) 1 .
có một vectơ chỉ phương MN = ( 3 − ; 3 − ; 2 − ) u = (9;9;6)
T =14a − 5b =14.9 − 5.9 = 81
Câu 48: Trong không gian Oxyz , cho mặt cầu 2 2 2
(S) : (x +1) + ( y − 9) + z = 18. và các điểm ( A 8;0;0), (4
B ; 4;0), Điểm M (x ; y ; z ) bất kì thuộc mặt cầu (S) . Biết MA + 3MB đạt giá trị nhỏ nhất M M M
tại điểm M có tọa độ (x ; y ; z ) . Giá trị của biểu thức T = 4x − 9 y bằng 0 0 0 0 0 A. T = 46. − B. T = 124. −
C. T = 46.
D. T = 124. Lời giải Chọn A
MA + 3MB = ( x − 8)2 + y + z + 3 ( x − 4)2 + ( y − 4)2 2 2 2 + z
= (x −8)2 + y + z + 8((x +1) + (y −9) + z )−144 + 3 (x − 4)2 + ( y − 4)2 2 2 2 2 2 2 + z
= x −16x + 64 + y + z + 8(x + 2x +1+ y −18y +81+ z )−144 + 3 (x − 4)2 + ( y − 4)2 2 2 2 2 2 2 2 + z
= 9x + 9y −144y + 9z + 576 + 3 (x − 4)2 + ( y − 4)2 2 2 2 2 + z
= 3 x + y −16y + z + 64 + 3 (x − 4)2 + ( y − 4)2 2 2 2 2 + z
= ( x +(y − )2 + z + ( − x)2 +( − y)2 2 2 2 3 8 4 4 + z ) 3 9 + 9 = 9 2 x = 2
Dấu bằng xảy ra khi: y = 6 T = 4x − 9y = 4.2 − 9.6 = 4 − 6 0 0 z = 1
Câu 49: Cho khối nón đỉnh S có đường cao bằng 3a . S ,
A SB là hai đường sinh của khối nón. Khoảng
cách từ tâm đường tròn đáy đến mặt phẳng (SAB) bằng a và diện tích tam giác SAB bằng 2
3a . Tính thể tích khối nón. 3 145 a 3 145 a 3 145 a 3 145 a A. . B. . C. . D. . 48 72 54 36 Lời giải Trang 23 Chọn B
Gọi O là hình chiếu của S trên mặt đáy và I là trung điểm AB , khi đó:
SO ⊥ AB và OI ⊥ AB AB ⊥ (SOI )
Kẻ OH ⊥ SI mà OH ⊥ AB( AB ⊥ (SOI )) OH ⊥ (SAB) d ( ,
O (SAB)) = OH = a .
Xét tam giác SOI vuông tại O , đường OH : 1 1 1 1 1 1 3a 2 9a 2 Ta có = + = + OI = SI = 2 2 2 2 2 2 OH OS OI a 9a OI 4 4 2 4a 2 2 2 2S 3 2.3a 4a 2 3a 2 a 290 Ta có SAB 2 2 AB = = =
OA = OI + IA = + = SI 9a 2 3 4 4 120 4 3 Khi đó 1 145a 2 V = . SO OA = . 3 72
Câu 50: Cho hàm số y = f ( x) có bảng biến thiên của hàm số g ( x) = f ( x − ) 1 + 2 như sau:
Giá trị lớn nhất của hàm số y = f (− 3 sin x − cos x + 2) + 2cos 2x + 4sin x −1 là: A. −9 . B. 2 − . C. 2 . D. 4 . Lời giải Chọn D
Từ bảng biến thiên của hàm số g ( x) ta có bảng biến thiên của hàm số f ( x) như sau: Trang 24 Đặ 3 1 t t = −
3 sin x − cos x + 2 = 2 − sin x − cos x + 2 = 2 − sin x − + 2 t 0;2 2 2 6
Từ bảng biến thiên ta có được f (t) f (2), t 0; 2
f (t ) đạt giá trị lớn nhất tại t = 2 hay sin x −
= 0 x − = k x = + k 6 6 6 x + x − = − x + x + = − ( x − )2 2 2 cos 2 4sin 1 4sin 4sin 1 2sin 1 + 2 2 x = + k2 1 Đẳ 6
ng thức xảy ra khi sin x = . 2 5 x = + k2 6
Ta có y = f (− 3 sin x − cos x + 2) + 2cos 2x + 4sin x −1 f (2) + 2 = 4 .
Hàm số đạt giá trị lớn nhất khi x = + k2 . 6
-----------------------HẾT----------------------- Trang 25