Đề thi Toán học kỳ II lớp 11

lOMoAR cPSD| 45619127 CTML
ĐỀ SỐ 6 ÔN THI HKI LỚP 11
Câu 1: Dãy số un ược gọi là dãy số tăng nếu với mọi số tự nhiên n :
A. un 1 un .
B. un 1 un .
C. un 1 un .
D. un 1 un .
Câu 2: Cho dãy số u 1 n , với u nn
.Mệnh ề nào dưới ây là úng ? n
A. Dãy un bị chặn trên và không bị chặn dưới. B. Dãy un bị chặn dưới và không bị chặn trên.
C. Dãy un bị chặn trên và bị chặn dưới. D. Dãy un không bị chặn.
Câu 3: Cho cấp số cộng un có số hạng ầu u1 3 và công sai d 2. Tổng của 2019 số hạng ầu bằng A. 4 080 399. B. 4 800 399. C. 4 399 080. D. 8 154 741.
Câu 4: Cho cấp số cộng un có: u1 3; d
. Khẳng ịnh nào sau ây là úng? A. 1 1 1 un 3
n 1 .B. un
3 n 1.C. un 3
n 1 .D. u nn 3 1 n 1 . 2 2 2 4
Câu 5: Xác ịnh số hạng ầu u1 và công sai d của cấp số cộng un có u9 5u2 và u13 2u6 5.
A. u1 3 và d 4.
B. u1 3 và d 5.
C. u1 4 và d 5.
D. u1 4 và d 3.
Câu 6: Có bao nhiêu giá trị thực của x ể 3 số a b c, , theo thứ tự ó lập thành một cấp số cộng với a 10
3x, b 2x2 3, c 7 4x? A. 2 . B. 0 . C. 1. D. 4 .
Câu 7: Cho tam giác ABC biết 3 góc của tam giác lập thành một cấp số cộng và có một góc bằng 25 .
Tìm 2 góc còn lại.
A. 65 ; 90 . B. 75 ; 80 . C. 60 ; 95 . D. 60 ; 90
Câu 8: Cho dãy số 1; 1 ; 1 ; 1 ; 1 . Khẳng ịnh nào sau ây là sai? 3 9 27 81
A. Dãy số không phải là một cấp số nhân. 1
B. Dãy số này là cấp số nhân có u1 1; q . 3 lOMoAR cPSD| 45619127 CTML
C. Số hạng tổng quát.u 1 n 1 n .
n 1 . D. Là dãy số không tăng, không giảm. 3
Câu 9: Cho cấp số nhân: 1; a ; 1 . Giá trị của a là: 5 125 1 A. a 5 . B. a . C. a . D. a 5.
Câu 10: Một tam giác có các góc lập thành một cấp số nhân với công bội là q 2. Khi ó số o các góc của
tam giác ấy tương ứng là bao nhiêu?
A. 30 ; 60 ; 90 . B. ; 2 ; 4 . C. ; 2 ; 4 . D. ; 2 ; 4 . 5 5 5 6 6 6 7 7 7
Câu 11: Tìm lim 4n n2 1 n . 9n2 3n A. . B. . C.0 . D. .
Câu 12: Ba số x , y , y theo thứ tự ó lập thành một CSN với công bội q ; q 1, ồng thời các số x , 2y , 3z
theo thứ tự ó lập thành một CSC với công sai d d, 0. Hãy tìm q ? A.2 . B. . C. . D. 0.
Câu 13: Tính tổng của cấp số nhân lùi vô hạn ( )un biết u1 1 và u u u1, 3, 4 theo thứ tự là ba số hạng liên
tiếp trong một cấp số cộng. A. 5 1 . B. 5 1. C. 1 . D. 2 . 2 2 5 1
Câu 14: Trong các mệnh ề sau, mệnh ề nào là mệnh ề Sai? A. lim 31 0 . B. lim
12 n 0 . C. lim 13 1. n n D. lim 1 n 0 n .
Câu 15: Giá trị của giới hạn lim n2 2n 1 2n2 n là: lOMoAR cPSD| 45619127 CTML A. 1. B. 1 2. C. D. . . 1 2 1 3 5 .... 2n 1 . C. . D. 1 . 3 3
Câu 16: Tính giới hạn:lim 2 . A. 0 . B. n n 1 3n 4 4 2 1 . 3n na 4 16
Câu 17: Tìm tất cả giá trị nguyên của a thuộc 0;2020 ể lim A. 2019. B. 2018. C. 2017. D. 2016.
Câu 18: Cho ường thẳng a là hình chiếu vuông góc của a lên mặt phẳng P . Xét tính úng sai của hai mệnh ề sau. I
b P b a . II
b P b a ' . b a b a A. B.
I sai, II úng.
I úng, II sai. C. cả hai ều sai. D. cả hai ều úng.
Câu 19: Trong các mệnh ề sau, mệnh ề nào úng?
A. Góc giữa hai ường thẳng a và b bằng góc giữa hai ường thẳng a và c khi b song song với c (hoặc b trùng vớic ).
B. Góc giữa hai ường thẳng a và b bằng góc giữa hai ường thẳng a và c thì b song song với c .
C. Góc giữa hai ường thẳng là góc nhọn.
D. Góc giữa hai ường thẳng bằng góc giữa hai véctơ chỉ phương của hai ường thẳng ó.
Câu 20: Cho tứ diện ABCD và I là trọng tâm tam giác ABC . Đẳng thức úng là.
A. SI SA SB SC .B.SI 3 SA SB SC .C.SI 1 SA 1 SB 1 SC .D. 6SI SA SB SC . 3 3 3
Câu 21: Cho tứ diện ABCD . Gọi M , N lần lượt là trung iểm của AB , CD và G là trung iểm của MN .
Trong các khẳng ịnh sau, khẳng ịnh nào sai?
A. GM GN 0.B. MA MB MC MD
4MG.C. GA GB GC
GD .D. GA GB GC GD 0.
Câu 22: Cho hình chóp SABCD. có cạnh SA x , tất cả các cạnh còn lại ều bằng a . Tính số o của góc giữa
hai ường thẳng SA và SC. A. 30 .0 A. 45 .0 A. 60 .0 A. 90 .0
Câu 23: Cho hình chóp S ABCD.
áy là hình vuông, cạnh bên SA vuông góc với áy, SA AB a .
Tính Tính góc giữa ường thẳng SC và mặt phẳng SBD . lOMoAR cPSD| 45619127 CTML A. arcsin 1 . B. arcsin 1 . C. arcsin 13 . 3 D. arcsin 32 . 4
Câu 24: Cho hình chóp SABCD.
có áy là hình vuông, cạnh bên SA vuông góc với áy (ABCD)
.Khẳng ịnh nào sau ây sai?
A. CD (SBC). B. SA ABC ( ).
C. BC (SAB) . D. BD SAC ( ).
Câu 25: Cho hình chóp tứ giác ều S ABCD. có cạnh áy bằng a , cạnh bên bằng 2a . Độ lớn của góc giữa
ường thẳng SA và mặt phẳng áy bằng A. 45 . B. 75 . C. 30 . D. 60 .
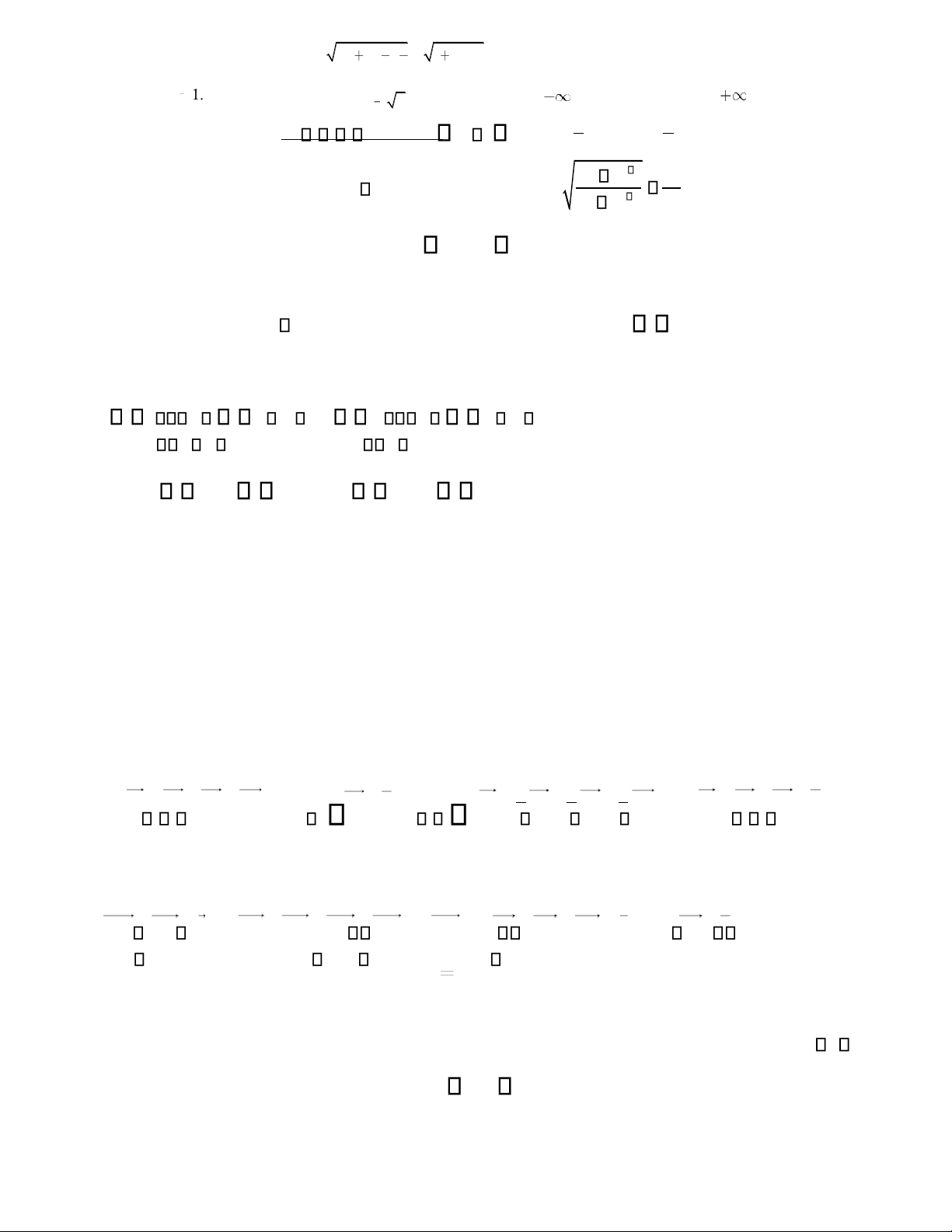
ĐÊ TỰ LU Ậ N n 1 3 n Câu 1: 2.7 1 Tìm các gi 2 ớ i h ạ n I n 3 3n I lim 1 lim 4 2 2 2 n 1 n 2 5.6 4.7 2 n 2 2 I lim2 n n 1 n 3n I lim4.5 3 4 4 n 7.3
Câu 2: a. Tìm x ể 3 số: 10 3x ; 2x2 3; 7 4x là 3 số hạng liên tiếp của một cấp số cộng
b. Cho cấp số cộng un biết u5 18, 4Sn S2n . Tìm số hạng ầu u1 và công sai d của cấp số cộng.
c. Tính tổng S 1002 992 982 972 .... 22 12
Câu 3: Cho cấp số nhân ( )un thỏa:
u4 272 . a) Viết năm số hạng ầu của cấp số. u3 243u8
b) Tính tổng 10 số hạng ầu của cấp số. c) Số
là số hạng thứ bao nhiêu của cấp số ? d
Câu 4: Cho tam gi¸c ABC vu«ng t¹i A . Trªn ®›êng th¼ng
(ABC) t¹i C lÊy mét
®iÓm D ( D C ). KÎ AO BC (víi O BC ), KÎ AM BD (víi M BD ). 1) Chøng minh BD (AOM).
2) §›êng th¼ng OM c¾t d t¹i E . Chøng minh AE BD vµ BE AD .
3) Gi¶ sö D thay ®æi trªn ®›êng th¼ng d . Chøng minh tÝch CDCE. kh«ng ®æi.
Câu 5: Cho tứ diện ABCD có AB CD 2 .a Gọi M N, lần lượt là trung iểm BC AD, . Biết rằng MN a
3. Tính góc của AB và CD.