Final Exam January 2022 - Quantitative Methods Questions | Microeconomics | Trường Đại học Quốc tế, Đại học Quốc gia Thành phố Hồ Chí Minh

CARDIFF SCHOOL OF MANAGEMENT Module Title: Quantitative Methods Module Number: BEC4003 Examination Period: January 2022 Examination Duration: 2 hours INSTRUCTIONS: 1.
This is a closed book examination. 2.
Non-programmable calculators are allowed. 3.
Answer all questions in Sections A and B. 4.
All numerical answers should be rounded to 4 decimal places unless
stated otherwise in the question. All probabilities should be
expressed in decimal form. 5.
Please show all your workings. 6.
Statistical tables and formulae are included on pages 2 – 3. 7.
A total of 100 marks is available. Page 1 of 6 Page 2 of 6 Formula:
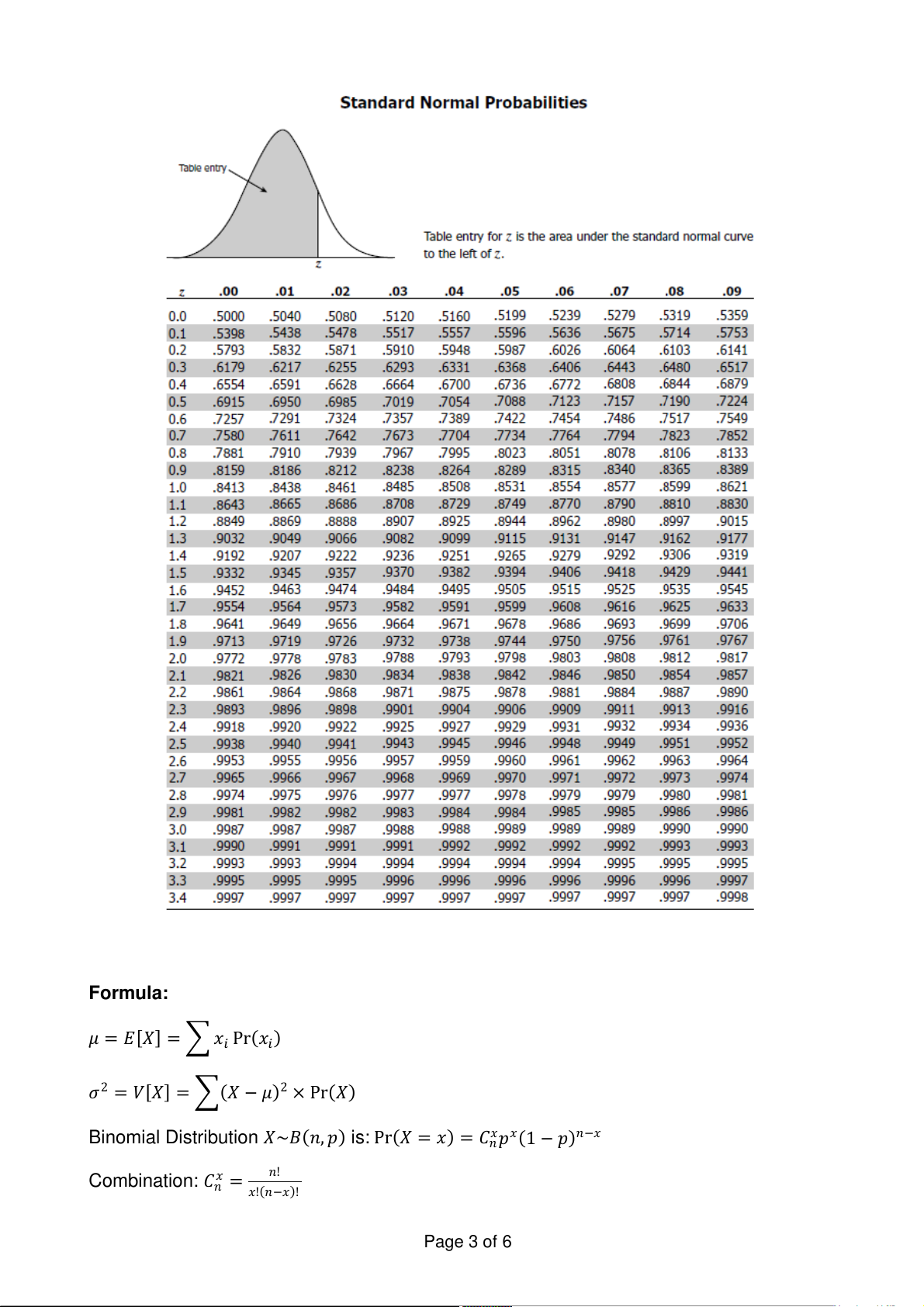
𝜇 = 𝐸[𝑋] = ∑ 𝑥𝑖 Pr(𝑥𝑖)
𝜎2 = 𝑉[𝑋] = ∑(𝑋 − 𝜇)2 × Pr(𝑋)
Binomial Distribution 𝑋~𝐵(𝑛, 𝑝) is: Pr(𝑋 = 𝑥) = 𝐶𝑥 𝑥
𝑛𝑝 (1 − 𝑝)𝑛−𝑥
Combination: 𝐶𝑥𝑛 = 𝑛! 𝑥!(𝑛−𝑥)! Page 3 of 6
SECTION A – MATHEMATICS: ANSWER ALL QUESTIONS IN THIS SECTION.
PLEASE SHOW YOUR WORKINGS FOR ALL QUESTIONS QUESTION 1
Simplify each of the fol owing expression:
a) 𝑎−3.1𝑏2𝑎1.2𝑏−1.7 (3 marks)
b) 4𝑎: 4 × 5𝑎−1 (3 marks) 𝑎2
c) [(2 − 2𝑎)𝑎 − 3(𝑎2 − 1)] ÷ (1 − 𝑎)2 (3 marks) 𝑛 d) 𝑥2𝑦 2𝑧𝑚 (3 marks) 𝑦𝑛𝑥2/3𝑧2𝑚
e) 3𝑧𝑥 + 7𝑧𝑦 − 4𝑥 𝑧 (3 marks) Total: 15 marks QUESTION 2
Solve the fol owing equations:
a) −2(𝑥 + 4) = 6 (5 marks)
b) 𝑥2 + 5𝑥 = 𝑥 − 4 (5 marks) c) 2𝑧 = 1 + 𝑧 (5 marks) 𝑧−1 1−𝑧 Total: 15 marks QUESTION 3
Write down an expression for the floor area of a two-room flat where the width of the second
room is twice that of the first room and the length of the second room is one and a half times
that of the first room. (Each room is rectangular.) Total: 10 marks Page 4 of 6 QUESTION 4
A project requires an initial outlay of £30,000 and is expected to produce a return of £34,000
in 2 years’ time. If the prevailing market rate is 3% compounded monthly, calculate the net
present value of the project and hence decide whether this investment is worthwhile. Total: 10 marks
SECTION B – PROBABILITY THEORY: ANSWER ALL QUESTIONS IN THIS SECTION.
PLEASE SHOW YOUR WORKINGS FOR ALL QUESTIONS. QUESTION 5
Suppose that the grades on the QM exam of a class consisting of 50 students were
summarised in the fol owing table: D (10 – 39) 2 students C (40 – 59) 10 students B (60 – 89) 30 students A (90 – 100) 8 students
A student fails if the grade is D. What is the probability that a randomly chosen student passes the QM exam? Total: 5 marks QUESTION 6
Suppose that 10% of students have to wear glasses. If we select 10 students at random, find
the probability that the number who have to wear glasses is: a) Exactly 2. (5 marks) b) At least 2. (10 marks) Total: 15 marks Page 5 of 6 QUESTION 7
A continuous random variable, 𝑋, takes any value between 15 and 45 and has the CDF 𝐹(𝑥) = 𝑥−15. 30
a) Calculate the probability that 𝑋 is smal er than 20. (5 marks)
b) Calculate the probability that 𝑋 lies between 25 and 30. (5 marks) Total: 10 marks QUESTION 8
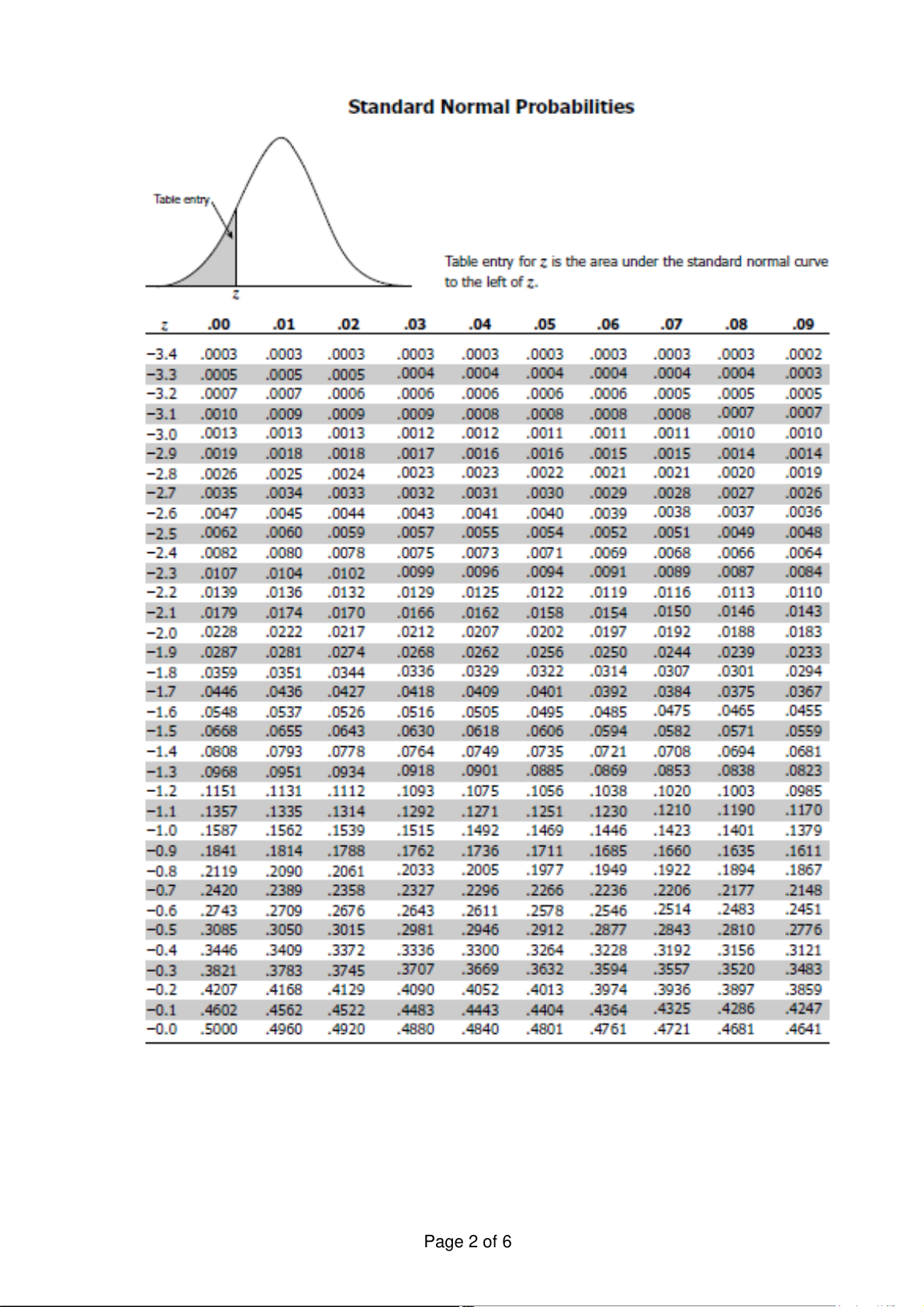
𝑋 fol ows a normal distribution with mean 20 and standard deviation 5, i.e. 𝑋~𝑁(20,52).
a) What is Pr(𝑋 > 25) and Pr(10 < 𝑋 < 22)? (15 marks)
b) What is the 𝑥 value such that Pr(𝑋 > 𝑥) = 0.1? (5 marks) Total: 20 marks
Please find the z table on pages 2 - 3.
--END OF PAPER-- Page 6 of 6